Измерение спектра и формы детерминированных сигналов

Вид материала

Документы

Содержание Анализаторы спектра последовательного действия Разрешающая способность Динамический диапазон Погрешность измерения уровней сигнала Цифровой анализ спектра Цифровые анализаторы спектра Анализаторы спектра на цифровых фильтрах Измерение нелинейных искажений

Подобный материал:

• Цифровая обработка сигналов, 25.15kb.
• Программа курса лекций (3 курс, 6 сем., 32 ч., диф зачет) Профессор Киричук Валерий, 72.05kb.
• Цифровая фильтрация, 139.58kb.
• Тема пространство и метрология сигналов физическая величина более точно определяется, 595.48kb.
• Обработка сигналов в радиотехнических системах, 126.5kb.
• Методические указания по выполнению лабораторной работы №2 по курсу "Цифровая обработка, 99.67kb.
• Измерение длины волны и ширины спектра лазерного излучения с помощью много лучевого, 102.41kb.
• Программа курса лекций, 51.42kb.
• Измерение фазового сдвига, 189.66kb.
• Цифровой вольтметр щ-304, 137.06kb.

Анализаторы спектра последовательного действия


А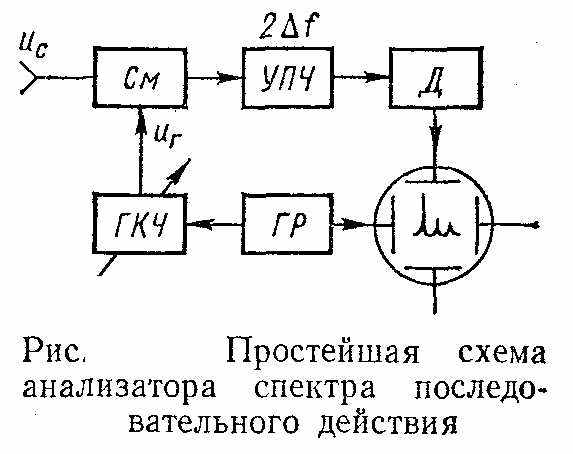нализаторы спектра последовательного действия применяются для исследования любых сигналов, спектр кото­рых не изменяется за время измерения (анализа). Простей­ший анализатор со­стоит из смесителя См, на один вход которого поступает ис­следуемый сигнал и_с, а на вто­рой — сигнал с линейно изме­няющейся частотой и_г от гене­ратора качающейся частоты ГКЧ. Изменение частоты генератора по закону f_г=f₀±af перемещает спектр сигнала относительно цент­ральной настройки усилителя промежуточной частоты УПЧ с полосой пропускания 2∆f_ф, и на выходе последнего последовательно выделяются со­ставляющие спектра сигнала при выполнении условия 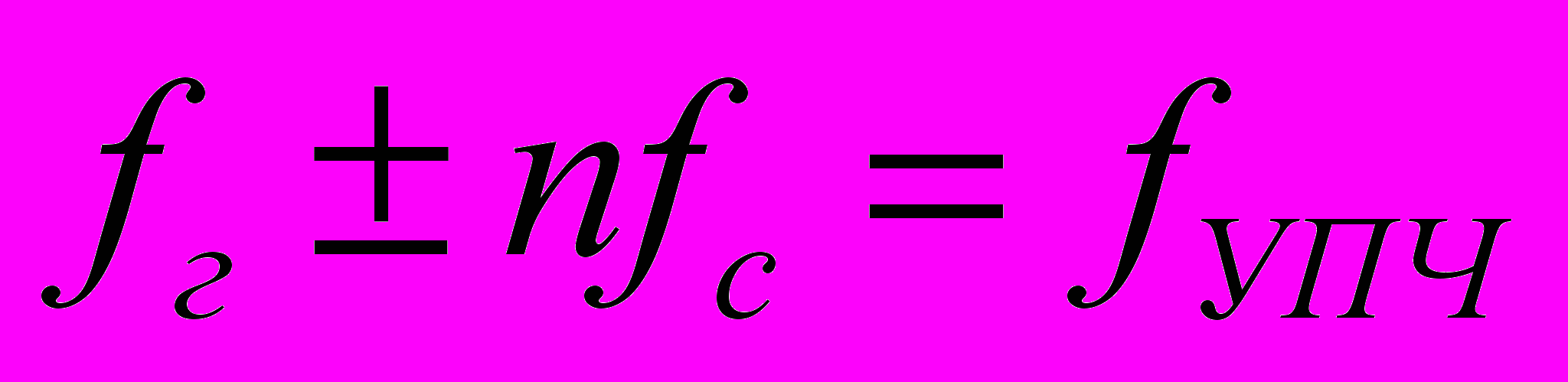, где п = 1, 2, 3, ... — номера гармоник. Спектральные составляющие поступают на де­тектор Д и затем на вертикально отклоняющие пластины осциллографического индикатора. Отклонение луча по го­ризонтали осуществляется генератором развертки ГР син­хронно с качанием частоты ГКЧ, благодаря чему линия развертки соответствует оси частот спектрограммы.

Если развертка калибрована в единицах частоты, а коэф­фициент передачи анализатора спектра от его входа до экра­на индикатора известен, то полученная осциллограмма будет точно соответствовать амплитудному спектру сиг­нала.

Имеются анализаторы спектра, генератор которых пере­страивают вручную, а в качестве индикатора используют стрелочный измеритель напряжения сигнала после детек­тора; такие приборы называют анализаторами гармоник.

Они подобны селективным вольт­метрам и постепенно вытесняются ими.

Основными характеристиками анализаторов спектра являются разрешающая способность, время анализа, динамический диапазон и погрешность измерения частоты и амплитуды.

Р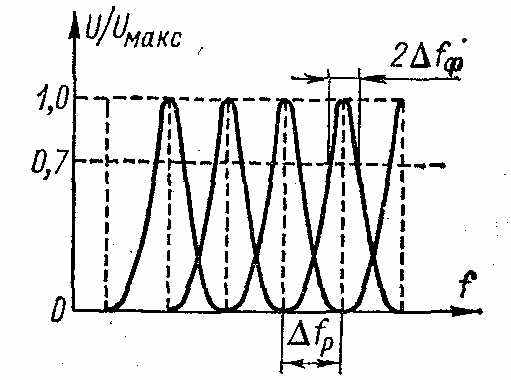азрешающая способность ∆f_р определяется минимальным рас­стоянием по оси частот (рис. 6-3), при котором можно выделить и из­мерить с заданной погрешностью две соседние составляющие спек­тра. Разрешающая способность прямо пропорциональна полосе пропускания фильтра 2∆f_ф усилителя промежуточной частоты: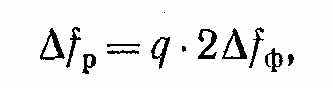



где q> 1.

Время анализа определяется полосой обзора, т. е. раз­ностью частот генератора f_г._макс — f_г.мин. и полосой про­пускания фильтра. Время ана­лиза в полосе пропускания фи­льтра равно 1/(2∆f_ф), а в поло­се обзора увеличивается в (f_г.макс-f_г.мин)/(2∆f_ф) раз и составляет Т_а =(f_г.макс-f_г.мин)/(2∆f_ф)². Очевидно, что стре­миться к сверх узкополосным фильтрам нецелесообразно, так как при 2∆f_ф < 1 Гц время ана­лиза слишком велико. Это об­стоятельство соответственно ог­раничивает частотный диапазон анализаторов снизу значением 10 Гц, а полосу пропуска­ния фильтра — 3 Гц.

Динамический диапазон анализатора спектра характери­зует его работу в линейном режиме. Нельзя допускать перегрузку смесителя анализатора, так как она может вызвать в выходном спектре сигналы на комбинационных частотах. Динамический диапазон



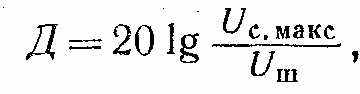
где U_c-макс — максимальный допустимый уровень исследуе­мого сигнала, поступающего на сместитель, при котором напряжение составляющих комбинационных частот соиз­меримо с напряжением соб­ственных шумов U_ш вход­ной цепи анализатора.

Погрешность измерения уровней сигнала состоит из многих составляющих: по­грешности калибровки чув­ствительности; неравномер­ности амплитудно-частот­ной характеристики трак­та; погрешности шкал ат­тенюаторов; погрешности шкалы индикатора; влия­ния собственных шумов. В конкретных случаях возможно исключение некоторых частных погрешностей. Например, если уровень выходного сигнала определяется методом сравнения с уровнем сиг­нала вспомогательного генератора, то погрешность анали­затора будет определяться только погрешностью шкалы индикатора и установки уровня вспомогательного генера­тора. Если исследуемый сигнал значительно превышает уровень шумов, то их можно не учитывать.

Во время анализа на усилитель промежуточной частоты поступает напряжение, частота которого непрерывно ме­няется. В фильтре с полосой пропускания 2∆f возникают переходные процессы, искажающие его резонансную ха­рактеристику: смещается и уменьшается ее максимум, расширяется полоса пропускания. Степень искажений зависит от скорости изменения частот генератора V; .

На рисунке приведены характеристики фильтра: ста­тическая 1 и динамическая 2. По оси ординат отложен ква­драт коэффициента передачи фильтра К, а по оси абсцисс — о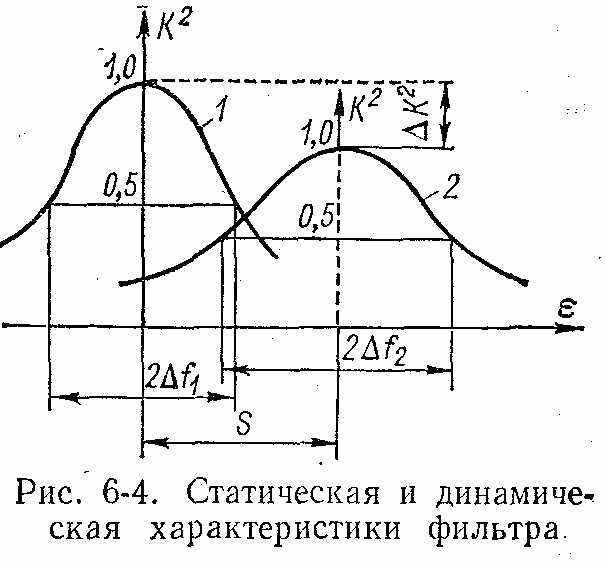бобщенная расстройка 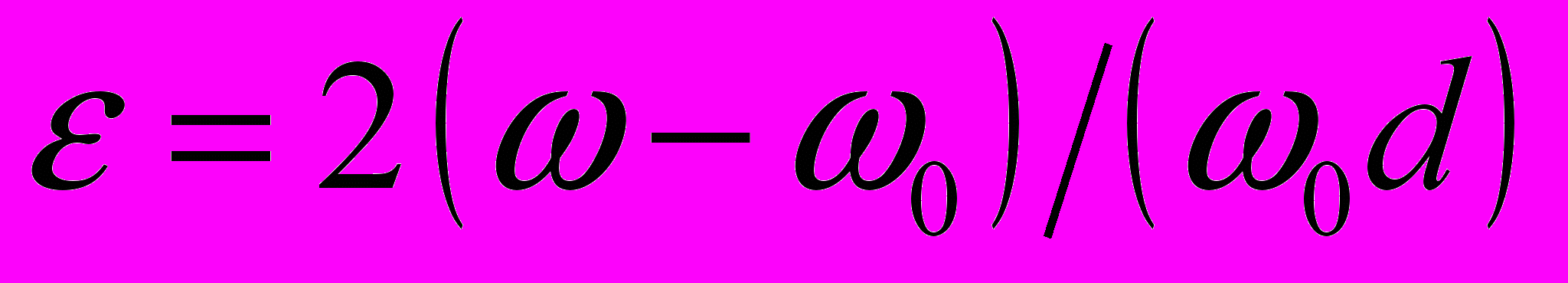, где ω₀ — резонансная частота фильтра, ω — текущая частота, d — затухание фильтра. Искажения вычисляются по следую­щим формулам: смещение максимума 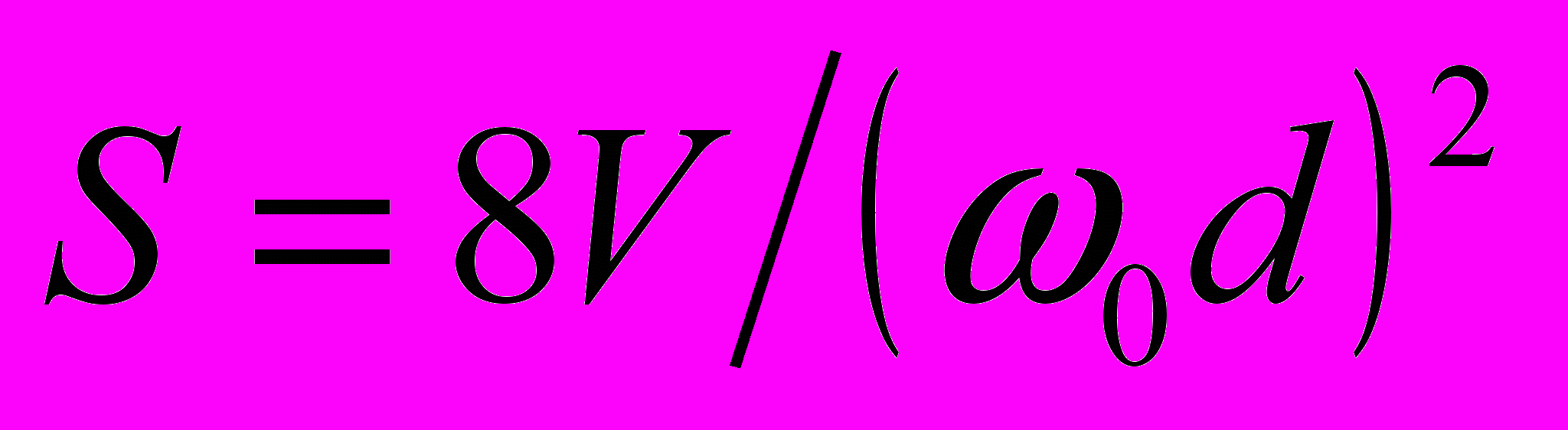; уменьшение максимума 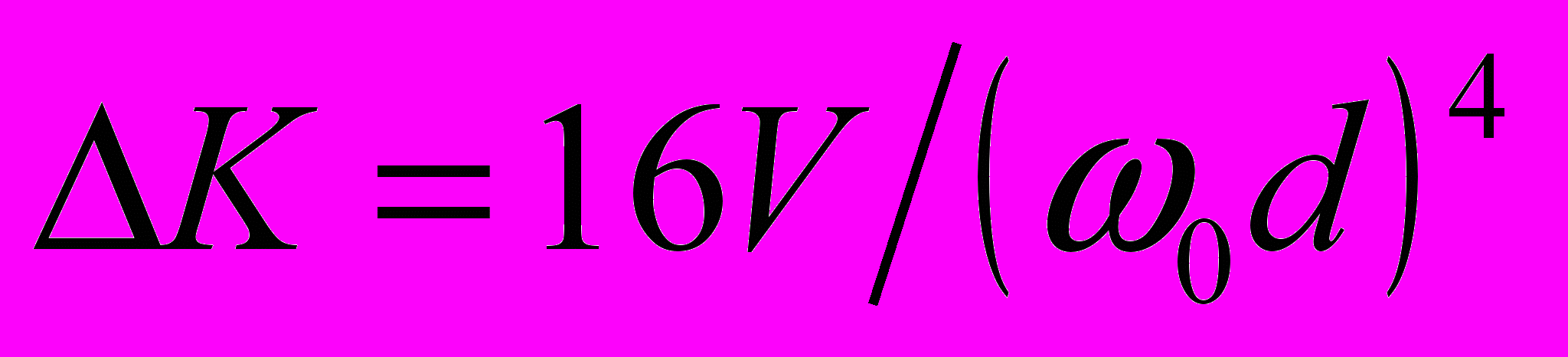; приращение относительной ширины полосы 2∆f₂ — 2∆f₁ = А∆К, где А зависит от типа фильтра.

Скорость изменения частоты генератора ГКЧ



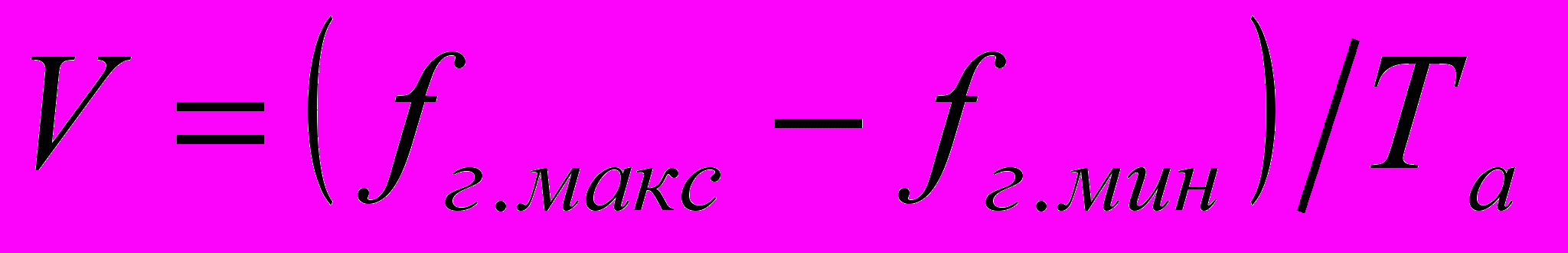
При правильном выборе полосы обзора и времени ана­лиза, которое равно длительности прямого хода луча, искажения резонансной кривой фильтра не вно­сят заметных искаже­ний в спектрограмму.

А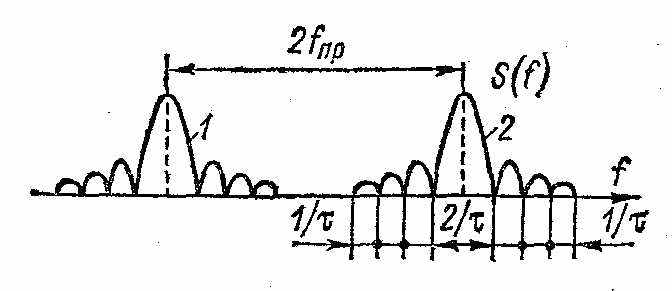нализатор спектра представляет собой су­пергетеродинный прием­ник, в котором при не­правильно выбранной промежуточной частоте возможно прохождение сигналов зеркального канала, отстоящего от основного на удвоенную промежуточную частоту 2f_пр . При исследовании спектра импульса, длительность которого τ, можно огра­ничиться тремя боковыми лепестками. Ширина основного лепестка равна 2/τ, а каждого из боковых — 1/τ. Таким образом, для исключения перекрытия спектров необхо­димо, чтобы f_пр > 4/τ. Полоса обзора определяется шири­ной спектра исследуемого сигнала. При трех лепестках она должна быть больше 8/τ. Частота развертки равна 1/Т_а и определяет число циклов качания частоты генератора в секунду.

В 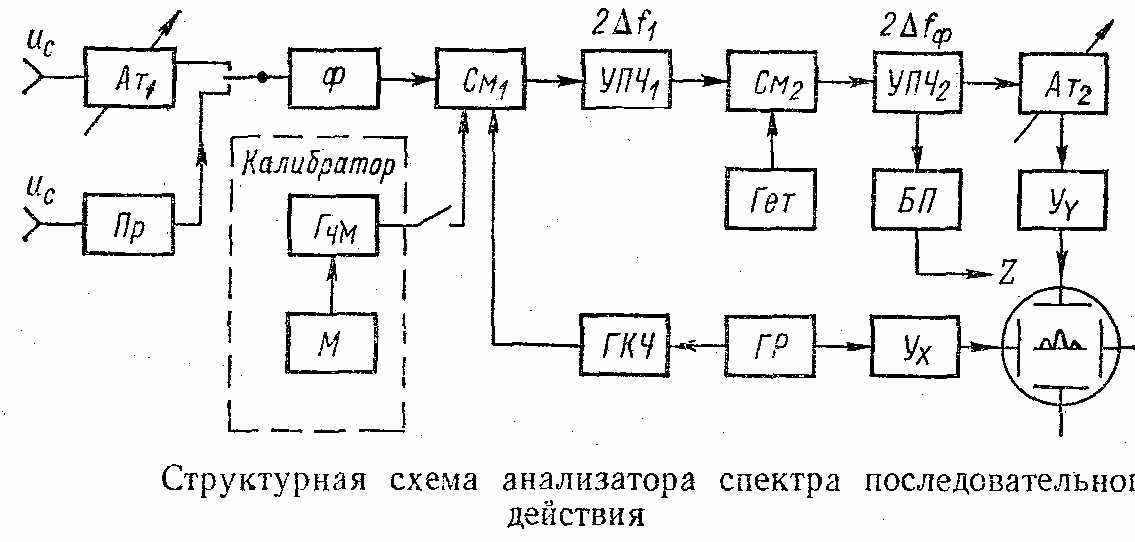качестве примера рассмотрим полную структурную схему анализатора спектра последовательного действия. Периодический сигнал сложной формы поступает через пробник Пр или через входной аттенюатор Ат₁ и фильтр нижних частот Ф на смеситель См₁ на второй вход которого подводится напряжение генератора качаю­щейся частоты ГКЧ. Линейное изменение частоты во вре­мени производится изменением пило­образного напряжения генератора развертки ГР. С выхода смесителя переменный по частоте сигнал поступает на первый усилитель проме­жуточной частоты УПЧ₁. Когда частота сигнала совпадает с частотой настройки УПЧ₁ на его выходе появляются составляющие спектра с полосой частот 2∆f₁. С помощью гетеродина Гem и смесителя См₂ они подвергаются вто­рому преобразованию с понижением частоты. Это облег­чает трудную задачу создания узкой полосы пропускания во втором усилителе промежуточной частоты УПЧ₂. В ка­честве избирательного устройства в нем используются LC-фильтры или кварцевые резонаторы. Ширина полосы пропускания этих устройств 2∆f_ф определяет разрешаю­щую способность и другие параметры анализатора.

После регулировки аттенюатором Ат₂ проходящие через фильтр составляющие детектируются, усиливаются и поступают на пластины Y электронно-лучевой трубки индикатора, образуя спектрограмму в виде светящихся вертикальных полосок, высота которых пропорциональна амплитудам составляющих сигнала. Для увеличения яр­кости осциллограммы сигнал с УПЧ₂ подают на блок подсвета БП, где он детектируется, формируется в прямо­угольный импульс для воздействия на модулятор трубки.

Калибратор предназначен для создания на экране трубки частотных меток. Он представляет собой генератор с ча­стотной модуляцией Г_Чм и модулятор М, вырабатываю­щий модулирующее синусоидальное напряжение. В спектре высокочастотного сигнала генератора при частотной моду­ляции появляются составляющие боковых частот, расстоя­ния между которыми равны частоте модулирующего коле­бания. Частота генератора Гчм и боковые полосы соз­дают на экране трубки опорные частотные метки с извест­ными фиксированными значениями частоты и интервалов между ними.

Промышленность выпускает анализаторы последователь­ного действия, перекрывающие диапазон частот от 10 Гц до 40 ГГц с полосой пропускания фильтров от единиц герц в низкочастотных анализаторах до 300 кГц и больше в ана­лизаторах СВЧ. Динамический диапазон 50—90 дБ. Время анализа 0,01—20 с. Погрешность измерения частоты 1—2 %, амплитуды—10—15%.


Анализ спектра в реальном времени

Анализ спектра сигналов в реальном времени осущест­вляется дисперсионно-временным методом. Дисперсией на­зывается зависимость фазовой скорости распространения электромагнитной волны от ее частоты. Фазовая скорость v_ф=ω/β, где β=2π/λ. Дисперсионно-временной анализ осуществляется с помощью дисперсионной линии задержки, в которой разные частотные составляющие распростра­няются с разными скоростями и потому на выходе линии последовательно появляются составляющие спектра со сдви­гом во времени. Огибающая этих составляющих соответ­ствует модулю спектра сигнала, поданного на вход. На основе дисперсионно-временного метода созданы анализа­торы спектра, с помощью которых можно исследовать быстро меняющиеся во времени сигналы, корот­кие радиоимпульсы и одиночные сигналы (на­пример, анализатор С4-47).

П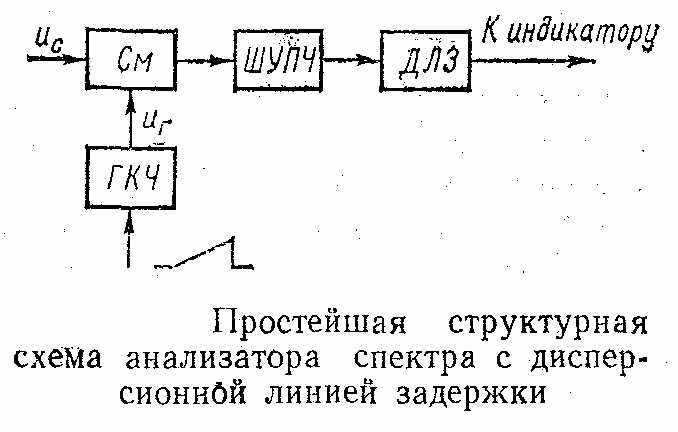ростейшая струк­турная схема диспер­сионного анализатора спектра состоит из смесителя См, на ко­торый подается исследуемый сигнал и_с и сигнал качаю­щейся частоты от ГКЧ. Выходной сигнал смесителя уси­ливается широкополосным усилителем ШУПЧ промежуточ­ной частоты и поступает на дисперсионную линию задерж­ки ДЛЗ. На выходе ДЛЗ появляются частотные составляю­щие исследуемого импульса, которые поступают в канал У осциллографического индикатора. В канал X для развертки луча по горизонтали подается пилообразное напряжение от генератора развертки, которое одновременно и синхронно модулирует частоту ГКЧ. Благодаря этому горизонталь­ная линия развертки является осью частот.

При импульсных сигналах запуск генератора раз­вертки и ГКЧ происходит в момент поступления импульса и он анализируется в течение одного хода луча, поэтому при трубке с достаточным послесвечением спектрограмма сохраняется в течение некоторого интервала времени, достаточного для фотографирования и рассмотре­ния. При периодически повторяющихся импульсах можно не только измерить спектрограмму, но и оценить происходящие изменения спектра от импульса к импульсу. При анализе спектра непрерывных сигналов ГК.Ч и ГР работают в периодическом режиме и часть спектра, при­ходящаяся на интервал времени обратного хода луча, теряется. Сигнал непрерывный разбивается на некоторые реализации длительностью τ, равной длитель­ности прямого хода.

Основное преимущество анализаторов с дисперсионной линией заключается в их большем быстродействии по срав­нению с анализаторами последовательного действия с узко­полосными фильтрами.


Цифровой анализ спектра

Бурное развитие цифровой вычислительной техники дало толчок для соз­дания цифровых анализаторов спектра. Цифровой метод анализа спектра состоит в преобразовании исследуемого сигнала в цифровой код и вычисле­нии составляющих спектра с помощью специализированных микропроцес­соров. Цифровые анализаторы спектра по совокупности дискретных отсчетов (выборок) аналогового сигнала вычисляют спектральную плотность путем замены интеграла на конечную сумму из некоторого числа выборок. Такие вычисления осуществляются с помощью алгоритмов дискретного и быстрого преобразований Фурье.

Алгоритм дискретного преобразования Фурье

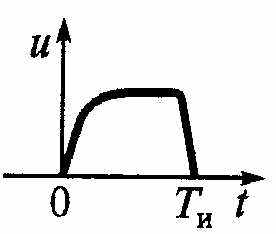
Е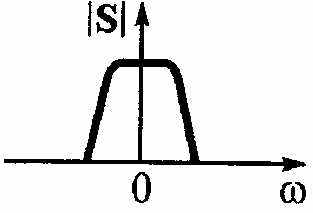сли сигнал u(t) со спектральной плотностью S(co) , яв­ляющийся непрерывной функцией времени в некотором ограниченном ин­тервале 0...Т_И, дискретизирован в соответствии с теоремой Котельникова и отражен своими N отсчетами {u(kAf)} = {щ} с частотой дискретизации юи = 2я /Ги = 2n/(NAt), то его можно представить в виде дискретного преобра­зования Фурье (ДПФ).

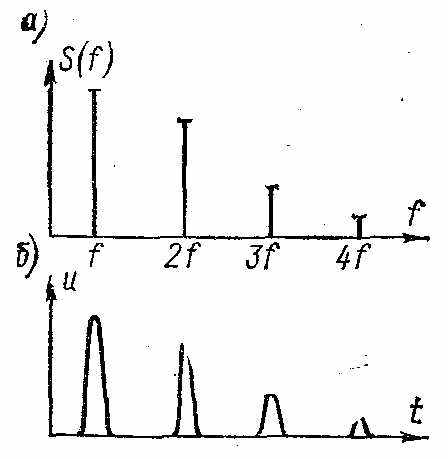
С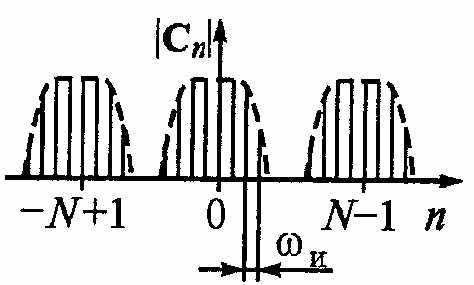пектр процесса, полученный численными методами в виде конечных сумм дискретных решетчатых функций (ДПФ), отличается от спектра, вы­численного интегральными преобразованиями. Спектр ДПФ непре­рывного сигнала периодически размножен: повторяется по оси частот с пе­риодом, равным частоте следования отсчетов. Алгоритм дискретного преоб­разования Фурье имеет вид: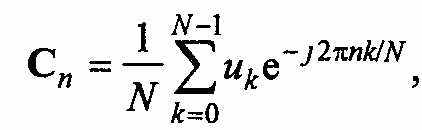



где С„ — комплексные гармонические составляющие исследуемого спектра; W = TJAt — необходимое число отсчетов, отвечающих требованиям теоремы Котельникова; п = 0, 1, 2,..., (N12 - 1) — номер спектральной составляющей.

Это фундаментальное для дискретных сигналов соотношение показано графически на рис. Дискретное преобразование Фурье по существу представляет собой алгоритм цифрового вычисления гармонических состав­ляющих спектра С„ по заданным дискретным отсчетам щ аналогового сигна­ла u(t), что значительно сокращает время и объем обработки.

Быстрое преобразование Фурье

Б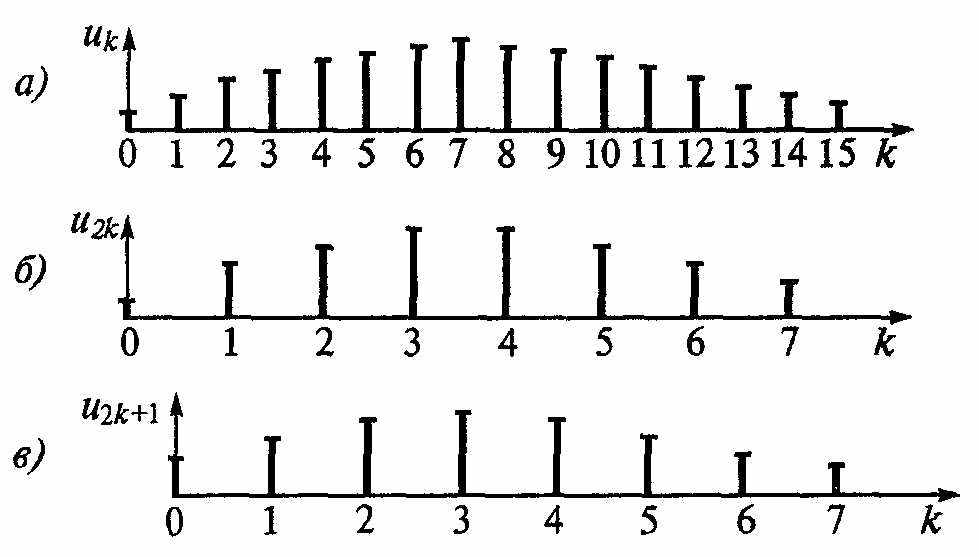ольшое время вычислений спектра препятствовало распространению цифровых методов спектрального анализа. Многократно сократить число операций позволяет быстрое преобразование Фурье (БПФ), обеспечивающее более скоростное и эффективное цифровое вычисление ДПФ. В основу алго­ритма положен принцип разбиения (прореживания во времени, или децимации — от греч. деци — доля) заданной последовательности отсчетов дис­кретного сигнала на ряд промежуточных последовательностей (подпоследо­вательностей). При этом число дискретов N разделяют на множители (на­пример, N = 8 = 2 2 2, N = 60 = 3 • 4 ■ 5). Затем определяют спектры этих промежуточных последовательностей и через них находят спектр всего сиг­нала. В зависимости от состава, числа и порядка следования множеств мож­но создать различные алгоритмы БПФ. В цифровой технике удобнее обраба­тывать сигнальные последовательности с числом отсчетов N, являющимися степенью с основанием два (4, 8, 16 и т.д.). Это позволяет многократно де­лить входную последовательность отсчетов на более мелкие подпоследова­тельности.

Пусть требуется вычислить ДПФ входной последовательности дискрет­ного сигнала {u(k∆t)} = {u_k}, имеющей четное число отсчетов (рис. а), причем N = 2^г где г — целое число (если это условие не выполняется, то по­следовательность искусственно дополняют нулями до требуемого значения N). Представим входную последовательность в виде двух подпоследователь­ностей с четными и нечетными номерами и половинным числом членов в каждой (рис. б, в):

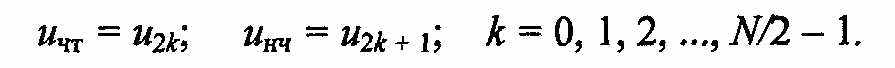
Коэффициенты ДПФ для подпоследовательностей с четными и нечетны­ми номерами запишем отдельно:



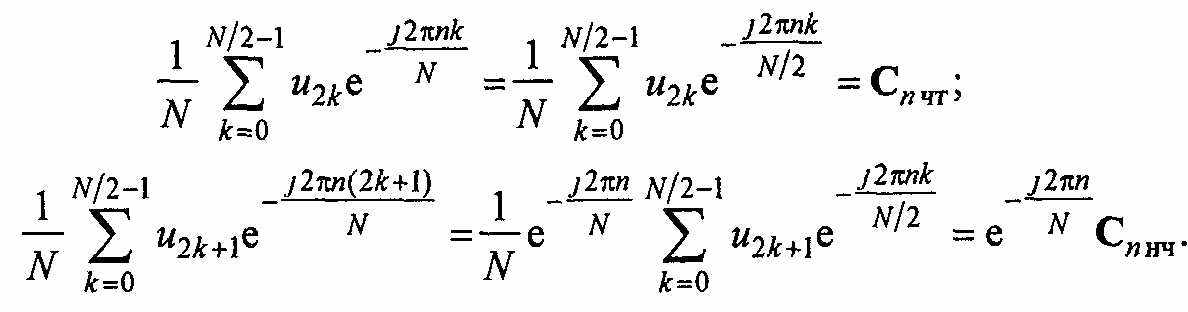
Коэффициенты С„ результирующего ДПФ входной последовательности можно выразить через параметры С„ „ и С„ т двух вновь введенных подпос­ледовательностей. Из последней формулы нетрудно заметить, что в диапазо­не номеров отсчетов от 0 до N/2-l, ДПФ входной последовательности опре­деляется соотношением



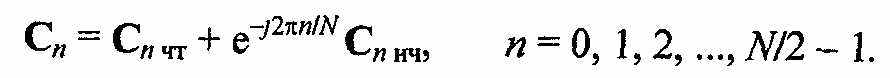
Так как ДПФ четной и нечетной подпоследовательностей являются пе­риодическими, имеющими период следования N12 то:



Запишем экспоненциальный множитель в формуле (11.10) при п = N12, т.е. для ДПФ С(дга + п)т,в виде:



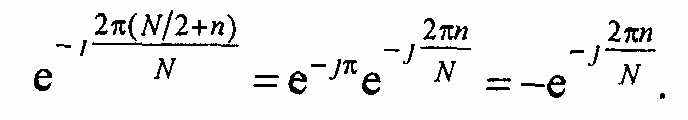
С учетом двух последних выражений находим ДПФ входной последова­тельности для отсчетов с номерами отN12 до TV- 1:



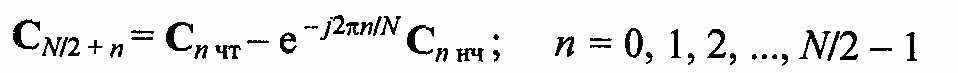
Соотношения (11.10) и (11.11) представляют алгоритмы БПФ. Отме­тим, что экспоненциальные фазовые множители e~j2™IN в этих алгоритмах учитывают влияние сдвига нечетной подпоследовательности относитель­но четной

Чтобы еще уменьшить число вычислений, четную и нечетную подпосле­довательности также разбивают на две промежуточные части. Разбиение продолжают вплоть до получения простейших двухэлементных последова­тельностей. Определив ДПФ данных простейших пар отсчетов, можно вы­числить ДПФ четырехэлементных, восьмиэлементных и так далее подпосле­довательностей. При объединении ДПФ четной и нечетной подпоследова­тельностей используют алгоритмы (11 10) и (11.11), подставляя в них соот­ветствующие значения номеров Nw.n

Можно заметить, что вычисление по формулам (11.9) не потребует опе­раций умножения, а только сложение и вычитание комплексных чисел. Учи­тываться же должны лишь операции умножения в алгоритмах (11.10) и (11.11) для различных п при разбиениях массива отчетов на мелкие подпос­ледовательности. Число этих операций при первом разбиении составляло N12. Тоже же число N12 операций требуется выполнить при каждом следую­щем разбиении. Итак, вдвое увеличивается число подпоследовательностей и вдвое сокращается наибольшее число п в формулах (11.10) и (11.11).

Вычисление коэффициентов ДПФ последовательности из N отсчетов по алгоритмам БПФ требует совершения примерно Nlog2N операций умноже­ния Алгоритмы БПФ сокращают число операций по сравнению с алгорит­мами ДПФ в N2I{N \og2N) = N/(log2N) раз. В частности, при количестве отсчетов N = 210, имеем log2iV = 10 и сокращение числа операций составляет N/(\og2N)« 100. При очень больших массивах отсчетов входного сигнала вы­игрыш в скорости обработки может достигать нескольких тысяч.

У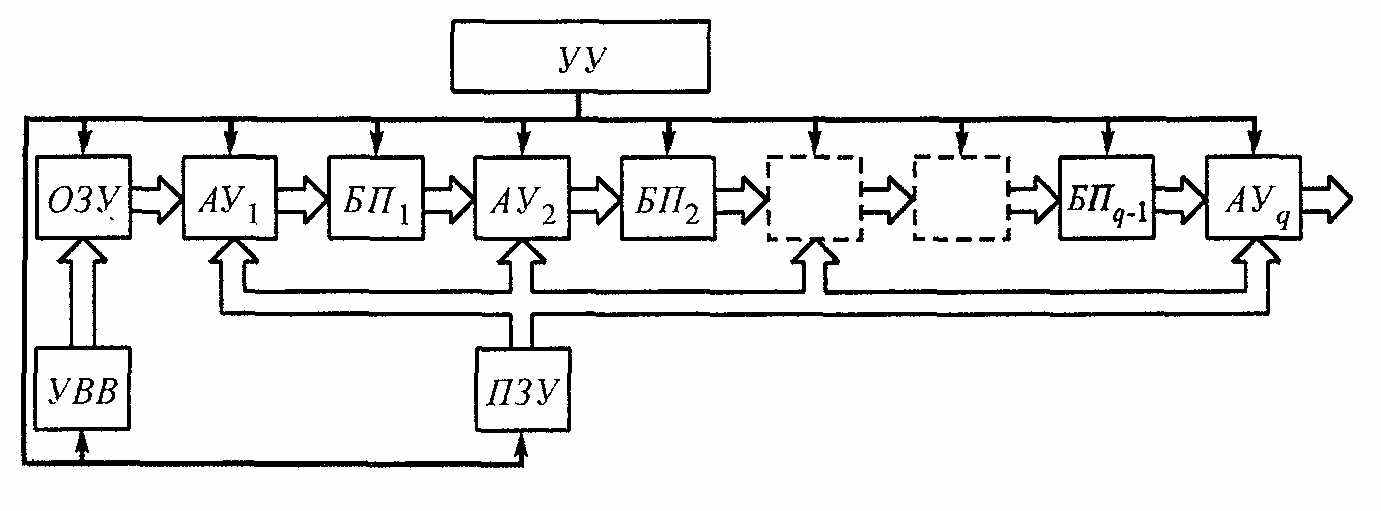прощенная струк­турная схема цифрового анализатора спектра, реали­зующая один из алгоритмов БПФ, показана на рис.


В схеме используются процессоры БПФ с каскадной структурой органи­зации параллельной работы и содержатся q = log₂N арифметических уст­ройств (АУ,), а также q -1 блоков памяти (БП_i) емкостью 2ⁱ комплексных слов каждый. В режиме реального времени все N отсчетов обрабатываемой группы через устройство ввода-вывода информации (УВВ) поступает в опе­ративное запоминающее устройство (ОЗУ). Последним тактом ввода группы отсчетов к ОЗУ последовательно подключаются арифметические устройства, которые осуществляют обработку информации в соответствии с заданным алгоритмом БПФ. Служебная информация о комплексных весовых коэффи­циентах exp(-j2πnk/N) вводится в арифметические устройства из постоянного запоминающего устройства (ПЗУ).

Вывод результатов обработки осуществляется непосредственно из АУ. Синхронизация работы всех устройств цифрового анализатора спектра вы­полняется командами, вырабатываемыми устройством управления (УУ).

Цифровые анализаторы спектра

Современный цифровой анализатор представляет собой качественно но­вый тип аппаратуры, в которой специфические функции многочисленных приборов моделируются с помощью набора компьютерных программ: для изменения характера функционирования достаточно вызвать соответствую­щую программу обработки без аппаратурной перестройки устройств. Ком­плекс программ современного цифрового анализатора спектра позволяет со­четать в одном приборе практически все функциональные возможности, не­обходимые для всестороннего исследования параметров различных сигналов и процессов.

Принцип действия цифрового анализатора спектра основан на вычисли­тельных процедурах определения параметров и характеристик различных сигналов и процессов. В функциональные возможности современного циф­рового анализатора заложены следующие алгоритмы:

• восстановление сигнала по его спектру, т.е. вычисление обратного пре­образования Фурье;

• анализ и синтез характеристик электрических цепей: определение им­пульсных (реакция цепи на элементарные сигналы), передаточных и фазовых характеристик цепей с сосредоточенными параметрами (постоянными); ана­лиз диаграмм Вольперта-Смитта (характеристики и параметры цепей с рас­пределенными постоянными); устойчивость цепей со звеньями обратных связей — анализ диаграммы (критерия устойчивости) Найквиста;

• цифровая обработка и фильтрация сигналов и вычисление произведения спектров (операция, обратная свертке);

• корреляционный анализ детерминированных и случайных сигналов: вы­числение корреляционных и взаимокорреляционных функций; определение фазовых соотношений сигналов (идентификация сигналов);

• спектральный анализ периодических, импульсных и случайных сигна­лов: анализ квадратурных составляющих — определение модуля спектра, фазового спектра, комплексного спектра; определение спектра мощности случайного процесса и его функции когерентности; вычисление взаимного спектра; усреднение спектра по полосе частот; определение кепстра сигналов — так называемый обобщенный или гомоморфный (гомоморфизм — неодно­значность) линейный анализ мультипликативных сигналов;

• измерение параметров сигналов (амплитуды, частоты, фазы, коэффици­ента или индекса модуляции, девиации (отклонения) частоты сигналов; опре­деление параметров импульсных сигналов — амплитуды, длительности, дли­тельностей переднего и заднего фронтов, периода следования и т.д.);

• анализ статистических характеристик случайных процессов; построение гистограмм (столбчатых распределений величин) мгновенных значений сиг­налов; определение одномерной плотности вероятности и интегральной функции распределения случайных процессов, характеристической функции.

Структурная схема современного цифрового анализатора спектра приве­дена на рисунке.

Исследуемые аналоговые сигналы по одному (А) или двум (А, Б) каналам подаются на соответствующие усилители с переменным коэффициентом уси­ления, которые приводят различные уровни входных сигналов (от 0,01 до 10 В) к стандартному значению, необходимому для нормальной работы последую­щих трактов. Затем сигналы поступают на ФНЧ, в котором выделяется поло­са частот, подлежащая анализу. По команде исследователя фильтр может быть выключен. С выхода фильтров сигналы поступают на АЦП, где они преобразуются в параллельный десятиразрядный двоичный код. Возможна работа как одного, так и обоих каналов. В последнем случае выборки мгно­венных значений сигнала проходят одновременно по обоим каналам, что по­зволяет сохранить в цифровом коде информацию о фазовых соотношениях сигналов, необходимую для измерения взаимных характеристик.

Ч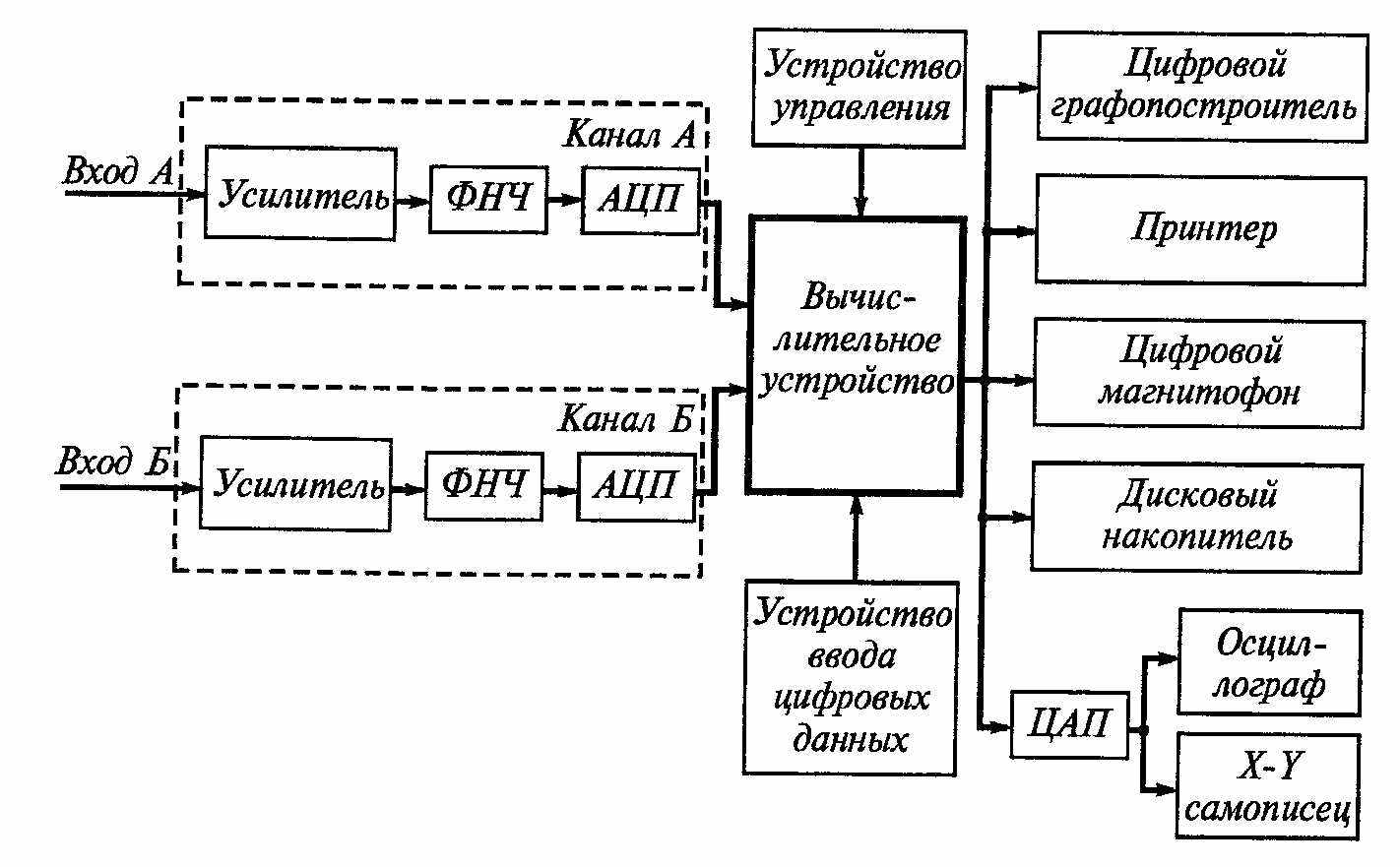астота выборки определяется кварцевым генератором и может изме­няться исследовате­лем в пределах 0,2... 100 кГц. Эта частота определяет отсчетный масштаб прибора во временной и частотной областях.

Тракт прохож­дения исследуемого сигнала от входа усилителей до выхода АЦП имеет калиброванные значения коэффициента передачи во всем диапа­зоне частот и уровней напряжений. Информация о значении коэффициента передачи и частота выборки вводятся в цифровое вычислительное устройст­во (микропроцессор) и учитываются при формировании конечного результа­та. Микропроцессор работает в соответствии с заложенной в него програм­мой. Программа состоит из ряда подпрограмм, организующих ту или иную вычислительную операцию (вычисление спектра, корреляционной функции, построение гистограммы и т.д.). Вызов необходимой подпрограммы осуще­ствляется с устройства управления. Результаты вычислений выводятся на индикаторное или регистрирующее устройство, в качестве которого может быть использован цифровой графопостроитель, принтер, цифровой магнито­фон, дисковый накопитель, осциллограф или самописец. Отметим, что по­следние два подключаются через ЦАП. Все результаты сопровождаются масштабным коэффициентом для перевода их в физические единицы.

При анализе сигналов, представленных в цифровом виде (в виде числово­го ряда), данные вводятся непосредственно в цифровое вычислительное уст­ройство с помощью устройства ввода цифровых данных с наборного табло пульта управления в десятичном коде.

Основные режимы работы цифрового анализатора спектра:

спектральный, статистический и корреляционный анализ;

измерение амплитудного и фазового спектров;

измерение передаточных функций электрических сигналов;

измерение свертки двух сигналов;

измерение спектра мощности, взаимного спектра;

измерение корреляционных функций;

измерение гистограмм амплитуд.


Анализаторы спектра на цифровых фильтрах

Внедрение цифровых методов обработки сигналов в измерительной технике привело к созданию эффективных и высокоскоростных анализаторов спектра на цифровых фильтрах. Цифровой фильтр имеет стабильную частотную характери­стику, не нуждается в подстройке, компенсирующей неточности из-за старения элементов и его универсальность намного выше аналогового фильтра. При пере­стройке цифрового фильтра нет необходимости менять элементы, а достаточно его перепрограммировать. Однако главное преимущество цифровой фильтрации в измерительной технике — применение высокоточных цифровых детекторов и устройств усреднения (цифровых интеграторов). Цифровой детектор измеряет практически истинное среднее квадратическое значение анализируемого сигнала без ограничений, связанных с его амплитудным значением.

Цифровое устройство усреднения, обеспечивающее усреднение анализи­руемого сигнала по линейному и экспоненциальному (или показательному) законам, отличается универсальностью и эффективностью, недостижимым для аналоговых усредняющих устройств.

Цифровая обработка сигналов в анализаторах спектров

Одним из важнейших методов цифровой обработки сигналов в современ­ной измерительной технике и, в частности, в анализаторах спектров, является цифровая фильтрация. Она заключается в цифровом преобразовании последо­вательности числовых отсчетов входного сигнала {u(k∆t)} = {u_k} в последова­тельность числовых отсчетов {у(k∆t)} = {у_к} выходного сигнала.

Рассмотрим упрощенную структурную схему цифровой обработки сиг­налов. Непрерывный сигнал u_вх(t) = u_вх (далее аргумент t опущен) поступает на вход АЦП, на выходе которого создается цифровой код в виде двоичного числа {u(k∆t)} = {u_т} = u_т с фиксированным количеством разря­дов, соответствующий дискретным отсчетам входного сигнала.



Последовательность закодированных определенными цифрами отсчетов {u_т} поступает в цифровой фильтр (ЦФ), представляющий собой, по сути дела, специализированный микрокомпьютер (раннее название — спецвычис­литель). В цифровом фильтре осуществляется цифровая обработка сигнала в соответствии с определенным алгоритмом, в результате чего на его выходе по­являются новые цифровые коды, соответствующие про­фильтрованному входному сигналу.

Обычно обрабатываемый сигнал с цифрового фильтра поступает на ЦАП, в котором цифровая форма сигнала преобразуется в аналоговую. Однако в измерительной технике часто используется преобразованный сиг­нал непосредственно в цифровой форме и при этом необходимость в ЦАП отпадает. Если же ЦАП включен в схему обработки, то на его выходе необхо­дим синтезирующий фильтр (СФ) низкой частоты (по существу это ФНЧ), который будет производить сглаживание полученного аналогового сигнала. В результате сглаживания форма кривой выходного сигнала uBax(t) = u_вых стано­вится плавной, а не ступенчатой.

Структурные схемы линейных цифровых фильтров

Цифровые фильтры делятся на два больших класса: нерекурсивные и ре­курсивные. Термин рекурсивный связан с известным математическим прие­мом — рекурсией — циклическим обращением к вычисленным данным, по­лученным на предыдущих этапах математических операций. Подробно о цифровых фильтрах в курсе схемотехники.


Измерение нелинейных искажений

Измерение ряда величин, характеризующих параметры сигналов или электрических цепей, осуществляют с помощью приборов, которые по по­строению аналогичны анализаторам спектра. К таким характеристикам относятся нелинейные искажения, которые возникают в цепях с нелинейной ам­плитудной характеристикой. При прохождении по таким цепям колебания теряют синусоидальную форму (искажаются) и в их спектре появляются высшие гармоники.

Возникающие при нелинейных искажениях гармоники можно исследо­вать и измерить с помощью анализаторов спектра. Известны несколько количественных показателей уровня нелинейных искажений. Наибольшее распространение получил такой показатель как коэффициент нелинейных искажений (коэффициент гармоник), представляющий собой отношение среднего квадратического значения всех высших гармоник напряжения (или тока)



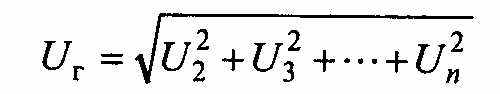
к среднему квадратическому значению его первой гармоники U₁.



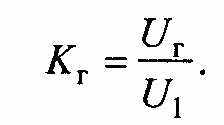
Для измерения относительного значения напряжения гармоник можно использовать анализатор спектра, если его разрешающая способность позво­ляет наблюдать раздельно спектральные составляющие. Если детектор ана­лизатора линейный, то вместо напряжений U₁, U₂,..., Un можно подставить значения их амплитуд, измеренных на экране анализатора в единицах длины.

Существуют специальные приборы, измеряющие коэффициент нели­нейных искажений, называемые измерителями нелинейных искажений.



Упрощенная структурная схема аналого-цифрового измерителя нели­нейных искажений.

В основе измерительной методики таких приборов лежит метод по­давления основной частоты исследуемого сигнала.

Входное устройство служит для согласования измерительного прибора с источником исследуемого сигнала. Перед измерением переключатель Кл ста­вят в положение Калибровка. Затем с помощью усилителя уровень исследуе­мого напряжения повышают до такого фиксированного значения, при кото­ром электронный цифровой вольтметр среднего квадратического значения будет проградуирован в величинах коэффициента нелинейных искажений. При этом измеряется среднее квадратическое значение напряжения всего исследуемого сигнала



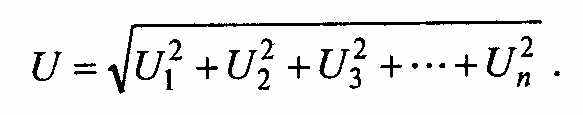
Затем переключатель Кл прибора ставят в положение Измерение. На­страивая заграждающий фильтр, подавляют напряжение основной частоты (первой гармоники U₁). Полное подавление гармоники U₁, будет при мини­мальном показании прибора. В этом случае цифровой вольтметр показывает среднее квадратическое значение суммы высших гармонических составляю­щих сигнала U_г.

Сравнивая показания во втором и первом случаях, находят коэффициент гармоник



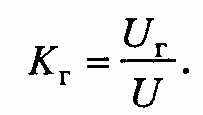
Практически при положении переключателя Кл Измерение будет изме­ряться коэффициент К_г1. При этом коэффициент гармоник К_г можно вычис­лить как:



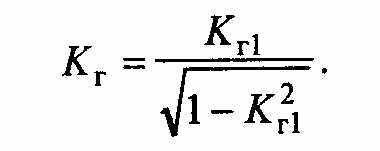
При небольших нелинейных искажениях исследуемого сигнала (К_г<0,1) коэффициенты К_т и К_т1 отличаются меньше чем на 1 %. Обычно измерите­ли нелинейных искажений применяются для измерения коэффициента гар­моник К_т в пределах 0,1...30 %, в диапазоне частот от 0,01 кГц до 25 МГц и более.


Контрольные вопросы

1. Для каких целей используется спектральный анализ сигналов?

2. Какой физический смысл лежит в основе прямого и обратного преобразова­ний Фурье?

3. Как аналитически записываются прямое и обратное преобразования Фурье?

4. На чем основан параллельный и последовательный анализ спектра исследуемых сигналов?

7. Как выглядит упрощенная структурная схема анализатора параллельного действия?

8. Что называется разрешающей способностью анализатора?

9. Как разрешающая способность связана с полосой пропускания фильтра анали­затора?

10. Какова упрощенная структурная схема анализатора спектра последовательно­го типа?

11. Как связана скорость анализа с полосой пропускания анализатора?

12. Чему равно время анализа в схемах последовательного типа?

13. На чем основан принцип построения гетеродинного анализатора спектра после­довательного типа?

14. Каковы основные характеристики гетеродинного анализатора?

17. Как записывается математическое выражение для коэффициента гармоник?

18. Каков алгоритм практического определения коэффициента гармоник?