Разработка и исследование метода одновременной оценки корней характеристического уравнения линейной системы
| Вид материала | Исследование |
- Сингулярность напряжений в вершине изотропных и анизотропных конусов, 61.15kb.
- 2 Семестр. Лекция n 25. Способы составления характеристического уравнения. Алгоритм, 68.85kb.
- Сафиуллин Николай Тахирович исследование, 64.17kb.
- Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
- Isbn 978-5-7262-1376 нейроинформатика 2011, 103.58kb.
- Метод оценки эффективности иерархической системы информационной и инженерно-технической, 93.19kb.
- Вдокладе представлен сравнительный анализ метода конечных объёмов и метода Галёркина, 27.76kb.
- Дискретная математическая модель распостронения эпидемических заболеваний, 30.62kb.
- С. В. Шешенин 1/2 года Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
- Разработка метода нечеткой оценки проектных характеристик обучаемого инженера для автоматизированных, 55.1kb.
На правах рукописи
Кокорев Сергей Алексеевич
РАЗРАБОТКА И ИССЛЕДОВАНИЕ МЕТОДА ОДНОВРЕМЕННОЙ ОЦЕНКИ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ ЛИНЕЙНОЙ СИСТЕМЫ
Специальность 05.13.01 - “Системный анализ, управление и обработка информации (энергетика, приборостроение, информатика, производственные процессы)”
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва – 2006
Работа выполнена в Московском энергетическом институте (техническом университете) на кафедре Управления и информатики.
Научный руководитель: доктор технических наук,
профессор Колосов Олег Сергеевич
Официальные оппоненты: доктор технических наук,
профессор Горицкий Юрий Александрович
кандидат технических наук,
доцент Тягунов Олег Аркадьевич
Ведущая организация: кафедра Кибернетики
Московского инженерно-физического института
(Государственного университета) (МИФИ (ГУ))
Защита состоится 15 марта 2007 г. в 16 час. 00 мин. на заседании диссертационного совета Д 212.157.08 при Московском энергетическом институте (техническом университете) по адресу:
г. Москва, ул. Красноказарменная, дом 14 в Малом актовом зале МЭИ
С диссертацией можно ознакомиться в библиотеке МЭИ (ТУ)
Отзывы на автореферат в двух экземплярах, заверенные печатью, просим направлять по адресу: 111250, г. Москва, ул. Красноказарменная, д. 14, Ученый совет МЭИ (ТУ).
Автореферат разослан “___” ________________ 2007 г.
Ученый секретарь диссертационного совета Беседин В.М.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность проблемы. При анализе линейных систем автоматического управления, а также при синтезе регуляторов для них, часто возникает задача поиска корней характеристического уравнения исследуемой системы, причем левая часть уравнения представляет собой алгебраический полином, а правая равна нулю. Среди имеющихся методов можно выделить методы, которые достаточно ясны для понимания, однако неэффективны с точки зрения количества выполняемых операций, а также методы, которые считаются достаточно эффективными, но при этом численная процедура, соответствующая им, является достаточно сложной для освоения и реализации. Предлагаемый метод имеет преимущества с точки зрения количества выполняемых операций по сравнению с методом собственных значений (сравниваются методы одновременного нахождения всех корней полинома) в случае многократных вычислений для характеристического уравнения системы с изменяющимися во времени коэффициентами, а также дает возможность более быстрого построения корневого годографа.
Целью работы является создание численного метода одновременного определения всех корней полиномиального уравнения, достаточно простого для понимания и эффективного.
Основные задачи работы:
- Проанализировать существующие методы нахождения корней полиномиальных уравнений, выявить их достоинства, недостатки и ограничения;
- Разработать эффективный алгоритм одновременного нахождения всех корней характеристического уравнения линейной системы автоматического управления;
- Разработать алгоритм для разделения множества корней полинома на подмножества, обладающие некоторыми общими свойствами (близость действительных частей корней, близость комплексных частей корней, комбинированный критерий).
Научная новизна работы состоит в том, что в ней предложен качественно новый метод решения полиномиальных уравнений, являющийся универсальным, то есть применять предложенный метод без потери им своих качеств возможно к любым полиномиальным алгебраическим уравнениям, а не только для получения корней характеристического полинома жесткой системы автоматического управления.
Практическая значимость работы состоит в возможности расширения функциональности популярных математических пакетов и средств анализа и синтеза систем автоматического управления с помощью новой предложенной методики. Также необходимо отметить, что идея предлагаемого метода достаточно легко воспринимается, а поэтому метод может быть предложен к использованию для обучения студентов. Кроме вычисления корней полинома с постоянными коэффициентами, в работе показана возможность использования метода для расчета корней “в темпе с объектом” для случая, когда коэффициенты характеристического уравнения изменяются с течением времени. Также представлена процедура разделения свободного движения линейной системы автоматического управления.
Основные положения, выводимые на защиту:
- Возможность переформулировки задачи одновременного нахождения всех корней полиномиального уравнения к задаче оптимизации.
- Применимость численных процедур оптимизации к поставленной задаче оптимизации.
- Возможность ухода от задачи оптимизации овражного критерия путем задания начальных условий при помощи быстрого расчета оценок корней с использованием деления промежуточного полинома на одночлен, содержащий оценку корня, полученную из одномерной численной процедуры для нахождения корней нелинейных алгебраических уравнений.
- Возможность быстрого построения корневого годографа линейной системы автоматического управления.
Апробация работы проведена на заседании семинара по теории автоматического управления кафедры управления и информатики ГОУ ВПО “Московский энергетический институт (технический университет)”, также материалы диссертации изложены на одиннадцатой международной научно-технической конференции студентов и аспирантов “Радиоэлектроника, электротехника и энергетика”, Москва, 2005 г. и на международных семинарах “Современные технологии в задачах управления, автоматики и обработки информации”, Алушта, 2005 г. Результаты работы используются при чтении лекций по курсу: “Системы автоматизации и управления”.
Структура и объем диссертации. Диссертация состоит из введения, 5 глав, заключения, списка источников и двух приложений. Диссертация изложена на 129 страницах машинописного текста без учета приложений, иллюстрирована 9 таблицами и 18 рисунками. В списке литературы приведено 67 источников, из них 53 отечественных и 14 иностранных.
Публикации. По теме диссертации опубликовано 3 печатные работы, одна из которых – в реферируемом ВАК журнале.
СОДЕРЖАНИЕ РАБОТЫ
В первой главе обсуждаются методы исследования устойчивости линейных систем автоматического управления, рассматривается случай, когда поиск корней характеристического полинома системы предпочтителен. На сегодняшний день имеется довольно много методов нахождения корней полиномиальных уравнений, которые можно разделить на две группы:
- Методы решения систем нелинейных уравнений общего вида.
- Специализированные методы решения полиномиальных уравнений.
Среди этих методов представлены одномерные процедуры, базирующиеся на последовательном нахождении всех корней полинома, а также метод собственных значений, обладающий следующими преимуществами:
- Одновременно находит все корни полинома;
- Не требует начальных приближений.
Однако и этот метод не лишен недостатков, среди которых требуется отметить высокую вычислительную сложность и неудовлетворительную работу метода с полиномами высокого порядка (за счет плохой обусловленности матрицы) и кратными корнями (за счет метода построения этой матрицы). Более того, при некоторых процедурах, проводимых в рамках анализа линейных систем автоматического управления (вычисление корней системы с изменяющимися во времени коэффициентами, построение корневого годографа) требуется на каждом шаге рассчитывать корни полинома, коэффициенты которого лишь немного отличаются от коэффициентов полинома на предыдущем шаге. При применении метода собственных значений всю вычислительную процедуру (в силу особенностей построения последней) требуется запускать заново. В работе предложен метод, который позволяет избежать этого за счет разделения численной процедуры на две стадии и возможности повторения второй стадии (уточнения корней) со значениями корней, полученными с предыдущего шага. Таким образом можно сократить количество вычислений на каждом шаге.
Во второй главе рассматривается основная идея метода, при этом изложены нижеследующие положения.
В работе используется следующая форма записи полинома:
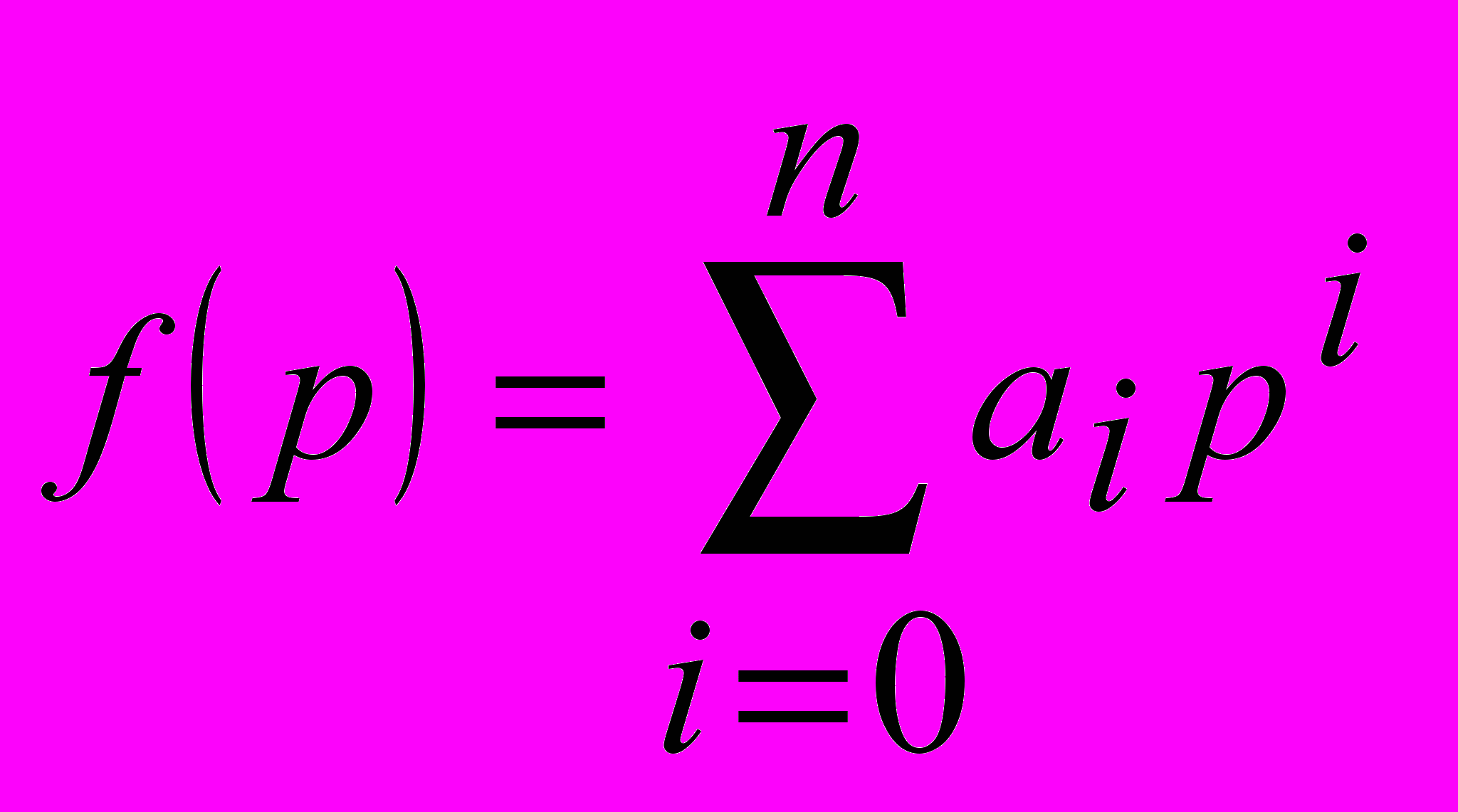 , (1)
, (1)при этом предполагается, что
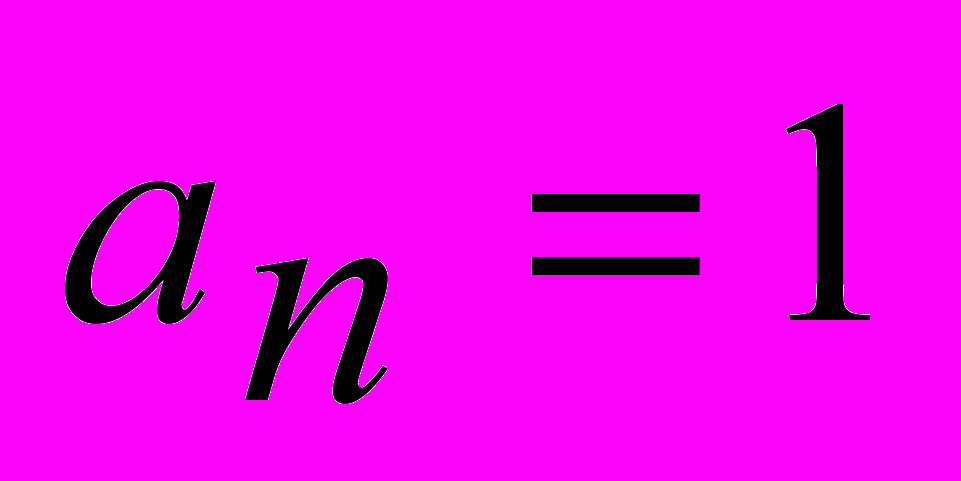 .
.Основная идея предложенного в работе метода заключается в использовании формул Виета, связывающих корни полинома с его коэффициентами для построения задачи оптимизации, решение которой впоследствии позволяет одновременно получить все корни полинома.
Формулы Виета в работе записываются в следующей форме:
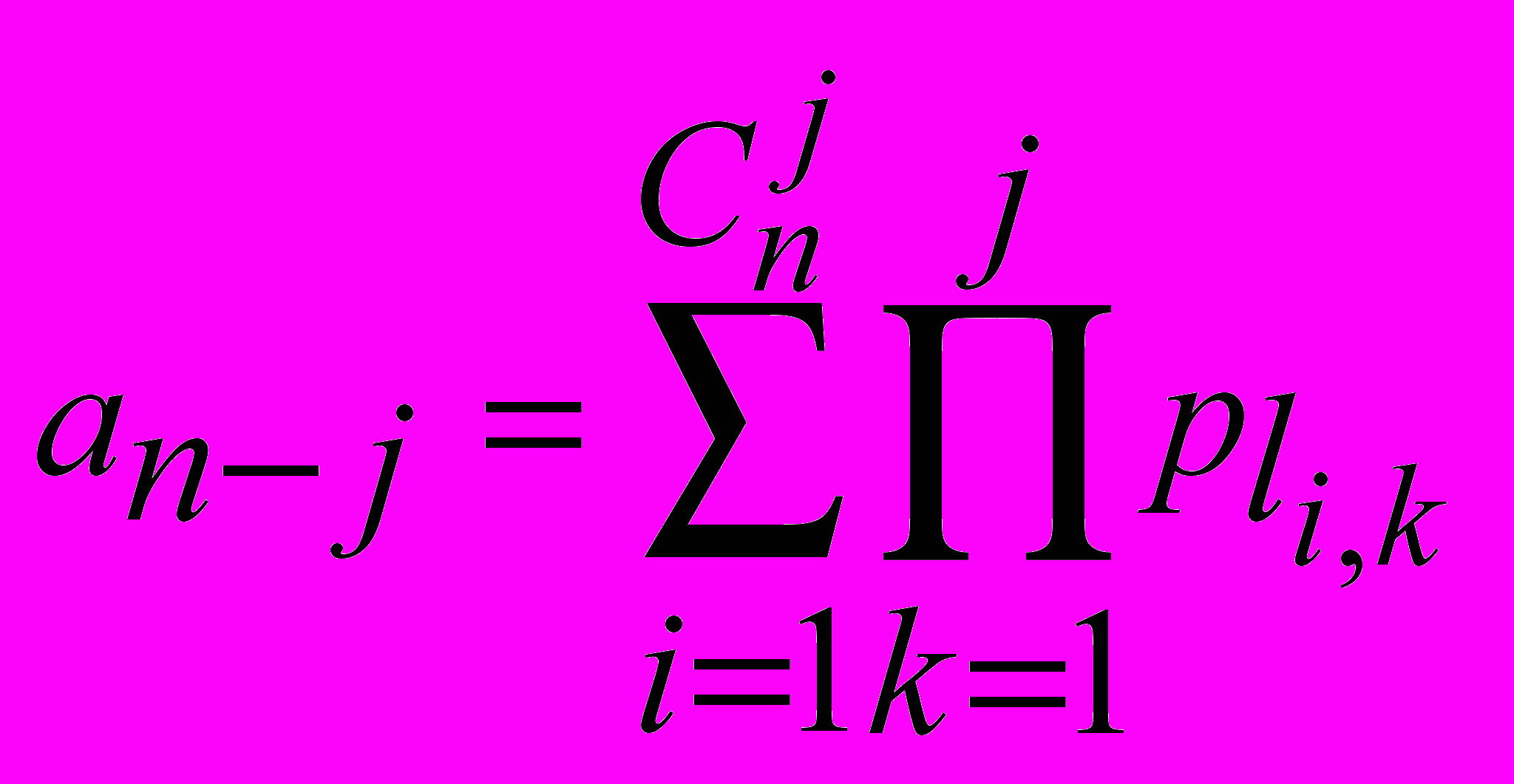 (2),
(2),где
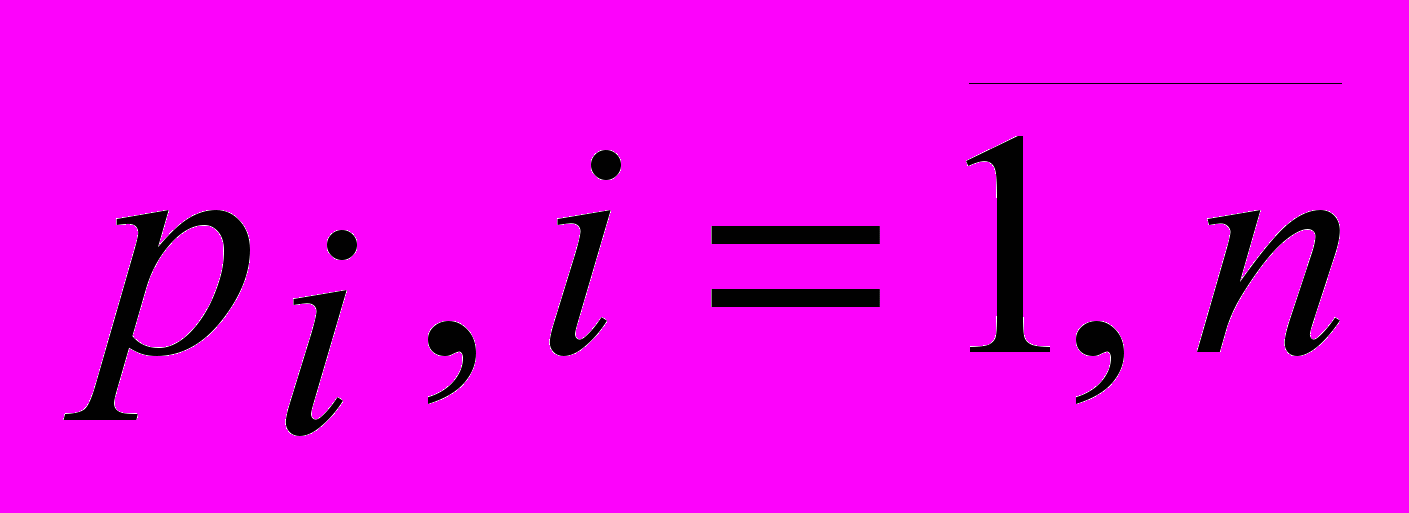 - корни уравнения (1) с противоположным знаком,
- корни уравнения (1) с противоположным знаком, 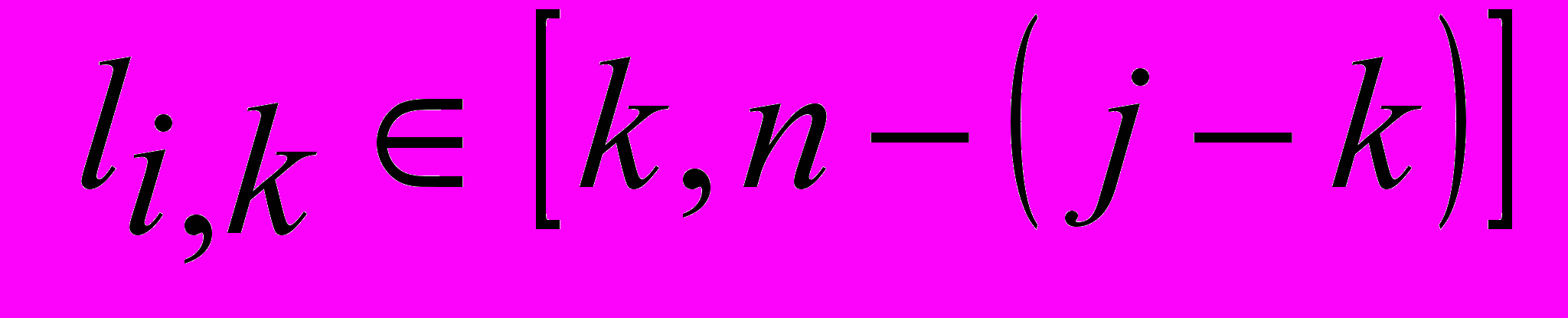 для
для 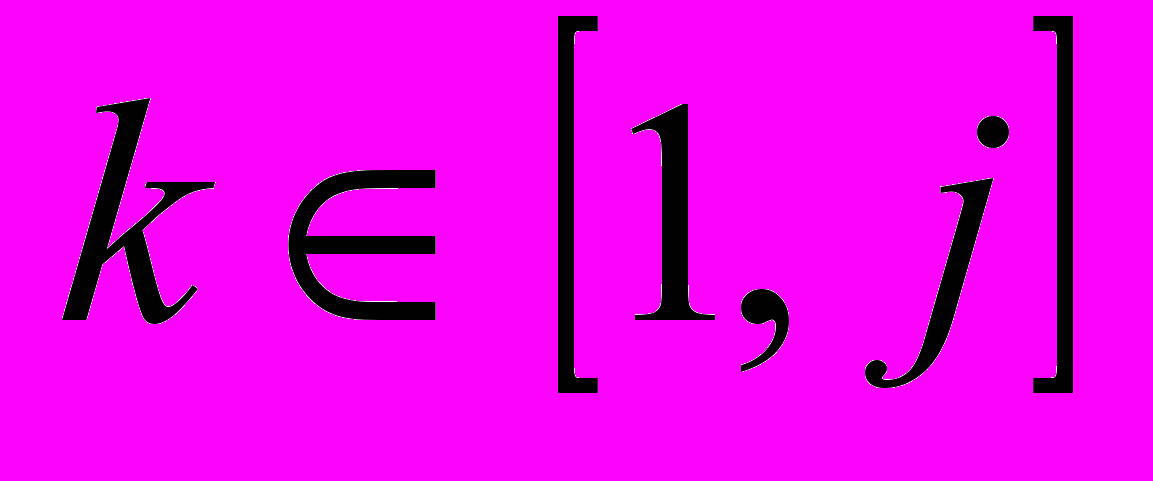 ,
,  , причем
, причем  для
для  .
.Матрица
 называется таблицей индексов для коэффициента полинома, которая может быть сгенерирована еще до начала вычисления корней на основе знания порядка полинома. Использование таблиц индексов для коэффициентов полинома и для частных производных позволяет избежать ошибок вычисления при численном дифференцировании в ходе численной процедуры, которая будет описана ниже.
называется таблицей индексов для коэффициента полинома, которая может быть сгенерирована еще до начала вычисления корней на основе знания порядка полинома. Использование таблиц индексов для коэффициентов полинома и для частных производных позволяет избежать ошибок вычисления при численном дифференцировании в ходе численной процедуры, которая будет описана ниже.На основе формулы (2) можно построить критерий оптимизации, удовлетворяющий следующим условиям:
- Критерий должен быть по крайней мере дважды непрерывно дифференцируем по всем своим параметрам и их сочетаниям. (При этом имеется возможность использовать для его оптимизации численные методы второго порядка).
- Критерий должен принимать наименьшее значение в точке значений всех корней полинома.
В работе предлагается следующая форма записи критерия оптимизации:
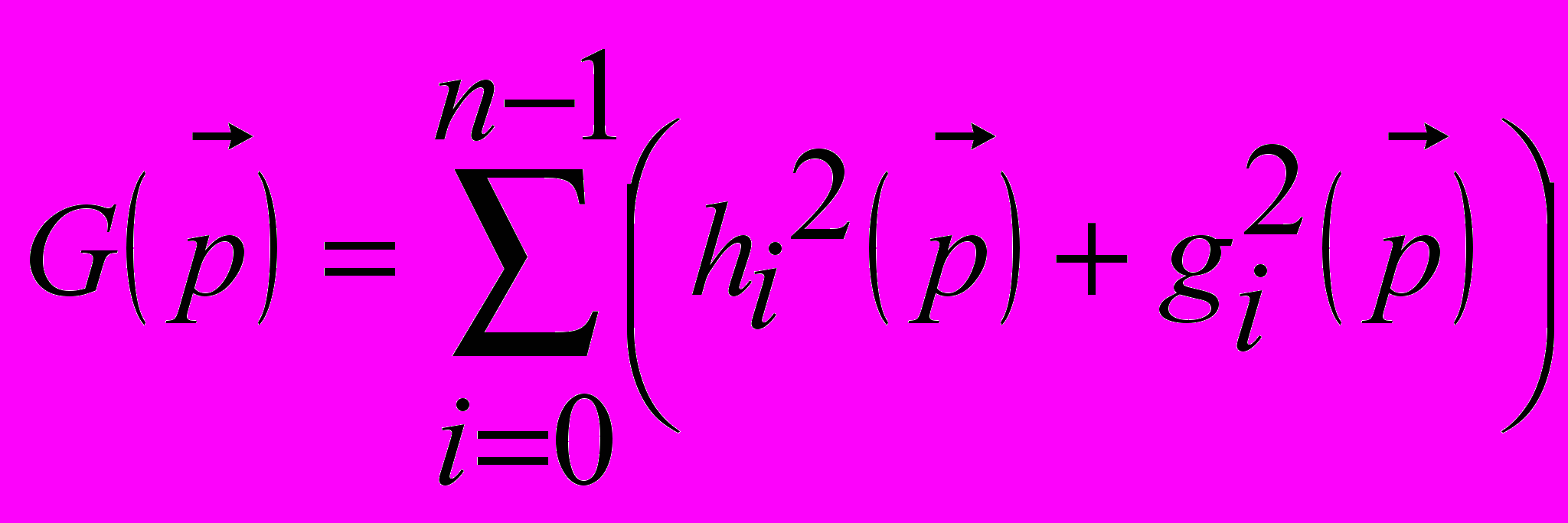 ,
,  , (3),
, (3),где
 ,
, 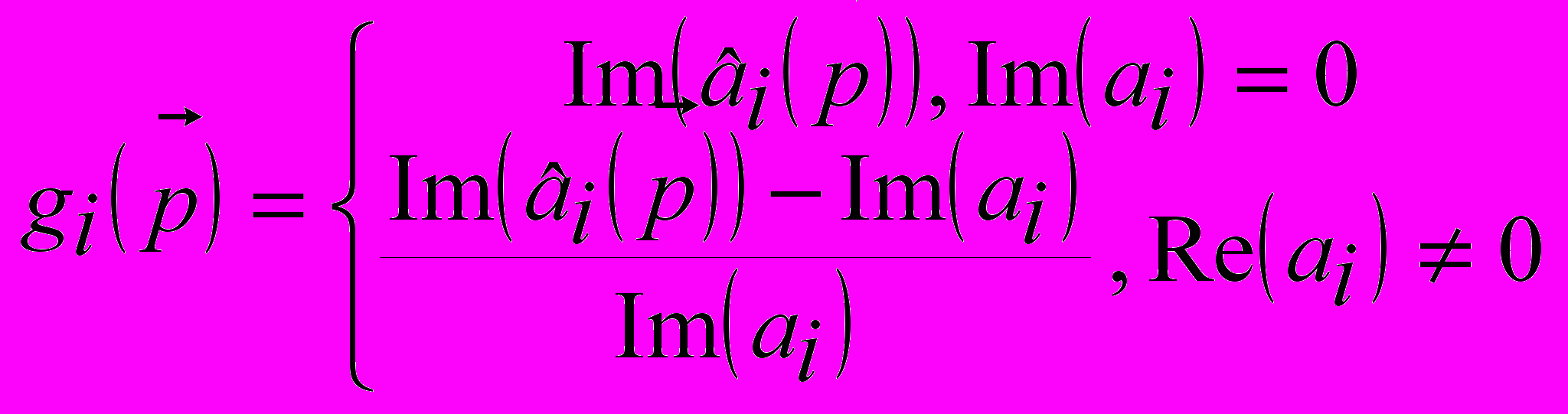 (4),
(4),рассчитанного на наличие комплексных корней и коэффициентов, а также адаптированного к случаю нулевых коэффициентов.
Из второго условия следует, что критерий имеет не единственную точку минимума, так как за счет перестановки корней, можно получить другую точку, в которой критерий принимает наименьшее значение. Не единственный минимум является здесь не помехой, а подспорьем для исследователя, так как оптимизационная процедура может сойтись к ближайшему минимуму, который в любом случае будет удовлетворять потребности нахождения всех корней полинома.
Принимая во внимание формулы (2), (3) и (4), задачу оптимизации можно сформулировать следующим образом:
 (5)
(5)Так как поиск в общем случае осуществляется для
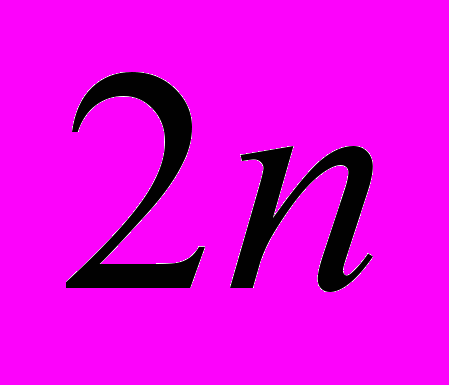 значений, то есть для
значений, то есть для 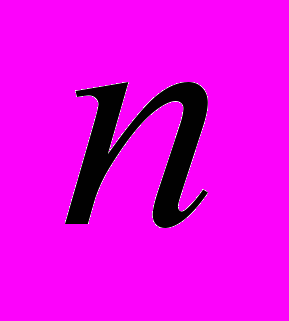 действительных частей и для
действительных частей и для 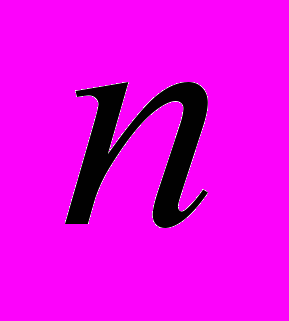 мнимых частей корней (1), то поиск производится в пространстве
мнимых частей корней (1), то поиск производится в пространстве 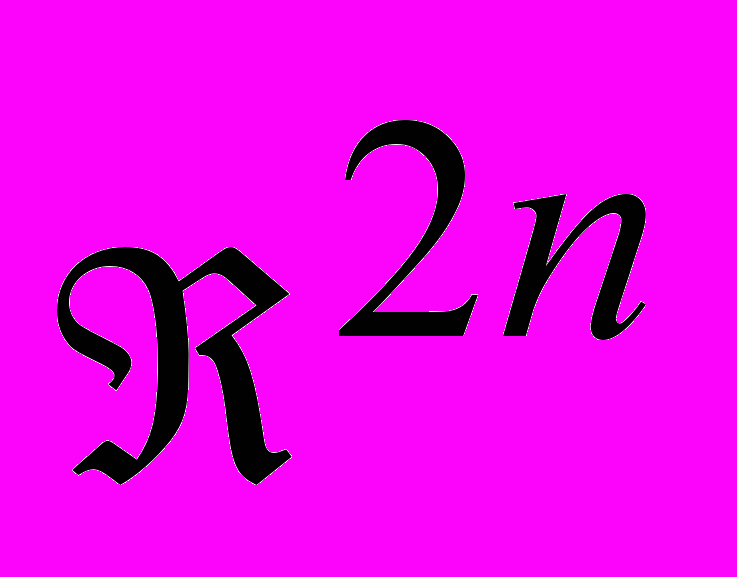 , при этом значение критерия всегда является вещественным числом.
, при этом значение критерия всегда является вещественным числом.Исследование поведения критерия показало, что задача оптимизации (5) имеет овражный характер, что можно достаточно легко продемонстрировать, построив на плоскости линии уровня критерия для случая
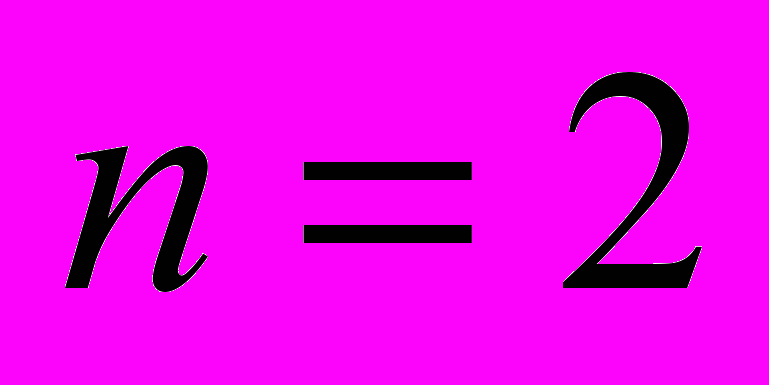 и вещественных корней, либо линии уровня в разрезе двух переменных. Для случая полинома пятого порядка с комплексными корнями такой срез показан на рис. 1.
и вещественных корней, либо линии уровня в разрезе двух переменных. Для случая полинома пятого порядка с комплексными корнями такой срез показан на рис. 1.
Рис. 1. Поведение критерия для случая полинома пятого порядка в разрезе двух составляющих вектора переменных.
В третьей главе исследуются возможности существующих методов для решения задачи оптимизации (5).
Произведенное исследование поведения метода Гельфанда и его модификаций при оптимизации подобных функций показало, что такие методики неэффективны и следует предложить другие способы оптимизации.
В работе для оптимизации полученного критерия был использован метод Левенберга-Марквардта, который на данный момент является одним из самых быстрых квазиньютоновских методов оптимизации. Для построения численной процедуры по этому методу требуется вычислять значения критерия и его якобиан в произвольной точке. Такие вычисления производятся по аналитическим формулам с помощью таблиц индексов для коэффициентов полинома, частных производных коэффициентов полинома по корням, а также матриц комплексных произведений. Последние позволяют хранить в виде тернарной матрицы (каждое значение элемента матрицы выбирается из множества
 ) аналитическую формулу произведения
) аналитическую формулу произведения 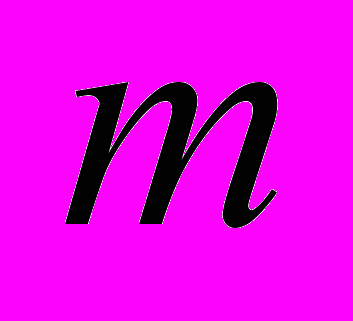 комплексных чисел.
комплексных чисел.Градиент критерия оптимизации (составляющие его якобиана) записывается в следующей форме:
 (6),
(6),где
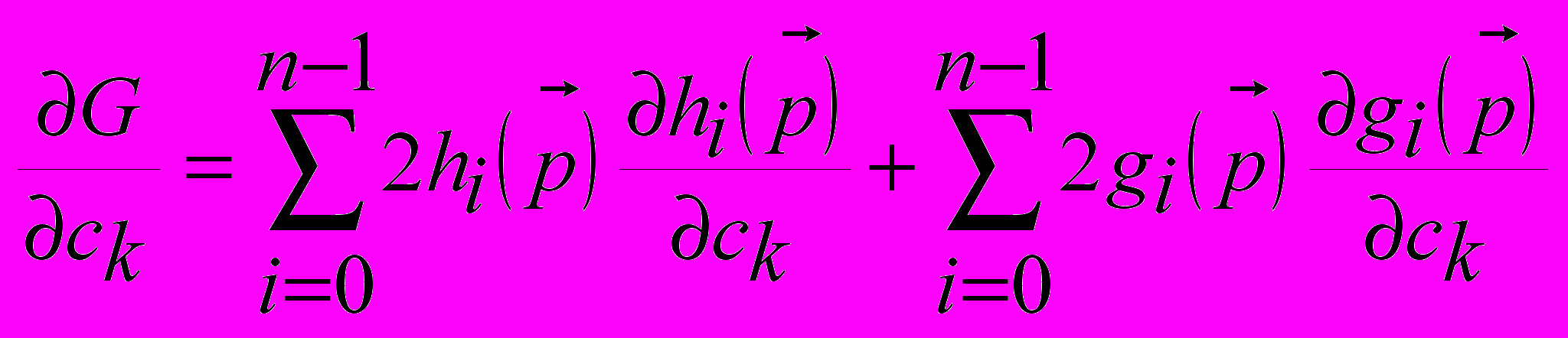 ,
, 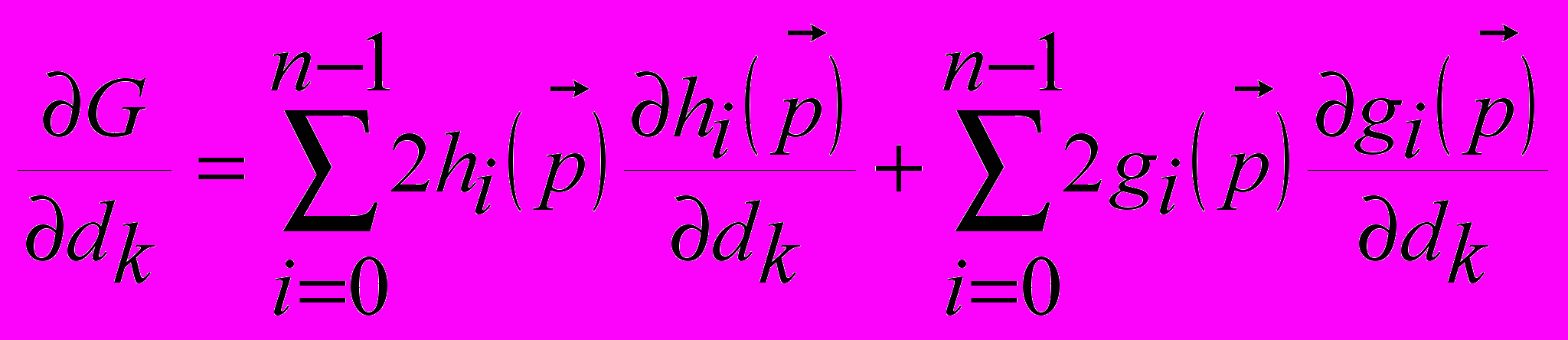 (7)
(7)и
 , где (8)
, где (8)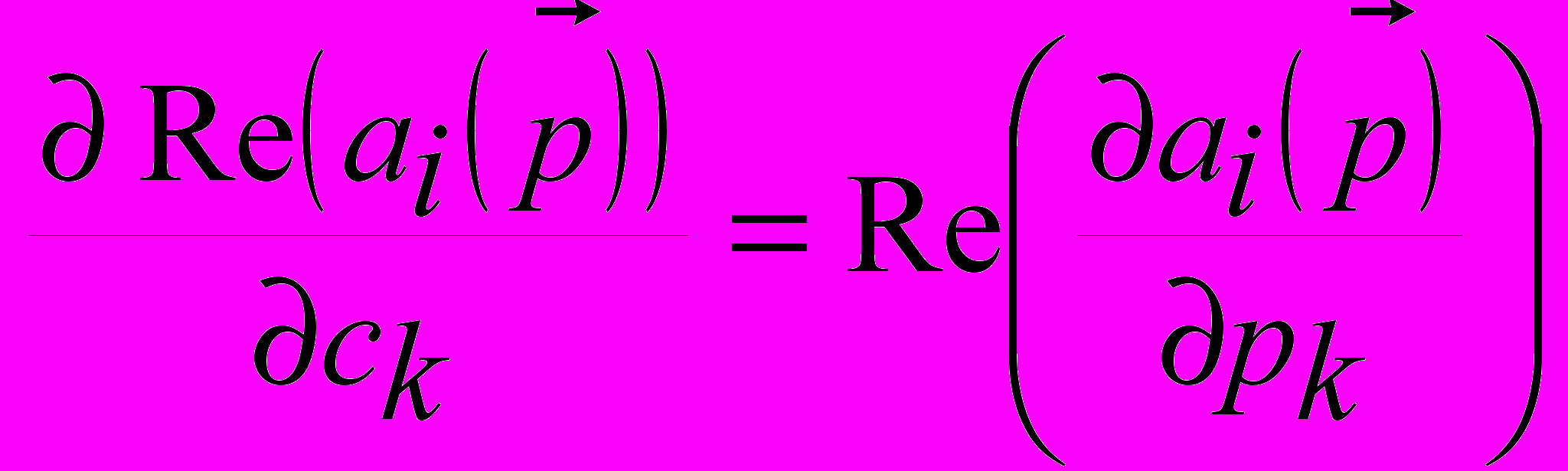 ,
,  , (9.1)
, (9.1) ,
,  . (9.2)
. (9.2)Правильность использования формул (9.1) и (9.2) в работе доказывается с помощью леммы, которая формулируется следующим образом:
Лемма. Пусть имеется произведение нескольких комплексных чисел
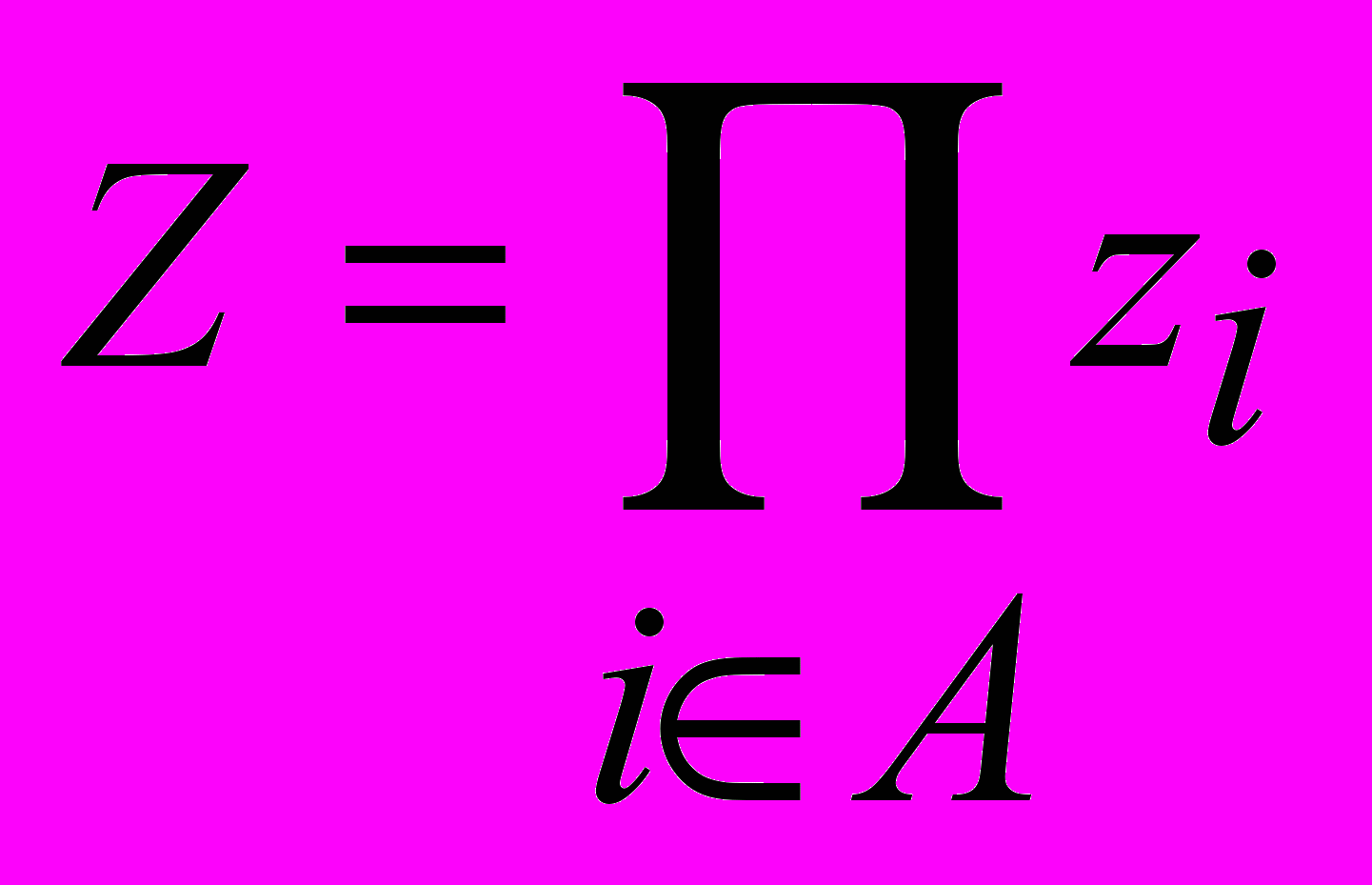 , где
, где  - некое множество целых чисел, используемых как индексы в произведении. Тогда
- некое множество целых чисел, используемых как индексы в произведении. Тогда 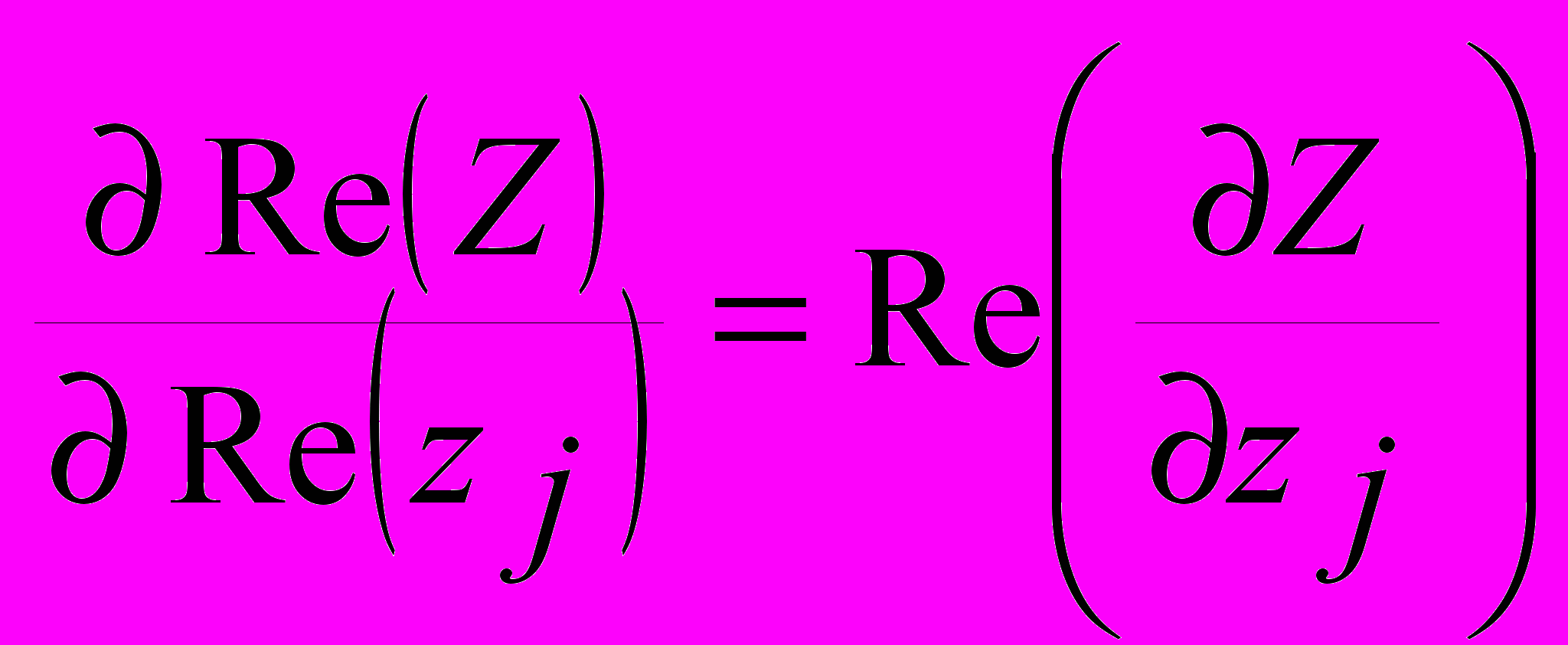 ,
, 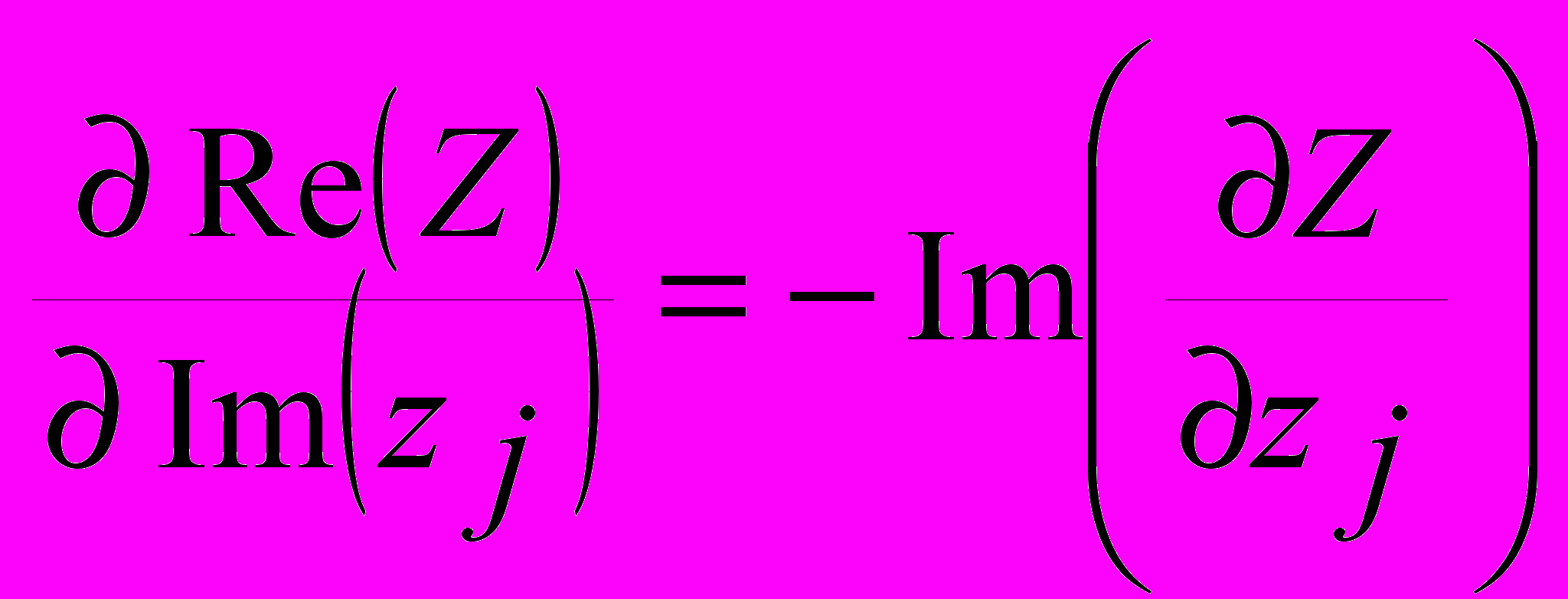 ,
, 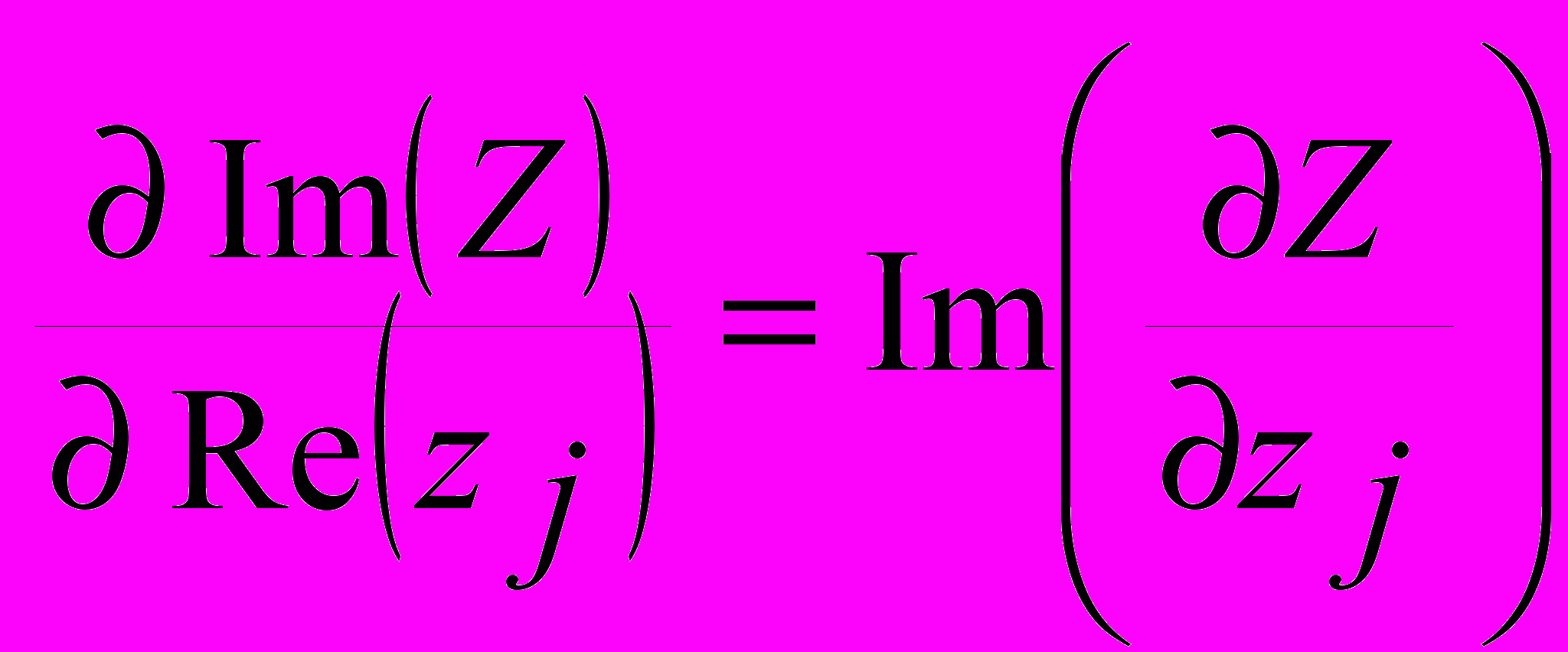 ,
,  где
где  .
.Теоретически, изменение формул расчета с помощью соотношений (9.1) и (9.2) не дает никакого существенного изменения самого процесса расчета, однако на практике применение этих соотношений позволяет рассчитывать необходимые частные производные, пользуясь аналогами таблиц индексов для коэффициентов, которые называются таблицами индексов для производных. Это позволяет рассчитывать составляющие вектора градиента (6) и, соответственно, якобиана для метода Левенберга-Марквардта, по аналитическим формулам.
Исследование поведения метода Левенберга-Марквардта показало, что последний достаточно быстро сходится для рассматриваемого критерия, в особенности, если начальная точка, из которой запускается численный процесс оптимизации находится в некоторой окрестности одной из точек минимума. Такая окрестность характеризуется довольно медленным изменением критерия оптимизации по всем направлениям. Для того, чтобы задать такую точку, используется модификация метода Мадсена-Рейда, заключающаяся в том, что в отличие от оригинального метода, процедура уточнения корней (обычно производящаяся по методу Ньютона-Рапсона) запускается только после оценки всех значений корней, и вместо стандартной одномерной процедуры, используется рассмотренная многомерная процедура минимизации по методу Левенберга-Маквардта.
В четвертой главе предлагаются алгоритмы генерации статической и динамической информации, требующейся для работы метода.
Для запуска рассмотренной численной процедуры минимизации требуются матрицы комплексных произведений и таблицы индексов для коэффициентов полинома и частных производных. В работе предложен алгоритм генерации таблиц индексов для коэффициентов полинома, работающий на основании перебора всех возможных уникальных сочетаний индексов корней полинома из
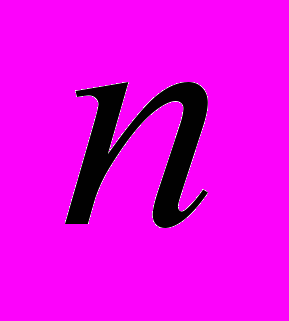 по
по  . Для генерации таблиц индексов для производных требуется взять таблицу индексов для коэффициентов и вычеркнуть оттуда соответствующую строку и столбец. Генерация матриц комплексных произведений осуществляется по формулам:
. Для генерации таблиц индексов для производных требуется взять таблицу индексов для коэффициентов и вычеркнуть оттуда соответствующую строку и столбец. Генерация матриц комплексных произведений осуществляется по формулам: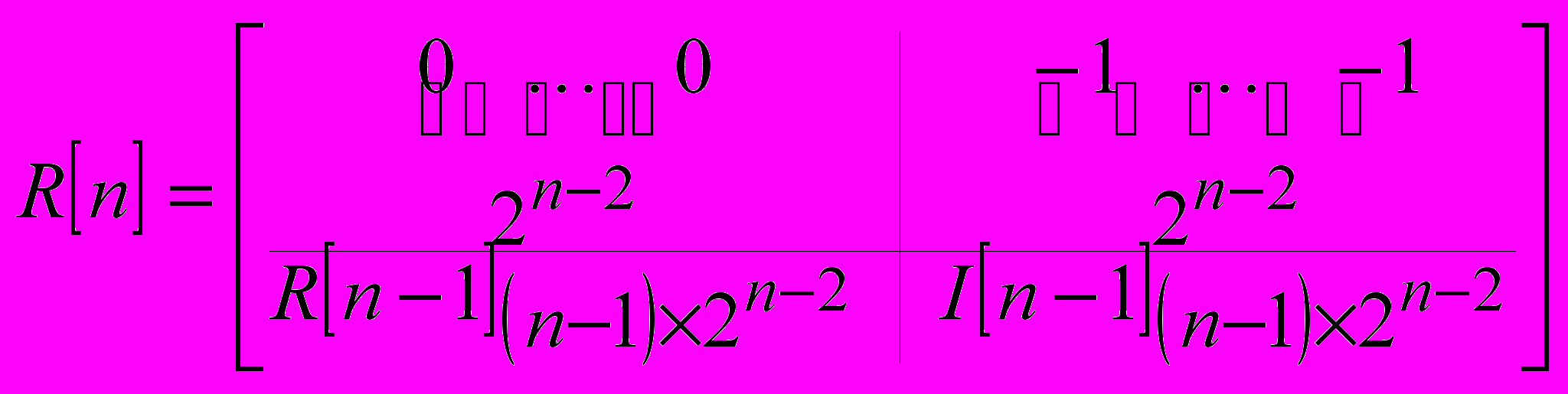 ,
, 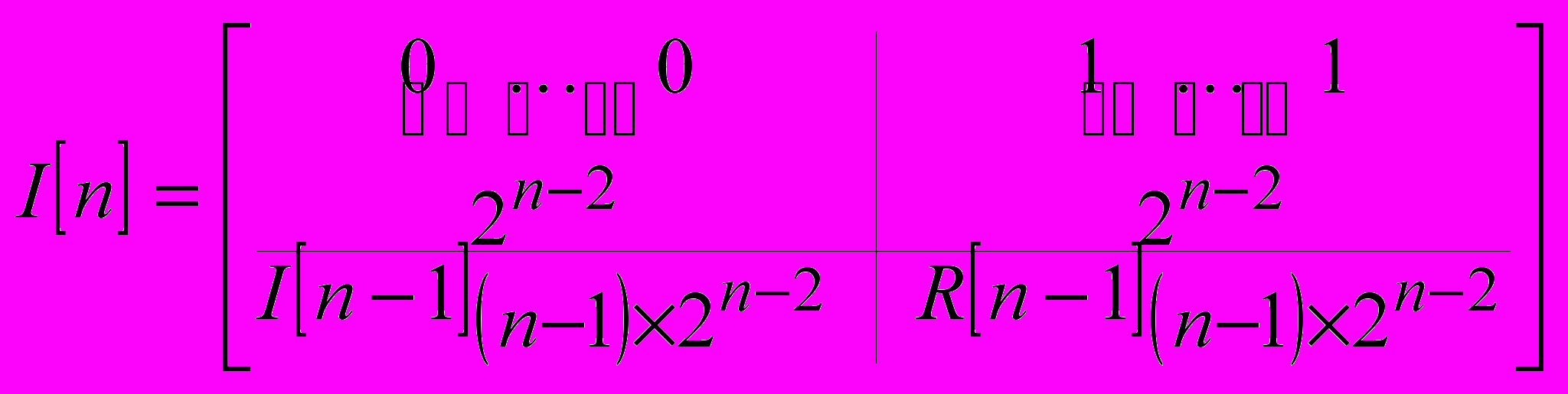 , (10)
, (10)где
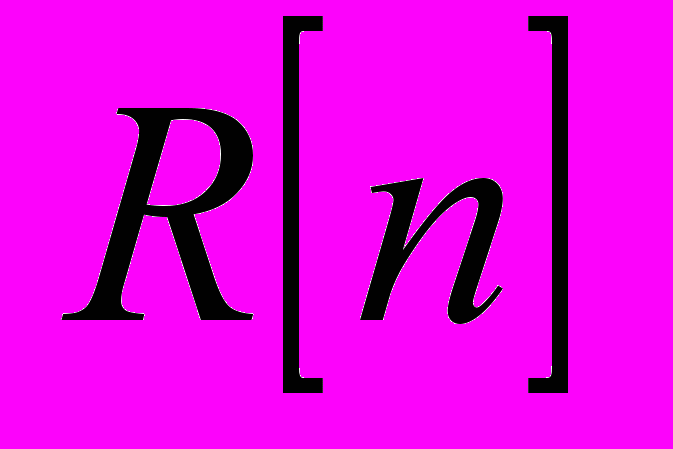 представляет из себя действительную часть числа, получившегося при перемножении
представляет из себя действительную часть числа, получившегося при перемножении  комплексных чисел в виде матрицы для генерации аналитической формулы, а
комплексных чисел в виде матрицы для генерации аналитической формулы, а  - мнимую.
- мнимую.При расчете таблиц индексов достаточно широко применяется расчет сочетаний, при этом известно, что при реализации такого расчета по формуле
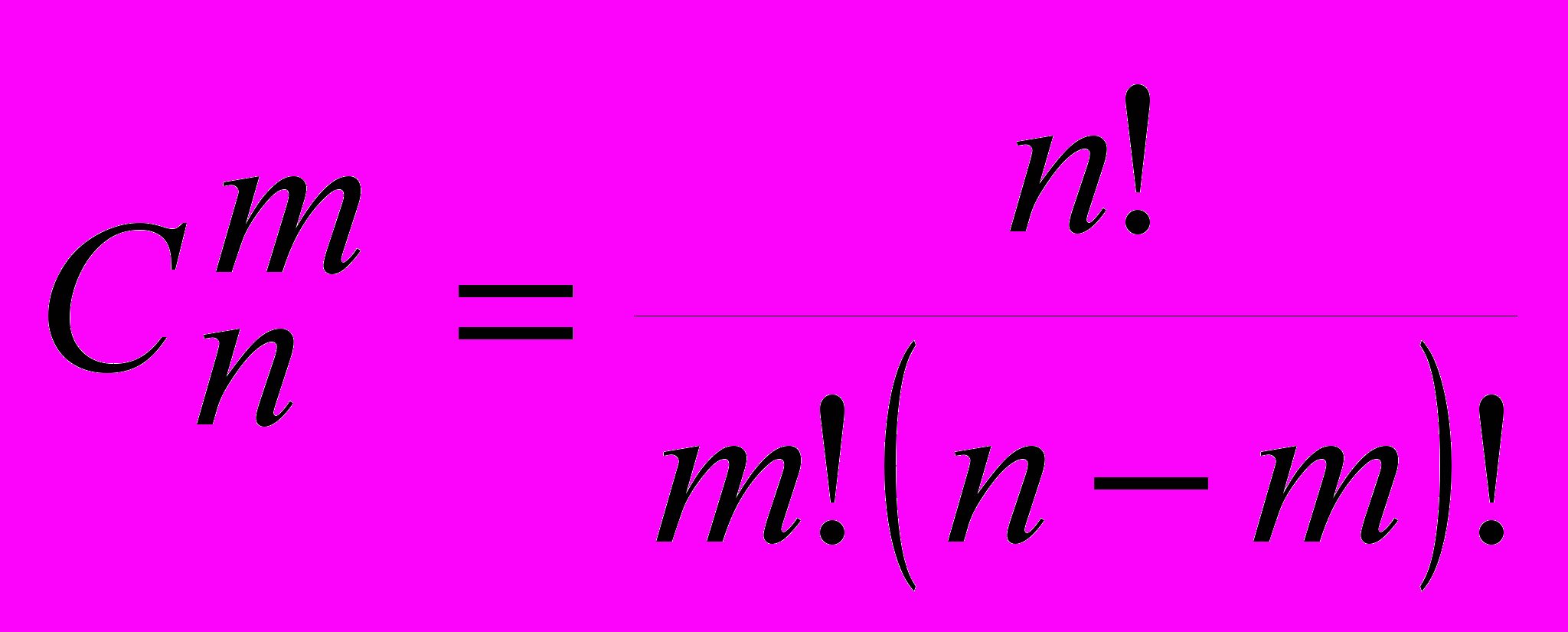 имеет место явление быстрого переполнения стека, поэтому в работе предлагается рассчитывать сочетания итеративно по формуле
имеет место явление быстрого переполнения стека, поэтому в работе предлагается рассчитывать сочетания итеративно по формуле  . Также, среди оптимизирующих вычислительный процесс процедур, следует выделить возможность расчета только половины якобиана для метода Левенберга-Марквардта. После расчета половины частных производных можно воспользоваться соотношениями
. Также, среди оптимизирующих вычислительный процесс процедур, следует выделить возможность расчета только половины якобиана для метода Левенберга-Марквардта. После расчета половины частных производных можно воспользоваться соотношениями 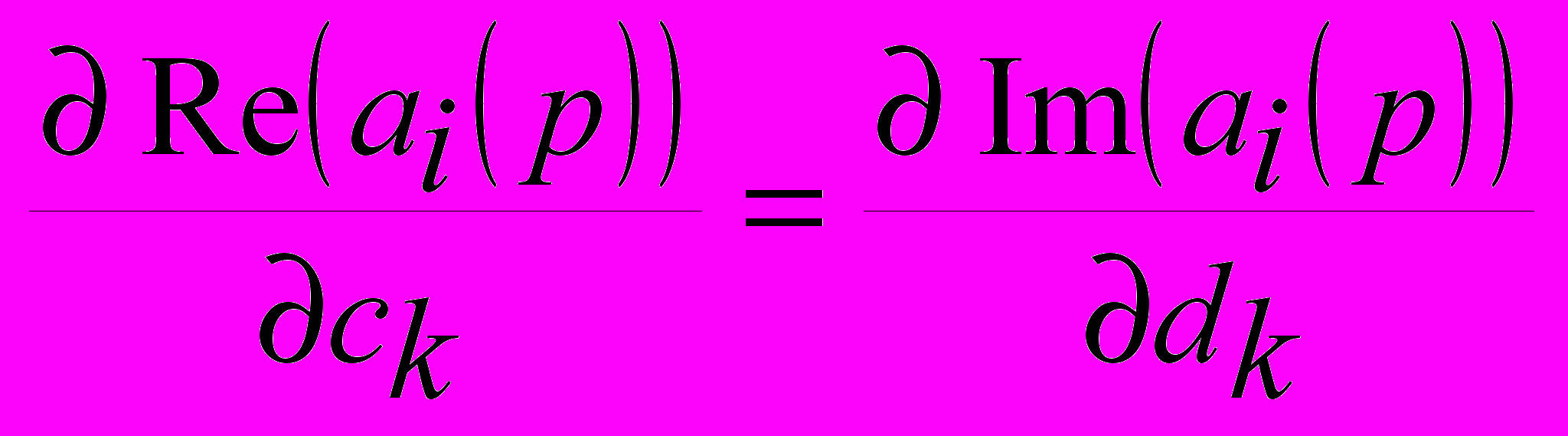 и
и 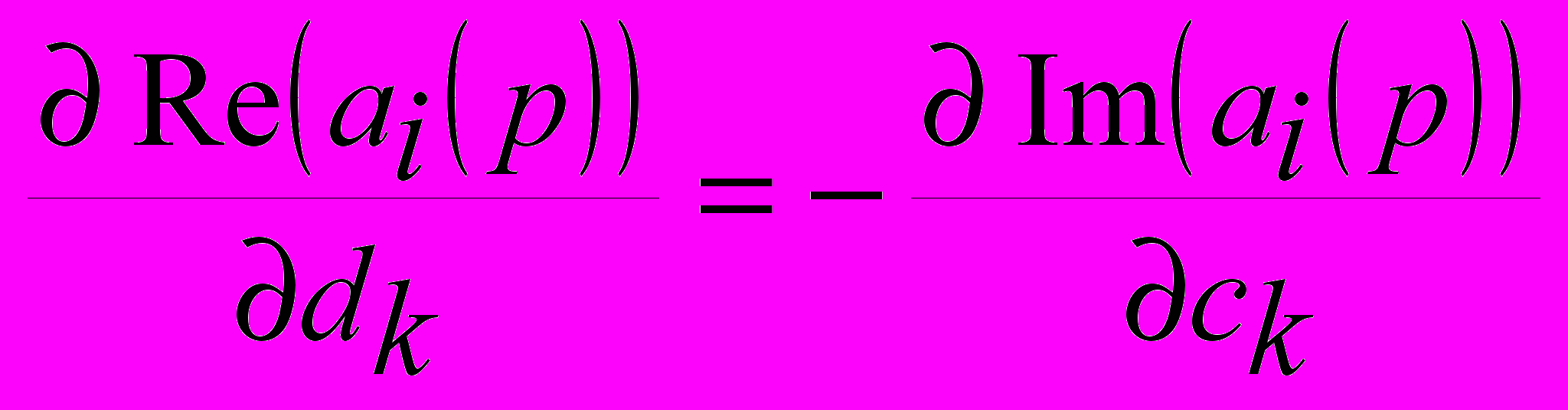 , которые вытекают из рассмотрения формул (9.1) и (9.2) и достаточно быстро заполнить вторую половину.
, которые вытекают из рассмотрения формул (9.1) и (9.2) и достаточно быстро заполнить вторую половину.В пятой главе рассматриваются применения предложенного метода. В частности, в работе рассматривается применение метода для разделения свободного движения линейной системы автоматического управления. На основе рассчитанных значений корней с помощью простого алгоритма сортировки можно разделить все корни характеристического полинома на группы таким образом, чтобы размер этих групп был существенно меньше расстояния между ними. Затем при получении констант для решения задачи Коши, образующейся из начального дифференциального уравнения, описывающего систему автоматического управления и начальных условий, можно изображать различные составляющие свободного движения системы (образовавшиеся из групп корней) раздельно и анализировать их поведение.
Предложено три способа сортировки корней:
- По действительной части (декременту затухания)
- По мнимой части (частоте колебаний)
- Комбинированный (сочетающий в себе первые два, при этом сперва применяется способ сортировки по декременту затухания, а затем в рамках получившихся групп – по частоте колебаний).
Группировка корней показана на рис. 2.
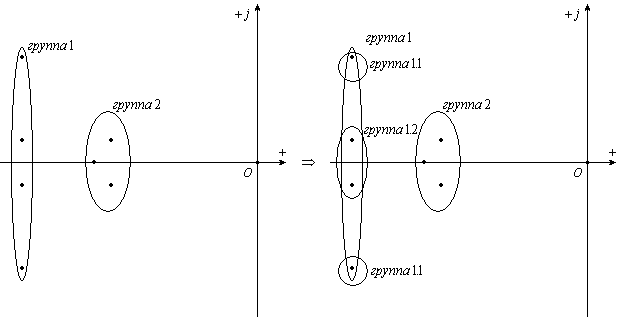
Рис. 2 Группировка корней: сперва по декременту затухания, а затем по частоте колебаний
Также метод применим (как это уже было сказано выше) для построения корневого годографа. В частности, в работе рассмотрен пример построения корневого годографа для системы автоматического управления лентопротяжным механизмом в устройстве памяти последовательного доступа. Указано, что при построении такого годографа метод собственных значений выполняет на каждом шаге около
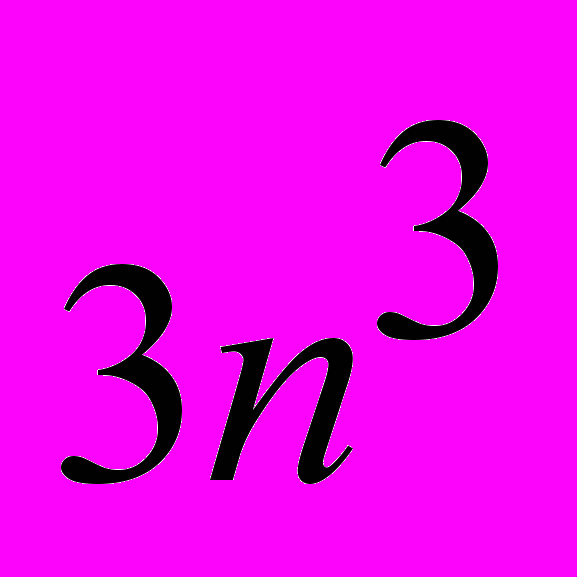 операций умножения (которые занимают большую часть времени вычислительного процесса), в то время как предлагаемый метод выполняет около
операций умножения (которые занимают большую часть времени вычислительного процесса), в то время как предлагаемый метод выполняет около 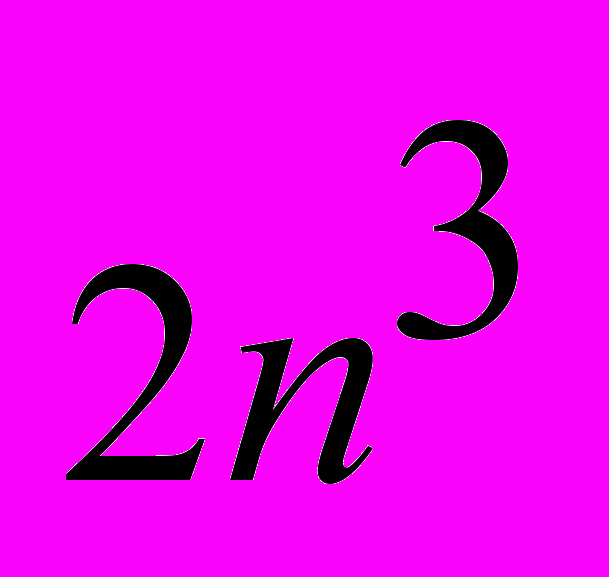 операций (из расчета 4-х итераций уточнения корней по методу Левенберга-Маквардта), что позволяет сократить время построения корневого годографа. Также подобная вычислительная процедура может применяться для целей адаптивного регулирования в линейной системе автоматического управления для вычисления корней системы “в темпе с объектом”. При этом следует выбирать временной интервал расчета таким, чтобы новые значения корней попадали в ранее упомянутую “почти плоскую окрестность” точки экстремума на предыдущем шаге. Это гарантирует быструю сходимость для процедуры уточнения корней.
операций (из расчета 4-х итераций уточнения корней по методу Левенберга-Маквардта), что позволяет сократить время построения корневого годографа. Также подобная вычислительная процедура может применяться для целей адаптивного регулирования в линейной системе автоматического управления для вычисления корней системы “в темпе с объектом”. При этом следует выбирать временной интервал расчета таким, чтобы новые значения корней попадали в ранее упомянутую “почти плоскую окрестность” точки экстремума на предыдущем шаге. Это гарантирует быструю сходимость для процедуры уточнения корней.Также был поставлен эксперимент, полагающий своей целью проверку работы предложенного метода в случае кратных корней. Для этого корни полинома
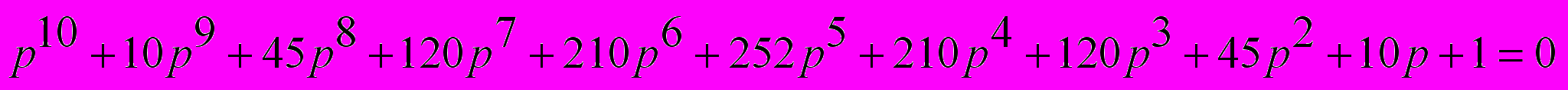
были рассчитаны по предложенной методике и по методу собственных значений (использовалась реализация математического пакета MathCad 2000).
Были получены следующие результаты:
- Предложенная методика выдала в качестве вектора корней десять значений, равных 1. (Напомним, что в методе используются значения корней с противоположным знаком, поэтому получен правильный результат, в чем можно убедиться, расписав треугольник Паскаля до 11-й строки).
- Метод собственных значений выдал следующий результат:
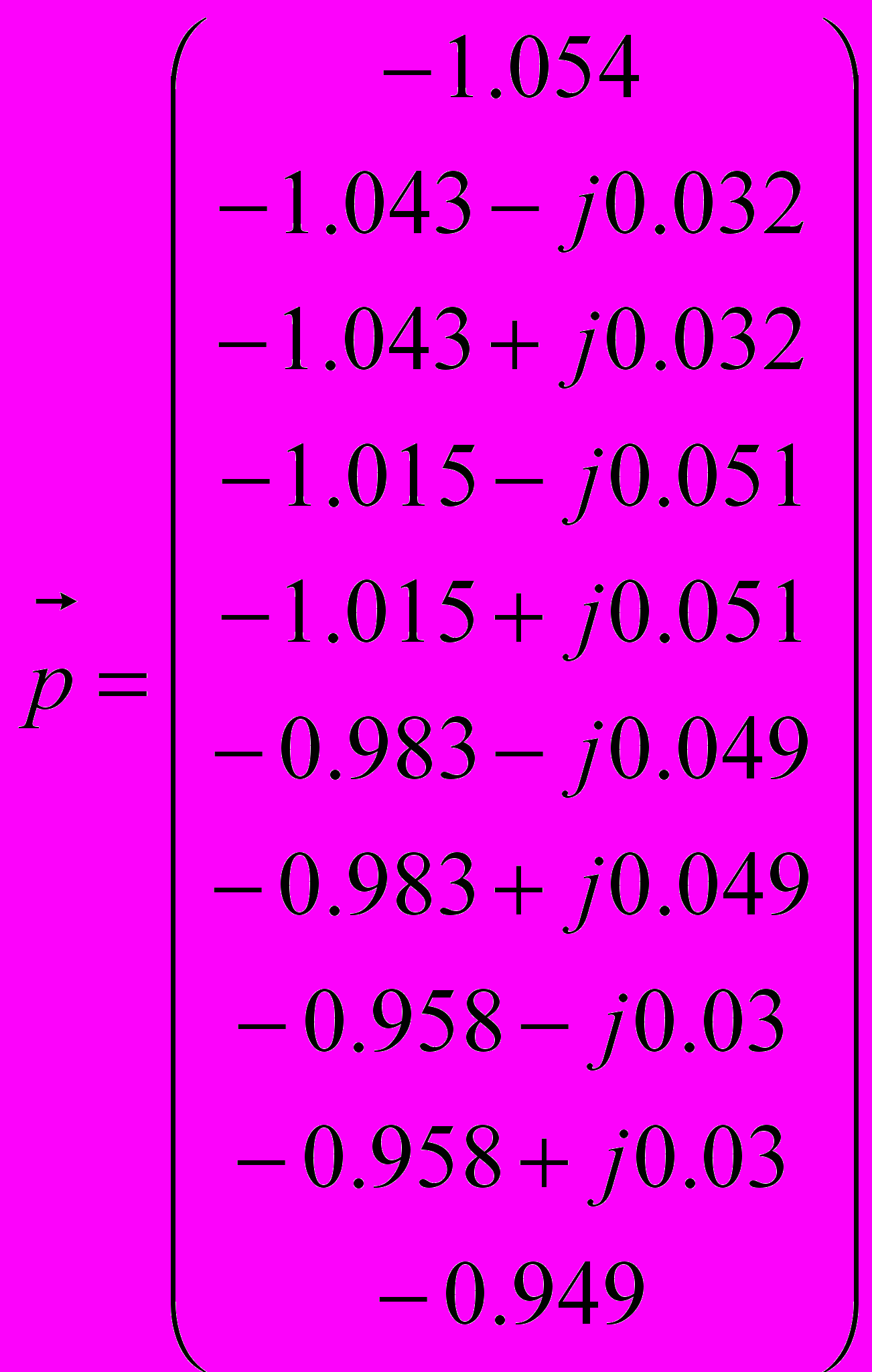
Результат этого эксперимента был вполне предсказуем, так как метод собственных значений известен своей плохой работой в условиях наличия кратных корней, хотя проблема вычисления корней полинома с корнями неединичной кратности относится не только к нему. С другой стороны, в силу своей независимости от обусловленности матриц, предложенный метод показал возможность работы с кратными корнями.
Одно из достоинств предложенного метода, а именно, возможность предварительного вычисления статической информации (матриц комплексных произведений, таблиц индексов для коэффициентов полинома, а также для частных производных), одновременно является и недостатком, ибо в случае предварительно вычисленных таблиц, последние занимают определенное место в оперативной памяти электронной вычислительной машины, в то время как расход памяти на метод собственных значений будет существенно меньшим.
В заключении приводятся основные результаты, полученные в ходе выполнения диссертационной работы.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
- Проанализированы существующие на данный момент методы решения полиномиальных уравнений, показано, что одни из самых популярных методов на сегодняшний день имеют некоторые недостатки, которые предполагалось компенсировать в предложенном в работе методе. Выявлены две группы методов решения поставленной задачи (методы решения систем нелинейных уравнений общего вида и специализированные методы), показаны различия между ними, а также найдена взаимосвязь между этими группами.
- Предложено математическое обоснование рассматриваемого в работе метода, качественно отличающееся от существующих подходов, сформулирована задача оптимизации, которую предстоит решать для нахождения всех корней полинома, выявлены особенности критерия оптимизации.
- Показана возможность аналитического вычисления оценки коэффициента полинома с помощью его корней, а также градиента сформулированного критерия оптимизации в произвольной точке.
- Проанализирована возможность применения существующих методов оптимизации для решения поставленной задачи. Выяснен овражный характер критерия оптимизации. Предложена модификация градиентного метода для оптимизации выбранного критерия. Показано, что скорость сходимости градиентного метода при продвижении к точке, содержащей значения всех корней, уменьшается. Предложено использование алгоритма Левенберга-Марквардта, как наиболее подходящего для поставленной задачи оптимизации, указаны особенности его применения.
- Разработаны алгоритмы для всех стадий работы метода, выяснено, что информация, используемая алгоритмом делится на статическую (которую возможно рассчитать до запуска численной процедуры) и динамическую (которая генерируется непосредственно в ходе вычислений). Предложены удобные способы хранения статической информации.
- Предложены процедуры, оптимизирующие вычислительный процесс, в частности, процедура быстрого расчета таблицы сочетаний и процедура минимизации вычислений при расчете частных производных.
- Предложены алгоритмы разделения свободного движения линейных систем автоматического управления: по декременту затухания, по частоте колебаний и комбинированный.
- Предложена процедура нахождения корней полинома – на первом шаге достаточно грубо вычисляются оценки корней полинома, на втором – оценки уточняются с помощью предложенной методики по методу Левенберга-Марквардта.
- Рассматривается вопрос применения предложенной методики для целей адаптивного регулирования линейных систем автоматического управления с изменяющимися в течение времени коэффициентами, а также для оптимизации реализации метода корневого годографа, имеющего некоторые преимущества применения для анализа двусвязных систем.
- Рассматривается возможность применения метода для нахождения собственных чисел действительных и комплексных матриц.
Все предложенные пути решения поставленной задачи проиллюстрированы численными примерами, которые составляют численный эксперимент, являющийся основным методом проверки результатов в работе.
СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ
- Кокорев С.А. Численный метод определения корней характеристического уравнения для жестких систем автоматического управления//XI Междунар. науч.-техн. конф. студентов и аспирантов “Радиоэлектроника, электротехника и энергетика”: Тез. докл. - М.: МЭИ, 2005 - Т.1. - С. 401-402.
- Кокорев С.А. Численный метод определения всех корней полиномиального уравнения произвольного порядка//Известия ТулГУ. Сер. Вычислительная техника. Информационные технологии. Системы управления. – Тула: ТулГУ, 2005 – Вып. 4 – С. 27-33.
- Кокорев С.А. Численный метод поиска корней характеристических уравнений жестких систем//XIV Международный научно-технический семинар “Современные технологии в задачах управления, автоматики и обработки информации”: Тез. докл. – Алушта – Самара: Самарский государственный аэрокосмический университет, 2005г. – С. 108.
