Geum.ru

Программа дисциплины по кафедре "Экономическая кибернетика" Методы исследования и моделирования

Вид материалаПрограмма дисциплины

Содержание


Цели и задача дисциплины
2. Требования к уровню освоения содержания дисциплины
3. Объем дисциплины и виды учебной работы
4. Содержание дисциплины
5. Практические занятия
Время выполнения заданий
Оценка. Формирует типологию межотраслевых отношений в регионе. Время выполнения задания
6. Контроль самостоятельной работы студентов-заочников
7. Контроль знаний студента
8. Учебно-методическое обеспечение дисциплины
9 Материально-техническое обеспечение дисциплины
10 Методические рекомендации по организации изучения дисциплины
11 Словарь терминов
Алгоритм максимального пото­ка
Базисное решение
Двойственные оценки
Детерминированные величи­ны
Дополнительные переменные
Достоверное событие
Задача оптимизации
...
Полное содержание
Подобный материал:
  1   2   3


ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Тихоокеанский государственный университет



Утверждаю

Проректор по учебной работе

______________ С.В. Шалобанов

“_____” ________________200_ г.



Программа дисциплины

по кафедре "Экономическая кибернетика"


Методы исследования и моделирования

национальной экономики


Утверждена научно-методическим советом университета для направлений подготовки (специальностей) в области экономики и управления


Специальность: 080103.65 «Национальная экономика»


Хабаровск 2007 г.


Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных программ и стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного технического университета.


Программу составил (и)
Порошина Л.А.



Старший преподаватель, кафедра «Экономическая кибернетика»




























Ф.И.О. автора (ов)
Ученая степень, звание, кафедра







Программа рассмотрена и утверждена на заседании кафедры

протокол № ______ от «____»__________________ 200_г

Завкафедрой__________«__»______ 200_г
________________

Подпись дата
Ф.И.О.







Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию

протокол № ______ от «____»_____________ 200_г

Председатель  УМК  _______«__»_______ 200_г
_________________

Подпись дата
Ф.И.О.




Директор  института  _______«__»_______ 200_г
Зубарев А.Е. _

(декан факультета) Подпись дата
Ф.И.О.

Директор  института  _______«__»_______ 200_г
____Лысак С.Г. _

(декан факультета) Подпись дата
Ф.И.О.

Директор  института  _______«__»_______ 200_г
_______Вайнер Л.Г.

(декан факультета) Подпись дата
Ф.И.О.






  1. ЦЕЛИ И ЗАДАЧА ДИСЦИПЛИНЫ

ГОСом предусмотрено, что студент специальности НЭ должен:
  • иметь системное представление о структурах и тенденциях развития российской и мировой экономик;
  • понимать многообразие экономических процессов в современном мире, их связь с другими процессами, происходящими в обществе;

Целью преподавания дисциплины является формирование знаний, умений и практических навыков моделирования управленческих решений.

Предметом изучения названной дисциплины являются количественные характеристики экономических процессов на основе экономико-математических методов и моделей. В курсе рассматриваются конкретные задачи и их экономико-математические модели. Это модели балансовые, имитационные, эконометрические.

Немалое место отводится моделям оптимального отрасле­вого и регионального регулирования – экономико-математическим моделям проекта развития отдельных отраслей народного хозяйства.

Освещаются модели народнохозяйственного регулирования (в частности, межотраслевого баланса, базовые, статистические и динамические модели, модели ценообразования на основе межотраслевого баланса, моделирование спроса и предложения). Представляется модель взаимосвя­зи конечного использования и валового продукта. Излагаются вопросы сингулярных моделей макроэкономического прогнозирования.

Основным понятием курса является понятие математи­ческой модели. В общем случае слово модель – это отражение реального объекта. Такое отражение объекта может быть пред­ставлено схемой, эскизом, фотографией, моделью описательно­го характера в виде графиков и таблиц и т. д. Математическая модель – это система математических уравнений, нера­венств, формул и различных математических выражении, опи­сывающих реальный объект, составляющие его характеристи­ки и взаимосвязи между ними. Процесс построения математи­ческой модели называют математическим моделированием. Естественно, моделирование и построение математической моде­ли экономического объекта позволяют свести экономический анализ производственных процессов к математическому ана­лизу и принятию эффективных решений.

2. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ

Студент должен знать:
  • методы моделирования экономических процессов на макро-, микро- и глобальном уровнях;
  • современные методы социально-экономического анализа, идентификации и распознавания образов, информационные технологии и вычислительные средства для обоснования принятия оптимальных решений в области управления и бизнеса.

Студент должен уметь и иметь опыт:
  • применения экономико-математических методов на предприятиях и в организациях различных отраслей экономики, включая Интернет-экономику;
  • построения балансовых моделей экономики;
  • разработки вариантов управленческих решений и обоснования их выбора по критериям социально-экономической эффективности.


3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ

Таблица 1. Объем дисциплины и виды учебной работы

Наименование

По учебным планам (УП)

с максимальной трудоёмкостью
с максимальной трудоёмкостью

Общая трудоёмкость дисциплины

по ГОС

по УП






Изучается в семестрах
8



Вид итогового контроля по семестрам

зачёт

экзамен

курсовой проект (КП)

курсовая работа (КР)

расчётно-графическая работа (РГР)

реферат (РФ)

домашние задания (ДЗ)


8



Аудиторные занятия по семестрам

Всего

лекции (Л)

лабораторные занятия (ЛР)

практические занятия (ПЗ)






68



34


34

Самостоятельная работа

Общий объем часов (С2)

В т.ч. на подготовку к лекциям

на подготовку к лабораторным занятиям

на подготовку к практическим занятиям

на выполнение КР

на выполнение РГР

на написание РФ

на выполнение ДЗ
8



68



34

-

34


4. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

4.1. Разделы дисциплины и виды занятий и работ


Таблица 2. Разделы дисциплины и виды занятий и работ

№
Раздел дисциплины
л
п/з
л/з
С2

1
Введение
*






*

2
Моделирование микроэкономических процессов и систем
*
*



*

3
Моделирование макроэкономических процессов и систем
*
*



*



    1. Содержание разделов дисциплин

4.2.1. Введение

Общая характеристика состояния и развития математического моделирования и оптимизации. Методология развития самостоятельных математических дисциплин, их место и роль в овладении студентами знаниями, умениями и навыками, необходимыми им в профессиональной деятельности, место дисциплины в межпредметных логических связях. Определение предмета, целей и задач читаемого определённому потоку курса «Экономико-математического моделирования». Классификация ЭММ. Этапы экономико-математического моделирования.

4.2.2. Моделирование микроэкономических процессов и систем.

Методы анализа и прогнозирования рыночной конъюнктуры, определения потребительских свойств продукции и ее качества. Методы оптимизации маркетинговых затрат (реклама, товародвижение и сбыт). Моделирование ценовой политики. Производственные системы, их структура. Технологии производства и их представление в экономико-математических моделях. Оптимизация производственных процессов. Модели управления производственными запасами с учётом спроса и цен на продукцию. Моделирование инвестиций и анализ их эффективности. Решение задач развития и размещения производства. Транспортно-производственные модели. Моделирование и оптимизация работы предприятий. Критерии оптимизации на основные ограничения, локальные и глобальные критерии.

4.2.3. Моделирование макроэкономических процессов и систем.

Моделирование развития национальной экономики и глобальных про­цессов. Модели совокупного спроса и предложения. Моделирование национальных сбережений и инвестиционного спроса. Модели рынка товаров и услуг. Модели рыночного равновесия и мультипликатора, их использование в стратегическом планировании. Макромодели рын­ка труда. Классический и кейнсианский подходы к моделирова­нию. Методы и модели оценки занятости и безработицы. Моделирова­ние финансового рынка. Модели макроспроса и макропредложения де­нег. Модели денежного мультипликатора. Модели инфляционных про­цессов и индексация заработной платы. Макроэкономическое модели­рование сценариев финансовой и монетарной политики. Моделирова­ние бюджетной экспансии, объемов производства и потребления. Мо­делирование сценариев антикризисной и стабилизационной политики. Межотраслевые модели экономики (балансовые модели, модели В.Леонтьева и т.д.). Модели размещения производственных сил. Мак­ромодели экономического роста и их основные характеристики. Моде­лирование международных взаимодействий (экспорт, импорт, внешне­торговый мультипликатор). Макромодели платежного баланса и внеш­него долга.


5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

Таблица 3. Практические занятия

№
№ раздела дисциплины
Тема практического занятия

1
1
Оптимизация производственных процессов

2
2
Межотраслевые модели экономики

3
3
Производственные функции


Краткие характеристики практических занятий.

Моделирование микроэкономических процессов и систем.

Задание. Разработка математической модели производственного процесса.

Исполнение. Решение производственной задачи с применением обоснованного математического инструментария. Интерпретация результатов решения. Обоснование устойчивости решения.

Оценка. Формируют необходимые представления о применимости того или иного математического инструментария к заданному классу производственных задач.

Время выполнения заданий: 11 часов.


Моделирование макроэкономических процессов и систем.

Задание. Разработка постановки задачи размещения производственных сил в регионе, обоснование исходных данных для постановки задачи.

Исполнение. Обоснование и выбор аппарата моделирования, инструментария решения задачи. Решение на ЭВМ. Интерпретация решения: объемов производства продукции и транспортировки потребителям.

Оценка. Формирует типологию межотраслевых отношений в регионе.

Время выполнения задания: 11 часов.


Производственные функции.

Задание. Проведение анализа производственных функции и функций затрат.

Исполнение: решение задачи. Использование математического инструментария подготовки исходных данных и метода решения. Интерпретация результатов решения.

Оценка. Формирует необходимые представления об используемом математическом аппарате.

Время выполнения заданий: 12 часов.


6. КОНТРОЛЬ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ-ЗАОЧНИКОВ

Для студентов-заочников предусмотрено выполнение контрольной работы по дисциплине. Целью контрольной работы является формирование и контроль знаний по основным разделам дисциплины. Студенту рекомендуется, руководствуясь предлагаемой программой и используя литературу, самостоятельно изучить ряд вопросов и примеров. Затем следует выполнить задание. Контрольная работа разработана и имеется в электронном виде на кафедре.

Контрольная работа предусматривает выполнение следующих заданий по вариантам:

Известны данные об изменении объёма спроса на товар (Qp) и его предложения (Qs) в зависимости от изменения цены (Р) товара.

На основании приведенных данных:
  1. Построить кривые спроса и предложения.
  2. Определить функции спроса и предложения, построить их графики.
  3. Определить равновесную цену и равновесный объем продаж.
  4. Определить ситуацию, которая установится на рынке, если цена товара составит 4 у.д.е. и 8 у.д.е.
  5. Определить, возможно ли достижение точки равновесия. Построить паутинообразную модель, в качестве исходной цены взять значение 6 у.д.е.
  6. Определить эластичность спроса и предложения относительно цены (в общем виде и по отдельным точкам значений цен).
  7. Пусть на рынке имеется второй товар. Его цена в определенный момент времени снизилась с 12 до 10 у.д.е. Отмечено, что объем спроса на первый товар при этом изменился следующим образом (по варианту):

1. Увеличился с 60 до 70 тыс.шт.

2. Снизился с 85 до 73 тыс.шт.

3. Снизился с 72 до 60 тыс.шт.

4. Увеличился с 48 до 58 тыс.шт.

5. Увеличился с 15 до 25 тыс.шт.

6. Снизился с 40 до 25 тыс.шт.

7. Снизился с 60 до 45 тыс.шт.

8. Увеличился с 80 до 95 тыс.шт.

9. Увеличился с 30 до 45 тыс.шт.

10. Снизился с 80 до 60 тыс.шт.

Определить перекрестную эластичность спроса.

Цена,

Р
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5

В месяц
В месяц
В месяц
В месяц
В месяц

спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs

10
14
99
10
98
10
90
10
100
2
40

9
25
88
25
87
22
81
27
89
7
35

8
35
80
41
79
35
68
40
78
11
29

7
46
69
55
66
47
56
52
65
16
26

6
58
61
62
57
60
44
65
58
21
22

5
70
50
77
45
70
33
75
44
28
18

4
83
37
92
35
83
23
89
28
35
13

3
92
28
105
26
95
12
100
13
40
10

2
103
19
111
19
106
7
113
6
47
6




Цена,

Р
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10

В месяц
В месяц
В месяц
В месяц
В месяц

спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs
спрос, Qd
предло-жение, Qs

10
8
88
20
48
16
81
20
50
56
95

9
22
80
27
44
27
73
24
46
62
90

8
35
70
33
41
35
66
27
43
70
84

7
46
51
40
38
50
62
31
40
74
80

6
57
38
46
35
62
55
34
38
81
78

5
67
23
50
32
74
50
40
35
86
75

4
79
13
55
28
85
41
43
33
88
70

3
93
8
59
23
100
36
46
30
96
66

2
105
5
62
20
112
30
50
26
102
60



По завершению изучения курса студенты-заочники сдают экзамен. Примерный тест на экзамен представлен ниже.
  • Какое из утверждений верно:

а) экономико-математическая модель – это образ реального объекта в материальной или идеальной форме, отражающей существенные свойства моделируемого объекта и замещающий его в ходе исследования;

б) экономико-математическая модель – это математическое описание экономического процесса, произведенное в целях его исследования;

в) экономико-математическая модель – это математическое описание экономического процесса, необходимое для доказательства гипотез экономической теории.
  • Динамическая модель обязательно включает:

а) переменные только одного временного периода;

б) переменные нескольких временных периодов.
  • В основе классификации экономико-математических моделей по содержательной проблеме лежит:

а) объект моделирования;

б) цель моделирования;

в) специальный программный комплекс.
  • Методологическое и методическое обоснование модели предполагает:

а) формализацию экономической проблемы;

б) изучение особенностей объекта моделирования и их отражение с помощью структуры разрабатываемой модели;

в) экспериментальные расчеты.
  • Производственная функция записывается в виде Y=f (x1,x2), где

а) x1 –стоимость основных производственных фондов,x2 – объём выпускаемой продукции, Y- численность промышленно-производственного персонала;

б) x1 – стоимость товарной продукции,x2 – численность промышленно-производственного персонала, Y- стоимость основных производственных фондов;

в) x1 –стоимость основных производственных фондов,x2 – численность промышленно-производственного персонала, Y- стоимость товарной продукции.
  • К характеристикам нулевого порядка производственной функции относятся:

а) средняя производительность труда;

б) предельная производительность ресурса;

в) средняя фондоотдача;

г) средняя норма замещения ресурсов;
  • К характеристикам первого порядка производственной функции относятся:

а) средняя фондоотдача;

б) предельная производительность ресурса;

в) предельная фондоотдача;

г) предельная норма замещения ресурса;
  • К характеристикам второго порядка производственной функции относятся:

а) предельная производительность ресурса;

б) предельная производительность ресурса;

в) эластичность замещения ресурсов;

г) средняя норма замещения ресурсов;
  • Оценка эластичности потребления ресурса по объему выпускаемой продукции, находиться по формуле:

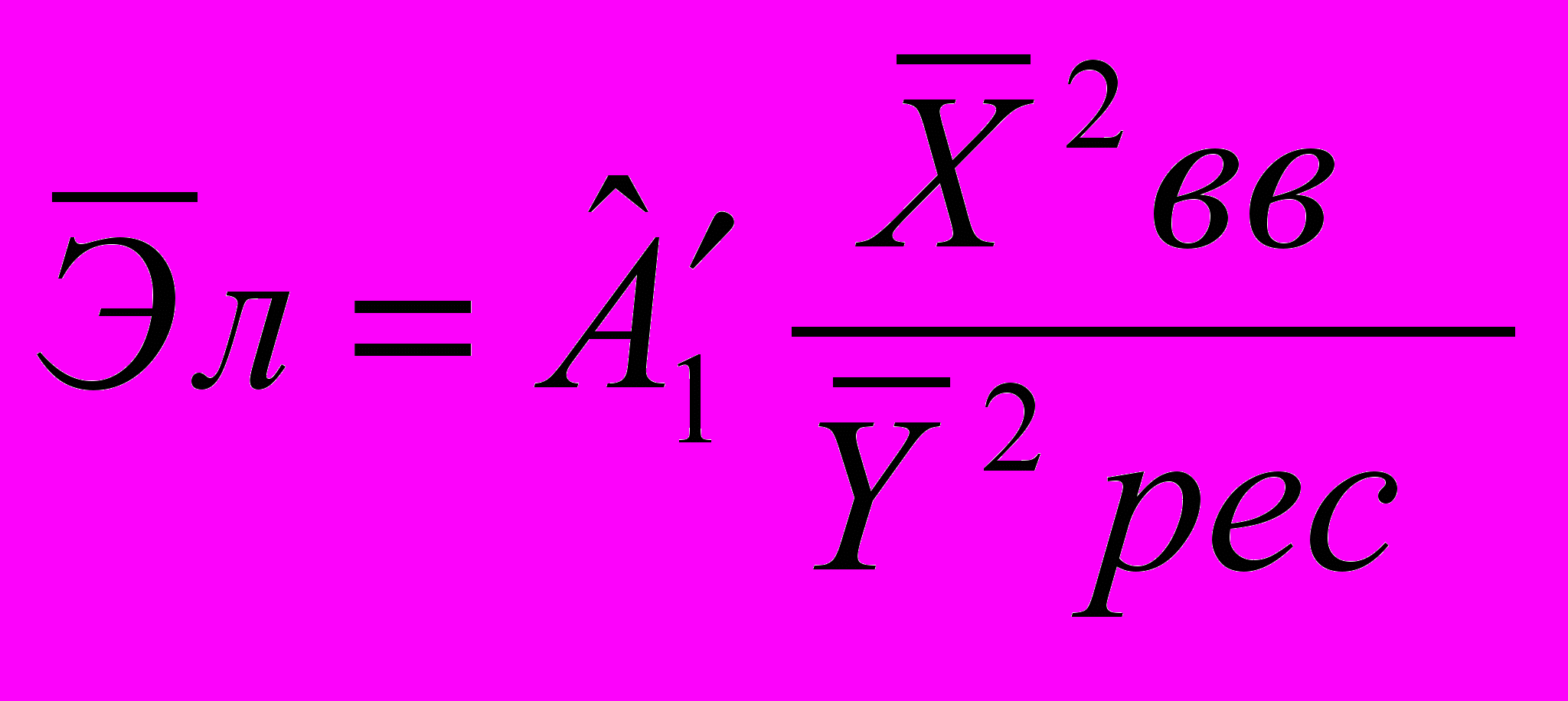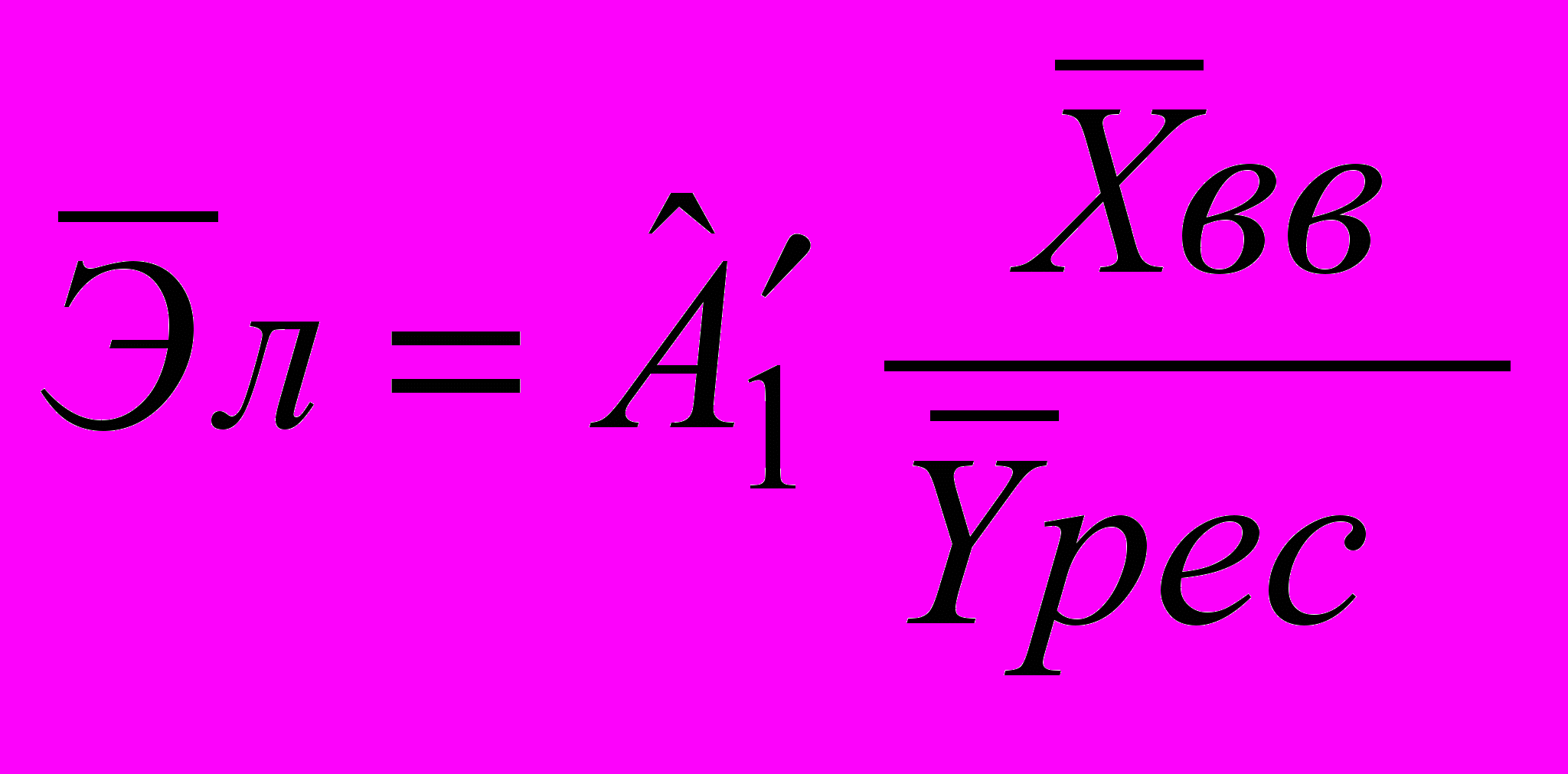а) ; б) ; в)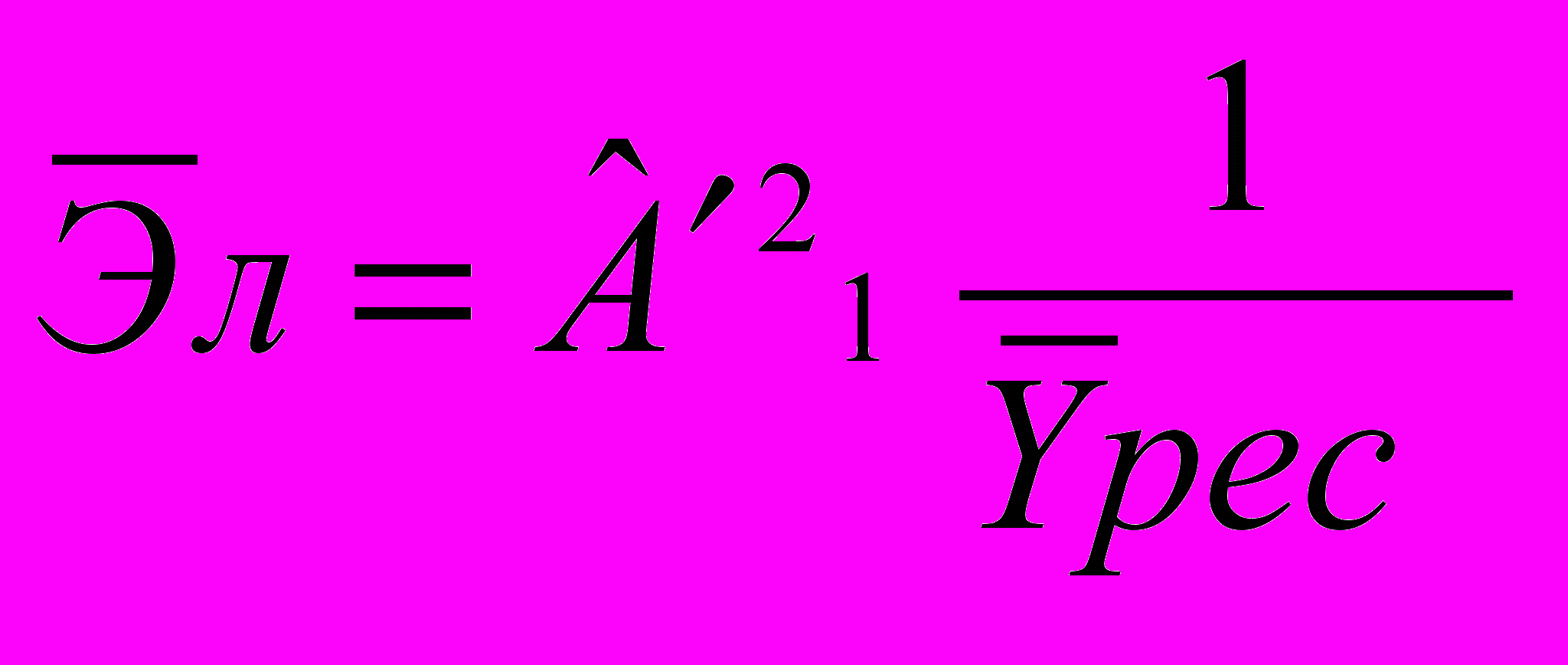
  • Производственная функция типа Кобба-Дугласа записывается в виде:

а) у=А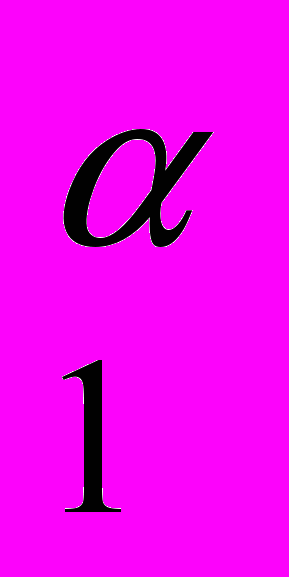х+Вх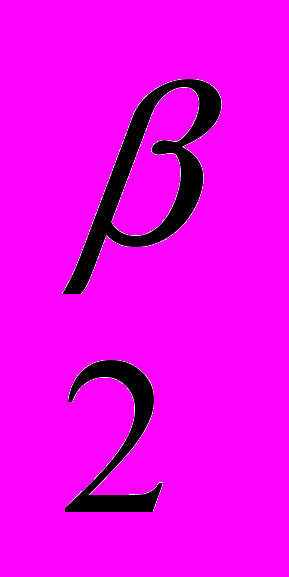; б) у=А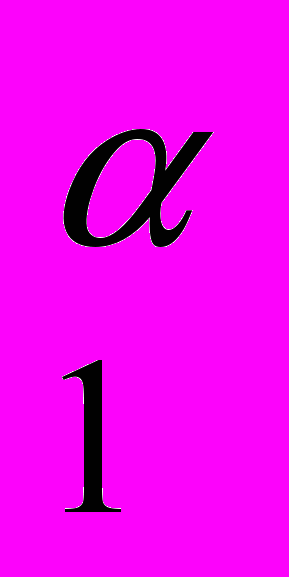хх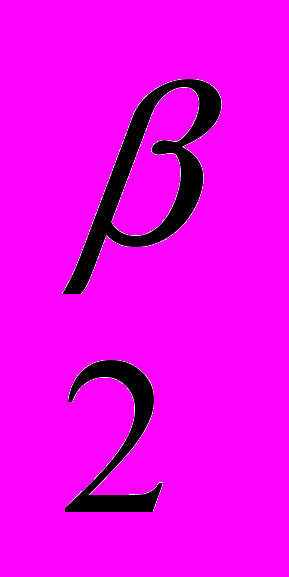; в) у=А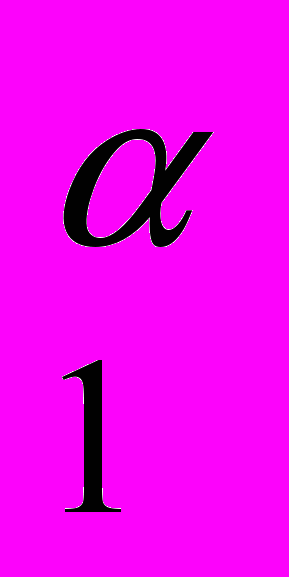х/Вх.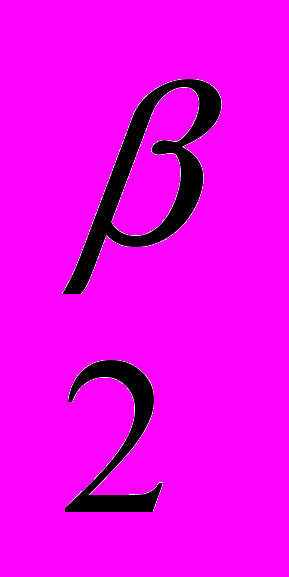
  • Расчет полиномиальных моделей основывается на использовании:

а) ортогональных на дискретном множестве полиномов Чебышева;

б) степенных полиномов Чебышева;
  • Полиномиальные модели записываются в виде:

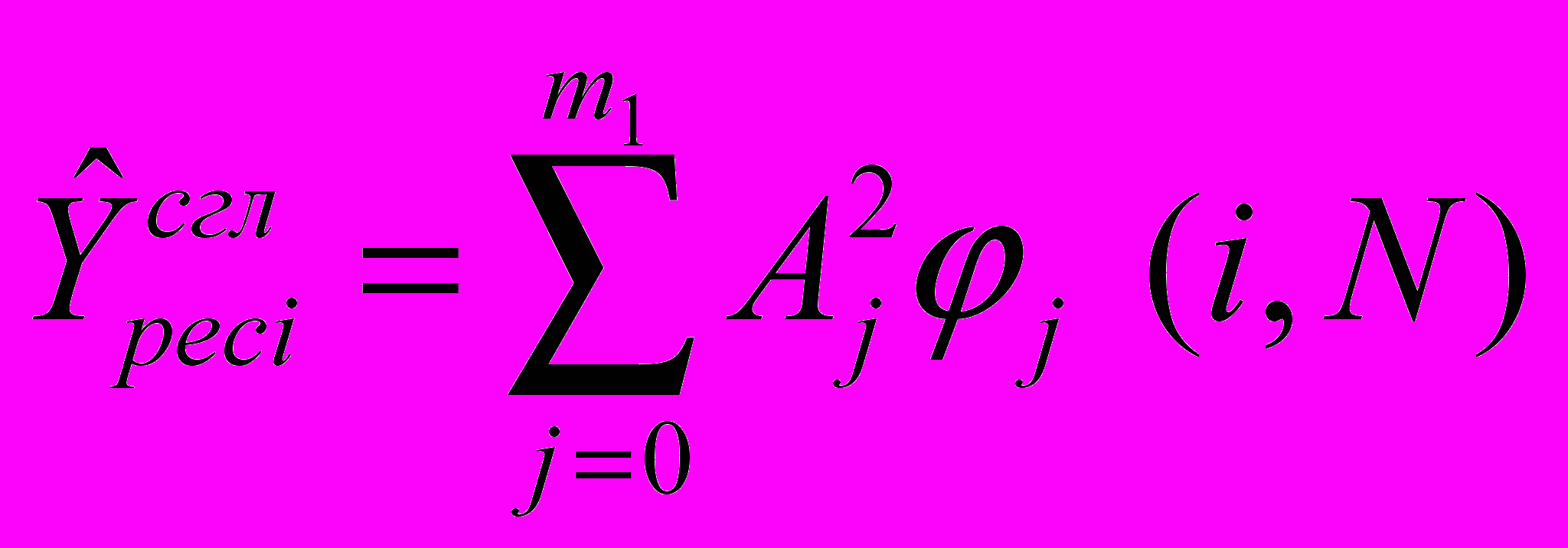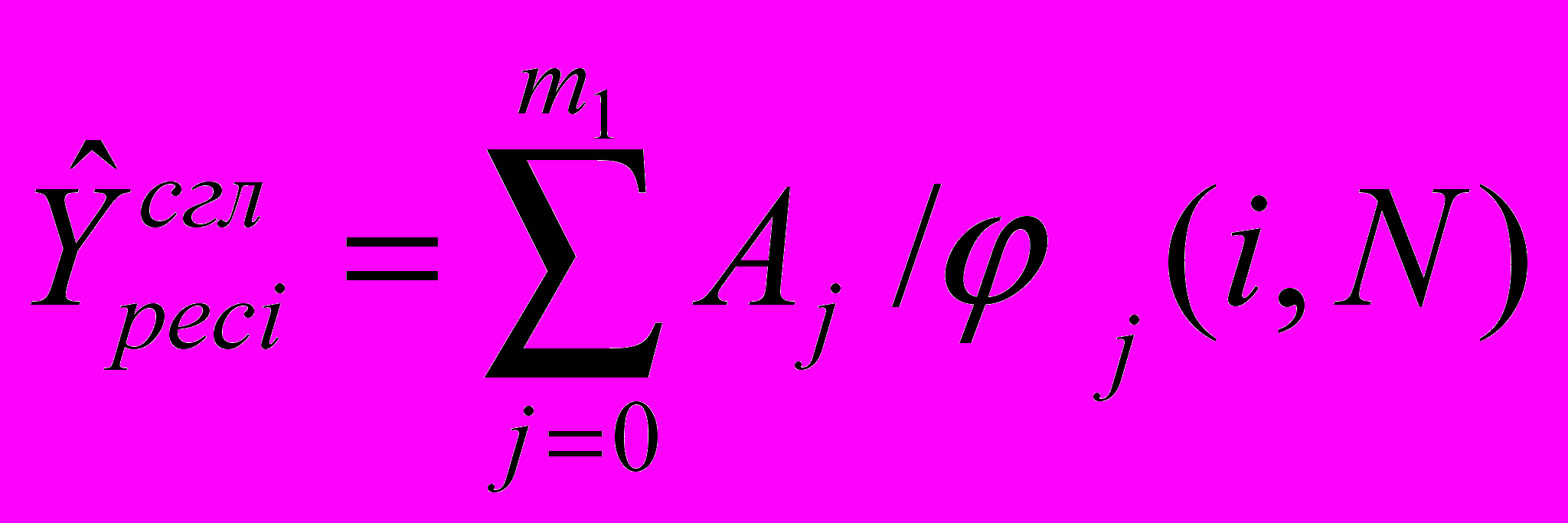а) ; б) ; в) .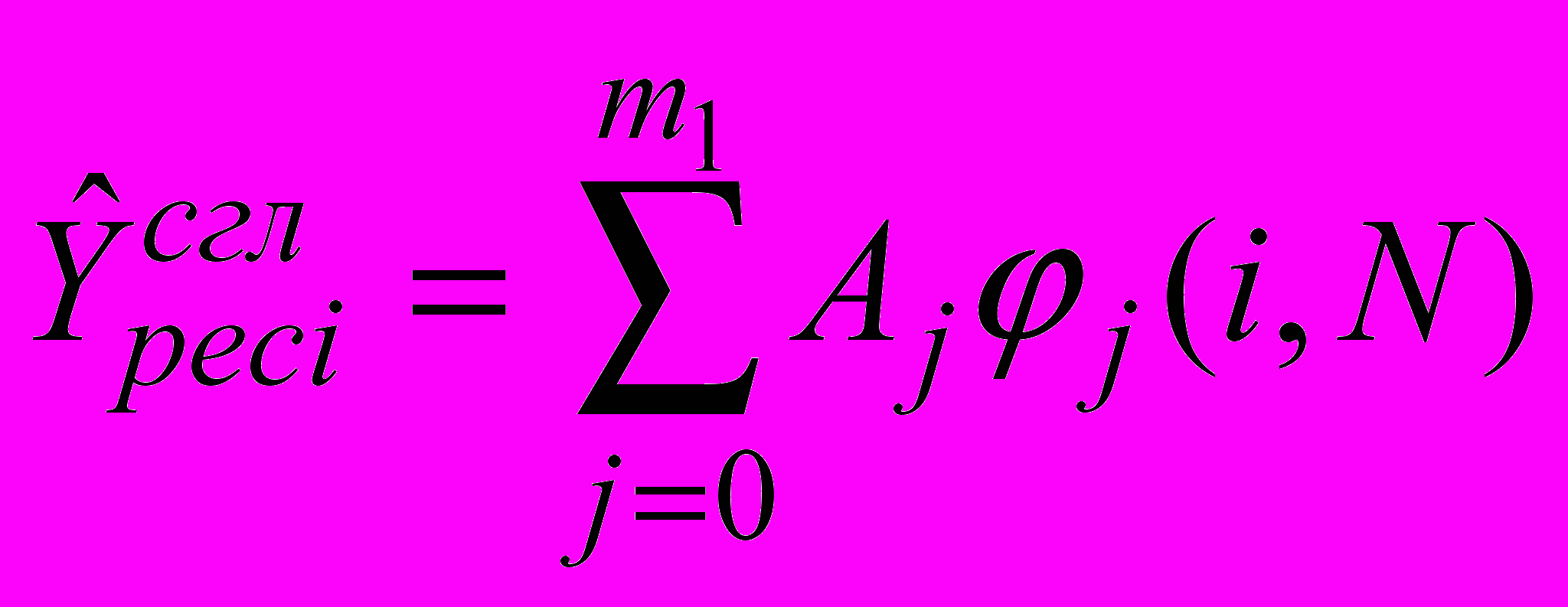
  • Предметом теории массового обслуживания является:

а) разработка математического и программного обеспечения;

б) построение математических моделей, связывающих заданные условия работы системы с показателями эффективности функционирования с целью нахождения наилучших вариантов управления этими системами;

в) построение оптимизационных моделей.
  • Каждая система массового обслуживания (СМО) состоит из одного или нескольких обслуживающих устройств, которые называются:

а) очередью;

б) входящим потоком заявок;

в) каналами обслуживания;

г) выходящим потоком обслуженных заявок.
  • Поток событий называется стационарным, если

а) его вероятностные характеристики зависят от времени;

б) его вероятностные характеристики не зависят от времени.
  • В основе математического обеспечения статической модели МОБ лежит:

а) математическая статистика;

б) линейная алгебра;

в) теория графов.
  • Коэффициент прямых затрат аij характеризует:

а) количество валовой продукции i -й отрасли, которое необходимо для производства единицы конечной продукции j- й отрасли;

б) количество валовой продукции i -й отрасли, которое необходимо для производства единицы валовой продукции j- й отрасли;

в) количество конечной продукции i -й отрасли, которое необходимо для производства единицы валовой продукции j- й отрасли.
  • Матрица прямых затрат А характеризует в экономике:

а) динамику финансовых процессов;

б) динамику технологических процессов;

в) воспроизводственные процессы.
  • Коэффициент полных затрат bij показывает:

а) объём валовой продукции i -й отрасли, необходимый для производства единицы конечной продукции j- й отрасли;

б) количество конечной продукции i -й отрасли, которое необходимо для производства единицы валовой продукции j- й отрасли.

в) объём валовой продукции i -й отрасли, необходимый для производства единицы валовой продукции j- й отрасли;