Geum.ru

Компьютерное моделирование химико-технологических процессов на основе дифференциальных уравнений в частных производных

Вид материалаКурсовая

Содержание


Решение уравнений первого порядка
Подобный материал:

Компьютерное моделирование химико-технологических процессов на основе дифференциальных уравнений в частных производных


Курсовая работа по дисциплине «Общая химическая технология»


ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ:

ДУЧП – дифференциальные уравнения в частных производных;

ХТП – химико-технологический процесс;

Содержание









Обозначения и сокращения
2




Введение
4

1
Компьютерное моделирование
5

1.1.
Понятие компьютерного моделирования
5

1.2.
Описание ХТП с применением ДУЧП
6

2.
Дифференциальные уравнения в частных производных
9

2.1.
Дифференциальные уравнения в частных производных:

классификация, граничные условия


9

2.2.
Разностный метод решения ДУЧП
13

2.2.1.

Решение уравнений первого порядка
17

2.2.2.

Решение эллиптического уравнения
19

2.2.3.
Решение гиперболического уравнения
23

2.2.4.
Решение параболического уравнения
26

3.
Применение ДУЧП для описания процессов проницаемости газов через полимерные мембраны
28

3.1.
Понятие о мембранных процессах
28

3.2.
Моделирование процесса проникновения газа через мембрану при экспоненциально падающей концентрации газа
30




Заключение
33




Список использованной литературы
34




Приложение
35



Введение

Одной из характерных черт третьего тысячелетия являются интеграционные процессы в мировой экономике и, одновременно, устойчивые тенденции роста цен на энергетические, материальные и другие природные ресурсы, необходимые для различных производственных процессов. Для химической и других отраслей промышленности задача снижения затрат на получение требуемых продуктов является первостепенной. Важнейшим условием успеха при этом является выбор, эксплуатация и, при необходимости, создание высокоэффективных энерго- и ресурсосберегающих технологий химических процессов.

Традиционные методы расчета ХТП, основанные на учете при вычислениях упрощенных механизмов их протекания, абсолютно не удовлетворяет современным требованиям. Только компьютерное моделирование дает возможность учесть наибольшее число факторов и явлений, влияющих на протекание реальных процессов, и обеспечить высокую точность предсказания их поведения при расчетах.

Одно из направлений методологии компьютерного моделирования – построение физико-химических моделей, базирующихся на знании закономерностей элементарных процессов (гидродинамики, массо- и теплопередачи, химической кинетики). Большинство данных процессов можно описать с помощью дифференциальных уравнений в частных производных.

Дифференциальные уравнения в частных производных составляют в настоящее время одну из наиболее быстро развивающихся направлений вычислительной математики. Области науки и техники, где решаются уравнения в частных производных, весьма многочисленны и важны. К ним относится и химическая технология.

1. Компьютерного моделирование

1.1. Понятие компьютерного моделирования

Компьютерное моделирование – моделирование протекания химико-технологических процессов на основе физико-химических закономерностей, а также данных лабораторных экспериментов с применением прикладных программ и вычислительных мощностей компьютеров.

В зависимости от степени изученности закономерностей процесса разрабатывают эмпирические или физико-химические модели. Эмпирические модели применяются тогда, когда закономерности процесса до конца не известны, а их дальнейшее изучение требует значительных инвестиций.

Физико-математические модели являются более привлекательны, тек как они основаны на учете действительных закономерностей протекающих процессов. При построении сначала изучается теория процесса, исходя из чего строится система уравнений математического описания, после которой разрабатывается моделирующий алгоритм ее решения. Моделирующий алгоритм представляет собой комбинацию известных численных методов решения стандартных задач вычислительной математики.

1.2. Описание ХТП с применением ДУЧП

При изучении процессов и аппаратов химической технологии для моделирования ХТП выделяются шесть основных типов процессов и аппаратов, при математическом описании которых используются уравнения в частных производных.

1. Гидромеханические процессы (разделение жидких неоднородных систем, разделение газовых неоднородных систем, оборудование для неоднородных систем, перемещение жидких систем, перемещение и сжатие газовых систем), в описании кинетики которых лежат уравнения гидродинамики.

Уравнение движения идеальной жидкости (уравнение Эйлера) которое в векторной форме имеет вид:

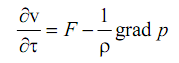(1.1)

или

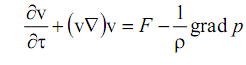(1.2)

где F – напряженность поля массовых сил; ρ – плотность жидкости или газа; p – давление; v – скорость,



Уравнение движения вязкой жидкости (уравнение Навье-Стокса) в векторной форме имеющее вид:

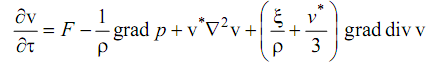(1.3)

где v*= ρ/η – кинематическая вязкость жидкости; η - динамическая вязкость; ξ – вторая вязкость;



2. Теплообменные процессы (теплообменные процессы без изменения агрегатного состояния, теплообменные процессы с изменением агрегатного состояния, холодильные процессы), скорость которых определяется законами теплопередачи и записывается в виде уравнения теплопередачи:

(2)

где Cp – коэффициент теплоемкости; λ – коэффициент теплопроводности; Q – источник или сток тепла.

3. Массообменные (диффузионные) процессы (тепломассообменные процессы, сорбционные процессы, экстракционные процессы, мембранные и электродиффузионные процессы), скорость которых определяется скоростью перехода вещества из одной фазы в другую и выражается в форме закона Фика:

(3)

где D – коэффициент диффузии; R – сток или приток вещества в результате взаимодействия.

4. Механические процессы (разделение твердых тел, измельчение, смешение, формообразование, дозирование), скорость которых определяется законами физического тела; среди базовых законов в первую очередь следует указать закон Гука, который в частном случае может быть записан в следующем виде:

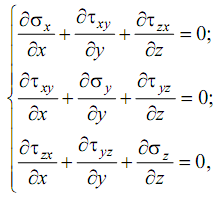(4)

5 Химические процессы, связанные с превращением веществ и изменением их химических свойств. Скорость этих процессов определяется закономерностями химической кинетики и законом Фика.

6 Биохимические процессы, связанные с синтезом веществ и осуществляемые под воздействием и при непосредственном участии живых микроорганизмов и выделенных из них ферментов. Скорость биохимических процессов, как и в предыдущем случае, определяется скоростью роста культуры в зависимости от концентрации одного или нескольких наиболее важных компонентов среды, обеспечивающих основу метаболизма. Эти компоненты получили название лимитирующих субстратов.

Как видно из представленного выше перечня задач, ДУЧП являются очень распространенными при описании различных процессов химической технологии. Без них невозможно описать практически ни один аппарат или процесс.

2. Дифференциальные уравнения в частных производных

2.1. Дифференциальные уравнения в частных производных:

классификация, граничные условия

Математическое описание целого ряда процессов химической технологии представляется дифференциальными уравнениями в частных производных второго порядка вида:

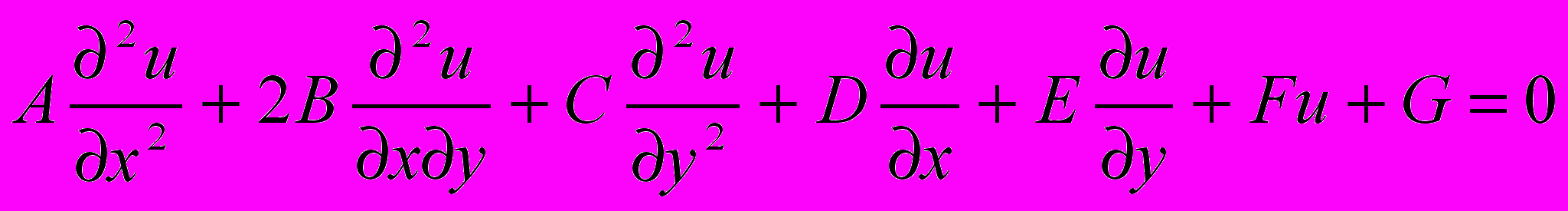(4)

где А, В,С, D, Е, F,G являются функциями только независимых переменных л и у, что удовлетворяет условию линейности уравнения (4). Функция u = u(х, у), которая определена внутри плоской области G переменных x, у (рис. 1), непрерывна, имеет непрерывные производные и удовлетворяет уравнению (4), является решением дифференциального уравнения в частных производных.



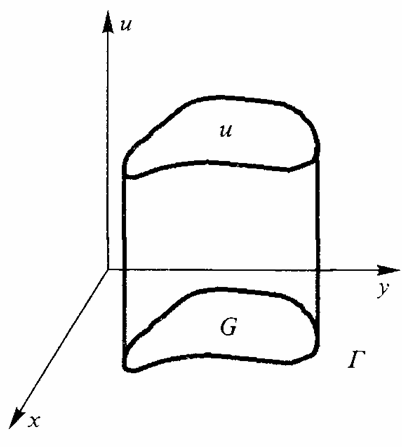
Рис. 1. Графическое представление функции решения дифференциального уравнения в частных производных второго порядка

Если функция u зависит от одной переменной, то уравнение (4) представляет собой обыкновенное дифференциальное уравнение, имеющее семейство решений.

Выбор единственного решения становится возможным при наличии начальных условий.

Аналогично при решении уравнений в частных производных получение единственного решения связано с заданием некоторых дополнительных условий на границе Г области G, внутри которой определена функция u(x, у), называемых граничными. Граничные условия могут накладываться на функции (граничные условия первого рода), на ее производные (граничные условия второго рода) или одновременно на функции и производные (граничные условия третьего рода). Граничные условия третьего рода или смешанные граничные условия задаются в виде:

(5)

где α и β — заданные функции в некоторой точке контура Г, F = F(x. у) — некоторая функция, значения которой в точках границы известны, — производная искомой функции по нормали к границе Г в рассматриваемой точке. Граничные условия первого рода являются частным случаем уравнения (5) при β=0, граничные условия второго рода - при α = 0.

Задание таких граничных условий дает возможность сформулировать три различные задачи с граничными условиями в зависимости от типа кривой контура Г области G. Граница области, вдоль которой известны граничные условия, может быть как замкнутой, так и незамкнутой, или «открытой» (рис. 2).



Рис. 2. Графическое изображение границы области известных граничных условий


Уравнения в частных производных вида (4) принято классифицировать по трем типам в зависимости от знака определителя, составленного из элементов уравнения (4):

(6)

При АС - В2<0 уравнение (1) называется гиперболическим, при АС – В2 =0 — параболическим, при АС – В2 >0 — эллиптическим.

Решить задачу с граничными условиями означает найти такую функцию u(х, у), которая удовлетворяет уравнению (4) и граничным условиям (5). Точные, или аналитические, методы решения краевых задач применимы лишь в некоторых частных случаях, и область их использования ограничена. Поэтому большое значение на практике имеют приближенные методы, которые разделяются на две группы:

• методы, в которых возможно получить приближенные аналитические выражения для искомой функции (здесь не рассматриваются);

• численные методы, в которых аналитические выражения для функций отсутствуют.

Вторая группа методов наиболее универсальна, так как пригодна для решения уравнений всех типов.

2.2. Разностный метод решения ДУЧП

Основная идея решения СДУЧП разностным методом заключается в том, что решается не исходное дифференциальное уравнение в частных производных (4), а соответствующее ему уравнение в конечных разностях, получаемых путем замены частных производных их выражениями через конечные разности. При этом осуществляется переход от поиска решения в виде непрерывной (интегральной) поверхности u(x, у) к поиску значений сеточной функции u(xi, yj) в дискретно расположенных точках (xi, yj), образующих прямоугольную сетку (рис. 3).



Рис. 3. Графическое представление значений сеточной функции


Для такого разбиения области определения G выбираются постоянные шаги разбиения: h в направлении х, t в направлении у. При этом точки имеют координаты:

(7)

где x0 и у0 — координаты начальной точки; i и j — номера узлов по направлениям x и у.

Значения функции в узловых точках обозначаются с указанием координат u(x0+ih,y0+jl) или сокращенно с помощью индексов:

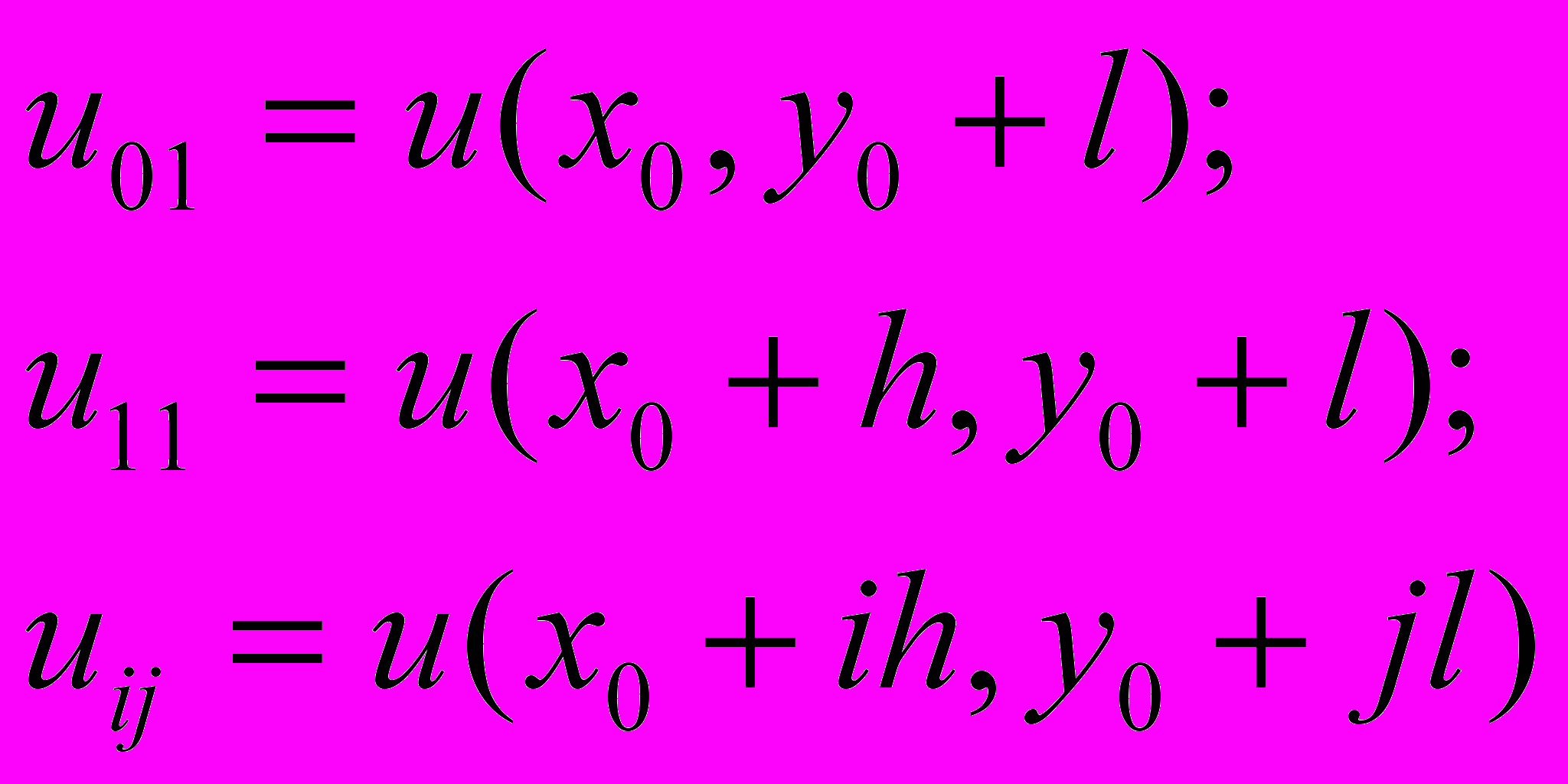(8)

Первые производные в сеточной области заменяются отношениями разностей между значениями функции в соседних узлах к величине шага сетки. Замена может быть выполнена тремя способами. Так, первая частная производная функции и в узле (х0,y0) выражается через конечные разности в направлении х в виде:

а) разностного отношения «вперед»

(9.1)

б) разностного отношения «назад»

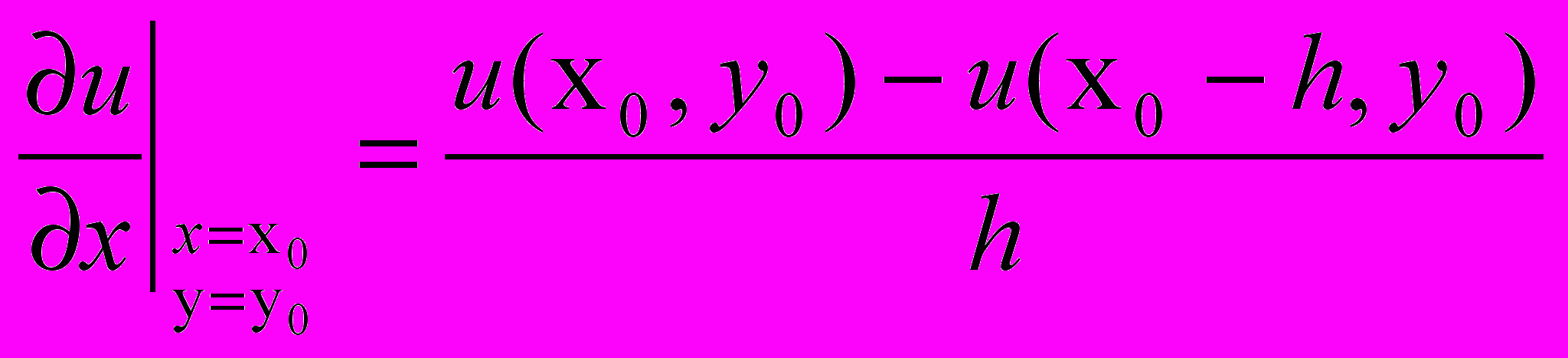(9.2)

в) симметричного разностного отношения

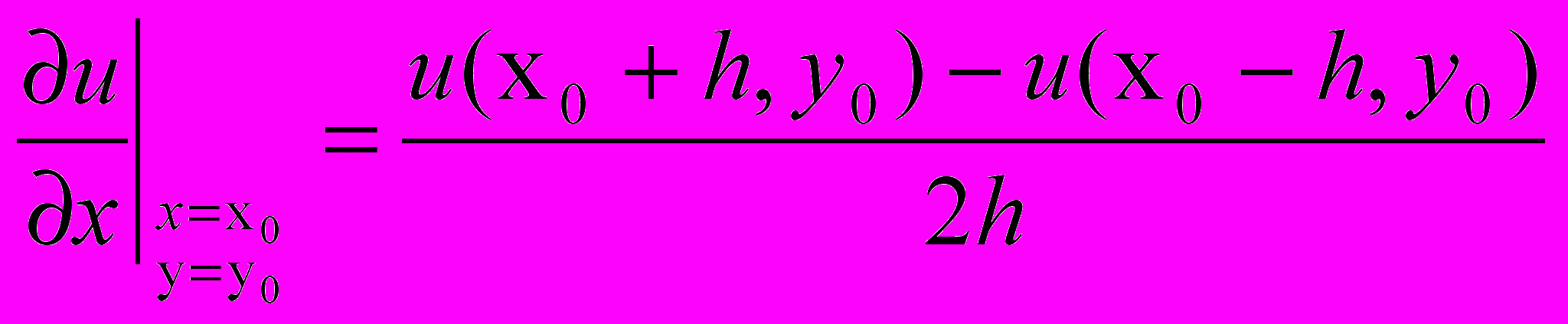(9.3)

Вторые частные производные в сеточной области определяются как отношения разностей первых производных к величине шага сетки. Например, вторая производная для узла (х0, у0) по направлению х определяется:

(10.1)

Для производной по направлению у выражение аналогично:

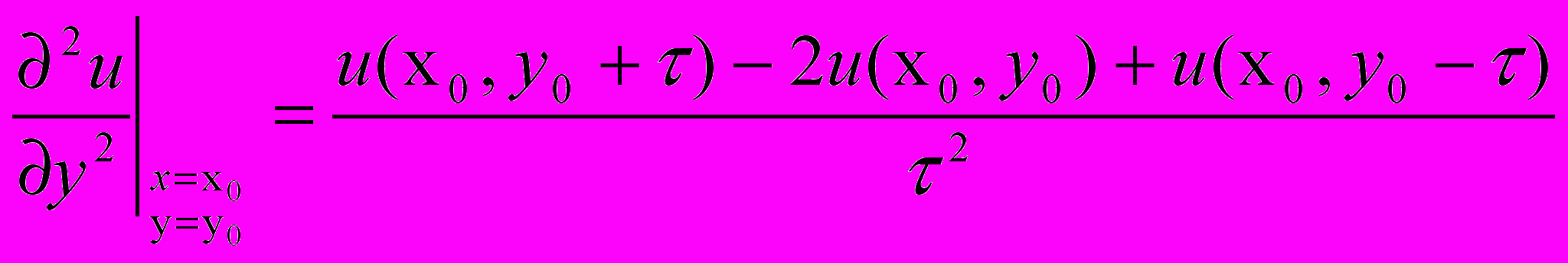(10.2)

Для смешанных частных производных разностное соотношение записывается следующим образом:

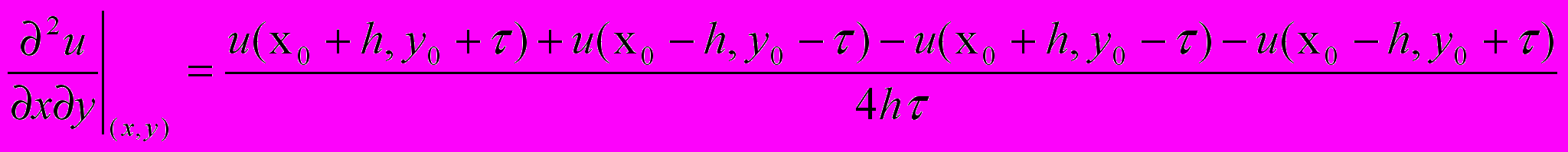(10.3)

Предположим, что область G, на которой определена функция и(х, у), прямоугольна (рис. 4).



Рис. 4. Графическое представление области, на

которой определена функция


На этой области строится сетка с параметрами h и l и узлами по горизонтали i = 0,1,2,...., n и по вертикали j = 0,1,2,…,m. Разностные уравнения связывают значения искомой функции в узлах сетки, число которых равно (n + 1)(m + 1). Решение задачи с граничными условиями заключается в отыскании этих значений при заданных значениях функции в граничных узлах. Таким образом, в замкнутой прямоугольной области остается (n-1)(m-1) неизвестных, для которых составляется и решается система (n-1)(m-1) разностных уравнений.

2.2.1. Решение уравнений первого порядка

Запишем дифференциальное уравнение в частных производных первого порядка:

(11)

Аппроксимация производных осуществляется по разностному соотношению (13.1) и уравнение для узла с координатами имеет вид:


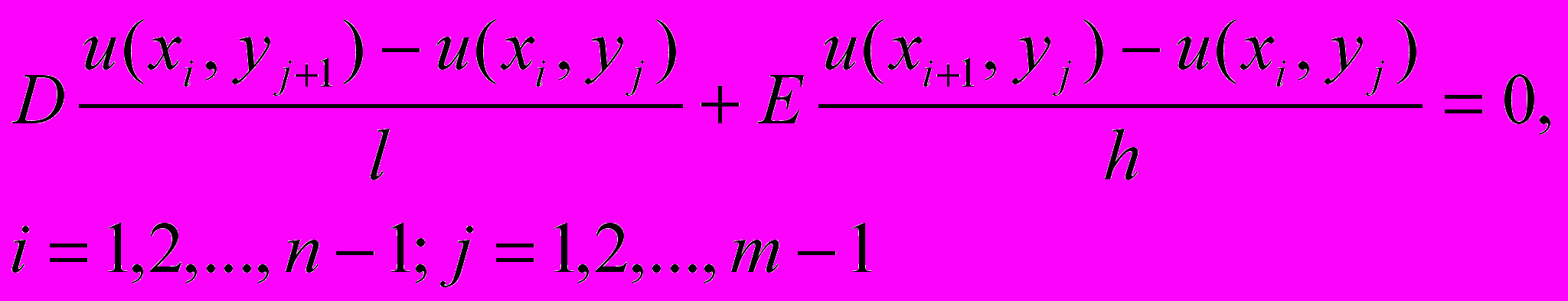(12)

Для простоты примем, что D/E = 1 и l/h = 1. Тогда значение функции в узле (i, j + 1) выражается (рис. 5):

(13)



Рис. 5. Соседние узлы сеточной функции


Решение уравнения (11) заключается в отыскании значений u(x, у), т.е. дискретных значений u(xi, yj) при i=1, 2,…,n и j = 1, 2,…m - см. (13), (14), по

заданным граничным значениям u(хi, у0) при i=1, 2,…,n.

2.2.2. Решение эллиптического уравнения

Одним из часто используемых дифференциальных уравнений эллиптического типа является уравнение Лапласа:

(14)

Аппроксимация производных выполняется с использованием формул (10.1) и (10.2), которые для узла (i,j) принимают вид

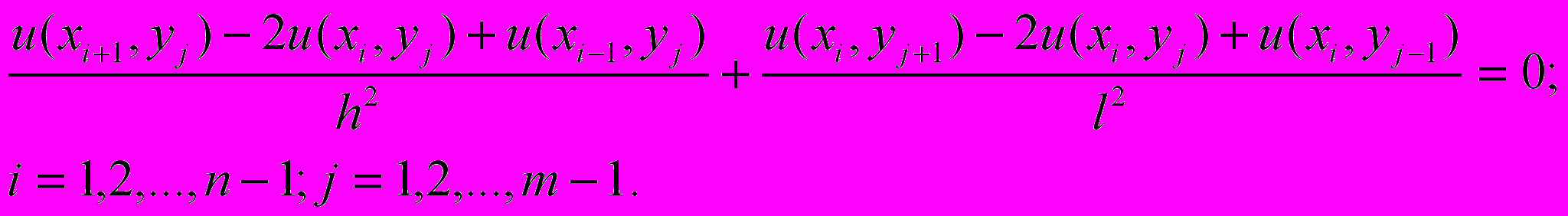(15)

Тогда значение функции в узле (i,j) при l/h = 1:

(16)

Таким образом, значение функции в каждом внутреннем узле сетки равно среднему арифметическому значений функции в четырех соседних узлах (рис. 6). Начало координат сетки (рис. 7) совпадает с точкой (x0,у0). Граничные условия (5) в разностной форме принимают вид:

а) для нижней границы ui0 = Fi0 = F(xi, у0); i = 0,1,2, ...,n;

б) для верхней границы uim = Fim = F(xi, ym); i = 0,1,2, ...,n;

в) для левой границы u0j = F0j, = F(x0, у j); j = 0, l, 2,..., m;

г) для правой границы unj = Fnj = F(xn,y0); j = 0, l, 2,..., m.



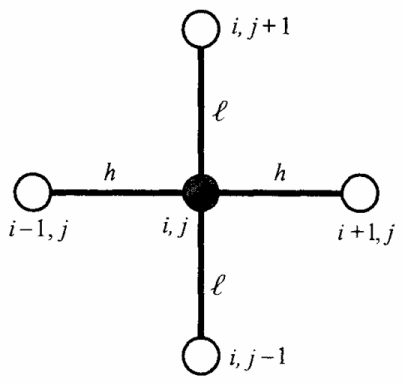
Рис. 6. Значение функций, определяющих значение

функции во внутреннем узле



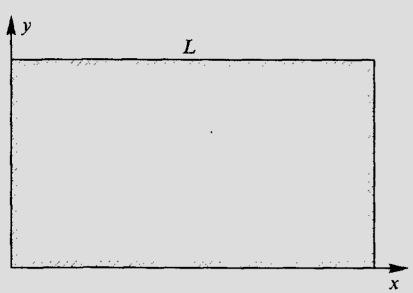
Рис. 7. Графическое изображение границ сетки

при решении эллиптического уравнения


Решается краевая задача с условием первого рода. Решение начинается с первого (нижнего) «слоя» сетки j = 1; i = 0,1,2, ...,n:

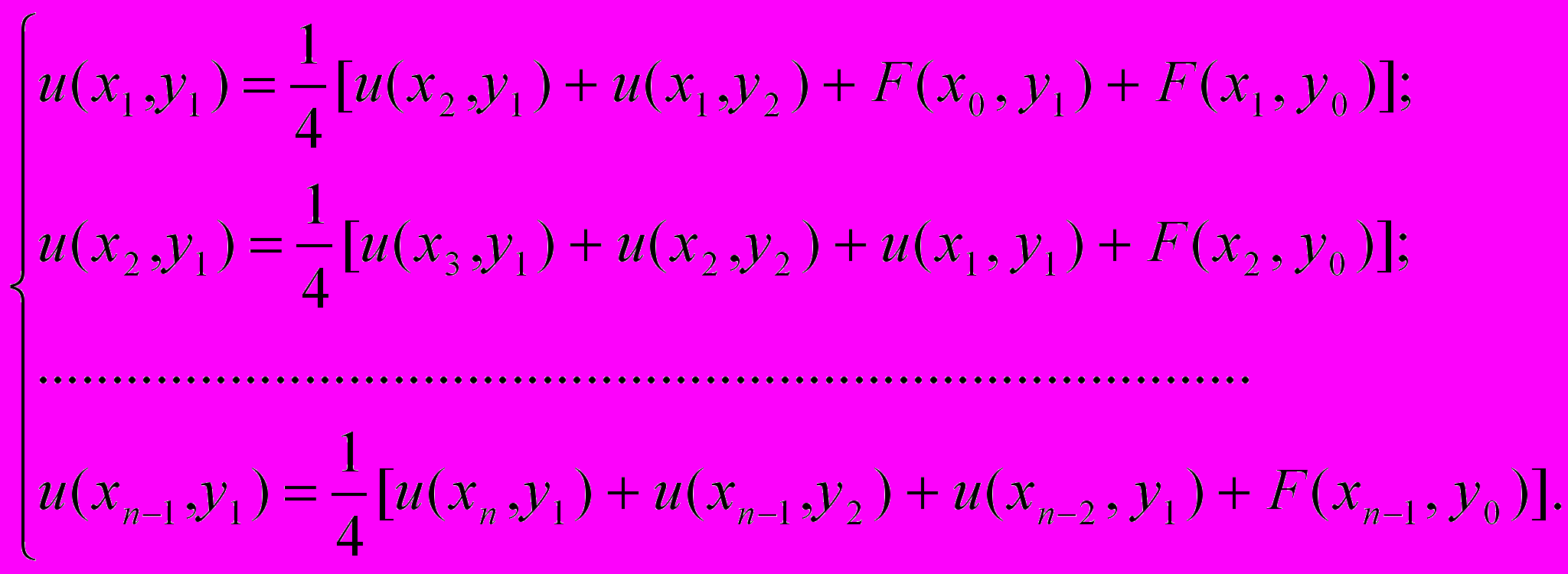(17)

Для второго слоя узлов сетки j = 2; i = 0,1,2, ...,n:

(18)


Подобным образом запишутся системы уравнений до слоя j = m - l. Доказано, что такая система, состоящая из (n - 1)(m - 1) линейных неоднородных уравнений с (n - 1)(m - 1) неизвестными, всегда совместна и имеет единственное решение. Так как большая часть коэффициентов системы равна нулю, то для ее решения наиболее целесообраз­но использование итерационных методов, в частности, метода Зейделя. Запишем часть уравнений системы (17) в приведенном виде, где верхний индекс показывает номер итерации. Все значения неизвестных в начале счета примем uij(0)=0. Тогда значе­ния функции в узловых точках на первой итерации будут следующими:

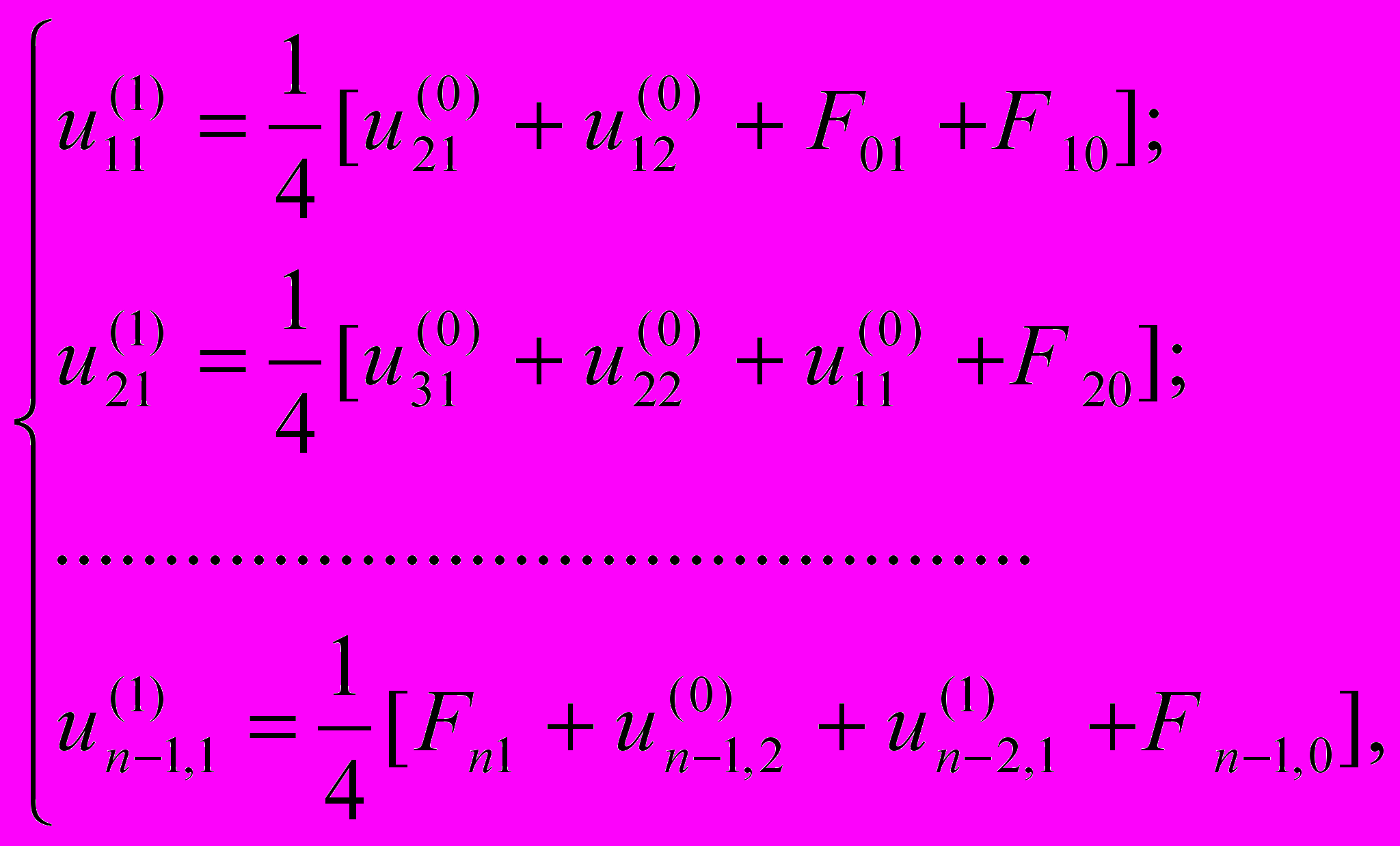(19)

(20)

Доказано, что при h→0 и l→0 решение разностного уравнения (системы линейных алгебраических уравнений) сходится к решению исходного дифференциального уравнения в частных производных без ограничений на величину отношения l/h.

2.2.3. Решение гиперболического уравнения

Уравнение гиперболического типа можно получить из уравнения (4), если переменную у трактовать как временную координату г, а переменную х - как пространственную координату

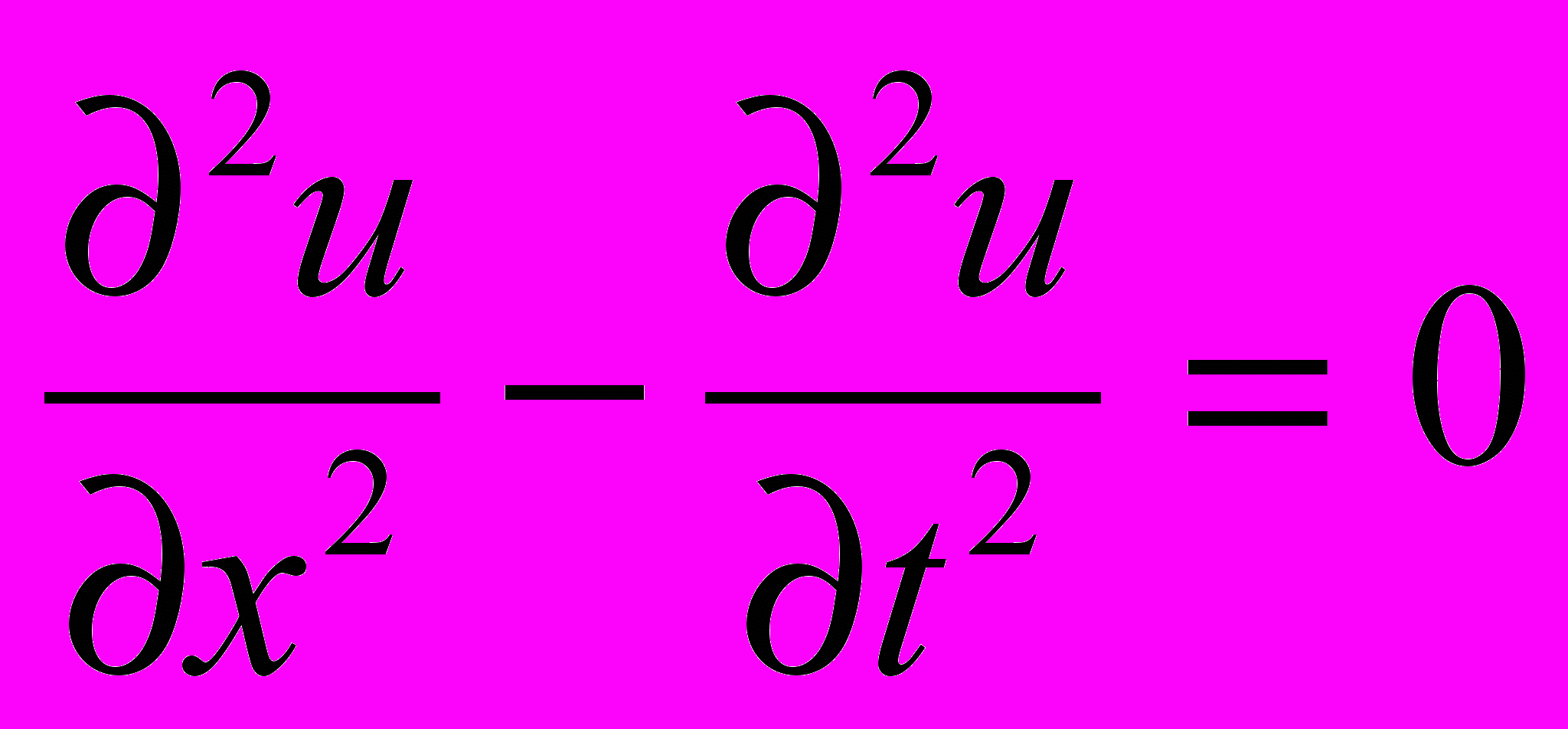(21)

Граница области, вдоль которой заданы краевые условия для уравнения (21), незамкнута по временной координате, и граничные условия представляются в виде:

u(0, t)= F(1)(t); u(L, t)= F{2)(t); t≥0 (22)

Граничные условия по временной координате относятся к фиксированному моменту времени и носят название начальных условий:

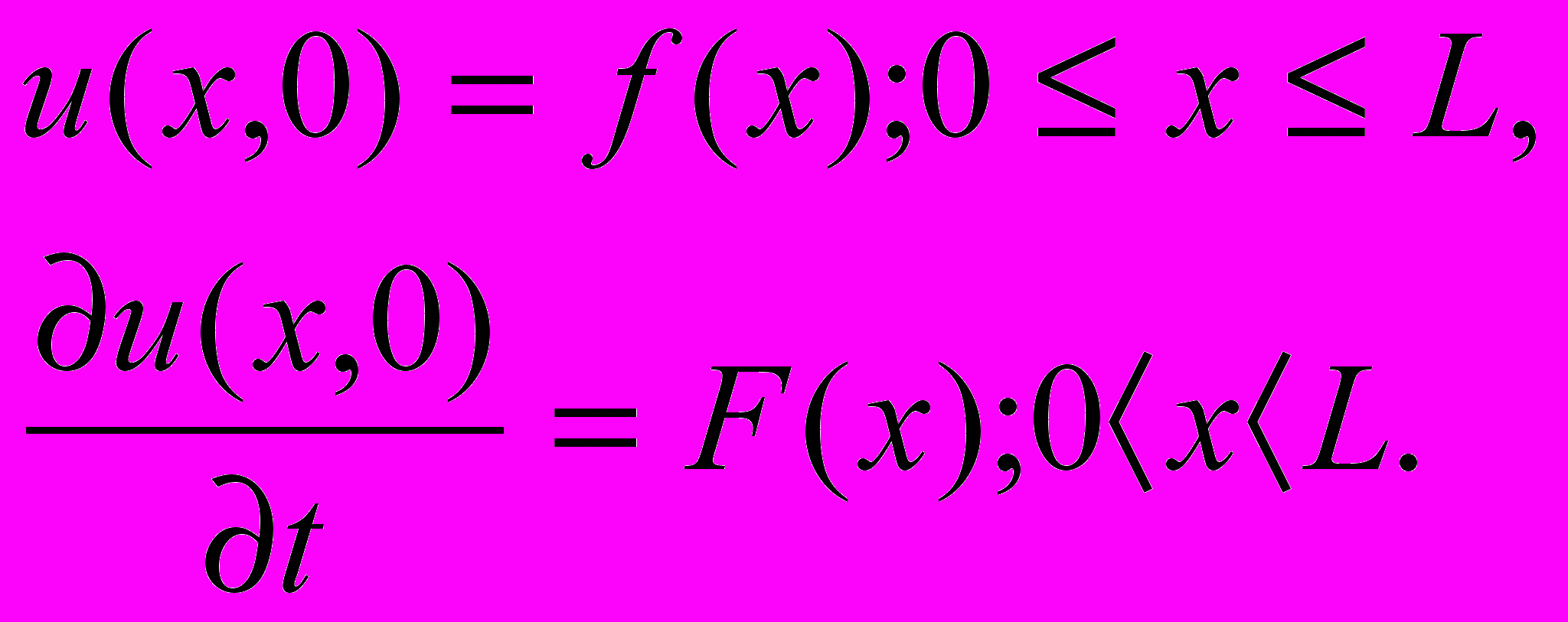(23)

Таким образом, имеем смешанную краевую задачу. Для численного решения уравнения (21) строится прямоугольная сетка в полуполосе t>0, 0


Рис. 8. Иллюстрация границы области при решении

гиперболического уравнения


Решение явной разностной схемы для уравнения (21) можно найти по следующей формуле:

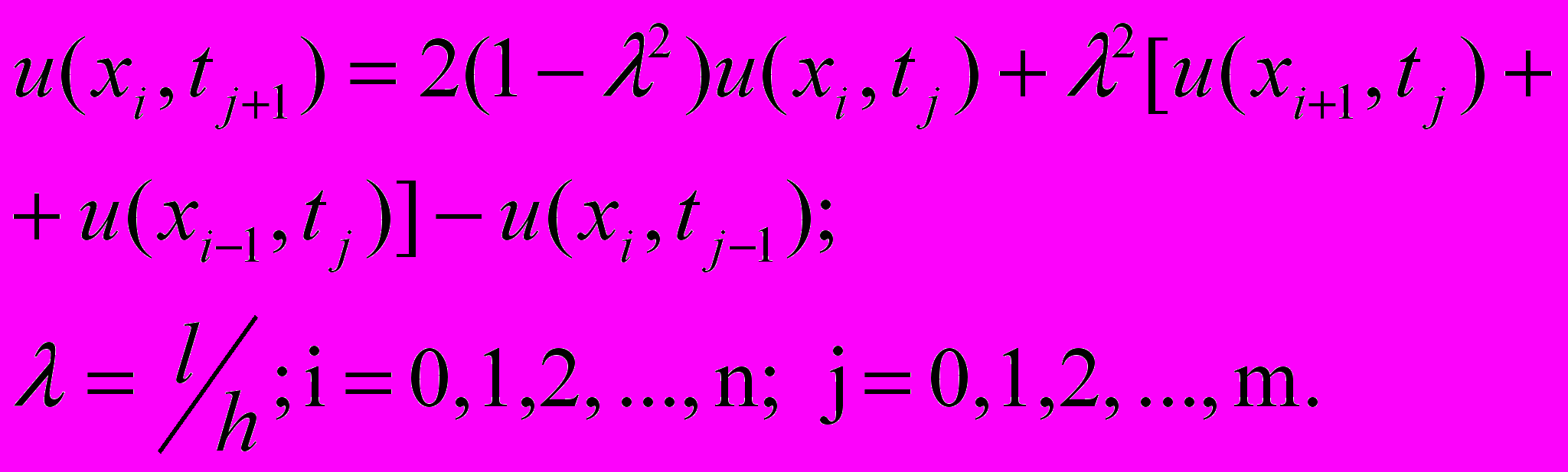(24)

Граничные и начальные условия представляются в разностной форме:

u0j=F0i(1)=F(1)(x0, tj);

unj=Fni(2)=F(2)(xn, tj), j=1, 2, … (25)

и

u10=fi0=f(xi, t0), i=1, 2, …, n-1;

1/ℓ[u(xi, t1)-u(xi, t0)]=F(xi, t0). (26)

Подставляя уравнение (25) в (26), получим

u(xi, tj) = f(xi, t0)+l*F(xi, t0). (27)

Далее из уравнения (25) определяются все значения функции u для нулевого слоя сетки при j = 0. Значения функции u для первого слоя при j = 1 определяются из уравнения (27). Значения функции ui2 соответствующие второму слою сетки, получаются из разностного уравнения (26) для j=1:

(28)

Таким образом, значения функции в каждом следующем слое вычисляются по значениям функции в двух предыдущих слоях. Существенно, что использование этой схемы не требует решения системы уравнений, так как значения искомой функции вычисляются в явном виде. Вычислительный процесс сходится при l
2.2.4. Решение параболического уравнения

Дифференциальное уравнение параболического типа имеет вид:

(29)

Разностное уравнение для узла (x, у) представляется в виде

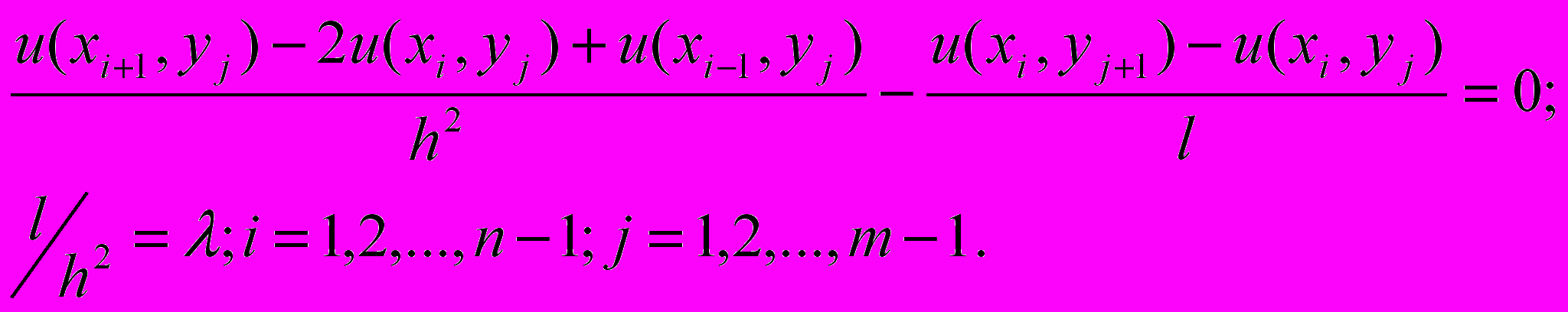(30)

Приведем уравнение (30) к форме (28):

(31)

Отсюда следует, что значение функции в узле (i, j+1) рассчитывается по трем значениям функции в соседних точках (i + 1, j), (i, j), (I - l, j) предыдущего слоя сетки (рис. 9).



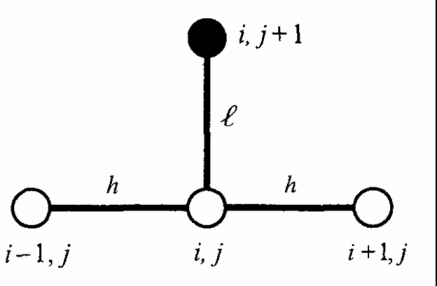
Рис. 9. Графическое изображение соседних узлов

сетки при решении параболического уравнения


Таким образом, решение параболического уравнения сводится к решению системы линейных алгебраических уравнений. Граница области, вдоль которой заданы граничные условия для уравнения этого типа, незамкнута, поэтому независимая переменная у трактуется как временная координата t. Тогда уравнение для узла имеет вид:

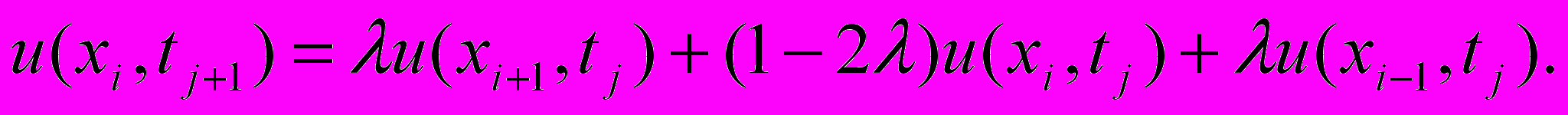(32)

Граничные условия:

u(0, t) = F(0);

u(L, t) = F(L), t≥0.

Начальное условие:

u(x, 0) = f(x), 0≤x≤L.

Решается краевая задача с граничными условиями первого рода. Строится прямоугольная сетка в полуполосе t ≥ 0, 0 ≥ х ≤ L (см. рис. 8).

Граничные и начальные условия в разностной форме принимают вид:

u(x0, tj)=F(0)(x0, tj);

u(xn, tj)=F(L)(xn, tj), j=1, 2, …;

u(xi, t0)=f(xi, t0), i=1, 2, …, n-1.

Значение функции вычисляется в явном виде u(xi, tj+1) по уравнению (32) аналогично случаю гиперболического уравнения. Решение для нулевого слоя j = 0 известно из граничных и начальных условий. Решение для первого слоя j = 1 получается из уравнения (32) при j = 0:

(33)

и так далее для каждого следующего слоя сетки решения находят по предыдущему слою. Доказано, что при решении параболического уравнения вычислительный процесс устойчив и сходится при l 2/2 или λ<1/2.

3.Применение ДУЧП для описания процессов проницаемости газов через полимерные мембраны

3.1. Понятие о мембранных процессах

Мембранные технологии разделения веществ характеризуются высокой эффективностью при низких энергозатратах (отсутствие фазовых переходов), малой материалоемкостью, мобильностью, модульной структурой и простотой управления и представляют собой новые наукоемкие перспективные технологии, ориентированные на активное практическое использование в ХХI веке.

Явления селективного переноса газов через полимерные мембраны могут быть рассмотрены на макроскопическом и микроскопическом уровне, а также с помощью молекулярного моделирования.

Рассмотрим макроскопический подход к описанию процесса. Макроскопический подход рассматривает среду мембраны как непрерывную, а процесс переноса газов через однородные непористые полимерные материалы представляется как диффузия молекул газа в конденсированной среде, обусловленная внешними движущими силами. Движущей силой массопереноса в общем случае является градиент химического потенциала диффундирующего вещества (пенетранта). Поток газа через мембрану, как правило, обусловлен градиентом концентраций (парциальных давлений газа).

Перенос газа через полимерную мембрану осуществляется по механизму «растворимость-диффузия» и включает адсорбцию и растворение газа в приповерхностном слое на границе раздела фаз газ/полимер на входе в мембрану, его диффузию в объеме мембраны к противоположной поверхности и десорбцию из пограничного слоя на выходе из мембраны.

Изменение концентрации газа по толщине x мембраны со временем описывается 2-м уравнением Фика (уравнением баланса массы):

(34)

Решение этого уравнения требует задания граничных и начальных условий. Уравнение решают методами разделения переменных с разложением в ряды Фурье или через операторы Лапласа.

Для одномерного потока через пленку толщиной h уравнение (34) решается при следующих начальных и граничных условиях:

(35)

где c1, с2 – концентрации газа на входной и выходной стороне мембраны, соответственно; f(x) – функция распределения концентрации диффундирующего газа в пленке в начальный момент времени.

Решение уравнения (34) с учетом условий (35) методом разделения переменных имеет следующий вид:

(36)

Полученное решение является очень громоздким по записи и неудобным в вычислении. Кроме того, оно не отражает динамику изменения концентрации газа в полимере при изменении концентрации данного газа в окружающем пространстве.

3.2. Моделирование процесса проникновения газа через мембрану при экспоненциально падающей концентрации газа

Рассмотрим решение уравнения (34) при следующих начальных и граничных условиях:

(37)

Уравнение (34) является параболическим, поэтому для его численного решения можно воспользоваться показанной в разделе 2.2.4. формулой для узла сетки:

,

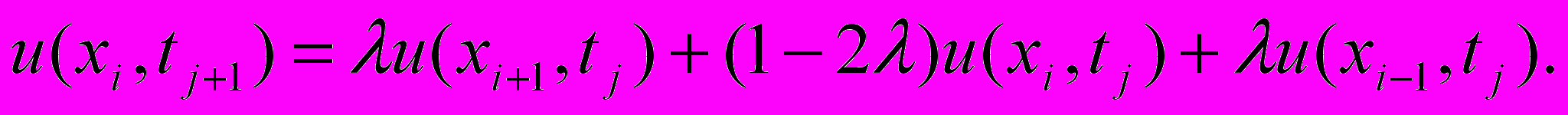где λ=D•ℓ/h2, h – шаг по оси х, ℓ - шаг по времени.

По условию задачи толщина мембраны равна 10мкм=0,001см, время, в течение которого происходит диффузия, равно 40 секунд.

Разбиваем интервал [0, 0,001] по оси x на 10 точек через 0,0001 см, при этом h=0,001/(10 – 1)=0,000111. 83239996,753510267023780537294051

Разбиваем интервал [0, 40] по оси t на 40 точек через 1 с, при этом ℓ=40/(40 – 1)=1,0256.

Сравним результаты вычислений при различных значениях коэффициента диффузии. D1= 1,2*10-9, D2= 3,6*10-9, D3= 5,4*10-9.

Вычисляем значения λ. λ1=0,1; λ2=0,3; λ3=0,45.

После подстановки полученных значений в программу, листинг которой приведен в приложении, были получены следующие результаты, выраженные в графической форме. Все вычисления производились в среде MATLAB.







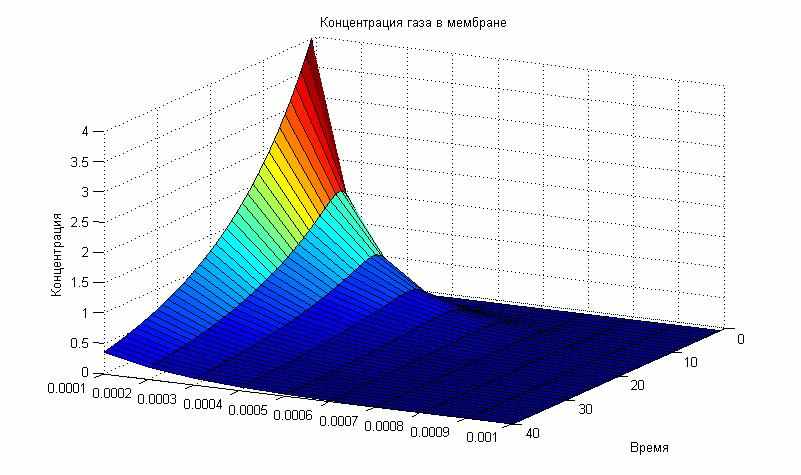
Рис. 10. Динамика проникания газа в мембрану.

а) D1= 1,2*10-9, б) D2= 3,6*10-9, в) D3= 5,4*10-9

Как видно из графиков, при увеличении коэффициента диффузии концентрация газа в мембране увеличивается. Кроме того, показана возможность моделирования процессов диффузии в нестационарных условиях. Это делает численные методы более привлекательными для моделирования ХТП по сравнению с аналитическими.

Заключение

Результатом данной курсовой работы явилось рассмотрение дифференциальных уравнений в частных производных как основы для компьютерного моделирования ХТС. В работе рассмотрены основные типы процессов и аппаратов, при математическом описании которых используются уравнения в частных производных. Таковыми являются:
  • Теплообменные процессы;
  • Гидромеханические процессы;
  • Массообменные (диффузионные) процессы;
  • Механические процессы;
  • Химические процессы;
  • Биохимические процессы.

В работе рассмотрен и применен разностный метод решения ДУЧП, который является очень распространенным и эффективным.

Проведенный в ходе данной работы анализ позволяет сделать заключение о том, что ДУЧП являются основой для описания и моделирования большинства ХТП, и точный расчет без привлечения численных методов становится все менее возможным.
  • Список использованной литературы

1. Байдакова Н. В. Общая химическая технология / М.: ВАХЗ. 2000.

2. Кутепов А. М. Общая химическая технология / А. М. Кутепов, Т. И. Бондарева, М. Г. Беренгартен. – М.: Высшая школа, 2000.

3. Гартман Т. Н. Основы компьютерного моделирования химико-технологических процессов: Учеб пособие для вузов / Т. Н. Гартман, Д. В. Клушин. – М.: ИКЦ «Академкнига», 2008. – 416 с.

4. Дьяконов В. П. MATLAB 6.5 SP1/7/7 SP1/7 SP2 + Simulink 5/6. Инструменты искусственного интеллекта и биоинформатики / В. П. Дьяконов, В. В. Круглов. – М.: СОЛОН-ПРЕСС, 2006. – 456с.

5. Тепляков В. В. Параметры селективного газопереноса в мембранных полимерных материалах: Учебное пособие / В.В. Тепляков, А.Ю. Алентьев. – М.: МГУ, 2006. – 36 с.

Приложение

Листинг программы.

>> x0=0;

xn=0.001;

t0=0;

>> tn=40;

>> n=10;

>> m=40;

>> g='4*exp(-0.06*t)';

>> x=x0:(xn-x0)/(n-1):xn;

>> t=t0:(tn-t0)/(m-1):tn;

>> F=inline(g,'t');

>> u=zeros(n,m);

>> for i=1:m

u(1,i)=F(t(i));

end

>> for i=2:n

for j=1:m-1

u(i,j+1)=0.45*(u(i+1,j)+u(i-1,j))+0.1*u(i,j);

end

end