2 Стандарты блочного шифрования
| Вид материала | Реферат |
- Системы блочного шифрования, 37.08kb.
- Реферат по дисциплине «Информационная безопасность» Тема: «Стандарты для алгоритмов, 241.55kb.
- Программа для демонстрации работы симметричного, 24.86kb.
- Методические указания к лабораторным работам по курсу «Теория информациии и основы, 449.11kb.
- Руководитель Касьян Владимир Николаевич подпись курсовой проект, 172.76kb.
- Классификация стандартов. Стандарты, регулирующие общие вопросы раскрытия информации., 385.43kb.
- Техническое задание «Разработка системы диагностики технического состояния маслонаполненного, 225.4kb.
- Введение. 2 Стандарты, нормы и правила., 167.3kb.
- Регламент второго съезда ит-директоров Украины, 76.58kb.
- Контрольная работа По дисциплине «Международные стандарты аудита» Тема «Классификация, 111.82kb.
4.2. Алгоритмы цифровой подписи
4.2.1. Цифровая подпись Эль-Гамаля
Рассмотрим систему цифровой подписи, носящую имя ее изобретателя Эль-Гамаля, основанную на схеме формирования открытых и секретных ключей, которая используется в методе Диффи-Хеллмана. Пусть мы имеем большое простое число p, такое, что разложение числа p – 1 содержит, по крайней мере, один большой простой множитель и первообразный корень
по модулю p.Механизм подписывания состоит в следующем. Некоторый абонент А выбирает секретный ключ xA, по которому формирует секретный ключ
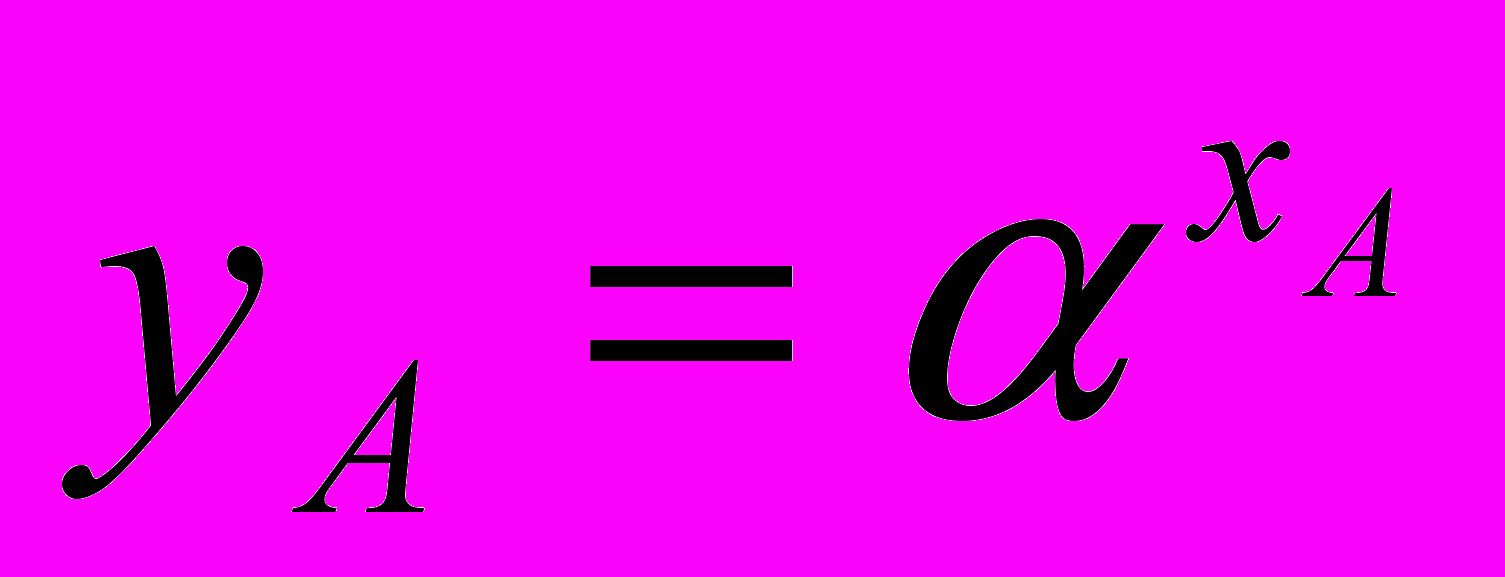. Подписью абонента А под документом M (подписываемое сообщение должно иметь длину меньше простого модуля p, т.е. M < p) служит пара чисел (r, s) (где 0 ≤ r < p - 1 и 0 ≤ s < p – 1), которая удовлетворяет уравнению 
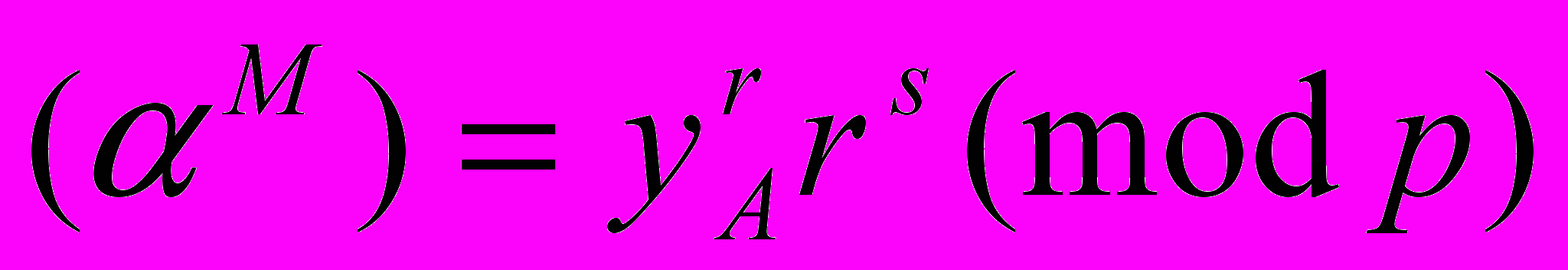.Это уравнение служит для проверки того факта, что документ подписан абонентом А.
Данная система электронной цифровой подписи основана на том, что только действительный владелец секретного ключа xA может выработать пару чисел (r, s), удовлетворяющую уравнению проверки подписи. Используя значение xA, абонент А вырабатывает подпись по следующему алгоритму:
- Сгенерировать случайное число k, удовлетворяющее условию:
0 < k < p – 1 и НОД(k, p – 1) = 1
- Вычислить
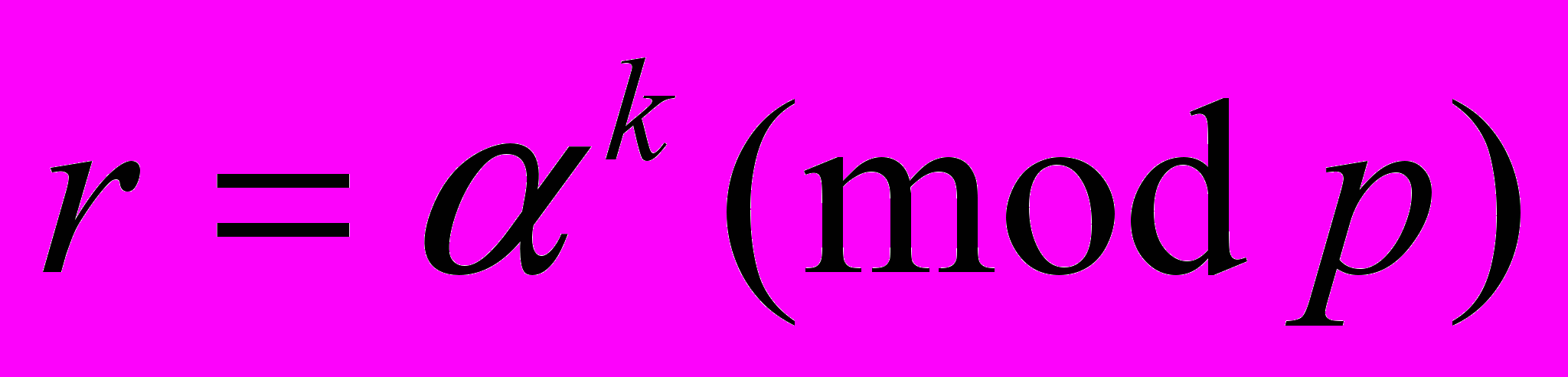
- Вычислить s из уравнения
.
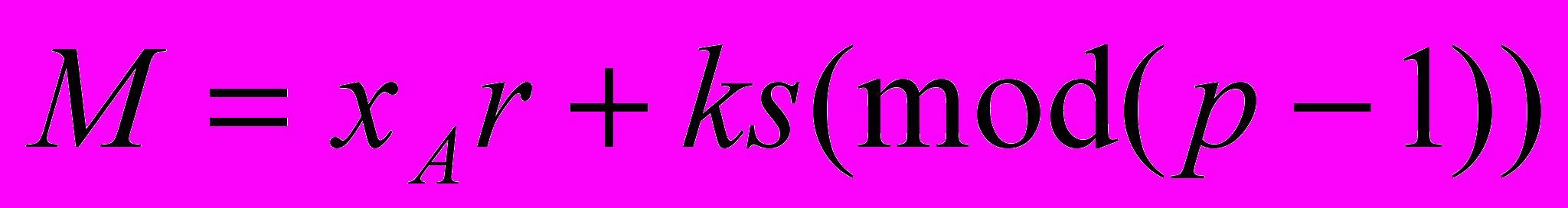Из теории чисел известно, что это уравнение имеет решение для s, если:
НОД(k, p – 1) = 1.
Владелец секретного ключа в состоянии подписать документ, а его подпись может быть проверена по его открытому ключу. Нахождение пары чисел (r, s) без знания секретного ключа вычислительно сложно. Различных подписей, соответствующих данному документу, может быть чрезвычайно много, т.к. k может иметь различные значения, но выработать правильную подпись способен только владелец секретного ключа. Множество возможных подписей отличаются значением r, но для данного r найти соответствующее значение s без знания секретного ключа практически невозможно. Для вычисления секретного ключа по открытому ключу необходимо решить задачу дискретного логарифмирования, которая является вычислительно сложной.
4.2.2. Алгоритм DSA
Этот алгоритм представляет собой аналог алгоритма, предложенного Эль-Гамалем, но с некоторыми изменениями, в частности за счет уменьшения числового порядка одного из параметров системы.
DSA является классическим примером схемы ЭЦП на основе использования хэш-функции и ассиметричного алгоритма шифрования.
Алгоритм использует следующие параметры:
P – простое число длиной L бит, где L принимает значение, кратное 64 в диапазоне от 512 до 1024.
Q – 160-битовое простое число – множитель p – 1
G =
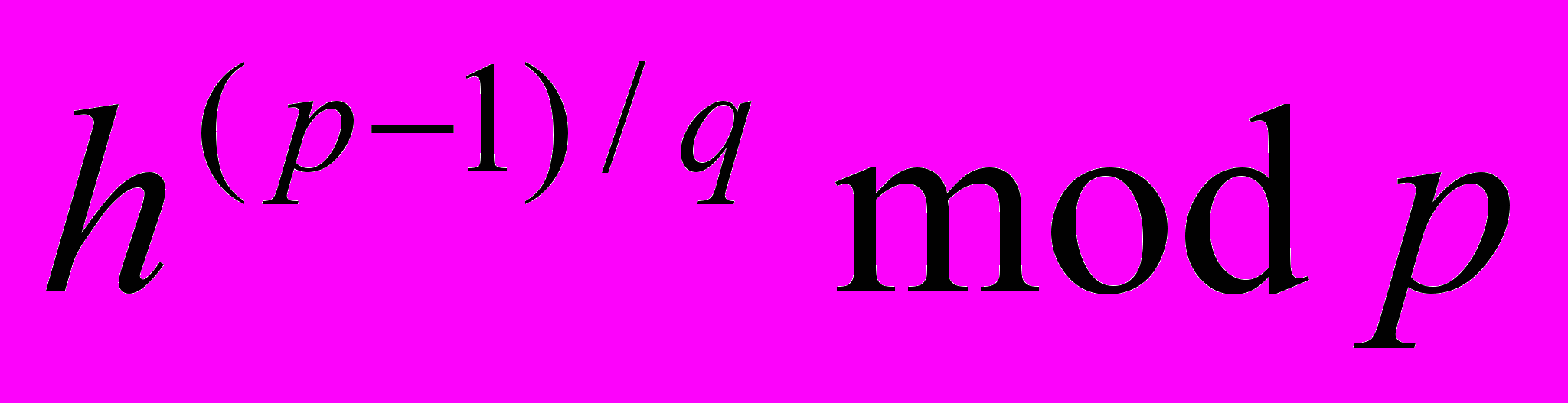, где h – любое число меньшее p – 1, для которого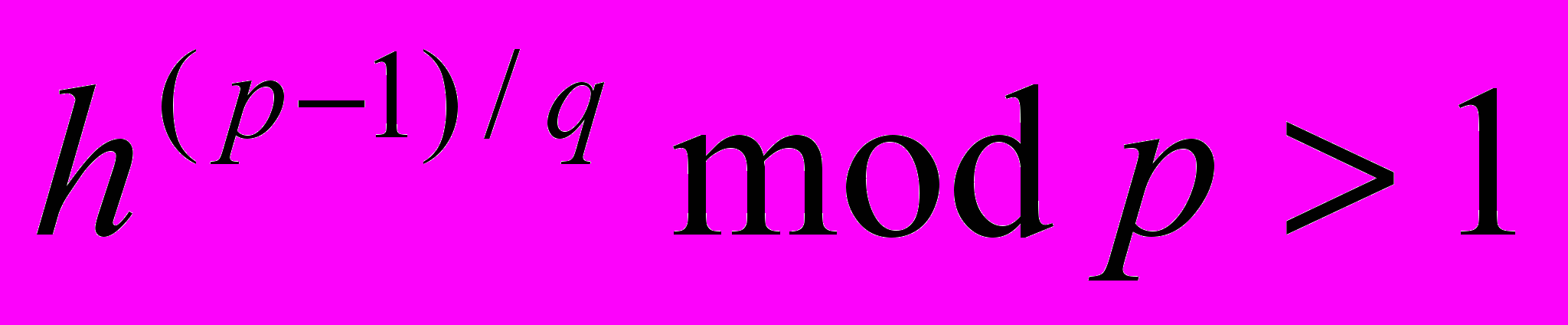 
X – число, меньшее q
Y -
В алгоритме также используется однонаправленная хэш-функция: H(m).
Первые три параметра p, q и g открыты и могут быть общими для пользователей сети. Закрытым является x, а открытым – y. Чтобы подписать сообщение m:
- Абонент А генерирует случайное число k < q
- Абонент А генерирует:
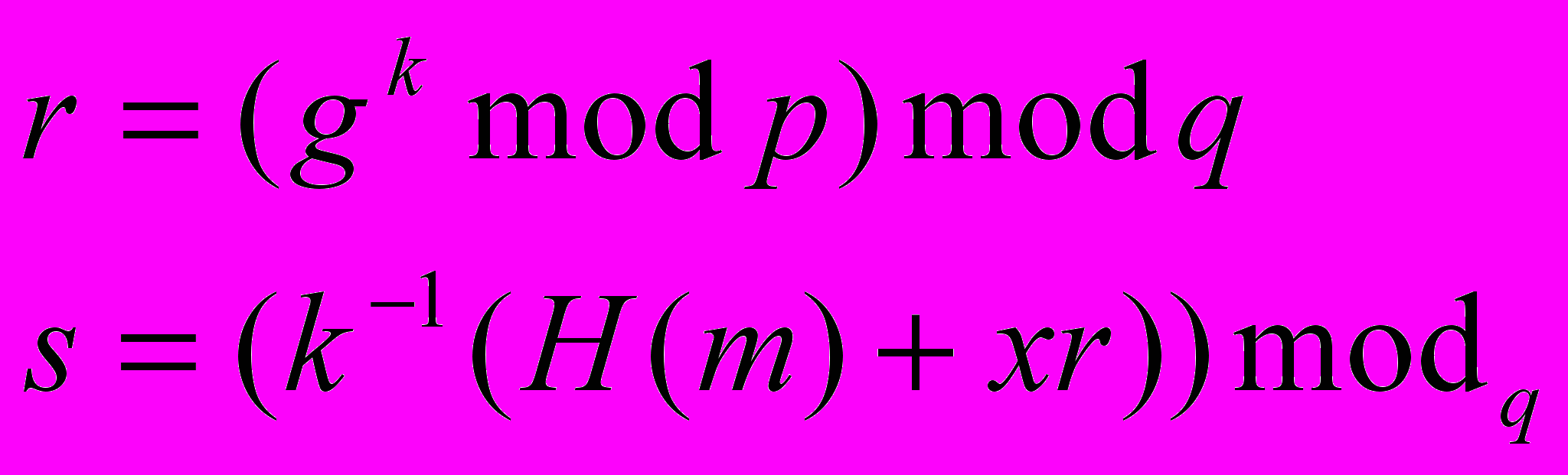
Его подписью служат параметры r и s, он посылает их абоненту Б.
- Абонент Б проверяет подпись, вычисляя:
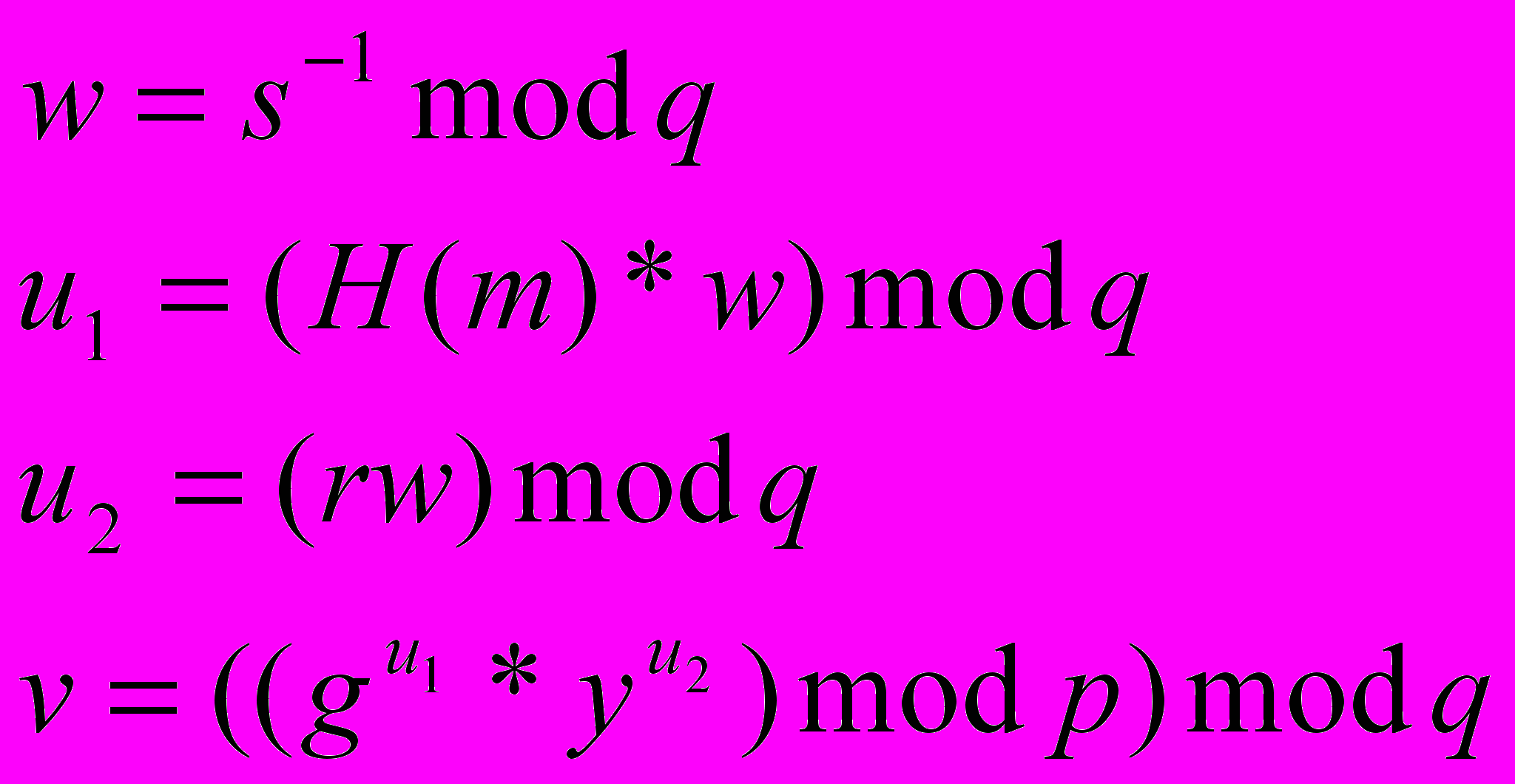
Если v = r, то подпись правильна.
4.2.3. Слепая подпись Чаума
Понятие слепой подписи было введено Д. Чаумом, который также предложил первые варианты ее реализации. Под слепой подписью понимается двухключевая криптосистема, которая позволяет осуществить подписывание электронных сообщений таким образом, чтобы подписывающая сторона не имела доступа к информации, содержащейся в подписываемом сообщении. Такое на первый взгляд нелепое требование в ряде криптографических систем имеет очень большое значение. Слепая подпись используется, например, в системах тайного электронного голосования и электронных деньгах, т.е. в таких криптографических системах, где требуется обеспечить решение задачи неотслеживаемости. Сама процедура слепой подписи требует от одного из участников согласия на то, что он может подвергнуться некоторым посягательствам путем приписывания ему определенных обязательств, которые он бы не хотел брать на себя.
Рассмотрим протокол слепой подписи Чаума, основанной на уже известной криптосистеме RSA. Пусть субъект А желает подписать некоторое сообщение M у субъекта Б. Для этого необходимо осуществить следующие шаги:
- Пользователь А (субъекты являются пользователями данной криптосистемы) генерирует случайное простое число k, такое, что НОД(k, N) = 1, где N – часть открытого ключа пользователя Б.
- Далее он вычисляет значение
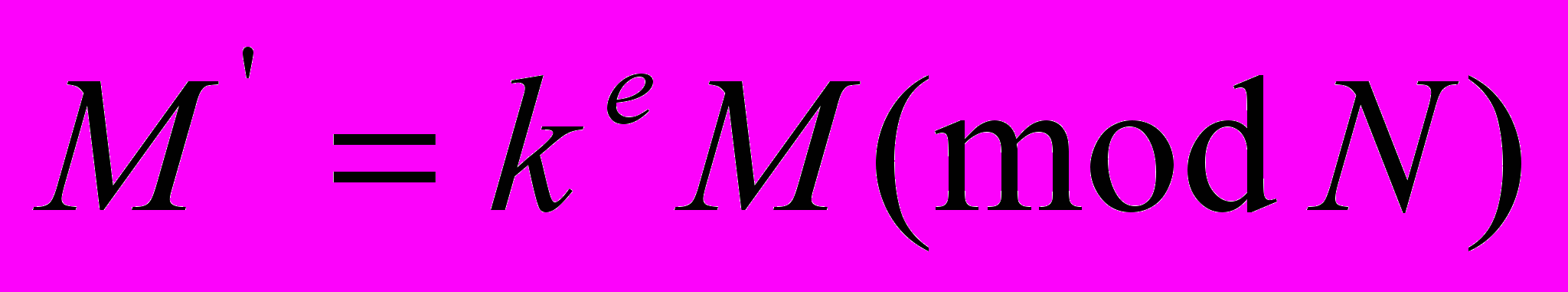, которое предоставляет для подписывания. Подписывающий не может получить доступ к сообщению M, поскольку оно зашифровано путем наложения на него "разового" ключа ke и использованием операции модульного умножения.
- Пользователь Б подписывает сообщение M' в соответствии с процедурой подписывания в криптосистеме RSA:
.
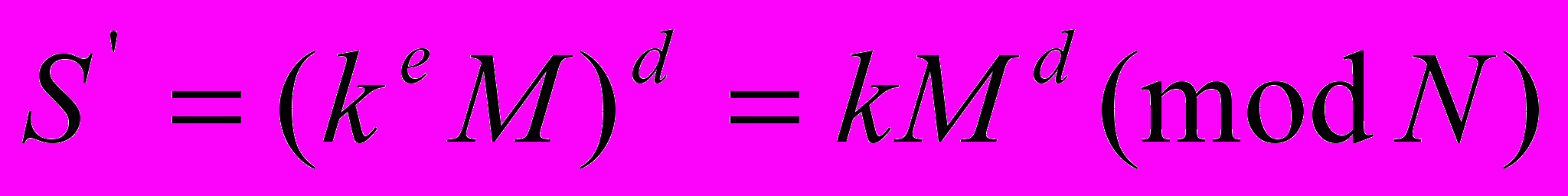Сформировав подпись S', подписывающий также не имеет возможности получить доступ к значению Md, поскольку оно зашифровано путем наложения на него "разового" ключа k.
- Используя расширенный алгоритм Евклида, пользователь Б вычисляет для числа k мультипликативно обратный элемент k-1 в поле вычетов по модулю N и восстанавливает подпись для сообщения M, а именно:
.
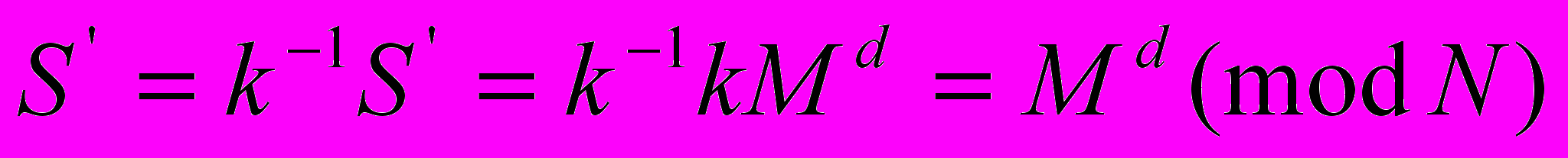Таким образом, цель достигнута – пользователь А сформировал правильную подпись пользователя Б, соответствующую сообщению M, причем он уверен, что подписывающий не знает содержания сообщения M.