2 Стандарты блочного шифрования
| Вид материала | Реферат |
- Системы блочного шифрования, 37.08kb.
- Реферат по дисциплине «Информационная безопасность» Тема: «Стандарты для алгоритмов, 241.55kb.
- Программа для демонстрации работы симметричного, 24.86kb.
- Методические указания к лабораторным работам по курсу «Теория информациии и основы, 449.11kb.
- Руководитель Касьян Владимир Николаевич подпись курсовой проект, 172.76kb.
- Классификация стандартов. Стандарты, регулирующие общие вопросы раскрытия информации., 385.43kb.
- Техническое задание «Разработка системы диагностики технического состояния маслонаполненного, 225.4kb.
- Введение. 2 Стандарты, нормы и правила., 167.3kb.
- Регламент второго съезда ит-директоров Украины, 76.58kb.
- Контрольная работа По дисциплине «Международные стандарты аудита» Тема «Классификация, 111.82kb.
6.3. Методы современного криптоанализа
Рассмотрим кратко методы, применяемые в современном криптоанализе. При их описании не будем вдаваться в математическое обоснование каждого метода, т.к. в некоторых случаях это требует серьезной математической подготовки, а ограничимся лишь общим обзором способов их применения.
6.3.1. Нетехнические методы взлома (Social Hacking)
Этот метод не имеет никакого отношения к математике, но, тем не менее, является очень распространенным. Состоит он в следующем:
Пользуясь человеческими слабостями и присущей каждому нормальному человеку склонностью к общению, злоумышленники не пренебрегают возможностью выудить у людей информацию, имеющую хотя бы косвенное отношение к паролям и ключевым словам. Людям, имеющим хорошую психологическую подготовку, не так уж сложно узнать, как зовут вашего супруга, детей, близких родственников, кота или собаку. Нередко какое-то из этих имен используется в качестве пароля. Злоумышленник, выудив эту информацию, получает возможность серьезно сузить зону поиска ключевых слов. Поэтому разумно не использовать в качестве пароля слова, так или иначе ассоциирующиеся с кругом ваших интересов.
6.3.2. Метод частотного анализа
Этот метод считается классическим еще со времен появления т.н. шифра Цезаря. Основан он на том, что в каждом языке существует определенная исторически сложившаяся статистическая структура, т.е. существуют определенные символы или комбинации символов, наиболее часто встречающиеся в естественной речи. При перехвате зашифрованного сообщения можно подсчитать частоту появления определенных символов12 и сопоставить их с вероятностями появления определенных символов или их комбинаций (биграммы, триграммы и т.д.), что в некоторых случаях может привести к однозначному дешифрованию отдельных участков зашифрованного сообщения.
Также этот метод основан на наличии вероятных слов. Речь идет о словах или выражениях, появление которых можно ожидать в сообщении с большой вероятностью. Так, в деловой переписке присутствуют шаблонные слова; в английском языке наиболее часто встречаются слова "and", "the", "are" и т.д.
В качестве классического примера использования частотного анализа может служить рассказ Э. По "Золотой жук".
6.3.3. Атака методом "грубой силы" (Brute Force Attack)
Данный метод является наиболее "грубым" с точки зрения криптоанализа. Он состоит в последовательном переборе всего ключевого пространства, с целью подбора использованного ключа. Основан он на все большем и большем развитии средств и возможностей вычислительной техники.
Скорость вскрытия методом грубой силы определяется двумя параметрами: количеством проверяемых ключей и скоростью проверки одного ключа. Большинство симметричных алгоритмов в качестве ключа могут использовать любую битовую последовательность фиксированной длины. Длина ключа, например, алгоритма DES составляет 56 бит, значит, всего может быть 256 возможных ключей. Длина ключей некоторых других алгоритмов равна 64 и 128 битам.
Скорость, с которой может быть проверен каждый ключ, имеет менее важное значение. Для проводимого анализа обычно предполагают, что скорость проверки ключа для каждого алгоритма примерно одинакова. В действительности скорость проверки ключей одного алгоритма может быть в два, три или даже десять раз больше, чем другого. Но так как для тех длин ключей, для которых ведется проверка, время поиска в миллионы раз больше, чем время проверки одного ключа, небольшие отличия в скорости проверки не имею значения.
Задача вскрытия грубой силой может быть хорошо реализована на параллельных процессорах. Каждый процессор проверяет подмножество пространства ключей. Процессорам не нужно обмениваться между собой информацией, единственным сообщением будет сообщение, сигнализирующее об успехе.
Однако стоимость таких многопроцессорных систем будет непомерно высокой и вряд ли окупит стоимость вскрытия зашифрованной информации. Хотя не стоит забывать, что мощь вычислительных средств непрерывно повышается, а стоимость их постоянно снижается.
6.3.4. Метод встречи посередине
Этот метод основан на следующем факте:
Если множество ключей криптоалгоритма замкнуто относительно композиции, то есть для любых ключей zi и zj найдется ключ zk такой, что результат шифрования любого текста последовательно на zi и zj равен шифрограмме этого же числа на zk, то есть
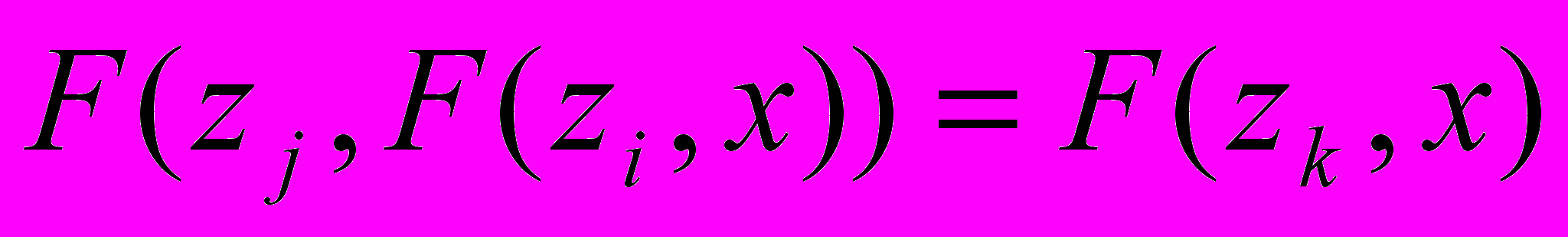 то можно воспользоваться этим свойством. Пусть нам нужно найти ключ zk. Тогда для нахождения ключа zk, необходимо найти эквивалентную ему пару ключей zi, zj. Данный метод криптоанализа основан на "парадоксе дней рождения". Известно, что если считать, что дни рождения распределены равномерно, то в группе из 24 человек с вероятностью 0,5 у двух человек дни рождения совпадут. В общем виде этот парадокс формулируется так: если a√n предметов выбираются с возвращением из некоторой совокупности размером n, то вероятность того что два из них совпадут, равна 1-exp(-a2 / 2) .
то можно воспользоваться этим свойством. Пусть нам нужно найти ключ zk. Тогда для нахождения ключа zk, необходимо найти эквивалентную ему пару ключей zi, zj. Данный метод криптоанализа основан на "парадоксе дней рождения". Известно, что если считать, что дни рождения распределены равномерно, то в группе из 24 человек с вероятностью 0,5 у двух человек дни рождения совпадут. В общем виде этот парадокс формулируется так: если a√n предметов выбираются с возвращением из некоторой совокупности размером n, то вероятность того что два из них совпадут, равна 1-exp(-a2 / 2) . Пусть известен открытый текст x и его шифрограмма y. Для текста x строим базу данных, содержащую случайное множество ключей z| и соответствующих шифрограмм w=F(z| , x), и упорядочиваем ее по шифрограммам w. Объем базы данных выбираем
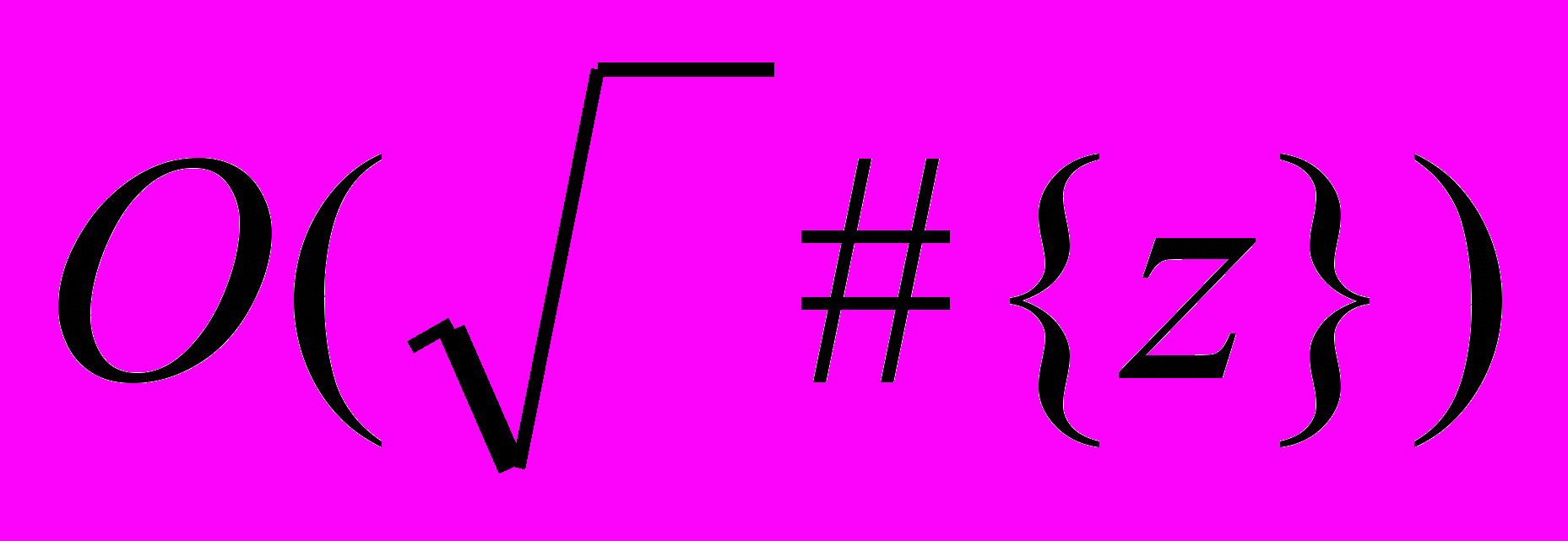 . Затем подбираем случайным образом ключи z| | для расшифровки текстов y и результат расшифрования v = F(z| | , y) сравниваем с базой данных. Если текст v окажется равным одной из шифрограмм w, то ключ z| z| | эквивалентен искомому ключу z. Временная сложность метода составляет О(√#{z}log#{z}). Множитель log#{z} учитывает сложность сортировки. Требуемая память равна О(√#{z}log#{z}) бит или О(√#{z}) блоков (предполагается, что длина блока и длина ключа различаются на ограниченную константу).
. Затем подбираем случайным образом ключи z| | для расшифровки текстов y и результат расшифрования v = F(z| | , y) сравниваем с базой данных. Если текст v окажется равным одной из шифрограмм w, то ключ z| z| | эквивалентен искомому ключу z. Временная сложность метода составляет О(√#{z}log#{z}). Множитель log#{z} учитывает сложность сортировки. Требуемая память равна О(√#{z}log#{z}) бит или О(√#{z}) блоков (предполагается, что длина блока и длина ключа различаются на ограниченную константу). Этот же метод применим, если множество ключей содержит достаточно большое подмножество, являющееся полугруппой.
Другое применение этого метода для множества, не являющегося полугруппой, можно продемонстрировать на хэш-функциях. Например, для подделки подписи надо найти два текста, обладающих одним хэш-образом. После этого можно подписанное сообщение заменить на другое, обладающее таким же хэш-образом. Поиск двух таких сообщений можно выполнить с использованием метода "встречи посередине". Сложность поиска равна О(√#{h}), где #{h} - число всевозможных хэш-образов.
6.3.5. Метод Полларда
Для нахождения ключа, например в криптоалгоритме, основанном на задаче логарифма на некоторой группе, достаточно решить задачу о встрече на графе случайного отображения. Для этого из двух разных стартовых точек x0|, x0| | строится траектория до входа в цикл. Затем одна из двух конечных точек, лежащих в цикле, фиксируется, а траектория другой продолжается до встречи с фиксированной точкой. Для функции f и точки входа x0 длина траектории составляет О(√#М ) шагов. Типичный вид этой траектории содержит предельный цикл длины О(√#М ) и отрезок до входа в цикл примерно такой же длины. В качестве индикатора замыкания траектории Поллард предложил использовать равенство xi = x2i , где xi - i-я точка траектории для входа x0. Это равенство будет выполняться всегда. Значение индекса i не превышает суммы длины пути до входа в цикл.
В среднем сложность нахождения равенства xi = x2i равна 3√(
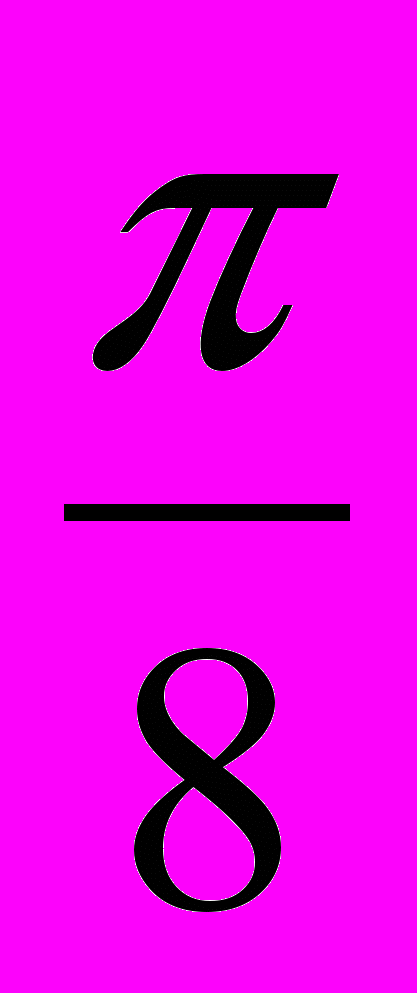 )#М. Сложность встречи, когда обе точки лежат в цикле, равна 0,5√(
)#М. Сложность встречи, когда обе точки лежат в цикле, равна 0,5√(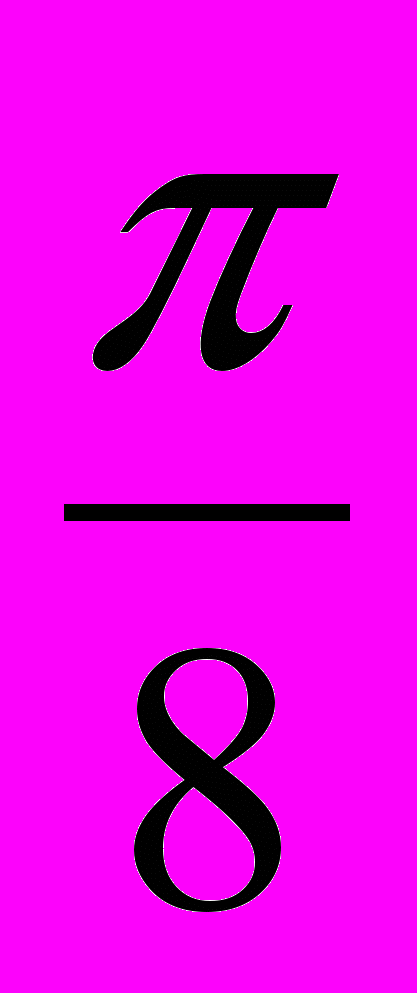 )#М. Таким образом, итоговая сложность равна 3,5 (
)#М. Таким образом, итоговая сложность равна 3,5 (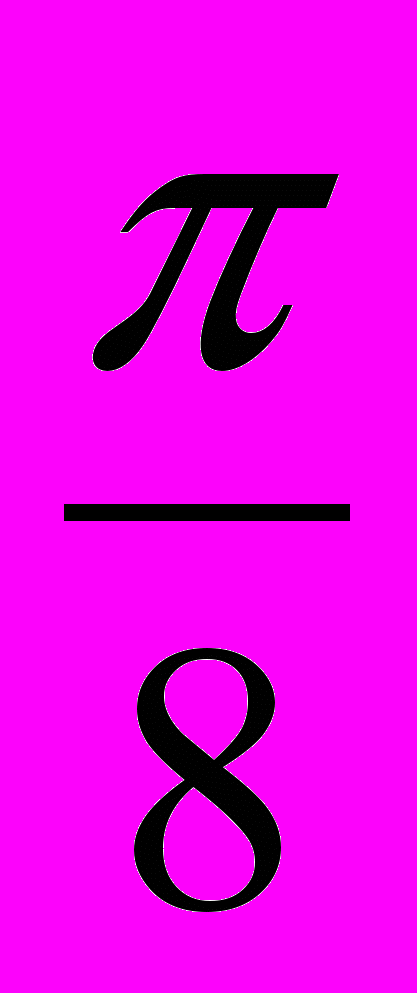 )#М.
)#М. 6.3.6. Дифференциальный криптоанализ
Дифференциальный метод криптоанализа (ДКА) был предложен Э.Бихамом и А.Шамиром в 1990 г. Дифференциальный криптоанализ - это попытка вскрытия секретного ключа блочных шифров, которые основаны на повторном применении криптографически слабой цифровой операции шифрования r раз. При анализе предполагается, что на каждом цикле используется свой подключ шифрования. ДКА может использовать как выбранные, так и известные открытые тексты.
Успех таких попыток вскрытия r-циклического шифра зависит от существования дифференциалов (r-1)-го цикла, которые имеют большую вероятность. Дифференциал i-го цикла определяется как пара (a, b)i такая, что пара различных открытых текстов x, x* c разностью a может привести к паре выходных текстов y, y* после i-ого цикла, имеющих разность b (для соответствующего понятия разности). Вероятность i-циклового дифференциала (a, b)i - это условная вероятность P(D y(i)=b | Dx=a ) того, что разность D y(i) пары шифротекстов (y, y*) после i-ого цикла равна b при условии, что пара текстов (x, x*) имеет разность Dx=a; открытый текст x и подключи циклов к(1) , к(2) ,...., к(i) независимыми и равновероятными.
Основная процедура ДКА r-циклического шифра с использованием выбранных открытых текстов может быть следующей:
1. На этапе предвычислений ищем множество (r-1)-цикловых дифференциалов
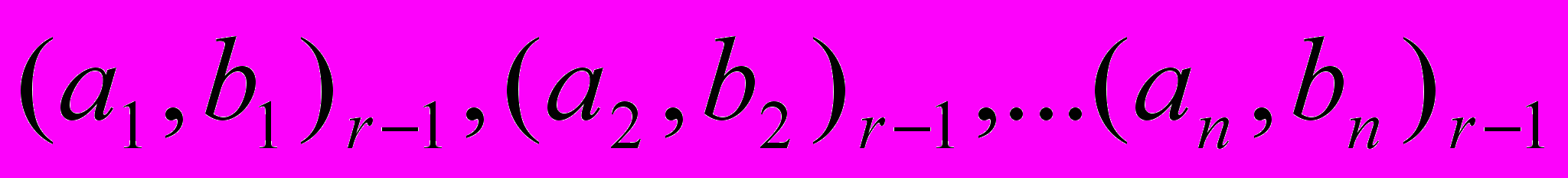 . Упорядочиваем это множество дифференциалов по величине их вероятности.
. Упорядочиваем это множество дифференциалов по величине их вероятности. 2. Выбираем открытый текст x произвольным образом и вычисляем x* так, чтобы разность между x и x* была равна a1. Тексты x и x* шифруются на подлинном ключе и после r циклов получаем пару шифртекстов y(r) , y*(r). Предполагаем, что на выходе предпоследнего (r-1)-ого цикла разность шифртекстов равна наиболее вероятной: Dy(r-1)=b1. Для тройки (D y(r-1), y(r), y*(r)) находим каждое возможное (если их несколько) значение подключа последнего цикла к(r). Добавляем его к количеству появлений каждого такого значения подключа к(r).
3. Повторяем п.2 до тех пор, пока одно или несколько значений подключа к(r) не станет появляться чаще других. Берем этот подключ или множество таких подключей в качестве криптографического решения для подключа к(r).
4. Повторяем пп.1-3 для предпоследнего цикла, при этом значения y(r-1) вычисляются расшифрованием шифртекстов на найденном подключе последнего цикла к(r). Далее действуем аналогично, пока не будут раскрыты ключи всех циклов шифрования.
6.3.7. Линейный криптоанализ
В открытой печати линейный метод криптоанализа впервые был предложен японским математиком Мацуи. Метод предполагает, что криптоаналитик знает открытые и соответствующие зашифрованные тексты.
Обычно при шифровании используется сложение по модулю 2 текста с ключом и операции рассеивания и перемешивания. Задача криптоаналитика - найти наилучшую линейную аппроксимацию (после всех циклов шифрования) выражения
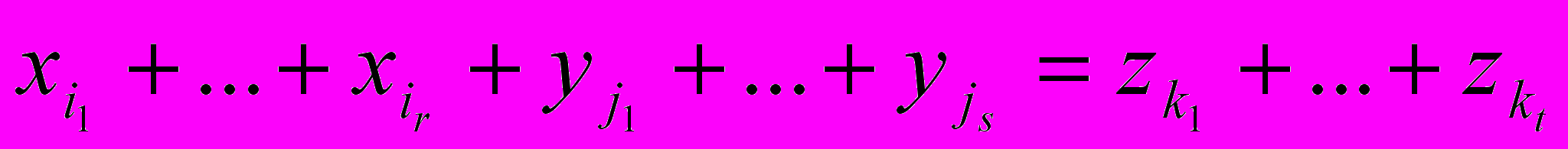
Пусть PL - вероятность того, что это равенство выполняется, при этом необходимо, чтобы PL - 1/2 и величина |PL-1/2| должна быть максимальна. Если |PL-1/2| достаточно велика, и криптоаналитику известно достаточное число пар открытых и соответствующих зашифрованных текстов, то сумма по модулю 2 бит ключа на соответствующей позиции в правой части равенства равна наиболее вероятному значению суммы по модулю 2 соответствующих бит открытых и зашифрованных текстов в левой части. Если PL > 1/2, то сумма бит ключа в правой части равна нулю. Для нахождения каждого бита собственно ключа теперь нужно решить систему линейных уравнений для известных линейных комбинаций этих бит, но эта процедура не представляет сложности, так как сложность решения системы линейных уравнений описывается полиномом не более третьей степени от длины ключа.
Требуемое для раскрытия ключа количество N пар открытых и зашифрованных текстов (блоков) оценивается выражением:
N
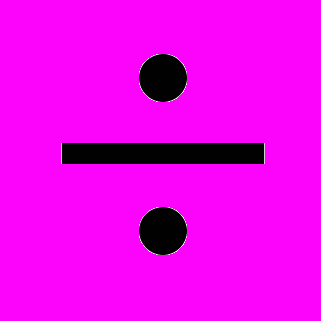 |PL-1/2| -2 .
|PL-1/2| -2 .Для раскрытия ключа шифра DES этим методом необходимо 247 пар известных открытых и зашифрованных текстов.
Итак, нами были рассмотрены наиболее употребительные методы современного криптоанализа. Разумеется, список этих методов далеко не полон и не претендует на исчерпывающее изложение. Перед нами стояла задача осветить лишь общие концепции их использования.
Следует отметить, что использование многих способов раскрытия шифров, особенно методов линейного и дифференциального криптоанализа, требует от криптоаналитика серьезной математической подготовки, что, разумеется, значительно осложняет возможности использования этих методов.
Заключение
Данная курсовая работа не претендует на исчерпывающее изложение содержания современной криптографии, являющейся чрезвычайно многообразным и сложным разделом современной прикладной математики. Я преследовал лишь цель в доступной форме изложить введение в общую проблематику и методологию криптографии.
При написании данной курсовой работы я имел намерение дать общую картину современной криптографии в таком изложении, которое было бы легко доступно людям, не имеющим специальной математической подготовки, а также рассмотреть некоторые моменты, связанные с разработкой современных скоростных блочных шифров, ориентированных на программную и/или аппаратную реализацию. К вопросам общего характера относится материал, посвященный значению криптографии в информационном обществе, двухключевой криптографии, электронной цифровой подписи и ряду хорошо известных одноключевых шифров. Рассмотрение же проблемы построения скоростных блочных шифров также представляет достаточно широкий интерес ввиду их большого значения в современных технологиях защиты информации.
Литература
- Аршинов Н. М., Садовский Л. Е. Коды и математика. – М.: Наука, 1983
- Жельников В. Криптография от папируса до компьютера. – М.: ABF, 1996
- Молдовян А. А., Молдовян Н. А., Гуц Н. Д., Изотов Б. В. Криптография. Скоростные шифры. – СПб.: БХВ-Петербург, 2002
- Петров А. А. Компьютерная безопасность. Криптографические методы защиты. – М.: ДМК, 2000
- Чепмен Д. Разработка защищенных приложений в среде Visual Basic. – Москва – Санкт-Петербург – Киев: Вильямс, 2000
- Шнайер Б. Прикладная криптография. – СПб.: БХВ-Петербург, 2002
- Информация, шифры, компьютеры // Chip. – июнь 2001
- tography.ru
1 Хотя это и может показаться парадоксальным, но для создания надежного алгоритма шифрования необходимо стремится к тому, чтобы он был известен как можно более широкому кругу специалистов. Здесь нет никакого противоречия – чем больше людей вовлечено в оценку качества алгоритма, тем больше вероятность того, что будут тщательно проанализированы его сильные, а самое главное, слабые стороны.
2 Шенноном был показан способ составления совершенно секретной криптограммы. Она должна быть избавлена как от избыточности исходного текста, так и от избыточности ключа. Способ, предложенный им, заключался в следующем: сначала устраняется избыточность текста с помощью применения к нему какого-либо метода эффективного кодирования. Вслед за этим к получившемуся безызбыточному тексту применяем шифр со случайным ключом, для которого (применительно к русскому алфавиту) Li=mi+ki (mod 31).В этом равенстве mi и li являются номерами i-ой буквы шифруемого текста и криптограммы соответственно, а каждое ki выбирается случайным образом среди чисел 0,1,2,…,30, так, что выбор любого из этих чисел одинаково возможен.
Недостатком такой совершенно секретной системы является то, что вместе с шифрованным сообщением требуется посылать такое же по объему сообщения, содержащее информацию о случайном ключе, поскольку он заранее неизвестен. Поэтому эта система практически неприемлема.
3 FPGA – чипы, обладающие возможностью перебирать до 30 млн. ключей в секунду
4 ASIC – чипы, способные перебирать до 200 млн. ключей в секунду
5 Обычно он равен 10-3 – 10-6 в зависимости от области применения
6 Статья "Новые направления в криптографии", 1967 г.
7 На основании свойства обратимости операции
8 В качестве такой функции У. Диффи и М. Хеллман предложили функцию дискретного возведения в степень
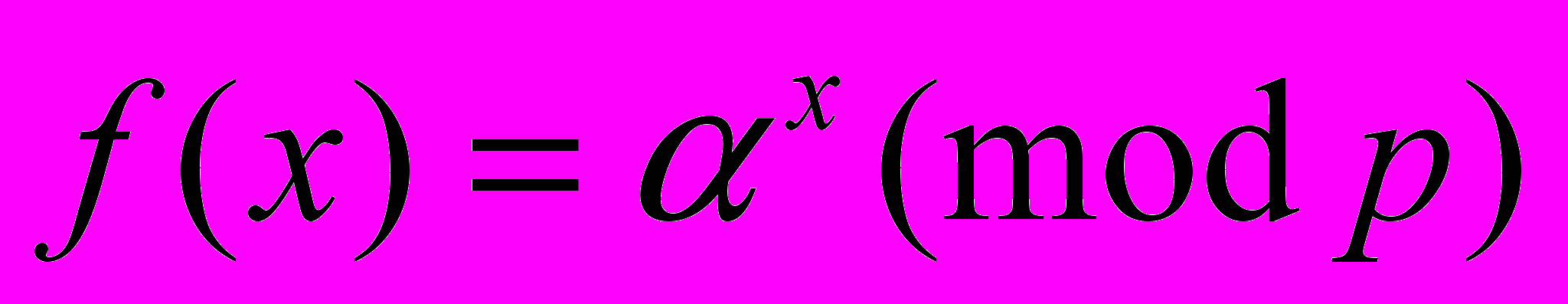 , где x – целое число, 1 ≤ x ≤ p – 1. Обратной к этой функции является функция f--1(y), которая ставит в соответствие заданному значению y такое значение x, для которого
, где x – целое число, 1 ≤ x ≤ p – 1. Обратной к этой функции является функция f--1(y), которая ставит в соответствие заданному значению y такое значение x, для которого 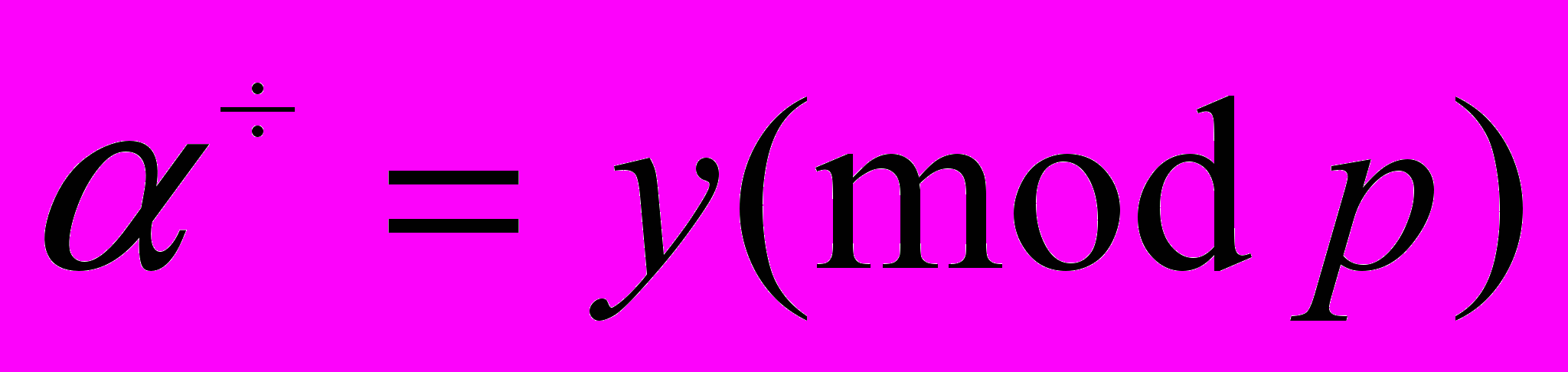 . Задача нахождения такого x называется задачей дискретного логарифмирования. Решение такой задачи является вычислительно неосуществимым для модулей p ≥ 512.
. Задача нахождения такого x называется задачей дискретного логарифмирования. Решение такой задачи является вычислительно неосуществимым для модулей p ≥ 512.9 См. приложение 1
10 Весом Хэмминга называется целочисленная функция WH, значение которой равно числу ненулевых компонентов вектора X.
11 См. пункт 1.2.
12 См. приложения 2, 3
