2 Стандарты блочного шифрования

Вид материала

Реферат

Содержание 2.2. Ассиметричные алгоритмы шифрования. Стандарт ассиметричного шифрования RSA Рисунок 5. Схема ассиметричного шифрования

Подобный материал:

• Системы блочного шифрования, 37.08kb.
• Реферат по дисциплине «Информационная безопасность» Тема: «Стандарты для алгоритмов, 241.55kb.
• Программа для демонстрации работы симметричного, 24.86kb.
• Методические указания к лабораторным работам по курсу «Теория информациии и основы, 449.11kb.
• Руководитель Касьян Владимир Николаевич подпись курсовой проект, 172.76kb.
• Классификация стандартов. Стандарты, регулирующие общие вопросы раскрытия информации., 385.43kb.
• Техническое задание «Разработка системы диагностики технического состояния маслонаполненного, 225.4kb.
• Введение. 2 Стандарты, нормы и правила., 167.3kb.
• Регламент второго съезда ит-директоров Украины, 76.58kb.
• Контрольная работа По дисциплине «Международные стандарты аудита» Тема «Классификация, 111.82kb.

2.2. Ассиметричные алгоритмы шифрования. Стандарт ассиметричного шифрования RSA

Ассиметричное шифрование предполагает наличие двух ключей. Первый ключ – открытый (public) – распространяется совершенно свободно, без всяких мер предосторожности, а второй – закрытый, личный (private), нужно держать в секрете. Любое сообщение, зашифрованное с использованием одного из этих ключей, может быть расшифровано только с использованием второго ключа. Как правило, отправитель сообщения пользуется открытым ключом получателя, а получатель – своим личным.

В ассиметричной схеме шифрования оба ключа являются производными от единого порождающего мастер-ключа (master-key), как это показано на рис. 6. Когда два ключа сформированы на основе одного, они зависимы в математическом смысле, но ни один из них не может быть вычислен на основе другого. После того, как вычислены оба ключа, мастер-ключ уничтожается и таким образом пресекается любая попытка восстановить в дальнейшем значения производных от него ключей.



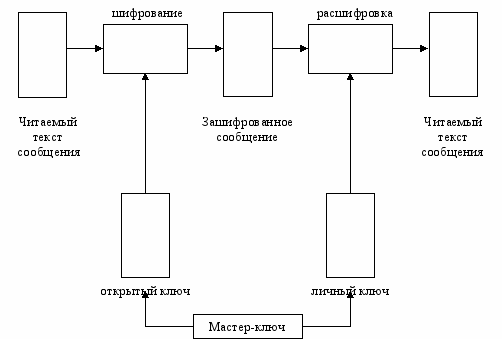
Рисунок 5. Схема ассиметричного шифрования

Идея асимметричных алгоритмов тесно связана с развитием теории односторонних функций и с теорией сложности. Под односторонней функцией мы будем понимать легковычисляемое отображение f(x): X Y, x  X, при этом обратное отображение является сложной задачей. Она называется трудновычисляемой, если нет алгоритма для ее решения с полиномиальным временем работы. Легковычисляемой будем называть задачу, имеющую алгоритм со временем работы, представленным в виде полинома низкой степени относительно входного размера задачи, а еще лучше алгоритм с линейным временем работы.

Развитием идеи односторонних функций явилось построение односторонних функций с секретом (с потайным ходом). Такой функцией называется f(x) = y⁸, значение которой, как и в предыдущем случае, легко вычислить, тогда как обратное значение без знания некоторого секрета трудно вычислить. Знание же секрета позволяет достаточно просто реализовывать операцию обращения односторонних функций с секретом. На практике при применении асимметричного алгоритма шифрования в роле секретного ключа выступает само знание секрета, а в роле открытого ключа – знание процедуры вычисления односторонней функции с секретом.

Вместе с тем необходимо отметить, что стойкость большинства современных асимметричных алгоритмов базируется на двух математических проблемах, которые на данном этапе являются трудновычисляемыми даже для метода “грубой силы”:

• дискретное логарифмирование в конечных полях;
  
• факторизация больших чисел.
  

Поскольку на сегодняшний день не существует эффективных алгоритмов решения данных задач либо их решения требуют привлечения больших вычислительных ресурсов или временных затрат, эти математические задачи нашли широкое применение в построении асимметричных алгоритмов. Их стойкость рассматривается как возможность свести проблему вскрытия алгоритмов к решению одной из вышеперечисленных математических головоломок.

Самым распространенным алгоритмом асимметричного шифрования является алгоритм RSA, названный по первым буквам имен его создателей (Rivest, Shamir, Adleman). Разработчиком данного алгоритма удалось эффективно воплотить идею односторонних функций с секретом. Стойкость RSA базируется на сложности факторизации больших целых чисел.

Каждый участник информационного обмена генерирует пару ключей (открытый и секретный) в соответствии со следующими правилами:

1. Выбираются два больших простых целых числа p и q приблизительно одинакового размера. Выбор чисел p и q определяется следующими соображениями:
   

• увеличение порядка чисел введет к замедлению операции зашифрования/расшифрования;
  
• увеличение порядка чисел p и q ведет к увеличению стойкости алгоритма, поэтому при выборе чисел следует руководствоваться практической необходимостью. Так, например, при реализации RSA в интеллектуальных карточках с точки зрения скоростных параметров системы не следует выбирать слишком большие p и q в связи с ограниченными вычислительными возможностями, заложенными в данных устройствах. На практике обычно рекомендуется выбирать числа, содержащие порядка 150-200 десятичных знаков.
  

2. Вычисляется модуль системы n = pq и (n) = (p-1)(q-1) – функция Эйлера
   
3. Выбирается достаточно большое число е, удовлетворяющее условию:
   

1 e (n), и взаимно простое с (n).

4. Используя расширенный алгоритм Евклида, вычисляется большое целое число d, отвечающее условию:
   

Ed = 1 (mod (n))

1 < d < (n)

Таким образом, секретным ключом является пара чисел (n,d), а открытым – пара чисел (n,e). Открытый ключ помещается в общедоступный справочник

После выбора параметров системы (n, e, d) абонент готов к приему зашифрованных сообщений. Их передача состоит из следующих шагов:

1. Входное сообщение разбивается на блоки m_i их размер определяется целым k, соответствующим неравенству 10^k-1< n < 10^k.
   
2. Вычисляется значение c = 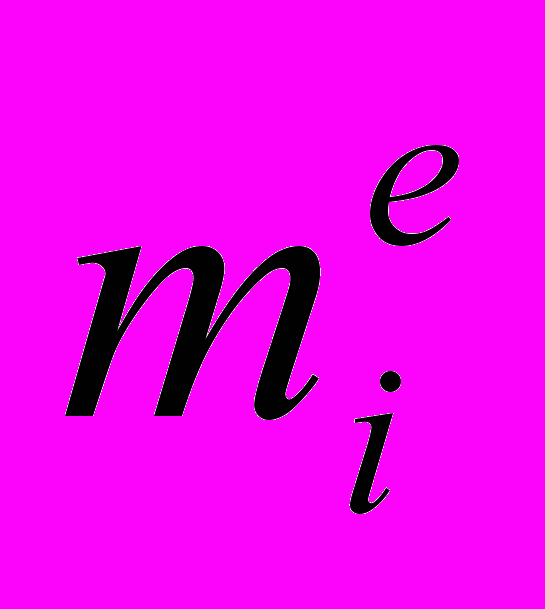mod n.
   
3. Значение c_i, которое является зашифрованным блоком сообщения, посылается по открытым каналам передачи данных.
   

Расшифрование заключается в вычислении значения m_i =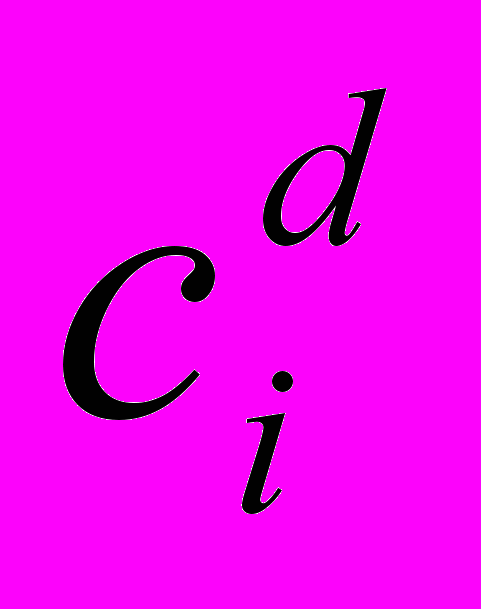mod n.

Доказательством того факта, что расшифрование выполняется только абонентом, знающим секретную экспоненту зашифрования d, является c_i^d mod n = m_i^{e d} mod n, с учетом, что ed = 1 (mod (n)). При этом получаем ed = 1 + k(n), где k - целое число, удовлетворяющее этому равенству. Поскольку m_i^(m) mod n – единичный элемент группы относительно операции умножения, элемент m_i тоже принадлежит к данной группе. В этом случае:

c_i^d mod n = m_im_i^k(m)mod n = m_i.

Среди наиболее известных недостатков алгоритма RSA можно выделить некорректный выбор значений p и q. Числа p и q должны быть простыми и не содержаться ни в одной из известных таблиц простых чисел. Эти числа также не должны быть близкими друг к другу. Если (p - q) / 2 мало и (p + q) / 2 немного больше, чем n, то при (p + q)² / 4 – n C (p – q)² / 4 левая часть равенства образует полный квадрат. При факторизации n перебираем целые числа на соответствие неравенству x  n до тех пор, пока не найдем такое значение, что x² – n = y². Тогда p = x + y и q = x – y . Учитывая изложенный факт, а также ряд других атак, основанных на неправильном выборе чисел p и q, сформулируем следующие требования к выбору чисел p и q:

1. Данные числа должны быть большими числами одинаковой длины.

2. Различие между p и q должно быть большим.

3. Числа p и q должны быть строго простыми. Число называется строго простым, если выполнены условия:

а) р – 1 должно иметь большой простой делитель (обозначим его через r);

б) р + 1 должно иметь большой простой делитель ;

в) r – 1 должно иметь большой простой делитель.

Требование а) обусловлено противодействием алгоритмам факторизации n (один из таких алгоритмов был предложен Поллардом). Аналогично обосновывается требование б). Выполнение на практике требования в) позволяет противостоять циклическим атакам.