А, поэтому необходимо вернуть астрономии статус самостоятельной дисциплины среди других дисциплин естественно-научного профиля в содержании среднего образования

Вид материала

Документы

Содержание Модель непрерывной поддержки и вовлечения школьников и студентовв научно-исследовательскую деятельность Теоретический блок Диагностический блок Блок методических разработок к лабораторным работам для профильных физико-математических 10-11-х классов Операционный блок Нормативный блок А. Методы обучения учащихся решению стандартных физических задач с помощиью алгоритмов и блоков Частный алгоритм Алгоритмические предписания решения задач на динамику Алгоритмические предписания решения задач на тему Памятка правил сложения векторов Таблица 2.4 Пример классификации задач по блокам

Подобный материал:

• Аннотация рабочей программы дисциплины математическое моделирование в расчетах на ЭВМ, 67.24kb.
• Аннотация рабочей программы дисциплины математические методы моделирования в геологии, 58.86kb.
• Учебная программа по специальностям: 020700 История историк, 177.18kb.
• Рабочая программа учебной дисциплины менеджмент для специальностей технического профиля, 111.78kb.
• Данный курс разработан для учащихся 9-х классов, ориентирован на выбор ими естественно, 170.71kb.
• Реализующих образовательные программы среднего профессионального образования на 2010/2011, 2581.19kb.
• Реализующих образовательные программы среднего профессионального образования на 2010/2011, 1360kb.
• Методические рекомендации для самостоятельной работы студентов, 532.2kb.
• «О структуре естественно-научного факультета», 54.97kb.
• Методическое объединение учителей предметов естественно научного цикла Банк данных, 489.05kb.

Рис. 2.7. Модель непрерывной поддержки и вовлечения школьников и студентов
в научно-исследовательскую деятельность

В такой системе осуществляется сквозное многоступенчатое непрерывное вовлечение учащихся в цепочку исследовательской деятельности «школьник – студент – аспирант – остепенённый учёный».

2.3.3. Элементы модульно-рейтинговой системы обучения


Модуль - вообще - отделяемая, относительно самостоятельная часть какой-нибудь системы, организации [8, с.361]. Термин «модуль» в педагогике употребляется в нескольких аспектах. Под модулем понимается единица учебного процесса, имеющая продолжительность 90 минут с двумя перерывами (30 + 30 + 30 минут) или имеющая продолжительность 1,5 часа с одним перерывом (45+45 минут), в течение которого осуществляется обучение одной дисциплине. В ФМК школы №40 временным модулем является 3-4 урока по 45 минут, в течение которых преподается одна дисциплина. Модульная система обеспечивает организационную сторону «моделей погружения» концентрированного обучения. Во-вторых, имеется в виду предметный модуль или интегративный курс-модуль, включающий в себя несколько близких предметов. Например, в учебном процессе ФМК школы №68 г. Ульяновска изучается курс радиотехники, на котором прививаются основы творческо-конструкторской деятельности и который по сути является интегрированным курсом-модулем, основными предметами которого являются физика, математика, лабраторный физический практикум.

Модульное обучение - одна из заметных педагогических инноваций. О преимуществах модульной системы обучения говорят многие исследователи. В диссертационном исследовании Н.В. Блохина [167] проведен концептуальный анализ модульного подхода в профессиональном обучении, сделан многоплановый сравнительный анализ эффективности модульного обучения с традиционным. Результаты исследований показали, что учащиеся экспериментальных групп по большинству показателей превосходили учащихся контрольных групп по развитию следующих профессионально важных навыков: активности, собранности, гибкости мышления, степени ответственности, самоконтролю, восприятию и памяти, распределению и переключению внимания.

В рамках инновационного педагогического поиска выступает модульно-рейтинговая технология. В данной технологии в целости и органическом единстве рассматриваются модульное обучение, рейтинговый контроль, который ориентирован не только на обеспечение прочных знаний, но и на подлинную индивидуализацию обучения школьников (студентов). Рейтинговый контроль знаний применяется, во-первых, при оценке олимпиадных работ: для трех туров олимпиад, проводимых среди 8- и 9-классников в целях отбора в ФМК, применяется метод рейтинговых оценок, являющихся интегральными оценками накопительного типа: победители определяются по сумме баллов трёх туров олимпиад. Рейтинговый контроль знаний применяется и при проверке контрольных работ: одна правильно решенная задача оценивается от 5 до 10 баллов в зависимости от трудности, затем сумма баллов переводится в оценку пятибалльной шкалы. Так учащиеся привыкают к оценке письменной работы по физике и математике на вступительных экзаменах в вуз. Традиционная пятибалльная (фактически - трёхбалльная шкала - 5, 4, 3) шкала уменьшает объективность оценки и не способствует активизации учащихся, оценка перестает быть сильным стимулирующим элементом учебного процесса.


2.3.4. Учебно-методический комплекс


Рассмотренные методы и формы интенсивного обучения способствуют развитию творческих способностей и раскрытию одарённости учащихся [168, 169]. Однако каждый преподаватель профильной дисциплины ФМК должен иметь эффективноее средство - учебно-методический комплекс (УМК) - в целях повышения результативности учебного процесса. В.Г. Скатецкий и В.И. Яшкин определяют УМК «как систему учебных пособий, дидактических средств, методик и организационных операций, органически связанных между собой», позволяющих обучаемому овладеть содержанием курса соответствующей дисциплины и «служащих для успешного решения задач, соответствующих данной специальности» [170].

В диссертации Л.Е. Солянкиной защищено положение об учебно-методическом комплексе как средстве учебно-методического обеспечения деятельности учащихся, как необходимого элемента программы профессионального саморазвития в инновационном учебном заведении [25, 171].

Качественное обучение в ФМК основным дисциплинам, входящим в блок профессионально значимых, невозможно без создания авторского УМК, так как содержание профессионально ориентированного образования отличается от содержания общего среднего образования. Кроме того, как было сказано выше, в основе организации учебного процесса в ФМК школы №40 лежат модели КО (по 3-4-х часовым блокам), что предполагает изучение предметов по специально созданным методикам с опорой на реальные методические рекомендации, учебные пособия, специально разработанные и изданные преподавателями УлГУ для успешного обучения в рамках моделей КО.

Главной целью УМК является обеспечение целенаправленной и качественной НПП учащихся профильных ФМК в короткие сроки.

Например, УМК автора настоящей работы состоит из следующих элементов:

1. Теоретический блок, включающий изданные учебные пособия (интенсивные курсы): «Механика и молекулярная физика» [172], «Электричество и магнетизм» [173], «Колебания и волны» [174], «Введение в теорию гравитации и космологию» [147], научные статьи [175 и др.].

2. Диагностический блок, включающий в себя:

• компьютерные тесты по физике по всему курсу физики (всего 11 тестов по 20 задач в каждом) в электронном варианте и изданные в виде отдельных брошюр в трех частях в соавторстве с преподавателем информатики Жарковой Г.А. [176, 177, 178];
  
• текстовые тесты по физике, составленные автором по всему курсу физики и изданные в виде брошюры (всего 14 тестов по 16 задач в каждом) [179];
  
• расчетно-графические задания по физике, разработанные автором и изданные в форме брошюры [180]. Вступительные задания по физике и математике в физико-математические классы УлГУ, изданные в двух брошюрах [181, 182];
  
• варианты контрольных работ разного уровня сложности по всему курсу физики;
  
• комплект вопросов для прохождения итогового и заключительного контроля знаний; пакет экзаменационных билетов вступительных экзаменов в УлГУ за прошлые годы.
  

3. Блок методических разработок к лабораторным работам для профильных физико-математических 10-11-х классов, включающий методическое пособие по молекулярной физике и термодинамике [183], а также 20 методических руководств в компьютерном варианте к лабораторным работам по другим разделам физики (5 из них в соавторстве). Каждое руководство включает в себя: целевой компонент, описание теории исследуемого процесса, описание экспериментальной установки или схемы, её принципа действия, методику эксперимента, методические рекомендации по оформлению отчёта, список контрольных вопросов. Освоение содержания методических руководств способствует развитию у учащихся начальных профессиональных умений и навыков научной экспериментальной работы: уровень экспериментальных заданий повышенной сложности по сравнению с общеобразовательным, требования к обработке эксперимента соответствуют вузовским (расчёт прямых и косвенных погрешностей, построение графиков и их спрямление в соответствующих координатах с целью установления математических зависимостей исследуемых процессов и определения из них требуемых физических параметров).

4. Операционный блок, включающий полный комплект отдельных методических разработок по физике и астрономии на каждое практическое занятие (компьютерный и рукописный варианты), а также методических рекомендаций к ним.

5. Нормативный блок, состоящий из нормативных документов МО РФ, программ, тематических планов, протоколов, журналов посещения занятий и других документов.

6. Методические рекомендации для работы над рефератами по физике и астрономии, для работы с опорами (блок относительной самостоятельности).

7. Архив: продукция учащихся ФМК (лучшие рефераты, доклады и т.д.).

Применение УМК повышает эффективность освоения учащимися учебного предмета. УМК для учителя-предметника - это многофункциональный объект, предназначенный для более эффективного осуществления профессиональной направленности преподавания физики, это система, от взаимодействия элементов которой зависит конечный результат - уровень НПП.

2.3.5. Метод опорных конспектов


В 1970-е годы В.Ф. Шаталовым была разработана система крупноблочного введения теоретических знаний, которая способствовала ускоренному обучению учащихся и формированию прочных знаний. Основу его методики составляет использование опорных конспектов (ОК) в процессе обучения. К.Г. Селевко к педагогическим технологиям, основывающимся на активизации и интенсификации деятельности учащихся относит технологию интенсификации обучения на основе схемных и знаковых моделей учебного материала В.Ф. Шаталова [154, с.69-73]. Система В.Ф. Шаталова получила широкое распространение среди преподавателей различных дисциплин в школах. В школе №40 г. Ульяновска по методике В.Ф. Шаталова работал Заслуженный учитель РФ, Соросовский учитель В.С. Тейтельман [184].

Опора - способ выделения существенного, главного в учебном материале и средство наглядности. Учебная опора является одновременно формой, методом и средством обучения, «она сочетает в себе наглядное знаково-символическое, схематическое, логически последовательное отображение главного, существенного в изучаемом материале с широким использованием ассоциаций и цветовой гаммы» [185, с.7]. В ОК включается только принципиально важный материал, расположенный в строгой логической последовательности. В диссертационном исследовании Н.А. Криволаповой [185] обосновывается возможность использования ОК в системе развивающего обучения как средства развития логического и творческого мышления учащихся путем привлечения учащихся к самостоятельной разработке опорных конспектов, реализуемых в различных формах. Ею также сформулированы принципы построения ОК:

1. Полное отражение основного (базового) содержания учебного материала в опорном конспекте с чётким выделением главного.

2. Строгая логическая последовательность в расположении материала (должны чётко прослеживаться причинно-следственные связи).

3. Оптимальная наглядность, лаконичность и яркость изложения: информация должна быть подана так, чтобы любой ученик мог самостоятельно усвоить и запомнить материал соответствующего блока знаний.

4. Развитие самостоятельности, инициативности и творческих способностей учащихся путём привлечения их к разработке ОК, а также путем включения в ОК вопросов, задач и заданий творческого характера.

5. Постепенное повышение степени самостоятельности учащихся и сложности заданий при разработке ОК.

Известно, что намеренное использование даже нескольких простых знаков расширяет возможности головного мозга и способности к размышлению: схема, рисунок, модель экономит время и усилия при восприятии, сокращает время эвристики. В диссертационном исследовании М.С. Атаманской на основании изучения состояния преподавания физики в 13 школах г. Ростова-на-Дону в течение 5 лет установлено [186, с.21]:

• информацию предметного содержания в форме эксперимента воспринимают 100% учащихся;
  
• в форме мысленного эксперимента - 40%;
  

• в виде картинок, фотографий - 95%; моделей - 95%; схем - 50%;
  
• в виде цифр и формул - 40%;
  
• динамику наблюдаемого процесса отображают в виде серии последовательных рисунков 70% учащихся, графиков - 20%, формул - 10%.
  

В.С. Тейтельман сочетал вузовскую методику: чтение лекций, семинаров, зачётов, проведение лабораторного спецпрактикума с методом опорных конспектов. Метод опор использовался, чтобы быстро и эффективно пройти теоретический материал всего курса физики за 1,5 года. Интенсификация обучения реализовывалась благодаря свойствам головного мозга воспринимать образную информацию с меньшим напряжением: учебный материал становился доступным и хорошо запоминался. В результате использования метода опор образовывались огромные резервы времени за счет того, что отпадала необходимость конспектировать новый материал, изучаемый на уроке, так как каждый учащийся имел готовые блоки опор за 10-й и за 11-й классы, в которых в сжатом виде содержалась теоретическая информация, и учитель с учениками работал по этим конспектам.

Работа с опорой отражала системно-деятельностный подход учителя и ученика к изучению теоретического материала: учащиеся в классе и дома дополняли содержание опор. При воспроизведении учебного материала срабатывала зрительная память: перед глазами возникала картинка-опора с графиками, рисунками, формулами, которая являлась стержнем, опорой в полном смысле этого слова в ответе учащегося. Но это было творческое воспроизведение, продуктивное, так как вокруг опоры разворачивался ответ с примерами, своими замечаниями, наблюдениями, обобщениями.

Учебная опора позволяла экономить время, которое затем использовалось на решение задач. Многолетние наблюдения за работой В.С. Тейтельмана показали, что при использовании метода опор в сочетании с вузовскими методами:

• повышается познавательная активность учащихся, возрастает их интерес к предмету, потому что он становится понятным;
  
• наблюдается рост интеллектуального развития учеников, развитие их творческого мышления;
  
• пропадает страх к предмету, появляется понимание предмета, желание понять глубже и вместе с ними - уверенность в себе, в своих силах и способностях.
  

Эффективность использования ОК в системе интенсивного обучения показывают результаты вступительных экзаменов в вузы выпускников ФМК В.С. Тейтельмана [125].


2.3.6. Информационные технологии


Само понятие «новые информационные технологии» (НИТ) предполагает повышение эффективности, оптимизацию учебно-воспитательного процесса в результате его компьютеризации. Под информационной компьютерной технологией понимается технология, предметом и продуктом труда которой является информация, а орудием труда - ЭВМ [187].

В течение последних 20 лет в развитии методов и хранения и использования информации произошла настоящая революция: информационная технология стала частью повседневной реальности. Решение проблемы повышения эффективности и обеспечения гарантированного качества обучения многие теоретики и практики- педагоги связывают сегодня с применением в учебном процессе новых информационных технологий, включающих в себя современные средства коммуникаций, компьютерные среды, интерактивное видео, системы видеотекста, мультимедиа и т.п.

В работах многих учёных анализируется практический опыт использования педагогических программных средств (ППС), а также автоматизированных учебных курсов (АУК) - компьютерных программ, которые включают в себя модули различного назначения: демонстрации, обучение, контроль знаний, умений, навыков. В работе [188] проведено исследование качественного и количественного анализа эффективности применения ППС и АУК при использовании в учебно-образовательном процессе естественно-научного направления. В результате сделаны выводы:

• использование АУК позволяет повысить качество знаний;
  
• использование компьютерных средств существенно сокращает временные затраты; освободившееся время используется на углубленное изучение материала, для решения задач повышенного уровня сложности;
  
• качественно изменяется контроль за учебной деятельностью, снижаются временные затраты преподавателя на проверку знаний учащихся при использовании компьютерного тестового контроля и обработке результатов контроля;
  
• учащиеся экспериментальных групп на подготовку домашних заданий затрачивали меньше времени, что снижало напряженность и утомляемость.
  

В работе [188] показано, что использование компьютерных технологий обеспечивает высокоэффективную подготовку учащихся к жизненному самоопределению, выбору профессиональной карьеры.

В школе №40 компьютерные технологии применяются в образовательном процессе НПП учащихся профильных ФМК для контроля знаний по физике. Автором данной работы был разработан комплекс тестов по основным разделам физики: механика - 3 варианта тестов по 22 задачи в каждом, молекулярная физика и термодинамика - 2 варианта по 17 задач в каждом, электричество - 1 тест, содержащий 20 задач, магнетизм и электромагнитные колебания - 2 варианта по 20 задач в каждом, оптика - 1 тест - 23 задачи. Всего в комплект тестов входит 183 задачи. Каждый тест содержит несколько качественных вопросов, остальные задачи расчётные: среднего и высокого уровня сложности. В целом тесты предназначены для учащихся специализированных ФМК и абитуриентов, готовящихся в вуз физико-технического профиля. Данные тесты по форме являются закрытыми, то есть из предлагаемых ответов нужно выбрать правильный. Чтобы уменьшить вероятность угадывания, число предлагаемых ответов в каждом задании варьируется от 5 до 7. Причём в их число входит позиция «У меня свой ответ» на случай, если ни один из ответов не устраивает испытуемого. Правильный ответ не выделяется среди дистракторов (других ответов): ответы-дистракторы подобраны так, что заставляют размышлять испытуемого, то есть являются работающими. Преподавателем информатики Г.А. Жарковой была составлена программа, с помощью которой данные тесты были выведены на компьютер, причём таким образом, что на компьютере происходит перемешивание как вопросов, так и ответов, что не позволяет при тестировании привыкать к их порядку, то есть у правильного ответа нет постоянного номера. Г.А. Жарковой также была описана процедура перевода тестов в компьютерный вариант и процедура компьютерного опроса. В результате возник блок дидактических материалов:

• методические пособия в трёх частях: часть I и часть II включают непосредственно содержание всех тестовых заданий [176-177], в части III описана процедура перевода тестов в компьютерный вариант [178];
  
• компьютерный вариант тестов на диске.
  

Чтобы успешно справиться с тестами, учащиеся должны хорошо владеть теоретическим материалом и алгоритмами решения стандартных задач и задач повышенной трудности. Каждый тест рассчитан на 45 минут - в среднем по 2 минуты на задачу.

Десятилетний опыт работы с компьютерными тестами показал их эффективность, надежность и валидность (пригодность для поставленной цели) и позволяет сделать следующие выводы:

1. Важнейшим аспектом в процессе обучения является обратная связь с учащимися, которая осуществляется преподавателем с помощью постоянного контроля знаний: в этой связи огромную роль приобретает компьютерное тестирование (КТ).
   
2. Для преподавателя КТ - возможность осуществить проверку большого объема знаний учащихся за короткое время, что существенно экономит учебное время и силы педагога: эффективный тест позволяет существенно уменьшить время, а, следовательно, стоимость проверки знаний испытуемых.
   
3. Для учащихся эта форма контроля наиболее интересна, так как является частью современных технологий обучения.
   

4. КТ позволяет наладить самоконтроль - самую гуманную форму контроля, так как исключает психологическое воздействие преподавателя и устраняет субъективность в оценке знаний.
   
5. В процессе работы с тестами закрепляются навыки работы с компьютером: знание клавиатуры, операционной системы, программных оболочек, текстовых и графических редакторов, математических пакетов, имеющих реальное применение к физическим процессам, что является условием формирования информационной культуры будущих специалистов-физиков.
   
6. Применение на уроках физики КТ приводит к повышению интереса к физике и формированию мотивации к углубленному изучению данного предмета у обучаемых [189-193].
   

2.3.7. Методы формирования умений решать задачи по физике


Физическая задача (ФЗ) – это небольшая проблема, которая решается на основе методов физики путем логических умозаключений, физического эксперимента и логических действий. Умение решать задачи отражает профессиональную компетентность будущего специалиста-физика.

По степени сложности ФЗ делятся на простые и сложные. Сложность оценивается по числу операций, которые необходимо выполнить при ее решении. Простые задачи - тренировочные, требуют знание формул и единиц физических величин и сводятся к вычислениям в одно действие (примеры). Решение сложных задач предполагает выполнение нескольких действий. К ним относятся комбинированные, творческие и олимпиадные.


А. Методы обучения учащихся решению стандартных физических задач
с помощиью алгоритмов и блоков

Технология обучения учащихся решению ФЗ – система приемов, реализация которых приводит к формированию у учащихся умений решать задачи в несколько этапов (поэтапное формирование умственных действий). Этапы решения задачи представляют собой последовательность действий, поэтому могут рассматриваться, как алгоритм. Общий алгоритм содержит последовательность действий, не зависящий от того, к какому разделу курса физики относится задача:

• 1-й этап: чтение и уяснение условия;
  
• 2-й этап: краткая запись условия задачи;
  
• 3-й этап: перевод заданных значений физических величин в систему СИ;
  
• 4-й этап: анализ описания задачной ситуации (какой физический объект описывается, обсуждаются факторы, которыми можно пренебречь, сопровождается рисунком или чертежом);
  
• 5-й этап: создание математической модели решения ФЗ (составление плана решения, запись уравнений, решение ФЗ в общем виде, получение общей формулы и ее проверка размерностью. Если проверка размерности не осуществляется, учащийся должен подставить в формулу численные значения величин с соответствующими единицами измерения);
  
• 6-й этап: вычисления;
  
• 7-й этап: проверка ответа и его анализ.
  

Частный алгоритм – относится к тому или иному разделу физики, фактически это алгоритм 5-го этапа - общепринятое выполнение в определенной последовательности элементарных операций для решения любой задачи, принадлежащей к определенному классу, типу или теме. Алгоритм решения задачи называют еще алгоритмическим предписанием. В качестве примера рассмотрим несколько частных алгоритмов решения задач, используемых автором настоящей работы.


Алгоритмические предписания решения задач на динамику:

1. 
   Сделать чертеж размером не менее 1/3–1/4 части тетрадного листа с указанием векторов всех сил, действующих на тело. Линейный размер векторов сил логически не связан с размерами самого рисунка. Для наглядности следует выбрать длину вектора не менее 1 см.
   

2. Написать уравнение Ньютона в векторной форме для данного случая:


åFi=ma (например: Fтяги + mg + Fтр +N = ma). (1)


3. Выбрать оси координат: ось X - по движению тела, ось У Х.

4. Спроецировать векторы всех сил на оси Х и У. Написать соответствующие уравнения для проекций. Если есть сила трения, дописать 3-е уравнение для неё:
   

Fтр=mN. (2)

5. Решить систему уравнений и найти искомую величину.


Алгоритмические предписания решения задач на тему:
«Принцип суперпозиции электростатических полей»:

1. Сделать чертеж, на котором указать векторы напряженностей электростатических полей Е1, Е2, Е3 … Еn, создаваемых зарядами q1, q2, q3,..qn. (Начало всех векторов находится в искомой точке! Векторы напряжённостей имеют направления сил, действующих на положительный единичный заря, помещённый в эту точку!)

2. Написать принцип суперпозиции в векторном виде:
   

Е0 = Е1 + Е2 + … + Еn. (3)

3. Геометрическим путем найти результирующий вектор Е0, изобразить его на чертеже и написать расчетную формулу для вычисления величины напряжённости Eо.
   
4. Найти величину напряжённости поля, создаваемого каждым зарядом
   

Е1, Е2 …. по формуле:

Ei = kqi / r², B/м (4)

5. Подставить числа в расчетную формулу и найти величину E0.

Опыт показывает, что каждому учащемуся целесообразно иметь банк памяток (формулы, таблицы, значения физических констант и прочий сопутствующий материал), который лучше всего разместить в конце тетради. В банк памяток следует поместить памятку правил сложения векторов.

Памятка правил сложения векторов:

а) Векторы E1 и E2 совпадают по направлению, тогда величина результирующего вектора напряжённости равна:

E0 = E1 + E2 ·®® (5)

б) Векторы E1 и E2 противоположны, тогда величина результирующего вектора напряжённости равна:

E0 = E1 - E2 ¬·® (6)

г) Векторы E1 и E2 направлены под углом друг к другу, тогда величина результирующего вектора напряжённости равна:

Eо = E1 + E2+ 2E1E2 (cosE1E2) (7)

E1 Ео



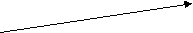
) µ

Е2


При изучении раздела «Молекулярная физика» все формулы лучше всего изобразить в виде лент 1 и 2 и красочно оформить. У каждого ученика в тетради на отдельной странице должны быть такие ленты формул: они не только хорошо запоминаются, но и являются работающими опорами в решении задач. В ленте 1 помещены формулы газовых законов.

Лента 1



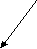
PV = nRT= NRT/Na = mRT/M = VRT/Vм = NkT


N/Na; m/M; V/Vм k=R/ Na


Изменение (D) в давлении Р или объеме V (слева) влечет за собой обязательное изменение какой-либо величины в уравнении справа. Это обстоятельство отражает лента формул 2.

Лента 2




D(P V) = nRDT = DNRT/Na = DmRT/M = DVRT/Vм = DNkT


Алгоритмические предписания решения задач на тему:
«Газовые законы, уравнение Клапейрона-Менделеева»

1. Выбрать подходящую ленту, вырезать из неё нужный кусок – уравнение с искомой и заданными величинами - и решить его относительно искомой величины.
   
2. Если даны 2 состояния газа – написать 2 уравнения для них и решить систему.
   
3. Если дана смесь газов, надо написать исходное уравнение для количества вещества смеси:
   

n = n1 + n2.

Аналогичные ленты формул создаются по теме «Термрдинамика» и на их основе – алгоритмы. Например, для внутренней энергии газа можно записать две таких ленты:

Лента 1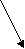


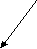U = 3/2 kTN = 3/2 PV = 3/2 n RT


N/Na m/M V/Vм


Лента 2 (изменение внутренней энергии)




D U =3/2 k D TN = 3/2 k TDN = 3/2 DPV = 3/2 PDV = 3/2 Dn RT = 3/2 n RDT


Ленту 2 можно подать в таком виде




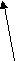
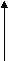
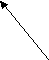
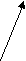
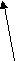
D U =3/2 k TN =3/2 PV =3/2 n RT = 3/2 RT N/Na = 3/2 RT m/M = 3/2 RT V/Vм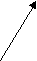

• D D
  

При решении ФЗ целесообразно обозначить чётко тему практического занятия и сгруппировать все задачи темы в блоки. Для каждого блока задач может быть выведен свой частный алгоритм или методические указания. Примеры деления задач на блоки показаны в табл.2.4. Сочетая блочный и алгоритмический методы, можно достичь высоких результатов в обучении учащихся решению задач. На дом задается по нескольку задач из каждого блока, номера задач умышленно не называются. Учащиеся должны сами выделить из задачника блоки, подобрать задачи по своим силам и оформить решения домашних задач в соответствии с номерами блоков.

Таблица 2.4

Пример классификации задач по блокам

№	Тема	Блок 1	Блок 2	Блок 3	Блок 4
1	Движение тела в поле тяготения Земли	Подблок А: Свободное падение; Подблок Б: Тело, брошенное горизонтально	Тело, брошенное вверх	Тело, брошенное под углом к горизонту	Комбинированные задачи (две в одной)
2	Динамика	Вертикальное движение без трения (лифт, блоки)	Движение по окружности: А) в вертикальной плоскости без трения; Б) в горизонтальной плоскости без трения и с трением	Движение по горизонтали с трением	Тело на наклонной плоскости: А) в покое или движется равномерно; Б) движется с ускорением
3	Движение заряженной частицы в магнитном поле	Частица движется вдоль силовой линии	Частица влетает в магнитное поле перпендикулярно силовым линиям	Частица влетает в магнитное поле под углом к силовым линиям	А) Совместные поля; Б) Частица предварительно ускорена продольным электрическим полем
4	Заряженная частица в поле плоского конденсатора	Частица находится в равновесии	Частица движется вдоль силовых линий	Частица влетает в конденсатор параллельно пластинам	Частица предварительно ускоренна продольным электрическим полем