Конспект урока Тема : Параллельность в пространстве
| Вид материала | Конспект |
СодержаниеХод урока Карточка №1 Карточка №2 |
- План-конспект урока по литературе в 11 классе Тема: «Отдавшая жизнь за единственный, 32.18kb.
- Конспект урока химии в 10 классе Тема урока, 54.04kb.
- План-конспект интегрированного урока в 1 классе Тема урока, 91.29kb.
- Как составить конспект урока русского языка. Конспект урока, 4218.04kb.
- План-конспект урока по информатике Тема урока: «Поисковые информационные системы», 228.6kb.
- Конспект урока литературы в 6 классе Учитель: Чечеткина, 20.47kb.
- План-конспект урока Тема программы: Рукоделие. Тема урока: Лоскутная пластика, 143.59kb.
- Конспект урока (11 класс) Тема урока: Основные типы алгоритмических структур, 40.57kb.
- Конспект урока обж для 7 класса Тема урока: «Вулканы», 127.36kb.
- Конспект урока в 1 классе Тема урока: Формирование правильной осанки, обучение технике, 30.04kb.
Конспект урока
Тема: Параллельность в пространстве
Урок №9 Параллельность прямой и плоскости
Автор Болышева Т.А.
Тип урока: комбинированный
Форма проведения урока: беседа
Цели: рассмотреть возможные случаи взаимного расположения прямой и плоскости в пространстве; ввести понятие параллельности прямой и плоскости; изучить признак параллельности прямой и плоскости. Показать применение теоретического материала при решении задач.
Развивать мышление, речь, умение анализировать, делать выводы.
Оборудование: инструменты, экран, диск со слайдами
Ход урока
| Этап урока | Время | Деятельность учителя | Деятельность учащегося |
| I Организационный момент | 31 | Отметить присутствующих. Проверить наличие учебных принадлежностей. Сообщить план урока | Приготовить все учебные принадлежности |
| II Актуализация знаний, проверка домашнего задания | 51 | Раздать задание на карточках двум учащимся. Провести фронтальный опрос по предыдущей теме: Вопросы (на экране): 1)Какие прямые называются параллельными в пространстве? 2) Сформулировать теорему о параллельности прямых 3) Сформулировать лемму о пересечении плоскости параллельными прямыми 4) Сформулировать теорему о параллельности трех прямых. Показать на экране условия и решение задач. Проверить ответы | Д  ва человека решают задачи по карточкам, остальные слушают и отвечают на вопросы ва человека решают задачи по карточкам, остальные слушают и отвечают на вопросыК |
| III Изложение нового материала | 51 51 51 51 | 1.Постановка цели урока 2.Предложить учащимся самим рассмотреть различные случаи расположения в пространстве прямой и плоскости На экране показать таблицу   Общие точки  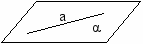 более одной 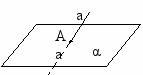  только одна 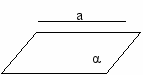  ни одной  3. Определение параллельности прямой и плоскости. Предложить учащимся сформулировать определение 4. Признак параллельности прямой и плоскости а) дать формулировку теорем б) показать на экране чертеж и доказательство теоремы в 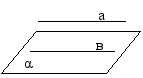 ) по чертежу пояснить доказательство ) по чертежу пояснить доказательство5 Сформулировать утверждение в форме теорем, полезные для решения задач 1 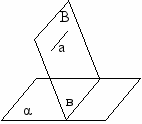 ) ) Дано: аIIα а β; β∩α=в Доказательство: а и в β Пусть в∩а, тогда а∩α, что противоречит условию. Значит вIIа 2 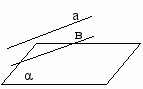 ) ) Дано: аIIв; аIIα Доказать: вIIα или в α Доказательство: если в∩α, то по лемме а α, что противоречит условию, значит вIIα, или в α | Учащимся продумывают различные способы расположения прямой и плоскости в пространстве и дают ответы всей группы. Учащиеся чертят таблицу в тетради Взаимное расположение Прямая лежит в плоскости а α Прямая и плоскость пересекаются а∩α=А Прямая параллельна плоскости аIIα Запись определения в конспекте. Запись чертежа, дано и доказательство в конспекте Дано: а α; в α; аIIв Доказать: аIIα Доказательство: а α, значит по лемме в α, что противоречит условию. значит аIIα Формулировка теоремы и запись условия с доказательством |
| IV Закрепление | | Задача (на экране) 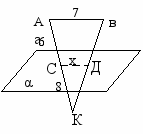 Дано: АВIIα ; АВ=7 см АВК∩α=СД; СД=6 см, СК=8 см Найти: СД Решение: Пусть СД=Х АВIIСД (утверждение 1) ∆ 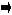 КСД ∞ ∆КАВ КСД ∞ ∆КАВАВ = АК → 7 = 14 СД СК Х 8 Х=7*8 Х= 4 см 14 | Во время решения ответить на вопросы: 1) Каково взаимное расположение АВ и СД? Почему? 2) Какие получаются ∆КСД и ∆ КАВ На основании чего? 3) Что следует из подобия треугольников? |
| V Итог урока | | Кратко повторить что изучалось на уроке. Выполнены ли цели. Дать анализ работы группы | |
| VI Домашнее задание | | п.4,5 повторить п. 6 учить №22 На экране показать условия задачи | 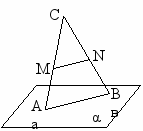 Дано: (А,В) α, с α М1-середина N-середина ВС Доказать МNIIα |

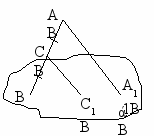 арточка №1
арточка №1 ешение:
ешение: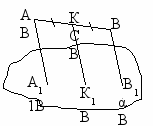 ано:
ано: