Рабочая учебная программа математика

Вид материала

Рабочая учебная программа

Содержание Основная цель Глава 6. Площадь. Глава 7. Подобные треугольники. Глава 8. Окружность. Основное содержание тем учебного курса Требования к уровню подготовки учащихся Требования к математической подготовке учащихся 8 класса Общеучебные умения, навыки и способы деятельности Контроль уровня обученности Учебно – программные материалы Учебно – теоретические материалы Учебно – практические материалы ГЕОМЕТРИЯ 9 класс Перечень практических работ по каждой изучаемой теме.

Подобный материал:

• Рабочая учебная программа дисциплины финансовая математика специальности 060400 «Финансы, 124.91kb.
• Жилина Аделя Фаритовна (Ф. И. О. учителя, категория) Заинск 2010 программа, 1059.96kb.
• Рабочая учебная программа предмета математика по специальности Химическая технология, 121.76kb.
• Рабочая учебная программа курса «Математика» для умк «Школа России», 536.26kb.
• Рабочая учебная программа по дисциплине вычислительная математика специальность: 230100, 133.73kb.
• Учебная программа для специальности: (рабочий вариант) 1-310301-02 Математика (научно-педагогическая, 120.64kb.
• Рабочая программа Программа лекционного курса План практических занятий, 825.14kb.
• Рабочая программа Программа лекционного курса План практических занятий, 1059.44kb.
• Рабочая учебная программа дисциплины (модуля) Математика. Часть, 210.81kb.
• Рабочая учебная программа дисциплины (модуля) Математика. Часть, 210.8kb.

Глава 5. Четырехугольники.

Основная цель - дать учащимся систематические сведения о четырехугольниках и их свойствах; сформировать представления о фигурах, симметричных относительно точки или прямой.

В результате изучения данной главы учащиеся должны:

• знать определения рассматриваемых четырехугольников; формулировки и доказательства теорем, выражающих признаки и свойства этих четырехугольников; определения симметричных точек и фигур относительно прямой и точки;
  
• уметь: распознавать на рисунке и по определению четырехугольники; применять признаки в решении задач; строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией
  

Глава 6. Площадь.

Основная цель - сформировать у учащихся понятие площади многоугольника, развить умение вычислять площади фигур, применяя изученные свойства и формулы, применять теорему Пифагора.

В результате изучения данной главы учащиеся должны:

• знать основные свойства площади, формулы площади прямоугольника, параллелограмма, треугольника, трапеции; формулировки теоремы Пифагора и обратной к ней теоремы;
  
• уметь применять их в решении задач.
  

Глава 7. Подобные треугольники.

Основная цель - сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольных треугольников.

В результате изучения данной главы учащиеся должны:

• знать определения пропорциональных отрезков, подобных треугольников, формулировки и доказательства теорем, выражающих признаки и свойства подобных треугольников; определения синуса, косинуса, тангенса острого угла прямоугольного треугольника;
  
• уметь воспроизводить доказательства признаков подобия треугольников, доказывать основное тригонометрическое тождество, применять их в решении задач.
  

Глава 8. Окружность.

Основная цель - дать учащимся систематизированные сведения об окружности и ее свойствах, вписанной и описанной окружностях.

В результате изучения данной главы учащиеся должны:

• знать случаи расположения прямой и окружности; определение, свойство и признак касательной; определения центрального, вписанного углов, теорему о вписанном угле и следствия из нее; какая окружность называется вписанной, описанной, теоремы о свойствах окружностей.
  
• уметь доказывать и применять их в решении задач.
  

3. .Основное содержание тем учебного курса
   

алгебра

№ п/п	Название темы	Количество часов	Контрольная работа	Дата проведения
1	Рациональные дроби.	23	№1, № 2
2	Квадратные корни.	20	№3, №4
3	Квадратные уравнения.	20	№5, №6
4	Неравенства.	19	№7, №8
5	Степень с целым показателем. Статистика, элементы комбинаторики	11	№9
6	Повторение. Решение задач.	5	Итоговая
	Итого	102	10

геометрия

№ п/п	Наименование разделов и тем	Всего ча­сов	В том числе на:		Примерное количе­ство часов на са­мостоятельные работы учащихся
			уроки	Контрольные работы количество часов
1.	Четырехугольники	14	13	1	1
2.	Площади фигур	14	13	1	1
3.	Подобные треугольники	19	18	1	2
4.	Окружность	17	16	1	2
5.	Повторение.	4	4
	Итого:	68	64	4	6

4. Требования к уровню подготовки учащихся
   

Требования к результатам обучения направлены на реализацию деятельностного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.

Рубрика «Знать/понимать» включает требования к учебному материалу, которые усваиваются и воспроизводятся учащимися.

Рубрика «Уметь» включает требования, основанные на более сложных видах деятельности, в том числе творческой: объяснять, изучать, распознавать и описывать, выявлять, сравнивать, определять, анализировать и оценивать, проводить самостоятельный поиск необходимой информации и т.д.

В рубрике «Использовать приобретенные знания и умения в практической деятельности и повседневной жизни» представлены требования, выходящие за рамки учебного процесса и нацеленные на решение разнообразных жизненных задач.

Требования к математической подготовке учащихся 8 класса

В результате изучения алгебры ученик должен

знать/понимать

• существо понятия математического доказательства; примеры доказательств;
  
• существо понятия алгоритма; примеры алгоритмов;
  
• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
  
• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
  
• как потребности практики привели математическую науку к необходимости расширения понятия числа;
  
• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
  
• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
  

• уметь
  

• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
  
• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
  
• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
  
• решать линейные неравенства с одной переменной и их системы;
  
• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
  
• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
  
• описывать свойства изученных функций, строить их графики;
  

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
  
• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
  
• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
  
• интерпретации графиков реальных зависимостей между величинами.
  

5. Общеучебные умения, навыки и способы деятельности
   

В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:

• привычно готовить рабочее место для занятий и труда;
  
• самостоятельно выполнять основные правила гигиены учебного труда режима дня;
  
• понимать учебную задачу, поставленную учителем, и действовать строго в соответствии с ней;
  
• работать в заданном темпе;
  
• учиться пооперационному контролю учебной работы (своей и товарища), оценивать учебные действия (свои и товарища) по образцу оценки учителя;
  
• уметь работать самостоятельно и вместе с товарищем;
  
• оказывать необходимую помощь учителю на уроке и вне его;
  
• самостоятельно обращаться к вопросам и заданиям учебника;
  
• работать с материалами приложения учебника;
  
• использовать образцы в процессе самостоятельной работы;
  
• отвечать на вопросы по тексту;
  
• учиться отвечать по плану связно;
  
• уметь выделять главное в тексте;
  
• уметь систематизировать материал;
  
• составлять схемы, диаграммы;
  
• подбирать дополнительный материал по теме.
  

6. Содержание тем учебного курса.
   

Глава 1. Рациональные дроби (23часов).

Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Преобразования рациональных выражений. Функция y= 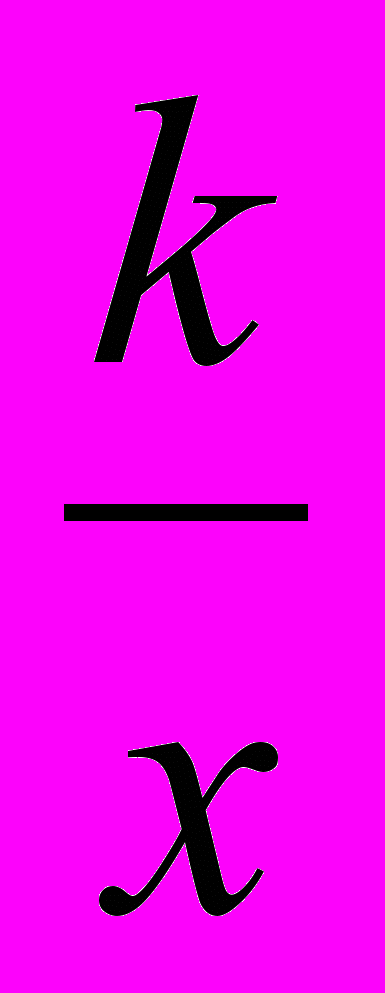и ее график.

Контрольная работа № 1 по теме: «Рациональные дроби. Сложение и вычитание дробей».

Контрольная работа № 2 по теме: «Рациональные дроби. Произведение и частное дробей».

Знать:

• определение целых, дробных и рациональных выражений;
  
• определение допустимых значений переменных;
  
• определение рациональной дроби;
  
• основное свойство дроби;
  
• определение тождества;
  
• правила сложения и вычитания дробей с одинаковыми знаменателями;
  
• правила сложения и вычитания дробей с разными знаменателями;
  
• правила умножения и деления дробей, возведения дроби в степень;
  
• определение обратной пропорциональности.
  

Уметь:

• находить значения рациональных выражений;
  
• определять целые, дробные и рациональные выражения;
  
• находить допустимые значения переменной;
  
• находить область определения функции;
  
• сокращать дроби;
  
• складывать и вычитать дроби с одинаковыми знаменателями;
  
• складывать и вычитать дроби с разными знаменателями;
  
• умножать и делить дроби, возводить дроби в степень;
  
• преобразовывать рациональные выражения;
  
• строить график функции y=.
  

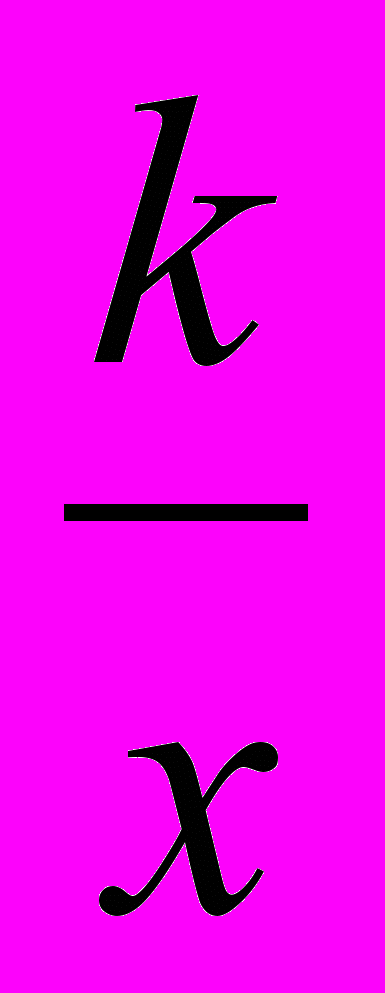Глава 2. Квадратные корни ( 20 часов).

Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция y = 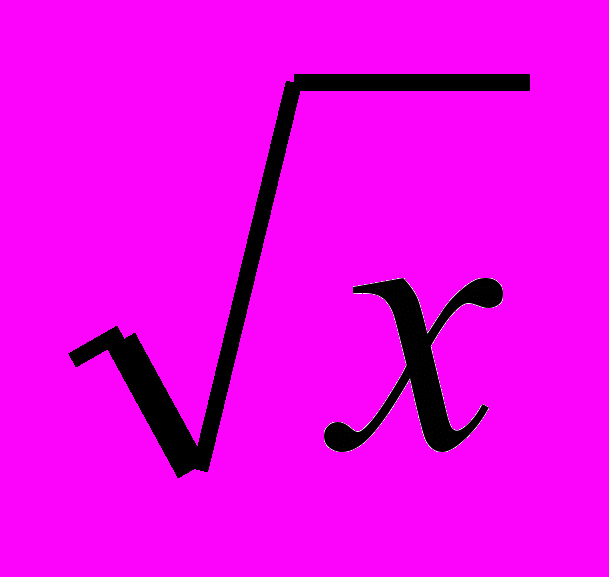, ее свойства и график.

Контрольная работа № 3 по теме: «Арифметический квадратный корень и его свойства».

Контрольная работа № 4 по теме: «Арифметический квадратный корень и его свойства».

Знать:

• определение натуральных, целых и рациональных чисел;
  
• определение иррациональных и действительных чисел;
  
• определение квадратного и арифметического квадратного корня из числа;
  
• свойства функции y = ;
  
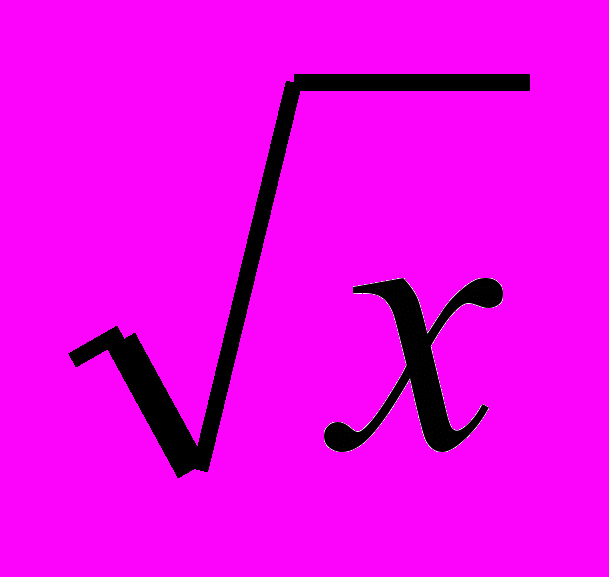• правила вычисления квадратного корня из произведения и дроби;
  
• правила вычисления квадратного корня из степени.
  

Уметь:

• сравнивать рациональные числа;
  
• представлять рациональные числа в виде бесконечной десятичной дроби;
  
• сравнивать иррациональные и действительные числа;
  
• вычислять квадратные корни;
  
• решать уравнения вида: x² = a;
  
• находить приближенное значение квадратного корня;
  
• строить график функции y = ;
  
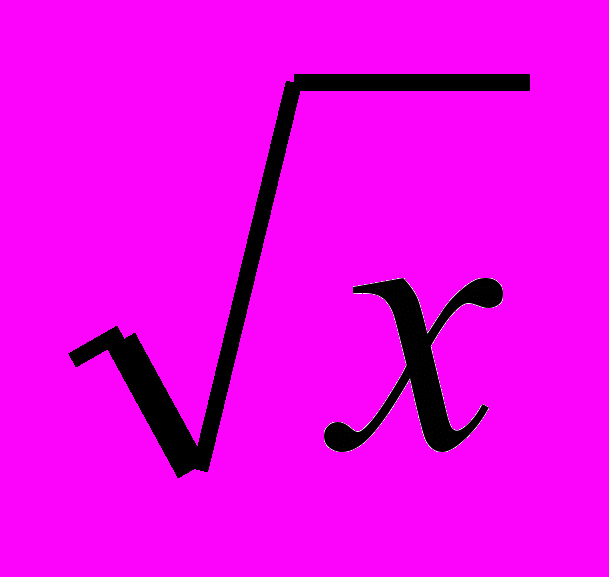• вычислять квадратный корень из произведения и дроби;
  
• вычислять квадратный корень из степени;
  
• выносить множитель из-под знака корня;
  
• вносить множитель под знак корня;
  
• преобразовывать выражения, содержащие квадратные корни.
  

Глава 3. Квадратные уравнения (20 часов).

Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям.


Контрольная работа № 5 по теме: «Квадратные уравнения».

Контрольная работа № 6 по теме: «Дробные рациональные уравнения».

Знать:

• определение квадратного уравнения;
  
• определение неполного квадратного уравнения;
  
• формулы полных и неполных квадратных уравнений;
  
• определение приведенного квадратного уравнения;
  
• определение дискриминанта квадратного уравнения;
  
• формулу дискриминанта квадратного уравнения;
  
• формулы корней квадратного уравнения;
  
• правило решения квадратного уравнения;
  
• теорему Виета и обратную ей теорему;
  
• определение целых и дробных рациональных уравнений;
  
• правило решения дробных рациональных уравнений.
  

Уметь:

• решать неполные квадратные уравнения;
  
• решать квадратные уравнения выделением квадрата двучлена,а также задачи на известные учащимся зависимости между величинами;
  
• решать квадратные уравнения по формуле;
  
• решать задачи с помощью квадратных уравнений;
  
• применять теорему Виета и обратную теорему;
  
• решать дробные рациональные уравнения;
  
• решать задачи с помощью рациональных уравнений;
  
• решать графически уравнения.
  

Глава 4. Неравенства (19 часа).

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.

Контрольная работа № 7 по теме: «Числовые неравенства и их свойства».

Контрольная работа №8 по теме: « Линейные неравенства и системы неравенств с одной переменной».

Знать:

• определение сравнения чисел;
  
• свойства числовых неравенств;
  
• теоремы о почленном сложении и умножении числовых неравенств;
  
• все виды числовых промежутков;
  
• определение пересечения и объединения множеств
  
• определение решения неравенства;
  
• свойства, используемые при решении неравенств;
  
• определение линейного неравенства с одной переменной;
  
• определение решения системы неравенств с одной переменной.
  

Уметь:

• доказывать неравенства;
  
• применять свойства числовых неравенств;
  
• оценивать значения выражений;
  
• складывать, вычитать, умножать и делить почленно числовые неравенства;
  
• изображать на координатной прямой числовые промежутки;
  
• записывать промежутки, изображенные на рисунке;
  
• решать линейные неравенства с одной переменной;
  
• решать системы неравенств с одной переменной.
  

Глава 5. Степень с целым показателем (11 часов).

Степень с целым показателем и ее свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями.

Контрольная работа № 9 по теме: «Степень с целым показателем».

Знать:

• определение степени с целым отрицательным показателем;
  
• свойства степени с целым показателем;
  
• определение стандартного вида числа.
  

Уметь:

• вычислять степени с целым отрицательным показателем;
  
• применять свойства степени с целым показателем;
  
• записывать числа в стандартном виде;
  
• выполнять действия с числами, записанными в стандартном виде;
  
• оценивать абсолютную и относительную погрешности приближенного значения;
  
• выполнять действия над приближенными значениями;
  
• выполнять действия над приближенными значениями на калькуляторе.
  

Повторение. (5 часов).

Цель: повторение и систематизация полученных в течение учебного года знаний.

Знать:

• Математические термины и формулы;
  
• Различные методы решения задач, уравнений и неравенств, систем уравнений и неравенств;
  
• Графики основных элементарных функций и их свойства;
  
• Преобразования выражений.
  

Уметь:

• Правильно употреблять математические термины и формулы;
  
• Применять различные методы при решении задач, уравнений и неравенств, систем уравнений и неравенств;
  
• Выполнять преобразования различных выражений;
  
• Выполнять действия с числами, корнями, степенями, многочленами, алгебраическими дробями, приближенными значениями;
  
• Осуществлять в выражениях и формулах числовые подстановки, выполнять соответствующие вычисления;
  
• Выражать из формул одни переменные через другие;
  
• Строить графики основных элементарных функций; опираясь на графики, описывать свойства этих функций, а также задачи на известные учащимся зависимости между величинами
  

7. Контроль уровня обученности
   

(система контролирующих материалов - основные дидактические единицы)

Контрольная работа №1 по теме: «Рациональные дроби. Сложение и вычитание дробей».

Контрольная работа №2 по теме: «Рациональные дроби. Произведение и частное дробей».

Контрольная работа №3 по теме: «Арифметический квадратный корень и его свойства».

Контрольная работа №4по теме: «Применение свойств арифметического квадратного корня».

Контрольная работа №5 по теме: «Квадратные уравнения».

Контрольная работа №6 по теме: «Дробные рациональные уравнения».

Контрольная работа №7 по теме: «Числовые неравенства и их свойства».

Контрольная работа №8 по теме: «Линейные неравенства и системы неравенств с одной переменной».

Контрольная работа №9 по теме: «Степень с целым показателем».

Итоговая контрольная работа.

8. Учебно – программные материалы:
   

1) Примерные программы основного общего образования по математике.

Вестник образования. №2, 2006г.

2) Сборник нормативных документов. Математика. Федеральный компонент государственного стандарта. Федеральный базисный план.

Москва. Дрофа, 2007г.

3) Программно- методические материалы. Математика 5 – 11 классы.

Москва. Дрофа, 2002г.

Учебно – теоретические материалы:

Учебник: Алгебра 8 класс

Авторы: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова.

Москва. Просвещение, 2002г.

Учебно – практические материалы:

1)Дидактические материалы по алгебре. 8 класс.

Авторы: В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк.

Москва. Просвещение, 2005г.

2) Тесты. Алгебра 7- 9 классы.

Автор: П. И. Алтынов.

Москва. Дрофа, 1997г.

3) Самостоятельные и контрольные работы. Алгебра. Геометрия. 8 класс.

Авторы: А. П. Ершова, В. В. Голобородько, А. С. Ершова.

Москва. Илекса. 2003г.

Учебно – справочные материалы:

1) Математический энциклопедический словарь.

Москва. Советская энциклопедия, 1995.

Учебно – наглядные материалы:

1. Таблицы, стенды.
   
2. Медиотека.
   

При разработке календарно-тематического планирования

по геометрии 8 классе использованы:

1. «Геометрия, 7-9 ».Учебник для общеобразовательных учреждений.
Авторы: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева, Э.Г.Позняк.
Издание подготовлено под научным руководством академика А.Н.Тихонова
Рекомендовано Министерством образования РФ, М.: Просвещение, 2006

2. Программы для общеобразовательных школ, гимназий, лицеев. Математика.
5-11 классы. Программы. Тематическое планирование.

Рекомендовано Департаментом общего и дошкольного образования Мини­стерства образования Российской Федерации- М.: Дрофа, 2004. Составители: Г.М. Кузнецова, Н. Г. Миндюк.

3. Журналы «Математика в школе», Учебно-методические газеты «Математика», Издательский дом «Первое сентября».

9 класс

АЛГЕБРА

Повторение курса алгебры 7-8 классов (3 часа).

Квадратичная функция (27 часов).

Область определения функции. Возрастание и убывание функции. Квадратный трёхчлен и его корни. Функция у=ах². Функция у=ах²+вх+с Построение графика квадратичной функции. Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов.

Уравнения и системы уравнений(21 час)

Целое уравнение и его корни. Уравнения, приводимые к квадратным. Графический способ решения систем. Решение систем уравнений 2 степени.

Арифметическая, и геометрическая прогрессии(18 часов)

Арифметическая прогрессия. Сумма n первых членов арифметической прогрессии.

Геометрическая прогрессия.Сумма n первых членов геометрической прогрессии.

Бесконечно убывающая геометрическая прогрессия.

Элементы комбинаторики и теории вероятностей. (13 часов)

Перестановки. Размещения. Сочетания.

Частота и вероятность. Сложение и умножение вероятностей.

Упражнения для повторения курса алгебры 7-9.(22 часа)

Решение упражнений.

ГЕОМЕТРИЯ 9 класс

Векторы. Метод координат. (19 уроков)

Вектор. Длина (модуль) вектора. Равенство векторов. Координаты вектора.  Операции над векторами: умножение вектора на число, сложение, разложение.

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.(15ч)

Синус, косинус и тангенс углов от 0^о до 180^о.Угол между векторами. Теорема синусов и теорема косинусов. Примеры их применения для вычисления элементов треугольника.       Формула, выражающая площадь треугольника через две стороны и угол между ними.      Скалярное произведение векторов.

Длина окружности и площадь круга(16ч)

  Вписанные и описанные многоугольники. Правильные многоугольники. Сумма углов правильного многоугольника. Длина окружности, число π; длина дуги. Площадь круга и площадь сектора. Вписанные и описанные окружности правильного многоугольника.

Движения(5 ч)

Примеры движения фигур. Центральная и осевая симметрия. Параллельный перенос. Поворот.

Повторение курса геометрии 7-9 класса (13 часов)

Начальные понятия и теоремы геометрии. Треугольник, его свойства. Равенство и подобие треугольников. Решение треугольника. Четырехугольники и многоугольники. Окружность и круг. Измерение геометрических величин. Векторы.

Так как тема «вектор» перенесена в программу 9 класса, то тема «движения» изучается обзорно.

3. Перечень практических работ по каждой изучаемой теме.