Достижение нового качества обучения математике в 5-6 классах по учебно-методическому комплекту Г. К. Муравина, О. В. Муравиной
| Вид материала | Документы |
- Программа по математике, 361.56kb.
- Учитель Матвеева Вера Анатольевна программа, 1253.42kb.
- Учитель Матвеева Вера Анатольевна программа, 748.53kb.
- Оисходит обновление содержания филологического образования, главной целью которого, 93.55kb.
- Календарно тематическое планирование на 2011 / 2012 учебный год Учебный предмет, 415.45kb.
- Календарно тематическое планирование на 2011 / 2012 учебный год Учебный предмет, 712.23kb.
- Методические особенности обучения школьников математике в классах естественно-научного, 9.62kb.
- Рабочая программа по русскому языку 11 класс По учебно-методическому комплексу под, 152.57kb.
- Учебно-методический комплекс опд. Р. 01. Теория и методика обучения русскому языку, 515.33kb.
- Доклад: Формирование логического мышления младших школьников на уроках математики, 40.14kb.
Достижение нового качества обучения математике в 5-6 классах
по учебно-методическому комплекту Г.К.Муравина, О.В.Муравиной
Вопросы отбора содержания математического образования и уровня его усвоения непосредственно связаны с методикой преподавания. Большая часть содержания математического образования школьников связана с выполнением более или менее сложных алгоритмов. При этом качество образования школьников, в основном, определяется умением сводить различные задачи к выполнению тех или иных алгоритмов и безошибочно их реализовывать. Сведение задачи к алгоритмам является творческой деятельностью, а выполнение алгоритмов – технической. Используя эту несколько упрощенную трактовку творческой и технической составляющих математической деятельности, можно утверждать, что эффективность обучения существенно повышается, если отделить формирование творческих умений от отработки технических навыков.
Определяющая роль в обучении математике принадлежит системе упражнений. С учетом выше сказанного, в ней должно находиться достаточное количество творческих заданий, не требующих от учеников переключения с интеллектуальной деятельности на техническую, так называемых, качественных заданий с существенно упрощенной технической стороной решения. Выполнение таких заданий, как правило, непосредственно связано с применением изученных идей. С другой стороны, выполнение стандартных, алгоритмических заданий не должно представлять для ученика интеллектуальных трудностей. Для этого должны быть предварительно проработаны все элементарные операции, из которых строится алгоритм, что тоже требует наличия в системе упражнений соответствующих заданий.
Понятно, что практическая реализация такого разделения потребовала создания новых учебных материалов и разработки технологии их использования в учебном процессе. Идея разделения интеллектуальных и технических целей в обучении явилась одной из центральных идей разработанной нами технологии обучения математике школьников, которые легли в основу учебно-методического комплекта Муравиных по математике для 5-11 классов. С 2007 года все семь учебников этого комплекта входят в Федеральный список учебников, рекомендованных Министерством образования и науки РФ.
Рассмотрим основные идеи упомянутой технологии на примере использования учебно-методического комплекта для 5 и 6 классов. Комплект состоит из программы, учебников, методических рекомендаций и рабочих тетрадей.
В программе курса описывается содержание каждой главы и пункта и требования к уровню подготовки учащихся по каждой теме. Это позволяет учителям акцентировать внимание на базовых умениях, не добиваясь от всех учеников усвоения материала пункта.
В учебниках математики 5 и 6 классов с учетом познавательных возможностей школьников материал излагается небольшими порциями с выделением определений, формул, правил, алгоритмов решения и оформления типовых задач. Небольшие порции позволяют ученикам схватывать основные идеи теоретических блоков, быстро пробегая их глазами и запоминая выделенные фрагменты.
Каждая порция материала отрабатывается поэтапно на творческих заданиях. После открытия и обсуждения способа их выполнения, ученики самостоятельно и осознанно применяют его, а затем обсуждают свои варианты решения или оформления. Способ рассуждения или решения, который они открыли, закрепляется в следующем задании, которое в учебнике уже сформулировано иначе, что дает простор творчеству школьников. Рассмотрим в качестве примера, как формируется система знаний и умений школьников в теме «Сравнение обыкновенных дробей» в учебнике 5 класса. Сравнение дробей осуществляется с применением различных приемов – это сравнение дробей с одинаковыми числителями, сравнение дробей с одинаковыми знаменателями, сравнение дробей приведением их к общему знаменателю, приведение дробей к общему числителю, сравнение дробей со вспомогательным числом 1,
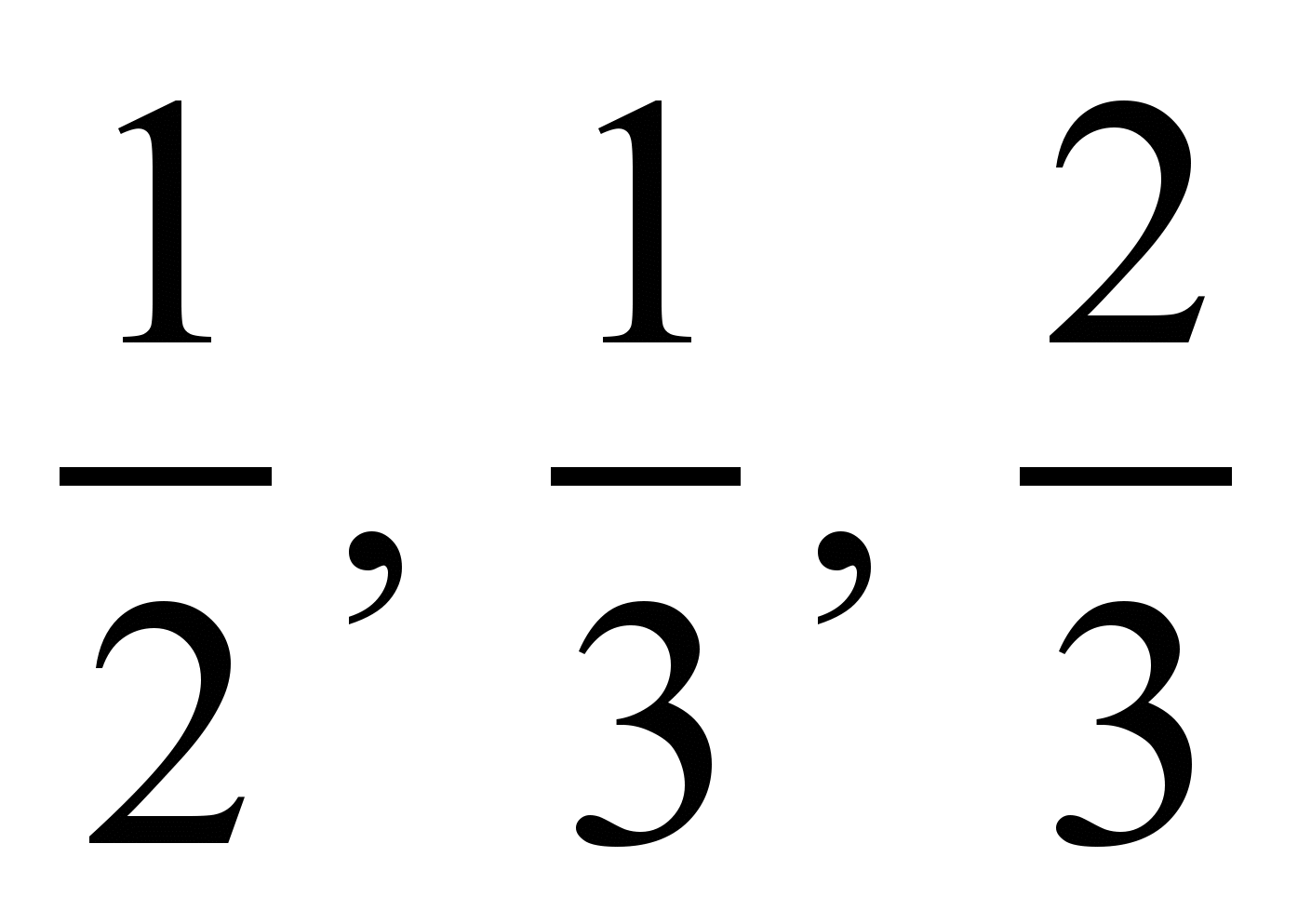 и т.п. К началу изучения материала школьники умеют выполнять арифметические действия с дробями, имеющими равные знаменатели, и понимают, что дробь можно рассматривать и как сумму долей, и как результат деления. Это позволяет им сравнивать дроби с равными знаменателями и с равными числителями. Основное свойство дроби используется ими для приведения дробей к общему числителю и к общему знаменателю, а умение изображать дроби на координатном луче дает возможность сравнивать дроби, используя вспомогательное число. Рамки публикации не позволяют привести полную систему упражнений учебника и рабочей тетради, поэтому ограничимся небольшим числом заданий указанных типов.
и т.п. К началу изучения материала школьники умеют выполнять арифметические действия с дробями, имеющими равные знаменатели, и понимают, что дробь можно рассматривать и как сумму долей, и как результат деления. Это позволяет им сравнивать дроби с равными знаменателями и с равными числителями. Основное свойство дроби используется ими для приведения дробей к общему числителю и к общему знаменателю, а умение изображать дроби на координатном луче дает возможность сравнивать дроби, используя вспомогательное число. Рамки публикации не позволяют привести полную систему упражнений учебника и рабочей тетради, поэтому ограничимся небольшим числом заданий указанных типов.Первое задание приводит к формулировке учениками правил сравнения дробей с равными числителями и дробей с равными знаменателями.
1. Что общего у дробей в каждой строке? Сравните дроби и сформулируйте правило сравнения таких дробей.
1) а)
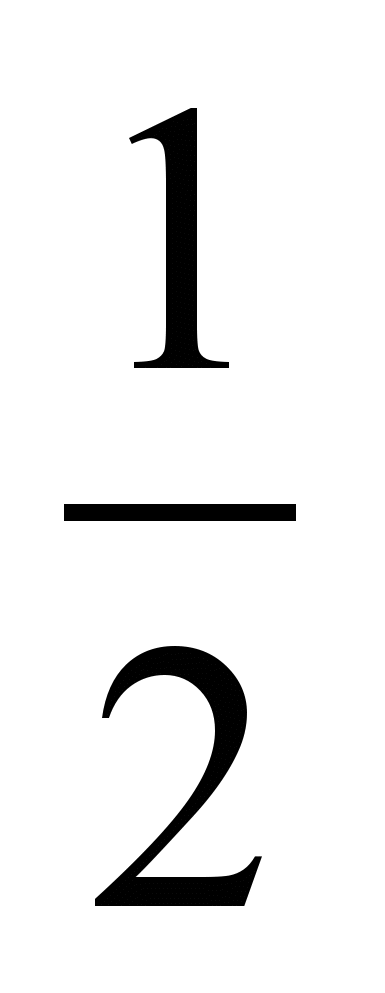 и
и 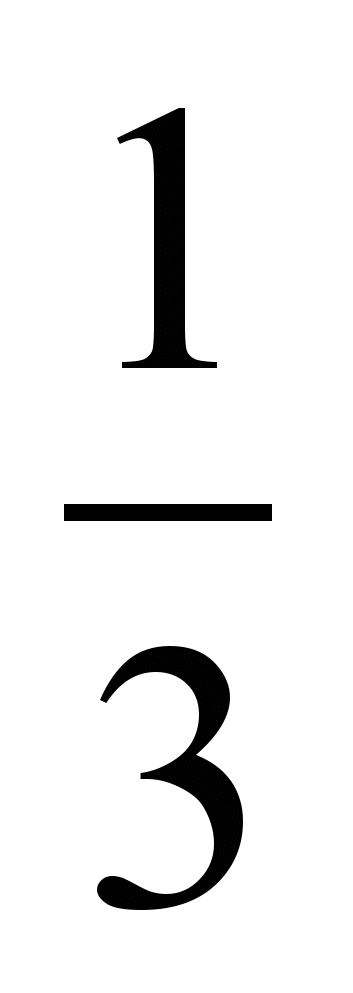 ; б)
; б) 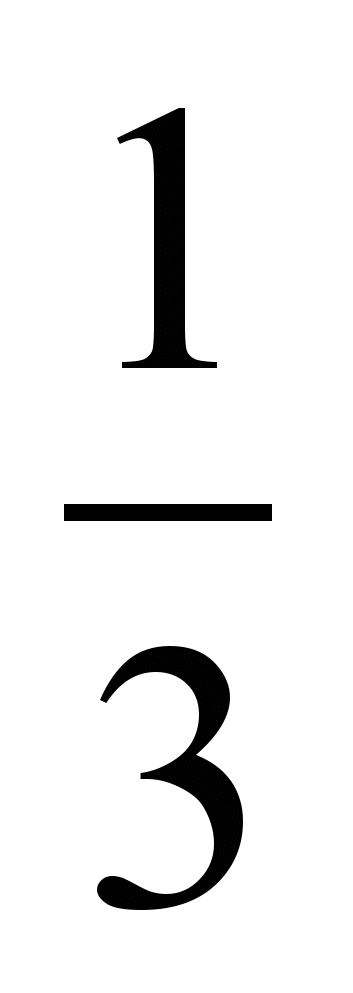 и
и  ; в)
; в)  и
и 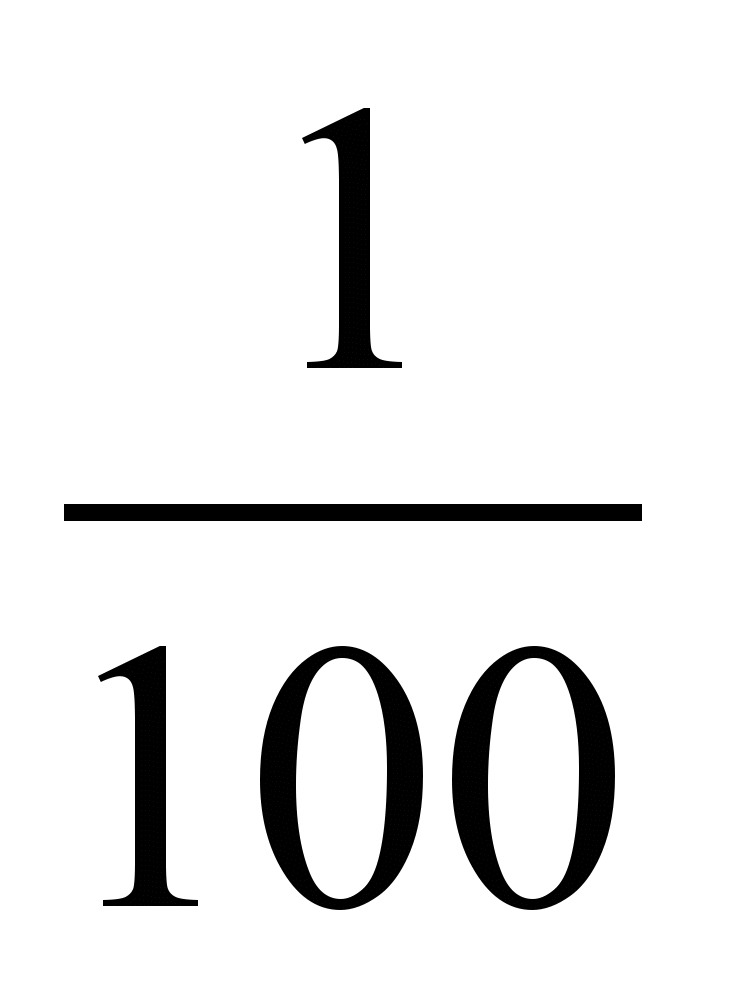 ; г)
; г)  и
и  ;
; 2) а)
 и
и 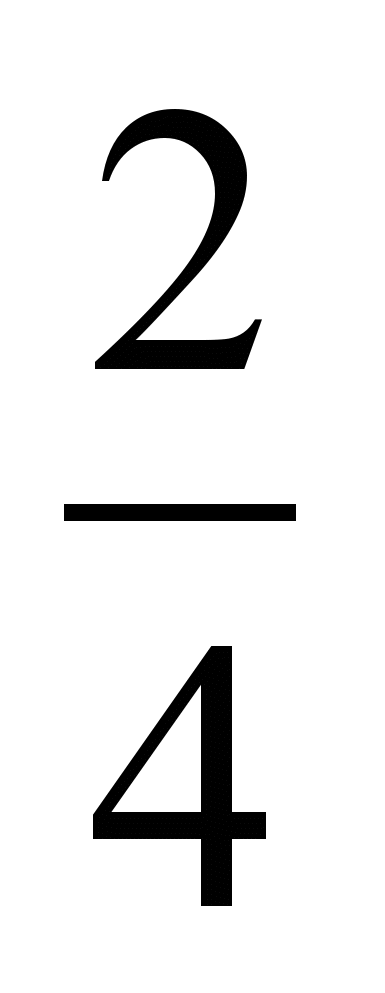 ; б)
; б) 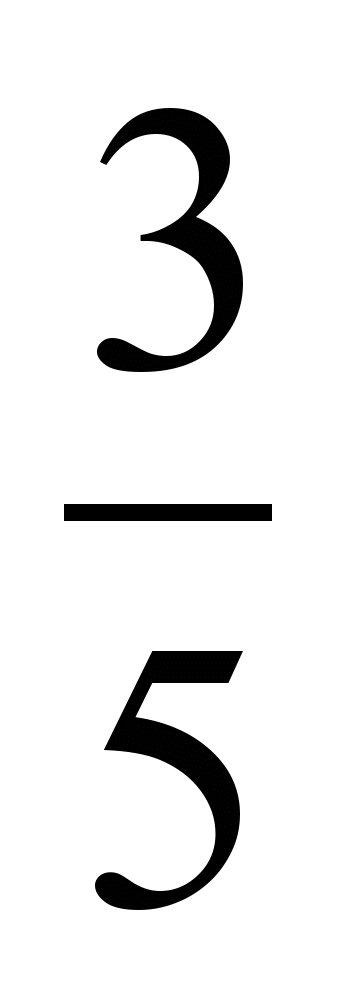 и
и 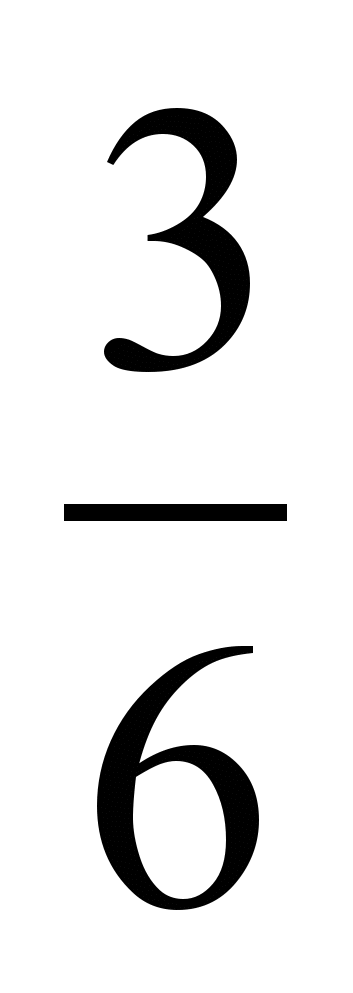 ; в)
; в) 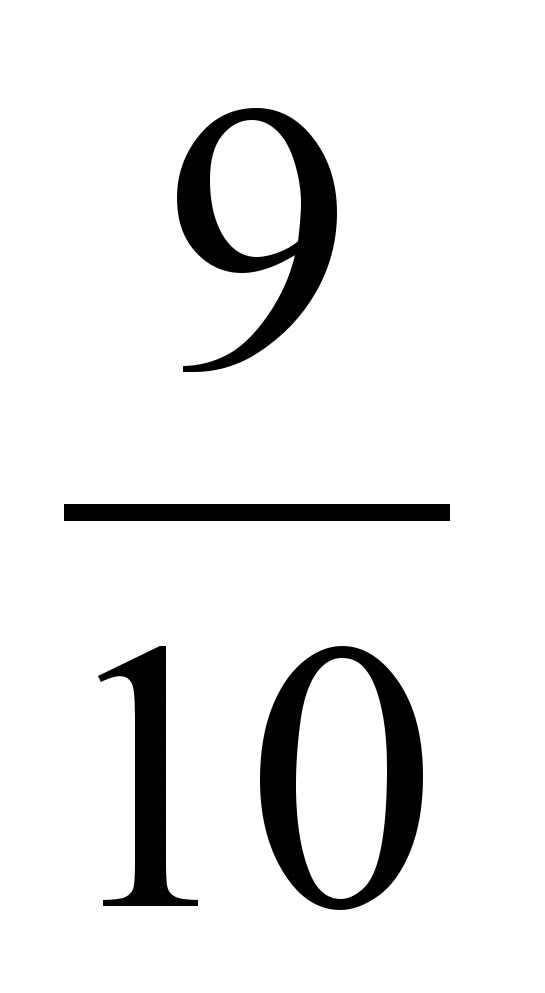 и
и 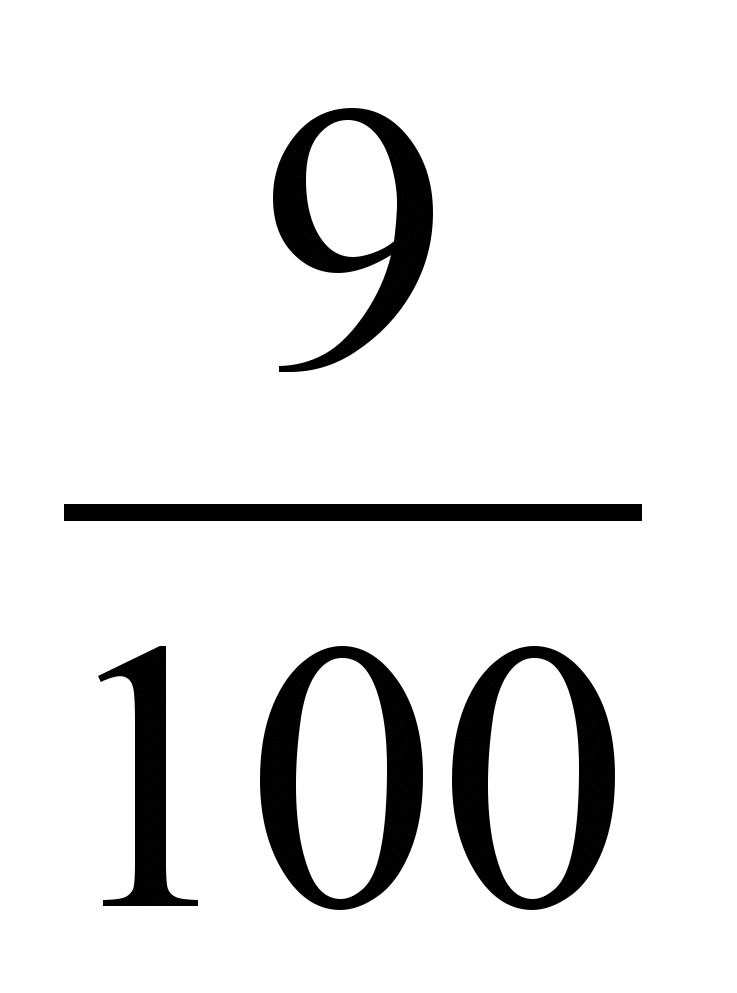 ; г)
; г)  и
и  ;
; 3) а)
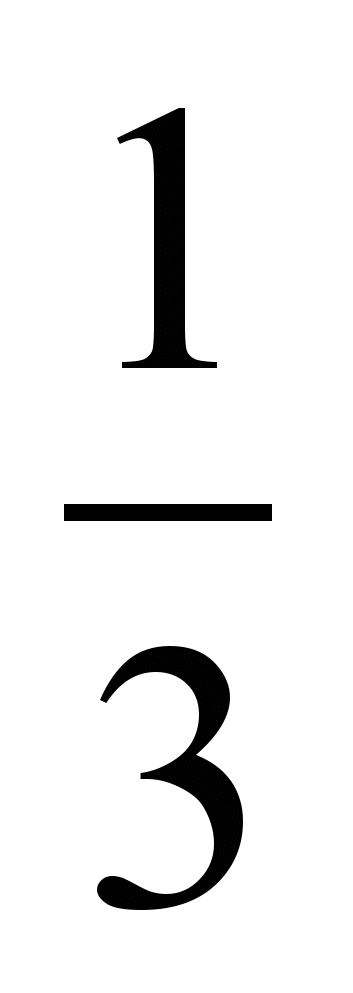 и
и 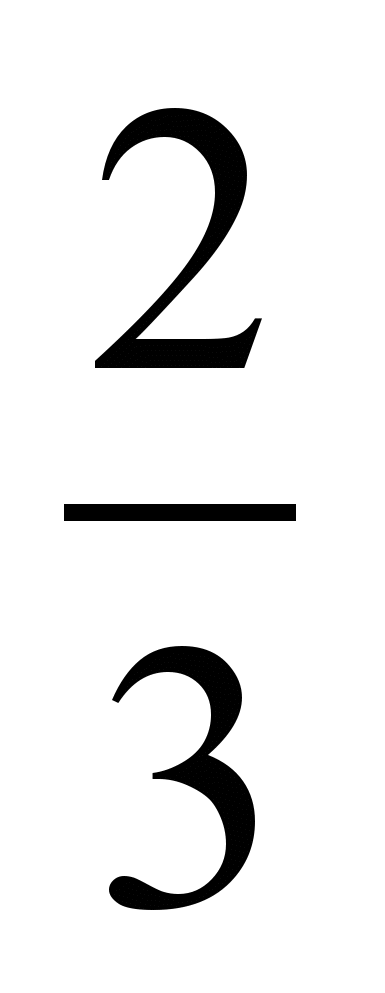 ; б)
; б) 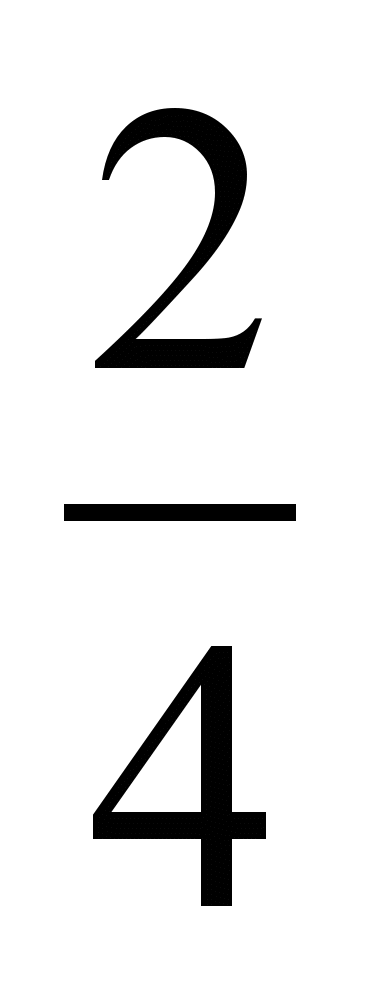 и
и  ; в)
; в)  и
и 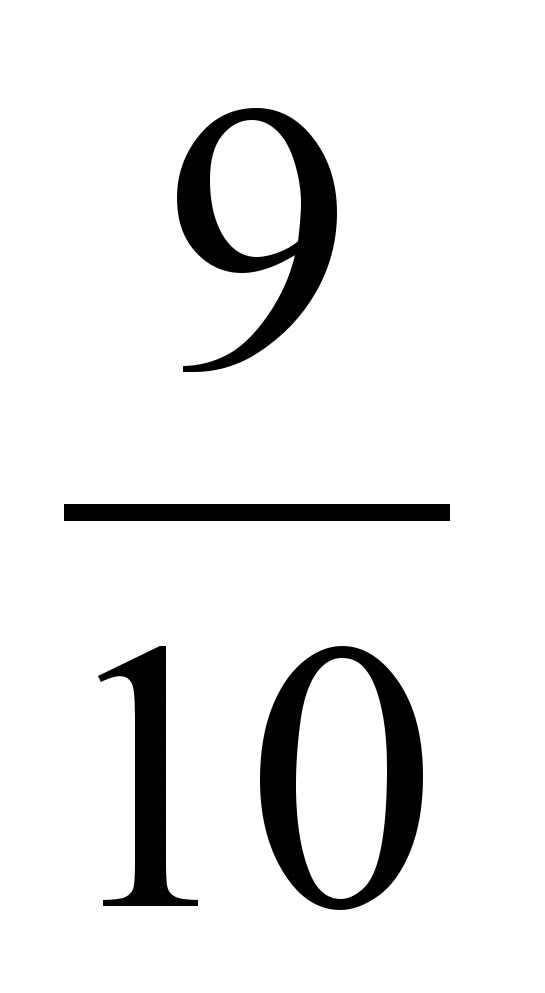 ; г)
; г)  и
и 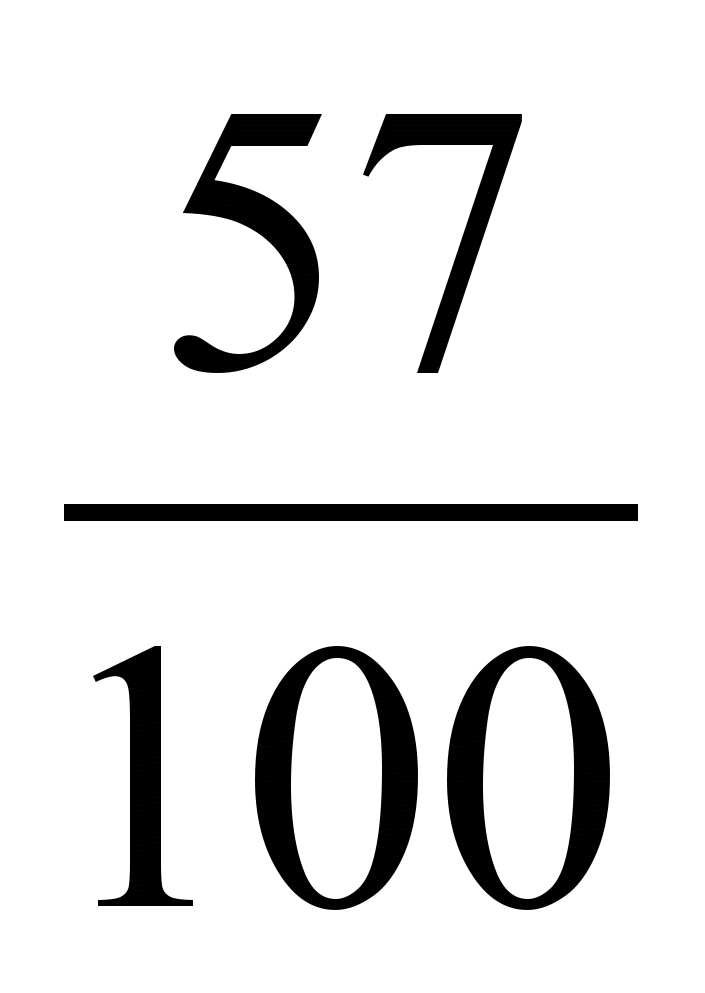 .
. Второе задание акцентирует внимание учеников на выборе рационального приема сравнения.
2. 1) Каким правилом вы будете пользоваться при сравнении дробей в каждом из следующих случаев? Сравните дроби.
а)
 в)
в)  ; д)
; д)  ;
;б)
 г)
г)  ; е)
; е)  ?
?В третьем и четвертом заданиях ученики встречаются с ситуацией сравнения не двух, а нескольких дробей.
3. Расположите в порядке возрастания числа:
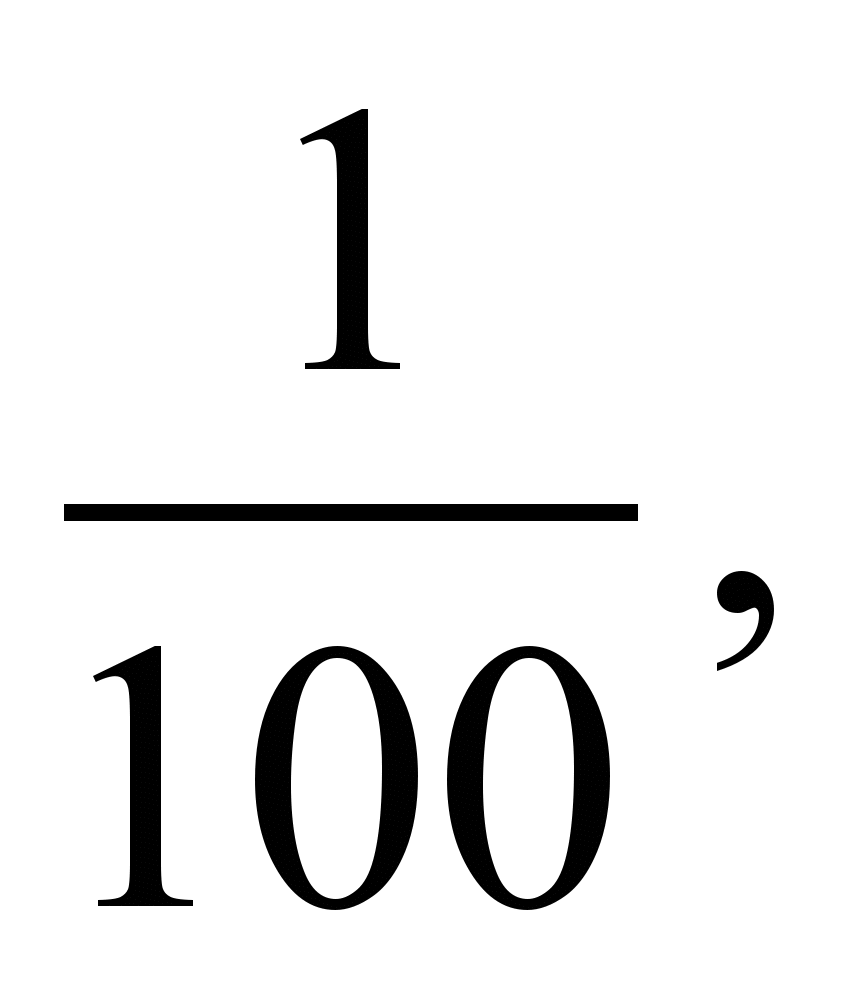
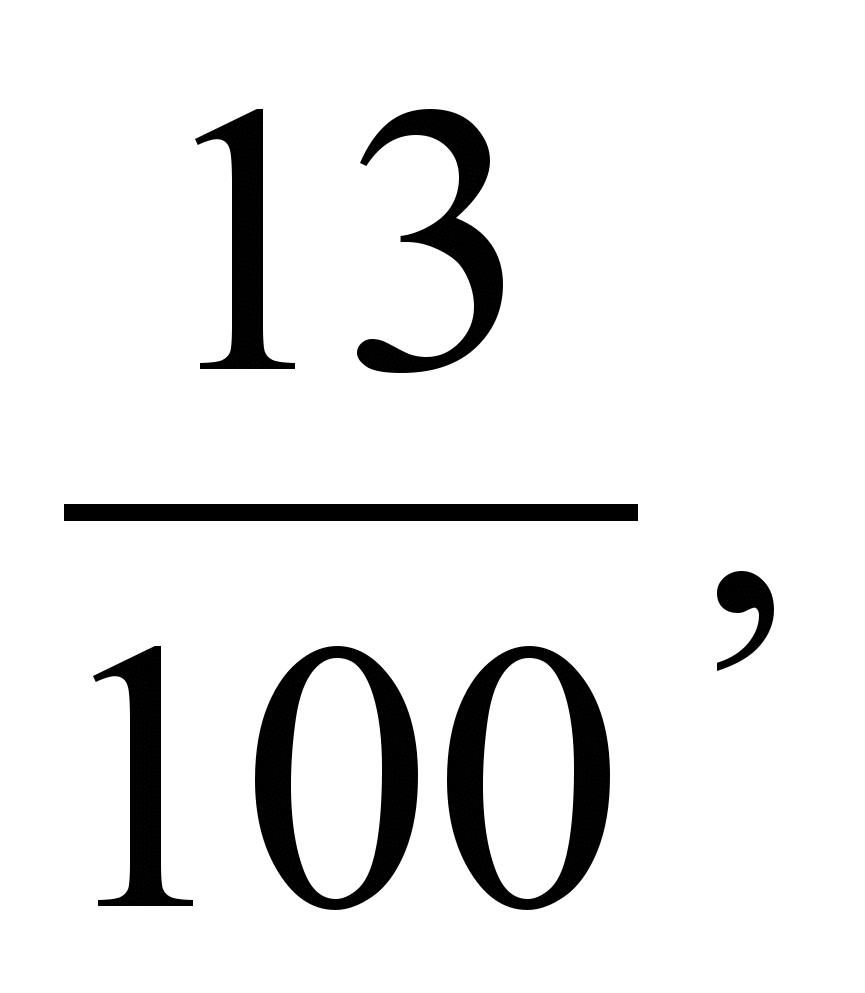
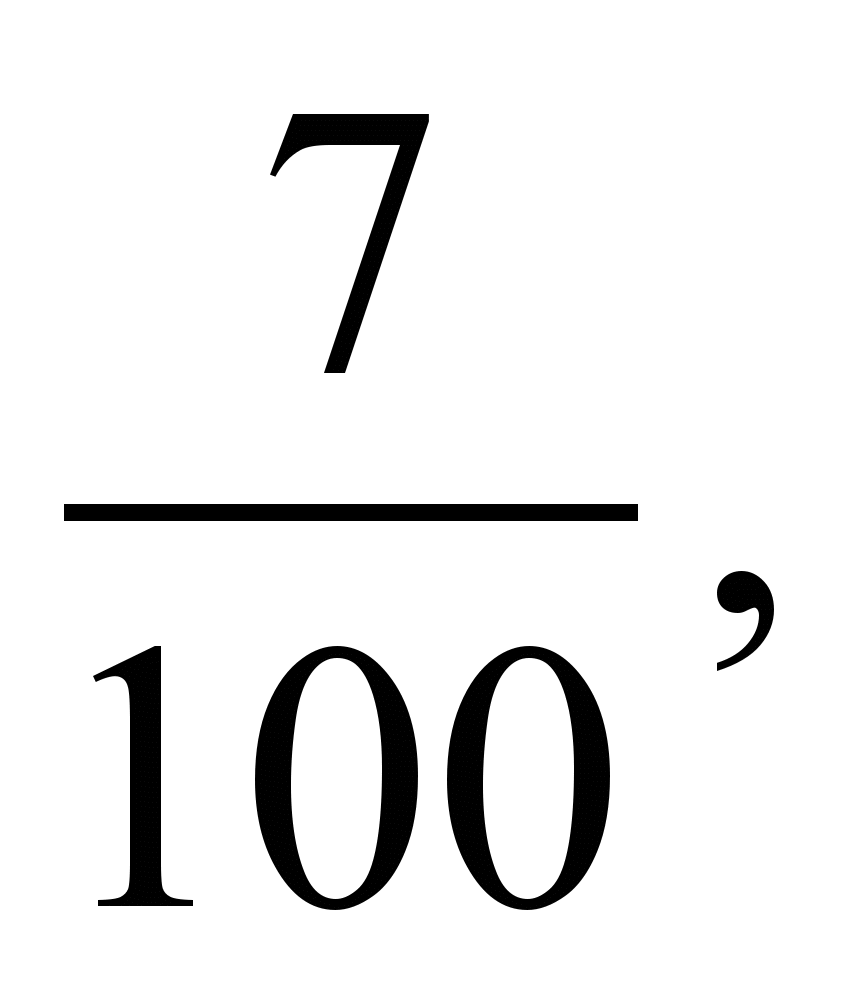
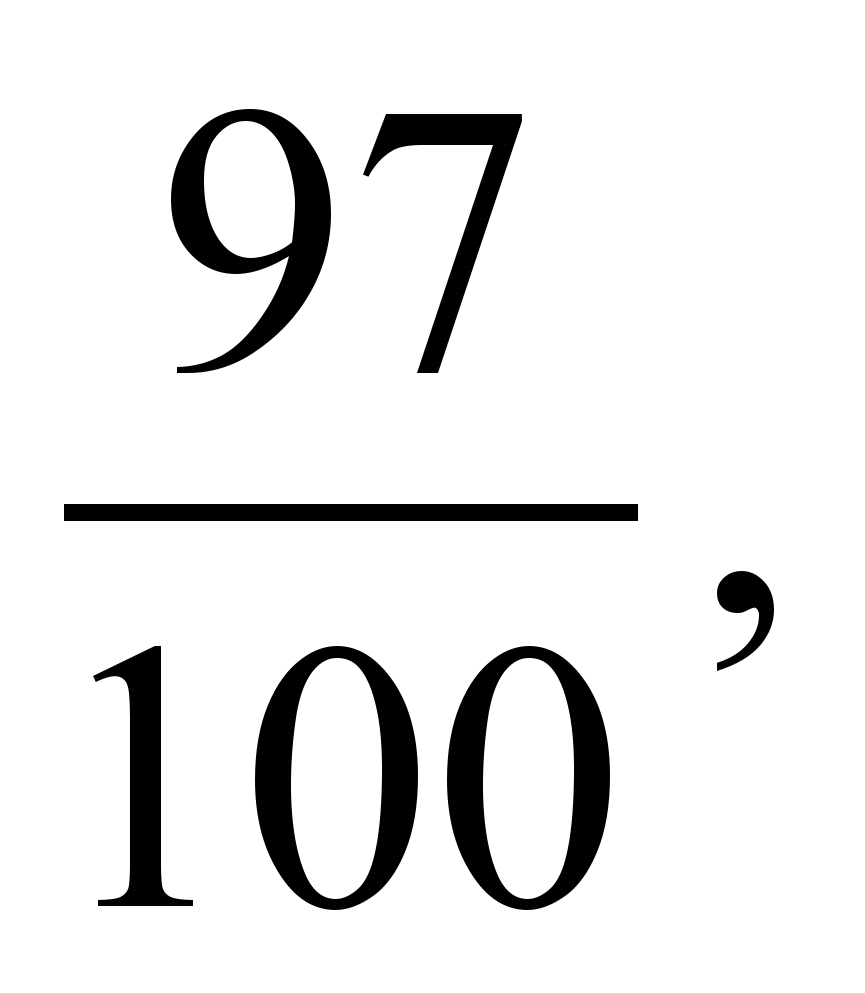
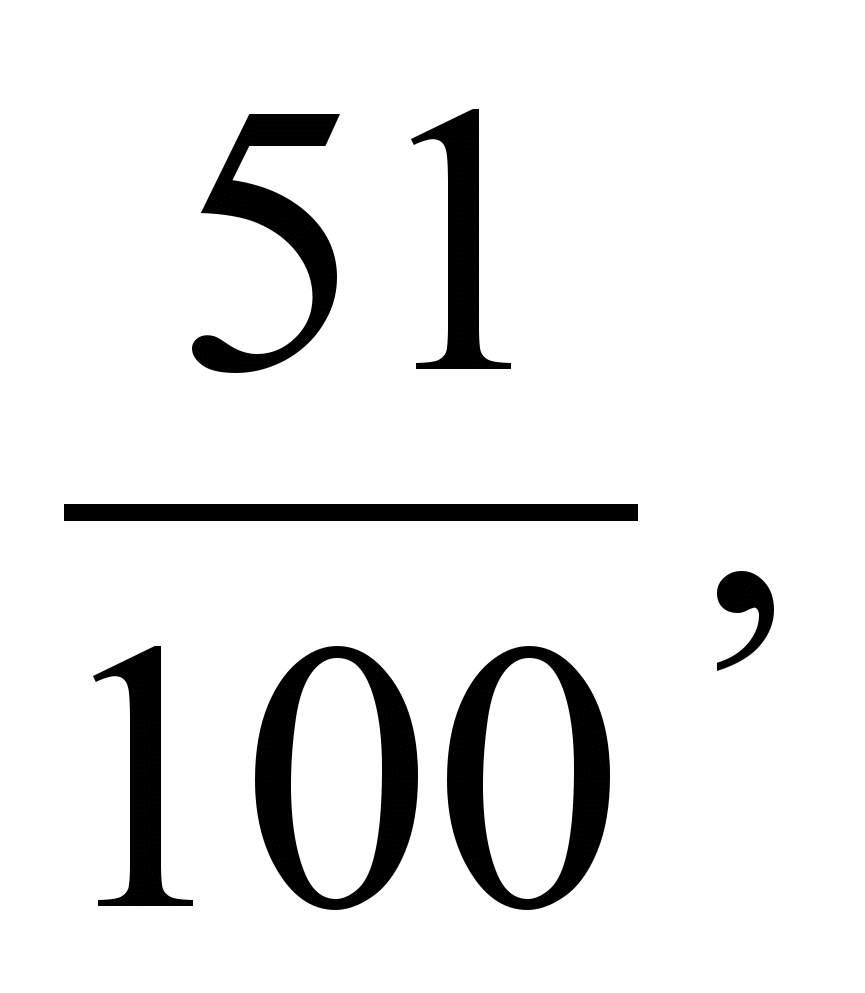
 .
.4. Из дробей



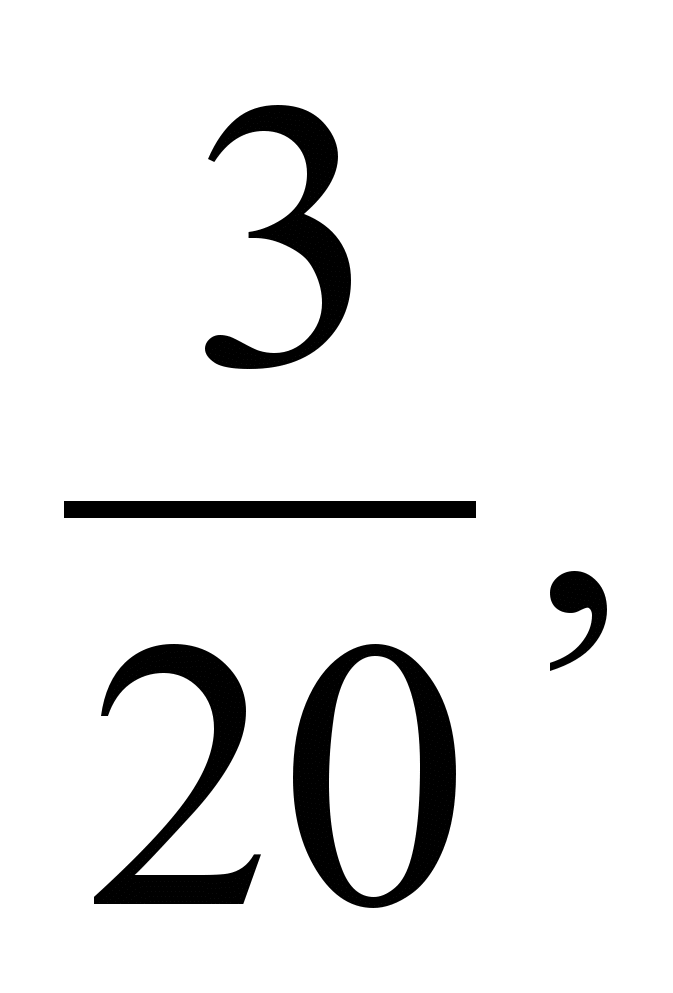

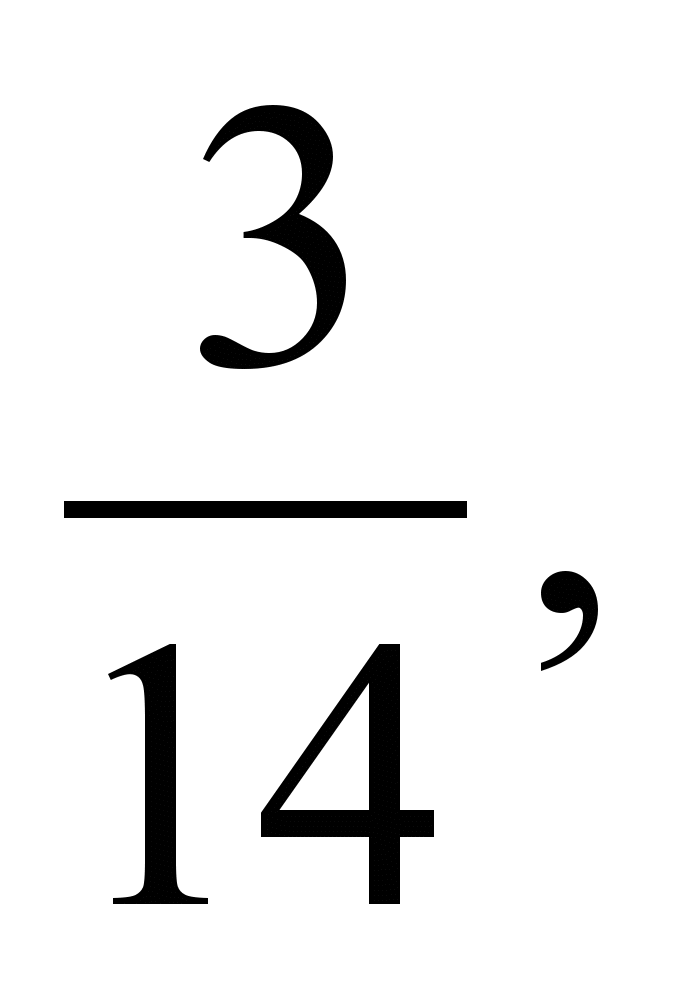
 выберите: 1) наибольшую; 2) наименьшую?
выберите: 1) наибольшую; 2) наименьшую?В пятом задании правила сравнения применяются в усложненной ситуации. Школьники должны выбрать правило и на его основе указать искомые значения переменных.
5. Найдите такие натуральные значения x, чтобы были верными неравенства:
1)
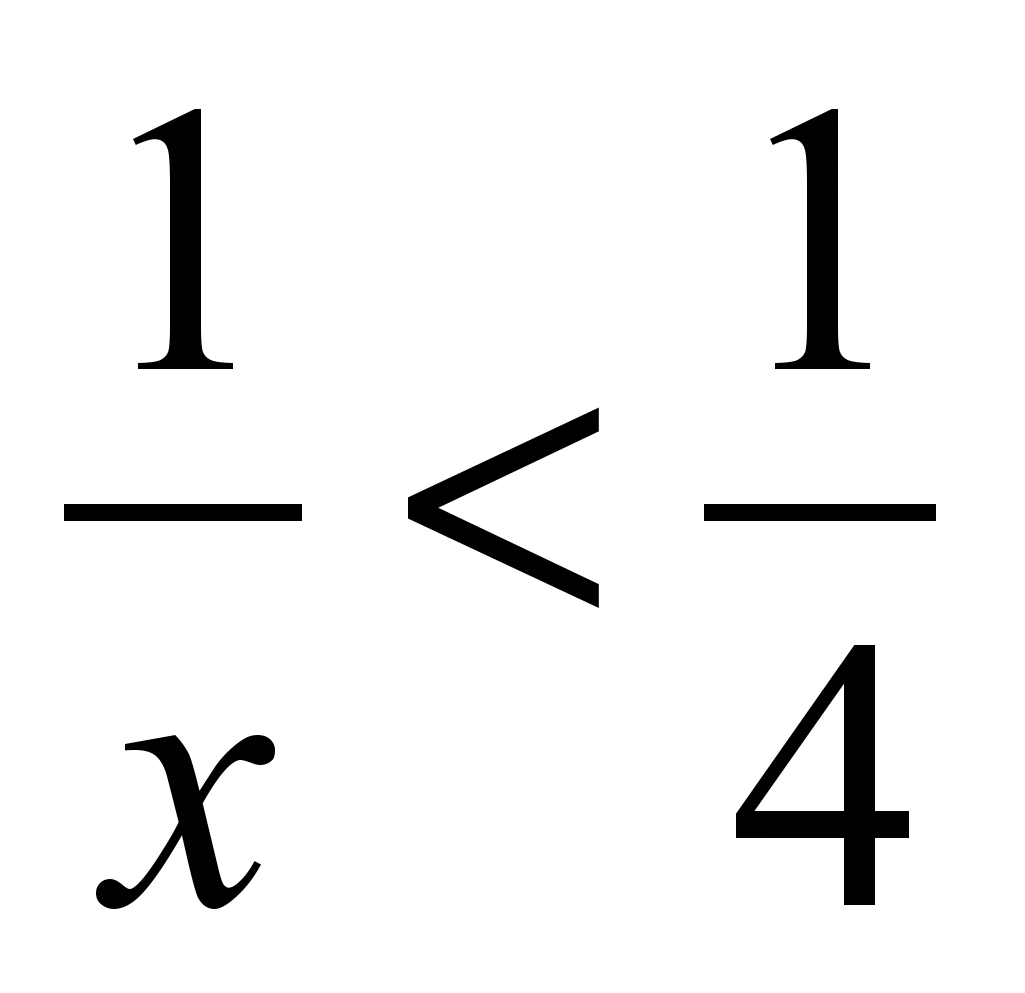 ; 2)
; 2)  ; 3)
; 3) 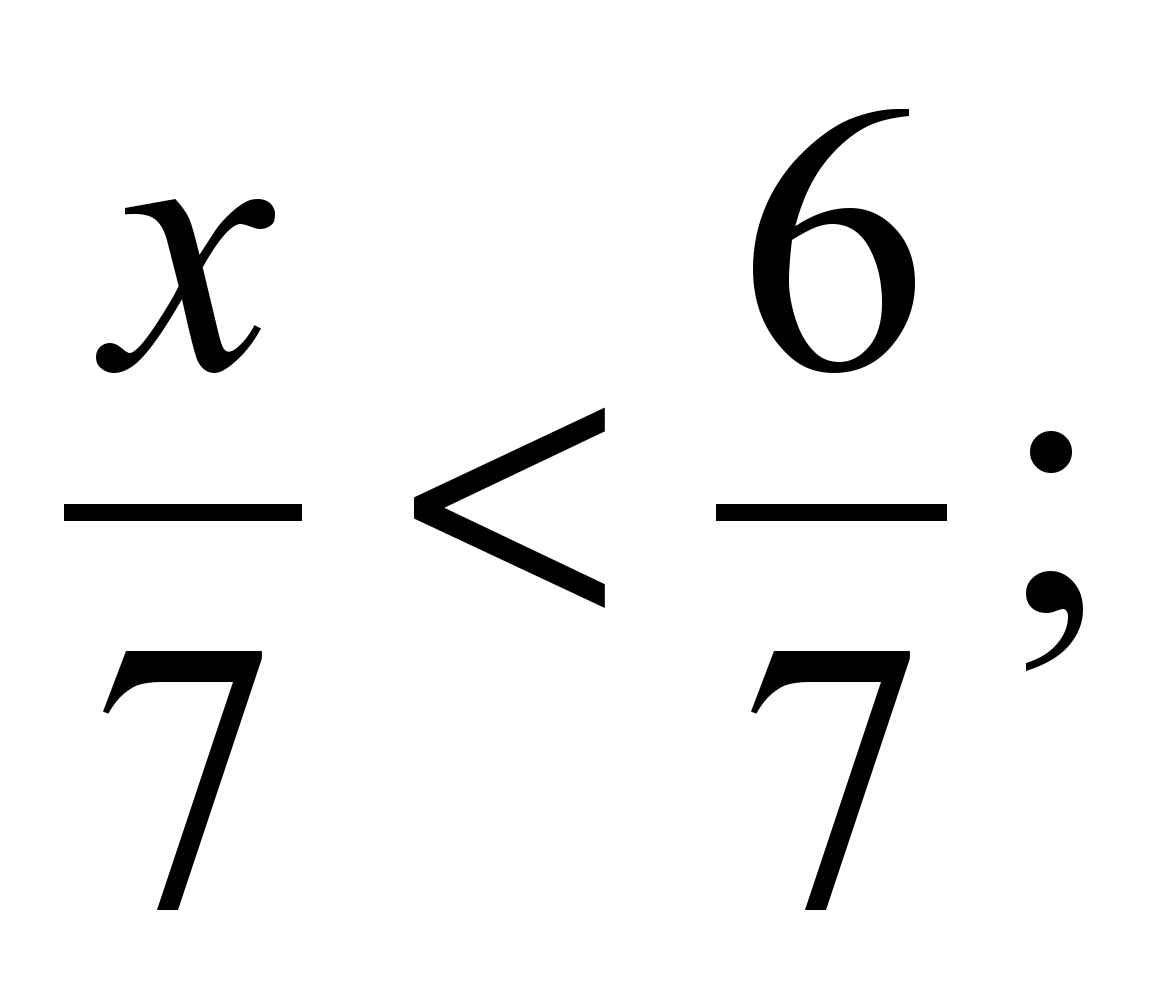 4)
4) 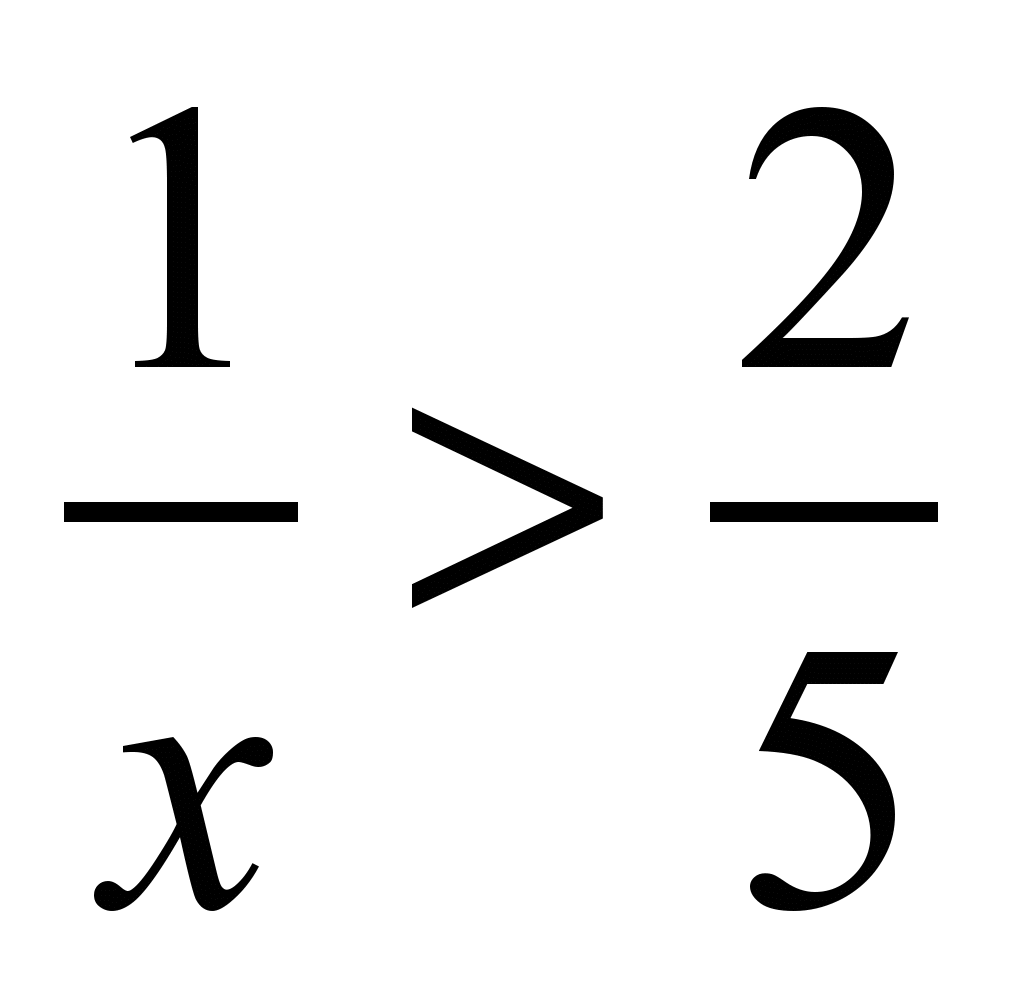 .
.Перед шестым заданием ученики рассматривают возможности использования основного свойства дроби для приведения дробей к равным числителям или знаменателям, а в самом задании сначала выбирают более простое из изученных преобразований, а затем выполняют его и делают вывод о результатах сравнения. Так в 1) и 3) проще приводить к одинаковым знаменателям, а в остальных случаях к одинаковым числителям
6. Сравните дроби: 1)
 ; 2)
; 2) 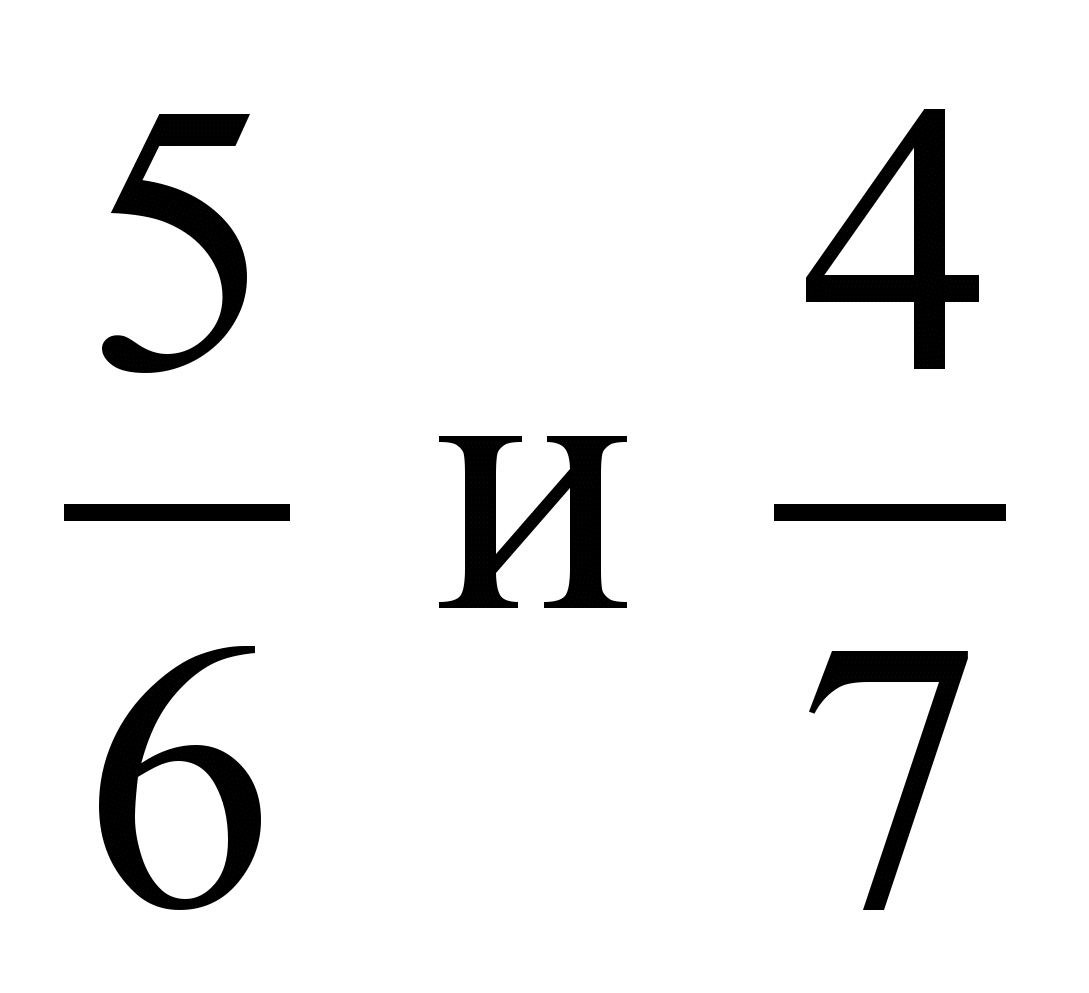 ; 3)
; 3)  ; 4)
; 4)  5)
5) 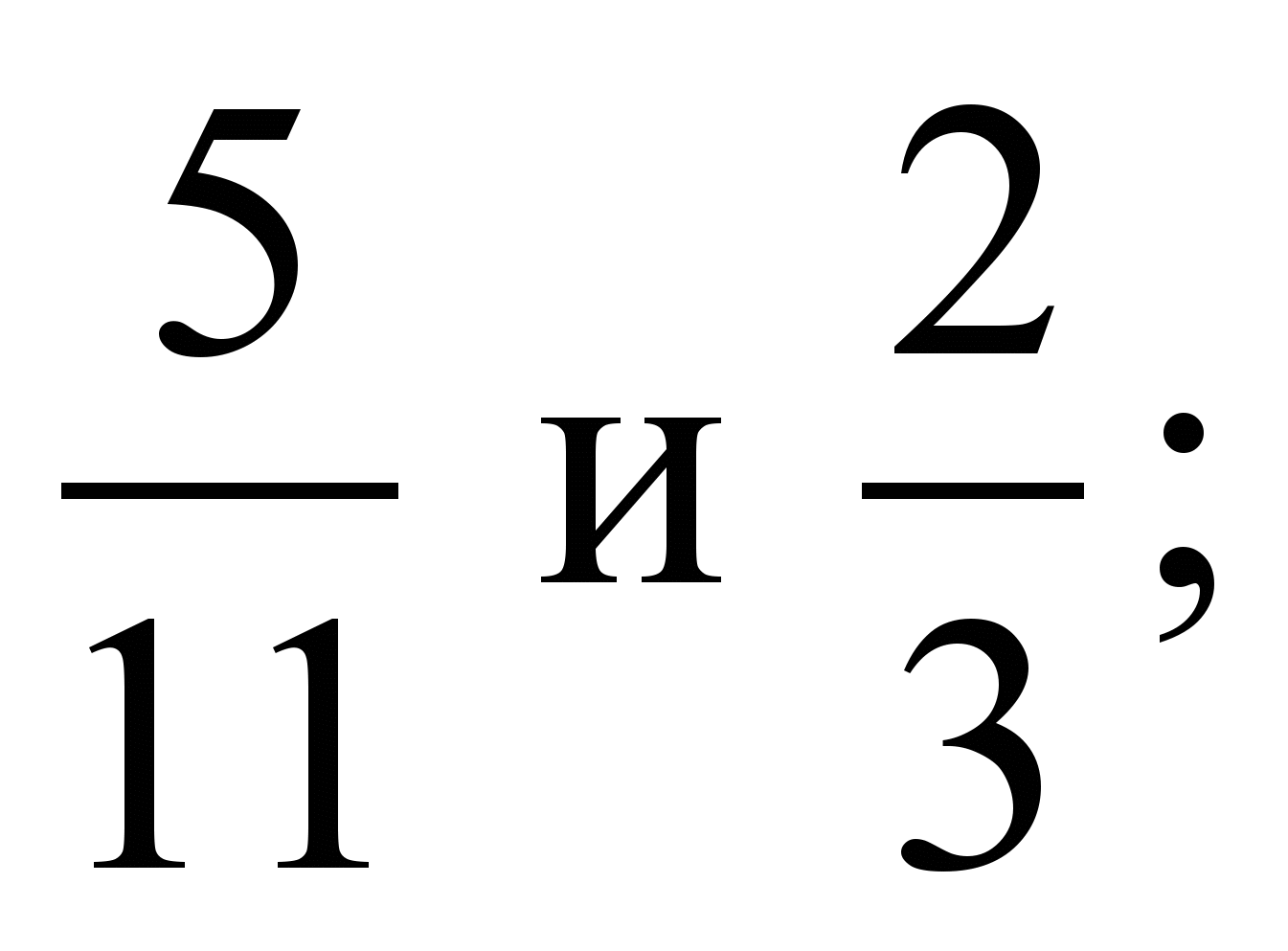
6)
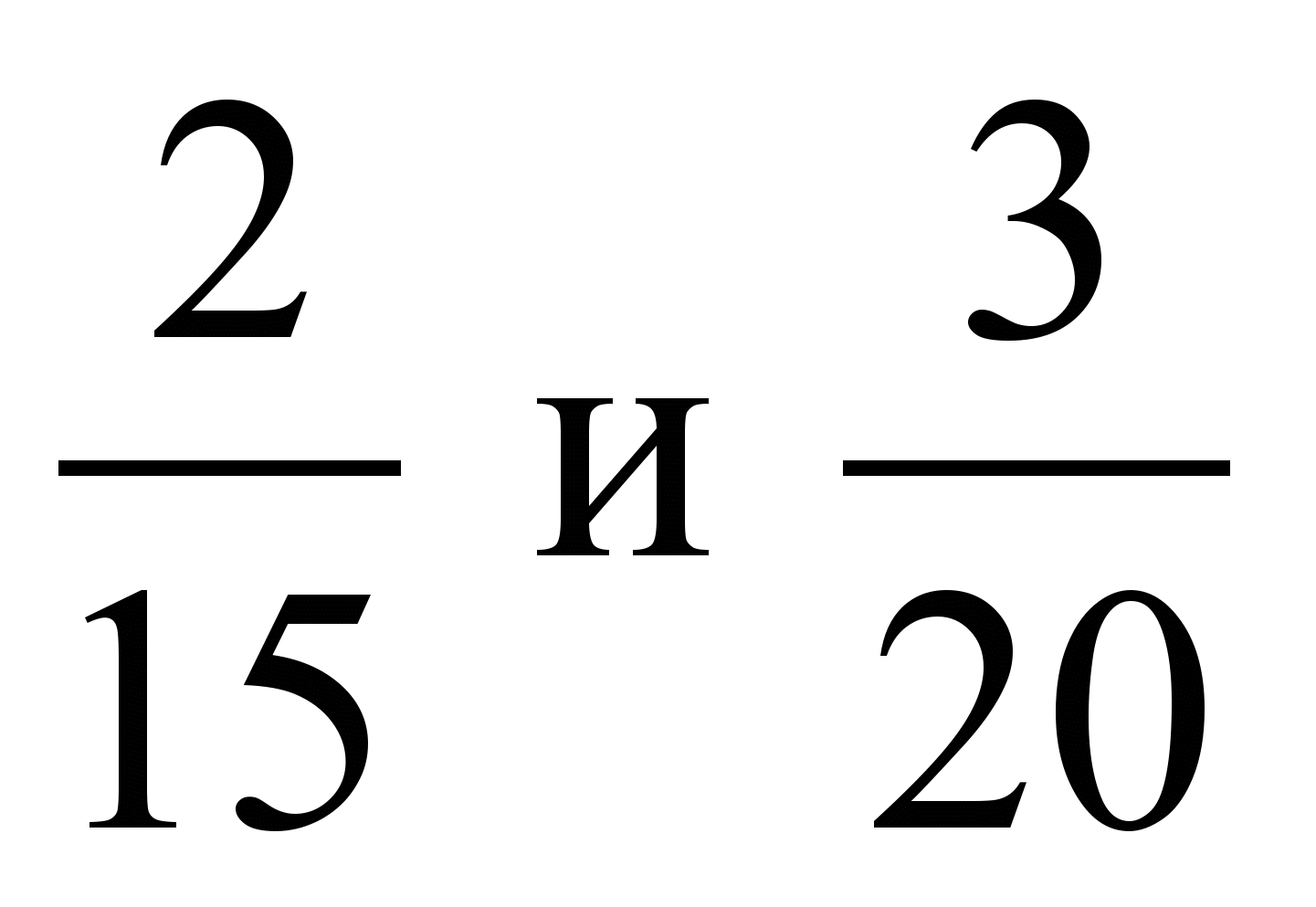 .
.Приведению к общему знаменателю в системе заданий уделяется большее внимание, поскольку этот навык найдет непосредственное применение при сложении и вычитании дробей в следующих пунктах.
7. Приведите к общему знаменателю и расположите в порядке возрастания дроби:
1)
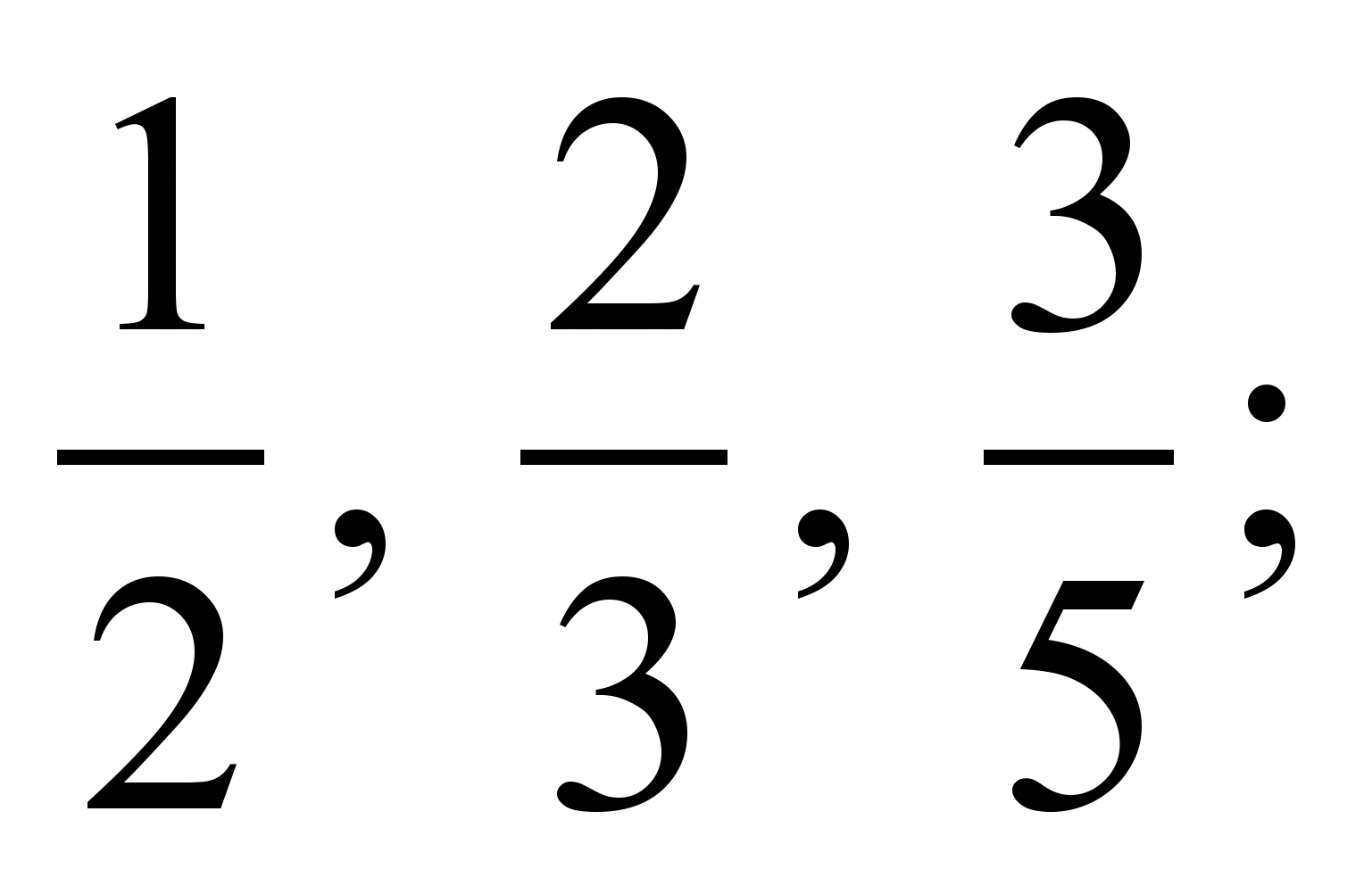 2)
2) 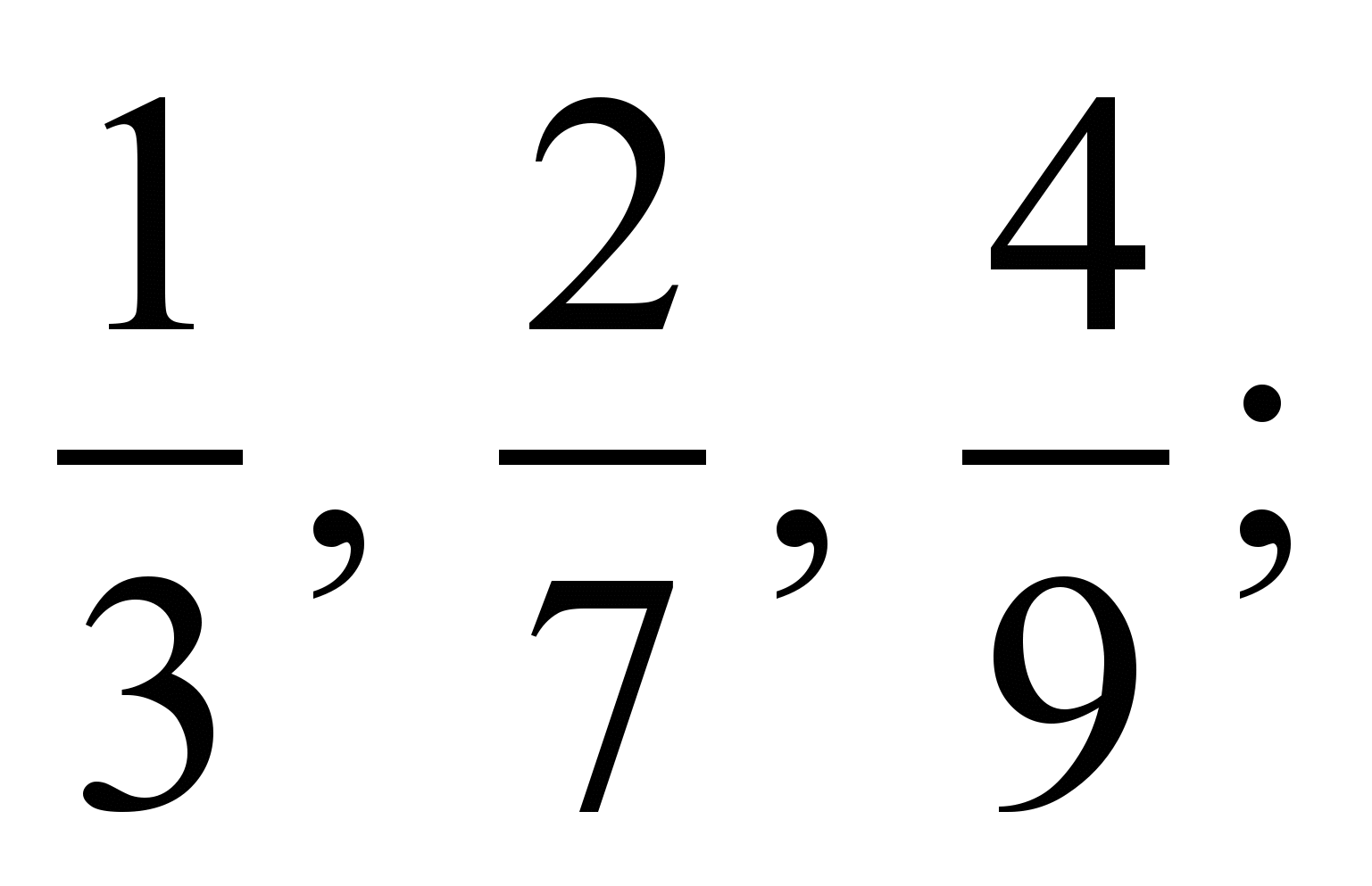 3)
3) 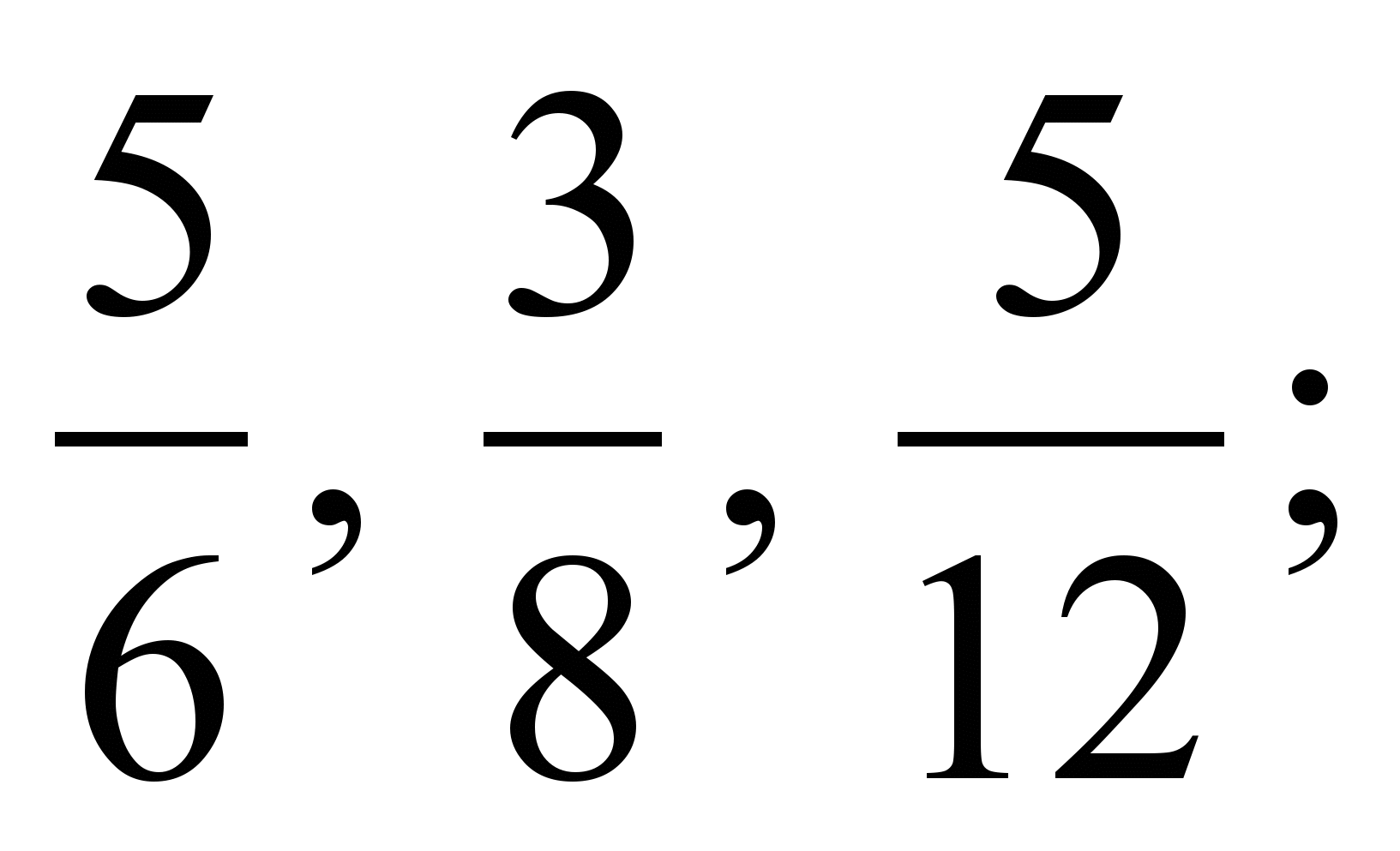 4)
4)  .
.8. 1) Приведите дроби
 ,
, 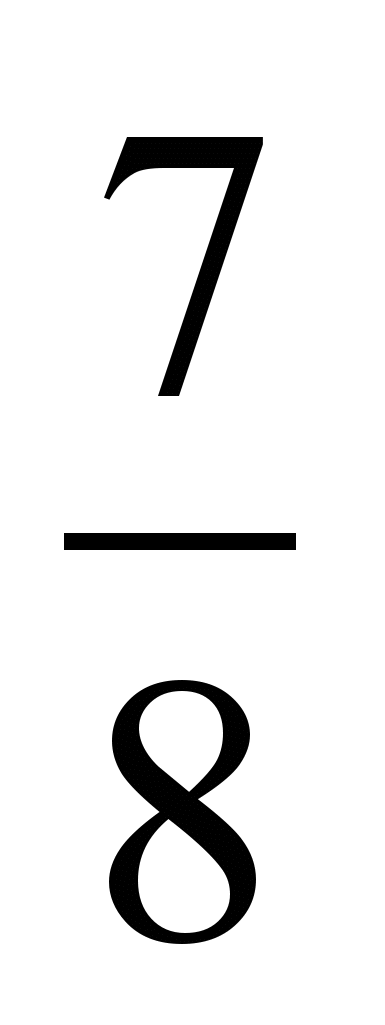 ,
,  ,
, 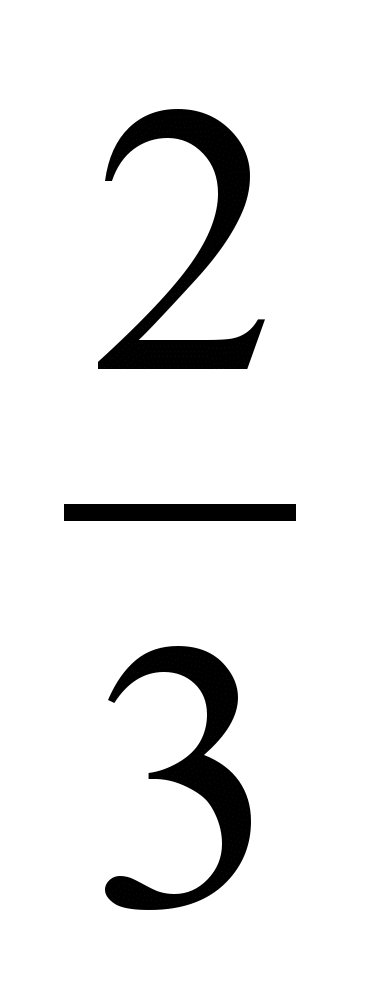 к общему знаменателю и запишите их в порядке возрастания.
к общему знаменателю и запишите их в порядке возрастания.2) Приведите дроби
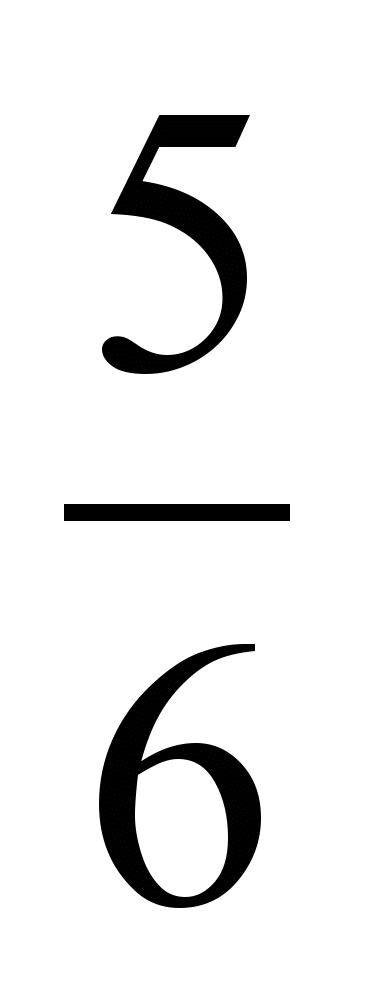 ,
, 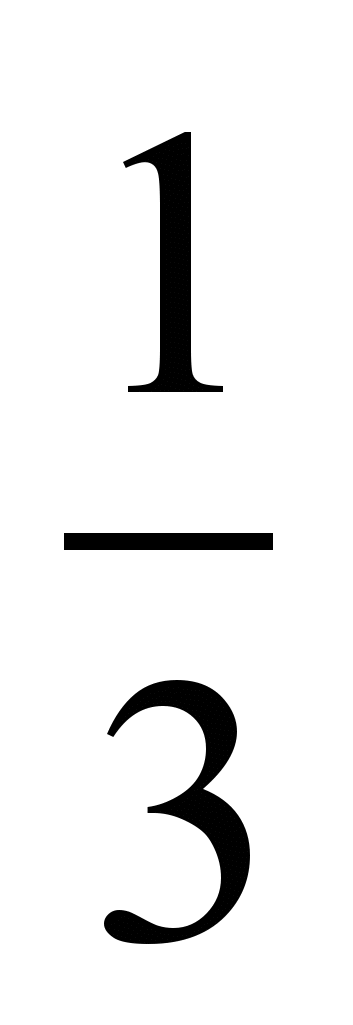 ,
, 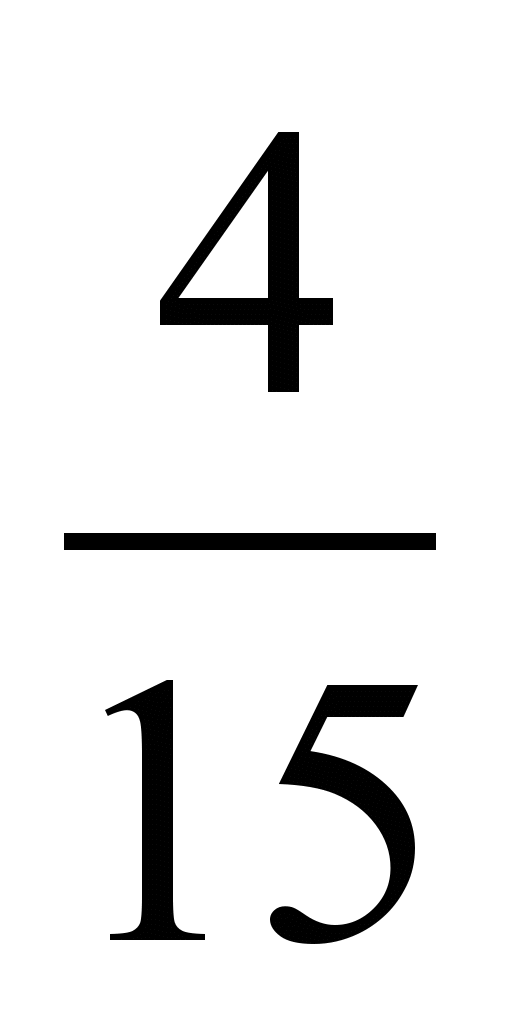 ,
, 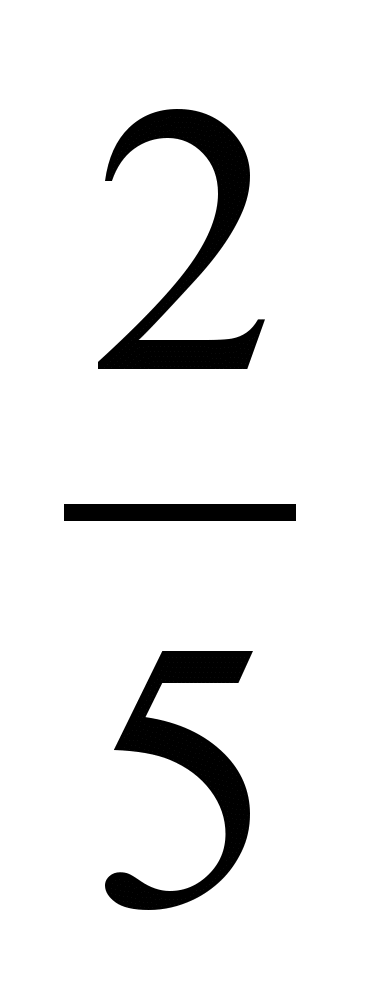 к общему знаменателю и запишите их в порядке убывания.
к общему знаменателю и запишите их в порядке убывания.Само по себе сравнение чисел в девятом задании не представляет трудностей, смысл задания в дополнительном вопросе.
9. Сравните числа и определите, на сколько одно из них больше другого:
1) 1 и
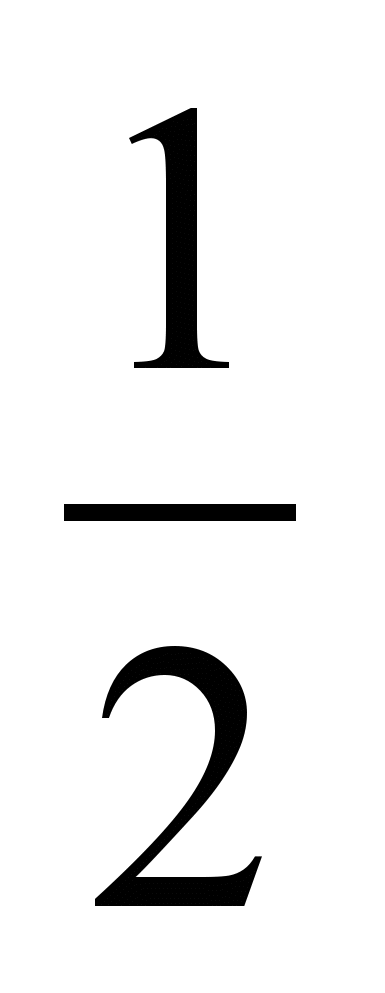 ; 2)
; 2) 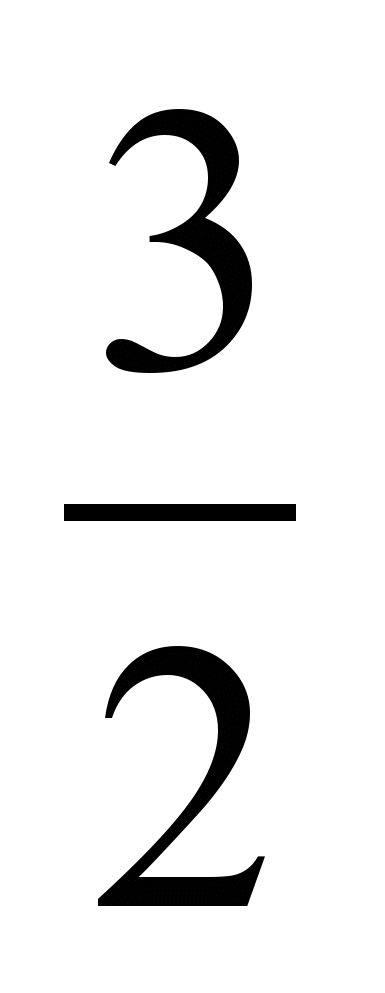 и 1; 3)
и 1; 3) 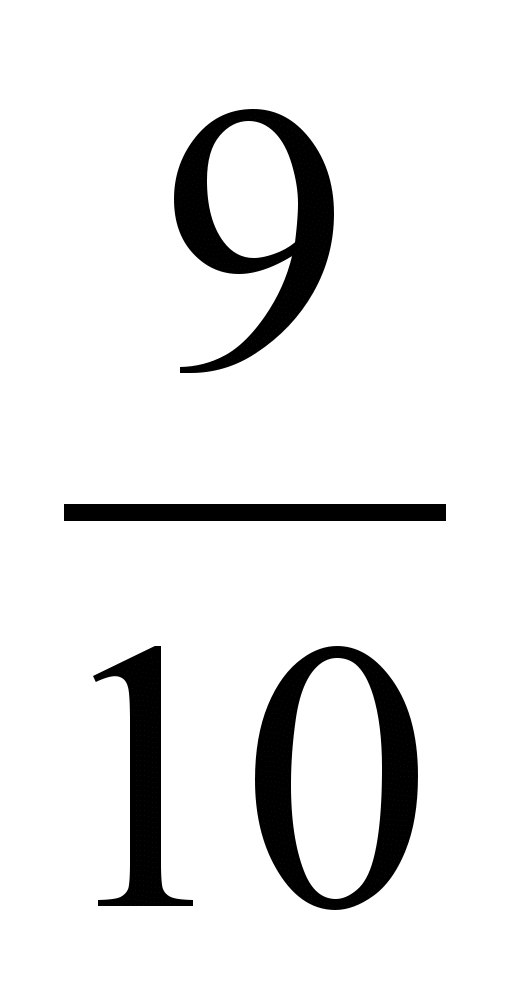 и 1; 4)
и 1; 4)  и 1; 5)
и 1; 5) 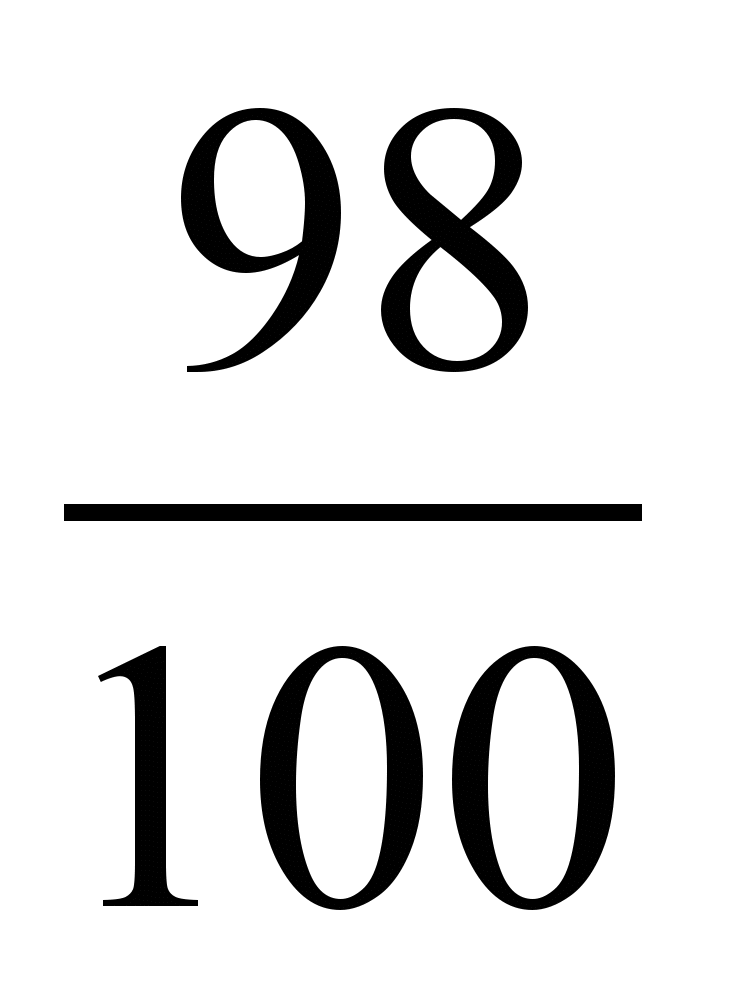 и 1; 6)
и 1; 6) 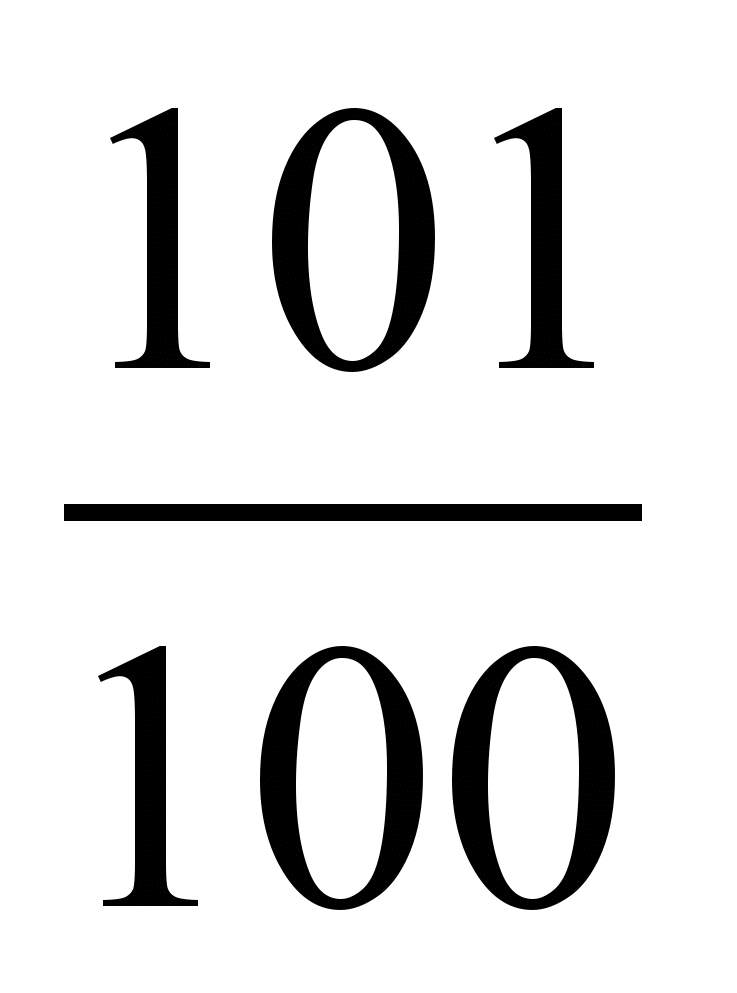 и 1.
и 1.Выясняя в задании 10, на сколько каждое из чисел больше или меньше 1, школьники располагают их на координатном луче.
10. 1) Сравните
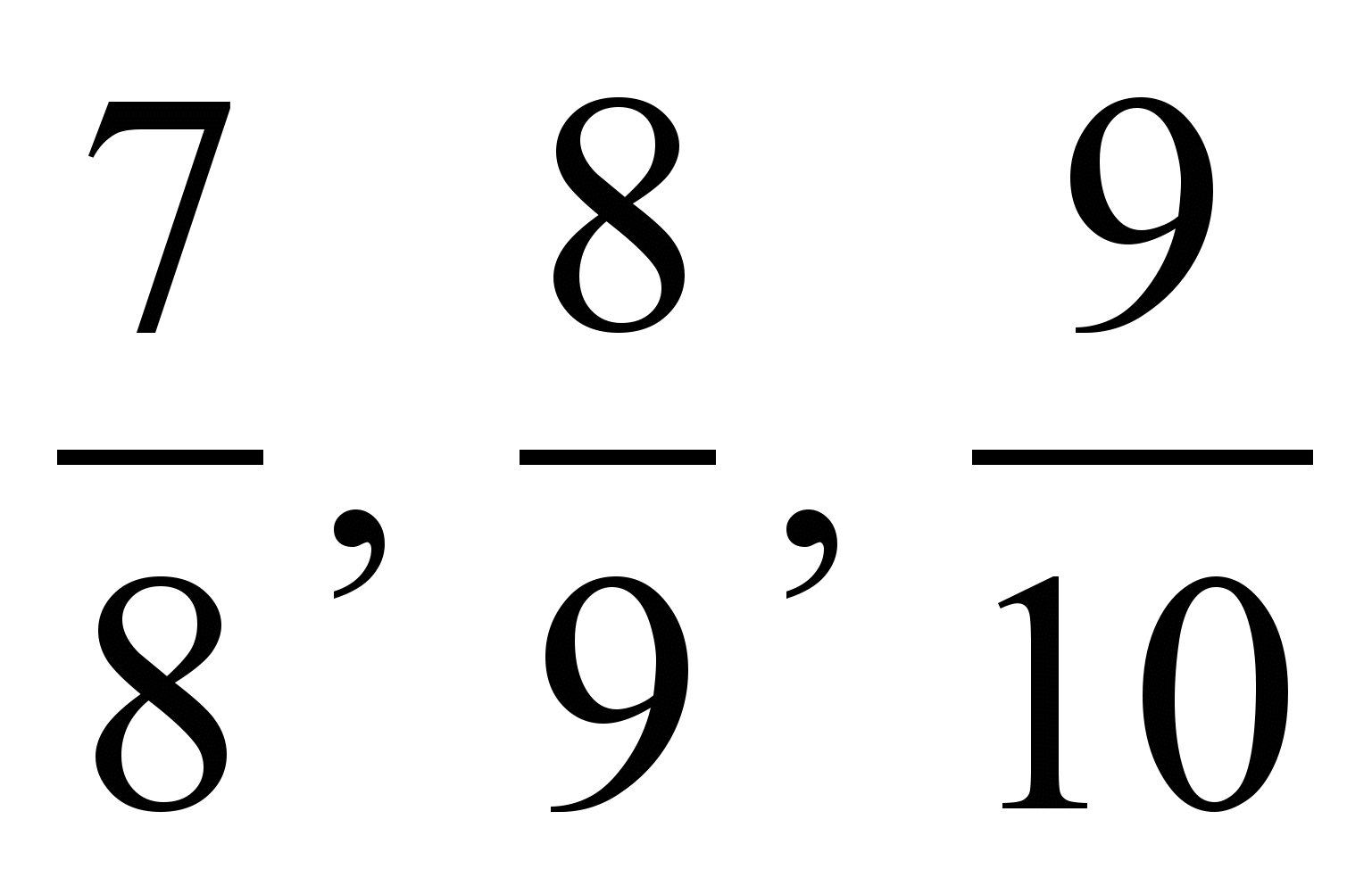 с единицей и узнайте, какая из дробей наибольшая.
с единицей и узнайте, какая из дробей наибольшая.2) Сравните
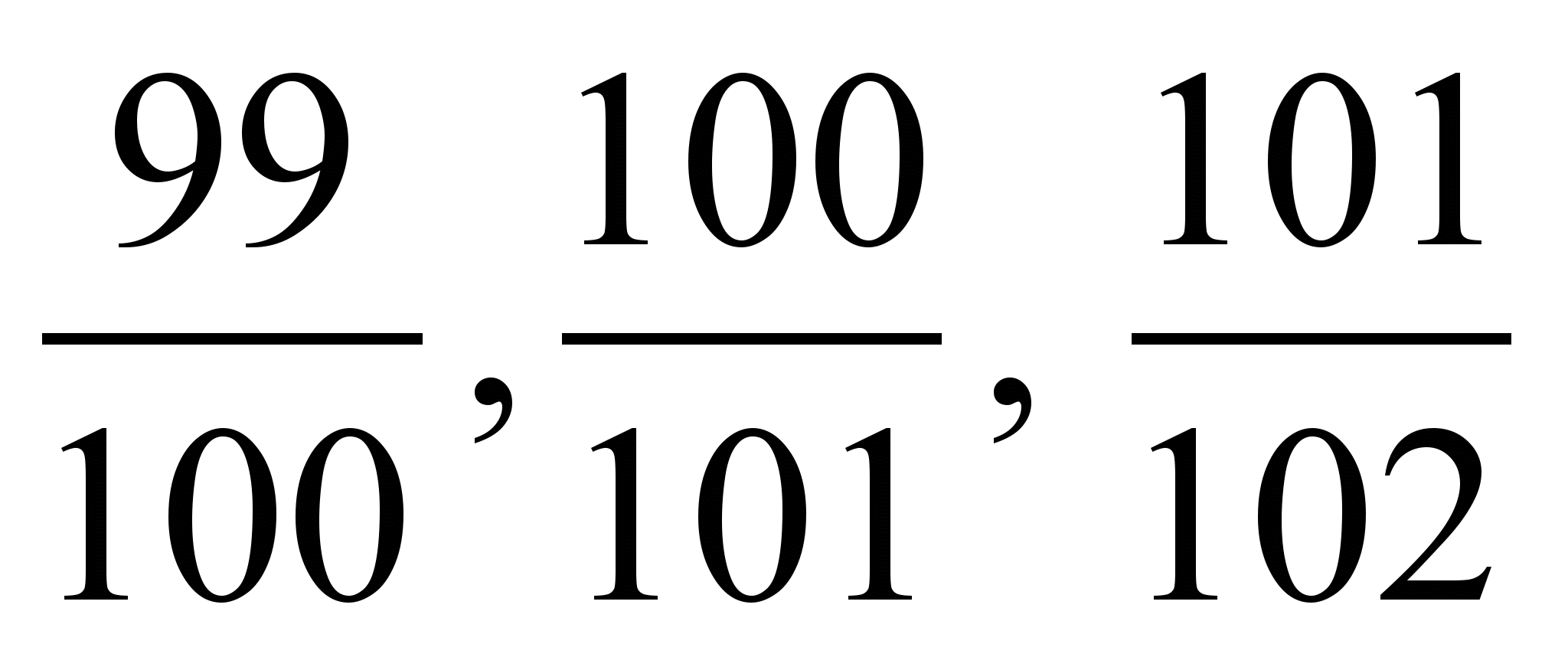 с единицей и узнайте, какая из дробей наименьшая.
с единицей и узнайте, какая из дробей наименьшая.3) Сравните числа
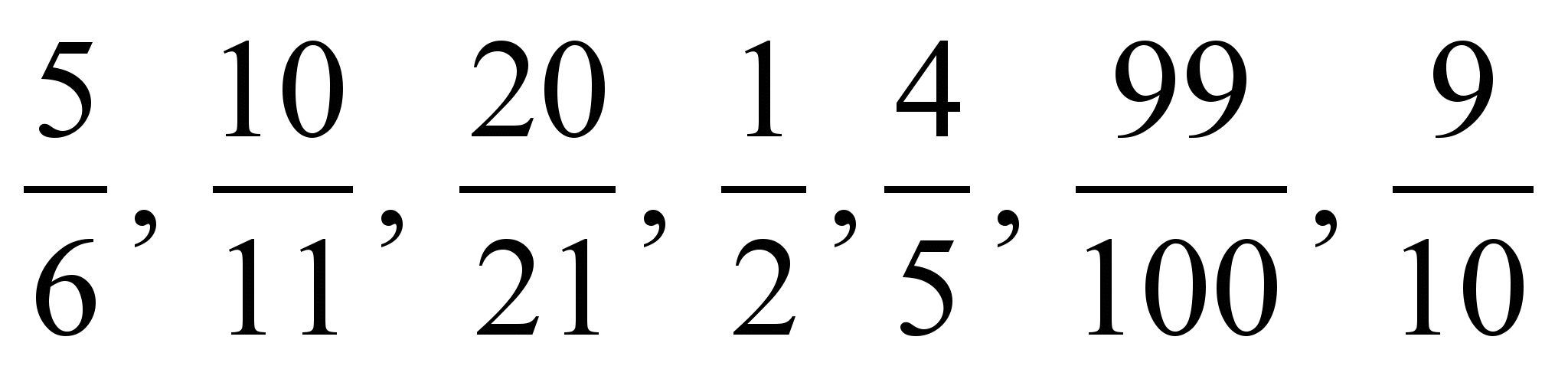 с единицей и расположите их в порядке убывания.
с единицей и расположите их в порядке убывания.В задании 11 аналогичная работа проводится при сравнении данных чисел с
 .
.11. 1) Сравните
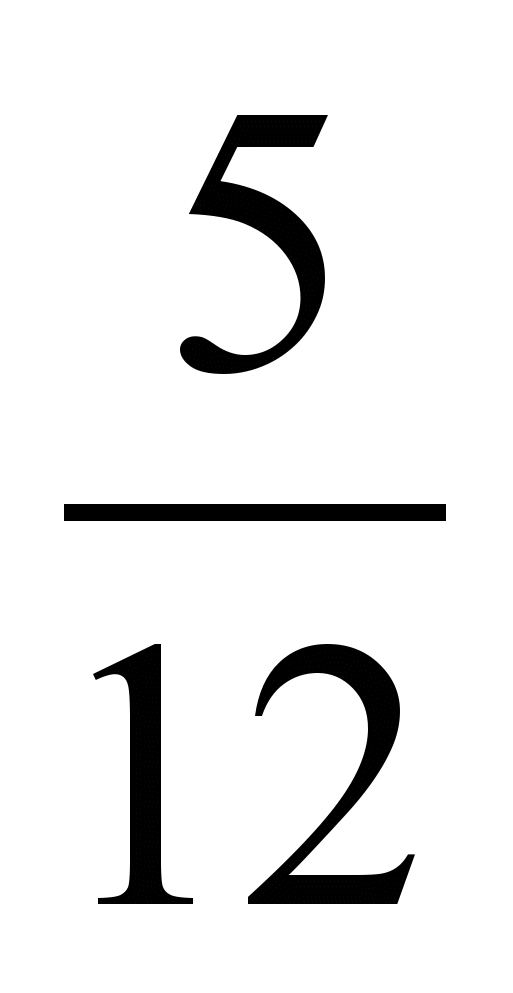 ,
,  ,
, 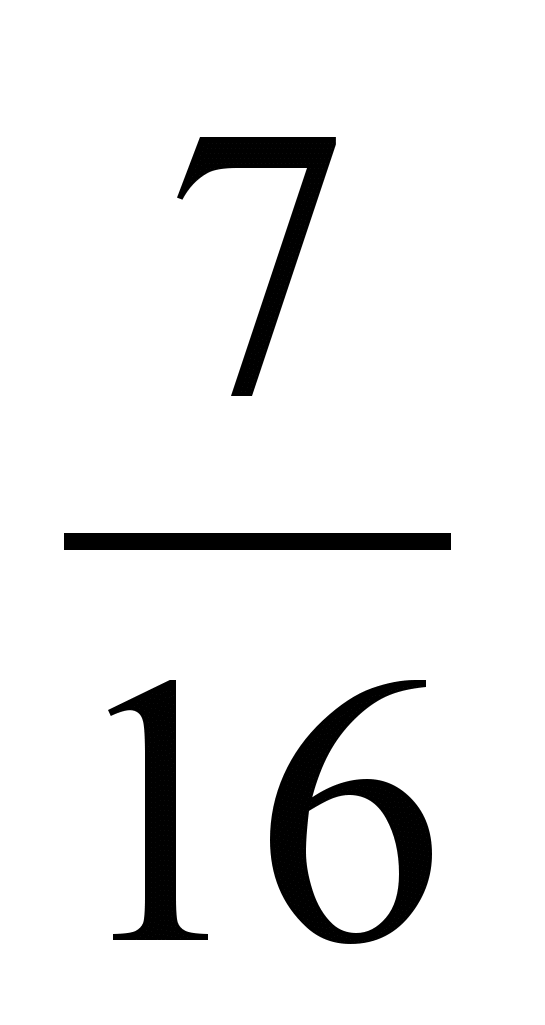 с дробью
с дробью  и узнайте, какая из дробей наибольшая.
и узнайте, какая из дробей наибольшая.2) Сравните
 ,
, 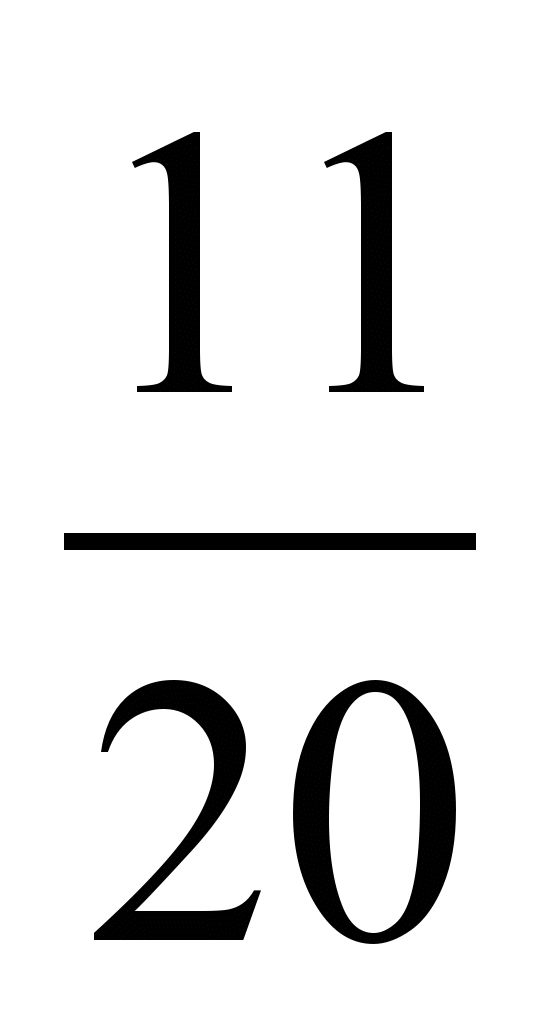 ,
, 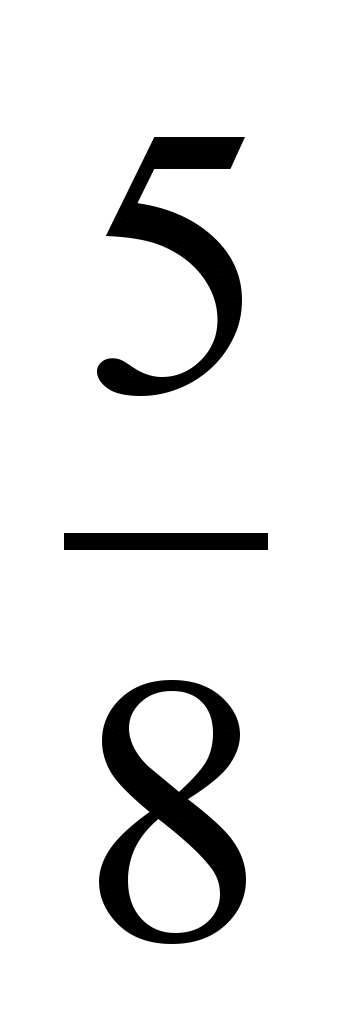 с дробью
с дробью  и узнайте, какая из дробей наименьшая.
и узнайте, какая из дробей наименьшая.В задании 12 школьники продолжают сравнивать дроби с использованием вспомогательного числа, но должны выбирать его самостоятельно.
12. 1) Не приводя дроби к общему знаменателю, сравните:
а)
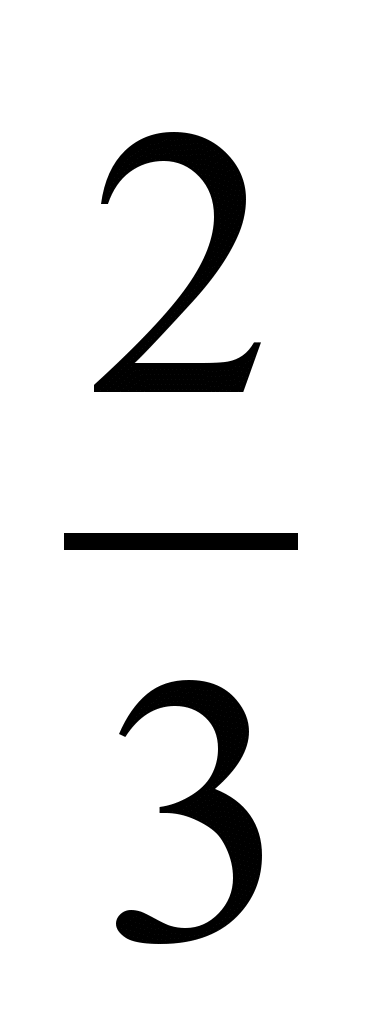 и
и 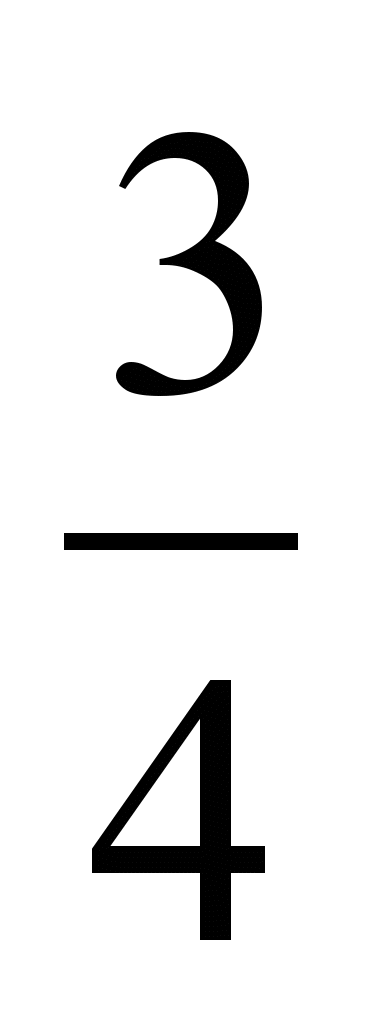 ; б)
; б)  и
и  ; в)
; в)  и
и  .
. 2) Составьте еще несколько пар дробей, которые можно сравнить без приведения их к общему знаменателю.
На этом этапе обучения все приемы сравнения дробей сформированы и в следующих заданиях и сюжетных задачах школьники будут выбирать наиболее рациональные пути сравнения обыкновенных дробей.
Мы показали на примере одной темы, как формируются умения и навыки пятиклассников, заложенные в государственный образовательный стандарт: интеллектуальные умения – при выборе рационального приема сравнения обыкновенных дробей, технические навыки – при выполнении этого приема.
Чередование интеллектуальной и технической деятельности при обучении математике снимает проблему перегрузки школьников.
