Методика обучения решению математических задач учащихся основной школы в условиях дифференциации образовательного процесса 13. 00. 02 Теория и методика обучения и воспитания (математика в системе начального, среднего и высшего образования)

Вид материала

Автореферат

Подобный материал:

• Методика дифференцированного обучения решению математических задач с использованием, 253.93kb.
• Методика создания и использования системы повторительных математических диктантов как, 452.55kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 154.39kb.
• Методика обучения геометрии в основной школе с использованием фузионистского подхода, 399.25kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.55kb.
• Программа-минимум кандидатского экзамена по специальности 13. 00. 02 «Теория и методика, 223.63kb.
• Взаимосвязанное обогащение синонимической лексикой родной и русской речи учащихся VI-VII, 389.12kb.
• Программа вступительного экзамена в аспирантуру по курсу теория и методика обучения, 45.44kb.
• Методическая система мониторинга математической подготовки студентов вуза 13. 00. 02 -, 435.72kb.
• Развитие интереса учащихся к математике через эстетический потенциал исторических задач, 468.64kb.

Сущность системного подхода к раскрытию понятия «задача» позволяет рассмотреть данное понятие как объект, орудие и результат познания.

В литературе по психологии существует несколько подходов к определению понятия «задача». Наиболее распространенным является понимание сущности задачи как цели мыслительной деятельности, в процессе которой идет поиск путей и средств ее разрешения для получения некоторого познавательного результата.

Общее психологическое определение задачи приводится в теории деятельности А.Н.Леонтьевым: задача - это «цель, данная в определенных условиях». Этим определением пользуется С.Л.Рубинштейн и рассматривает задачу как «цель для мыслительной деятельности индивида, соотнесенную с условиями, которыми она задана». Для К.К.Платонова «задача - цель, поставленная в конкретных условиях, требующая исполнения, решения». Ряд психологов (В.В.Давыдов, А.В.Запорожец, В.П.Зинченко, А.Р.Лурия, А.М.Матюшкин, А.В.Петровский) приводят такое определение задачи: «задача (проблема) - цель деятельности, данная в определенных условиях и требующая для своего достижения использования адекватных этим условиям средств».

Понятие задачи в психологии характеризует направленность и цель деятельности человека, достижение результата которой осуществляется определенными средствами.

Анализируя понятие «задача» в общей и частных дидактиках, будем иметь в виду учебную задачу. Учебная задача отличается по своей структуре и функциональному назначению от понятия задачи. Учебная задача является элементом учебной деятельности. В.В.Давыдов отмечает, что учебная задача требует определенных способов умственной деятельности, ориентированных на овладение наиболее общими отношениями предметной действительности. Учебная задача предполагает открытие и освоение общих способов решения относительно широкого круга проблем научной и практической области.

По В.В.Давыдову, «учебная задача, с постановки которой начинает разворачиваться учебная деятельность, направлена на анализ школьником условий происхождения теоретических понятий и на овладение соответствующими обобщенными способами действий, ориентированными на некоторые общие отношения осваиваемой предметной области. Иными словами, существенной характеристикой учебной задачи служит овладение школьниками содержательно (теоретически) обобщенным способом решения некоторого класса конкретно-практических задач».

В дидактической литературе задача представляет метод обучения, направленный на достижение образовательных целей.

В частных дидактиках оперируют различными определениями учебной задачи. Чаще всего встречается определение задачи через структуру изучаемого предмета. Математики определяют задачу через ее структурные элементы (В.М.Брадис, В.В.Репьев, А.А.Столяр, Л.М.Фридман). Например, А.А.Столяр в определении задачи выделяет ее требование. В.В.Репьев указывает на необходимость функциональной зависимости между ее искомыми и данными величинами. Б.М.Брадис определяет задачу через математический вопрос, не называя при этом ее признаков. Л.М.Фридман выделяет структурные элементы задачи. «Всякую знаковую модель проблемной ситуации мы будем называть задачей», - отмечает Л.М.Фридман.

Под задачей будем понимать объект мыслительной деятельности, в котором в диалектическом единстве представлены составные элементы (предмет, условие и требование), и получение познавательного результата возможно при раскрытии отношения между известными и неизвестными элементами задачи (рисунок 1).



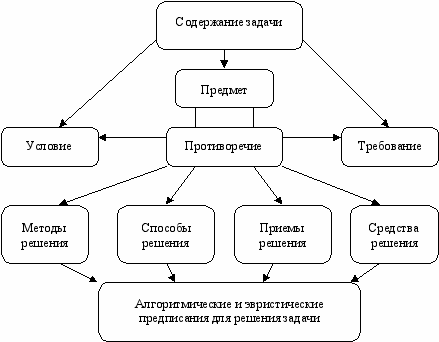
Рисунок 1 - Структурные единицы задачной и решающей систем

Задача - сложная дидактическая система, где в единстве, взаимосвязи, взаимозависимости и взаимодействии представлены компоненты (задачная и решающая системы), каждая из которых в свою очередь состоит из находящихся в такой же динамической зависимости элементов: предмета, условия и требования задачи, с одной стороны, методов, способов, приемов и средств ее решения - с другой. Важно отметить, что заданная и решающая системы являются структурными образованиями различной степени сложности.

Следовательно, сущность и статус понятия «задача» могут быть определены на структурном и функциональном уровнях.

В исследованиях ученых-философов существует несколько определений понятий «решение» и «решение задачи». «Решение, процесс и результат выбора цели и способа действий».

Так, С.Л.Рубинштейн относит всякий мыслительный акт к решению задачи, а в «процессе ее решения объективное предметное содержание задачи опосредует и определяет мыслительный процесс». Далее он продолжает: «Разрешение задачи требует сплошь и рядом значительного волевого усилия для преодоления встающих перед мышлением трудностей». Таким образом, в психологии решение задачи рассматривается как некоторое волевое усилие, направленное на разрешение противоречий между условиями и требованиями задачи.

Понятие «решение задачи» следует рассматривать как процесс и его результат.

Решение задачи представляет собой процесс преобразования объекта, описанного в содержании задачи. Преобразование этого объекта осуществляется определенными методами, способами и средствами. Решение задачи предполагает познание самого процесса преобразования. Оно осуществляется с помощью определенных мыслительных действий и операций, которые могут быть представлены в виде эвристических или алгоритмических предписаний. Таким образом, решение задачи является сложным процессом мыслительной деятельности человеке» направленным на преобразование объекта, на разрешение противоречия между условием и требованием задачи.

Мы придерживаемся точки зрения Л.М.Фридмана и выделяем четыре действия в решении задачи: ознакомление с задачей, составление плана ее решения, осуществление решения, анализ полученного результата.

Анализируя психологическую теорию решения задач, можно в каждом действии выделить основные операции: ориентирование, планирование, исполнение, контроль.

Четвертую операцию предлагаем дополнить самоконтролем, что обеспечивает личностно-ориентированный подход в обучении решению задач (рисунок 2).

Решение задач выполняет определенные функции в учебно-воспитательном процессе.

Основные функции решения задач следующие:

а) вводно-мотивационная;

б) познавательная;



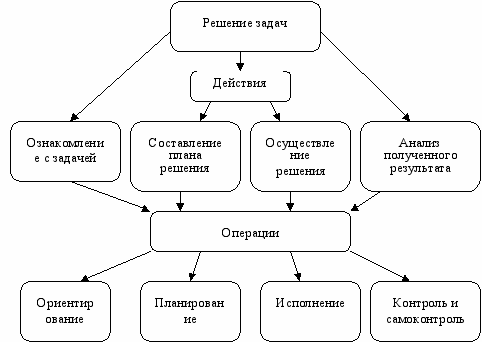
Рисунок 2 – Содержательные элементы деятельности по решению задач


в) развивающая;

г) воспитывающая;

д) управляющая;

е) иллюстративная;

ж) контрольно-оценочная.

В диссертации раскрыты сущности всех выше приведенных функций.

В диссертационном исследовании также рассмотрены дидактические принципы построения системы задач: целостность, многофункциональность, многоуровневость и множественность

Анализ методической литературы приводит к заключению, что обобщенный прием решения задач - это определенная система последовательных действий, без выполнения которой не может быть получен положительный результат, разрешено противоречие между данными и искомыми величинами, представленными в содержании задачи.

Обобщенный прием решения задач состоит из основных действий (ознакомление- с задачей, составление плана решений, осуществление решения, анализ результата), включающих в свою очередь операции, структура и содержание которых отличаются для каждого вида и типа задач.

Учитывая возрастные особенности и уровень знаний и умений учащихся средней школы, можно сказать о свернутой мыслительной деятельности при решении задач, которые необходимо при осуществлении дифференциации обучения.

Содержание школьного курса математики состоит из двух частей. Первая - теоретический материал, включающий в себя понятия и определения, математические факты и теоремы, методы доказательства утверждений и решения задач. Вторая часть представляет собой задачи, соответствующие теоретическому материалу учебного курса.

Успех обучения математике в определенной мере зависит от того, какие задачи, в какой последовательности и в каком количестве даются учащимся для работы на уроке и дома.

Поэтому при организации процесса обучение учащихся решению математических задач учитель в первую очередь сталкивается с необходимостью отбора задач, их упорядочивания, анализа тех умственных действий, которые должны будут выполнить учащиеся в процессе решения задач и т.д. Это требует проведения классификации задач, которая помогла бы учителю осуществить их отбор в соответствии с поставленной дидактической целью.

В дидактике и методике преподавания математики особое значение имеют обобщенные ассоциации, в которых фиксируется наиболее общие функциональные связи, обладающие широким спектром применения. Обобщенные ассоциации можно рассматривать как свернутые умозаключения, которые в случае необходимости легко разворачиваются в полное логическое рассуждение. Такое свернутое умозаключение может быть получено только в результате активной мыслительной деятельности учащегося.

Рассматривая обобщенную ассоциацию как свернутое умозаключение, мы приходим к выводу, что процесс решения математической задачи можно рассматривать как актуализацию необходимых ассоциаций, выстроенных в определенном порядке. Отсюда следует, что успех ученика при решении задачи во многом будет определяться наличием у него достаточного количества обобщенных ассоциаций и способностью ученика к их актуализации в нужный момент.

Реализуя данное положение на практике, многие учителя выделяют в учебном материале «опоры», которые по тем или иным причинам играют особую роль в учебном процессе. Это может быть задача, решение которой является удачной иллюстрацией метода или приёма. Опорой может быть конфигурация с реализуемыми на ней отношениями и т.д. Если такая опора, с одной стороны, обладает определенной универсальностью, а с другой, учащимися была проведена достаточная работа с ней, то она может служить базой для формирования обобщенной ассоциации.

Установление разнообразных связей в учебном материале основано на переработке математической информации. Способность перерабатывать информацию, особенно математическую, проявляется по-разному у разных учеников. Одни «с ходу» выделяют основное в учебном материале, другим требуется время для осмысления и выделения главного, третьи нуждаются в дополнительных вопросах, которые организовали бы и направили их умственную деятельность. Поэтому учебный процесс должен строиться с учетом индивидуальных особенностей учащихся. Например, таких, как особенности восприятия математической информации, её аналитико-синтетического осмысления, обобщения и т.п.

Запоминание найденных связей также требует учёта индивидуальных особенностей памяти ученика, учёта его интереса и мотивации.

Сказанное выше позволяет утверждать, что формирование обобщенных ассоциаций объективно требует дифференцированного подхода к ученикам.

Важную роль при формировании обобщенных ассоциаций играют стимулирующие звенья. Стимулирующим звеном называют промежуточный мыслительный процесс, который вводится между двумя другими процессам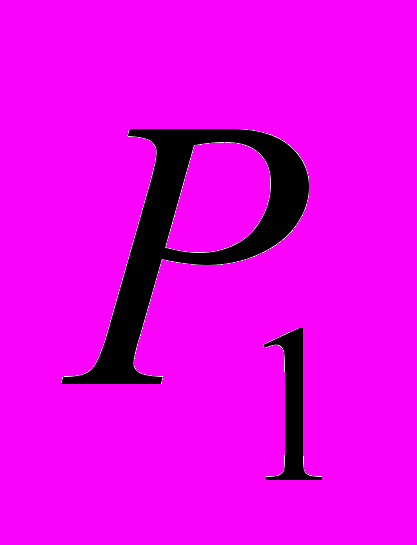и и 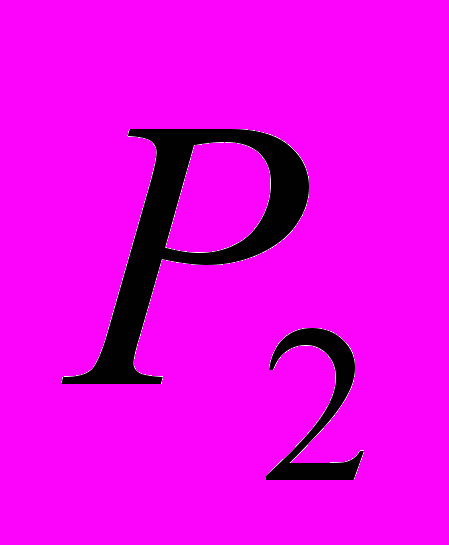, помогая установить связь между ними и активизируя мышление.

Активизируя мыслительную деятельность учащихся с помощью стимулирующих звеньев, учитель тем самым способствует формированию прочных ассоциаций, согласно закономерностям II.8 и 9.

Использование стимулирующих звеньев при дифференцированном обучении приводит к понятию «дозированная помощь». Такая помощь должна организовываться для каждой типологической группы учащихся с учетом тех индивидуальных особенностей, которые были положены в основу данной типизации. Дозированная помощь может отличаться объемом, формой предъявления (вербальной, графической), конкретикой и т.д.

Каждая математическая идея имеет вполне конкретную реализацию (часто не единственную). Поэтому учитель, желающий познакомить учеников с новым для них приёмом или методом решения должен отобрать наиболее подходящую, с его точки зрения, задачу, пример. Но одна задача, как правило, не может вскрыть всей полноты и глубины рассматриваемого метода, а является лишь его более или менее удачной иллюстрацией в конкретной математической ситуации. Для полного и глубокого усвоения учениками рассматриваемого метода необходимо показать его во всём многообразии его приложений. Это приводит к необходимости рассматривать ряд задач (блоки, циклы, серии, системы), объединенных общей дидактической целью.

Система задач, систематизированных и организованных с учетом поставленной дидактическои цели, приобретает новое качество, и его дидактическая ценность возрастает. Это было давно замечено учителями и использовано в учебном процессе. С тех пор дидактические проблемы, связанные с использованием систем задач в обучении, традиционно являются объектом исследований педагогов, методистов, учителей. Одним из первых в Русской методике применил в обучении системы задач известный методист С.И.Шохор-Троцкий. В его работах получила развитие идея целесообразно подобранных задач. Им был предложен метод построения курса арифметики на основе специально подобранных задач («метод целесообразных задач»).

В процессе работы с этими задачами ученики не только усваивали приёмы и методы решения арифметических задач, но и знакомились с теоретическими сведениями из арифметики.

Аналогичный курс разрабатывался С.И.Шохор-Троцким и для геометрии.

В настоящее время всё чаще внимание учёных, методистов, учителей обращается к системам задач, их методическому обоснованию и использованию в учебном процессе.

К системе задач должны быть предъявлены две группы требований: первая группа определяет состав и последовательность заданий с позиций содержания курса; вторая группа требований отражает особенности используемых задач.

При организации дифференцированного обучения к двум группам требований следует добавить, по нашему мнению, третью группу, в которой были бы отражены требования, учитывающие специфические особенности организации учебного процесса с различными типологическими группами учащихся в классе.

Особую роль приобретает использование систем взаимосвязанных задач в преподавании геометрии. Это вызвано рядом обстоятельств, которые оказывают существенное влияние на процесс обучения геометрии.

Прежде всего, отметим широкую зону ориентировочной основы действия при решении геометрической задачи. Блок взаимосвязанных задач позволяет сузить её, но не указывает однозначно направление поиска и выбора пути решения задачи. Т.е. система способствует формированию общих умений решения геометрических задач: учит сравнивать, обобщать, переносить известные приемы решения в новые условия и т.д. Благодаря тому, что задачи системы идейно достаточно близки, у учеников оттачивается механизм догадки, формируются элементы эвристики.

При обучении решению геометрических задач необходимо предусмотреть возможность перехода от одной задачи к другой для учащихся с разными способностями к математике. Обязательно должен выполняться принцип постоянного нарастания сложности заданий, причем этот принцип должен быть индивидуализирован.

В целях лучшей организации работы учащихся с системой взаимосвязанных задач удобно разделить его на две части: основную и творческую. Основная часть включает в себя программный материал и определяет уровень обязательных результатов обучения. Здесь содержится вся необходимая информация, являющаяся основой для успешной работы с задачами творческой части. Постепенно усложняющиеся задания, систематизирующие связи между ними, необходимое методическое обеспечение, создают основу для активной самостоятельной работы учеников с задачами основной части. Для контроля и коррекции деятельности учеников учитель со всем классом обсуждает полученные решения, анализирует их, сравнивает, выбирает среди них получше, разъясняет наиболее сложные. Активная самостоятельная работа учащихся с возможностью последующей коррекции собственных результатов дает возможность формировать индивидуальный стиль мышления учащихся, развивать их творческие способности.

В диссертации сформулированы методические требования, которым должны удовлетворять системы азпимосвязанных задач.

Специальным образом организованная уровневая дифференциация обучения предполагает выбор критерия, дифференцирующего учащихся в процессе обучения и формирования на основе этого критерия типологических групп обучаемых. В качестве дифференцирующего критерия одни исследователи выбирают уровень знаний, другие - обучаемость, третьи выбирают социально-мотивационные критерии и т.д. Исходя из выбранного критерия, строится методика обучения, основанная на учете индивидуальных особенностей, с помощью которых проведено формирование типологических групп учащихся.

В нашем исследовании в качестве дифференцирующего критерия был выбран критерий, который состоит из следующих слагаемых:

• уровень знаний;
  

• умение работать с чертежом, т.е. умение проводить комплексный анализ чертежа;
  
• количество актуализируемых обобщенных ассоциаций (первым членом которых является восприятие геометрической конфигурации, а вторым - актуализированные представления оперативных навыков, связанных с этой конфигурацией).
  

Организация активной аналитико-синтетической деятельности ученика при дифференцированном обучении связана с созданием условий, при которых учащиеся из разных типологичесхих групп активно были бы включены в учебный процесс. Один из путей повышения мыслительной активности учащихся связан с использованием стимулирующих звеньев. Это может происходить, например, в форме оказания дозированной помощи ученику на разных этапах решения задачи: на этапе предъявления задачи, на этапе поиска решения, на этапе анализа и исследования решения и его обобщения. Иными словами, дозированная помощь может оказываться на этапе восприятия математической информации, ее переработки и хранения. Эта помощь должна сопрягать типологические особенности ученика со специфическими особенностями учебного материала.

Для проверки выдвинутых предположений проводился педагогический эксперимент с последующей статистической обработкой результатов. В ходе эксперимента проверялась гипотеза о том, что дифференцированный подход к учащимся в процессе обучения решению математических задач с использованием системы взаимосвязанных задач позволяет:

- повысить качество знаний учащихся по математике в основной школе;

- формировать положительную мотивацию учащихся к обучению математике.

Первый этап констатирующего экспериментального исследования был проведён в 2006-2007 гг. Основная задача первого этапа эксперимента состояла в выявлении условий повышения качества знаний учащихся по решению математических задач, проверялось владение учащимися приёмами работы над задачей, влияние использования рациональных и нерациональных способов решения задачи на формирование умений решать математические задачи. Изучался опыт формирования этого умения, выявлялись затруднения учителей связанные с организацией учебной деятельности учащихся.

Основными методами исследования на данном этапе были: наблюдение уроков математики в 7-9 классах, беседы с учителями и учащимися по вопросам, связанными с формированием приёмов учебной деятельности учащихся, постановкой самостоятельных работ учащихся, анализ контрольных и рабочих тетрадей учеников, анкетирование учителей и учащихся, анализ программ и учебников по математике в 7-9 классах, обработка и анализ имеющейся литературы по данной теме и полученных данных. На первом этапе было посещено 150 уроков математики в 5-9 классах г. Шымкента.

Результаты исследования показали, что у учащихся этих классов имеются определённые знания о задаче и приёмах её решения, но они недостаточны для овладения школьниками умения учиться. Процесс формирования приёмов учебной деятельности (УД) учащихся 7-9 классов при обучении математике проходит стихийно, хотя большинство учителей считают необходимым такое обучение, при котором специально формируются приёмы учебной деятельности; вопросы систематизации учебного материала не рассматриваются учителем как необходимое условие повышения качества знаний учащихся по решению математических задач и как условие формирования приёмов учебной деятельности; в ходе изучения математических задач учителя преимущественно используют в обучении фронтальную форму деятельности. В то же время наблюдения за работой передовых учителей математики показали, что формированию приёмов работы над задачей способствует определённая схематизация текста задачи, представление некоторых приёмов поиска решения в виде совокупности действий и правил. Это обеспечивает высокий уровень формирования знаний и умений по математике.

Цель поискового эксперимента (2007-2008) – определить необходимые компоненты методики формирования приёмов учебной деятельности учащихся, как основы формирования знаний, умений и навыков, уточнение разработанной методики формирования приемов учебной деятельности учащихся 7-9 классов при обучении поиску решения текстовых алгебраических задач.

В ходе этого этапа эксперимента корректировать приёмы учебной деятельности, требования к системе, как текстовых алгебраических задач, так и учебных заданий к ним, проверялись различные системы текстовых задач, ориентированные на формирование указанных приёмов учебной деятельности, проверялись условия формирования приёмов учебной деятельности в самостоятельной работе учащихся, исследовались условия эффективной взаимосвязи рациональных и нерациональных решений задачи.

Установлено, что процесс формирования приёмов учебной деятельности учащихся должен сопровождаться системами учебных задач, обладающих свойством структурной полноты и удовлетворяющих выделенным основным требованиям; что система текстовых алгебраических задач, предложенная в школьных учебниках, не обладает свойством структурной полноты (нарушена иерархия сложности и имеются много повторов задач малой сложности, нет учебных заданий к ним).

При проведении обучающего эксперимента широко использовались такие методы исследования, как:

- наблюдение за учебным процессом и деятельностью учащегося;

- разработка, проведение н анализ письменных проверочных работ, анализ устных ответов учащихся;

- поэлементный анализ письменных работ учащихся;

- беседы с учителями.

Всё это вместе взятое позволило усовершенствовать отдельные стороны предлагаемой методики обучения решению математических задач.

В экспериментальных классах: а) обучение велось по системе задач, удовлетворяющей выделенным требованиям; б) формирование приёмов учебной деятельности осуществлялось сначала в условиях фронтальной деятельности учащихся, затем групповой и, наконец, в условиях индивидуальной деятельности (самостоятельные работы) – все выполнялось в соответствии с разработанной методикой с учётом уровней познавательной деятельности учащихся.

В контрольных классах: а) обучение осуществлялось на системе задач действующих учебников, которая не систематизирована и обладает рядом недостатков (но в конце обучения учителю предложено решить отсутствующие в учебнике задачи); б) приёмы учебной деятельности отрабатывались учителем традиционно, без чёткого соблюдения учителем последовательности форм деятельности учащихся (фронтальная, групповая, индивидуальная); в) обучение осуществлялось без чёткого выделения уровней познавательной деятельности учащихся.

Охвачено 129 учащихся в экспериментальных классах и 119 учащихся в контрольных классах.

В таблице 1 приведены результаты контрольной работы в экспериментальных и контрольных классах.


Таблица 1 – Результаты контрольной работы № 4

№ пп	Действия	Результаты к/р № 4 в %
контрольн. кл.	эксперимент. кл.
1. 2. 3.	Приёмы поиска выполнены Уравнение составлено верно Задача решена верно	67 78 76	86 86 82

По результатам выполнения контрольной работы учащиеся экспериментальной группы имеют более высокие показатели, чем учащиеся контрольной группы.

Таким образом, проведённая экспериментальная работа с учащимися 7-9 классов показала эффективность выделенных приёмов учебной деятельности при обучении решению текстовых алгебраических задач. Использование их повысило качество обучения решению текстовых алгебраических задач при развитии положительных мотивов к процессу и результату решения математических задач.

В эксперименте была доказана эффективность использования системы учебных задач.

В начале и в конце эксперимента среди учащихся экспериментальных классов был проведен опрос, который показал повышение интереса обучаемых к изучению геометрии.

Вопросы	2007-2008 учебный год
сентябрь	май
Проявляют интерес к обучению геометрии Нравится решать геометрические задачи Считают, что геометрические задачи более трудные, чем алгабраические	22 % 13 % 84 %	46 % 47 % 63 %

Эти данные позволяют говорить о том, что дифференцированное обучение решению геометрических задач позволяет формировать положительную мотивацию к изучению геометрии.

Таким образом, методика обучения решению геометрических задач и использованием систем взаимосвязанных задач основана на дифференцированном подходе к учащимся и приводит к:

• повышению качества знаний учащихся;
  
• способствует формированию положительной мотивации учеников к изучению геометрии.