Методика взаимосвязанного изучения свойств плоских и пространственных фигур в системе преподавания геометрического материала в технических колледжах

Вид материала

Автореферат

Содержание Общая характеристика работы Проблема исследования Апробация и внедрение результатов исследования На защиту выносятся следующие положения Основное содержание работы

Подобный материал:

• Урок в 10 «А» классе по геометрии На тему «Изображение пространственных фигур на плоскости», 72.61kb.
• Методика применения новых технологий изучения английского языка в колледжах города, 849.26kb.
• Методика преподавания древней русской литературы и фольклора с. Методика преподавания, 1259.52kb.
• Учебно-методический комплекс дисциплины «методика преподавания психологии», 166.81kb.
• Методика преподавания экономики в высшей школе Код, 19.08kb.
• Методика изучения правильных многоугольников в курсе планиметрии Курсовая работа, 313.94kb.
• Правила построения изображений пространственных фигур на плоскости чертежа, 95.16kb.
• Методика чтения лекции. Типичные недостатки. Личность лектора и ее влияние на восприятие, 20.92kb.
• Методика изучения алгебраического материала Анализ программы, 11.01kb.
• Учебная программа (Syllabus) Дисциплина: Методика преподавания психологии Специальность, 205.75kb.

На правах рукописи

БУЛЫЧЕВА ЮЛИЯ ВЛАДИМИРОВНА

МЕТОДИКА ВЗАИМОСВЯЗАННОГО ИЗУЧЕНИЯ СВОЙСТВ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ФИГУР В СИСТЕМЕ ПРЕПОДАВАНИЯ ГЕОМЕТРИЧЕСКОГО МАТЕРИАЛА

В ТЕХНИЧЕСКИХ КОЛЛЕДЖАХ


Специальность: 13.00.02 – теория и методика обучения и воспитания

(математика, уровень профессионального образования)


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата педагогических наук


Астрахань – 2006

Работа выполнена на кафедре математического анализа

факультета математики и информационных технологий Астраханского

государственного университета


Научный руководитель: доктор педагогических наук,

профессор Аммосова Н.В.


Официальные оппоненты: доктор физико-математических наук,

профессор Мантуров О.В.,

кандидат педагогических наук,

Тасмуратова С.С.


Ведущая организация: Московский педагогический

государственный университет


Защита диссертации состоится 15 сентября 2006 года на заседании диссертационного совета ДМ 212.009.05 при Астраханском государственном университете по адресу: 414056, г. Астрахань, ул. Татищева, д. 20 а.

Отзывы на автореферат присылать по адресу: 414056, г. Астрахань, ул. Татищева, д. 20 а.


С диссертацией можно ознакомиться в библиотеке Астраханского государственного университета.


Автореферат разослан « 18 » июня 2006 года.


Ученый секретарь диссертационного совета Крутова И.А.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования. У вчерашних школьников, студентов первого курса технического колледжа, с обретением нового статуса существенно меняется мотивация обучения. Получение профессиональных знаний, их реализация в практических условиях - основной побудительный момент их учебной деятельности. Прагматизм, свойственный студентам технических специальностей, ведет к снижению интереса к дисциплинам общеобразовательного цикла, не имеющих прямого отношения к производственной деятельности.

Геометрии как отдельной дисциплины в системе подготовки специалистов в технических колледжах не существует. Геометрические разделы составляют лишь небольшую часть общей программы дисциплины «Математика». В то же время именно геометрическая культура и развитие являются профессионально значимыми для многих современных специальностей, могут служить стимулом к постоянному саморазвитию и самообразованию.

Недостаточный уровень геометрической подготовки студентов младших курсов (на базе основной школы) в технических колледжах, на наш взгляд, определяется тремя основными причинами: 1) небольшим объемом учебного времени, выделяемого на изучение математики на первых курсах; 2) изначальным разноуровневым (в качественном и количественном отношении) геометрическим развитием студентов; 3) отсутствием учебной и методической литературы по геометрии, ориентированной на обучение в техническом колледже и соответствующей современным тенденциям в школьном геометрическом образовании.

Одной из важных проблем построения школьного курса геометрии является взаимоотношение двух разделов: планиметрии и стереометрии. Взаимосвязанное изучение свойств плоских и пространственных фигур является средством разрешения проблемы, связанной с искусственным разделением геометрии на планиметрию и стереометрию. В последнее время многие учителя предпринимают попытки одновременного исследования плоских и пространственных объектов на занятиях. Но для того, чтобы полностью перестроить курс геометрии или создать альтернативные курсы, воспитать качественно новое поколение учащихся, необходимо время и единая методическая система для всех уровней обучения геометрии в школе.

В настоящее время обучение геометрическому материалу в технических колледжах должно осуществляться с учетом обеспечения преемственности между школьными знаниями учащихся о пространстве и знаниями, приобретаемыми в колледже, а также с учетом возможности сокращения максимальным образом разрыва между планиметрией, изученной в школе, и стереометрией.

Представление о любой науке как о системе закономерно возникает у человека на заключительном этапе ее изучения. По нашему мнению, наиболее благоприятным для реализации идеи взаимосвязанного изучения свойств плоских и пространственных фигур является именно заключительный этап школьного курса геометрии, цель которого – накопление и систематизация общегеометрических (синтез планиметрических и стереометрических) знаний и умений, формирование представления о геометрии как о целостной системе. Кроме того, взаимосвязанное изучение свойств плоских и пространственных фигур предполагает рассмотрение и анализ большого количества вариантов их взаимного расположения. В силу большего жизненного опыта старшим школьникам легче мыслить альтернативами.

Идея построения курса геометрии, основанного на взаимосвязанном изучении свойств плоских и пространственных фигур, не является новой. Несмотря на это, реализации в научно-методической и учебной литературе по математике для средних специальных учебных заведений она еще не нашла. Большинство учебных пособий до сих пор сохранило классическую схему изложения стереометрического материала и составлено по аналогии со школьными учебниками. Профессиональная направленность процесса обучения геометрии осуществляется только за счет включения в него задач производственного характера.

Противоречия между требованиями практики к уровню геометрического образования будущих специалистов и реально существующей подготовкой по геометрии в колледже, необходимость расширения возможностей для обеспечения связей общеобразовательных знаний с профессиональными и отсутствие методической базы для этого, важность обеспечения преемственности между школьным геометрическим образованием и обучением геометрии в технических колледжах, недостаточная разработанность проблемы взаимосвязанного изучения свойств плоских и пространственных фигур в теории и практике методики обучения геометрическому материалу в средних специальных учебных заведениях определяют выбор и актуальность темы данного исследования.

Проблема исследования состоит в выявлении и раскрытии возможных путей реализации взаимосвязанного изучения свойств плоских и пространственных фигур при обучении геометрическому материалу в технических колледжах (базовый уровень).

Объектом данного исследования является процесс обучения геометрическому материалу студентов первых курсов технических колледжей.

Предмет исследования состоит в разработке методических приемов и средств реализации взаимосвязанного изучения свойств плоских и пространственных фигур, обеспечивающих эффективное формирование геометрических знаний студентов технических колледжей.

Цель исследования - выявление и обоснование особенностей содержания геометрического материала на первом курсе технических колледжей, реализующего взаимосвязанное изучение плоских и объемных фигур; разработка соответствующей методики обучения геометрии студентов колледжей технического профиля.

Анализ теоретических и практических аспектов рассматриваемой проблемы позволяет сформулировать гипотезу исследования: эффективность обучения геометрии в технических колледжах повысится, будет успешнее осуществляться связь между общеобразовательными и профессиональными знаниями учащихся, если в процессе геометрической деятельности студентов обеспечивать единство наглядно - образной и логико-интуитивной сторон, проводить целенаправленную работу по следующим направлениям:

- изучение основных геометрических фигур (точки, прямой и плоскости) и их свойств в составе плоских и пространственных конфигураций;

- построение конструктивных определений пространственных фигур с помощью плоских фигур;

- выявление закономерностей изображения плоских и пространственных фигур;

- рассмотрение взаимосвязи свойств многоугольников и многогранников в процессе их триангуляции; при построении сечений многогранников.

Проблема, предмет и гипотеза исследования определяют следующие задачи исследования:

1) проанализировать существующие на данный момент взгляды в теории методики обучения математике на проблему использования взаимосвязанного изучения свойств плоских и пространственных фигур в преподавании геометрии в старших классах средней школы и в средних профессиональных учебных заведениях;

2) выявить психолого-педагогические условия реализации взаимосвязанного изучения свойств плоских и пространственных фигур в старшем школьном возрасте;

3) проанализировать и теоретически обосновать возможность разработки методики обучения геометрическому материалу в технических колледжах на основе использования взаимосвязанного изучения свойств плоских и пространственных фигур;

4) разработать основные пути реализации взаимосвязанного изучения свойств плоских и пространственных фигур при изучении неопределяемых понятий, многогранников, круглых фигур на первых курсах технических колледжей;

5) разработать систему дидактических материалов и методику их применения в процессе обучения геометрии, ориентированном на взаимосвязанное изучение плоских и пространственных фигур по указанным выше направлениям;

6) экспериментально проверить доступность и эффективность разработанных дидактических материалов и методики их использования.

Теоретико-методологической базой диссертационного исследования являются: психологические исследования в области проблем мышления

(С.Л. Рубинштейн, П.Я. Гальперин, А.В. Брушлинский); исследования проблемы использования идеи фузионизма в школьном образовании (В.А. Гусев, С.В. Гуревич, В.Н. Фрундин); исследования проблемы развития пространственных представлений (А.Н. Леонтьев, Б.Г. Ананьев, Е.Ф. Рыбалко, И.Я. Каплунович, А.Д. Глейзер, И.С. Якиманская); исследования по проблеме усвоения математических понятий (З.И. Слепкань, Н.Ф.Талызина, А.И. Раев); исследования проблем развития конструктивных умений и навыков (В.Г. Коровина, В.А. Далингер), интуиции (А.Д. Мышкис, П.М. Эрдниев).

В ходе решения поставленных задач используются следующие методы:

- теоретическое исследование проблемы на основе анализа математической, психологической, педагогической, методической литературы, программ и учебных пособий по математике для школ и средних специальных учебных заведений;

- учет личного опыта автора как преподавателя; изучение и обобщение опыта работы учителей математики средней школы и преподавателей средних специальных образовательных учреждений;

- наблюдение за деятельностью студентов в процессе изучения геометрического материала;

- проведение тестирования и лабораторных работ с целью выявления динамики в геометрическом развитии студентов;

- проведение анкетирования среди студентов с целью выявления мотивации к изучению геометрического материала;

- проведение эксперимента с целью подтверждения гипотезы исследования.

Обоснованность и достоверность результатов исследования обеспечивается: построением исследований на основе положений современной психологии, дидактики и методики; согласованностью полученных выводов с основными положениями методики обучения математике и концепцией среднего специального математического образования; положительной оценкой преподавателями средних специальных учебных заведений и математических кафедр университетов разработанных учебных материалов и методики их использования; результатами опытного обучения и внедрения в практику преподавания геометрических разделов дисциплины «Математика» технических колледжей г. Астрахань.

Научная новизна исследования:

1) теоретически и практически обоснована эффективность реализации взаимосвязанного изучения свойств плоских и пространственных фигур при обучении геометрическому материалу в технических колледжах, состоящая:

- в четком понимании студентами общих закономерностей построения курса геометрии;

- в устранении дублирования при изложении учебного материала, связанного с изучением свойств плоских и пространственных фигур;

- в обеспечении эффективных приложений курса геометрии, так как традиционные приложения свойств плоских фигур являются весьма искусственными;

- в учете возрастных особенностей учащихся при изучении геометрического материала, например, в процессе моделирования и конструирования многогранников;

2) выявлены и раскрыты основные пути использования взаимосвязанного изучения свойств плоских и пространственных фигур в рамках геометрических разделов дисциплины «Математика» на первых курсах колледжей технического профиля, а также разработана методика изложения выше указанного материала, включающая в себя:

- рассмотрение геометрической фигуры как произвольного множества точек;

- использование плоских фигур для конструктивного определения пространственных фигур, в частности: а) рассмотрение взаимосвязи при изучении свойств многоугольников и многогранников; б) использование свойств отрезка при определении конкретных видов многогранников и круглых фигур;

- закономерности изображения плоских и пространственных фигур.

Теоретическая значимость исследования: в диссертации получены результаты, которые позволяют реализовать взаимосвязанное изучение свойств плоских и пространственных фигур в системе преподавания геометрии, совершенствовать процесс обучения геометрическому материалу в технических колледжах; получено экспериментальное подтверждение гипотезы об условиях эффективного применения взаимосвязанного изучения свойств плоских и пространственных фигур при обучении геометрическому материалу на первых курсах технических колледжей.

Практическая значимость исследования состоит в том, что разработаны блоки задач, лабораторные работы, методические рекомендации по организации геометрической деятельности студентов в условиях взаимосвязанного изучения свойств плоских и объемных фигур и обеспечения возможности дальнейшего использования полученных геометрических знаний и умений в освоении общепрофессиональных, специальных дисциплин колледжа. Предложенный материал может быть использован в практике преподавания математики в образовательных учреждениях среднего профессионального звена, а также при обучении геометрии в старших классах средней школы.

Апробация и внедрение результатов исследования проводились поэтапно в процессе проведения занятий на первых курсах технического колледжа г. Астрахань, колледжа строительства и экономики г. Астрахань, Астраханского речного училища, Каспийского филиала «Морская государственная академия имени адмирала Ф.Ф. Ушакова».

Основные положения диссертации, результаты педагогического эксперимента и сделанные по ним выводы получили отражение на заседаниях цикловой комиссии математических и общих естественнонаучных дисциплин Астраханского технического колледжа, заседаниях городского методического объединения преподавателей математики колледжей, заседаниях кафедры математического анализа Астраханского государственного университета, а также в докладах: на научно-практической конференции преподавателей, студентов и аспирантов АГУ (г. Астрахань, 2003 г.), ежегодных Международных конференциях «Математика. Компьютеры. Образование» (г. Пущино, 2003 г., 2005 г., г. Дубна, 2004 г., 2006 г.), ежегодных научных конференциях по проблемам математики, информатики, физики, химии и методики преподавания естественнонаучных дисциплин (г. Москва, 2003 г., 2004 г.), IX Всероссийской научно-практической конференции «Наука. Экология. Образование» (г. Краснодар, 2004 г.), VIII, X междисциплинарных научно-практических конференциях «Нелинейный мир» (г. Астрахань, 2003 г., г. Нижний Новгород, 2005 г.), Первой Всероссийской научно-практической конференции «Образование. Синергетика и новое мировидение» (г. Астрахань, 2006 г.).

На защиту выносятся следующие положения:

1. Методика обучения геометрическому материалу в технических колледжах, основанная на взаимосвязанном изучении свойств плоских и пространственных фигур, способствует повышению уровня геометрических знаний студентов, четкому пониманию учащимися общих закономерностей построения курса геометрии, роли геометрии в познании окружающего мира. Сущность этой методики состоит в рассмотрении геометрической фигуры как произвольного множества точек; в использовании плоских фигур для определения пространственных фигур; выявлении закономерностей изображения плоских и пространственных фигур; совместном изучении свойств многоугольников и многогранников, связанных с их триангуляцией и процессом построения сечений многогранников.

2. Органичное сочетание в структуре геометрической деятельности студентов конструктивного, интуитивного компонентов и идеи взаимосвязи свойств плоских и пространственных фигур в содержании геометрического материала позволяют обеспечивать связь общеобразовательных и профессиональных знаний студентов. Это достигается за счет включения в геометрический материал конструктивных определений плоских и пространственных фигур; задач на конструирование фигуры (плоской и пространственной); лабораторных работ, предполагающих конструктивную работу с многогранниками, экспериментальное изучение параллельных проекций плоских и пространственных фигур.

3. Эффективность применения разработанной методики изучения геометрического материала обеспечивается комплексом методических средств:

- учебные материалы, включающие схему изучения неопределяемых понятий, определения плоских и пространственных фигур;

- блоки задач, основанные на геометрическом материале, содержащем идею взаимосвязанного изучения свойств плоских и пространственных фигур;

- лабораторные работы «Триангуляция многогранников», «Методы проектирования. Свойства параллельных проекций», «Сечения многогранников».

Структура диссертации обусловлена логикой и последовательностью поставленных задач и состоит из введения, двух глав, заключения, библиографии.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы исследования, определены цель, объект, предмет, гипотеза, задачи исследования; указаны использованные методы, раскрыты научная новизна, теоретическая и практическая значимость работы; приведены сведения об апробации и внедрении результатов исследования, а также положения, выносимые на защиту.

В первой главе «Взаимосвязанное изучение свойств плоских и пространственных фигур в системе преподавания геометрического материала в технических колледжах, пути его реализации» теоретически обосновывается целесообразность одновременного рассмотрения свойств плоских и объемных фигур при изучении геометрического материала на первых курсах технических колледжей; выявляются и описываются психолого-педагогические условия, методические пути использования взаимосвязанного изучения свойств плоских и пространственных фигур в рамках геометрических разделов дисциплины «Математика» на первых курсах колледжей технического профиля.

Еще в древности существовали два пути определения понятий. Первый путь вел от фигур высшего порядка к фигурам низшего и состоял в том, что поверхность рассматривалась как граница тела, линия – как граница поверхности, концы же линии – как точки. Второй путь вел, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т.д. Существовал и третий путь, который предполагал осуществление двусторонних связей между плоскими и пространственными фигурами.

Учитывая, что в старшем школьном возрасте укрепляются и совершенствуются все психические процессы, мы считаем целесообразным рассмотрение связей между плоскими и пространственными фигурами при изучении геометрического материала на первых курсах технических колледжей (базовый уровень) осуществлять в двух направлениях.

Путь, ведущий от пространственной фигуры к плоской, при котором первая фигура выступает в качестве опорного элемента, заключающего в себе основные свойства последней, соответствует интуитивному уровню познания пространства. Он является приемлемым на этапе накопления информации о стереометрическом объекте.

Любая геометрическая фигура есть абстракция, результат предельного перехода, недостижимый в действительности. Пространственные фигуры по сравнению с плоскими аналогами – более низкая степень абстракции, так как трехмерное геометрическое пространство является моделью реального пространства. Поэтому стереометрические фигуры посредством их материальных моделей являются для учащихся неким средством связи с действительным миром. Курс геометрии, построенный на идее совместного рассмотрения двумерных и трехмерных фигур существенно расширяет возможности использования накопленного жизненного опыта обучаемого за счет установления связей между объективным пространством и абстрактным геометрическим пространством.

Студенты первого курса технического колледжа приступают к изучению геометрических разделов дисциплины «Математика» с основным запасом сведений из планиметрии. Их представление о геометрии плоскости как о системе не должно ограничиваться пониманием ее самодостаточности, возможности развития только за счет собственных средств, независимо от стереометрии. Необходимо научить их использовать плоские фигуры для нахождения общих принципов и закономерностей геометрического пространства (например, закономерностей во взаимном расположении геометрических фигур).

При изучении стереометрии важным становится осознание учащимися того факта, что любая геометрическая фигура - это совокупность других менее «сложных» по своей структуре фигур, предельными вариантами которых могут служить точка, прямая, плоскость или их части. Плоская фигура может быть разложена только на плоские составляющие. Частью пространственной фигуры может быть не только геометрический объект того же измерения, но и двумерная или одномерная фигура.

Оперирование долгое время плоскими фигурами позволит учащимся без особого труда разложить плоский объект на части и синтезировать его из частей. Однако процессу синтеза пространственного объекта из частей должно предшествовать его выделение, выявление из множества других объектов, т.е. стадия анализа. Решение данного вопроса мы непосредственно связываем с проблемой создания оптимальных условий восприятия пространства учащимися старшего школьного возраста, при котором будет обеспечиваться эффективное формирование, накопление или корректировка пространственных представлений.

Вслед за Ж. Пиаже, мы считаем, что воздействие сенсорно-моторного интеллекта на абстрактное мышление человека характерно для любого его возрастного периода. Поэтому важным условием для развития трехмерных представлений студентов первого курса является разнообразная конструктивная работа с моделями фигур, включающая комплекс действий над ними: созерцание, непосредственные манипуляции, мыслительные операции. Простое наблюдение пространственного объекта необходимо сочетать с предметно-чувственным познавательным геометрическим экспериментом, составляющим основу разработанных нами лабораторных работ.

В ходе исследования мы констатируем, что основанием для развития теоретических знаний студентов о пространстве является обогащение сознания учащихся системой наглядных устойчивых представлений пространственных форм. Следуя Л.М. Фридману, мы рассматриваем наглядность как особое свойство психических образов, создаваемых в процессе восприятия, памяти, мышления и воображения при познании объектов окружающего мира. Исследуя различные пути создания у учащихся наглядных образов фигур, мы отмечаем, что наглядность образа геометрического объекта у студентов первых курсов может достигаться за счет формирования у них понимания качественных различий между моделью объекта и самим объектом, между материальными и идеальными моделями фигур, формирования умений постепенного отвлечения от несущественных свойств реального объекта.

Представление – не механическая репродукция восприятия, а изменчивое динамическое образование, каждый раз при определенных условиях вновь создающееся и отражающее сложную жизнь личности. Видение объемных фигур, их изображений возникает в результате длительного обучения, в процессе которого действия переходят в мысленную сферу. Основой такого перехода является работа по созданию и оперированию пространственными образами. Оперирование пространственным образом составляет основное содержание пространственного мышления.

Из всех показателей уровня развития пространственного мышления, которыми располагает психология, мы выбираем два, которые являются, на наш взгляд, наиболее значимыми: тип и вид оперирования образом.

В соответствии с важным дидактическим правилом последовательного и постепенного усложнения типа оперирования образом для задач, связанных с взаимным расположением плоских и пространственных фигур, мы определяем следующую последовательность: 1) задачи на взаимное расположение плоских и пространственных фигур без изменения их структуры; 2) задачи на взаимное расположение плоских и пространственных фигур с изменением их структуры.

Эти типы задач предполагают не только возрастание уровня сложности действий, осуществляемых над образом, но и наличие у студентов умений ориентироваться в пространстве. Важен полный перебор возможных вариантов расположения фигур. Успешность выполнения данной работы связана с овладением внешним оперированием, при котором изучение пространственных характеристик тела осуществляется, исходя из анализа его отношений с другими геометрическими телами.

В нашем исследовании мы заключаем, что старшем школьном возрасте совершенствуется абстрактно-теоретическое мышление. Но его развитие не может идти в отрыве от наглядно-образного мышления. Рассмотрение большого количества вариантов расположения фигур в пространстве требует от студентов постоянной работы мысли, всестороннего анализа геометрической ситуации, оценки полноты набора решений. Установление причинно-следственных связей, безусловно, должно сопровождаться наглядным представлением ситуации, не всегда связанным с изображением.

Учитывая, что обучение в колледже ориентировано на получение профессиональной подготовки, в своем исследовании мы уточняем характер связи наглядного и абстрактного мышления как двух аспектов единого развивающегося мышления студентов.

Необходимость взаимосвязи общеобразовательной и профессиональной подготовки в технических колледжах заложена в специфике этих учебных заведений, следовательно, обучение и математике (геометрии, в частности) должно содействовать установлению связи между общеобразовательными и профессиональными знаниями студентов. По нашему мнению, эта связь может быть опосредованной и заключаться в формировании с помощью геометрии отдельных свойств мышления, которые позволят студентам колледжа осуществлять математизацию произвольных ситуаций не только при изучении общепрофессиональных, специальных дисциплин, но и в будущей профессиональной деятельности.

По Г.Д. Глейзеру, А. Пуанкаре, И.С. Якиманской геометрическая деятельность может осуществляться в различных направлениях и приводить к развитию определенных способностей учащихся в зависимости от преобладания в ее структуре некоторых из компонентов: пространственного, конструктивного, метрического, логического, интуитивного и символического. Учитывая приоритет развития конструктивного и интуитивного компонентов мышления, обеспечивающих единство наглядно-образной и логико-интуитивной сторон геометрической деятельности студентов технических колледжей в процессе обучения, в качестве основных путей использования взаимосвязанного изучения свойств плоских и пространственных фигур, мы выделяем:

1) изучение основных геометрических фигур (точки, прямой и плоскости) и их свойств в составе плоских и пространственных конфигураций;

2) построение конструктивных определений пространственных фигур с помощью плоских фигур;

3) выявление закономерностей изображения плоских и пространственных фигур;

4) рассмотрение взаимосвязи свойств многоугольников и многогранников в процессе их триангуляции; при построении сечений многогранников.

Из школьного курса планиметрии учащимся известно два неопределяемых понятия: точка и прямая. Плоскость воспринимается учащимися лишь как объект, содержащий фигуры, свойства которых изучались в планиметрии. В этой ситуации целесообразным является включение всех трех неопределяемых понятий в общую систему связей, демонстрирующую логику построения геометрии в целом. Процесс изучения данных понятий можно выразить следующим образом. Основные объекты (точки, прямые и плоскости) включаются в различные плоские и пространственные конфигурации. Известные ранее свойства основных объектов позволяют получить новую информацию о конфигурациях; в свою очередь, обогащение конфигураций позволяет выявить новые свойства основных объектов.

Необходимыми условиями для осуществления данной работы мы считаем:

1) усвоение студентами понятия геометрической фигуры как произвольного множества точек, а также понятий пересечения и объединения фигур;

2) наличие системы заданий, направленных на формирование умения у студентов воссоздавать объект по образу при различных степенях определенности конструируемой фигуры (указана только форма фигуры; указана форма фигуры и фигуры, участвующие в ее образовании и т.д.).

Рассмотрение любой геометрической фигуры как множества точек, как результата объединения или пересечения других фигур разных измерений, большого количества примеров, подтверждающих факт образования не только плоских, но и пространственных фигур из точек, прямых и плоскостей является первой частью подготовительной работы по использованию плоских фигур (отрезков) для конструктивного определения пространственных фигур (конкретных видов многогранников и круглых фигур). Второй частью данной работы является решение проблемы, связанной с осознанием учащимися факта возможности и мотива определения геометрических фигур с помощью отрезков.

Свойство любой геометрической фигуры – являться множеством точек, не всегда позволяет однозначно определить ее форму. Необходимо задать характерное свойство, которым должны обладать точки. Сделать это не всегда представляется возможным. Перед студентами мотивированно встает задача отыскания другой основной фигуры или ее части, которая могла бы образовывать большее количество плоских и пространственных фигур. Фигурой, обладающей данным свойством является отрезок. Множество отрезков, наделенных определенным свойством, может являться плоской или пространственной фигурой заданной формы.

Определение, которое характеризует предмет тем способом, каким он может быть построен, А.Д. Александров называет конструктивным. Рассматривая возможные пути определения понятия многогранника в курсе стереометрии, мы отмечаем, что построение конструктивного определения данного понятия способствует установлению связи между плоскими и пространственными фигурами. Основная идея состоит в проведении аналогии между способом получения многоугольника и многогранника. В связи с введением конструктивных определений многоугольника и многогранника возникает задача отыскания способов разбиения многогранников (многоугольников) на тетраэдры (треугольники). Эту задачу мы называем так же, как и В.А. Гусев в своем учебнике, задачей триангуляции.

Эффективность используемых в нашей методике конструктивных определений пространственных фигур обусловлена тем, что: 1) определение, иллюстрирующее способ образования фигуры, является более наглядным для студентов, «внутренне» убедительным; 2) конструктивное определение фигуры, в котором используются свойства отрезков, показывает, что эта фигура является частью общей системы, в которой точки, прямые и плоскости играют основную роль; 3) конструктивный метод определения понятий позволяет показать общие закономерности в получении фигур различных форм (многоугольника и многогранника, пирамиды и конуса, призмы и цилиндра); 4) формулировка конструктивного определения содержит минимум других понятий, что значительно упрощает ее усвоение студентами.

Традиционное изложение темы стереометрии, связанной с изображением фигур в пространстве, зачастую ограничивается рассмотрением в «готовом виде» параллельного проектирования и его свойств. Очевидные вопросы о том, какие виды проекций существуют, каково их происхождение и почему именно параллельная проекция является оптимальной для изображения фигур в геометрии, остаются без ответов в процессе обучения.

Для изучения свойств фигур, связанных с параллельным проектированием, мы используем лабораторный метод. Для более детального ознакомления с параллельным проектированием и вывода свойств параллельного проектирования студентам предлагается провести эксперимент с помощью проекционного аппарата. В каждом из трех заданий лабораторной работы «Метод проектирования. Свойства параллельных проекций» студенты должны получить всевозможные проекции определенного набора фигур: прямой и двух прямых (параллельных, пересекающихся и скрещивающихся); плоскости, правильного треугольника и четырехугольника, круга; тетраэдра, куба, прямого кругового конуса и цилиндра. В первых двух заданиях пространство помогает устанавливать свойства плоских фигур, в том числе и плоскости. В третьем задании уже плоские фигуры помогают выявить свойства пространственных фигур, гранями и основаниями которых служат треугольники, квадраты, круги. Студенты должны установить, какой вид проекции дает фигура при определенном расположении ее относительно направления проектирования и плоскости проекций.

Анализируя геометрический материал, связанный с построением сечений, мы отмечаем, что эффективное изучение указанного материала невозможно без рассмотрения связей между плоскими и пространственными фигурами. Это подтверждается необходимостью фиксации свойств плоскости, связанных с процессом построения сечений пространственных фигур, а также необходимостью сопоставления и анализа формы пространственных фигур и формы их сечений. Процессу построения и анализа разнообразных сечений многогранника в действующих пособиях по математике для технических колледжей уделяется, на наш взгляд, недостаточно внимания. В своей методике мы пытаемся восполнить этот пробел.

Во второй главе «Методика взаимосвязанного изучения свойств плоских и пространственных фигур при обучении геометрическому материалу в технических колледжах» описана методика изучения свойств неопределяемых понятий, многогранников и круглых фигур на первых курсах технических колледжей, включающая приемы организации деятельности студентов по изучению теоретического материала, решению задач, выполнению лабораторных работ, содержащих идею совместного рассмотрения свойств плоских и пространственных фигур.

Представление о любом элементе курса геометрии должно быть наглядным, логически организованным и укладываться в некоторую схему связей между элементами. Мы предлагаем схему изучения основных геометрических фигур (точки, прямой и плоскости), которая позволяет: рассматривать все указанные фигуры по одним и тем же позициям; формировать у студентов понятие модели фигуры, понимание качественных различий между разными видами моделей одной и той же фигуры; систематизировать свойства основных фигур, связанные с их взаимным расположением в пространстве; выявить способы получения плоских и пространственных фигур с помощью основных геометрических фигур; выявить способы получения основных геометрических фигур или их частей с помощью других плоских и пространственных фигур. Данная схема охватывает следующие темы геометрического материала, изучаемого на первых курсах технических колледжей: «Аксиомы стереометрии и простейшие следствия из них», «Взаимное расположение двух прямых в пространстве», «Взаимное расположение прямой и плоскости», Взаимное расположение двух плоскостей».

• Название фигуры.
  

• Идеальная модель фигуры.
  
• Условная графическая модель фигуры.
  
• Символическая модель фигуры.
  
• Натуральные модели фигуры.
  
• Свойства данной фигуры, выраженные в аксиомах или следующие из аксиом.
  
• Примеры других геометрических фигур, в образовании которых участвует данная фигура.
  
• Примеры фигур, пересечением и объединением которых может служить данная фигура или ее часть.
  
• Способы задания фигуры.
  

Студенты должны иметь четкое представление о том, что в геометрии они имеют дело с моделями, отличными от предметов реального мира. Методическим приемом для формирования у студентов умений отождествлять реальный объект с различными геометрическими фигурами, и, наоборот, воспринимать одну геометрическую фигуру как идеальный образ целого класса реальных объектов, является поиск натуральных моделей, соответствующих разным степеням абстрагирования, для каждой из основных геометрических фигур.

Известно, что основные свойства неопределяемых понятий выражены в аксиомах. В своей методике мы используем группу аксиом, которые характеризуют взаимное расположение точек, прямых и плоскостей. Их список приведен в действующем учебном пособии по геометрии для 10 – 11 классов средней школы Л.С. Атанасяна, В.Ф. Бутузова и др. авторов, на материал которого мы опираемся в своем эксперименте. Методика работы по данному пункту схемы должна включать логический анализ аксиом и фиксацию основных свойств, связанных с взаимным расположением основных геометрических фигур в пространстве.

После рассмотрения свойств основных геометрических фигур, связанных с их взаимным расположением, логичной оказывается систематизация возможных случаев такого расположения. Эту работу мы разбиваем на два этапа.

На первом этапе выясняется, каким образом определенное расположение в пространстве основных геометрических фигур приводит к образованию других фигур; вводится понятие фигуры как произвольного множества точек. Второй этап предполагает введение понятий объединения и пересечения фигур, которые позволяют студентам выявить способы получения точки, прямой и плоскости с помощью других фигур, а также убедиться, что точка является частью любой фигуры. Это закрепляет представление студентов о геометрической фигуре как о множестве точек.

Итогом работы по данной схеме является систематизация студентами случаев взаимного расположения двух прямых, прямой и плоскости, двух плоскостей.

В своей методике мы также используем теоретические задачи на взаимное расположение трех основных геометрических фигур, в том числе задачи с неполными данными, заданными в символической и графической форме. Они позволяют осуществлять постепенное композиционное усложнение конфигураций из плоских фигур в пространстве. При этом дополнение указанной конфигурации многогранником значительно увеличивает количество возможных вариантов взаимного расположения основных фигур и возможности для логического анализа геометрической ситуации.

1) А, В, САВ. Сделайте рисунок, соответствующий символической записи.

2) А, В, где  - плоскость верхнего основания треугольной призмы.

Методика изучения многогранников и круглых фигур включает рассмотрение основных вопросов, составляющих содержание темы «Геометрические тела и их поверхности» учебной программы дисциплины «Математика» для первых курсов колледжей. При изучении данного материала мы выделяем следующие основные направления работы: 1) формирование понятия многогранника, ознакомление с различными видами многогранников, триангуляция многогранников; 2) формирование понятий призмы, пирамиды; ознакомление с различными видами этих многогранников; 3) построение сечений многогранников (призм и пирамид); 4) формирование понятий цилиндра, цилиндрической поверхности; конуса, конической поверхности; построение сечений цилиндра и конуса.

При изложении данного материала мы учитываем следующие положения: 1) процесс формирования выше перечисленных понятий должен осуществляться по схеме: восприятия – представления – понятие – слово; 2) необходимо расширение представлений студентов о существующих видах многогранников и круглых фигур, в том числе за счет системы задач на определение факта принадлежности данного объекта к понятию и на поиск фигур, не принадлежащих данному понятию.

Одной из основных трудностей усвоения понятия многогранника в курсе стереометрии учащимися является большое количество других понятий, составляющих определение многогранника. Мы предлагаем конструктивный путь определения многогранника, который способствует наглядному выявлению его связей с многоугольником. В нашей методике определения двух указанных понятий рассматриваются одновременно. Приведем лишь определение многогранника, сформулированное А.Д. Александровым.

Многогранник – это фигура, составленная из тетраэдров так, что:

1) каждые два тетраэдра либо не имеют общих точек, либо имеют только одну общую вершину, или одно общее ребро, или одну общую грань;

2) от каждого тетраэдра к каждому можно пройти по тетраэдрам, последовательно прилегающим один к другому по целым граням.

Для отыскания возможных способов разбиения любого многогранника (выпуклого и невыпуклого) на тетраэдры мы предлагаем студентам лабораторную работу «Триангуляция многогранников». Триангуляция многоугольников является частным случаем разбиения на тетраэдры многогранников. Возможен и обратный ход выполнения работы – обобщение результатов триангуляции многоугольников для пространственного случая.

Анализ учебных пособий для колледжей и школ показывает, что в курсе стереометрии нередко даются такие формулировки определений, которые не позволяют учащемуся распознавать соответствующие объекты. Следуя В.А. Далингеру, мы считаем, что определения должны даваться по принципу: если в определении опустить определяемое понятие, то по оставшемуся тексту учащиеся должны узнать, известную им фигуру. К определениям, обладающим таким свойством, можно отнести конструктивные определения геометрических фигур.

До введения четкого определения понятия у учащихся должна накопиться достаточная наглядная и теоретическая информация, связанная с ним. Например, до более детального знакомства с пирамидой, студенты систематизируют в течение некоторого количества занятий различные способы получения данного многогранника с помощью нескольких полупространств; плоскости и конической поверхности, у которой направляющей служит многоугольник; многогранного угла (выпуклого или невыпуклого) и плоскости, не проходящей через его вершину; отрезков; некоторого числа тетраэдров. Они также используют пирамиду в качестве основного элемента в задаче о триангуляции многогранников.

Завершающим этапом формирования понятия пирамиды является следующее определение. Пирамида – это фигура, полученная объединением всех отрезков, один конец которых принадлежит некоторому многоугольнику, а другой - одной и той же точке пространства, не лежащей в плоскости этого многоугольника. Аналогичное определение имеет и конус. Конус – это фигура, полученная объединением всех отрезков, один конец которых принадлежит некоторой плоской фигуре, ограниченной замкнутой кривой, а другой - одной и той же точке пространства, не лежащей в плоскости этой фигуры.

Одним из проявлений интуиции человека является оценка ситуации – «прикидка» результатов. Оценка полноты полученных решений важна в задачах на сечения, когда анализируется полнота списка фигур, получаемых в пересечении данного многогранника и плоскости. Задачи на сечения относятся к задачам на конструирование фигуры и являются базовыми для изучения «Инженерной графики». Нами разработан блок пропедевтических задач по теме: «Сечения многогранников», который находит свое продолжение в лабораторной работе с одноименным названием.

В задачах на построение сечений четко проявляется идея взаимосвязи плоских и пространственных фигур. По форме плоской фигуры можно сформировать класс пространственных объектов, сечением которых является данная фигура. В свою очередь, без пространственных фигур невозможно изучить вид, свойства многоугольника, являющегося сечением. Так как в качестве приоритетных мы выбрали интуитивный и конструктивный компоненты умственной деятельности, то встает задача об изучении формы фигуры, а именно зон расположения точек на поверхности многогранника, при которых получается та или иная форма многоугольника в сечении. Эта зона может быть как плоской фигурой, так и пространственной. Задачи такого плана использованы нами в лабораторной работе «Сечения многогранников».

Для проверки эффективности разработанной методики и подтверждения гипотезы, выдвинутой в начале исследования, был организован педагогический эксперимент. В ходе констатирующего эксперимента выявлялось наличие у студентов мотивации к изучению геометрического материала, понимания значимости геометрических знаний и умений для освоения их будущей профессии, представлений о взаимосвязи разделов геометрии; определялся первоначальный уровень конструктивных умений студентов, используемых при изучении геометрического материала, основанного на идее совместного рассмотрения свойств плоских и пространственных фигур. К участию в эксперименте было привлечено восемь групп студентов первого курса.

В результате диагностики на констатирующем этапе эксперимента были получены примерно одинаково низкие результаты участников экспериментальной и контрольной групп по всем измеряемым параметрам.

Для экспериментальной проверки разработанной методики были взяты такие критерии: умение представлять геометрическую фигуру, мысленно преобразовывать плоскую и пространственную геометрические фигуры, умение разложить объект на части и синтезировать объект из частей, умение узнавать фигуру в новой ситуации и рассматривать ее с новых позиций, способность к вариативному построению, умение изображать фигуру.

После контрольной диагностики уровня сформированности конструктивных умений и навыков, которая проводилась по параметрам констатирующего эксперимента, мы получили следующие результаты, приведенные на гистограмме и графике.





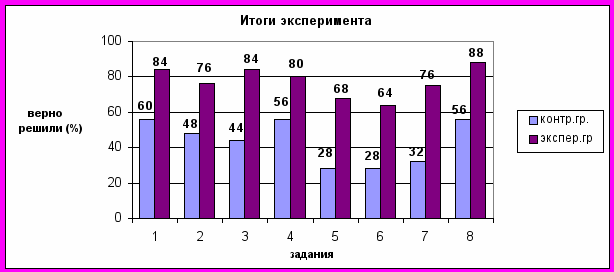
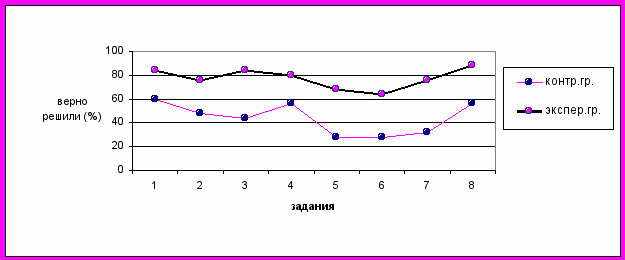
Анализ полученных данных свидетельствует, что в экспериментальных группах студенты намного успешнее, чем в контрольных группах выполняют задания, предполагающие одновременное исследование свойств плоских и пространственных фигур и требующие от них умений представлять и преобразовывать фигуру, синтезировать и раскладывать объект на части, узнавать фигуру в новой ситуации, вариативных умений анализа геометрической ситуации и умений изображать фигуры и конструкции из них различными способами.

Статистическая обработка полученных данных проводилась с помощью критерия ² (хи-квадрат) и позволила подтвердить эффективность разработанных нами учебных материалов, методики их использования.

Теоретический анализ и опытная работа позволили в заключении подвести следующие итоги:

1. Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей. Современные тенденции в школьном геометрическом образовании, низкий уровень геометрической подготовки будущих выпускников технических колледжей требуют пересмотра принципов изучения геометрических разделов дисциплины «Математика» на первых курсах.

2. Взаимосвязанное изучение свойств плоских и пространственных фигур при обучении геометрическому материалу на первых курсах технических колледжей способствует сокращению разрыва между планиметрией и стереометрией и приводит к четкому пониманию студентами общих закономерностей построения курса геометрии; обеспечивает эффективные приложения курса геометрии.

3. Органичное сочетание конструктивного, интуитивного компонентов в структуре геометрической деятельности студентов и взаимосвязанного изучения свойств плоских и пространственных фигур при обучении геометрическому материалу позволяют обеспечивать связь общеобразовательных и профессиональных знаний будущих выпускников колледжей. Это достигается за счет включения в геометрический материал конструктивных определений плоских и пространственных фигур, задач на конструирование фигур (плоских и пространственных), лабораторных работ, предполагающих конструктивную работу с многогранниками; экспериментальное изучение параллельных проекций плоских и пространственных фигур, выявление условий, обусловливающих эти проекции.

4. Эффективность применения разработанной методики изучения геометрического материала обеспечивается комплексом методических средств: учебными материалами, включающими схему изучения неопределяемых понятий, определения плоских и пространственных фигур; блоками задач, реализующими взаимосвязанное изучение свойств плоских и пространственных фигур; лабораторными работами «Триангуляция многогранников», «Методы проектирования. Свойства параллельных проекций», «Сечения многогранников».


Основные положения диссертации отражены в следующих публикациях автора:

1. Использование графических моделей пространственных фигур при решении геометрических задач // Математика, компьютер, образование: Труды Международной конференции. - Москва – Ижевск: Научно-издательский центр «Регулярная и хаотическая динамика», 2003. – Вып. 10, ч.1. - C. 21-28. – 0,5 п.л.

2. О построении курса математики в техническом колледже, ориентированного на профессиональную подготовку студентов // Образование. Экология. Экономика. Информатика: материалы VIII Международной конференции из серии «Нелинейный мир». 15 – 20 сентября 2003 г. - Астрахань: ИПЦ «Факел», 2004. - С.16-22. – 0,44 п.л.

3. О реализации идеи фузионизма при обучении геометрическому материалу студентов технических колледжей // Наука Кубани: Сборник научных трудов. - Краснодар, 2005. - Вып. 2. - С. 15 – 20. – 0, 38 п.л.

4. О проведении первых занятий по геометрии на первых курсах технических колледжей // Математика в образовании: Сборник статей / под ред. И.С. Емельяновой. - Чебоксары: Из-во Чуваш. ун-та, 2006. – Вып.2. – С. 158 - 161.- 0, 25 п.л.

5. Развитие самостоятельности студентов при изучении геометрического материала в технических колледжах // Синергетические идеи в образовании: Сборник научных трудов Первой Всероссийской научно-практической конференции «Образование. Синергетика и новое мировидение», 13 – 15 апреля 2006 г. – Астрахань: Изд-во АИПКП, 2006. – С. 154-159. – 0, 38 п.л.

6. Формирование понятия многогранника в процессе обучения геометрическому материалу студентов технических колледжей // Вестник АГТУ. - Астрахань: изд-во АГТУ, 2006. - № 4 (33) . – С. 339-343. – 0, 31 п.л.