Чертова Ольга Георгиевна, учитель математики, высшая квалификационная категория. Краткая аннотация проекта Основная задача

Вид материала

Задача

Содержание Краткая аннотация проекта Описание учреждения (организации) Кадровый потенциал Постановка проблемы Цель и задачи проекта Задачи проекта SMART Board. Ожидаемые результаты и их практическая значимость

Подобный материал:

• Гусева Ольга Владимировна, учитель химии и биологии, высшая квалификационная категория, 158.84kb.
• Шаблеева Марина Вячеславовна (высшая квалификационная категория) Название: Ю. Я. Яковлев, 138.9kb.
• План-конспект урока педагогическая мастерская «Кошки это кошки» Тема, 70.6kb.
• Сангаджиева Любовь Батовна, учитель физики, высшая квалификационная категория. Москва, 1226.42kb.
• Разработчики рабочей программы: Голубева Г. П. учитель истории и обществознания сош, 479.43kb.
• Дурягина Галина Алексеевна, высшая квалификационная категория. Тема урок, 57.77kb.
• Смирнова Любовь Васильевна, учитель математики, высшая квалификационная категория Утверждено:, 109.31kb.
• Урока английского языка и изобразительного искусства по теме: «наши выходные», 218.23kb.
• Еремеева Марина Валерьевна Квалификационная категория: высшая программа, 966.28kb.
• Ржевский Владимир Иванович учитель математики II квалификационная категория 2010 2011, 395.74kb.

Полное наименование учреждения в соответствии с уставом: Муниципальное бюджетное общеобразовательное учреждение города Новосибирска «Средняя общеобразовательная школа № 141 с углубленным изучением математики»;

район: Первомайский;

юридический адрес: 630068, город Новосибирск, улица Пришвина, дом 3.

контактные данные: телефон 8(383)3388651, телефон приёмной 8 (383)33-88-651, телефон бухгалтерии 8 (383)33-89-646, E-mail: sch141alisa@mail.ru, e-mail – sch_141_nsk@nios.ru,

номинация: «Обновление содержания образования и внедрения современных образовательных технологий»

название проекта:

«Мультимедийное сопровождение факультативного курса

«Наглядная геометрия»

автор проекта:

Чертова Ольга Георгиевна, учитель математики, высшая квалификационная категория.


Краткая аннотация проекта


Основная задача данного проекта - обеспечить условия для непрерывного и наглядного изучения геометрии, сделать пропедевтический курс наглядной геометрии действительно наглядным, разрабатывая уроки так, чтобы практически каждый урок сопровождался мультимедийной поддержкой.

К сожалению, современная школа очень далека от реализации платоновского принципа: «Не знающий геометрии– не выпускается из школы. Современная «школьная» геометрия не отражает логику ее исторического становления как науки. В нынешнем систематическом курсе геометрии в школе представлен лишь евклидов этап истории геометрии, а доевклидов этап практически не рассматривается. В связи с этим упускается существенный этап в развитии геометрии как науки. Включение его в качестве специального курса наглядно-практической геометрии для ознакомления со всеми объектами изучения перед систематическим курсом поможет восстановить логику развития науки и облегчит учащимся освоение систематического курса. Подобная работа и станет основой пропедевтического курса геометрии.

Вместе с тем, поскольку XXI век по праву считают веком высоких компьютерных технологий, необходимо по-новому рассматривать вопрос о том, как учить в современной школе. Поэтому поиску новых эффективных методик, в том числе и преподавания наглядной геометрии, уделяется большое внимание. Одной из таких методик можно считать методику преподавания геометрии с использованием новых информационных компьютерных технологий.

Что касается необходимых компьютерных программ, то недавно разработанный ресурс «Наглядная геометрия 5-6» в ГОУ ВПО Томского государственного педагогического университета позволяет легко проектировать индивидуальную траекторию построения урока учителем.

Данный ресурс разработан в рамках конкурса НФПК «Разработка Инновационных учебно-методических комплексов (ИУМК) для системы общего образования». Он состоит из семи интерактивных обучающих программ, имеющих модульную структуру. С появлением этого ресурса стало возможным разработать систему уроков факультативного курса «Наглядная геометрия» с соответствующей мультимедийной поддержкой каждого урока, а значит, есть возможность осуществить данный проект.

Основная цель данного проекта:


Используя современные образовательные технологии, осуществить в полном объёме эффективную реализацию пропедевтического курса «Наглядная геометрия», необходимого обучающимся для полноценного образования.

Задачи:

• Разработка системы уроков пропедевтического курса «Наглядная геометрия» с использованием информационных технологий на каждом уроке.
  
• Мониторинг получаемых знаний, умений и навыков учащихся, широко использующих информационные технологии в процессе изучения курса «Наглядная геометрия».
  
• Создание самостоятельной мотивированной деятельности учащихся с использованием полученных знаний, умений и навыков в социальной деятельности учащихся и в процессе дальнейшего обучения.
  
• Организация учебно-исследовательской деятельности обучающихся.
  
• Разработка программы пропедевтического курса геометрии для 5-6 классов.
  
• Проведение эксперимента по апробации программы.
  

На апробацию программы потребуется три года :

1. 2009-2010 уч.г.- разработка программы пропедевтического курса геометрии для 5-6 классов.
   
2. 2010-2012 уч г.- внедрение программы в учебный процесс и подведение итогов работы.
   

В связи с этим, учитывая материально-техническую базу нашей школы, необходимо приобрести:

	Наименование	Количество	Общая стоимость
	Мультимедийный проектор EPSON-Х6	1	28000 руб
	Программное обеспечение для быстрой графической формализации идей SMART Ideas	1	4400 руб.
	Устройство для одновременного включения интерактивной доски 6 серии, компьютера и проектора	1	5200 руб
	Потолочная штанга для крепления проектора	1	7000 руб
	Провода, 20 м	1	900 руб
	Итого		45500 руб

Описание учреждения (организации)

Муниципальное бюджетное общеобразовательное учреждение города Новосибирска «Средняя общеобразовательная школа № 141 с углублённым изучением математики». В декабре 2008 года школа прошла аттестацию и государственную аккредитацию, по результатам которой установлен следующий государственный статус: муниципальное бюджетное общеобразовательное учреждение города Новосибирска «Средняя общеобразовательная школа №141 с углублённым изучением математики», действующая на ос­новании Устава. Школа имеет лицензию серия А № 309976, регистрационный № 3429 от 11.12.2008 г. на право осуществ­ления образовательной деятельности по государственным образовательным программам начального основного общего и среднего (полного) общего обра­зования на уровне государственных и региональных стандартов образования. МБОУ СОШ №141 с углублённым изучением математики - вид общеобразовательного учреждения в системе непрерывного образования, ориентированного на обучение и воспитание детей, способных к активному интеллектуальному труду, на формирование личности, готовой к творческой и исследовательской деятельности в разных областях фундамен­тальных наук, обеспечивающая углублённую подготовку обучающихся по математике.

Режим работы школы – шестидневная рабочая неделя. Начальные классы учатся по пятидневной рабочей неделе.

В школе – 50 учебных кабинетов и учебных помещений, из них специализированных: 20, учебные кабинеты: 30, не учебные кабинеты: 4

В школе имеется библиотека (читальный зал и абонемент), столовая, актовый зал, кабинет психолога, комнаты совета старшеклассников и младших школьников, кабинет директора, 2 кабинета заместителей директора, кабинет социальных педагогов. При школе имеется хоккейная коробка, баскетбольная площадка, футбольное поле, полоса препятствия.

Школа I ступени – 14 классов; Школа II ступени – 14 классов (из них – 12 классов общеобразовательных, два класса (8-М, 9-М) с углубленным изучением математики; Школа III ступени - 2 класса с углубленным изучением математики).

Все классы занимаются по программе Министерства образования РФ.

Кадровый потенциал:

Школа укомплектована кадрами полностью. В настоящее время в школе работает 43 педагога. В их числе:

- «Заслуженный учитель» - 1;

- «Почетный работник общего образования» - 2;

- награжденные «Почетной грамотой министерства образования» - 4;

- «Отличник образования» - 4;

- получили награды в городском конкурсе «Учитель года» - 7;

- награждены благодарственными письмами Главного управления образования города Новосибирска – 7;

- награждены благодарственными письмами администрации Новосибирской области – 7;

- удостоены Премии мэра г. Новосибирска – 8.

- победили в конкурсе «Лучшие учителя России» - 2

Современный этап развития общества ставит перед школой новые, сложные задачи, решить которые можно только при анализе имеющихся достижений и на основе чётко спланированной деятельности. Видеть будущее школы - важнейшая творческая задача, решение которой зависит от организации инновационной, исследовательской работы, способности и возможности изменить структуру, статус и назначение школы.

Постановка проблемы


Ни для кого не секрет, что изучение курса геометрии в 7 классе всегда вызывает у учащихся определённые трудности: непонимание необходимости доказательств, отсутствие геометрической зоркости, интуиции, геометрического воображения, неумение выстраивать чёткие логические рассуждения, а в старших классах ещё добавляется проблема пространственного мышления. На сегодняшний день это одна из самых актуальных проблем современного математического образования. Академик А.Д.Александров говорил о том, что задача преподавания геометрии - развивать у учащихся три качества: пространственное воображение, практическое понимание и логическое мышление, причём пространственное мышление ставил на первое место. К 12-13 годам, когда ученик приступает к изучению геометрии, непосредственный интерес к ее освоению уже практически утрачен, еще по-настоящему не проявившись. Если рассматривать изучение геометрии с точки зрения психологически благоприятного момента, то становится очевидным, что ни один предмет не начинают изучать в школе с таким запозданием, как геометрию. Поскольку наглядно-образное мышление и воображение наиболее полно развиваются на стыке старшего дошкольного и младшего школьного возраста, то очевидно, что, наряду с систематическим курсом геометрии, в младших классах педагогически целесообразно широкое содержательное изучение наглядной геометрии. В его основе должна лежать максимально конкретная практическая деятельность ребенка, связанная с различными геометрическими объектами.

Сформулированные противоречия обусловили актуальность проблемы, связанной с разработкой проекта, направленного на эффективную реализацию пропедевтического курса геометрии с мультимедийной поддержкой.

Необходимость пропедевтического курса геометрии, который мог бы служить фундаментом для изучения систематического курса, неоднократно обосновывалась многими методистами. Не раз отмечалось, что начинать изучение геометрии абстрактно-дедуктивным методом нецелесообразно, что необходим подготовительный курс геометрии, который должен носить наглядно индуктивный характер.

Методика преподавания наглядной геометрии в России началась в эпоху школьной реформы середины девятнадцатого века. Первым российским учебником по начальному курсу геометрии стала книга барона М.О. Косинского. В 1871 году под непосредственным руководством К.Д. Ушинского, он составляет свое руководство по «Наглядной геометрии.

В 1873 году выходят учебники З.Б. Вулиха («Краткий курс геометрии и собрание геометрических задач»), В. Борышкевича («Курс элементарной геометрии с практическими задачами») и Е. Волкова («Образовательный курс наглядной геометрии»).

В защиту наглядных курсов геометрии и против замены их сокращенными учебниками евклидовского дедуктивного курса выступал видный методист того времени Евтушевский. Он считал необходимым составлять различные типы учебников по наглядной геометрии: курс наглядной геометрии для начальной школы, курс прагматического характера для практической жизни и пропедевтический курс по наглядной геометрии как подготовке к дальнейшему слушанию научно построенных систематических курсов евклидовского типа. Но вопрос так и остался открытым и нерешенным.

С 1917 года в трудовых школах раннего советского периода, был принят принцип наглядного преподавания всех дисциплин и геометрии, в частности. Наглядная геометрия в течение семи лет, с первого по седьмой класс, опиралась на опытно-наглядную базу. Каждое геометрическое свойство сначала наблюдалось и исследовалось, а только затем доказывалось. Но была допущена крупная методическая ошибка в период увлечения комплексно-лабораторной системой. Геометрия в трудовой школе превратилась в «опытную» дисциплину, у учащихся постепенно терялся интерес к теоретическому, дедуктивному доказательству. Начиная с 1934 года, эта ошибка была исправлена методистами того времени, и наглядная геометрия заняла свое законное место в обучении

Уже после революции, в 1923-1924 гг. была опубликована «Наглядная геометрия» и задачник профессора А.М. Астряба.

В 1955 г. вышла работа П.А. Карасева «Элементы наглядной геометрии в школе: пособие для учителя», в основу которой были положены «живое» созерцание, конструирование, моделирование, построения и измерения.

К сожалению, эти работы по созданию самостоятельного пропедевтического курса геометрии не нашли должного понимания и лишь в настоящее время начинают вновь обретать свою значимость.

Все большее внимание современная школа начинает обращать на методические разработки курса наглядной геометрии. На страницах приложения к газете «Первое сентября» «Математика» в последние годы нередки публикации о пропедевтике геометрии, также появляются авторские разработки и программы. Издательство «Просвещение» выпустило в 1999 г. «Методическую разработку курса наглядной геометрии: книга для учителя» Е.С. Смирновой. Появился учебник «Геометрия, 5» Т.Г. Ходота, В.Л. Велиховской, Н.А. Кайсина и А.Ю.Ходот.

Все это свидетельствует о возрождении интереса к курсу наглядной геометрии и о необходимости дальнейшей разработки одной из важнейших проблем школьного образования-пропедевтики геометрии.


Цель и задачи проекта


Цель проекта


Разработать пропедевтический курс «Наглядная геометрия» для 5-6 классов среднего звена с мультимедийной поддержкой каждого урока с учётом структуры программного комплекса «Наглядная геометрия 5-6»

Задачи проекта

С целью создания условий преемственности и для обеспечения непрерывного изучения геометрии:

1. Изучить педагогические, психологические, методические литературные источники по проблеме.

2. Исследовать актуальность проблемы в рамках нашей школы.

4. Скорректировать программу пропедевтического курса по геометрии для 5-6 классов.

5. Провести эксперимент по апробации программы.


Методы реализации проекта


Во все времена геометрии отводилась особая роль в воспитании и обучении юного поколения. Именно геометрия всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, являясь ключом к образованию системы мышления, способной адекватно и гармонично воспринимать и познавать окружающий мир. Поэтому поиску новых эффективных методик преподавания геометрии уделяется большое влияние. Одной из таких методик можно считать методику преподавания геометрии с использованием новых информационных компьютерных технологий, которая позволяет видоизменять весь процесс преподавания, реализовывать модель личностно-ориентированного обучения, интенсифицировать занятия, а главное – совершенствовать самоподготовку обучающихся.

Рассмотрим некоторые преимущества компьютерных моделей пространственных геометрических фигур, по сравнению с традиционными моделями (развертки, модели из дерева или металла, пластмасса), а также чертежами и рисунками, выполненными на доске или на бумаге учебника.

1. Возможность быстрого создания большого количества разнообразных компьютерных моделей геометрических фигур, что затруднено в случае с материальными моделями как в техническом, так и материальном плане.

2. Неоднократное обращение к компьютерной модели с целью ее демонстрации, что вызывает трудности с традиционными моделями.

3. Моментальное копирование компьютерных моделей для индивидуальной работы в классе, что невозможно при работе с материальными моделями и затруднено с чертежами и рисунками.

4. Возможность динамического изменения количественных характеристик модели объекта, которая полностью исключена в случае с традиционными моделями.

Компьютер можно использовать в различных режимах обучения, а самое главное – в режиме графической иллюстрации изучаемого материала, т. к. возможности компьютера при иллюстрировании намного превосходят возможности любого бумажного учебника, рисунков на школьной доске. Компьютер как чертежный прибор имеет ряд преимуществ по сравнению с циркулем и линейкой. Так, для изображения тел вращения требуется построить изображение окружности являющееся эллипсом. Однако циркулем и линейкой можно построить приближенное изображение эллипса, не всегда отличающегося хорошим качеством. С помощью компьютера можно создать большое количество разнообразных моделей геометрических фигур, что затруднено в случае с материальными моделями, как в техническом, так и в материальном плане.

Если говорить конкретно о системе уроков пропедевтического курса «Наглядная геометрия», то следует немного рассказать о соответствующем программном продукте.

Данный программный комплекс предназначен для компьютерной поддержки курса «Наглядная геометрия», который изучается в 5-6-х классах общеобразовательных учреждений.

Курс «Наглядная геометрия» ориентирован на пропедевтику основных понятий, идей и методов школьного курса геометрии и призван создать базу для успешного изучения геометрии в школе. Поэтому (в силу возрастных особенностей учащихся) тип формируемого геометрического знания школьников определяется и сведениями эмпирического характера, и некоторыми теоретическими положениями геометрии. Чтобы учесть основные принципы формирования геометрического знания школьников, концепцией курса предусмотрено обогащение познавательного опыта детей в разных аспектах сенсорно - персептивном, эмоциональном, интуитивном, интеллектуальном.

Чтобы показать, как данный комплекс программ можно использовать в учебном процессе, необходимо привести некоторые факты. Во-первых, нужно подчеркнуть, что создание геометрических абстракций невозможно без смены уровней познавательной активности ученика в процессе обучения. Поэтому в курсе «Наглядная геометрия» уровень опознания и описания объектов, событий и явлений постепенно сменяется уровнем конструирования и логического объяснения. Заданиями курса предусмотрено развитие навыков как реального- наглядного конструирования, так и идеального -мысленного, абстрактного конструирования.

Во-вторых, нужно отметить, что в курсе «Наглядная геометрия» в качестве основного элемента знания выбрано понятие геометрической фигуры. Сначала создается наглядный образ фигуры, затем этот образ включается в систему связей и только после этого формулируется определение. При этом обогащение познавательного опыта школьников осуществляется в соответствии с основными линиями развития восприятия пространства, которые определяются переходом: от трехмерного пространства к двумерному, от наглядных изображений к условно-схематическим и обратно, от фиксированной на себе системы отсчета к другим системам отсчета. Курс начинается с изучения пространственных геометрических фигур, затем вводятся плоские фигуры и в дальнейшем проводится их параллельное исследование.

В-третьих, необходимо заметить, что успешное изучение геометрии в школе определяется многими факторами и, в частности, требует особого стиля и культуры мышления. Поэтому, чтобы обеспечить плавный переход от наблюдения и произвольных рассуждений к логической (дедуктивной) строгости вывода, в этом курсе важная роль отводится наглядно-содержательной стороне предлагаемых учебных материалов. И в компьютерных программах, наряду с учебными текстами, широко используются фотографии, рисунки, таблицы, схемы, чертежи. Данный иллюстративный ряд помогает организовать познавательную деятельность так, чтобы усиление логической составляющей формируемого знания школьников происходило за счет активизации его образной составляющей. Такое уравновешивание интеллектуальной активности необходимо для гармоничного развития школьников этого возраста (согласно рекомендациям психологов).

Программный комплекс «Наглядная геометрия» состоит из семи компьютерных программ, имеющих модульную структуру.

Программа «Геометрия и моделирование» начинается с повторения учебного материала, организованного в виде ответов на анкету. Задания этого модуля связаны с формированием начальных представлений о пространственных геометрических фигурах. Чтобы обеспечить панорамность и обобщенность представлений, в программу включен альбом с фотографиями различных зданий, отдельные части которых имеют форму тех или иных геометрических фигур. После просмотра альбома школьникам предлагается смоделировать здания определенной формы, по образцу, по собственному замыслу. Используется выбор фигур, заполнение пропусков в предложении, игра «Геометрическая ромашка»





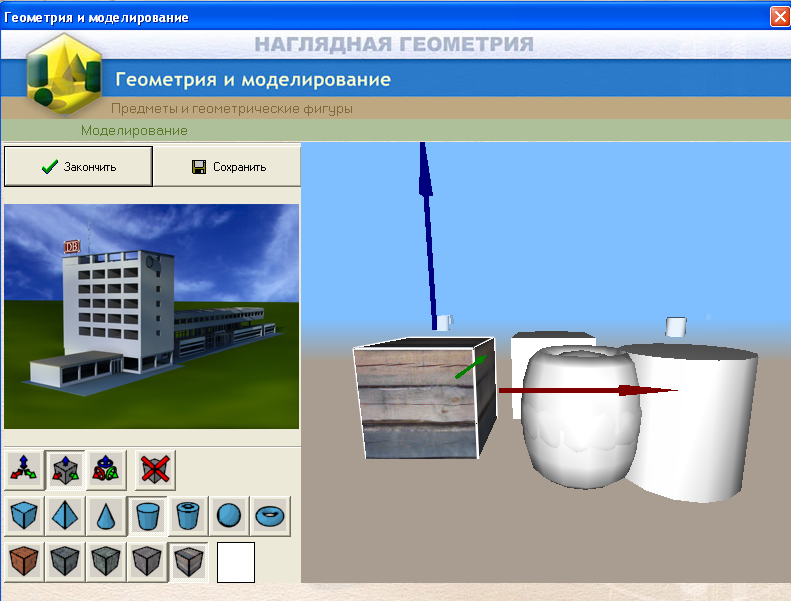
Второй модуль программы посвящен разверткам поверхности геометрических тел; здесь учащимся предоставляется возможность наблюдать динамику процесса развертывания поверхностей, опознавать и выбирать геометрические тела и развертки их поверхности, решать разные задачи о развертках. В этих задачах учащиеся оперируют рисунками и чертежами: разрезают, восстанавливают, достраивают, перекраивают разные фигуры. Третий модуль этой программы посвящен обсуждению проблемы размерности геометрических фигур.

В программе «Измерение геометрических величин» предусмотрена работа с текстом учебника в интерактивном режиме, выполнение заданий разного уровня сложности на действия с отрезками и углами, разрезание и перекраивание геометрических фигур, преобразование единиц измерения, вычисление с помощью формул и составление новых формул, а также выполнение контрольных работ и творческих проектов



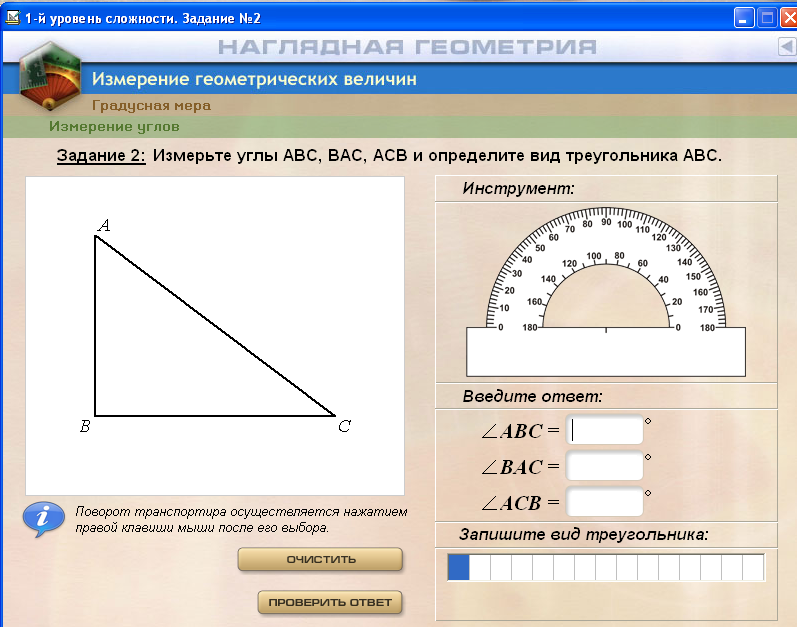
Программа «Конструкции из кубиков и шашек» предназначена для развития пространственных представлений и воображения учащихся. В данной программе учебные задания направлены на развитие умений создавать образ и оперировать им в процессе решения задачи. Для этого на основе действий с виртуальными кубиками и шашками учащимся предоставляется возможность кодировать пространственные отношения с помощью плоских схем.



Создаваемые конструкции можно повернуть в любую сторону, «посмотреть сверху», изобразить виды. Начиная с построения по образцу, учащиеся постепенно переходят к поиску разных конструкций по трем и двум заданным видам. В этой последней части сначала предлагаются задачи, в которых в качестве искомой выступает единственная конструкция. Затем появляются задания с многовариантным ответом. Такие задания предназначены для коллективного обсуждения и выполнения. Программой предусмотрено фиксирование ошибок, подсказки, самостоятельное знакомство с особенностями работы с конструкциями из кубиков и шашек.

Программа «Графические диктанты и Танграм» посвящена пропедевтике метода координат на плоскости. В первых модулях этой программы содержатся задания, которые направлены на совершенствование навыков ориентировки на листе в клетку. Эти задания имеют форму графических диктантов и предполагают изображение контура некоторой плоской фигуры.



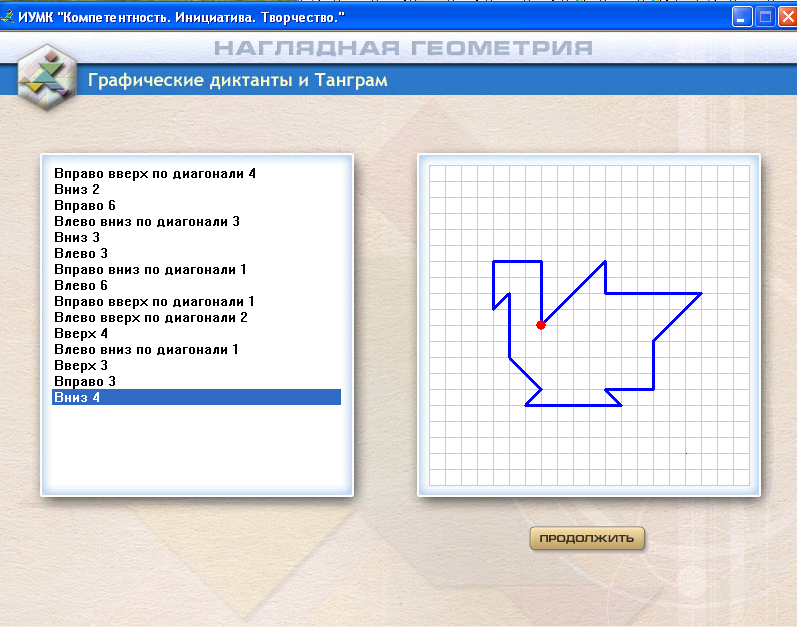
Сначала это происходит на основе словесного описания направления движения карандаша по странице. Затем вводятся две шкалы отсчета - вертикальная и горизонтальная, и координаты точки. Начинается эта часть программы с графических диктантов по заданному тексту, а завершается - шифровкой предложенных рисунков.

Рассмотрение нарисованной фигуры с позиций разных игр на составление из частей придает большую воображаемую подвижность создаваемому образу и помогает привлечь внимание учащихся к координатам как одному из средств ориентировки и конструирования. После того как плоская фигура будет изображена на листе в клетку, учащимся предлагается составить ее из семи частей квадрата (как в игре «Танграм») или двенадцати элементов пентамино. Программой предусмотрен выбор тематики рисунка, дизайн, подсказки, обучение.

Программа «Геометрические конструкции на плоскости и в пространстве» предназначена для расширения представлений учащихся о геометрии как отдельной отрасли знания, где существуют свои понятия , законы и методы исследования. Использование этой программы рассматривается как отдельный этап формирования познавательного опыта учащихся в области геометрии. В это время уже создан наглядный образ исследуемых объектов и учащиеся имеют возможность работать с определением и некоторыми его свойствами .



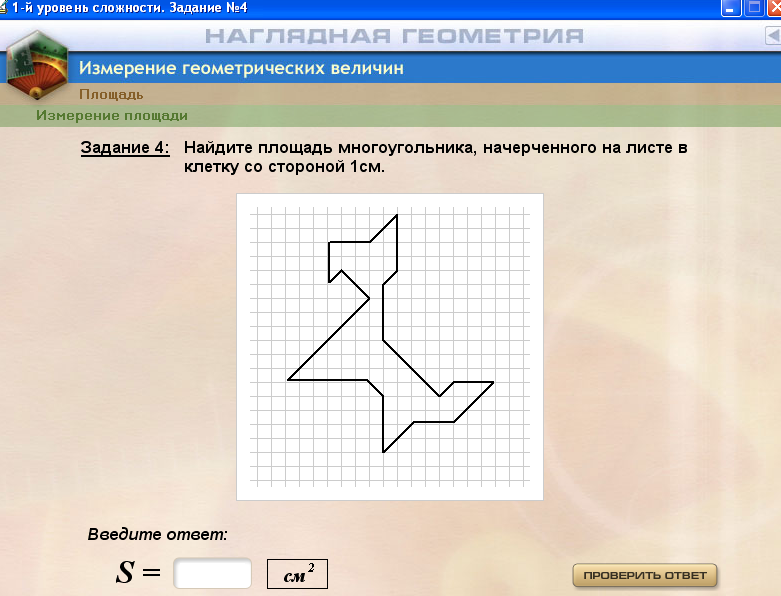
Программа «Математическое вышивание» предназначена для обогащения образного мышления и воображения школьников. В первом модуле этой программы обобщаются представления учащихся об окружности и круге. Следующий модуль программы посвящен алгоритмам метода математического вышивания. Учащимся предлагается повторить или познакомиться с алгоритмами построения некоторых кривых на плоскости , а затем обобщить эти алгоритмы на основе изменения параметров исходной конструкции . В последнем модуле программы учащимся предоставляется возможность познакомиться с тем, как можно использовать геометрические фигуры в прикладном творчестве. Используя инструментарий программы, они могут создавать различные композиции из фигур



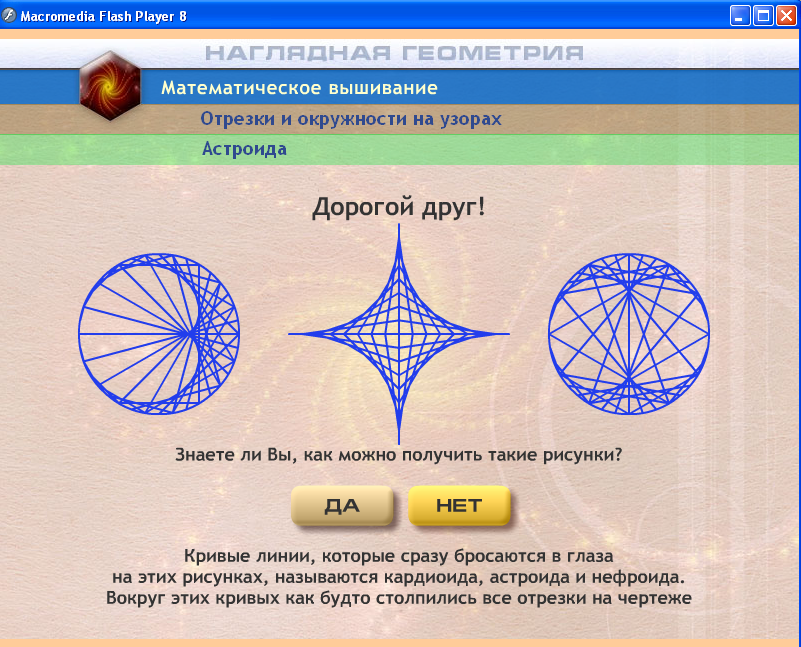
В данной программе предоставлен инструментарий для динамической визуализации свойств плоских и пространственных геометрических фигур. В первом модуле программы обобщаются представления о ломаных и многоугольниках, конструируются ломаные на поверхности куба. Решаются задачи на изображение видов и построение по трем видам пространственных ломаных



Второй модуль программы посвящен основным конфигурациям из прямых на плоскости; здесь рассматриваются пересекающиеся и параллельные прямые и некоторые четырехугольники как конструкции из параллельных прямых. Предусмотрена работа с текстом учебника ,содержатся задания трех уровней сложности, в том числе предлагаются задания на разработку специальных исследовательских проектов. В третьем модуле рассматривается взаимное рас положение прямых и плоскостей в пространстве. Учащиеся получают возможность наблюдать и исследовать с помощью инструментария программы отношения между основными геометрическими фигурами в пространстве.

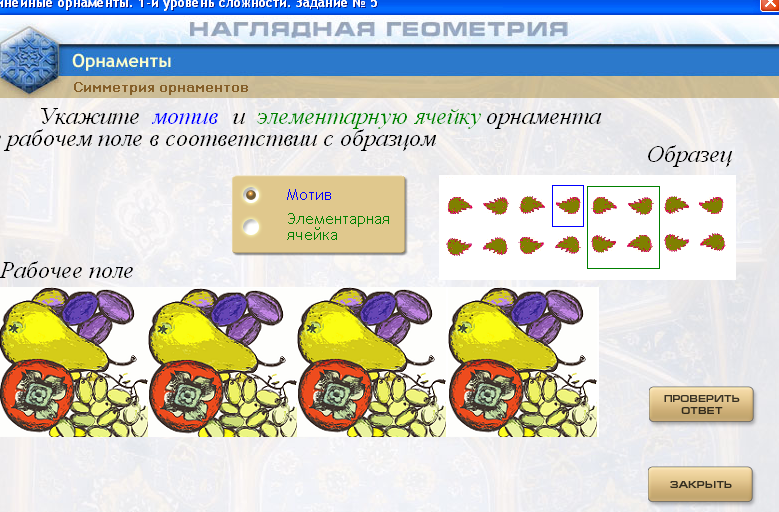
Программа «Орнаменты» посвящена формированию представлений учащихся об эстетическом потенциале и практической значимости геометрии. В данной программе содержится материал и предлагается инструментарий, который позволяет привлечь внимание детей к геометрии и геометрическим проектам. При работе по этой программе учащиеся получают возможность не только наблюдать процесс создания различных образов, но и непосредственно принимать участие в их конструировании на основе понятий, идей и законов геометрии.

В первом модуле этой программы учащиеся знакомятся с орнаментальной росписью памятников архитектуры. Второй модуль посвящен обобщению представлений о различных видах движения фигур на плоскости. В третьем модуле исследуются линейные и сетчатые орнаменты и паркеты; решаются вопросы их классификации и построения с помощью виртуальных инструментов



Рассматриваемые компьютерные программы построены таким образом, чтобы учитель имел возможность использовать каждую из них по-разному, в соответствии с уровнем геометрической подготовки и осведомленности своих детей. Программы можно применять как для повторения учебного материала и систематизации знаний учащихся, так и для знакомства с новой информацией и обогащения геометрических знаний и умений школьников новыми фактами, элементами и приемами.

В заключен6ие следует отметить, что данный программный комплекс по своему содержанию ближе к учебным текстам из книги «Математика: наглядная геометрия» (учебное пособие для 5-6 классов общеобразовательных учреждений / [В.А. Панчищина, Э.Г. Гельфман, В.Н. Ксенева и др.] – М.: Просвещение, 2006. – 175 с.).

Более того, в дополнение к этому учебному пособию в 2008 году Томский государственный педагогический университет выпустил тетради «Наглядная геометрия: рабочая тетрадь по математике. 5-6 класс.» Но, учитывая небольшое количество часов, отводимых на пропедевтический курс геометрии, и отсутствие тетрадей в массовой продаже, можно часть выбранных из них заданий распечатывать по мере необходимости. В связи с этим, претворяя данный проект , необходимо рассмотреть целесообразность перехода к этим учебным комплектам.

Реализация проекта должна быть основана на активной деятельности детей. Она должна быть ориентирована на накопление информации по геометрии, на её осмысление и некоторую систематизацию. Тогда эта программа будет служить не только цели обучения началам геометрии, но и повлияет на общее развитие детей.

Реализуя данный проект в нашей школе мы можем при проведении уроков использовать потенциал электронной интерактивной доски SMART Board.

Перечислим следующие виды образовательной деятельности, доступные при использовании электронной интерактивной доски:

Работа с текстом и изображениями

Создание заметок с помощью электронных чернил

Сохранение сделанных заметок для передачи по электронной почте, размещения в Интернете или печати

Коллективный просмотр Web-сайтов

Свобода передвижения по классу при демонстрации программного обеспечения или работе с ним перед аудиторией

Создание с помощью шаблонов и изображений собственных заданий для занятий

Демонстрация и нанесение заметок поверх образовательных видеоклипов

Использование встроенного в программное обеспечение интерактивной доски презентационного инструментария для обогащения дидактического материала

Демонстрация презентаций, созданных учащимися.

Разнообразие цветов, доступных на интерактивной доске, позволяет преподавателям выделять важные области и привлекать внимание к ней, связывать общие идеи или показывать их отличие и демонстрировать ход размышления.

С помощью доски можно значительно усилить подачу материала. На интерактивных досках также можно захватывать видео - изображения и отображать их статично, чтобы иметь возможность обсуждать и добавлять к нему записи. Тест, схему или рисунок на интерактивной доске можно выделить. Это позволяет преподавателям и ученикам фокусироваться на отдельных аспектах темы. Часть экрана можно скрыть и показать его, когда будет нужно. Программное обеспечение для интерактивных досок включает фигуры, которые могут помочь учащимся сконцентрироваться на определенной области экрана. Используя инструмент "прожектор" можно выделить определенные участки экрана и сфокусировать внимание на них.

Объекты можно вырезать и стирать с экрана, копировать и вставлять, действия - отменять или возвращать. Это придает учащимся больше уверенности - они знают, что всегда могут вернуться на шаг назад или изменить что-нибудь. Доска помогает учащимся группировать идеи, определять достоинства и недостатки, сходства и различия, подписывать карты, рисунки, схемы и многое другое.

Электронные интерактивные доски SMART Board поддерживают в классе атмосферу оживленного общения и вызывают дискуссии - это существенно помогает при ознакомлении обучающихся с новым материалом.

Интерактивные SMART-технологии - это уникальный инструмент, который позволит репродуктивную деятельность сменить на креативную.


Ожидаемые результаты и их практическая значимость


Внедрение программы в учебный процесс призвано обеспечить, прежде всего, безболезненный переход из начальной школы в основную ступень. У детей будет сформирован механизм адаптации к учебным проблемам, снят психологический барьер для принятия собственного решения. У детей будет положительная реакция в том случае, если усвоение учебного материала произойдёт не сразу. Они смогут создать для себя установку «не могу, так как пока этого не знаю» и наметить конкретный план для решения учебной проблемной ситуации. Они смогут научиться нешаблонно мыслить и интерпретировать мыслительные действия.

Усилится связь между школой и родителями, так как родители, заинтересованные в успешности детей, примут ещё большее участие в учебном процессе, помогая решать нестандартные задачи и оказывая методическую поддержку в домашних условиях.

Внедрение программы позволит сформировать более раннюю потребность у детей в изучении геометрии, поможет детям и их родителям увидеть перспективу изучения математики и её роль для успешного обучения в основной и средней школе.

Таким образом, образуется некий фундамент для дальнейшего успешного обучения математике и «опережающее» развитие будет происходить за счёт функциональных связей, которые значительно обогатят тот комплекс понятий, которая начинает формироваться у младших школьников.