До курсового проектування за курсом "Моделювання І прогнозування стану навколишнього середовища" для студентів 4 курсу хіміко-технологічного факультету / Уклад

Вид материала

Документы

Содержание 4.2. Математичний опис реверс-процесу Розподіленість системи Теплова інерційність шару Перенос тепла в шарі

Подобный материал:

• Єльнікової Тетяни Олександрівни з курсу "Моделювання та прогнозування стану довкілля", 33.26kb.
• Робоча навчальна програма з раціонального використання та відтворення водних ресурсів, 401.96kb.
• Укладач О. О. Кузьменко, 590.11kb.
• Л. М. Чуніхіна Рецензент М. М. Латишева, 719.95kb.
• Комп’ютерне моделювання фізичних процесів Для студентів ІV курсу спеціальності 070100, 219.13kb.
• Юрія Федьковича «затверджую», 632.92kb.
• Програма та плани семінарських занять для студентів Філософського факультету львів, 361.9kb.
• Кабінет міністрів україни постанова від 2012 р. № Київ Про затвердження Порядку проведення, 11.23kb.
• Програма стабілізації екологічного стану навколишнього середовища та підвищення рівня, 68.98kb.
• Ї праці студентів й виконання курсової роботи з дисципліни „Загальна екологія й основи, 517.37kb.

4.2. Математичний опис реверс-процесу

Нестаціонарний спосіб здійснення каталітичних реакцій засновано на використанні динамічних властивостей нерухомого шару каталізатора.

Математичні моделі, що описують динамічні процеси в шарі зернистого каталізатора, що розробляються на основі ієрархічного підходу, повинні враховувати наступні фактори.

1. Гетерогенний характер системи — наявність твердої і газоподібної фаз.
   
2. Наявність джерел (стоків) речовин — результат хімічних перетворень реагентів, що протікають на каталізаторі.
   
3. Наявність джерел тепла, загальний тепловий потік яких визначається як добуток теплових ефектів реакцій на швидкості їх протікання.
   
4. Розподіленість системи. Основним об'єктом вивчення є процес міграції теплових полів по шару каталізатора. Неоднорідність температурних і концентраційних полів у шарі може бути врахована тільки просторово розподіленою системою.
   
5. Теплова інерційність шару. Висока швидкість хімічного перетворення в зоні реакцій забезпечується досить високою температурою. Теплова енергія в зоні реакції, що рухається в напрямку фільтрації газу, складається з енергії реакції й енергії, накопиченої шаром раніше. Перепад температур у зоні реакції виявляється вище адіабатичного розігріву. Нагромадження значної кількості тепла шаром можливо тільки при досить великій тепловій ємності шару. Велика теплова інерційність шару забезпечує більш повільну в порівнянні зі швидкістю подачі реакційної суміші міграцію високотемпературної зони реакції.
   
6. Конвекція. Подача реакційної суміші в шар каталізатора здійснюється за рахунок фільтрації газу. У математичній моделі це може бути враховано конвекційними членами.
   
7. Перенос тепла в шарі. У результаті екзотермічної реакції в шарі каталізатора виникає високотемпературна зона. Щоб виключити необмежене зростання температури в зоні реакції, потрібно врахувати можливі механізми переносу тепла в шарі каталізатора: теплопровідність по «каркасу» шару, зовнішній теплообмін між зовнішньою поверхнею гранул каталізатора і реакційною сумішшю, внутрішній перенос тепла в гранулах. Під «каркасом» розуміється сукупність зовнішньої поверхні всіх зерен і непроточних зон між ними. Передача тепла здійснюється за рахунок наявності пульсуючих вихрів, що утворюються в непроточних зонах, поблизу місць контакту окремих гранул. Механізм переносу тепла можна в цьому випадку описати ефективною подовжньою теплопровідністю по «каркасу» шару.
   

Якщо процеси на зерні каталізатора описуються моделлю швидкості хімічного перетворення, що спостерігається, W_н (θ, Y), а дифузією і теплопереносом у газі можна зневажити, то математичний опис буде мати такий вид:

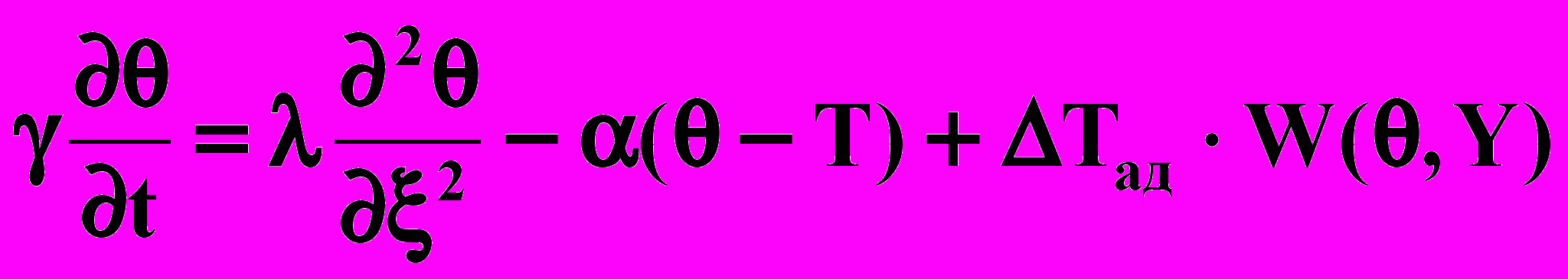	(4.1)
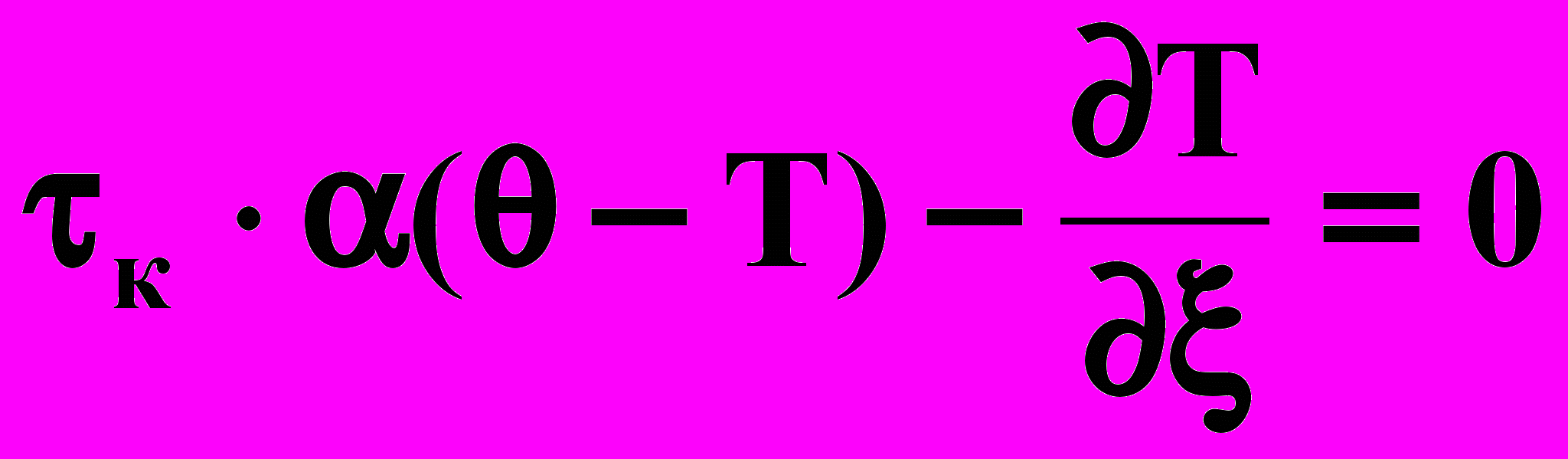	(4.2)
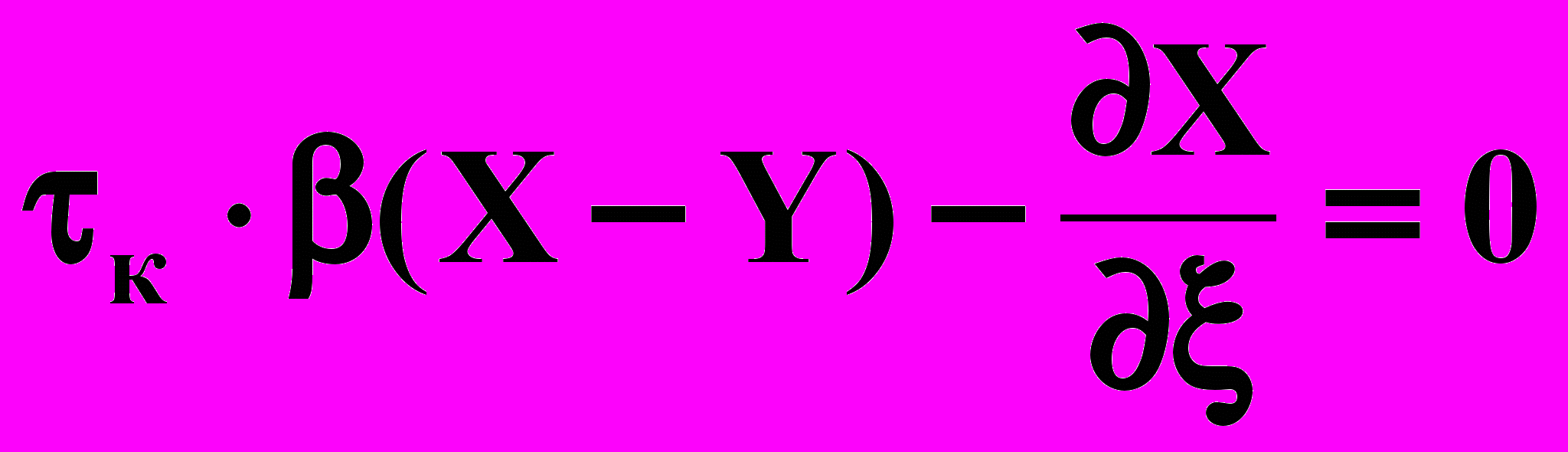	(4.3)
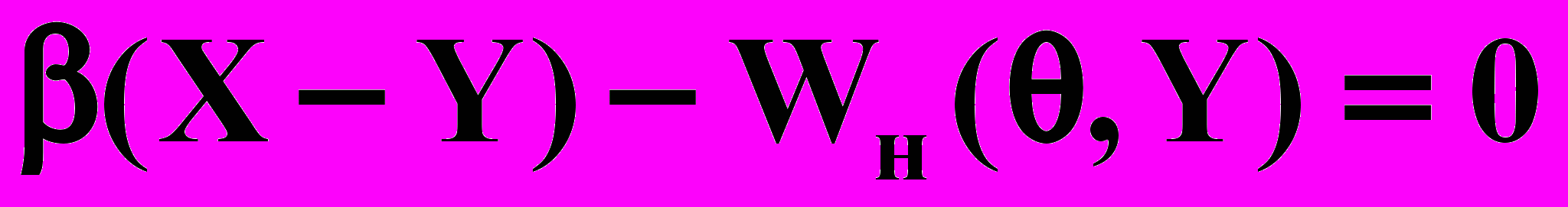	(4.4)

с граничними умовами:

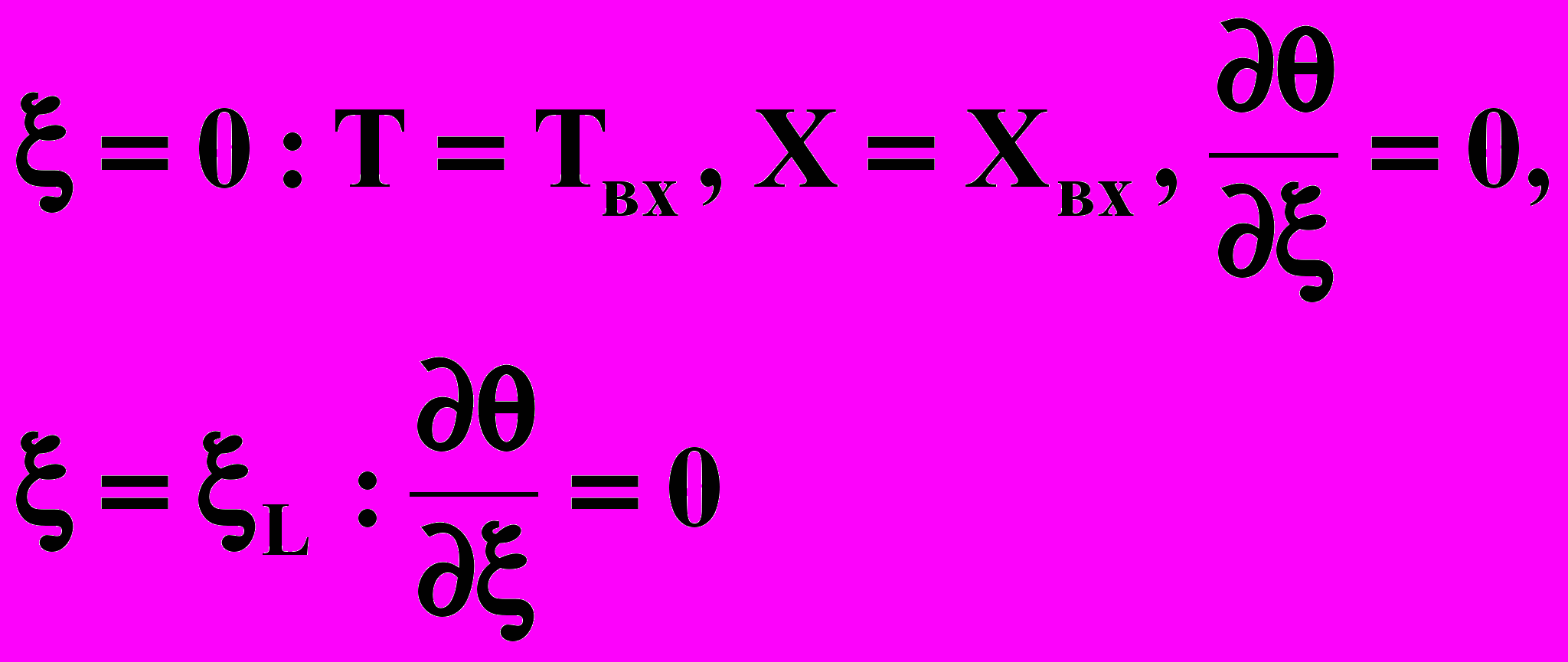(4.5)

початковими умовами:

.

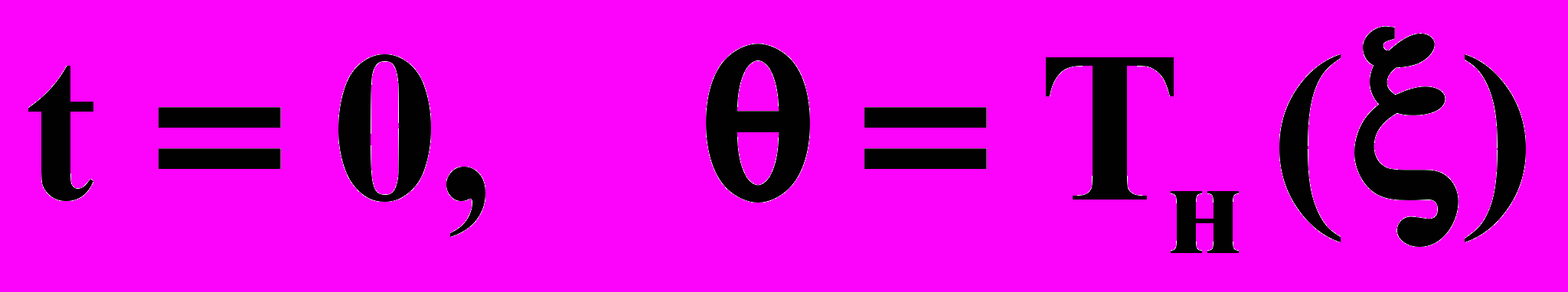(4.6)

Для аналізу нестаціонарних режимів у реакторі з розміщеним по торцях шару каталізатора інертом система рівнянь (4.1)–(4.6) доповнюється граничною умовою «склейки» У крапках між каталізатором і інертом (ξ = ξ₁ і ξ = ξ₂₎ умови «склейки» мають вид:

(4.7)

Крім того, для шару інертного матеріалу вираження

W_н(θ,Y) =0.

Для чисельного розрахунку нестаціонарних процесів знешкодження по моделі (4.1)–(4.7) використовується комбінований числено-аналітичний метод. Рішення всієї системи знаходиться таким способом. З рішення рівняння (4.1) знаходиться наближення до 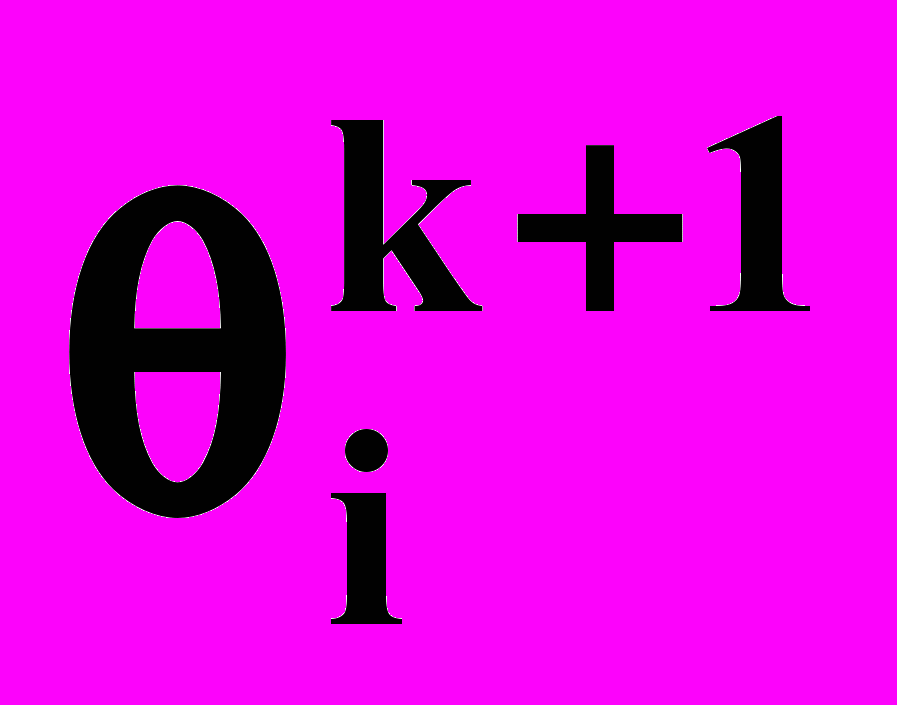. З цим наближенням вирішується рівняння (4.2) і знаходиться приблизно 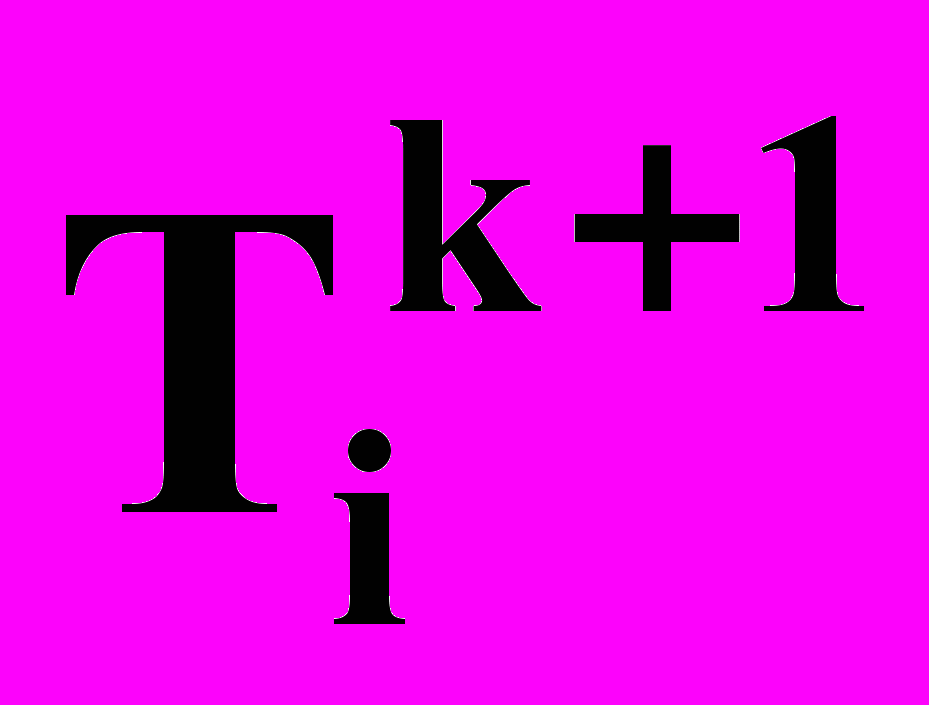, що використовується для більш точного рішення першого рівняння. Ітераційний процес здійснюють до виконання умови

,

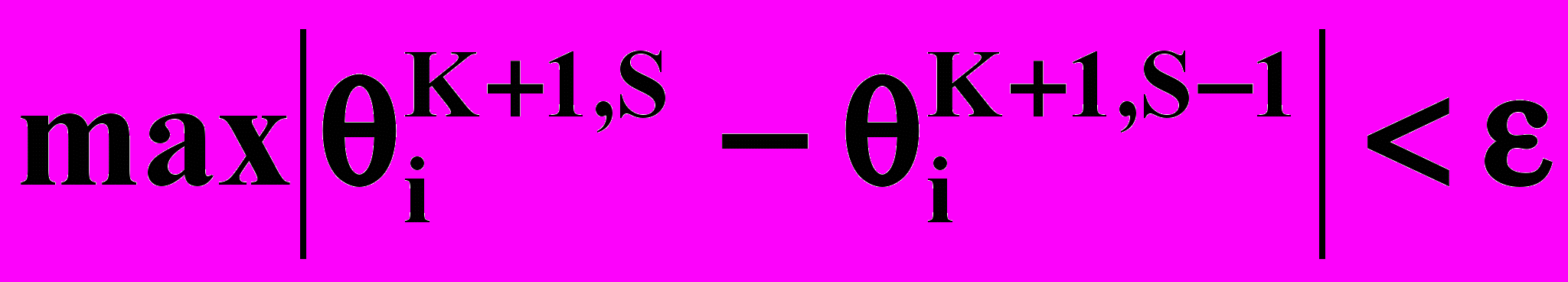(4.8)

де s – номер ітерації. Після встановлення ітерацій вирішують рівняння (4.3), (4.4) і переходять до наступного кроку за часом.