Аннотации программ дисциплин
| Вид материала | Документы |
- Аннотации программ учебных дисциплин основной образовательной программы по направлению, 5252.4kb.
- Аннотации примерных программ дисциплин профессионального цикла (вариативная (профильная), 110.56kb.
- Аннотации программ дисциплин, 849.25kb.
- Аннотации программ дисциплин, 1084.05kb.
- Направление: Информатика и вычислительная техника (552800), 659.51kb.
- Аннотации рабочих программ дисциплин подготовки бакалавров по направлению 150100, 1497.02kb.
- Аннотации рабочих программ дисциплин подготовки бакалавров по направлению 150400., 1630.48kb.
- Аннотации программ дисциплин по направлению 231300. 62 Прикладная математика, 505.37kb.
- 032700. 62. 01 Отечественная филология: русский язык и литература аннотации рабочих, 1833kb.
- Аннотации программ дисциплин Аннотация дисциплины, 37.75kb.
“Численные методы решения уравнений математической физики и химии”
Рекомендуется для направления подготовки 230400 «Информационные системы и технологии» как дисциплина по выбору математического и естественнонаучного цикла
Квалификация (степень) - бакалавр
1. Введение.
Современные тенденции в развитии численных методов, программирования и вычислительной техники. Формализация этапов разработки математической модели химико-технологического процесса. Классификация уравнений математических моделей ХТП. Классификация граничных условий. Примеры математических моделей ХТП. Выбор численного метода решения. Оценка точности вычислений.
2. Теоретические основы.
Приведение уравнений к безразмерному виду. Разностная аппроксимация дифференциальных операторов 1-го и 2-го порядков. Понятие порядка аппроксимации. Понятия разностной сетки и разностной схемы. Явные и неявные разностные схемы. Аппроксимация начальных и граничных условий.
Понятия устойчивости разностных схем и сходимости решения разностной схемы к решению исходного дифференциального уравнения. Спектральный метод (метод гармоник) анализа устойчивости разностных схем. Исследование устойчивости явной и неявной разностных схем, аппроксимирующих дифференциальное уравнение параболического типа.
3. Решение дифференциальных уравнений параболического типа (одномерных по пространству) и дифференциальных уравнений в частных производных 1-го порядка.
Примеры дифференциальных уравнений параболического типа применительно к процессам химической технологии. Явная разностная схема, исследование устойчивости схемы, метод ее решения. Неявная разностная схема, исследование устойчивости схемы. Метод прогонки как метод решения неявной разностной схемы. Метод решения на основе схем Кранка-Николсона и Саульева. Построение алгоритмов для решения задач теплопроводности и диффузии.
Примеры дифференциальных уравнений в частных производных 1-го порядка применительно к процессам химической технологии. Явные разностные схемы, исследование устойчивости разностных схем, метод решения. Неявные разностные схемы, устойчивость разностных схем, метод решения. Построение алгоритмов для решения задач, связанных с расчетом уравнений баланса числа частиц в химических реакторах.
4. Решение многомерных дифференциальных уравнений параболического типа и многомерных уравнений в частных производных 1-го порядка.
Примеры многомерных дифференциальных уравнений параболического типа применительно к процессам химической технологии. Явные разностные схемы, исследование устойчивости, метод решения. Схемы расщепления. Схема со стабилизирующей добавкой, схема предиктор-корректор. Исследование устойчивости схем, метод их решения. Сравнительная характеристика изученных разностных схем. Построение алгоритмов для решения многомерных задач диффузии, вихря скорости с учетом явлений конвекции.
Примеры многомерных дифференциальных уравнений в частных производных 1-го порядка применительно к процессам химической технологии. Явные разностные схемы, исследование устойчивости, метод расщепления. Схемы расщепления, исследование устойчивости, метод решения. Построение алгоритмов для решения многомерных задач расчетов функций распределения частиц по размерам и по толщине пленок на них в процессе разложения апатита и получения экстракционной фосфорной кислоты.
5. Решение дифференциальных уравнений эллиптического типа.
Примеры дифференциальных уравнений эллиптического типа применительно к задачам химической технологии. Методы установления с использованием явной разностной схемы (метод простой итерации), с использованием схем расщепления. Сравнительная характеристика методов. Построение алгоритмов для решения задач расчета концентрационных и тепловых профилей в проточных трубчатых реакторах, расчета функции тока для решения задач гидродинамики.
6. Решение интегро-дифференциальных уравнений.
Примеры интегро-дифференциальных уравнений применительно к задачам химической технологии. Разностные схемы для решения интегро-дифференциальных уравнений, методы решений. Построение алгоритмов для расчета уравнений для функций распределения включений по размерам с учетом явлений агломерации и дробления в химических реакторах.
7. Решение сложных систем уравнений.
Приведение системы уравнений к безразмерному виду. Построение разностных схем, аппроксимирующих систему уравнений. Определение устойчивости разностных схем с помощью тестовых задач. Метод тестовых задач. Разработка алгоритма для решения уравнений математической модели процесса массовой кристаллизации из раствора (уравнение изменения концентрации в растворе, уравнение баланса числа частица, уравнение изменения температуры раствора).
Авторы программы:
Профессор Э.М. Кольцова (кафедра ИКТ РХТУ им. Д.И. Менделеева)
Доцент А.С. Скичко (кафедра КХТП РХТУ им. Д.И. Менделеева)
“Численные методы решения уравнений в частных производных 2-го порядка”
Рекомендуется для направления подготовки 230400 «Информационные системы и технологии»
как дисциплина по выбору математического и естественнонаучного цикла
Квалификация (степень) – бакалавр
1. Введение.
Цели и задачи курса. Классификация уравнений в частных производных 2-го порядка. Классификация граничных условий.
2. Теоретические основы.
Разностная аппроксимация дифференциальных операторов 1-го и 2-го порядков. Понятие порядка аппроксимации. Понятия разностной сетки и разностной схемы. Явные и неявные разностные схемы. Аппроксимация начальных и граничных условий.
Понятия устойчивости разностных схем и сходимости решения разностной схемы к решению исходного дифференциального уравнения. Спектральный метод (метод гармоник) анализа устойчивости разностных схем. Исследование устойчивости явной и неявной разностных схем, аппроксимирующих дифференциальное уравнение параболического типа.
3. Решение дифференциальных уравнений параболического типа (одномерных по пространству).
Явная разностная схема, исследование устойчивости схемы, метод ее решения. Неявная разностная схема, исследование устойчивости схемы. Метод прогонки как метод решения неявной разностной схемы. Метод решения на основе схем Кранка-Николсона и Саульева. Построение алгоритмов для решения задач теплопроводности и диффузии.
4. Решение многомерных дифференциальных уравнений параболического типа.
Явные разностные схемы, исследование устойчивости, метод решения. Схемы расщепления. Схема со стабилизирующей добавкой, схема предиктор-корректор. Исследование устойчивости схем, метод их решения. Сравнительная характеристика изученных разностных схем. Построение алгоритмов для решения многомерных задач диффузии, вихря скорости с учетом явлений конвекции.
5. Решение дифференциальных уравнений эллиптического типа.
Методы установления с использованием явной разностной схемы (метод простой итерации), с использованием схем расщепления. Сравнительная характеристика методов. Построение алгоритмов для решения задач расчета концентрационных и тепловых профилей и расчета функции тока.
6. Решение дифференциальных уравнений гиперболического типа.
Разностная аппроксимация оператора
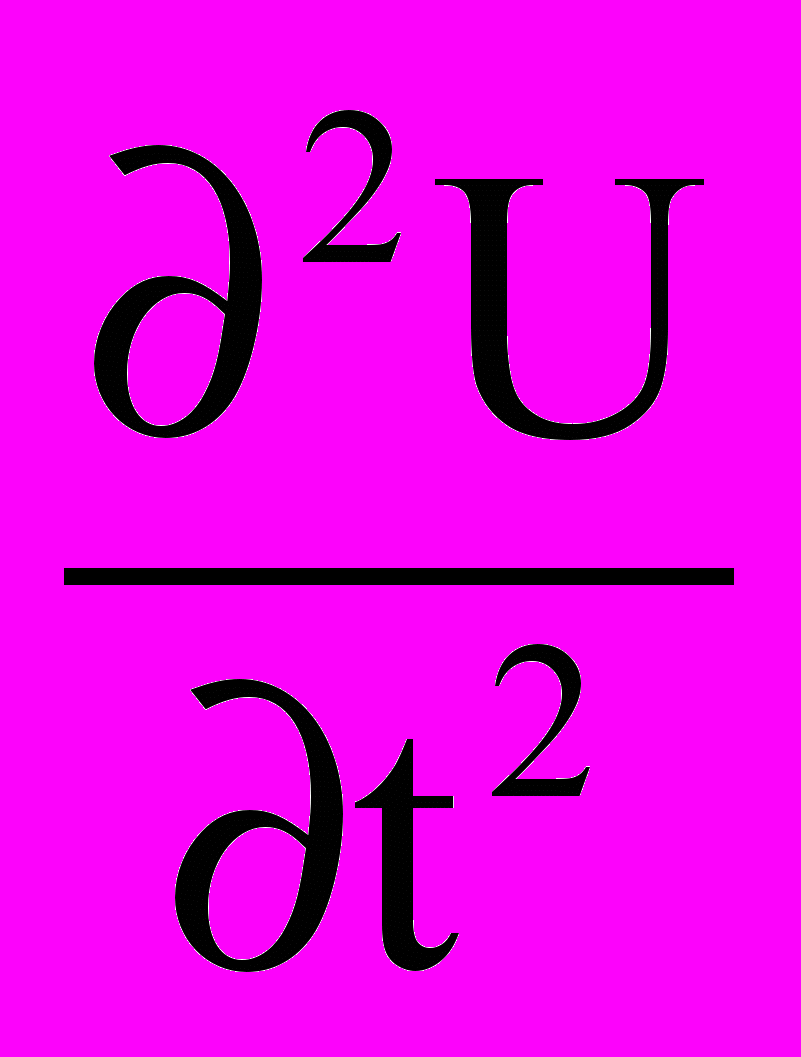. Явная и неявная разностные схемы. Устойчивость разностных схем. Метод характеристик для решения гиперболических уравнений. Сравнительная характеристика методов. Построение алгоритмов для решения задач упругости твердого тела.7. Решение дифференциальных уравнений с дробной производной по времени.
Разностная аппроксимация оператора
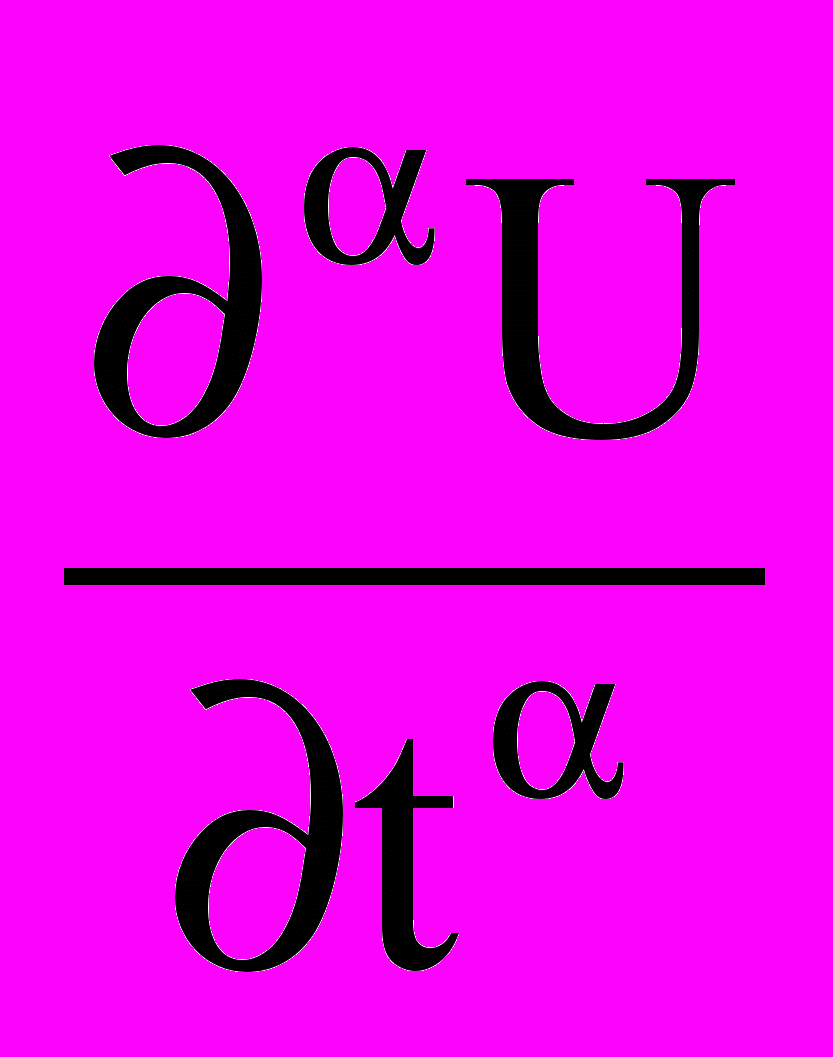. Явная и неявная разностные схемы. Исследование устойчивости разностных схем. Сравнительная характеристика разностных схем. Построение алгоритма для решения задач массопереноса в фрактальных средах.Автор программы:
Профессор Э.М. Кольцова (кафедра ИКТ РХТУ им. Д.И. Менделеева)
Аннотация рабочей программы учебной дисциплины
«Вычислительная математика»
Рекомендуется для направления подготовки 230400 «Информационные системы и технологии » как дисциплина вариативной части математического и естественнонаучного цикла
Квалификация (степень) - бакалавр
- Введение в вычислительную математику. Место численных методов в научных исследованиях. Источники погрешности результата вычислений.
- Основы теории погрешностей. Прямая задача теории погрешностей. Решение обратной задачи теории погрешностей. Знакомство с MATLAB.
- Решение систем линейных алгебраических уравнений (СЛАУ). Согласованные нормы векторов и матриц. Обусловленность СЛАУ. Прямые методы решения. Итерационные методы. Собственные значения и собственные векторы. Решение СЛАУ в MATLAB.
- Методы решения нелинейных уравнений. Отделение корней уравнения. Уточнение корней. Решение нелинейных уравнений в MATLAB.
- Решение систем нелинейных уравнений. Условия сходимости. Возможности MATLAB для решения систем нелинейных уравнений.
- Интерполирование функций. Полином Лагранжа. Конечные разности. Полином Ньютона. Остаточный член и его оценки для конечноразностной интерполяции. Глобальная и кусочно-полиномиальная интерполяция. Интерполяция сплайнами. Реализация интерполяции в MATLAB.
- Аппроксимация экспериментальных данных. Сглаживание опытных данных методом наименьших квадратов. Аппроксимация ортогональными классическими полиномами. Реализация аппроксимации МНК в MATLAB.
- Численное дифференцирование. Метод Рунге уточнения формул численного дифференцирования. Численное дифференцирование в MATLAB.
- Численное интегрирование функций. Процедура Рунге оценки погрешности и уточнения формул численного интегрирования. Численное интегрирование в MATLAB.
- Численные методы оптимизации. Поиск минимума функций одной и нескольких переменных. Поиск минимума функций в MATLAB.
- Численные методы решения дифференциальных уравнений первого порядка. Методы Рунге-Кутта. Локальная и глобальная погрешности метода. Решение дифференциальных уравнений в MATLAB.
- Решение нормальных систем ОДУ. Выбор шага численного интегрирования задач Коши. Процедура Рунге оценки погрешности и уточнения численного решения задач Коши. Обусловленность численных методов решения ОДУ. Устойчивость решений дифференциальных уравнений по Ляпунову. Жёсткие системы ОДУ.
Автор программы: доцент Филиппова Е.Б. (кафедра информационных компьютерных технологий РХТУ им. Д.И.Менделеева)
Аннотация рабочей программы учебной дисциплины
«Методы вычислительной математики
и пакеты прикладных программ»
Рекомендуется для направления подготовки 230400 «Информационные системы и технологии» как вариативная дисциплина по выбору цикла
математических и естественно-научных дисциплин
Квалификация (степень) – бакалавр
Введение.
Цели и задачи курса. Классы задач, решаемых методами вычислительной математики. Основные понятия, определения, терминология.
1. Методы обработки экспериментальных данных. Интерполирование и аппроксимация.
Обработка экспериментальных данных с целью идентификации математической модели. Интерполирование экспериментальных зависимостей (интерполирующая зависимость в виде ломаной, интерполяционные многочлены Лагранжа и Ньютона, сплайн-интерполяция). Аппроксимация экспериментальных данных. Метод наименьших квадратов для решения задачи аппроксимации. Матричная форма записи и решения задачи аппроксимации методом наименьших квадратов. Корреляционный анализ и определение адекватности регрессионной модели.
2. Численные методы решения линейных и нелинейных уравнений и систем уравнений.
Классификация методов решения уравнений с одним неизвестным. Методы решения уравнений с одним неизвестным (половинного деления, пропорциональных частей, простых итераций, касательных). Классификация методов решения систем алгебраических уравнений. Методы решения систем линейных алгебраических уравнений (Крамера, обратной матрицы, Жордана-Гаусса, Гаусса, простых итераций, Гаусса-Зейделя). Методы решения систем нелинейных алгебраических уравнений (простых итераций, Ньютона-Рафсона).
3. Методы вычисления определённых интегралов.
Вычисление определённых интегралов методами прямоугольников и его вариациями, трапеций, парабол. Сравнение точности методов. Способы повышения точности вычисления определённых интегралов.
4. Численные методы решения дифференциальных уравнений и систем уравнений.
Методы решения обыкновенных дифференциальных уравнений (Эйлера, Эйлера-Коши, модифицированный Эйлера, Рунге-Кутты). Решение систем дифференциальных уравнений. Задача Коши. Краевая задача.
5. Численные методы оптимизации функций одной и нескольких переменных.
Постановка задачи оптимизации. Классификация методов решения задач оптимизации. Методы оптимизации функции одной переменной (локализации экстремума, золотого сечения, поиска экстремума с использованием чисел Фибоначчи). Градиентные методы оптимизации функции нескольких переменных (релаксации, градиента, наискорейшего спуска). Оптимизация методами детерминированного поиска (поочерёдного изменения переменных, сканирования, симплексный и его модификация). Оптимизация методами случайного поиска (случайных направлений и его модификация, спуск с наказанием случайностью). Решение системы нелинейных алгебраических уравнений как задача оптимизации функции нескольких переменных.
6. Основы работы с электронными документами, таблицами и мультимедийными презентациями. Программный пакет Microsoft Office.
Подготовка научно-технической документации. Особенности работы с электронными документами. Типы и форматы электронных документов. Основные правила профессиональной вёрстки текста. Редактор текстов Microsoft Word: назначение, версии, интерфейс программы, обзор функциональных возможностей. Редактор табличных данных Microsoft Excel: назначение, основные функциональные возможности, интерфейс программы. Реализация методов вычислительной математики в табличном процессоре Microsoft Excel. Визуализация табличных данных. Подготовка электронных мультимедийных презентаций в программе Microsoft PowerPoint. Основные принципы и правила оформления презентаций.
Заключение.
Заключительная лекция по подведению итогов курса.
Автор программы:
Доцент С. П. Дударов (кафедра ИКТ РХТУ им. Д. И. Менделеева)
Аннотация рабочей программы учебной дисциплины