Метод матричной прогонки является одним из широко применяемых точных методов решения систем уравнений с блочными матрицами ленточной структуры

Вид материала

Документы

Содержание LU-разложение. Если разбить матрицу системы на блоки, то можно построить блочное LU L = blocktridiag{-Li, 0, 0}; U Алгоритм матричной прогонки Тогда алгоритм матричной прогонки корректен, а для прогоночных коэффициентов справедливы неравенства Пусть также для матрицы Якоби Для любой блочной трехдиагональной матрицы вида (14) при условии, что Матрица K положительно определена. Блоки полного блочного разложения T Список использованных литературных источников Ample conditions of existence of the complete

Подобный материал:

• Решение систем линейных алгебраических уравнений методом прогонки, 112.31kb.
• Операции с матрицами Решение систем линейных уравнений с помощью матриц Операции, 131.32kb.
• Практических: 0 Лабораторных:, 21.53kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• Для решения систем линейных алгебраических уравнений с ленточной матрицей, с понятием, 89.58kb.
• Решение систем нелинейных уравнений, 119.58kb.
• Метод касательных гиперплоскостей для решения систем нелинейных алгебраических уравнений, 25.48kb.
• Точные решения некоторых нелинейных эволюционных уравнений, встречающихся при описании, 28.05kb.
• Удк 519. 6 Механизмы управления длиной шага в параллельных алгоритмах решения дифференциальных, 40.83kb.
• Методические рекомендации к проведению урока: «Методы решения уравнений и неравенств., 15.21kb.

УДК 519.615.5


ДОСТАТОЧНЫЕ УСЛОВИЯ КОРРЕКТНОСТИ
МЕТОДА МАТРИЧНОЙ ПРОГОНКИ٭

^


Е.А. Васильева


Метод матричной прогонки является одним из широко применяемых точных методов решения систем уравнений с блочными матрицами ленточной структуры. В статье сформулированы и доказаны более общие условия корректности метода матричной прогонки, сводящиеся к проверке существования обычного LU - разложения для матрицы Якоби, элементами которой являются значения матричных норм для блоков исходной матрицы системы уравнений.


метод матричной прогонки, полное блочное разложение


Одним из методов решения систем алгебраических уравнений является метод Гаусса или, как его вариант, LU-разложение. Если разбить матрицу системы на блоки, то можно построить блочное LU-разложение, которое мы в дальнейшем будем называть полным разложением.

Пусть матрица системы уравнений

K u = f (1)

имеет вид

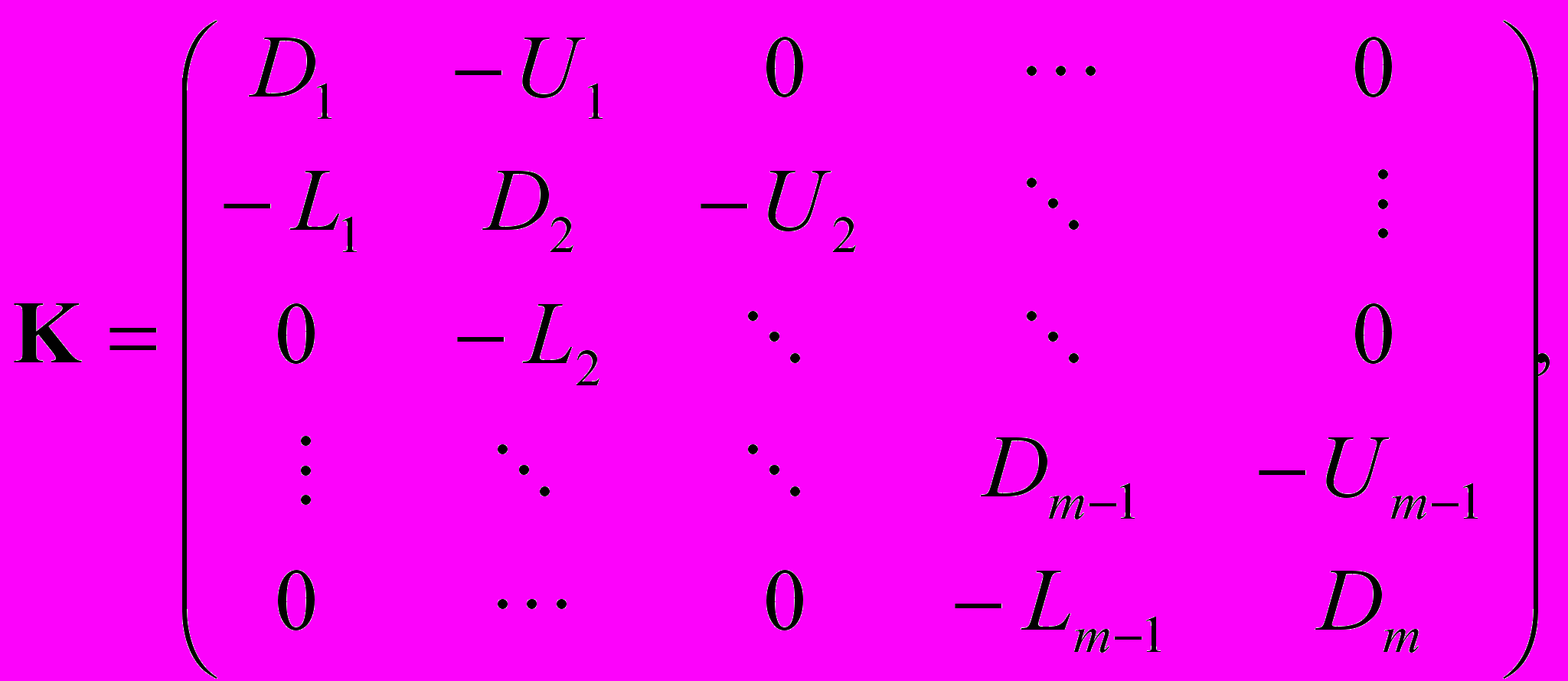(2)


где L_i-1, D_i, U_i . Тогда полное блочное разложение матрицы K, если оно существует, можно представить в виде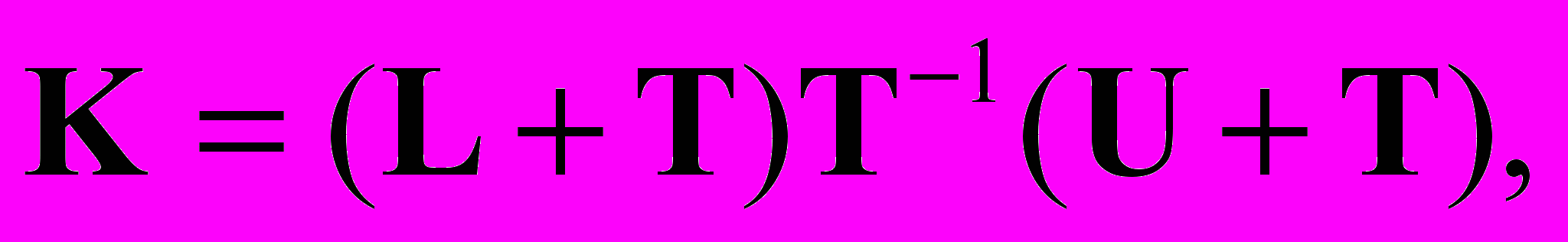

(3)

где L = blocktridiag{-L_i, 0, 0}; U = blocktridiag{0, 0, -U_i}; T = blockdiag{T_i}. Приравнивая соответствующие блоки в левой и правой части (3), получим выражения для блоков полного блочного разложения T_i

(4)

Если ввести обозначение



то процесс решения системы (1) разбивается на два этапа:



Покомпонентно каждый из них можно записать в следующем виде:

для вычисления  последовательно выполняются действия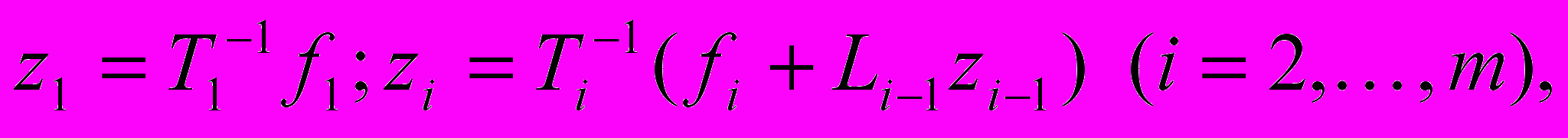

(5)

а для вычисления можно воспользоваться следующими рекуррентными формулами: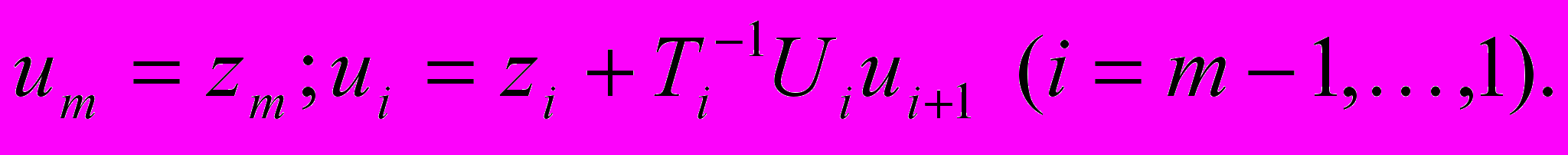

(6)

Отсюда видно, что для решения системы уравнений (1) нам требуется уметь вычислять не саму матрицу , а ее произведение на вектор. С полным блочным разложением тесно связан метод матричной прогонки (напр., [1, 2]), алгоритм которого можно записать в следующем виде.

Алгоритм матричной прогонки. Пусть требуется решить систему линейных алгебраических уравнений с блочной трехдиагональной матрицей вида (2)

(Ku)_i = -L_i-1 u_{i -1} + D_iu_i  U_iu_i+1 = f_i (i = 1,…, m); L_m = U_m = 0 . (7)

Здесь u_i и f_i  суть подвекторы в общем случае различных порядков n_i. Тогда решение этой системы уравнений находится рекуррентно по формулам



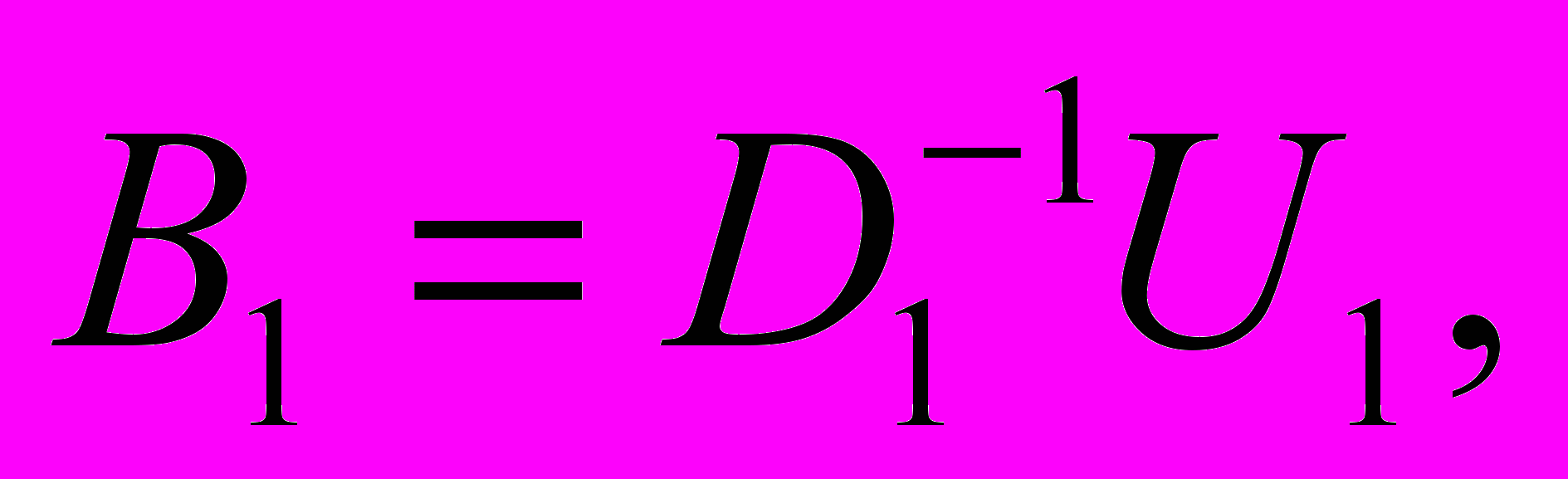
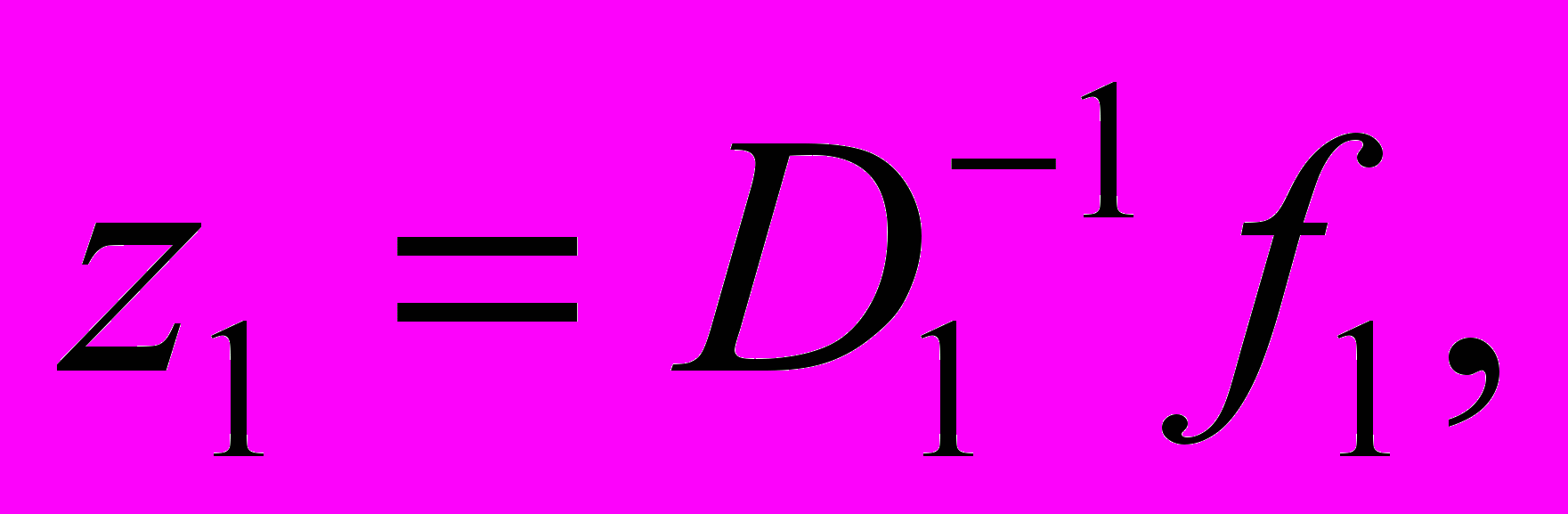
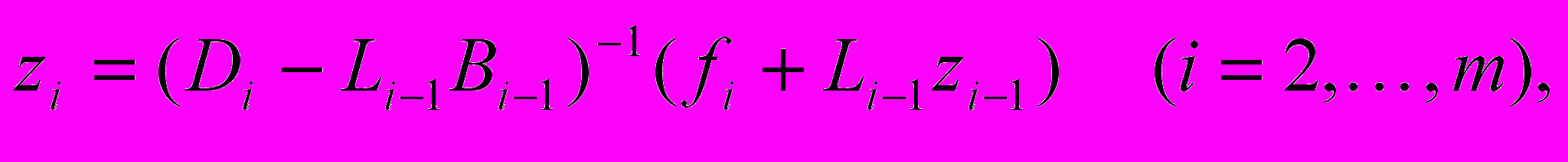(8)



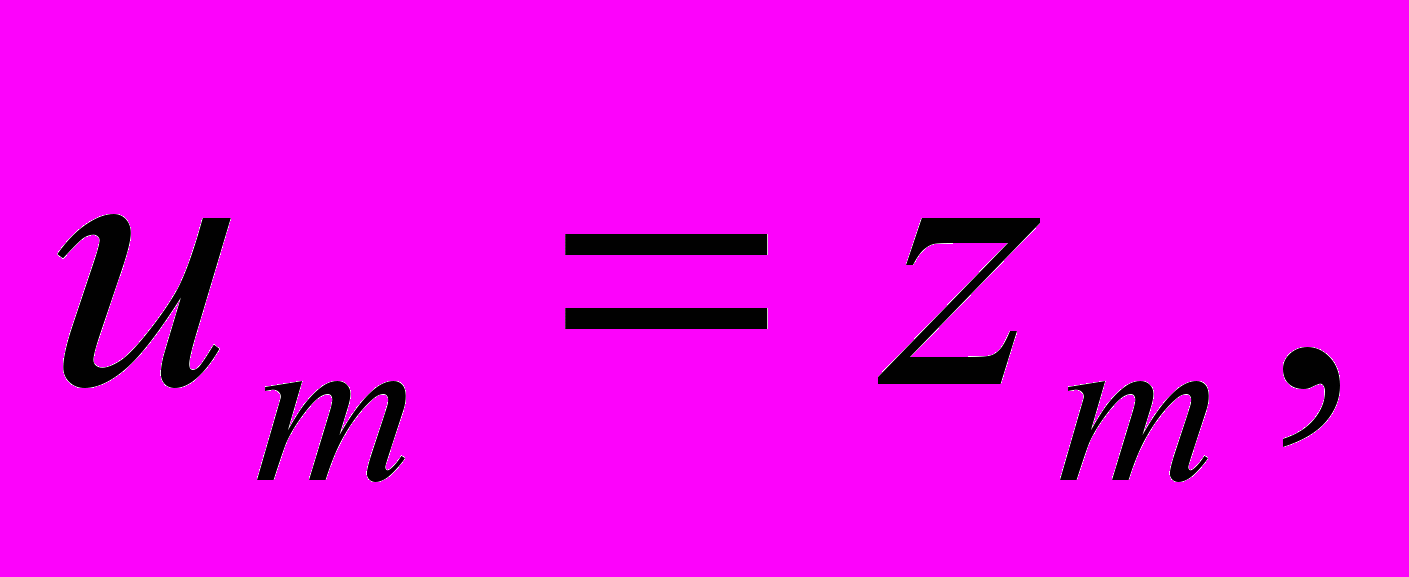
Матрицы B_i обычно называют прогоночными коэффициентами.

Перепишем выражение для z_i из (8) в виде



Тогда, если сравнить его с выражением для z_i из (5) и выражениями для  u_i из (6) и (8), можно сделать вывод, что матричные прогоночные коэффициенты B_i и матрицы T_i полного блочного разложения связаны простым соотношением

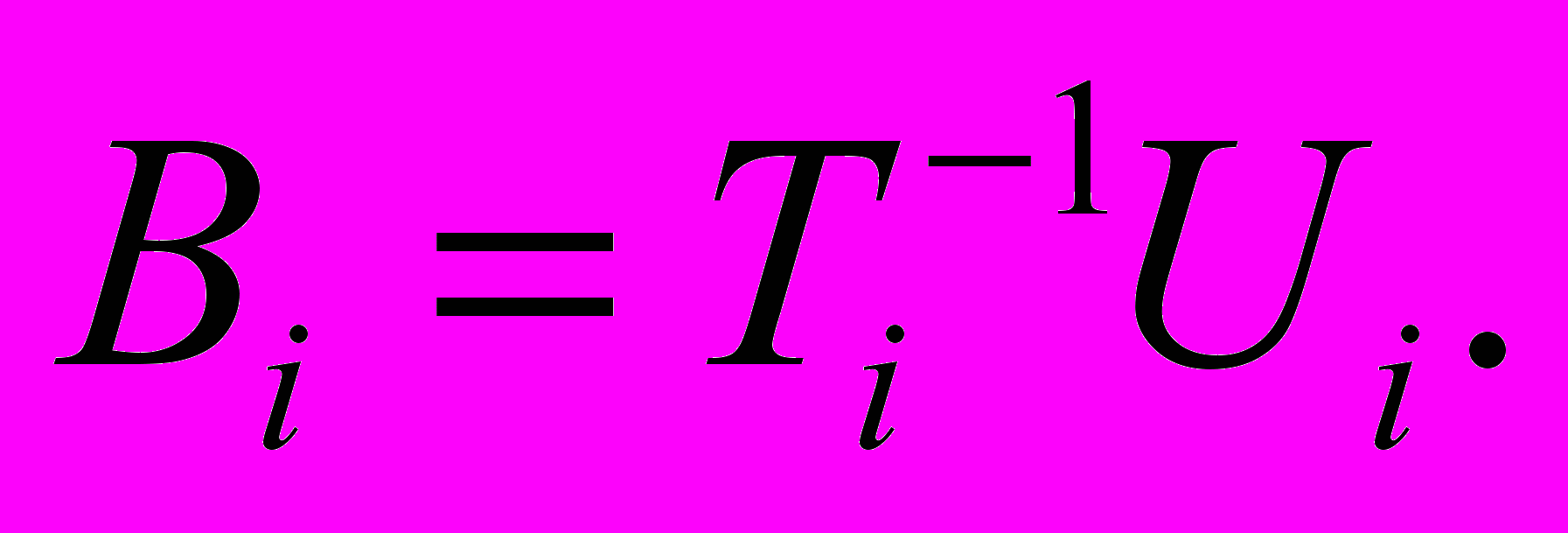(9)

Тогда метод матричной прогонки (8) в матричном виде можно записать как

(L + T)z = f; (I + B)u = z,

откуда видно, что вспомогательный вектор z в обоих случаях один и тот же. Поэтому полное блочное разложение можно рассматривать как один из вариантов метода матричной прогонки (или наоборот). В связи с этим, вопрос существования полного блочного разложения (невырожденности матриц T_i) однозначно связан с обоснованием корректности метода матричных прогонок (существованием B_i).

Наиболее общим условием существования полного блочного разложения для матрицы K является отличие от нуля всех ее главных миноров. Однако это условие является трудно проверяемым. Поэтому на практике предпочтение отдают условиям, сформулированным в следующей теореме (напр., [2]), которые для скалярных трехдиагональных матриц соответствуют условию (слабого) диагонального преобладания.

Теорема 1 (Самарский). Если D_i для 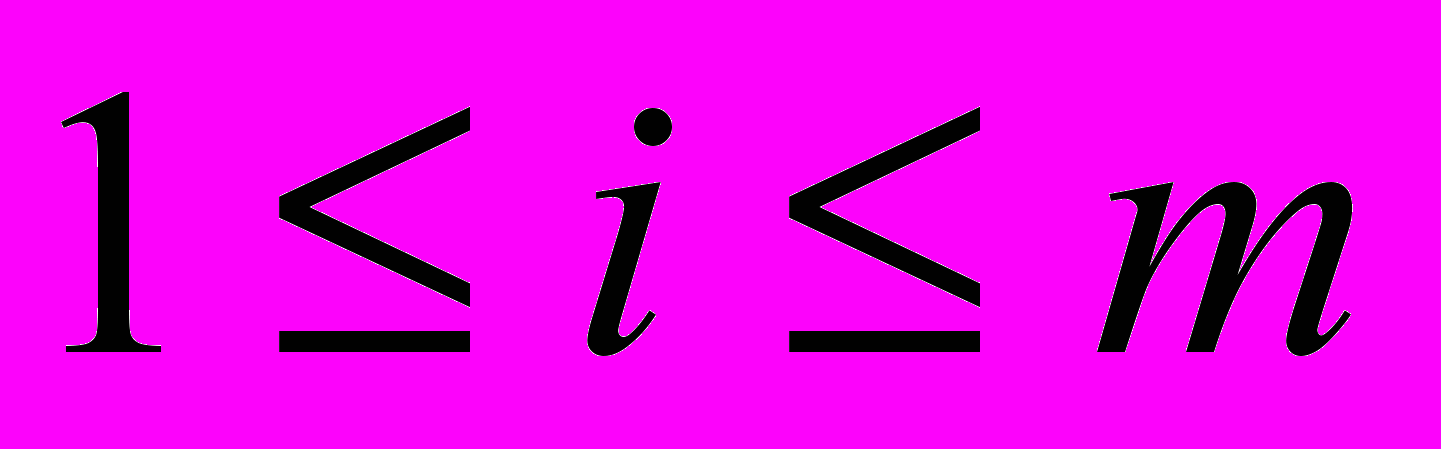– невырожденные матрицы, а L_i и U_i  - ненулевые матрицы, для которых выполнены условия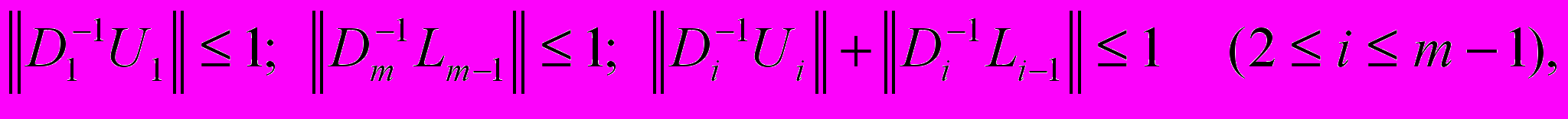



где   некоторая матричная норма, причем хотя бы в одном из неравенств имеет место строгое неравенство, то алгоритм метода матричной прогонки корректен.

Эта теорема имеет следующий недостаток: если рассмотреть трехдиагональную матрицу , которая получается из K заменой блоков L_i   L_i и 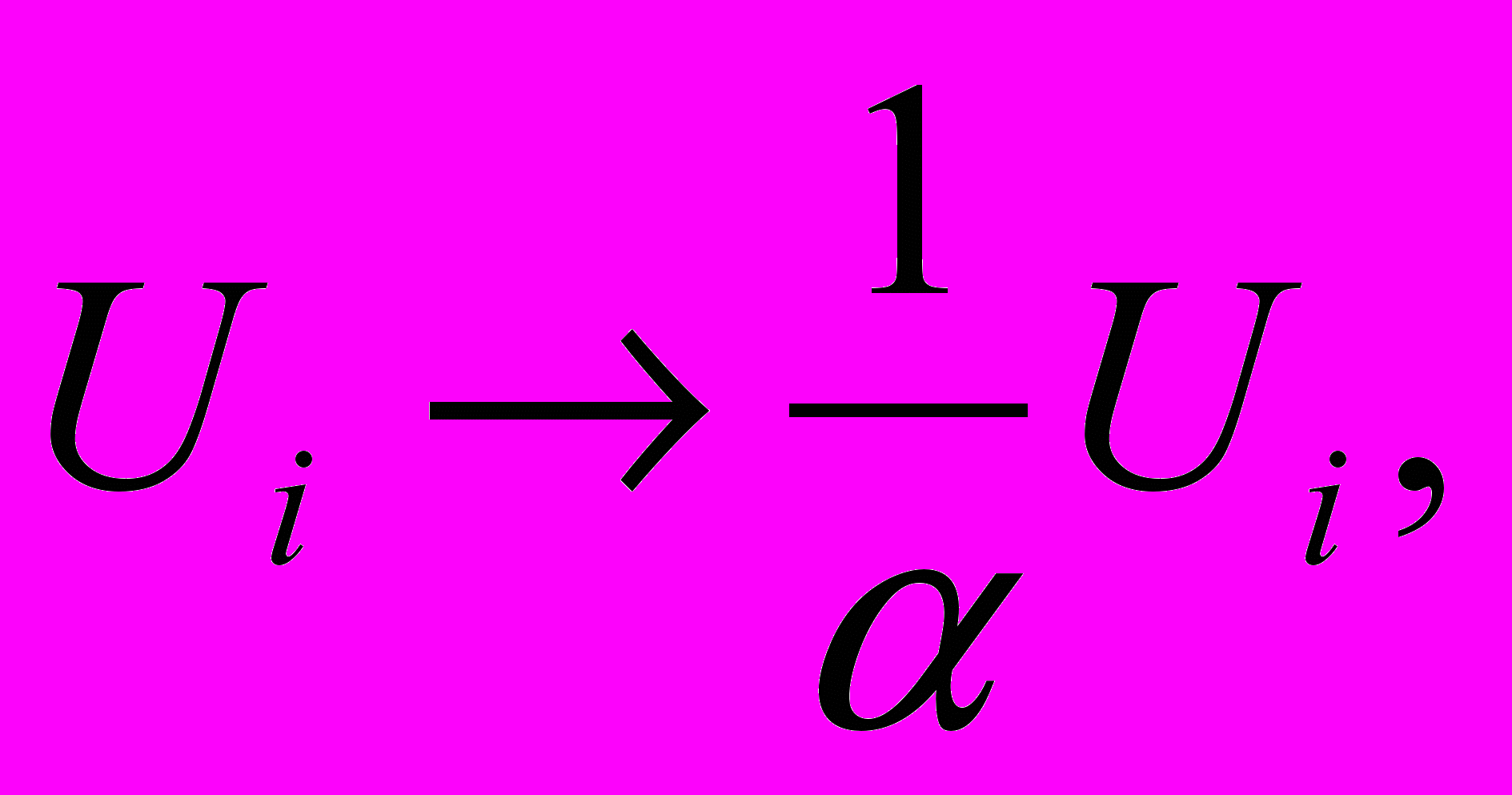 то выражения для блоков ее полного блочного разложения (4) будут такими же, как для матрицы K, а условия теоремы 1 при достаточно больших  могут не выполняться. Частично этот недостаток исправлен в следующей теореме (см. [3]).

Теорема 2 (Джангава). Пусть матрицы B_i определяются соотношениями (8) и пусть выполняются условия



Тогда алгоритм матричной прогонки корректен, а для прогоночных коэффициентов справедливы неравенства



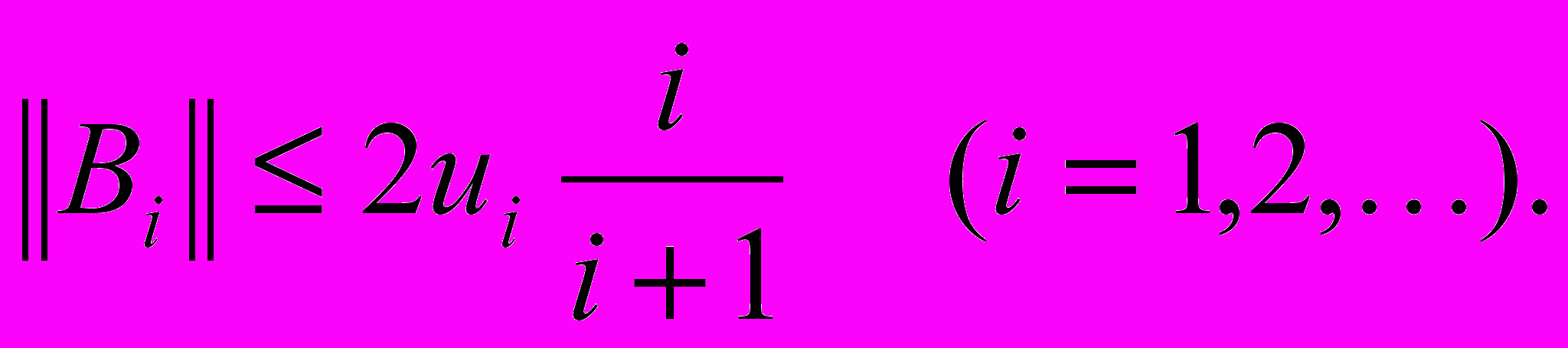
Сформулируем и докажем новую теорему, обобщающую теоремы 1-2 и гарантирующую существование полного блочного разложения при условии существования обычного LU – разложения для некоторой трехдиагональной матрицы Якоби.

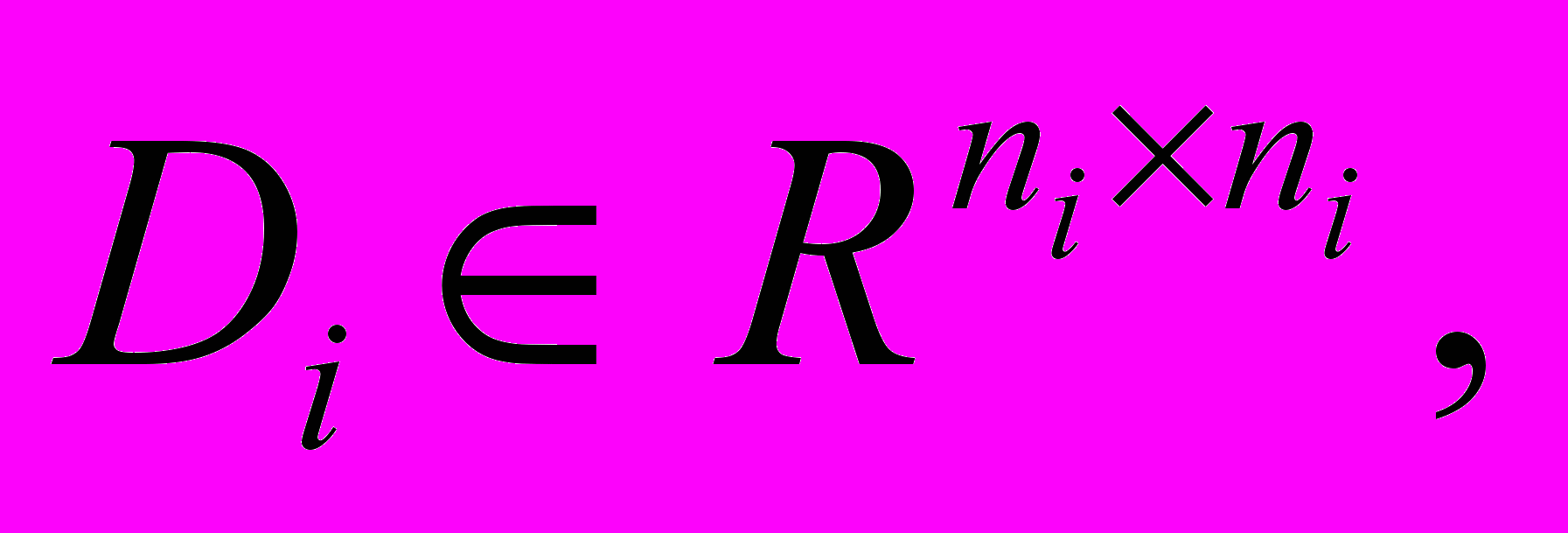
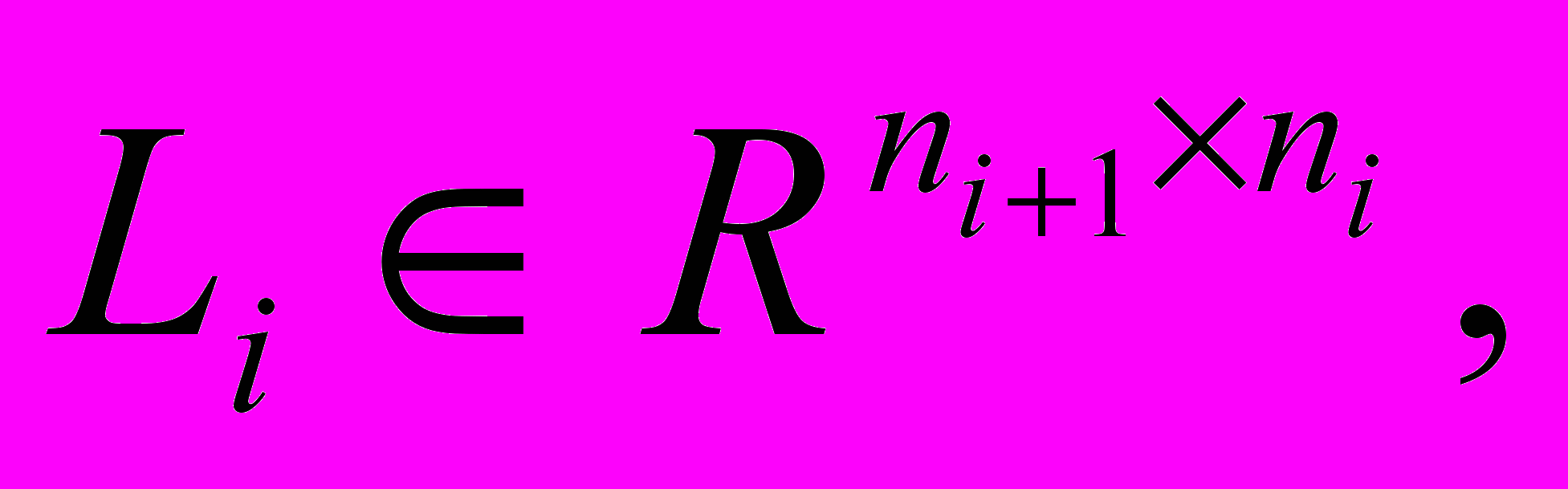
Теорема 3. Пусть матрица системы K имеет вид (2), где блоки регулярные. Обозначим через какую - либо из матричных норм, а через



Пусть также для матрицы Якоби J¹




существует LU - разложение J = L D ^1 U, а для элементов d_i диагональной матрицы D выполняются условия

(i > 1). (10)

Тогда для любой блочно - трехдиагональной матрицы вида (2) существует ее полное блочное разложение (3). Матрица K регулярная. Блоки T_i полного блочного разложения удовлетворяют следующей оценке:

(11)

а для коэффициентов матричной прогонки B_i будет справедлива следующая оценка:

(12)

Доказательство. Покажем индуктивно, что блоки T_i регулярные и что они удовлетворяют оценке (11). При i = 1 утверждения верны. По индуктивному предположению блоки T_i-1 регулярные и выполняется неравенство 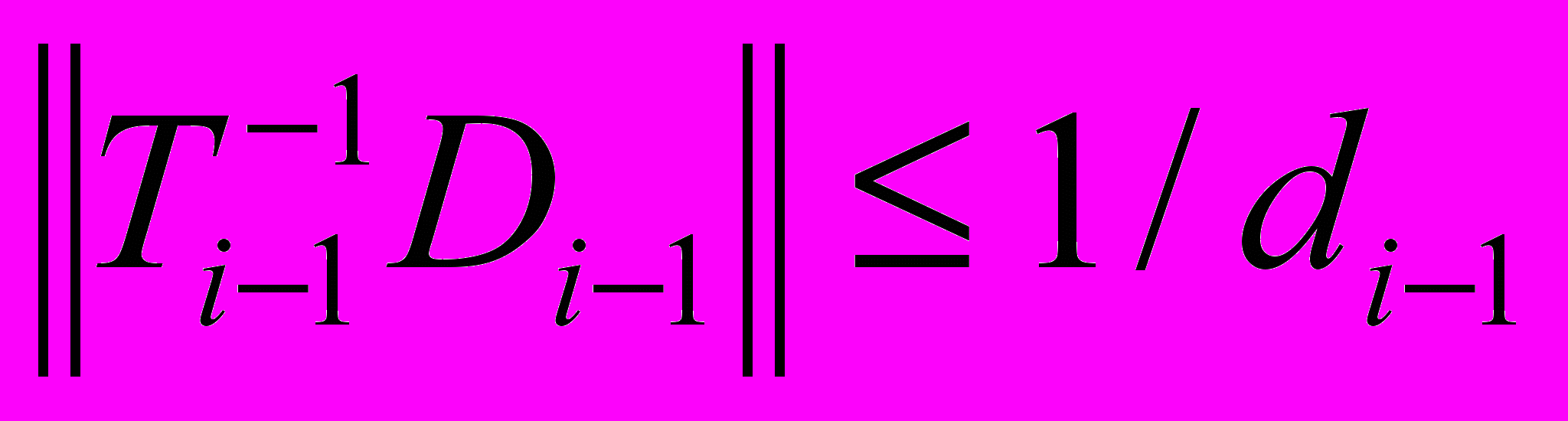. Следовательно,

(13)

В силу (10) справедливы неравенства _i-1 _i-1 / d_i-1 < 1, поэтому матрица 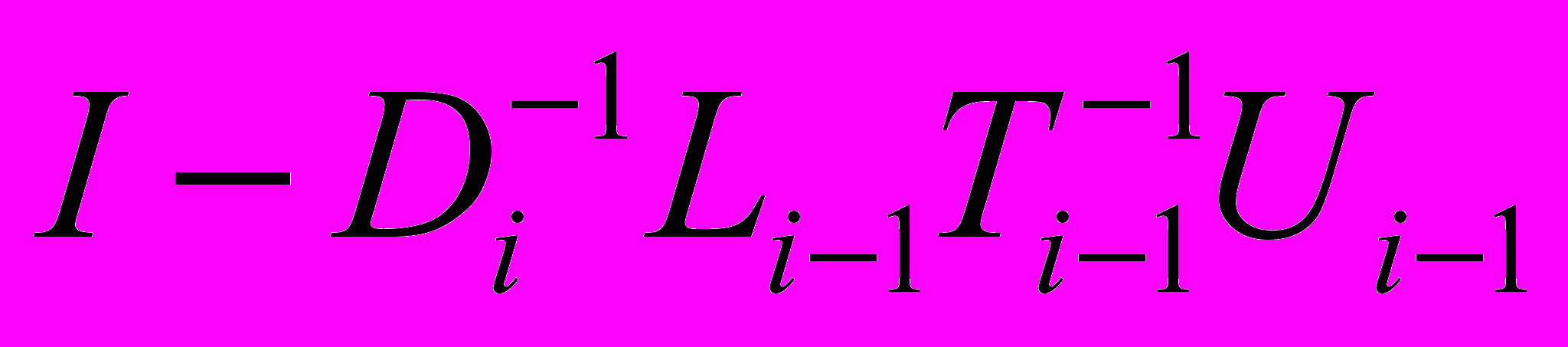 регулярная. Так как блоки D_i регулярные, регулярными будут и матрицы .

Так как любая матрица A, для которой ||A|| < 1 удовлетворяет неравенству 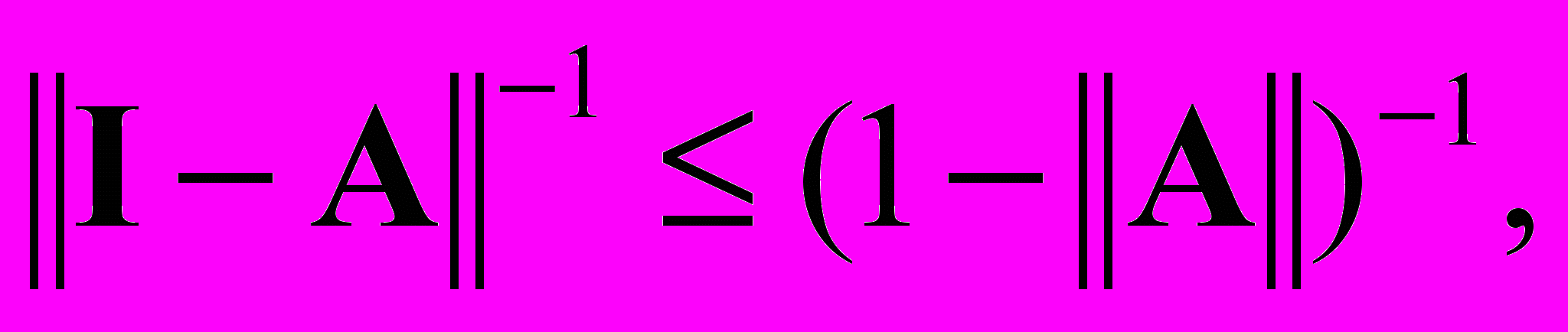 то оценка (11) будет следовать из

.

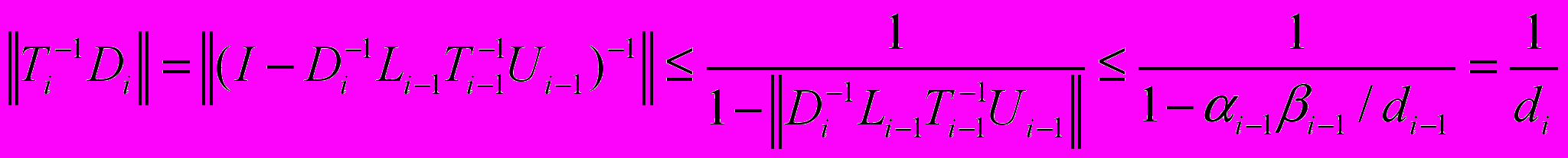Воспользовавшись этим результатом, покажем справедливость оценки (12):



Замечание. Пусть а также выполнено условие (10). Тогда можно аналогично доказательству теоремы 3 показать, что блоки T_i полного блочного разложения регулярные и удовлетворяют оценке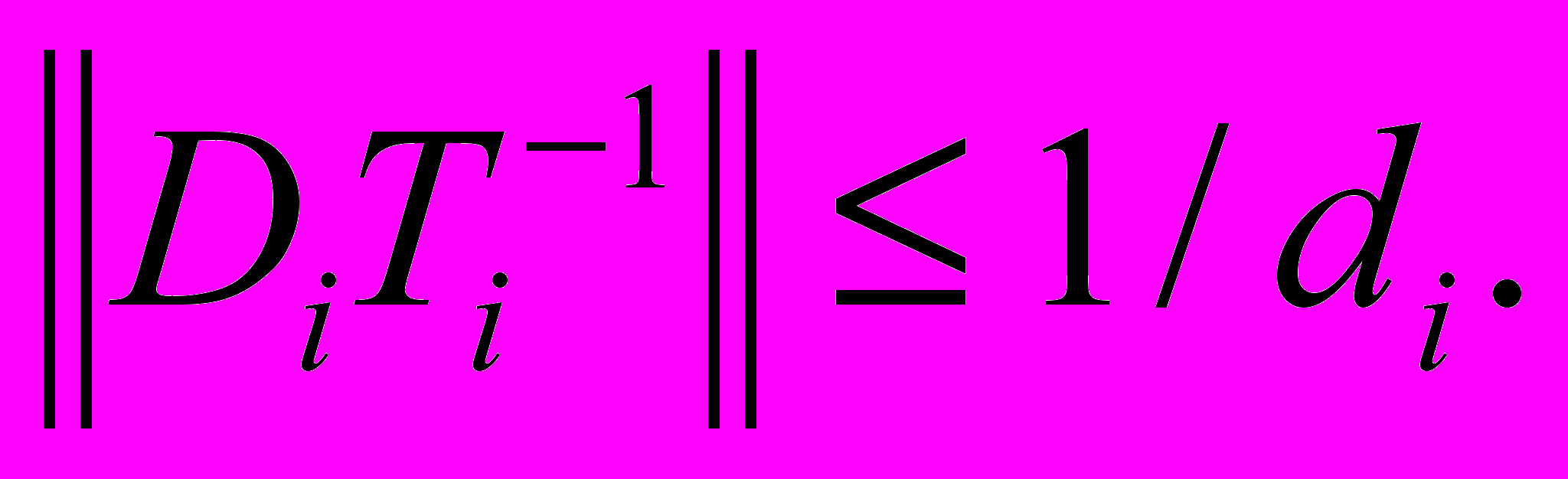 

Мы видим, что теорема 3 действительно является обобщением теоремы 2. В самом деле, пусть для матрицы K выполнены условия теоремы 2. Покажем по индукции справедливость в этом случае следующего неравенства:



При i = 1 индуктивное предположение выполняется, так как d₁ = 1. Пусть для i = k - 1 неравенство выполняется: 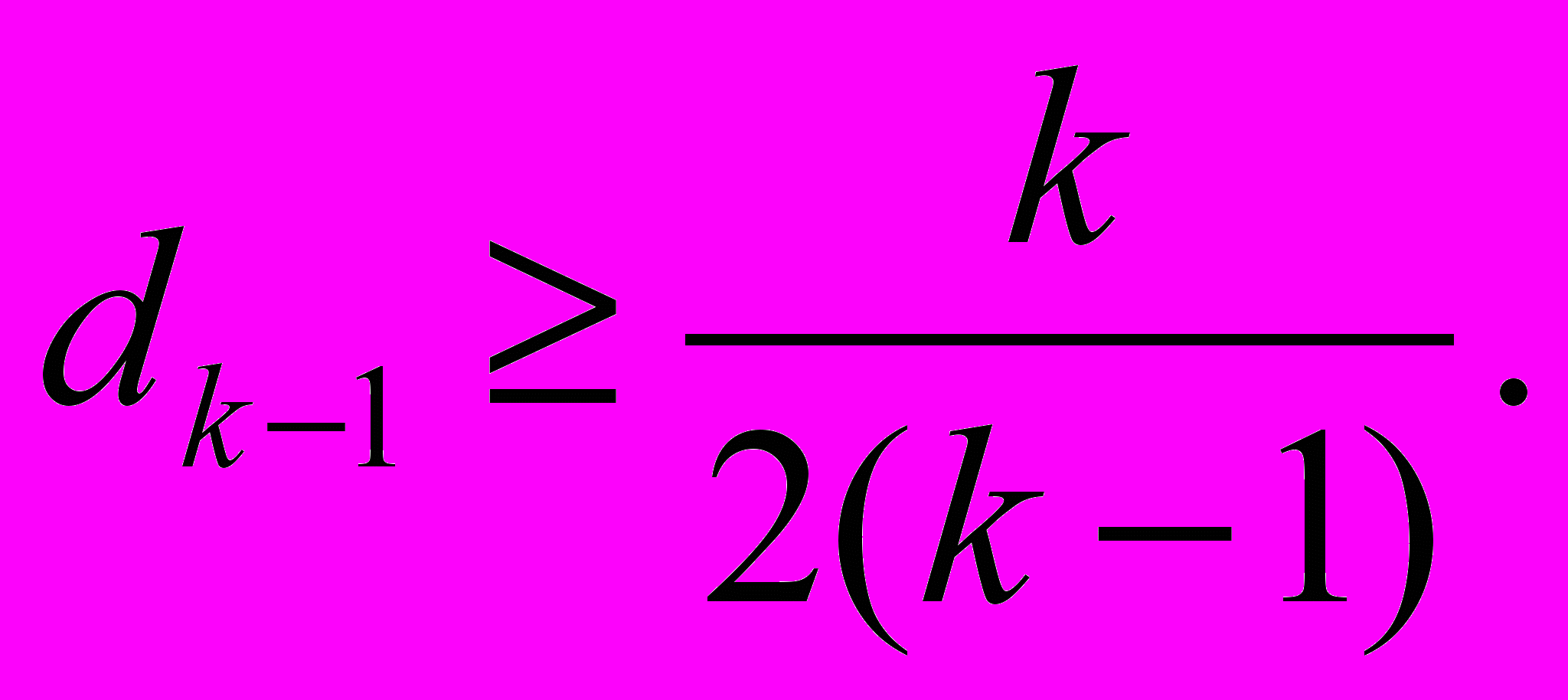Тогда из условия теоремы 2 и индуктивного предположения следует, что



Отсюда и из оценки (12) следует справедливость теоремы 2.

Для более частного вида матрицы K условия теоремы 3 можно сформулировать следующим образом.

Теорема 4. Пусть матрица системы K имеет вид

(14)


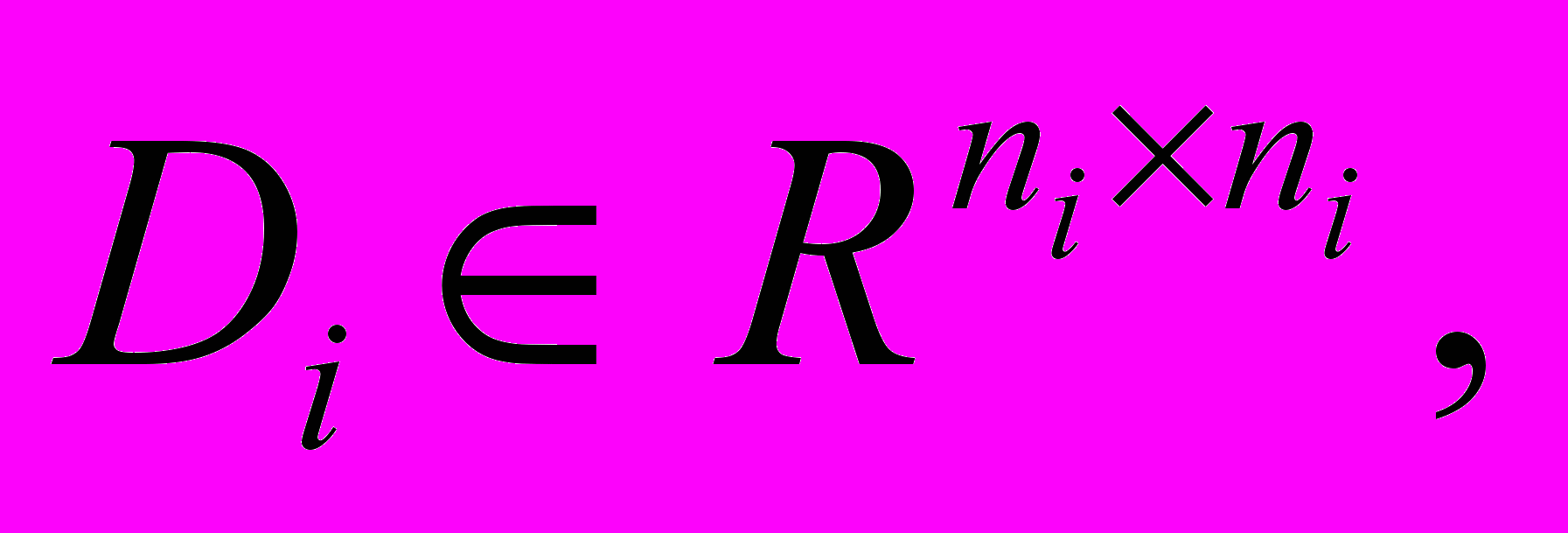
где 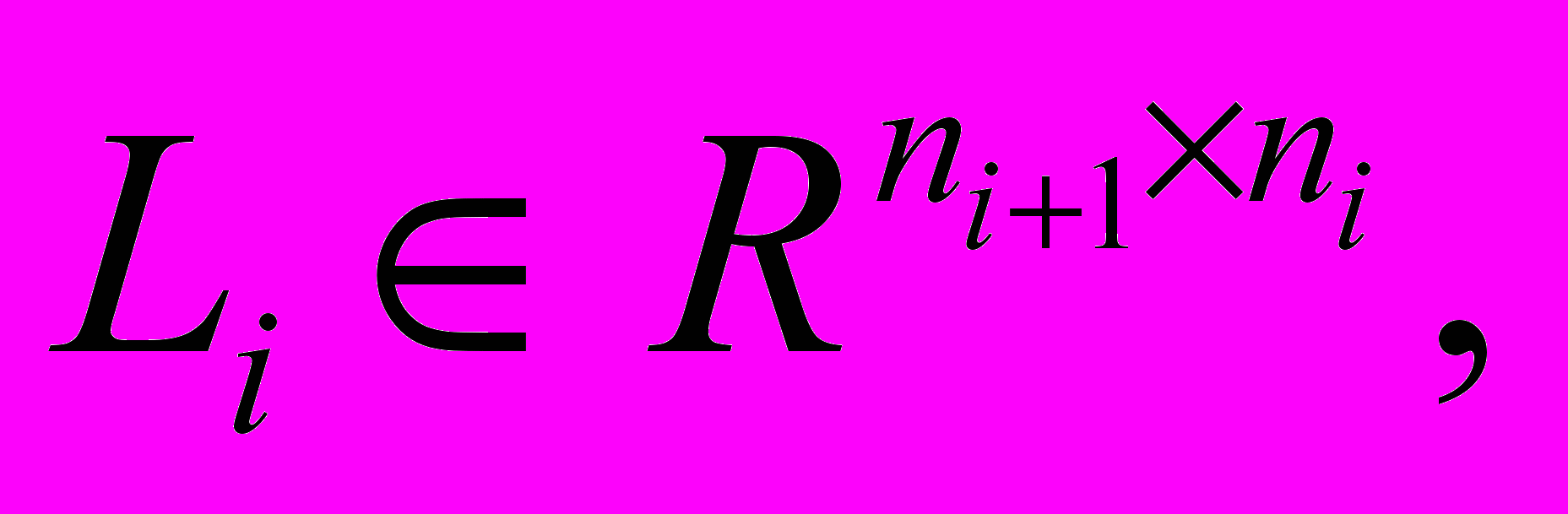D_i > 0. Обозначим через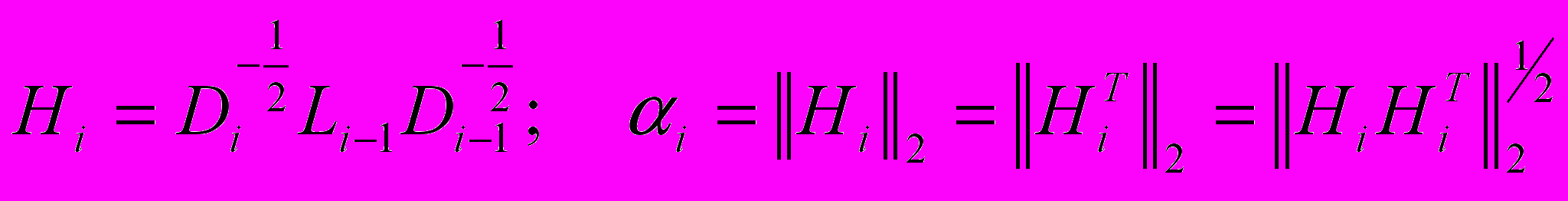



и построим трехдиагональную матрицу Якоби J = tridiag{_i-1, 1, _i}. Обозначим через d_i элементы диагональной матрицы D LU - разложения

J = L D^{ -1} L^T.

Эти элементы удовлетворяют следующей рекурсии:

d₁ = 1 ; (15)

Для любой блочной трехдиагональной матрицы вида (14) при условии, что J > 0, существует полное блочное разложение

(16)

Матрица K положительно определена. Блоки полного блочного разложения T_i удовлетворяют следующей оценке:

T_i  d_i D_i, (17)

где d_i из (15).

Доказательство. Так как матрица J положительно определена, все элементы d_i > 0. Предположим далее, что справедлива оценка (17). Тогда в силу того, что D_i > 0, будет следовать, что K > 0. Поэтому остается доказать лишь оценку (17).

Блоки T_i удовлетворяют следующей рекурсии:

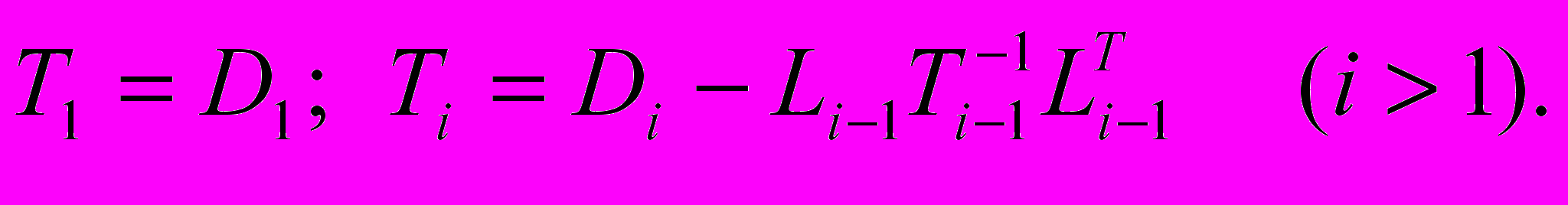(18)

Первое равенство позволяет утверждать, что при k = 1 неравенство (17) выполняется.

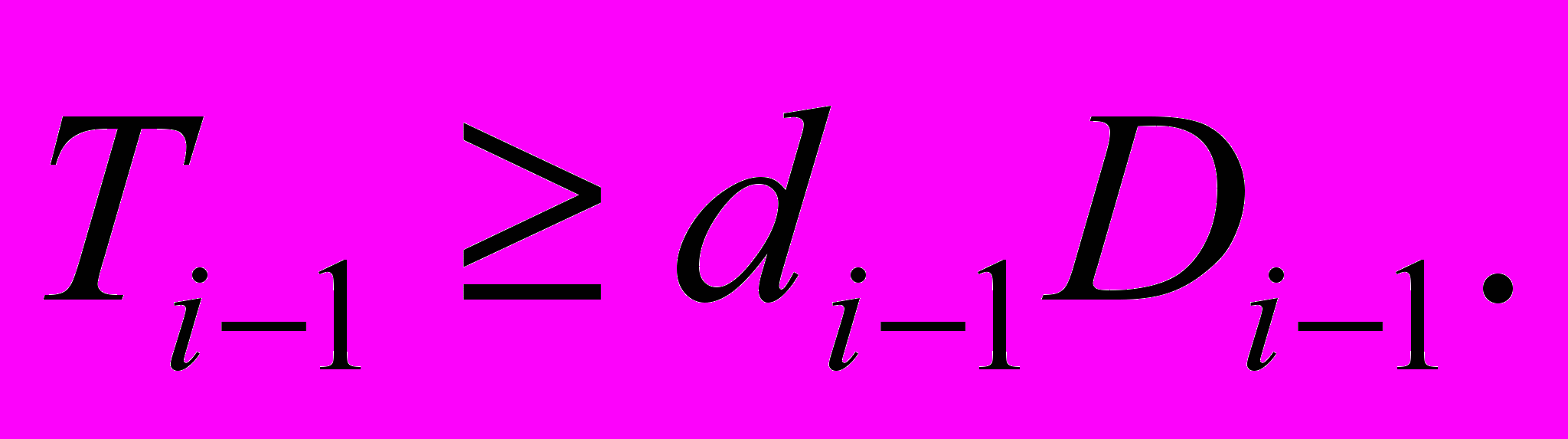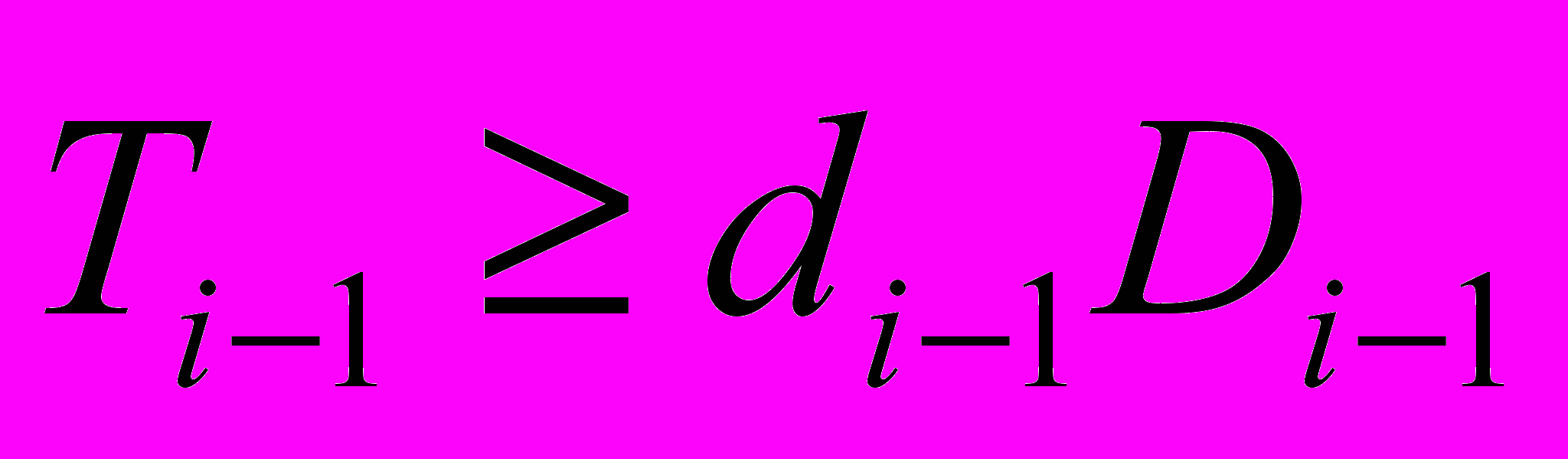В силу индуктивного предположения при k = i - 1 справедливы неравенства Так как для любой положительно определенной матрицы A из неравенства A   I следует , то из неравенств следует выполнение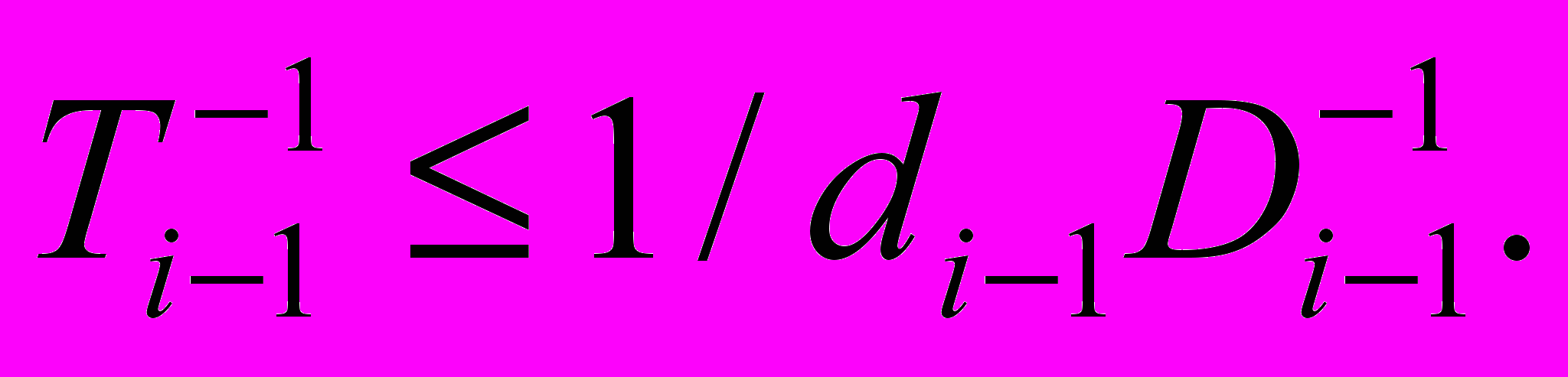

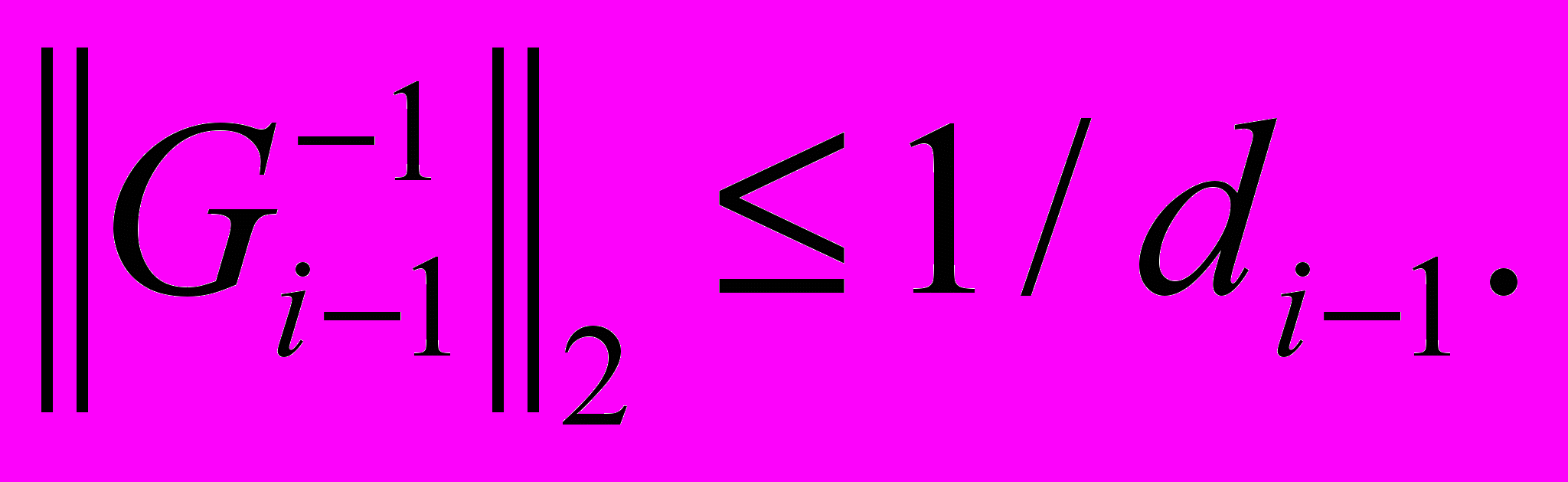Воспользовавшись обозначением последние неравенства можно переписать в виде откуда следует Учитывая эти неравенства и равенства (15), получим



СПИСОК ИСПОЛЬЗОВАННЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ


1. Ильин В.П. Методы конечных разностей и конечных объемов для эллиптических уравнений. – Новосибирск: Изд-во Института математики, 2000. – 344 c.

2. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений.– М.: Наука, 1978. – 591 с.

3. Джангава П.В. Об одном свойстве коэффициентов метода прогонки // Труды Вычислительного центра ГрАН СССР. – Тбилиси, 1976.

4. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления.– М.: Наука, 1984. – 318 c.


AMPLE CONDITIONS OF EXISTENCE OF THE COMPLETE
BLOCK DECOMPOSITION


E.A. Vasilieva


The method of the complete block decomposition is one of the popular exact methods of solution of the systems of equations with block matrices with belt structure. There are some conditions of existence of this method (e.g. [1-3]). In this article have been formulated and proved more general conditions of the existence of the complete block decomposition, that come to the testing of existence of the usual LU - decomposition of the Jacobi matrix, which elements are values of matrix norms for the blocks of the initial matrix of the system of equations.


complete block decomposition