Для решения систем линейных алгебраических уравнений с ленточной матрицей, с понятием сплайна, получение навыков решения задач вычислительной математики на ЭВМ

Вид материала

Содержание

2 Описание метода
Алгоритм построения интерполяционного кубического сплайна
8(n-1) арифметических операций: 3(n-1)

Подобный материал:

Министерство образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Лабораторные работы №1

ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ С ПОМОЩЬЮ СПЛАЙНА

Выполнила студентка

группы ВМ-226 т:

Курамшина А.Р.

Проверил

преподаватель:

Шерыхалина Н.М.

Уфа 2006

1 Цель работы:

Целью работы является ознакомление студентов с задачей интерполяции функций, с методом прогонки для решения систем линейных алгебраических уравнений с ленточной матрицей, с понятием сплайна, получение навыков решения задач вычислительной математики на ЭВМ.

2 Описание метода:

Пусть отрезок [a,b] разбит на n равных частей [x_i, x_i+1], где x_i=a+ih, i=0,...,n, x_n=b, h=(b-a)/n.

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a,b], а на каждом частичном отрезке [x_i, x_i+1] в отдельности является некоторым алгебраическим многочленом.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной - дефектом сплайна.

Определение. Функция S_n_,_(x) называется сплайном степени n дефекта  (-целое число, 0n+1) с узлами на сетке  (: a=x₀< _i<..._n=b), если:

а) на каждом отрезке [x_i,x _i+1] функция S_n,_ (x) является многочленом степени n, то есть

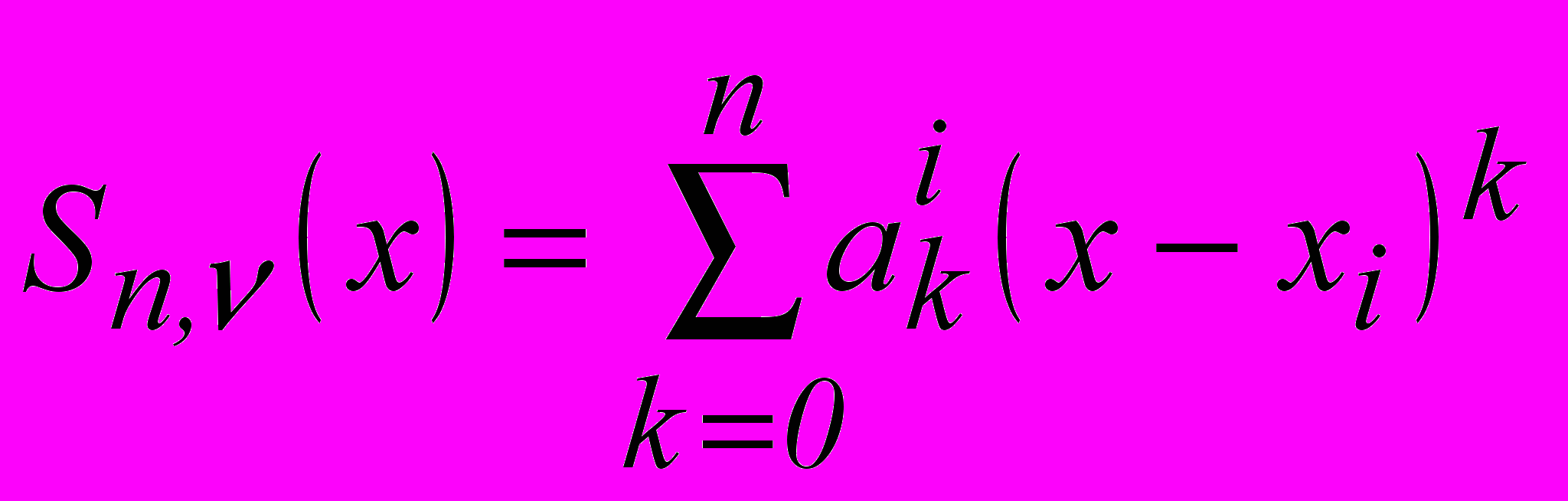для x[x_i, x_i+1] , i=0,...,n-1;

б) S_n_,_(x)Cⁿ^-^v[a,b]

(для целого k>0 через C^k =C^k[a,b] обозначается множество k раз непрерывно дифференцируемых на [a,b] функций).

Интерполяция сплайном

На практике широкое распространение получили сплайны третьей степени, имеющие на [a,b] непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими и обозначаются S₃(x) (без указания дефекта).

Пусть на отрезке [a,b] в узлах сетки  заданы значения некоторой функции

f_i =f(x_i), i=0,...,n.

Интерполяционным кубическим сплайном S₃(x) называется сплайн

S₃(x)=а_i0 +а_i1(x - x_i)+а_i2(x - x_i)² +а_i3(x - x_i)³, x[x_i, x_i+1], (1.1)

удовлетворяющий условиям

S₃(x_i)=f(x_i), i=0,...,n. (1.2)

Сплайн (1.1) на каждом из отрезков [x_i, x_i₊₁], i=0,...,n-1 определяется четырьмя коэффициентами, и поэтому для его построения на всем промежутке [a,b] необходимо определить 4n коэффициентов. Для их однозначного определения необходимо задать 4n уравнений.

Условие (1.2) дает 2n уравнений, при этом функция S₃(x_i), удовлетворяющая этим условиям, будет непрерывна во всех внутренних узлах.

Условие непрерывности производных сплайна , r=1,2 во всех внутренних узлах x_i, i=1,...,n-1 сетки  дает 2(n-1) равенств.

Вместе получается 4N-2 уравнений.

Два дополнительных условия обычно задаются в виде ограничений на значение производных сплайна на концах промежутка [a,b] и называются краевыми условиями.

Наиболее употребительны следующие типы краевых условий:

а) S'₃(а)=f'(а), S'(b)=f'(b) ;

б) S"₃(а)=f"(а), S"(b)=f"(b) ;

в) ;

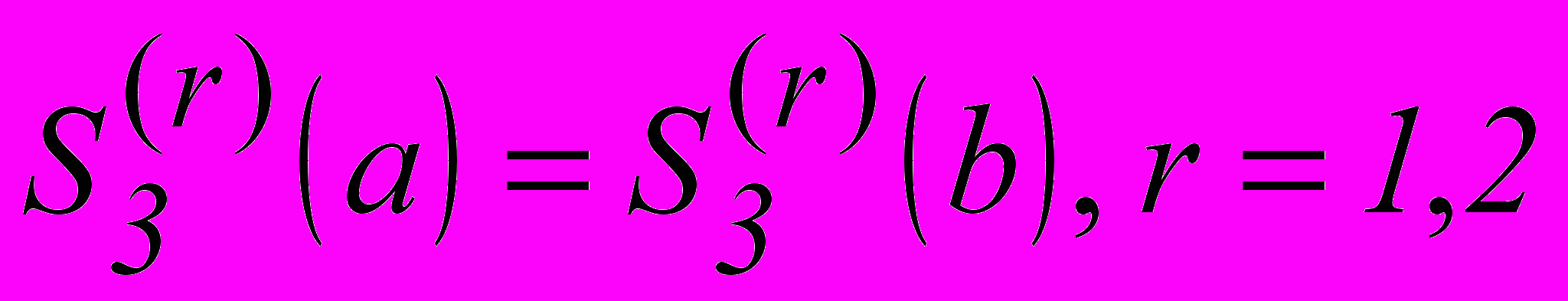г) S'''₃(x_p₊₀)=S'''₃(x_p_-0), р =1, n-1.

Через краевые условия в конструкцию сплайна включаются параметры, выбирая которые можно управлять его поведением, особенно возле концов отрезка [a,b].

Условия типа в) носят названия периодических. Естественно требовать их выполнения в том случае, когда интерполируемая функция периодическая с периодом (b-a).

Если известны f'(x) или f"(x) в точках а и b, то естественно воспользоваться краевыми условиями типа а) или б).

Если производные неизвестны, то в большинстве случаев наилучшим решением будет применение краевых условий типа г).

Вместо значений производных можно использовать их разностные аналоги. При этом точность интерполяции вблизи концов падает.

Иногда предлагается принимать

S"₃(а)=S"₃(b)=0 .

В этом случае вблизи концов точность интерполяции функции и ее первой производной уменьшается и становится соизмеримой с точностью интерполяции сплайном первой степени, что резко ухудшает всю картину.

Алгоритм построения интерполяционного кубического сплайна

Пусть каждому значению аргумента x_i, i=0,...,n соответствуют значения функции f(x_i)=y_i и требуется найти функциональную зависимость в виде сплайна (1.1), удовлетворяющего перечисленным ниже требованиям:

а) функция S₃(x_i) непрерывна вместе со своими производными до второго порядка включительно;

б) S₃(x_i)=y_i, i=0,1,...,n;

в) S"₃(x₀)=S"₃(x_n)=0.

Сформулированная выше задача имеет единственное решение.

Вторая производная S"₃(x) непрерывна и, как видно из выражения (1.1), линейна на каждом отрезке [x_i-1, x_i], (i=1,...,n), поэтому представим ее в виде

, (1.4)

где h_i = x_i- x_i-1 , m_i= S"₃(x_i).

Интегрируя обе части равенства (1.4), получим

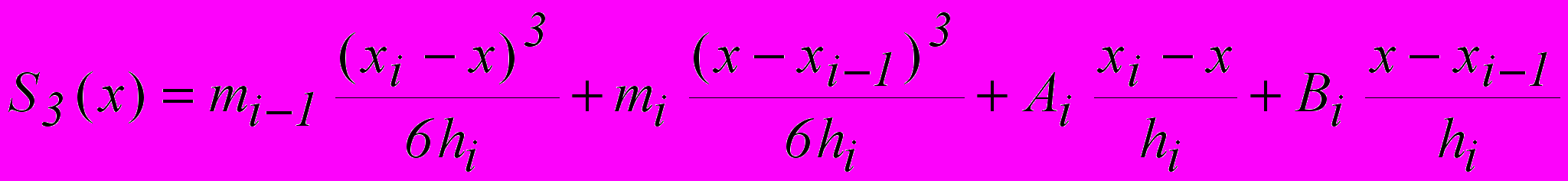, (1.5)

где A_i и B_i - постоянные интегрирования.

Пусть в (1.5) x=x_i и x=x_i_-1, тогда используя условия б), получим

, i=1,...,n.

Из этих уравнений находим A_i и B_i, и окончательно формула (1.5) принимает вид

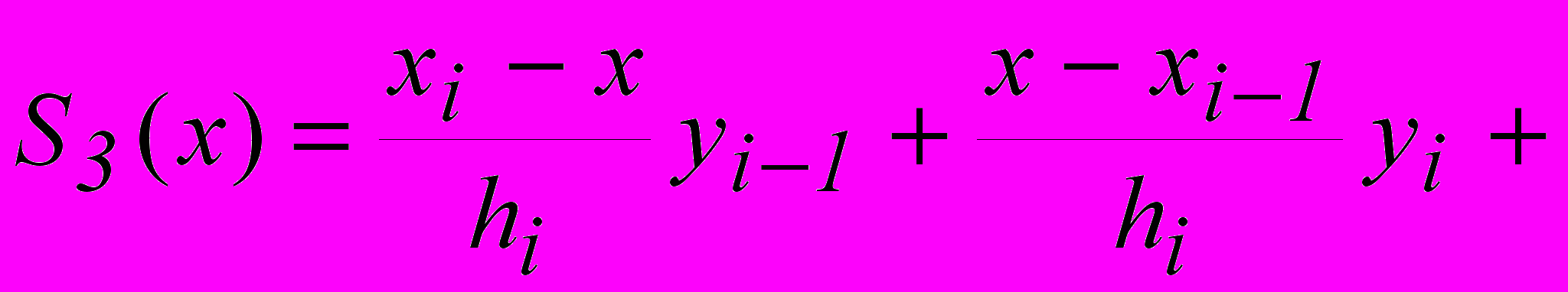
. (1.6)

Из формулы (1.6) находим односторонние пределы производной в точках x₁,x₂ ,...,x_n_-1:

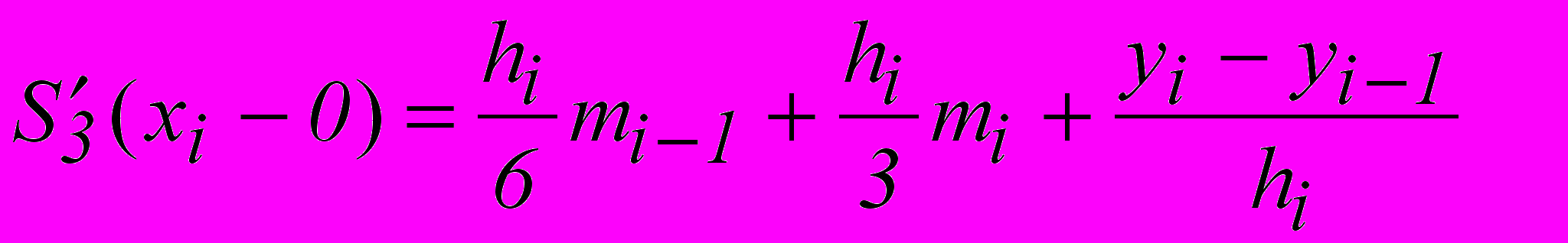, (1.7)

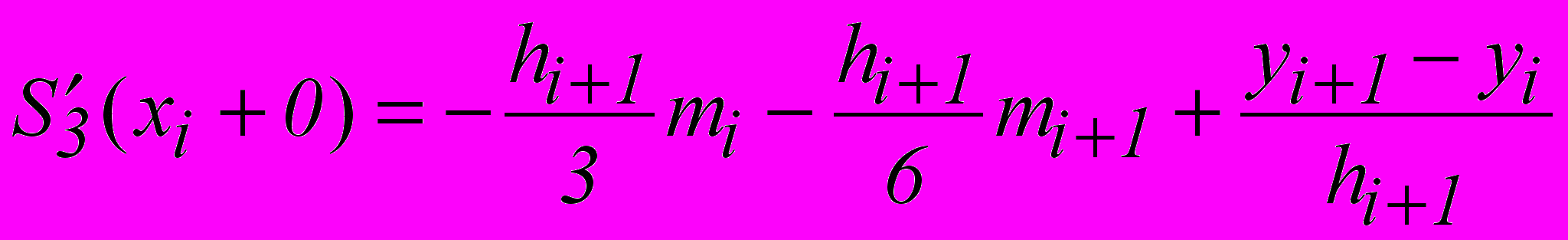. (1.8)

Приравнивая выражения (1.7) и (1.8) для i=1,...,n-1, получим n-1 уравнение

(1.9)

с n-1 неизвестными m_i (i=1,...,n-1). Согласно условию (1.4) m₀=m_n=0.

Система линейных алгебраических уравнений (1.9) имеет трехдиагональную матрицу с диагональным преобладанием. Такие матрицы являются неособенными. Поэтому неизвестные m₁, m₂, ... , m_n_-1 находятся из системы (1.9) однозначно. Они могут быть найдены итерационными и прямыми методами решения систем линейных алгебраических уравнений, в том числе и методом прогонки. После определения m_i функция S₃(x) восстанавливается по формуле (1.6).

Метод прогонки

Пусть имеется система уравнений, записанная в матричном виде:

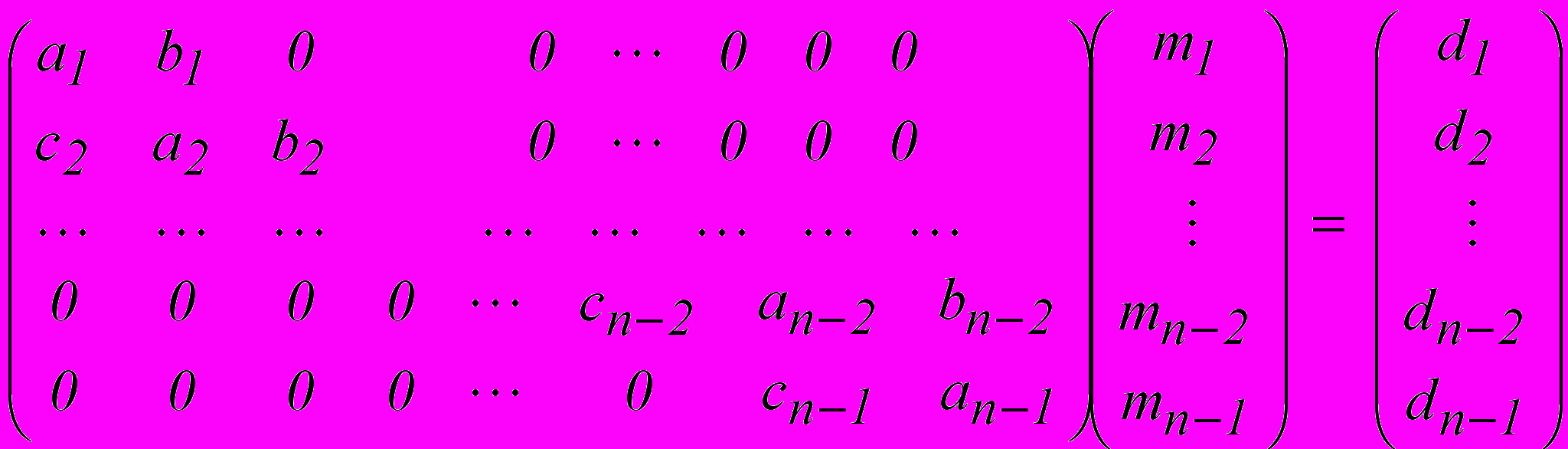. (1.10)

В нашем случае согласно (1.9)

Решение системы ищется в виде

m_i = _i m_i₊₁ + _i , i=1,...,N-1, (1.11)

где A_i , B_i - прогоночные коэффициенты. Используя выражение для m_i-1 из (1.11), исключим это неизвестное из i го уравнения системы. Получаем

(a_i +c_i _i-1)m_i + b_i m_i+1 = d_i -c_i_i-1.

Сравнивая это соотношение с (1.11), выводим рекуррентные формулы для прогоночных коэффициентов _i, _i (прямая прогонка):

₀=₀=0, 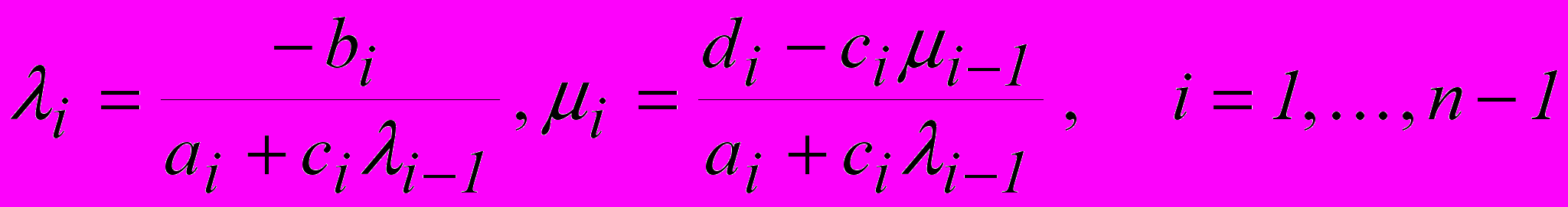. (1.12)

Очевидно, что m_n_-1=_n_-1 (при с_n_-1=0). Все остальные неизвестные находим по формулам (1.11), используя выражения для прогоночных коэффициентов (1.12).

Для реализации алгоритма требуется выполнить 8(n-1) арифметических операций: 3(n-1) сложений, 3(n-1) умножений, 2(n-1) делений.

Величины _i и a_i +c_i_i-1 не зависят от правой части системы. Поэтому если вычислить их и запомнить, то для решения систем, отличающихся только правыми частями, потребуется 5(n-1) арифметических операций.

Листинг программы:

#include

#include

#include

#include

float d[99999];

float l[99999];

float m[99999];

double f[99999];

float s[99999],mu[99999];

void main()

{

system("cls");

int n;

float c,a,b,shag;

float h;

cout<<"Vvedite shag h:=";

cin>>h;

cout<<"Vvedite kolichestvo znachenii n:=";

cin>>n;

shag=h/2;

c=h/6;

a=2*h/3;

b=h/6;

cout<<"c="<
po=(float)(h*i);

cout<<"S["<

}

system("PAUSE");

}

Проверим правильность выполнения программы на примере функции y(x)=sinx, в качестве узловых точек возьмем точки из интервала (0;Π] с шагом h=Π/8. Найдем значения функции в промежуточных точках при помощи интерполяции функции сплайном:

Пример

Vvedite shag h:=0.3925

Vvedite kolichestvo znachenii n:=8

c=0.0654167 a=0.261667 b=0.0654167

Vvedite Y[0.3925]:=0.38249949727

Vvedite Y[0.785]:=0.7068251811

Vvedite Y[1.1775]:=0.92365

Vvedite Y[1.57]:=0.999999

Vvedite Y[1.9625]:=0.9246

Vvedite Y[2.355]:=0.70795

Vvedite Y[2.7475]:=0.38397

Vvedite Y[3.14]:=0.00159

S[0.58875]=1.49443

S[0.785]= 0.706825

S[0.98125]=2.10928

S[1.1775]= 0.92365

S[1.37375]=2.35328

S[1.57]= 0.999999

S[1.76625]=2.25135

S[1.9625]= 0.9246

S[2.15875]=1.80784

S[2.355]= 0.70795

S[2.55125]=1.087

S[2.7475]= 0.38397

Для продолжения нажмите любую клавишу . . .

Вывод: Как мы видим, значения функции, полученные нами в промежуточных точках, не совпадают с теоретическими значениями, это вызвано тем, что функция y(x)=sinx является периодической, что влечет собой достаточно большую погрешность при интерполировании.

Проверим также метод интерполяции на более монотонной функции, например на функции y(x)=x². В качестве узловых точек возьмем точки из отрезка [1;8], с шагом h=1:

Vvedite shag h:=1

Vvedite kolichestvo znachenii n:=8

c=0.166667 a=0.666667 b=0.166667

Vvedite Y[1]:=1

Vvedite Y[2]:=4

Vvedite Y[3]:=9

Vvedite Y[4]:=16

Vvedite Y[5]:=25

Vvedite Y[6]:=36

Vvedite Y[7]:=49

Vvedite Y[8]:=64

S[1.5]=2.35101

S[2]= 4

S[2.5]=6.18125

S[3]= 9

S[3.5]=12.2424

S[4]= 16

S[4.5]=20.2242

S[5]= 25

S[5.5]=30.2359

S[6]= 36

S[6.5]=42.2074

S[7]= 49

Для продолжения нажмите любую клавишу . . .

Вывод: Как мы можем заметить, при интерполировании более монотонной функции, погрешность расчетов оказалось относительно небольшой.

Blog

Для решения систем линейных алгебраических уравнений с ленточной матрицей, с понятием сплайна, получение навыков решения задач вычислительной математики на ЭВМ

Содержание

Уфа 2006