Тема Модели статистической взаимосвязи и их корреляционно-регрессионный анализ

Вид материала

Документы

Содержание 6.2.Модель аналитической группировки (МАГ) 6.3. Модель линейной регрессии (МЛР) 6.4. Дисперсионный анализ МАГ Общая дисперсия результативного признака равна F-критерием Фишера 6.5. Корреляционный анализ МЛР Тарифный разряд Коэффициент обеспече Контрольные вопросы

Подобный материал:

• Тематическийплан по видам занятий курса "Статистика" Наименование разделов и тем, 202.52kb.
• Лабораторная работа №2 по дисциплине дискретный анализ Тема: «Линейный регрессионный, 100.15kb.
• Анализ данных маркетинговых исследований: Корреляционно-регрессионный анализ и анализ, 91.98kb.
• Корреляционно-регрессионный анализ в ms excel, 34.62kb.
• По данным наблюдения провести корреляционно-регрессионный анализ (кра) зависимости, 134.2kb.
• Методические указания по выбору темы и написанию курсовых проектов по дисциплине «Эконометрика, 61.07kb.
• Аннотация гридасов В. М., Подгайко Н. В. Модель расчета коэффициента дисконтирования, 218.5kb.
• Тема 41. Предпосылки модели экономики с экзогенными ценами (кейнсианская модель равновесия, 96.08kb.
• Однофакторный регрессионный анализ можно осуществлять с помощью "Мастера функций" ппп, 29.02kb.
• М. Н. Узяков Проблемы построения межотраслевой модели, 310.25kb.

Тема 6. Модели статистической взаимосвязи и их

корреляционно-регрессионный анализ


6.1. Типы взаимосвязи между явлениями


В природе и обществе существует множество взаимосвязанных явлений. Урожайность зависит от погоды и агрокультуры, производитель-ность труда – от технической оснащенности, рынок – от спроса, уровень преступности – от солнечной активности и т.д. Существует известная притча о взаимосвязи явлений. Подгулявшего соотечественника в полночь задер-живает страж порядка с вопросом:

-Что это Вы тут песни поете?

-А отчего прогресс на земле? – отвечает вопросом тот. – От того, что работают заводы и фабрики. А отчего они работают? От того, что ученый до глубокой ночи не спит и мысль думает. А от чего он не спит? От того, что я под его окном стою и песни пою. Как же я могу позволить себе не выпить и не спеть хоть раз? Прогресс на земле остановится!

Слово “связь” относится к числу самых обиходных в русском языке. Нашим предметом не будет почтовая, голубиная, cотовая связь и даже связь поколений. Пожалуй, нет ни одной науки, не изучающей какие-то виды связи. Статистика занимается изучением статистической (стохастической) связи между массовыми явлениями. Когда исследуется влияние какого-то фактора на интересующий нас результат, то говорят о причинно-следст-венной связи между факторным Х и результативным Y признаками.

Управленческие решения всегда принимаются на основе учета множе-ства факторов, как объективных, так и субъективных (для последних харак-терными бывают так называемые волюнтаристские решения). Нельзя, разу-меется, отрицать интуиции, как нельзя отрицать и здравого смысла. Грамотное решение всегда требует тщательного анализа и расчета. Статистика как раз и дает методологию анализа, основанную на построении экономических (или других) моделей. Такие модели, отображающие взаимо-связи между явлениями или процессами, полезны для прогноза и управле-ния.

Различают функциональную (детерминированную) и статистичес-кую связь. Под функциональной связью понимают зависимость y=y(x), при которой каждому значению аргумента х (фактора) ставится в соответствие известное (детерминированное) значение функции, рис.6.1а. Например, закон Ньютона a=F/m (ускорение тела а пропорционально силе F и обратно пропорционально массе m) является примером прямой функциональной зависимости между a (функцией) и F (аргументом). Связь называют статис-тической, если для каждого фиксированного значения xX существует мно-жество возможных значений результативного признака Y, рис.6.1б. Часто есть основания рассматривать Y как случайную величину, имеющую для каждого фиксированного х распределение условных вероятностей P{Y=y_k| x} или плотности вероятности f(y|x). Если при изменении факторного признака х существенно изменяется и распределение результативного Y, то говорят о наличии статистической связи между X и Y. О такой связи можно в первом приближении судить уже по изменению среднего значения признака Y –


y (x) (а) Y (б)




m_y(x)




y₀













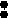
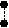
0 x₀ x 0 x₀ X

Рис.6.1

у
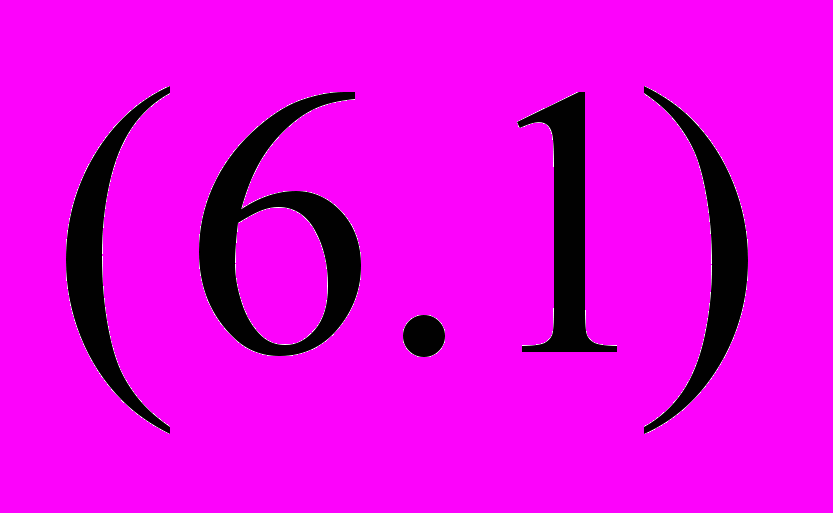
словного математического ожидания

к
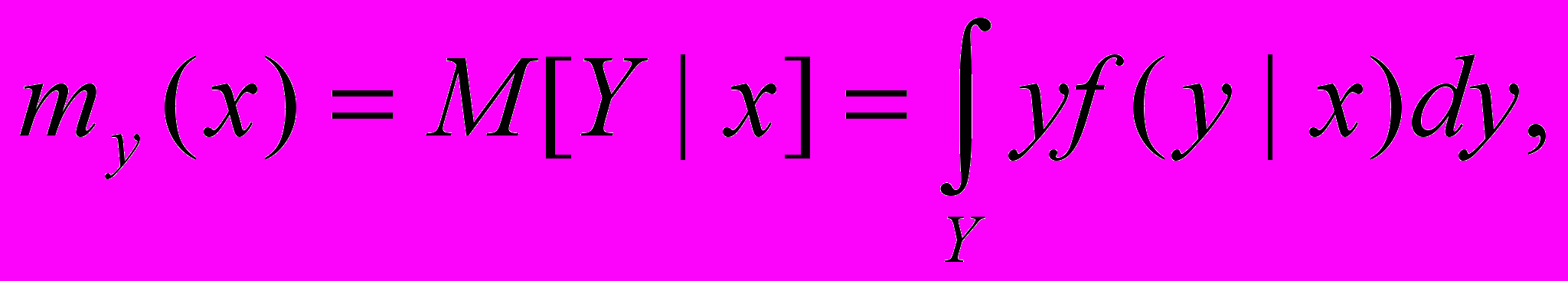
оторое здесь записано для непрерывной случайной величины Y. Эту зависимость как функцию аргумента х в теории вероятностей называют линией регрессии. Она изображена в качестве примера на рис.6.1 б.

Как уже отмечалось, в статистике приходится иметь дело с выборками ограниченного объема n и вместо вероятностей (плотностей вероятности) оперировать их оценками – частостями. При этом на основе выборки также можно построить линию регрессии или ее аппроксимацию (приближенную функцию линии регрессии). Такие линии регрессии называют моделями статистической зависимости между факторным Х и результативным Y признаками. Они служат для различных оценок и прогнозов в экономичес-ких и финансовых расчетах.

Частным случаем статистической связи является корреляционная связь. Она оценивается коэффициентом корреляции (см.п.6.4), характе-ризующим степень линейной статистической связи.

Подчеркнем различие между причинно-следственной и статистической связью. В теории вероятностей и статистике хорошо известно, что если Y зависит от X, то и X зависит от Y (статистически). Например, тот факт, что преступность зависит от солнечной активности, был обнаружен случайно. Один из европейских астрономов оказался как-то в полицейском участке, в котором увидел график уровней преступности за многолетний период. Этот график с 11-летним периодом максимумов оказался очень близким к его графику изменения солнечной активности. В дальнейшем исследования психологов подтвердили влияние активности Солнца на агрессивность человека. Налицо причинно-следственная связь. Однако на основе статисти-ки можно утвержать и обратное: солнечная активность зависит от преступности (статистически !). Условно говоря, астроном может поменять свое рабочее место на полицейский участок и там изучать периоды изменения солнечной активности. По следствию можно судить и о причине.

При изучении взаимосвязей между социально-экономическими яв-лениями решаются следующие задачи:

• выбор типа модели регрессии;
  
• построение модели выбранного типа;
  
• дисперсионно-корреляционный анализ модели и установление существенности связи между факторным и результативным признаками.
  

В данной теме мы рассмотрим самые распространенные в статистике модели регрессии:

• модель аналитической группировки (МАГ);
  
• модель линейной регрессии (МЛР).
  

6.2.Модель аналитической группировки (МАГ)


В простейшем случае изучаются статистические связи между одним факторным и результативным признаками. Соответствующие модели называют моделями парной регрессии. На практике чаще приходится учитывать множество факторов, влияющих на результативный признак. В таких случаях строются модели множественной регрессии. В данной теме мы рассмотрим более простые модели парной регрессии.

Метод построения модели аналитической группировки очень прост: для каждого значения x_k дискретной величины или интервала [x_{k min}, x_{k max}] определяются условные средние y(x_k), после чего соседние значения условных средних соединяются отрезками прямых. Для наглядности удобней пользоваться графическим представлением выборки. Каждая точка выборки задается двумя координатами (x_i, y_i).

Пример 6.1. Показатели рентабельности предприятия y_i % в зависимо-сти от числа x_i выпускаемых в день автомобилей отражены на рис.6.2. Здесь


4 y



3

МАГ

2




1



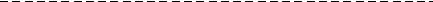
-1 МЛР




-2


-3

20 30 40 50 x авт/день

Рис.6.2

для проcтоты и наглядности расчетов точки выборки расположены в узлах решетки. Требуется построить МАГ с разбиением признака х на три интервала группирования.

Чтобы избежать неясностей на границах интервалов, ширину интервалов принимаем h=11, тогда в первый интервал попадают целые значения x_i[20,21,…30], во второй - значения x_i [31,…,41], и в третий -

x_i [42,…,52]. Число точек выборки в интервалах: n₁=9, n₂=6, n₃=7, общее число точек n=22.

Для каждого из интервалов рассчитываем средние групповые величи-ны. Для первого интервала






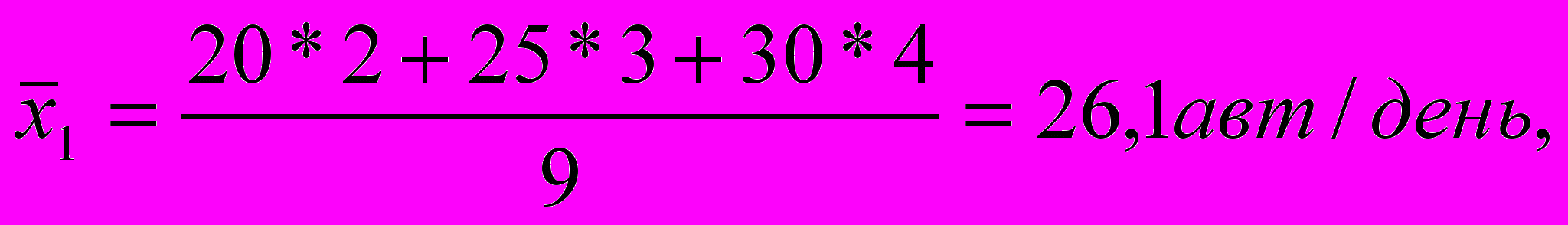
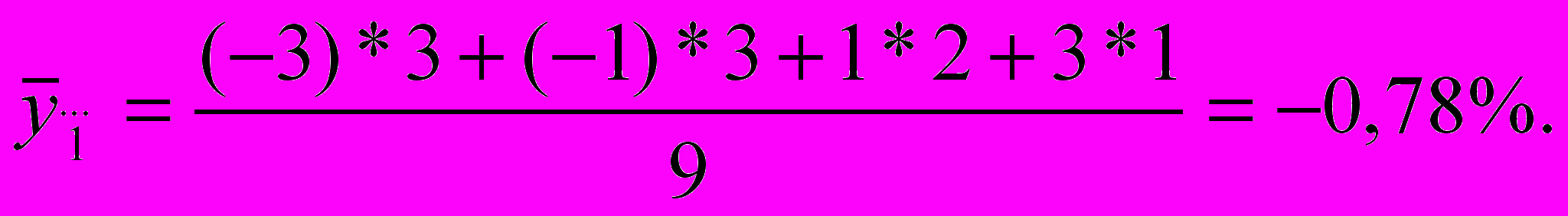
Аналогичные расчеты для всех интервалов сводим в таблицу 6.1.

Таблица 6.1

Номер интервала K	1	2	3
Границы интерв.	20-30	31-41	42-52
Средние xk	26,1	37,5	47,1
Cредние yk	-0,78	1,5	2,14
Число точек nk	9	6	7

Точки (x_k,y_k) отмечаем на рис.6.2 и соединяем отрезками прямых. Эта кусочно-ломаная зависимость и называется моделью аналитической группировки.

Т
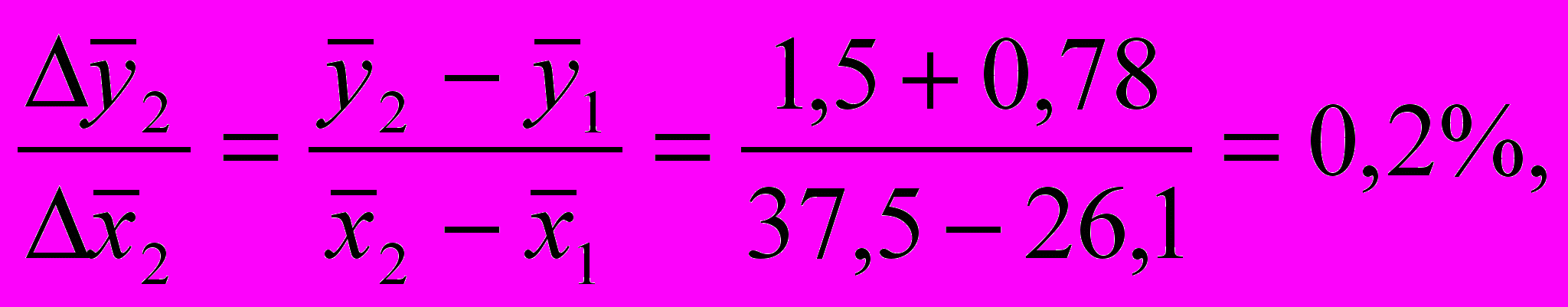
аким образом, чтобы достичь рентабельности выше 2%, нужно выпускать не менее 45 автомобилей в день. Можно рассчитать прирост рентабельности за счет выпуска одного автомобиля

С
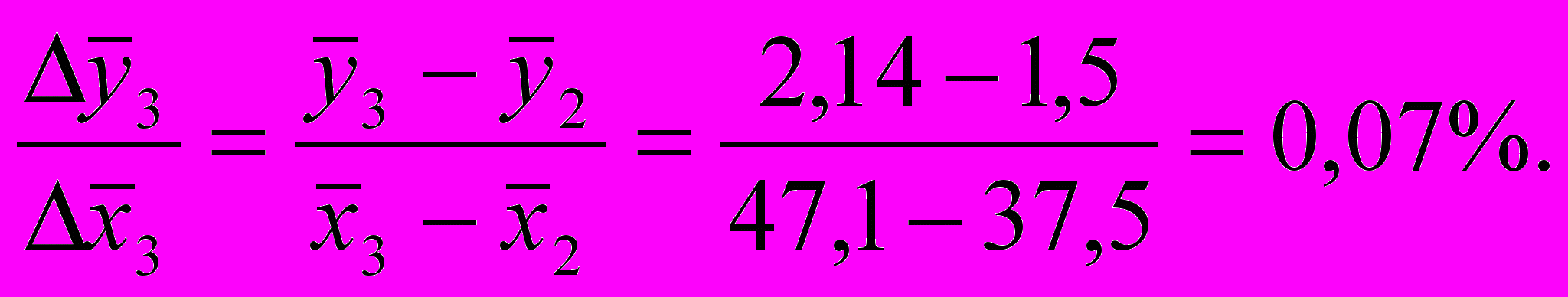
ледовательно, дополнительный выпуск одного автомобиля в день дает прирост рентабельности от 0,07 до 0,2% (прирост больше при меньших значениях производительности).


6.3. Модель линейной регрессии (МЛР)


Эта модель является наиболее распространенной регрессионной моделью. Во-первых, она привлекает своей простотой, так как нет проще функции, чем линейная (уравнение прямой линии). Во-вторых, при линейной аппроксимации легко удается получить минимальную среднеквадратичную ошибку.

Модель линейной регрессии является по существу линейной аппроксимацией (приближением) реальной линии регрессии y(x). Она описывается уравнением прямой

г
де множитель а называется коэффициентом регрессии. Прямая (6.2) должна проходить так, чтобы по отношению к точкам выборки

{X_i,Y_i}⁽ⁿ⁾={ (x₁,y₁)_, (x₂,y₂)_,… (x_n,y_n) }

о
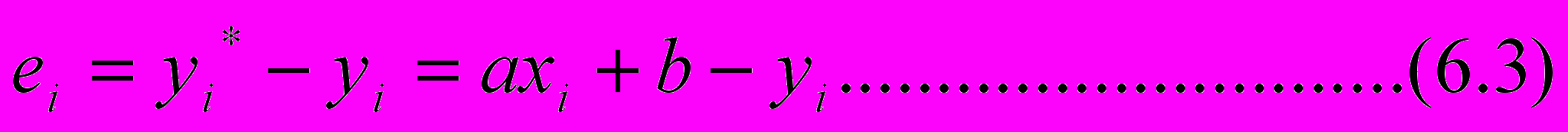
беспечить минимальную СКО. Для каждой точки выборки ошибка результативного признака равна

Эта ошибка для i-й точки представлена на рис.6.3.


Y


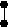
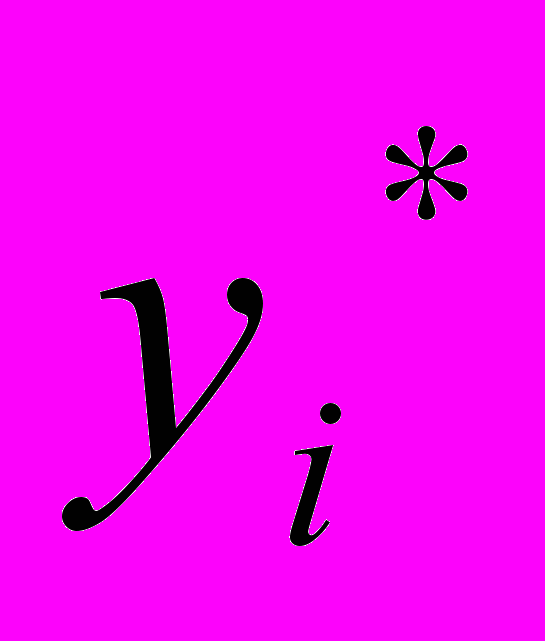
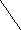y_i e_i




b





0 x_i x

Рис.6.3

Средний квадрат ошибки аппроксимации пропорционален сумме квадратов ошибок

E(a,b)=n^-1_i e_i²=n^-1_i(ax_i+b-y_i)². (6.4)

О
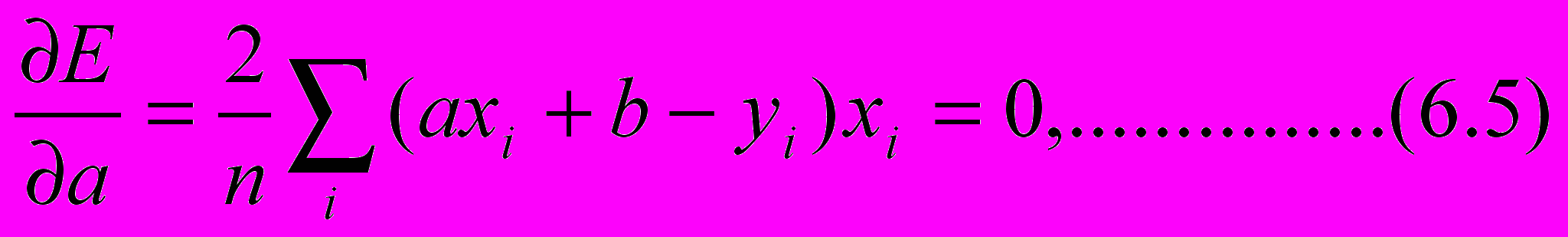
пределение параметров a и b модели осуществляется методом наименьших квадратов (МНК). Так как минимум функции (6.4) при вариации a и b имеет место в точке нулевых частных производных, то получим систему двух линейных относительно a и b уравнений

И

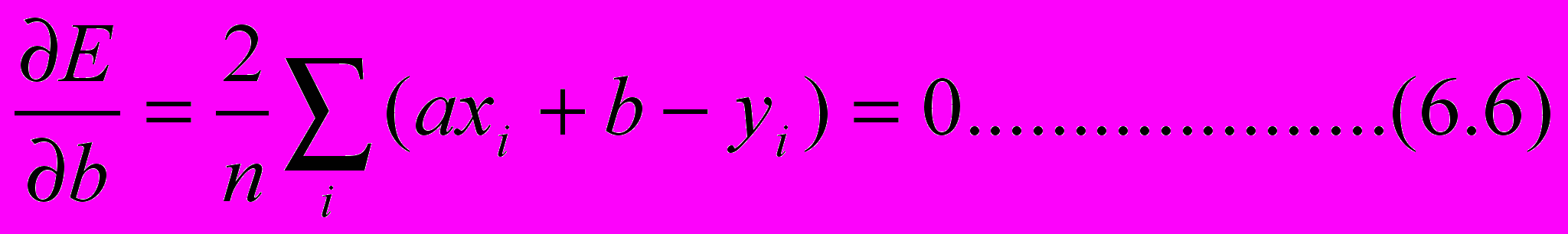
з второго уравнения, в частности, следует, что суммарная ошибка аппроксимации

т.е. оценка МНК является несмещенной. Кроме того, оно дает соот-ношение между средними значениями признаков X и Y



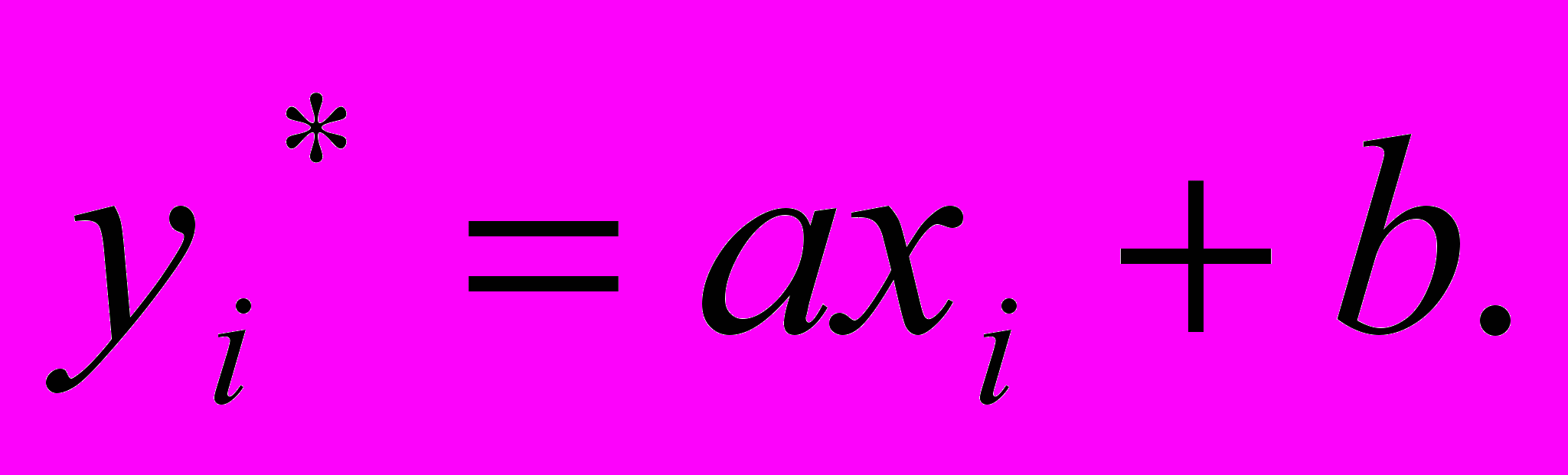
Значение теоретической прямой в i-й точке

В
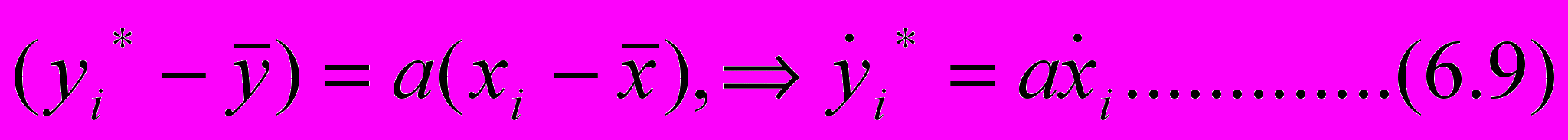
ычитая из этого уравнения (6.8), получим связь между центрирован-ными величинами (отклонениями)

Следовательно, отклонения от средних связаны коэффициентом регрессии. Это соотношение будет использовано в корреляционном анализе.

Р
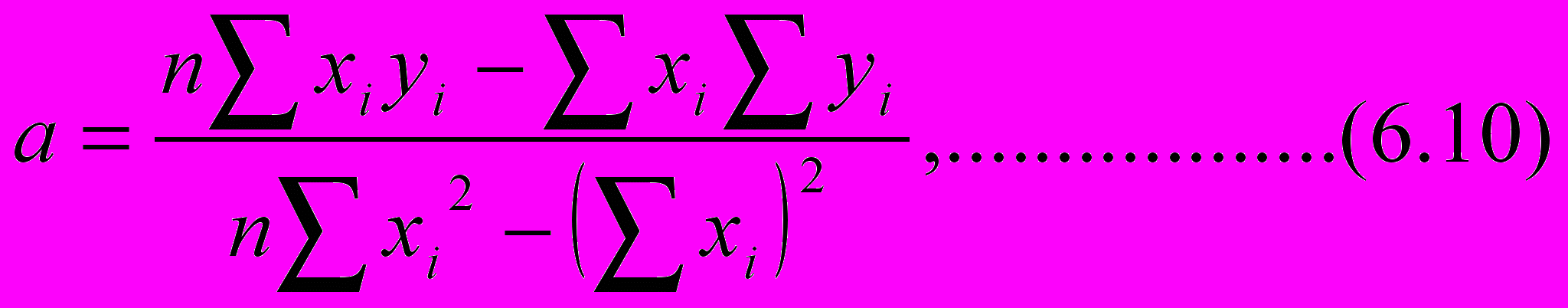
ешение системы уравнений (6.5), (6.6) имеет вид


З

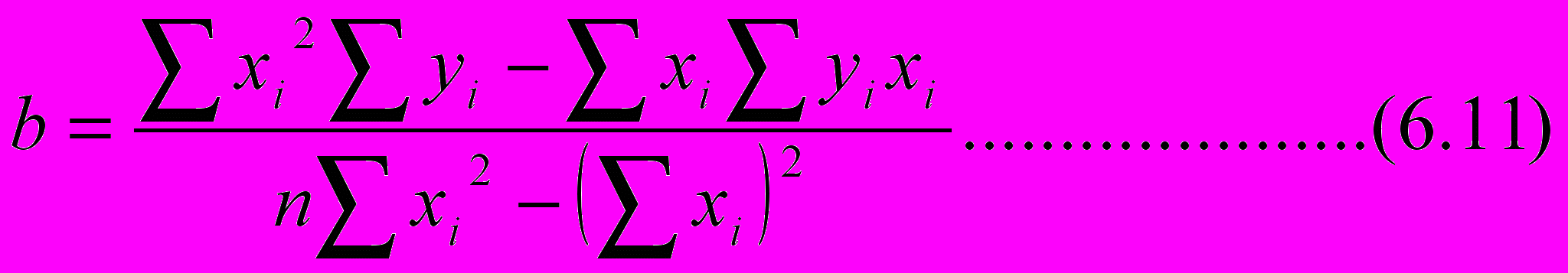
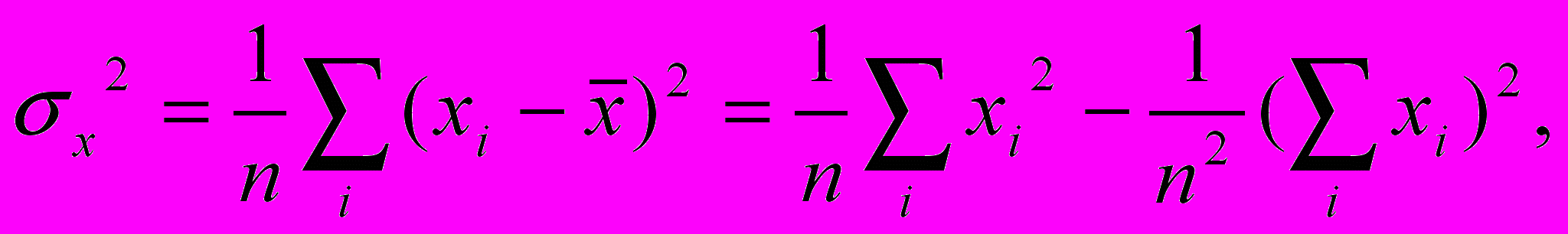
наменатели в этих выражениях пропорциональны дисперсии факторного признака


а
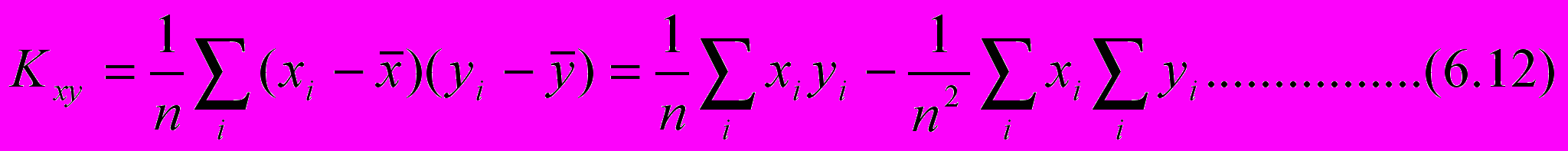
числитель (6.10) пропорционален моменту корреляции между признаками X и Y

З
десь использовано свойство несмещенности оценок x и y. C учетом последних соотношений коэффициент регрессии можно выразить как

После определения a для расчета b удобней вместо (6.11) пользоваться (6.8).

Пример 6.2. Рассчитаем параметры a и b модели линейной регрессии по данным примера 6.1. Сведем расчеты в таблицу 6.2.

Таблица 6.2

I	xi	yi	xi2	yi2	xiyi
1	20	-3	400	9	-60
2	20	-1	400	1	-20
3	25	-3	625	9	-75
4	25	-1	625	1	-25
5	25	1	625	1	25
6	30	-3	900	9	-90
7	30	-1	900	1	-30
8	30	1	900	1	30
9	30	3	900	9	90
10	35	-1	1225	1	-35
11	35	1	1225	1	35
12	35	3	1225	9	105
13	40	-1	1600	1	-40
14	40	1	1600	1	40
15	40	3	1600	9	120
16	45	-1	2025	1	-45
17	45	1	2025	1	45
18	45	3	2025	9	135
19	45	4	2025	16	180
20	50	1	2500	1	50
21	50	3	2500	9	150
22	50	4	2500	16	200
	790	14	30350	116	785

По результатам расчета находим







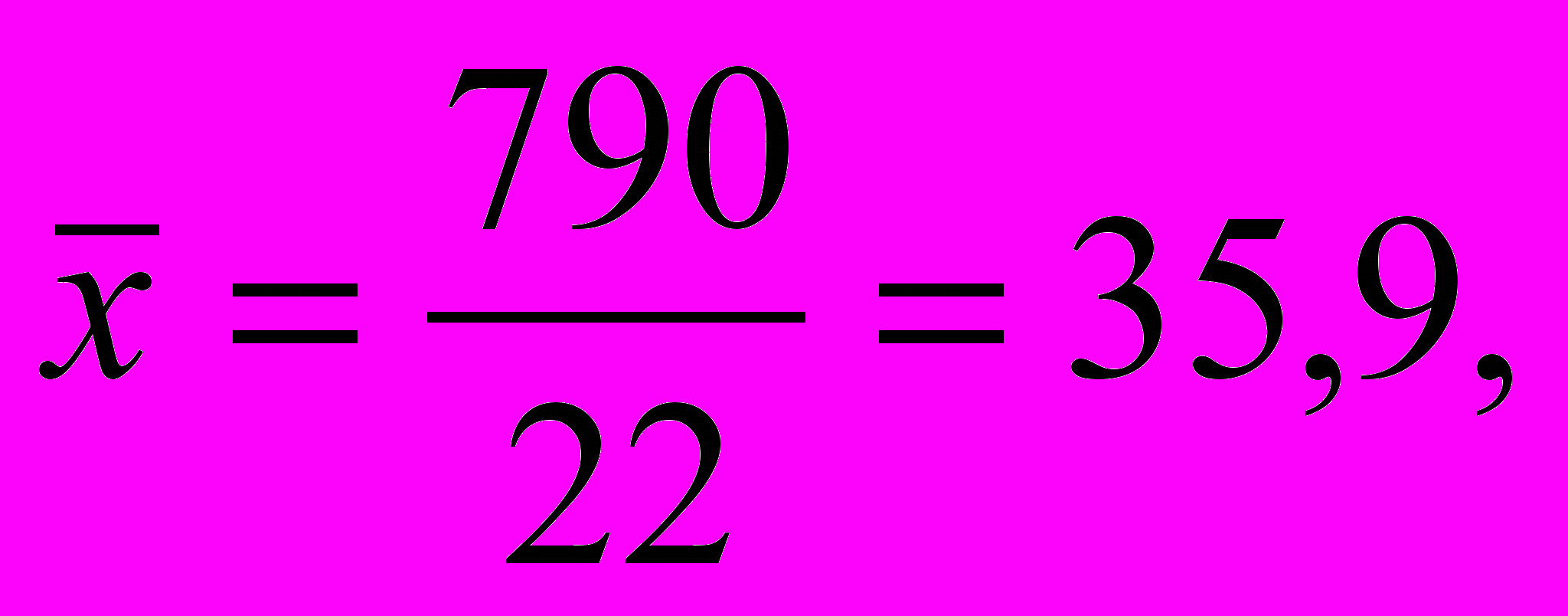
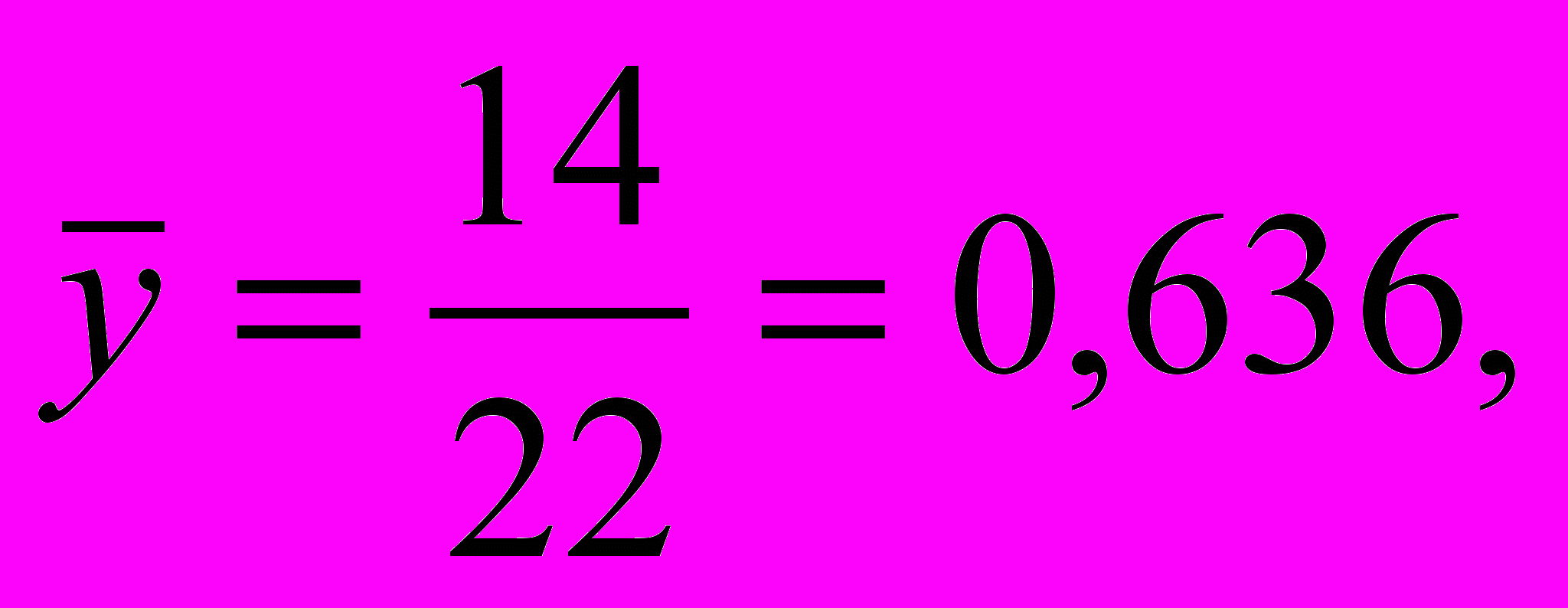
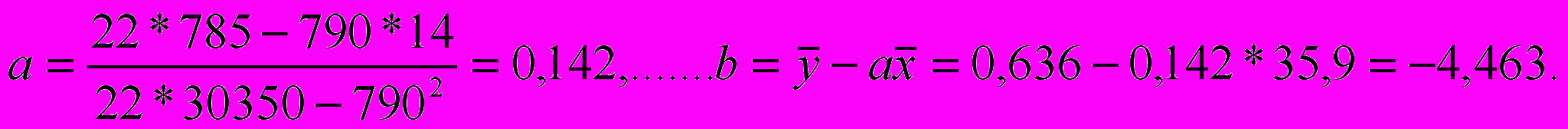
Т
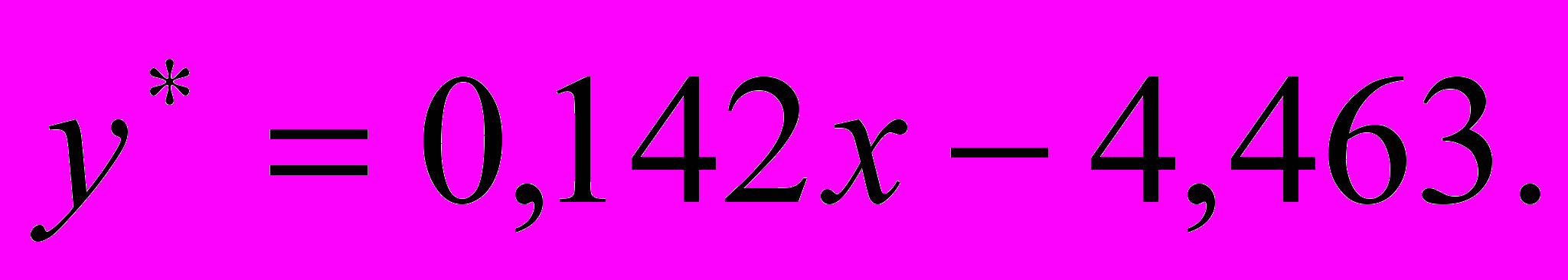
аким образом, уравнение модели линейной регрессии можно записать в виде

частности, при х=20 и х=50

Э
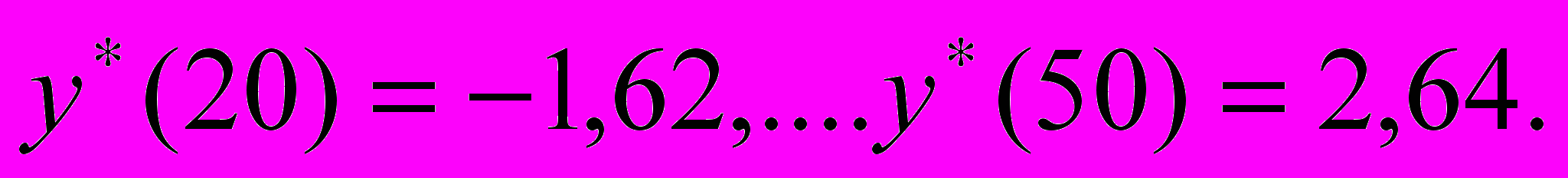
та прямая, определяющая МЛР, изображена на рис.6.2.

Коэффициент регрессии a имеет смысл производной функции y(x), т.е. является отношением приращений y/x. В нашем примере он означает прирост рентабельности в 0,142 % за счет выпуска одного автомобиля в день (для МАГ мы получили для разных интервалов значения 0,2 и 0,07).

Сравнивая рассмотренные модели, отметим, что МАГ является более универсальной, так как может описывать существенно нелинейные линии регрессии. Вместе с тем в распространенных на практике случаях множественной регрессии МЛР имеет преимущественное применение в силу возможности минимизировать ошибки аппроксимации.


6.4. Дисперсионный анализ МАГ


После этапа построения моделей линии регрессии остается решить еще одну задачу: определить, является ли статистическая связь между X и Y существенной? Иначе говоря, следует ли учитывать Х при анализе экономической ситуации и прогнозировании как фактор, влияющий на интересующий нас показатель (результат Y)? При положительном ответе на этот вопрос данный фактор включается в более сложную модель множественной регрессии, в противном случае – не рассматривается.

Теория существенности (тесноты) статистической связи разработана английским математиком Р.Фишером. В ее основе лежит теория проверки статистических гипотез. Для принятия решения о том, существенна ли связь, по результатам анализа МАГ определяется корреляционное отношение ², которое сравнивается затем с некоторым порогом или критическим значением _кр², которое находится из таблиц Фишера.

Сначала проанализируем составляющие дисперсии результативного признака после группировки на интервалы

В
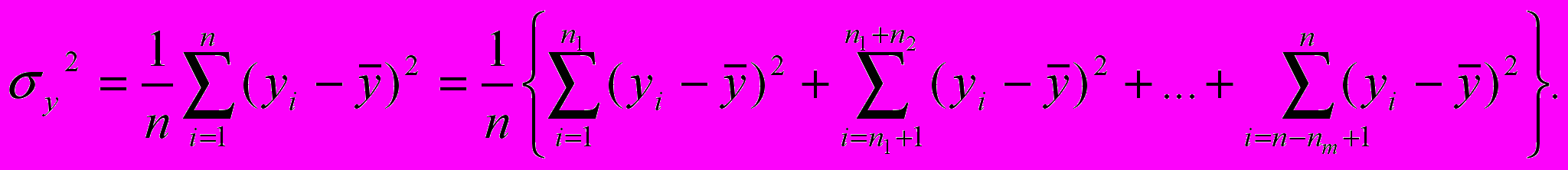
нутри первой группы сумма n₁ слагаемых может быть представлена





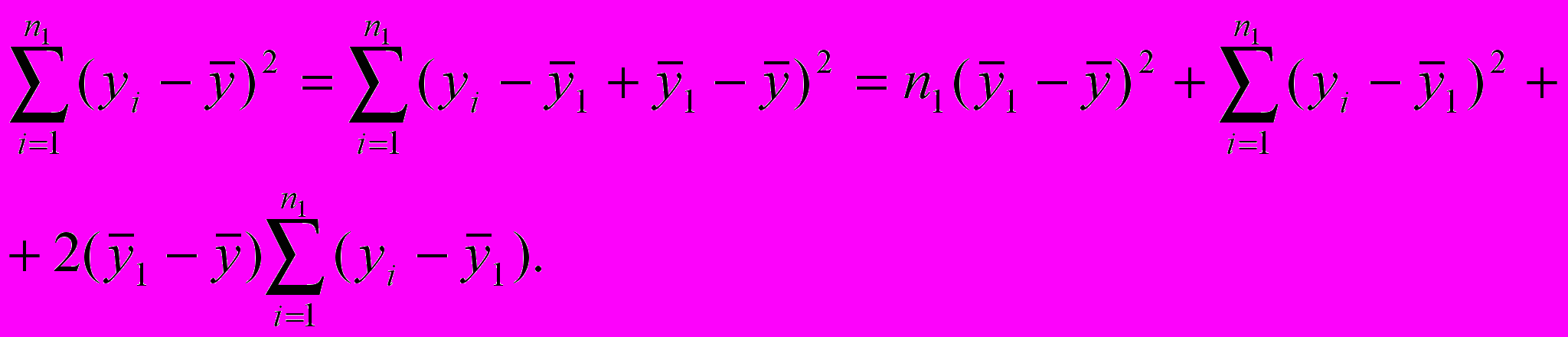
О
чевидно, последнее слагаемое здесь равно 0, поэтому общая дисперсия имеет два слагаемых

г
де

м
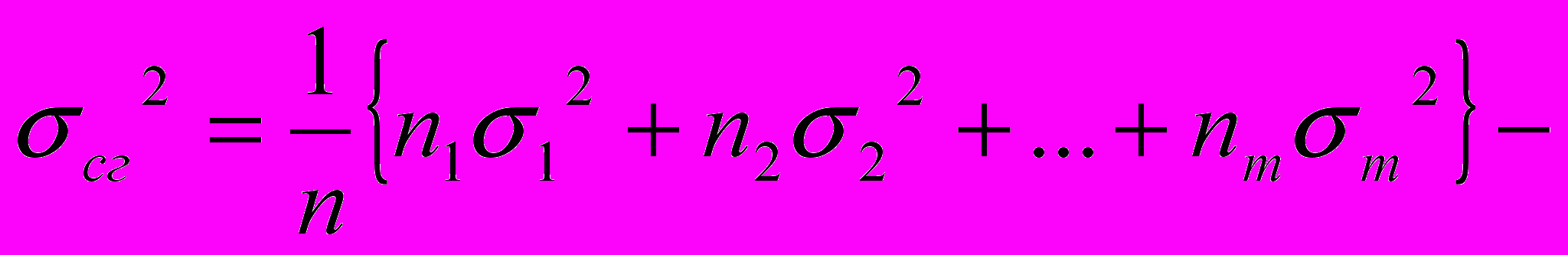
ежгрупповая дисперсия,

средняя из групповых дисперсий. Здесь m – число групп МАГ.

Д
ва слагаемых в (6.14) некоррелированы и содержат разную информацию. Средняя из групповых дисперсий определяется как взвешенная средняя дисперсия всех групп и, следовательно, характеризует случайность разброса элементов выборки относительно средних групповых. При изменении факторного признака эта дисперсия может не изменяться или изменяться незначительно. Совершенно другого рода информация содержится в межгрупповой дисперсии (6.15). Действительно, она пропорциональна степени изменения групповых средних и, следовательно, изменению линии регрессии. В частности, если все групповые средние одинаковы и равны общей средней величине, межгрупповая дисперсия равна 0. В этом случае линия регрессии параллельна оси абсцисс и можно констатировать, что Y не зависит от X. Наоборот, чем круче изменяется зависимость y_i(x), тем больше межгрупповая дисперсия. Ее доля в общей дисперсии тем выше, чем меньше фактор случайного разброса относительно линии регрессии. Следовательно, показателем закономерной связи между факторным и результативным признаками может служить относительная доля межгрупповой дисперсии в общей дисперсии. Она определяется как корреляционное отношение

Этот коэффициент, очевидно, может принимать значения в пределах от 0 до 1. В первом случае говорят об отсутствии корреляционной связи между X и Y, во втором предельном случае статистическая связь вырождается в функциональную. Чем ближе к 1 корреляционное отношение, тем сильнее (тесней) связь между признаками. Это, однако, лишь тенденция. А что можно сказать о взаимосвязи, если, к примеру, расчеты привели к значениям ² =0,1 или ²=0,3 ? Существенна ли такая связь?

Ответ на этот вопрос может оказаться различным в зависимости от объема выборки и числа интервалов группирования. Не вдаваясь в теорию оценивания тесноты связи, отметим лишь, что она основана на выборе с допустимой вероятностью ошибки наиболее правдоподобной гипотезы:

• H₀ – гипотеза о том, что связи нет;
  
• H₁ – гипотеза о том, что связь есть.
  

Для каждого набора параметров n,m рассчитаны значения критического корреляционного отношения _кр², и при

²>_кр²

принимается гипотеза H₁ о том, что связь есть (или существенна). При этом допустимая вероятность ошибки

=Р{²>_кр²|H₀}

называется коэффициентом значимости. Наиболее часто используют два значения этого коэффициента =0,05 или =0,01. Это значит, что если рассчитанное по результатам дисперсионного анализа значение ² оказалось больше _кр², то наше заключение о том, что связь существенна, может быть ошибочным в 5% случаев (или в 1%).

Входными параметрами в таблицы критических значений корреляци-онного отношения являются степени свободы

k₁ =m-1, k₂=n-m. (6.17)

Значения критических корреляционных отношений для =0,05 приведены в приложении I.

Пример 6.3. Определим тесноту стохастической связи для МАГ, построенной в примере 6.1.

О
бщая дисперсия результативного признака равна

Межгрупповая дисперсия согласно (6.15) определяется как

²={(-0,78-0,636)²*9+(1,5-0,636)²*6+(2,14-0,636)²*7}/22=1,74.

Таким образом, корреляционное отношение

²=² /_y²=1,74/4,87=0,36.

По входным параметрам k₁=m-1=2, k₂=n-m=19 определяем по таблице (Приложение I) значение критического корреляционного отношения при вероятности ошибки =0,05

_кр²=0,283.

Так как ²>_кр², то с вероятностью 0,95 заключаем, что статистическая связь существенна.

Если в результате расчетов оказывается, что ²<_кр², то полагают, что связь между X и Y не установлена.

И
ногда вместо корреляционного отношения ² удобней пользоваться обобщенным параметром – F-критерием Фишера

для которого также рассчитаны табличные критические значения (Приложение II). Заключение о существенности связи принимается при F>F_кр. Таблицы для F-критерия оказываются более компактными, чем для корреляционного отношения.


6.5. Корреляционный анализ МЛР


Как и в предыдущем параграфе, этот анализ имеет целью установление существенности (тесноты) корреляционной связи между факторным и результативным признаками. Основное отличие состоит в том, что вместо корреляционного отношения для этой цели используется другой параметр - коэффициент детерминации.

П
ользуясь обозначениями п.6.2, разложим общую дисперсию _y² на две некоррелированные составляющие

И

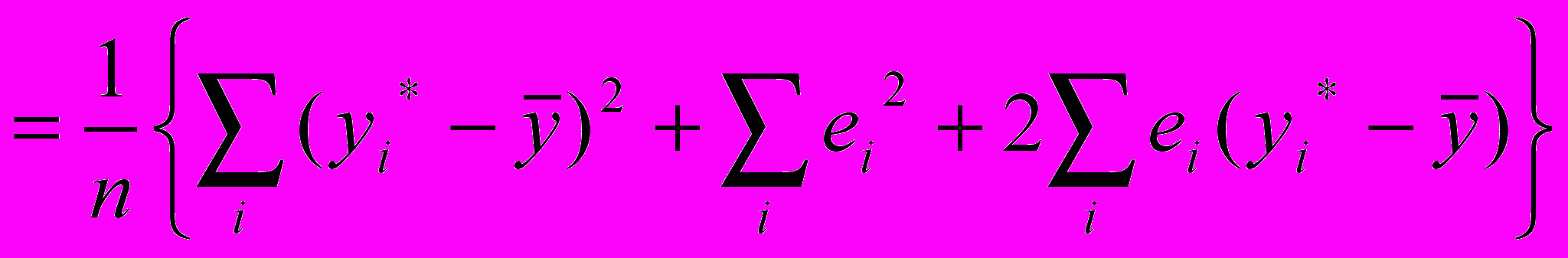
з (6.5), (6.7) следует, что последняя сумма в этом разложении равна 0, поэтому

г
де

Т

аким образом, общая дисперсия результативного признака складывается из двух составляющих, характеризующих разные свойства корреляционного поля. Составляющая (6.21) характеризует степень разброса точек у_i относительно теоретической прямой и, следовательно, выражает свойство случайности совокупности. Составляющая (6.20), напротив, пропорциональна квадрату разности между линией регрессии и постоянной средней, т.е. характеризует свойство закономерности связи. Ее доля в общей дисперсии, определяемая как коэффициент детерминации

я
вляется параметром, определяющим существенность связи. Его можно выразить через коэффициент регрессии а, если учесть, что возведение в квадрат (6.9) и усреднение дает

Т
огда

и
ли, учитывая (6.13)

Т
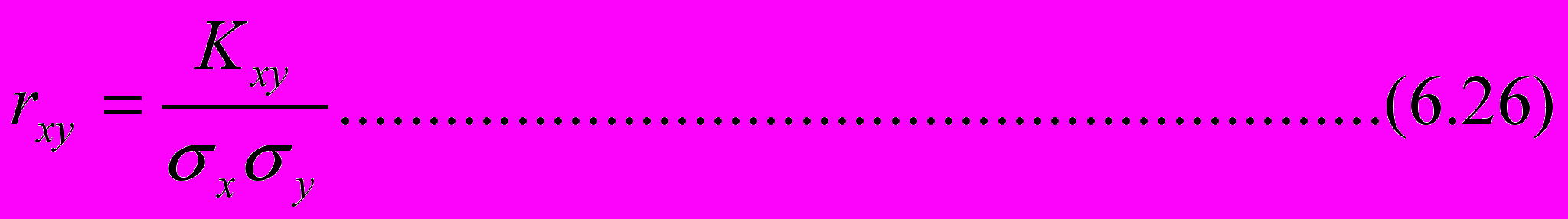
аким образом, коэффициент детерминации равен квадрату коэффициента корреляции

Коэффициент корреляции характеризует степень линейной статисти-ческой связи. Он принимает значения в интервале

-1  r_xy 1.

В крайних точках r_xy =1 статистическая связь становится линейной функциональной, положительной (r_xy =1, а0 ) или отрицательной (r_xy =-1, а0 ). При r_xy =0 говорят, что признаки X и Y некоррелированы. Независимые величины всегда некоррелированы (обратное утверждение верно лишь в частных случаях, например, для нормальных случайных величин). Обычно полагают, что при |r_xy|< 0,3 корреляционная связь слабая, при |r_xy|=(0,30,7) – средняя, а при |r_xy|> 0,7 – сильная.

О
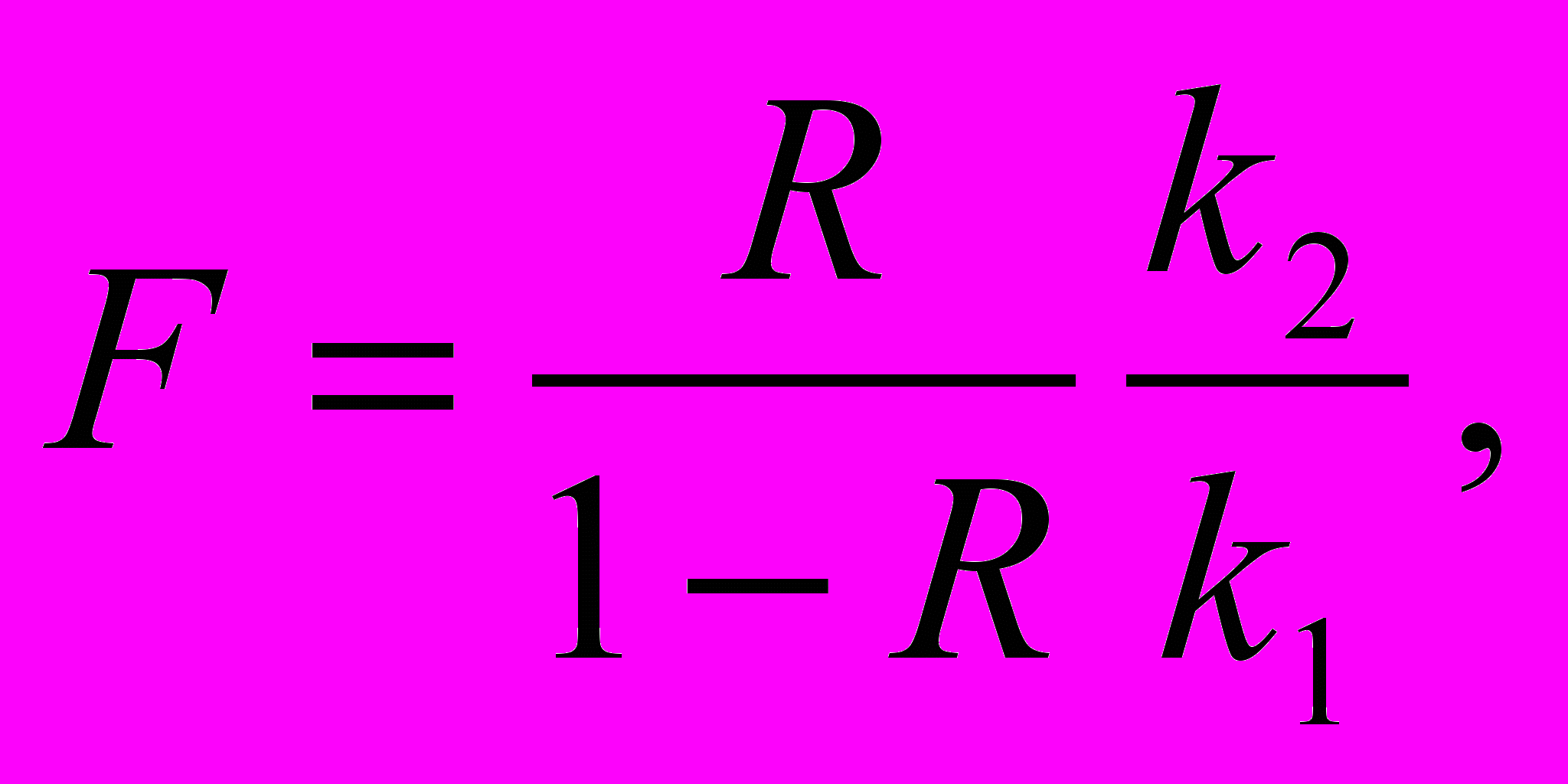
пределение существенности связи для МЛР осуществляется по той же методике, что и для МАГ. Вместо корреляционного отношения в этом случае используется коэффициент детерминации, который затем сравнивается с критическим коэффициентом детерминации R_кр. Последний находится по той же таблице (Приложение I), что и корреляционное отношение. Отличие состоит лишь в том, что число степеней свободы m принимается равным 2, так как МЛР имеет два параметра: a и b. Как и в МАГ, коэффициент детерминации можно пересчитать в F-критерий Фишера

который сравнивается с критическим (Приложение II). При R>R_кр или F>F_кр делается вывод, что связь существенна, в противном случае говорят, что связь не установлена.

П
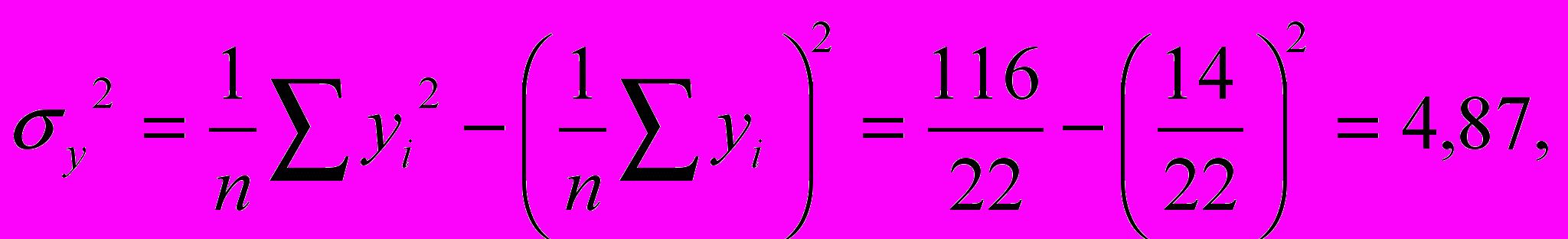
ример 6.4. Определим существенность связи для построенной в параграфе 6.2 МЛР (пример 6.2). Согласно данных таблицы 6.2 определяем дисперсии

П
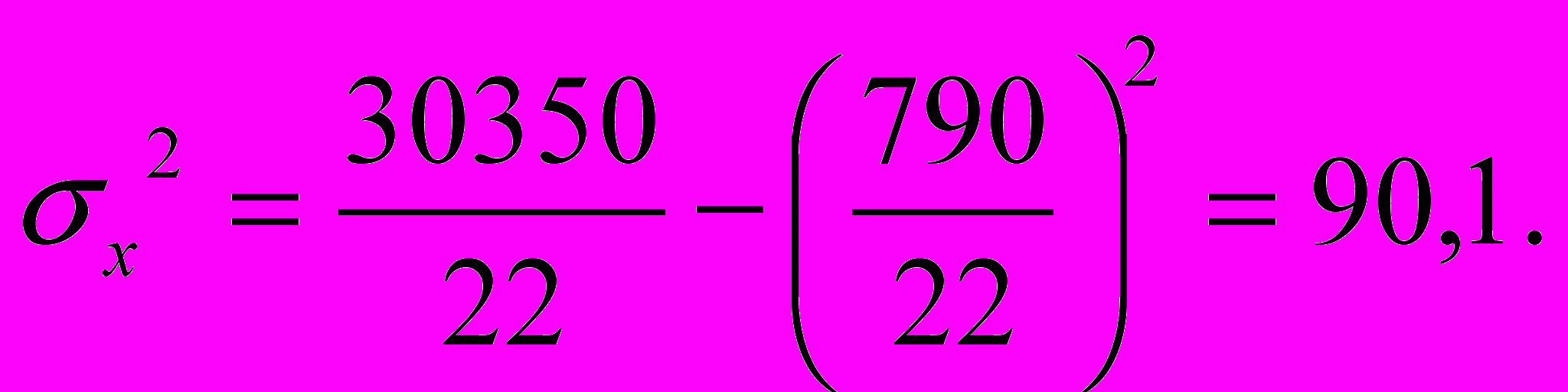
о формуле (6.24) получим






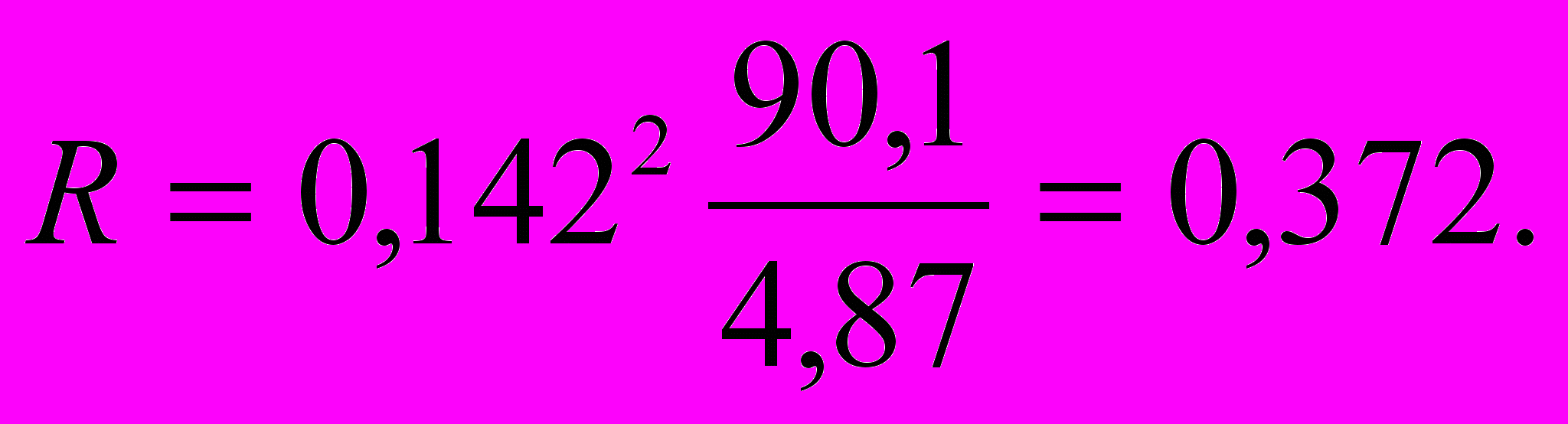
По входным данным k₁=m-1=1, k₂=n-m=20 таблицы (Приложение 1) находим критическое значение коэффициента детерминации при =0,05

R_кр=0,179.

Так как R>R_кр, заключаем, что связь между выпуском автомобилей в день и рентабельностью завода существенна с вероятностью 0,95.

Рассмотренную в данной теме модель парной регрессии можно обобщить на случай множественной регрессии. Одномерный факторный признак при этом заменяется вектором, линейная модель становится многопараметрической, а ее параметры находятся из системы матричных уравнений. Подробнее эти вопросы изучаются в курсе «Эконометрия».

Задачи

1. Для выборки из 10 специалистов с тарифными разрядами от 2-го до 6-го их заработки составляли

Тарифный разряд	2	3	4	5	6
Заработок,у.е.	150	200 280	300 400 460	400 500	500 700

Построить модель линейной регрессии, определить существенность корреляционной связи между уровнем квалификации и зарплатой (с вероятностью 0,95).

2. По данным годовых отчетов уровень рентабельности 100 предприятий связан с коэффициентом обеспечения ресурсами следующим образом

Коэффициент обеспече- ния ресурсами	<0,9	0,9 – 1,1	>1,1
Уровень рентабельности, %	5	12	22
Число предприятий	31	45	24

Общая дисперсия рентабельности предприятий равна 86.

Определить:

• межгрупповую дисперсию;
  
• корреляционное отношение.
  

Проверить существенность связи с вероятностью 0,95, пояснить экономический смысл корреляционного отношения.

3. Возраст (x_i, лет) и вес (y_i, кг) 12 школьников описываются выборкой

{x_i, y_i}⁽¹²⁾={(10, 28), (10, 32), (11, 34), (11, 35), (11, 36), (12, 36), (13, 39), (14, 41), (14, 44), (15, 46), (15, 48), (15, 50)}. Построить МЛР веса детей в зависимости от возраста, определить коэффициент корреляции между этими признаками, сделать выводы.

Контрольные вопросы

1.Какая связзь называется:

• функциональной;
  
• стохастической?
  

2. Что такое линия регрессии? Что называется линейной (нелинейной) регрессией?

3. Как строится модель аналитической группировки? Как на ее основе можно прогнозировать экономические явления?

4. Дайте определение:

• межгрупповой дисперсии;
  
• средней из групповых дисперсий;
  
• корреляционного отношения.
  

Поясните их математический и экономический смысл.

5. Как установить существенность связи для МАГ? От чего зависит критическое корреляционное отношение? Как определяются параметры таблиц Фишера? Как определяется критерий Фишера?

6. Как строится модель парной линейной регрессии? В чем суть метода наименьших квадратов?

7. Дайте определение:

• коэффициента регрессии;
  
• коэффициента детерминации;
  
• коэффициента корреляции.
  

Поясните их экономический смысл. Как они связаны друг с другом?

8. Какой из двух параметров (коэффициент детерминации или коэффициент корреляции) содержит больше информации и почему?

9. Какие явления называют некоррелированными? Являются ли они статистически независимыми?

10. Как проверяется существенность связи для МЛР? Как определяются входные параметры k_i при использовании таблиц Фишера?