Однофакторный регрессионный анализ можно осуществлять с помощью "Мастера функций" ппп excel

Вид материала

Документы

Содержание Известные_значения_y –

Подобный материал:

• Однофакторный линейный регрессионный анализ © 2008 г. А. М. Гржибовский, 208.29kb.
• Краткие теоретические сведения по выполнению заданий, 279.04kb.
• Запуск Excel, 203.99kb.
• Как создать мультфильм с помощью макроса, 44.99kb.
• Microsoft Office Excel 2007, 13.85kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Корреляционно-регрессионный анализ в ms excel, 34.62kb.
• Задание Изучить правила работы с мастером функций и оформления отчетов в Excel, 24.9kb.
• Методические указания по выбору темы и написанию курсовых проектов по дисциплине «Эконометрика, 61.07kb.
• Лабораторная работа «Построение и оформление графиков математических функций», 17.39kb.

ОДНОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

С ПРИМЕНЕНИЕМ “МАСТЕРА ФУНКЦИЙ”


Однофакторный регрессионный анализ можно осуществлять с помощью “Мастера функций” ППП Excel.

Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии y=a+bx. Порядок вычисления следующий:

1. введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
   
2. выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1х2 – для получения только оценок коэффициентов регрессии;
   
3. активизируйте Мастер функций любым из способов:
   

а) в главном меню выберите Вставка/ Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;

4. в окне Категория (рис. 34) выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните по кнопке ОК;
   
5. заполните аргументы функции (рис. 35):
   

Известные_значения_y – диапазон, содержащий данные результативного признака;

Известные_значения_x – диапазон, содержащий данные факторов независимого признака;

Константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении; если Константа = 1, то свободные член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щелкните по кнопке ОК;

6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите клавишу , а затем – на комбинацию клавиш ++.





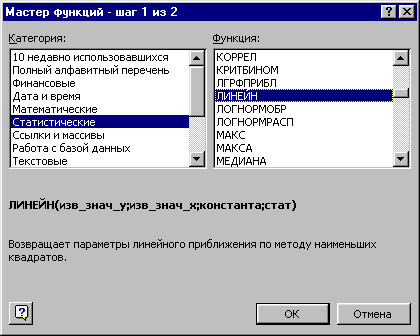
Рисунок 34 – Диалоговое окно Мастер функций





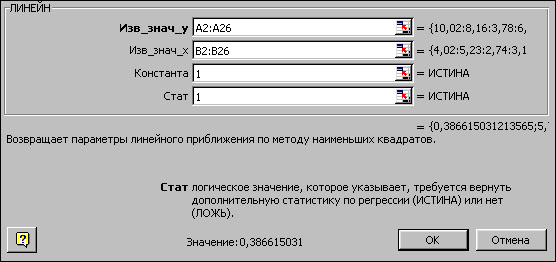
Рисунок 35 – Диалоговое окно ввода аргументов функции ЛИНЕЙН


Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Таблица 5

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F- статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для вычисления параметров экспоненциальной кривой 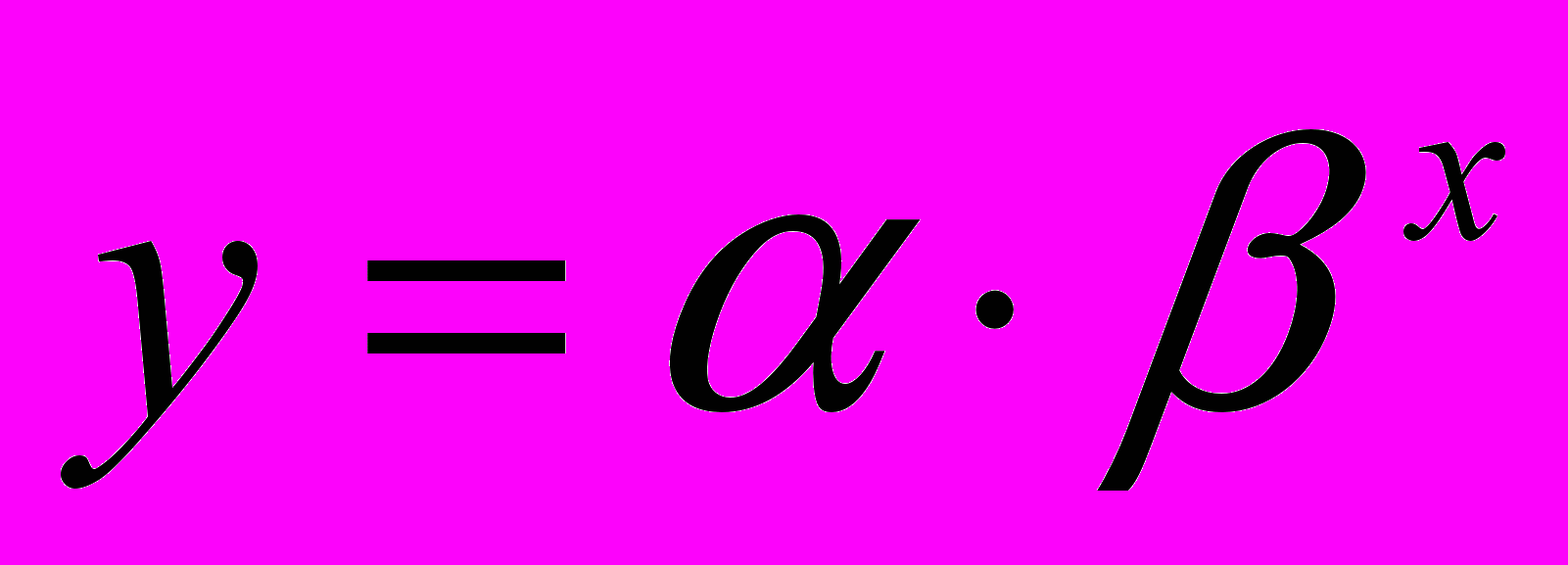в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

Для данных из нашего примера результат вычисления функции ЛИНЕЙН представлен на рис. 36, функции ЛГРФПРИБЛ – на рис. 37.





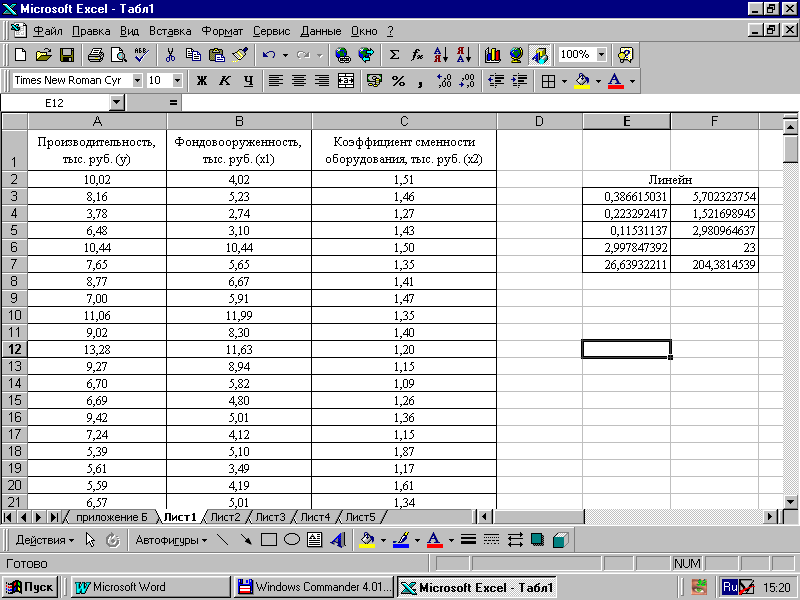
Рисунок 36 – Результат вычисления функции ЛИНЕЙН


Р
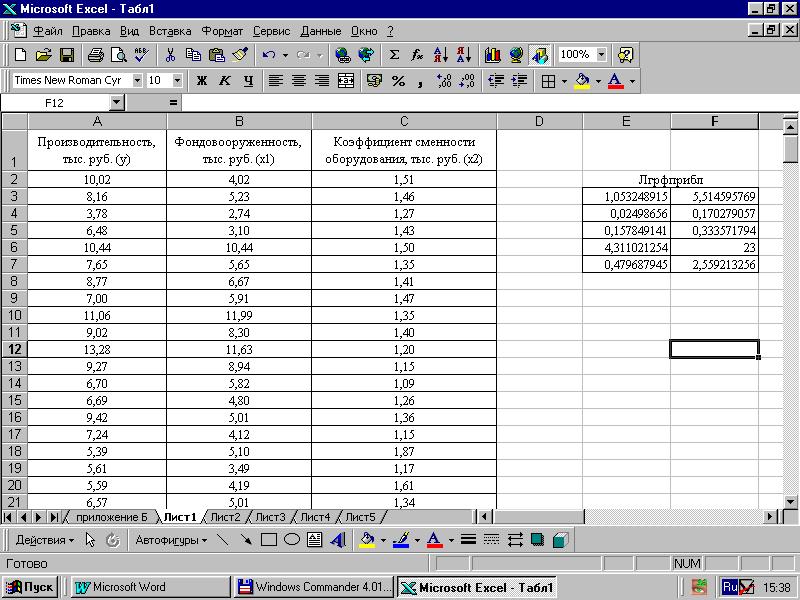
исунок 37 – Результат вычисления функции ЛГРФПРИБЛ


МНОГОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ


Эта операция производится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии. описанной выше, только в отличие от парной регрессии в диалоговом окне при заполнении параметра входной интервал X следует указать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены в приложении Д.