Geum.ru

Рабочая программа учебной дисциплины дпп. Ф. 08 Числовые системы ооп

Вид материалаРабочая программа

Содержание


Математика Курс
«31» января 2005 г
1. Пояснительная записка
1.2 Цели и задачи преподавания дисциплины
1.3 Принципы построения дисциплины
Тематический план
Тематический план
Тематический план
Содержание учебной дисциплины
Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
Содержание учебной дисциплины
Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
Содержание учебной дисциплины
Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
Содержание учебной дисциплины
Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
Методические рекомендации преподавателю
Методические материалы и рекомендации для преподавателя для по модульно-рейтинговой системе оценки знаний студентов покурсу «Чис
Формы и методы самостоятельной работы
Коллоквиум по теме "Системы действительных и комплексных чисел. Алгебра кватернионов"
...
Полное содержание
Подобный материал:
  1   2   3

Министерство образования и науки РФ

Федеральное агентство по образованию

Псковский государственный педагогический университет им.С.М.Кирова

Физико-математический факультет

Кафедра алгебры и геометрии


«Утверждаю»

Декан физико-математического факультета

_____________Медведева И.Н.

«____»____________200 г.


РАБОЧАЯ ПРОГРАММА

учебной дисциплины

ДПП.Ф.08 Числовые системы

ООП 032100.00 Математика с дополнительной специальностью

(код ОКСО 050201)

Факультет: физико-математический

Форма обучения: очная

Курс III, семестр 6

Специальность
Кол - во часов

 
Трудоемкость
ЛК
ПР
СР

Математика с дополнительной специальностью физика Курс III, семестр 6
90
32
16
42

Математика Курс IV, семестр 7
128
42
22
64

Физика с дополнительной специальностью математика Курс III, семестр 6
94
28
20
46

Информатика с дополнительной специальностью математика Курс IV, семестр 8
60
20
10
30



ПСКОВ

2007

Рабочая программа составлена на основании ГОС ВПО по специальности 032100.00 Математика с дополнительной специальностью (код ОКСО 050201)


Номер государственной регистрации

№ 692 пед/сп (новый)

«31» января 2005 г




ДПП.Ф.08. Числовые системы

Рабочая программа принята на заседании кафедры алгебры и геометрии, протокол № ____ от «___» ___________200 г. и представлена на утверждение.




Программу разработал

старший преподаватель кафедры алгебры и геометрии,

кандидат пед. наук ____________Мартынюк О.И.




Зав.кафедрой _______________ /Медведева И.Н.


1. Пояснительная записка


1.1 Требования к содержанию учебной дисциплины из государственного образовательного стандарта



ДПП.Ф.08
Числовые системы

Аксиоматическая теория натуральных чисел. Формулировка аксиоматической теории натуральных чисел. Сложение и умножение натуральных чисел. Неравенства на множестве натуральных чисел. Натуральные кратные и степени элементов полугруппы, их свойства. Категоричность аксиоматической теории натуральных чисел. Независимость аксиомы индукции и ее роль в арифметике. Эквивалентность аксиомы индукции и теоремы о наименьшем элементе. Упорядоченные множества и системы. Аксиоматическая теория целых чисел. Свойства целых чисел, теорема о порядке. Непротиворечивость и категоричность аксиоматической теории целых чисел. Аксиоматическая теория рациональных чисел. Первичные термины и аксиомы. Свойства рациональных чисел. Плотность поля рациональных чисел. Непротиворечивость и категоричность аксиоматической теории рациональных чисел. Последовательности в нормированных полях. Аксиоматическая теория действительных чисел. Действительное число как предел последовательности рациональных чисел, существование корня натуральной степени из положительного действительного числа. Аксиоматическая теория комплексных чисел. Линейные алгебры над полями. Теорема Фробениуса.
90


1.2 Цели и задачи преподавания дисциплины


Одним из основных понятий изучаемых в школьном курсе математики, является понятие числа.

В соответствии с Государственным образовательным стандартом выпускник, получивший квалификацию учителя математики и ___ (в соответствии с дополнительной специальностью), подготовлен к выполнению основных видов профессиональной деятельности учителя математики и ___ (в соответствии с дополнительной специальностью), решению типовых профессиональных задач в учреждениях среднего общего (полного) образования. Выпускник подготовлен для продолжения образования в аспирантуре.

В связи с этим общей целью обучения теории чисел студентов является формирование общепрофессиональных и специальных компетентностей.

Задачи изучения дисциплины:

В результате изучения теории чисел обучающиеся должны:
  • Иметь представление о различных подходах в построении числовых систем.
  • Владеть основными понятиями, характеризующими числовые системы.
  • Уметь проводить доказательства с использованием понятий математической логики.
  • Уметь использовать знания по числовым системам при рассмотрении понятия числа в ШКМ.
  • Уметь использовать знания по числовым системам при изучении смежных дисциплин.
  • Уметь ориентироваться в информационном потоке, находить и перерабатывать информацию, критически относится к полученной информации, владеть новыми информационными технологиями.
  • Иметь опыт употребления символики математической логики для записи определений и теорем.
  • Иметь опыт аргументировать свои действия и предположения.
  • Иметь опыт использования знаний из смежных дисциплин.
  • Иметь опыт ответственного отношения к процессу обучения, выполнения всех требований, предъявляемых в процессе обучения, самоорганизации.


1.3 Принципы построения дисциплины

Числовые системы относятся к дисциплинам предметного блока. Изучение данного курса опирается на знания по математике, полученные студентами в средней школе, при изучении математической логики, алгебры, математического анализа. Полученные знания способствуют формированию специальных компетентностей будущего специалиста.

Материал данной дисциплины является теоретической основой для введения понятия числа в ШКМ, метода математической индукции при проведении доказательства.


Тематический план

Специальность математика


Тема
Трудоем.
ЛК
ПР
СР




128
42
22
64

1. Упорядоченные множества, группы, кольца, поля.
22
9
2
11

2. Система натуральных чисел.
24
8
4
12

3. Система целых чисел.
18
5
4
9

4. Система рациональных чисел.
20
6
4
10

5. Система действительных чисел.
16
6
2
8

6. Система комплексных чисел.
12
4
2
6

7. Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.

16

4

4

8


Тематический план

Специальность: математика с дополнительной специальностью физика


Тема
Трудоем.
ЛК
ПР
СР




90
32
16
42

1. Упорядоченные множества, группы, кольца, поля.
14
6
2
6

2.   Система натуральных чисел.
16
7
2
7

3.   Система целых чисел.
11
4
2
5

4.   Система рациональных чисел.
11
4
2
5

5.   Система действительных чисел.
14
5
2
7

6.   Система комплексных чисел.
10
3
2
5

7.   Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
14
3
4
7


Тематический план

Специальность: физика с дополнительной специальностью математика


Тема
Трудоем.
ЛК
ПР
СР




94
32
16
46

1. Упорядоченные множества, группы, кольца, поля.
14
6
2
6

2.   Система натуральных чисел.
16
7
2
8

3.   Система целых чисел.
11
4
2
6

4.   Система рациональных чисел.
11
4
2
6

5.   Система действительных чисел.
14
5
2
8

6.   Система комплексных чисел.
10
3
2
5

7.   Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
14
3
4
7


Тематический план

Специальность: информатика с дополнительной специальностью математика

Тема
Кол - во часов

 
Трудоем.
ЛК
ПР
СР




60
20
10
30

1.  Упорядоченные множества, группы, кольца, поля.
6
2
1
3

2.   Система натуральных чисел.
12
4
2
6

3.   Система целых чисел.
10
3
2
5

4.   Система рациональных чисел.
10
3
2
5

5.   Система действительных чисел.
10
4
1
5

6.   Система комплексных чисел.
6
2
1
3

7.   Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
6
2
1
3



Содержание учебной дисциплины

Специальность математика


Тема
Кол - во часов




Общее
ЛК
ПР
СР

IV курс, VII семестр
128
44
20
64
  1. Упорядоченные множества, группы, кольца, поля.
22
9
2
11

1.1. Бинарные отношения, их свойства. Примеры. Отношения порядка. Примеры.
5
2
0,5
2,5

1.2. Упорядоченная группа. Упорядоченные кольца и поля. Примеры. Свойства упорядоченной группы, кольца, поля.
5
2
0,5
2,5

1.3. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.

5
2
0,5
2,5

1.4. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.
7
3
0,5
3,5
  1. Система натуральных чисел.
24
8
4
12

2.1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
4
2
–
2

2.2. Сложение натуральных чисел. Существование суммы. Свойства: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых.

6
2
1
3

2.3. Умножение натуральных чисел. Существование произведения. Свойства: коммутативность, дистрибутивность, ассоциативность.
5
1,5
1
2,5

2.4. Вычитание натуральных чисел. Существование разности. Деление натуральных чисел. Существование частного.
4
1
1
2

2.5. Отношение порядка на множестве натуральных чисел. Определение, свойства: монотонность относительно сложения и умножения, 1 – наименьшее натуральное число, теорема Архимеда.
5
1,5
1
2,5
  1. Система целых чисел.
18
5
4
9

3.1. Определение системы целых чисел. Несобственные свойства. Представимость целого числа как разности двух натуральных чисел.
6
2
1
3

3.2. Упорядоченность кольца целых чисел.
6
2
1
3

3.3 Модель системы целых чисел.
6
1
2
3
  1. Система рациональных чисел.
20
6
4
10

4.1. Определение системы рациональных чисел. Несобственные свойства. Представимость рационального числа как частного от деления двух целых чисел.
6
2
1
3

4.2. Упорядоченность поля рациональных чисел.
6
2
1
3

4.3. Всякое линейно и строго упорядоченное поле включает в себя поле рациональных чисел.
2
1



1

4.4. Модель теории рациональных чисел.
6
1
2
3
  1. Система действительных чисел.
16
6
2
8

5.1. Нормированные поля и свойства последовательностей в нормированных полях.
2
1
–
1

5.2. Определение системы действительных чисел. Теорема о продолжении порядка .
1
0,5
–
0,5

5.3. Свойства действительных чисел: действительное число – предел последовательности рациональных чисел, теорема о существовании корня. Определение арифметического корня, рациональной и действительной степени действительного числа, их свойства.
6
2
1
3

5.4. Свойства действительных чисел: теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
5
2,5
1
2,5
  1. Система комплексных чисел.
12
4
2
6

6.1. Определение системы комплексных чисел. Представимость комплексного числа в виде 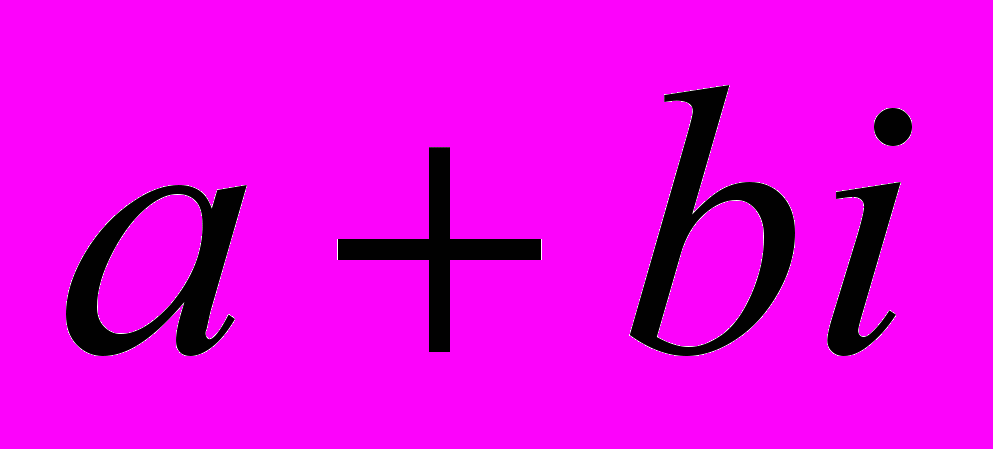. Невозможность упорядочивания. Модели теории комплексных чисел.
12
4
2
6
  1. Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.

16

4

4

8

7.1. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
4
1
1
2

7.2. Алгебры с делением. Алгебра кватернионов.
5
1,5
1
2,5

7.3. Теорема Фробениуса.
3
1,5
–
1,5

7.4. Контрольная работа.
4
–
2
2


Содержание учебной дисциплины

Специальность математика с дополнительной специальностью физика



Тема
Кол - во часов




Общее
ЛК
ПР
СР




90
32
16
42
  1. Упорядоченные множества, группы, кольца, поля.
14
6
2
6

1.1. Бинарные отношения, их свойства. Примеры. Отношения порядка. Примеры.
2,5
1
0,5
1

1.2. Упорядоченная группа. Упорядоченные кольца и поля. Примеры. Свойства упорядоченной группы, кольца, поля.
2,5
1
0,5
1

1.3. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.

4,5
2
0,5
2

1.4. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.
4,5
2
0,5
2
  1. Система натуральных чисел.
16
7
2
7

2.1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
2
2
–



2.2. Сложение натуральных чисел. Существование суммы. Свойства: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых.

4,5
2
0,5
2

2.3. Умножение натуральных чисел. Существование произведения. Свойства: коммутативность, дистрибутивность, ассоциативность.
3,5
1
0,5
2

2.4. Вычитание натуральных чисел. Существование разности. Деление натуральных чисел. Существование частного.
2,5
1
0,5
1

2.5. Отношение порядка на множестве натуральных чисел. Определение, свойства: монотонность относительно сложения и умножения, 1 – наименьшее натуральное число, теорема Архимеда.
3,5
1
0,5
2
  1. Система целых чисел.
11
4
2
5

3.1. Определение системы целых чисел. Несобственные свойства. Представимость целого числа как разности двух натуральных чисел.
3
1
1
1

3.2. Упорядоченность кольца целых чисел.
4

2
1
1

3.3 Модель системы целых чисел.
4
1



3
  1. Система рациональных чисел.
11
4
2
5

4.1. Определение системы рациональных чисел. Несобственные свойства. Представимость рационального числа как частного от деления двух целых чисел.
3
1
1
1

4.2. Упорядоченность поля рациональных чисел.
3
1
1
1

4.3. Всякое линейно и строго упорядоченное поле включает в себя поле рациональных чисел.
2
1



1

4.4. Модель теории рациональных чисел.
3
1



2
  1. Система действительных чисел.
14
5
2
7

5.1. Нормированные поля и свойства последовательностей в нормированных полях.
1
0,5
–
0,5

5.2. Определение системы действительных чисел. Теорема о продолжении порядка .
1
0,5
–
0,5

5.3. Свойства действительных чисел: действительное число – предел последовательности рациональных чисел, теорема о существовании корня. Определение арифметического корня, рациональной и действительной степени действительного числа, их свойства.
6
2
1
3

5.4. Свойства действительных чисел: теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
6
2
1
3
  1. Система комплексных чисел.
10
3
2
5

6.1. Определение системы комплексных чисел. Представимость комплексного числа в виде 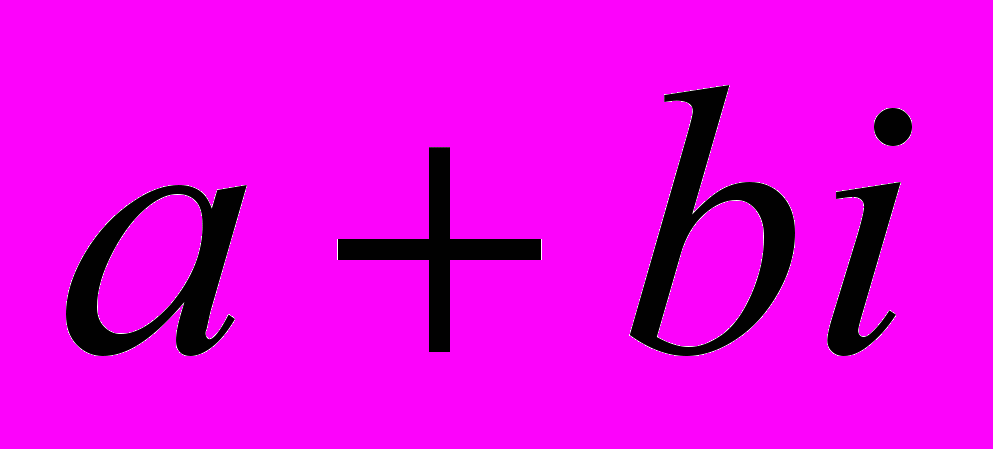. Невозможность упорядочивания.

4
2



2

6.2 Модели теории комплексных чисел
6
1
2
3
  1. Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
14
3
4
7

7.1. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
3
0,5
1
1,5

7.2. Алгебры с делением. Алгебра кватернионов.
4
1
1
2

7.3. Теорема Фробениуса.
3
1,5
–
1,5

7.4. Контрольная работа.
4
–
2
2



Содержание учебной дисциплины

Специальность физика с дополнительной специальностью математика


Тема
Кол - во часов




Общее
ЛК
ПР
СР




94
32
16
46
  1. Упорядоченные множества, группы, кольца, поля.
14
6
2
6

1.1. Бинарные отношения, их свойства. Примеры. Отношения порядка. Примеры.
2,5
1
0,5
1

1.2. Упорядоченная группа. Упорядоченные кольца и поля. Примеры. Свойства упорядоченной группы, кольца, поля.
2,5
1
0,5
1

1.3. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.

4,5
2
0,5
2

1.4. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.
4,5
2
0,5
2
  1. Система натуральных чисел.
16
7
2
8

2.1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
2
2
–



2.2. Сложение натуральных чисел. Существование суммы. Свойства: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых.

4,5
2
0,5
2,5

2.3. Умножение натуральных чисел. Существование произведения. Свойства: коммутативность, дистрибутивность, ассоциативность.
3,5
1
0,5
2,5

2.4. Вычитание натуральных чисел. Существование разности. Деление натуральных чисел. Существование частного.
2,5
1
0,5
1

2.5. Отношение порядка на множестве натуральных чисел. Определение, свойства: монотонность относительно сложения и умножения, 1 – наименьшее натуральное число, теорема Архимеда.
3,5
1
0,5
2
  1. Система целых чисел.
11
4
2
6

3.1. Определение системы целых чисел. Несобственные свойства. Представимость целого числа как разности двух натуральных чисел.
3
1
1
1

3.2. Упорядоченность кольца целых чисел.
4

2
1
2

3.3 Модель системы целых чисел.
4
1



3
  1. Система рациональных чисел.
11
4
2
6

4.1. Определение системы рациональных чисел. Несобственные свойства. Представимость рационального числа как частного от деления двух целых чисел.
3
1
1
1,5

4.2. Упорядоченность поля рациональных чисел.
3
1
1
1,5

4.3. Всякое линейно и строго упорядоченное поле включает в себя поле рациональных чисел.
2
1



1

4.4. Модель теории рациональных чисел.
3
1



2
  1. Система действительных чисел.
14
5
2
8

5.1. Нормированные поля и свойства последовательностей в нормированных полях.
1
0,5
–
1

5.2. Определение системы действительных чисел. Теорема о продолжении порядка .
1
0,5
–
1

5.3. Свойства действительных чисел: действительное число – предел последовательности рациональных чисел, теорема о существовании корня. Определение арифметического корня, рациональной и действительной степени действительного числа, их свойства.
6
2
1
3

5.4. Свойства действительных чисел: теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
6
2
1
3
  1. Система комплексных чисел.
10
3
2
5

6.1. Определение системы комплексных чисел. Представимость комплексного числа в виде 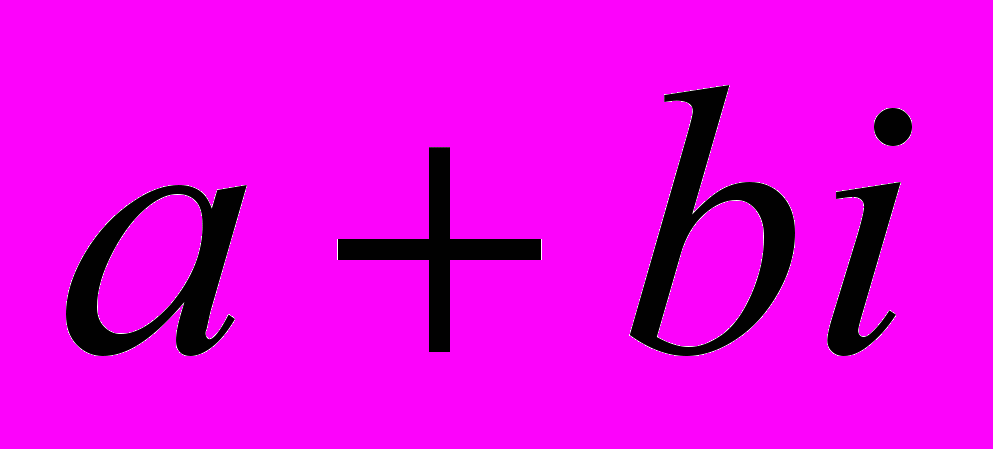. Невозможность упорядочивания.

4
2



2

6.2 Модели теории комплексных чисел
6
1
2
3
  1. Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
14
3
4
7

7.1. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
3
0,5
1
1,5

7.2. Алгебры с делением. Алгебра кватернионов.
4
1
1
2

7.3. Теорема Фробениуса.
3
1,5
–
1,5

7.4. Контрольная работа.
4
–
2
2


Содержание учебной дисциплины

Специальность информатика с дополнительной специальностью математика



Тема
Кол - во часов




Общее
ЛК
ПР
СР

IV курс, VII семестр
60
20
10
30
  1. Упорядоченные множества, группы, кольца, поля.
6
2
1
3

1.1. Отношения порядка. Примеры. Упорядоченная группа. Упорядоченные кольца и поля. Примеры. Свойства упорядоченной группы, кольца, поля.
2
0,5
0,5
1

1.2. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.
1
0,5



0,5

1.3. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.

3
1
0,5
1,5
  1. Система натуральных чисел.
12
4
2
6

2.1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
2
1



1

2.2. Сложение и умножение натуральных чисел. Свойства: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых, дистрибутивность.

4
1
1
2

2.3. Вычитание, деление натуральных чисел. Свойства.
2
1



1

2.4. Отношение порядка на множестве натуральных чисел. Определение, свойства: монотонность относительно сложения и умножения, 1 – наименьшее натуральное число, теорема Архимеда.
4
1
1
2
  1. Система целых чисел.
10
3
2
5

3.1. Определение системы целых чисел. Несобственные свойства. Представимость целого числа как разности двух натуральных чисел.
5
1,5
1
2,5

3.2. Упорядоченность кольца целых чисел. Модель системы целых чисел.
5
1,5
1
2,5
  1. Система рациональных чисел.
10
3
2
5

4.1. Определение системы рациональных чисел. Несобственные свойства. Представимость рационального числа как частного от деления двух целых чисел.
4
1
1
2

4.2. Упорядоченность поля рациональных чисел.
5
1,5
1
2,5

4.3. Всякое линейно и строго упорядоченное поле включает в себя поле рациональных чисел.
1
0,5



0,5
  1. Система действительных чисел.
10
4
1
5

5.1. Определение системы действительных чисел. Теорема о продолжении порядка. Свойства действительных чисел.
3
1,5
–
1,5

5.2. Теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
7
2,5
1
3,5
  1. Система комплексных чисел.
6
2
1
3

6.1. Определение системы комплексных чисел. Представимость комплексного числа в виде 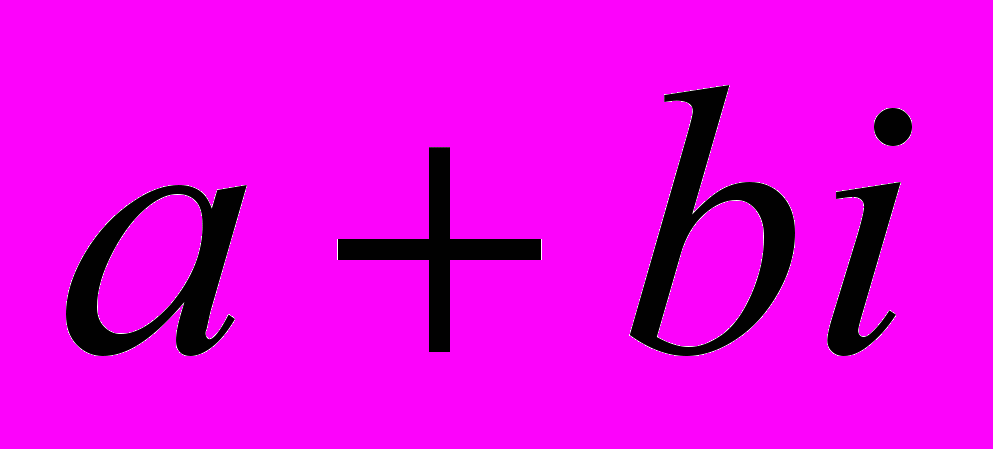. Невозможность упорядочивания. Модели теории комплексных чисел.
6
2
1
3
  1. Линейные алгебры конечного ранга над полем действительных чисел. Алгебра кватернионов.
6
2
1
3

7.1. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
1
0,5



0,5

7.2. Алгебры с делением. Алгебра кватернионов.
4
1
1
2

7.3. Теорема Фробениуса.
1
0,5
–
0,5