Рабочая программа учебной дисциплины дпп. Ф. 08 Числовые системы ооп

Вид материала

Рабочая программа

Содержание Основная часть Защита научно-исследовательской работы Оценка научно-исследовательской работы Защита выпускной квалификационной (дипломной) работы Итоговая оценка выпускной квалификационной (дипломной) работы Контролирующие материалы для аттестации студентов по дисциплине.

Подобный материал:

• Рабочая программа учебной дисциплины дпп. Ф. 07. Теория чисел ооп, 386.12kb.
• Рабочая программа учебной дисциплины дпп. Ф. 06. Геометрия ооп, 265.11kb.
• Программа дисциплины дпп ф. 09 «числовые системы» Специальность 032100 (050201. 65), 121.39kb.
• Рабочая программа учебной дисциплины дпп. Ддс. 04. Геометрия ооп, 258.07kb.
• Учебно-методический комплекс учебной дисциплины дпп. Р. 01. Математическое конструирование, 83.94kb.
• Рабочая программа учебной дисциплины Сетевое программирование и программное обеспечение, 390.77kb.
• Рабочая программа учебной дисциплины программно аппаратные средства защиты информационных, 135.7kb.
• Рабочая программа учебной дисциплины наименование учебной дисциплины Кафедра-разработчик, 301.9kb.
• Рабочая программа учебной дисциплины наименование учебной дисциплины Кафедра-разработчик, 336.98kb.
• Рабочая программа по учебной дисциплине Автоматизированные системы финансового анализа, 744.4kb.

Литература


Основная литература

1. Демидов И.Т. Основания арифметики/Учебное пособие для физ.-мат. фак. Пед. ин-тов/М., Учпедгиз, 1963. - 159с.
   
2. Ларин С.В. Числовые системы. Издат. Центр "Академия". 2001. - 160 с.
   
3. Нечаев В.И. Числовые системы. Учеб. пособие для ст-тов физ. Мат. фак-тов. Пед. инст-тов. М.: Просвещение, 1975
   

Доплнительная литература

1. И.Т. Демидов. Основания арифметики. – М.: Учпедгиз, 1963


Методические рекомендации по подготовке курсовых и дипломных работ (проектов). Проблематика курсовых и дипломных работ.

1. Метод математической индукции.
   
2. Аксиоматический метод построения теорий.
   
3. Модели теории комплексных чисел.
   
4. Тестовый контроль знаний по теме «Числовые системы».
   
5. Тестовый контроль знаний по теме «Рациональные числа» в школьном курсе математики.
   
6. Представление числовой линии в материалах единого государственного экзамена.
   

Структура и содержание научно-исследовательской, курсовой и выпускной квалификационной работы

1. Титульный лист
   
2. Оглавление
   
3. Введение предполагает изложение в любой удобной для автора после­довательности актуальности темы, ее относительной научной новизны, теоретического и практического значения; выявление противоречия и проблемы; определение цели, задач; указание объекта и предмета исследования; пере­числение этапов и объема работы, методов ее выполнения
   
4. Основная частьобычно включает 2-3 главы:
   

1-я – изложение краткой истории исследуемой проблемы, теоретическое обоснование работы, которое выводит на основной предмет исследования;

2-я – описание содержания и хода опытно-экспериментальной работы:

1) характеристику исследуемого объекта в той или иной степени глубины, что зависит от поставленных цели и задач;

2) характеристику этапов исследования с указанием частных цели и задач для каждого из них; описание содержания каждого этапа;

3) описание конкретных методик, способов и приемов, используемых при организации исследования;

3-я – представление результатов работы, их анализ и обобщение, обсуждение

5. Заключение представляет собой последовательное, логически стройное изложение полученных итогов и их соотношение с целью, задачами, научной новизной, теоретической значимостью и практической ценностью, сформулированными во введении
   
6. Приложение – это часть основного текста, которая имеет дополнительное (обычно справочное) значение, но является необходимой для более полного освещения темы; содержит материалы, не являющиеся насущно важными для понимания решения научной задачи.
   

Защита научно-исследовательской работы предполагает:

1). изложение основных положений работы в течении 7-10 минут;

2). ответы на вопросы преподавателей и прочих присутствующих.

Оценка научно-исследовательской работы определяется:

1) глубиной содержания;

2) четкостью выступления;

3) степенью самостоятельности при выполнении исследования (это отра­жается, как правило, в отзыве научного руководителя);

4) глубиной знаний, которые студент демонстрирует в тексте и в ответах на вопросы;

5) качеством практической части работы;

6) оформлением работы в целом.

Защита выпускной квалификационной (дипломной) работы

проходит на открытом заседании Государственной аттестационной комиссии. Для выступления предоставляется 10 минут. Затем зачи­тываются отзыв и внешняя рецензия, и выпускник отвечает на вопросы членов ко­миссии и присутствующих, а также на замечания, имеющиеся в отзыве и рецензии.

Итоговая оценка выпускной квалификационной (дипломной) работы учитывает:

- доклад;

- ответы на вопросы;

- оценку рецензента;

- оценку руководителя.


Контролирующие материалы для аттестации студентов по дисциплине.


Вопросы к экзамену по курсу «Числовые системы»

1. Отношение порядка. Определение, свойства, примеры.
   
2. Упорядоченная группа. Определение, свойства.
   
3. Упорядоченное кольцо. Определение, свойства.
   
4. Упорядоченное поле. Определение, свойства.
   
5. Абсолютная величина. Эквивалентность определений. Свойство модуля суммы.
   
6. Абсолютная величина. Свойства: модуль разности, произведения.
   
7. Критерий возможности упорядочивания кольца.
   
8. Критерий однозначности порядка.
   
9. Критерий продолжения порядка.
   
10. Система натуральных чисел. Определение. Свойства, вытекающие из определения.
    
11. Сложение натуральных чисел. Существование и однозначность суммы.
    
12. Сложение натуральных чисел. Основные свойства.
    
13. Умножение натуральных чисел. Существование и однозначность произведения.
    
14. Умножение натуральных чисел. Основные свойства.
    
15. Отношение порядка на множестве натуральных чисел. Теоремы о монотонности.
    
16. Отношение порядка на множестве натуральных чисел. Свойства неравенств, теорема Архимеда.
    
17. Вычитание натуральных чисел.
    
18. Деление натуральных чисел.
    
19. Кратное и степень натурального числа. Свойства.
    
20. Система целых чисел. Собственные свойства.
    
21. Упорядоченность кольца целых чисел.
    
22. Модель теории целых чисел.
    
23. Система рациональных чисел. Представимость рационального числа.
    
24. Упорядоченность поля рациональных чисел.
    
25. Всякое линейно упорядоченное поле включает в себя…
    
26. Модель теории рациональных чисел.
    
27. Система действительных чисел. Связь с полем рациональных чисел.
    
28. Теорема о существовании корня.
    
29. Определение корня и его свойства.
    
30. Определение и свойства рациональной степени.
    
31. Упорядоченность поля действительных чисел.
    
32. Теорема о двойной последовательности. Примеры построения последовательностей.
    
33. Теорема о рубеже сечения.
    
34. Система комплексных чисел. Свойства.
    
35. Модель теории комплексных чисел.
    
36. Алгебра кватернионов.
    

Глоссарий

Бинарное отношение	Любое подмножество декартова квадрата данного множества
Отношение порядка	Бинарное отношение , обладающее свойствами антисимметричности и транзитивности
Упорядоченная группа	Группа, в которой введено отношение порядка, монотонное относительно групповой операции
Упорядоченное кольцо, поле	Кольцо (поле), в котором введено отношение порядка монотонное сложения и монотонное относительно умножения на положительные элементы
Система натуральных чисел	Непустое множество, элементы которого называются натуральными числами, с введенным отношением «следовать за» и аксиомами Пиано
Система целых чисел	Кольцо, являющееся наименьшим расширением полукольца натуральных чисел
Система рациональных чисел	Поле, являющееся наименьшим расширением кольца целых чисел
Система действительных чисел	Архимедовски линейно и строго упорядоченное поле, в котором каждая фундаментальная последовательность является сходящейся
Система комплексных чисел	Поле, являющееся наименьшим расширением поля действительных чисел и содержащее элемент i, такой что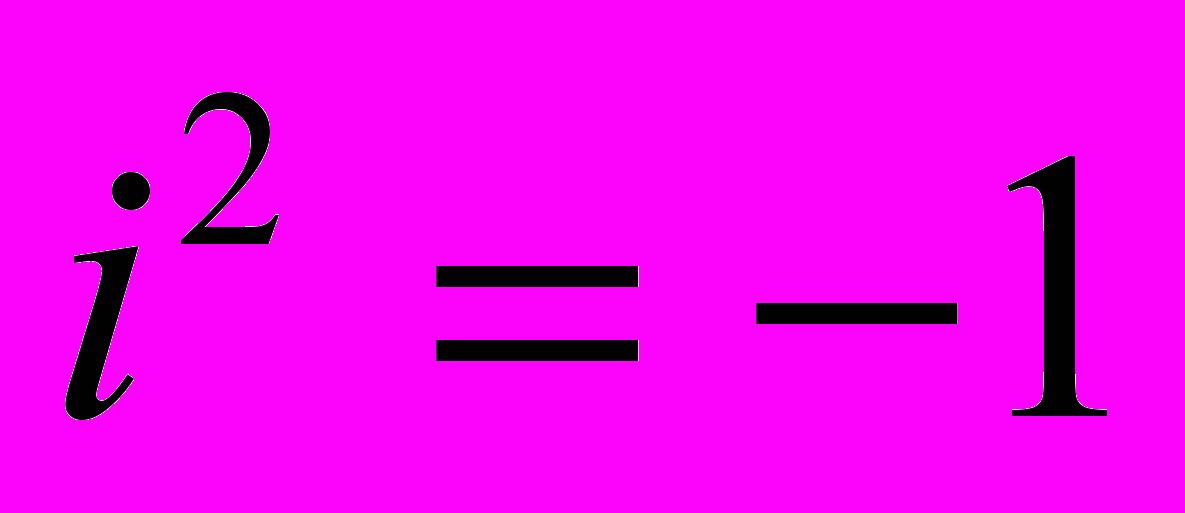
Алгебра кватернионов	Алгебра ранга 4 над полем действительных чисел.