Рабочая программа учебной дисциплины дпп. Ф. 08 Числовые системы ооп
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины дпп. Ф. 07. Теория чисел ооп, 386.12kb.
- Рабочая программа учебной дисциплины дпп. Ф. 06. Геометрия ооп, 265.11kb.
- Программа дисциплины дпп ф. 09 «числовые системы» Специальность 032100 (050201. 65), 121.39kb.
- Рабочая программа учебной дисциплины дпп. Ддс. 04. Геометрия ооп, 258.07kb.
- Учебно-методический комплекс учебной дисциплины дпп. Р. 01. Математическое конструирование, 83.94kb.
- Рабочая программа учебной дисциплины Сетевое программирование и программное обеспечение, 390.77kb.
- Рабочая программа учебной дисциплины программно аппаратные средства защиты информационных, 135.7kb.
- Рабочая программа учебной дисциплины наименование учебной дисциплины Кафедра-разработчик, 301.9kb.
- Рабочая программа учебной дисциплины наименование учебной дисциплины Кафедра-разработчик, 336.98kb.
- Рабочая программа по учебной дисциплине Автоматизированные системы финансового анализа, 744.4kb.
Методические рекомендации преподавателю
Курс «Числовые системы» является одним из базовых математических курсов, поэтому его изучению должно придаваться особое значение.
Главная цель курса дать студентам современные знания и хорошую практическую подготовку, необходимую будущему учителю для преподавания математики, алгебры в средней школе и квалифицированного проведения факультативных курсов.
При построении лекционного курса важно продумать не только содержание, но и построение лекционного курса, логику изложения материала каждого его раздела. Изложение курса рекомендуется начать с темы «Упорядоченные геруппы, кольца, поля», опираясь на данный материал при чтении других тем курса.
Чтение лекционного курса должно проводиться на достаточно высоком научном уровне, однако строгость изложения материала необходимо сочетать с его доступностью. Особое внимание необходимо обратить на прочность получаемых студентами знаний. Данные разделы курса алгебры обладают богатством внутрипредметных и межпредметных связей.
Для активизации самостоятельной работы студентов и экономии времени, отводимого на лекционный курс, ряд тем выносится на самостоятельное изучение. Доказательства свойств степени и кратного натуральных чисел, построение моделей систем целых, рациональных, комплексных чисел, а также доказательства свойств арифметического кроня и рациональной степени действитеольного числа выносятся на самостоятельное изучение. Самостоятельная работа со студентами проводится в часы самостоятельной работы в форме консультаций. Распределение часов руководства самостоятельной работой учитывает важность рассматриваемой темы и возможную сложность при освоении ее студентами.
Для контроля за самостоятельной работой над теоретическим материалом целесообразно проводить коллоквиумы по разделам курса.
Текущий контроль результатов освоения курса проводится на практических занятиях. В начале каждого практического занятия рекомендуется проводить небольшие самостоятельные работы по теоретическим вопросам, относящимся к теме занятия. Особое внимание следует уделить проверке знаний основных определений, теоретических фактов, формул.
Традиционными формами контроля являются коллоквиумы. При проведении контрольной работы целесообразно предлагать задачи средней сложности рассматриваемые на практических занятиях.
Методические материалы и рекомендации для преподавателя для по модульно-рейтинговой системе оценки знаний студентов по
курсу «Числовые системы»
Педагогический контроль является важным элементом учебного процесса, благодаря которому реализуется обратная связь в обучении, позволяющая регулировать и корректировать ход обучения. Одной из разновидностей контроля качества знаний является модульно-рейтинговая система.
Весь материал курса разбит на 4 блока (модуля):
- Упорядоченные множества, группы, кольца, поля.
- Система натуральных чисел.
- Система целых чисел. Система рациональных чисел.
- Система действительных чисел. Система комплексных чисел. Алгебра кватернионов.
Рейтинговая оценка успеваемости студентов по данному курсу включает в себя лекторский, текущий, блочный контроль. Максимальное количество баллов – 100. Лекторский контроль предполагает проведение проверочной работы по лекционному материалу, текущий контроль: проведение самостоятельных работ по материалу предыдущего практического занятия или домашней работе. Каждая из таких работ оценивается в 3 балла. Блочный контроль предполагает проведение коллоквиума по каждому блоку.
Блоки в зависимости от объёма материала оцениваются определенным количеством баллов.
В начале семестра студентам предлагается технологическая карта и правила перевода полученных ими баллов в экзаменационные оценки.
| | Технологическая карта (Числовые системы) | |||
| | Вид отчетности | Сроки | количество баллов | |
| 1 | Упорядоченные группы, кольца, поля | коллоквиум | | 8 |
| тест | | 5 | ||
| 2 | Система натуральных чисел | | 12 | |
| 3 | Системы целых и рациональных чисел | | 12 | |
| 4 | Системы действительных, комплексных чисел, алгебра кватернионов | | 15 | |
| 5 | Тест | | 10 | |
| 6 | Контрольная работа | | 8 | |
| 8 | Текущий контроль | | 30 | |
| | Максимальное количество баллов | | 100 |
Итоговая оценка ставится следующим образом:
| Проценты | Баллы | Оценка |
| 60-75 | 60-75 | удовлетворительно |
| 76 –85 | 76 –85 | хорошо |
| 86 –100 | 86 –100 | отлично |
Курс «Числовые системы» является теоретическим, все практические задания – это задания на доказательство. В связи с этим, при обычной форме контроля знаний мотивация студентов во время семестра слабая. Проведение небольших самостоятельных работ по материалу предыдущей лекции или практического занятия может существенно повысить заинтересованность студентов, заставит их разбираться в материале, как прошедшей, так и текущей лекции.
По каждому блоку предполагается проведение коллоквиума. Поскольку объём материала различный, то каждый коллоквиум оценивается разным числом баллов. По первой теме кроме сдачи коллоквиума предполагается написание теста «Группы, кольца, поля». Материал, изучаемый студентами на младших курсах и используемый при изучении данной темы. При сдаче 2 и 3 коллоквиумов студентам может быть предложено практическое задание по материалу данных тем. Студенты претендующие на высокие оценки, как правило успешно с ним справляются. При сдаче 4 коллоквиума предлагаются для доказательства свойства арифметического корня и рациональной степени, которые студенты при подготовке к коллоквиуму должны доказать самостоятельно. А также для студентов претендующих на экзамене на оценку «отлично» можно предложить для самостоятельного изучения доказательство теоремы Фробениуса.
Контрольная работа включает в себя те практические задания, которые разбираются в семестре. Каждый вариант состоял из 4 таких заданий, оцениваемых каждое из 2 баллов.
В конце семестра студентам предлагается тест по данному курсу.
Студенты, набравшие более 60 баллов могут согласиться с полученной оценкой или сдавать экзамен. Студенты, набравшие от 35 до 59 баллов, сдают экзамен.
Если количество баллов, набранных студентом в течение семестра, было ниже «порога успеваемости» – 35 %, то перед сдачей экзамена студент должен «добрать баллы» до порога успеваемости в интерактивном режиме.
Например, в случае, если студент во время семестра набрал 23 балла, то он должен ответить на 12 дополнительных вопросов.
Формы и методы самостоятельной работы
Курс «Числовые системы» теоретический, объемный поэтому целесообразно ряд тем вынести на самостоятельное изучение.
- Свойства степени и кратного натуральных чисел.
- Построение модели теории целых чисел.
- Построение модели теории рациональных чисел.
- Построение последовательностей рациональных чисел.
- Свойства арифметического корня из действительного числа.
- Свойства рациональной степени действительного числа.
- Построение модели теории комплексных чисел.
- Решение линейных уравнений в алгебре кватернионов.
Рекомендации по организации самостоятельной работы студентов по курсу «Числовые системы»
Самостоятельная работа со студентами проводится в часы самостоятельной работы в форме консультаций. Распределение часов руководства самостоятельной работой учитывает важность рассматриваемой темы и возможную сложность при освоении ее студентами. Текущий контроль результатов освоения курса проводится на практических занятиях.
Вопросы к коллоквиуму по теме «Упорядоченные группы, кольца, поля»
1. Бинарные отношения, их свойства. Примеры. Отношения порядка. Примеры.
2. Упорядоченная группа. Свойства.
3. Упорядоченные кольца и поля. Свойства.
4. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.
5. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.
Вопросы к коллоквиуму по теме «Система натуральных чисел».
1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
2. Сложение натуральных чисел. Существование суммы.
3. Свойства сложения: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых.
4. Умножение натуральных чисел. Существование произведения.
5. Свойства умножения: коммутативность, дистрибутивность, ассоциативность.
6. Вычитание натуральных чисел. Существование разности.
7. Деление натуральных чисел. Существование частного.
8. Отношение порядка на множестве натуральных чисел. Определение, свойства.
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Вопросы к коллоквиуму по теме «Системы целых и рациональных чисел».
1. Определение системы целых чисел. Несобственные свойства.
2. Представимость целого числа как разности двух натуральных чисел.
3. Упорядоченность кольца целых чисел.
4. Модель системы целых чисел.
5.Определение системы рациональных чисел. Несобственные свойства.
6. Представимость рационального числа как частного от деления двух целых чисел.
7. Упорядоченность поля рациональных чисел.
8. Модель теории рациональных чисел
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Вопросы к коллоквиуму по теме «Системы действительных и комплексных чисел. Алгебра кватернионов.».
1. Нормированные поля и свойства последовательностей в нормированных полях.
2. Определение системы действительных чисел. Теорема о продолжении порядка .
3. Свойства действительных чисел: действительное число – предел последовательности рациональных чисел, теорема о существовании корня.
4. Определение арифметического корня, рациональной и действительной степени действительного числа, их свойства.
5. Свойства действительных чисел: теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
6. Определение системы комплексных чисел. Представимость комплексного числа в виде
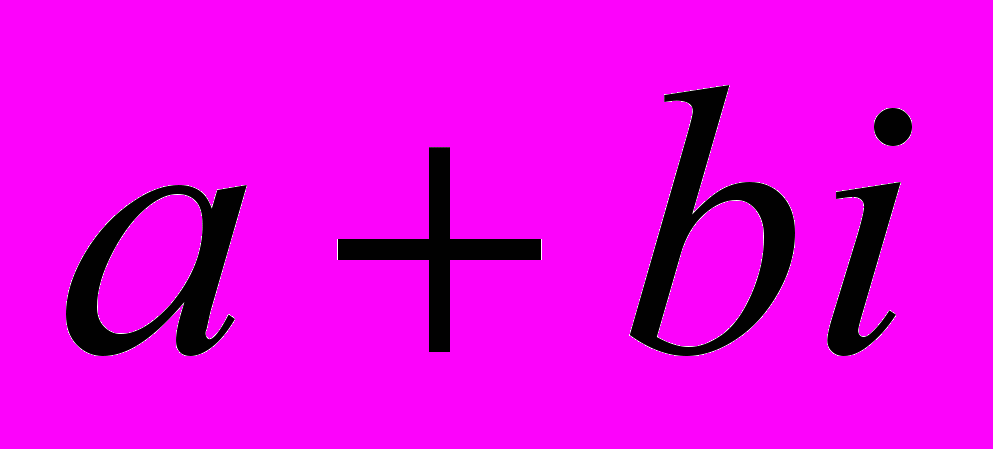 .
.7. Невозможность упорядочивания. Модели теории комплексных чисел.
8. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
9. Алгебры с делением. Алгебра кватернионов.
10. Теорема Фробениуса.
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Формы текущего, промежуточного и итогового контроля.
Весь материал курса разбит на 4 блока:
- Упорядоченные множества, группы, кольца, поля.
- Система натуральных чисел.
- Система целых чисел. Система рациональных чисел.
- Система действительных чисел. Система комплексных чисел. Алгебра кватернионов.
Каждый блок в зависимости от объёма материала оценивается определенным количеством баллов.
| | | Вид отчетности |
| 1 | Упорядоченные группы, кольца, поля | коллоквиум |
| тест | ||
| 2 | Система натуральных чисел | коллоквиум |
| 3 | Системы целых и рациональных чисел | коллоквиум |
| 4 | Системы действительных, комплексных чисел, алгебра кватернионов | коллоквиум |
| 5 | Итоговый тест по курсу | |
| 6 | Контрольная работа | |
| 8 | Текущий контроль | |
Лекторский контроль предполагает проведение проверочной работы по материалу предыдущей лекции (3 балла). Текущий контроль: проведение самостоятельных работ по материалу предыдущего занятия или домашней работе (3 балла). Блочный контроль: проведение коллоквиума по каждому блоку.
Вопросы к коллоквиуму по теме «Упорядоченные группы, кольца, поля»
1. Бинарные отношения, их свойства. Примеры. Отношения порядка. Примеры.
2. Упорядоченная группа. Свойства.
3. Упорядоченные кольца и поля. Свойства.
4. Абсолютная величина элемента линейно и строго упорядоченного кольца. Свойства абсолютной величины.
5. Критерии возможности упорядочивания кольца (поля), однозначности порядка, продолжения порядка.
Вопросы к коллоквиуму по теме «Система натуральных чисел».
1. Определение системы натуральных чисел. Свойства, вытекающие из определения. Принцип математической индукции.
2. Сложение натуральных чисел. Существование суммы.
3. Свойства сложения: ассоциативность, коммутативность, отличие суммы от каждого из слагаемых.
4. Умножение натуральных чисел. Существование произведения.
5. Свойства умножения: коммутативность, дистрибутивность, ассоциативность.
6. Вычитание натуральных чисел. Существование разности.
7. Деление натуральных чисел. Существование частного.
8. Отношение порядка на множестве натуральных чисел. Определение, свойства.
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Вопросы к коллоквиуму по теме «Системы целых и рациональных чисел».
1. Определение системы целых чисел. Несобственные свойства.
2. Представимость целого числа как разности двух натуральных чисел.
3. Упорядоченность кольца целых чисел.
4. Модель системы целых чисел.
5.Определение системы рациональных чисел. Несобственные свойства.
6. Представимость рационального числа как частного от деления двух целых чисел.
7. Упорядоченность поля рациональных чисел.
8. Модель теории рациональных чисел
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Вопросы к коллоквиуму по теме «Системы действительных и комплексных чисел. Алгебра кватернионов.».
1. Нормированные поля и свойства последовательностей в нормированных полях.
2. Определение системы действительных чисел. Теорема о продолжении порядка .
3. Свойства действительных чисел: действительное число – предел последовательности рациональных чисел, теорема о существовании корня.
4. Определение арифметического корня, рациональной и действительной степени действительного числа, их свойства.
5. Свойства действительных чисел: теоремы о двойной последовательности, о рубеже сечения. Построение последовательностей рациональных чисел. О моделях системы действительных чисел.
6. Определение системы комплексных чисел. Представимость комплексного числа в виде
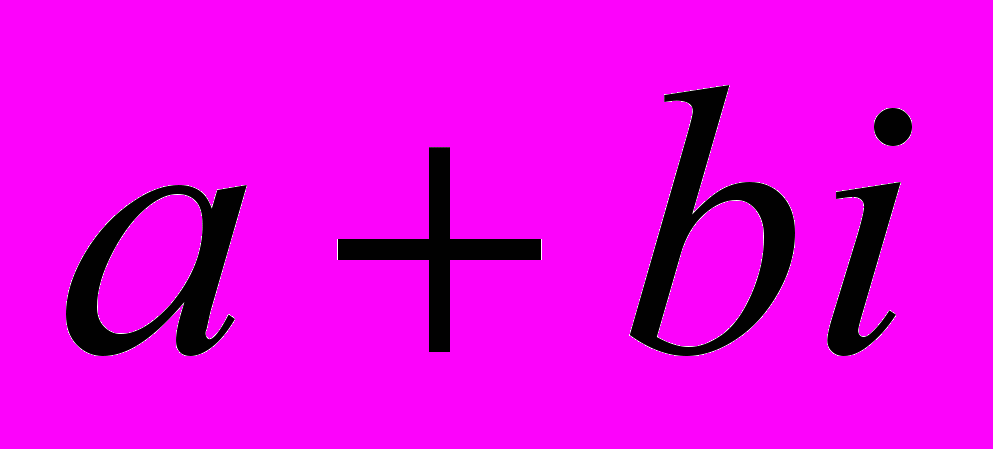 .
.7. Невозможность упорядочивания. Модели теории комплексных чисел.
8. Определение алгебры конечного ранга над полем, примеры алгебр над полем действительных чисел.
9. Алгебры с делением. Алгебра кватернионов.
10. Теорема Фробениуса.
В качестве задания на коллоквиуме студент получает теоретический вопрос и практическое задание.
Коллоквиум по теме «Системы действительных и комплексных чисел. Алгебра кватернионов.». может приниматься также и в форме математического КВНа. Далее предложена технологическая карта для сдачи коллоквиума в такой форме.
| | Коллоквиум по теме "Системы действительных и комплексных чисел. Алгебра кватернионов" | |||
| | | | | |
| | Название | Содержание | Оценка | Примечание |
| 1 | Визитка | Представление команд должно содержать термины используемые в алгебре с их расшифровкой (необязательно математической) | 4 | Оценивается общая идея и использование терминов |
| 2 | Разминка | 3 вопроса команд друг другу по заранее известной теме (например: доказательство теоремы о рубеже сечения) | 0-3 | В случае, если команда соперника не отвечает на поставленный вопрос может быть выбран любой представитель команды задававшей вопрос для ответа |
| 3 | 2 вопроса преподавателя обеим командам по заранее известной теме | 0-2 | Вопросы могут быть одинаковыми: тогда ответы письменно. Либо вопросы "вытягиваются" командами, тогда они разные | |
| 4 | Теоретический | Доказательство свойств корня и рациональной степени (каждому 2 свойства) | 0-4 | 1 свойство корня и одно свойство степени, каждое оценивается до 3 баллов |
| 5 | Кто больше? | Доказательство свойств натуральных, целых и рациональных чисел. Свойства формулируются заранее. Каждое доказательство оценивается отдельно (1 или 2 балла). Чем больше доказательств, тем больше очков заработает команда. | 0-2 и дополнительно за каждое "иное" доказательство | Каждая команда при подготовке к конкурсу оформляет свои доказательства письменно. Во время конкурса может быть вызван любой участник команды для доказательства свойств |
| 6 | Домашнее задание | Командам предлагаются определения, формулировки теорем, которые они должны использовать при создании сюжета. Тема свободная. Форма свободная: стихотворная, прозаическая… | 4 | |
| | | | | |
| | Баллы заработанные командой по итогам конкурсов 1-3 и 5-6 ставятся каждому участнику команды + индивидуальные баллы каждого полученные в 4 конкурсе. | | |
