Построение погрешностей для перемещений дискретных моделей двумерных композитов регулярной структуры с применением функций верхних и нижних оценок

Вид материала

Документы

Содержание Список литературы

Подобный материал:

• Цифровая обработка сигналов, 25.15kb.
• 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.
• Программа вступительного экзамена в магистратуру элементы теории погрешностей, 51.03kb.
• Математика и компьютерные науки, 102.47kb.
• Изменения структуры и свойств цементных композитов под влиянием углеродных наномодификаторов, 69.63kb.
• Методические указания к практическим занятиям для студентов медицинских факультетов, 1032.27kb.
• Рентгенографические исследования и построение моделей структуры ряда углеродных материалов, 315.25kb.
• План изучения дисциплины № п/п, 155.57kb.
• Изучение математических функций с использованием км-школы в VII-VIII классах, 166.32kb.
• Основными задачами данного цикла лекций являются: изложение основных положений метода, 18.46kb.

ПОСТРОЕНИЕ ПОГРЕШНОСТЕЙ ДЛЯ ПЕРЕМЕЩЕНИЙ ДИСКРЕТНЫХ МОДЕЛЕЙ ДВУМЕРНЫХ КОМПОЗИТОВ РЕГУЛЯРНОЙ СТРУКТУРЫ

С ПРИМЕНЕНИЕМ ФУНКЦИЙ ВЕРХНИХ И НИЖНИХ ОЦЕНОК

А.Д. Матвеев

ИВМ СО РАН
660036, Красноярск,
e-mail: mtv @ icm.krasn.ru


В настоящее время при расчете композитов с учетом структуры широко используют метод конечных элементов (МКЭ) [1,2]. В ряде случаев для инженерной практики важно знать точное значение относительной погрешности для перемещений в тех узлах дискретной модели композита, в которых возникают большие перемещения. Пусть 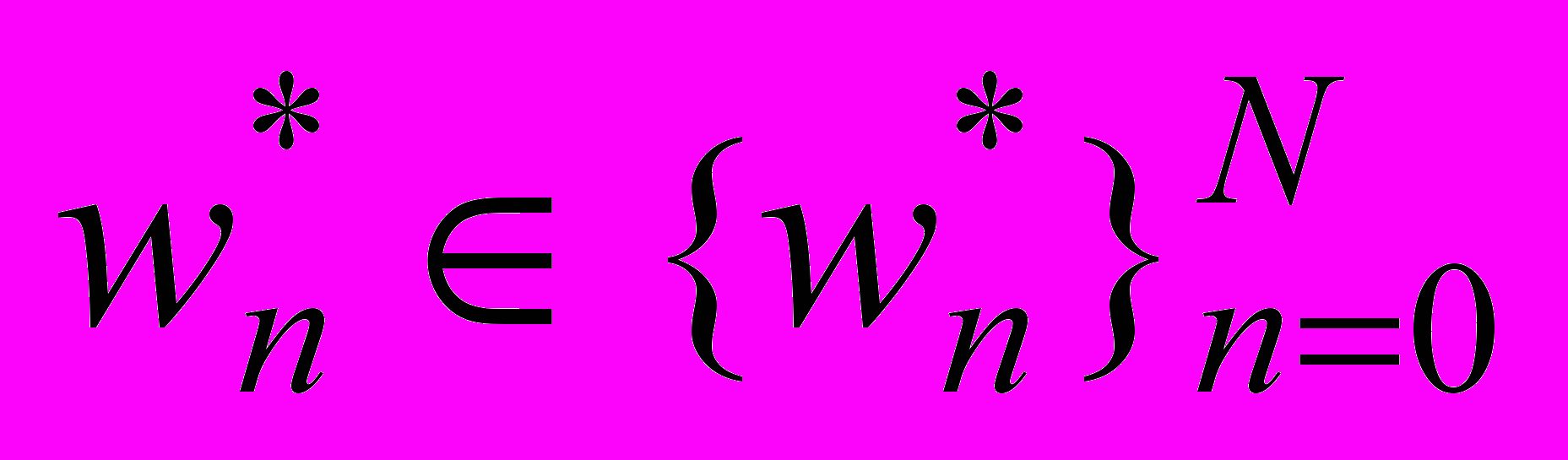сеточное решение плоской задачи теории упругости, построенное (по микроподходу) с помощью МКЭ для регулярного разбиения 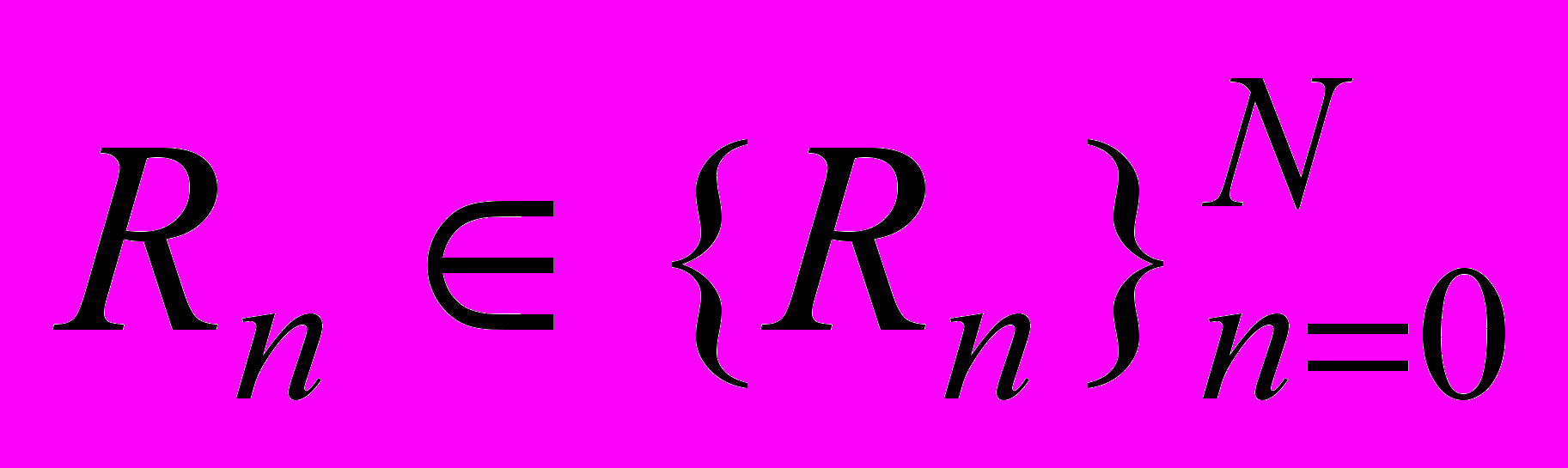двумерного композита, имеющего гладкую границу и регулярную структуру заданного вида; 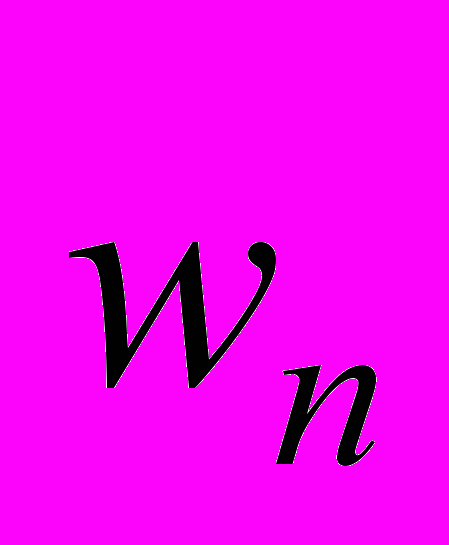- максимальное значение (по модулю) сеточной функции 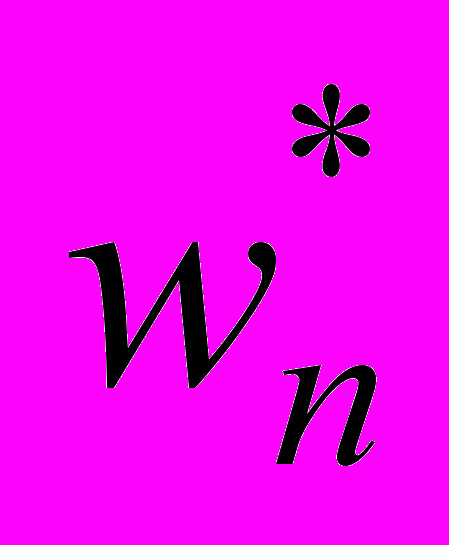; пусть 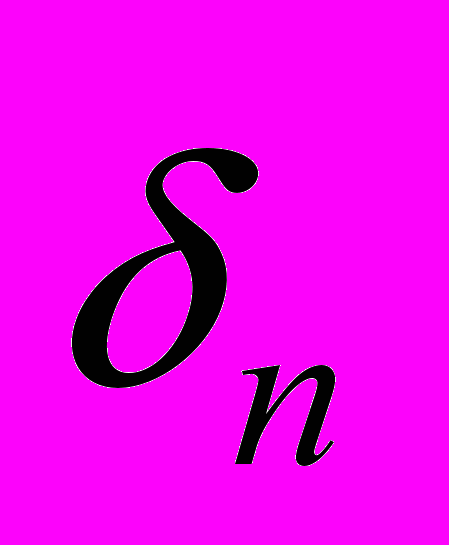- относительная погрешность (по модулю) для решения 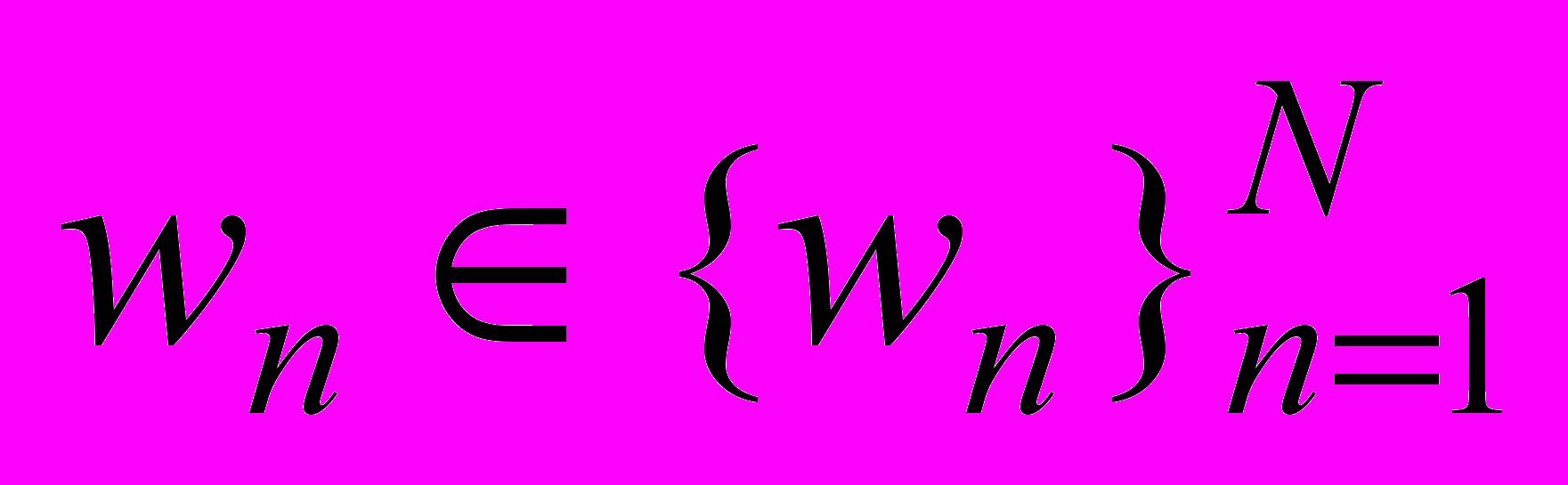, т. е.

,

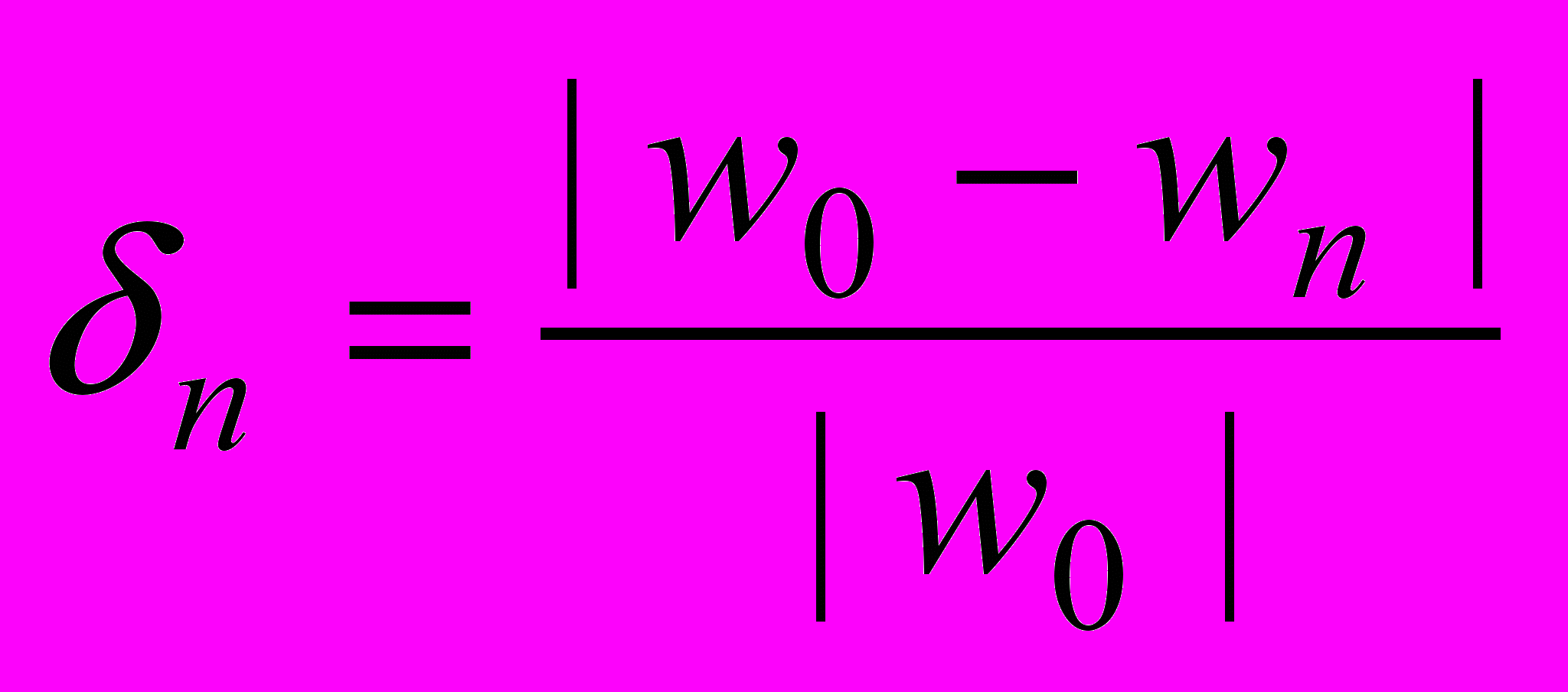где 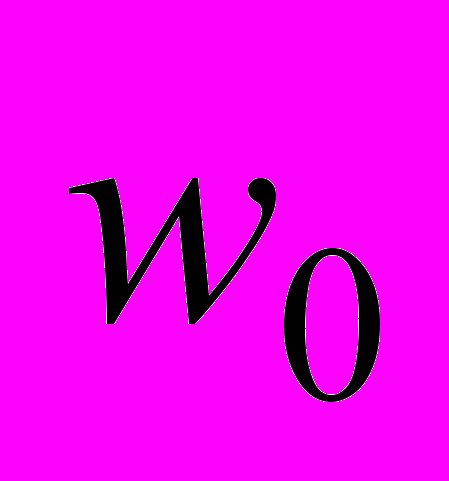- точное решение для ,

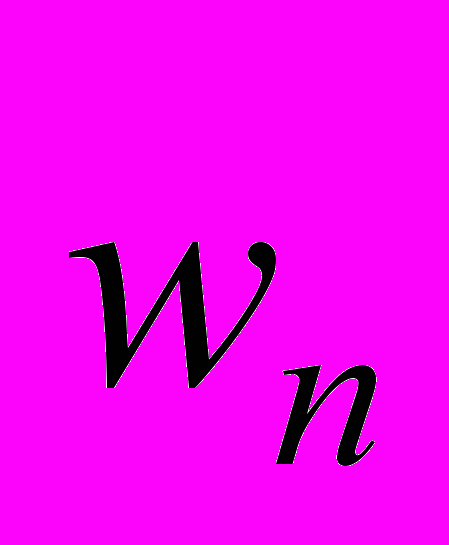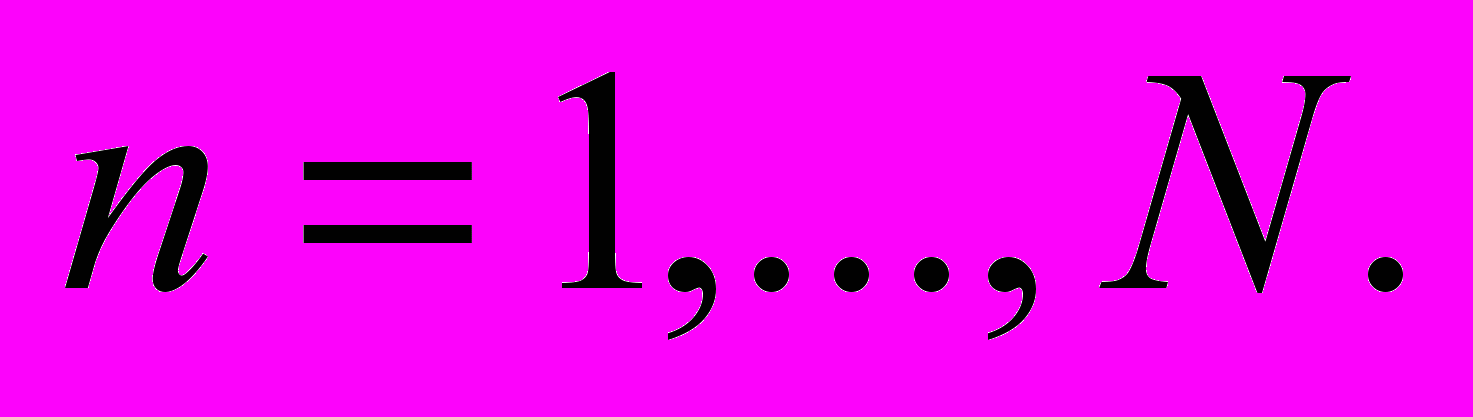
Определить точное значение погрешности 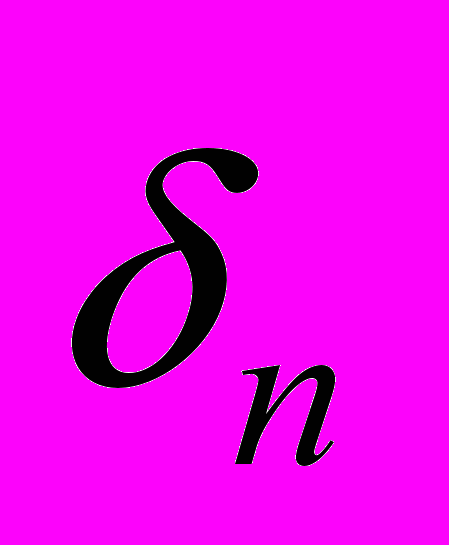очень сложно и поэтому в инженерных расчетах применяют погрешность 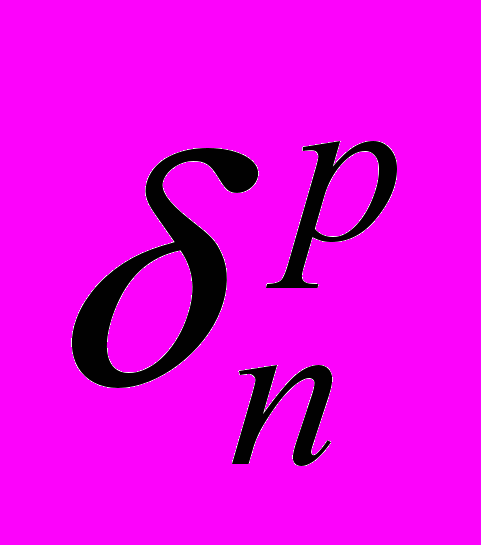, которая приближенно представляет истинную 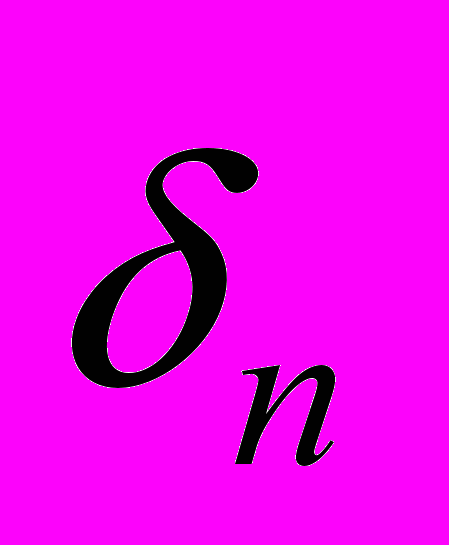, т. е. 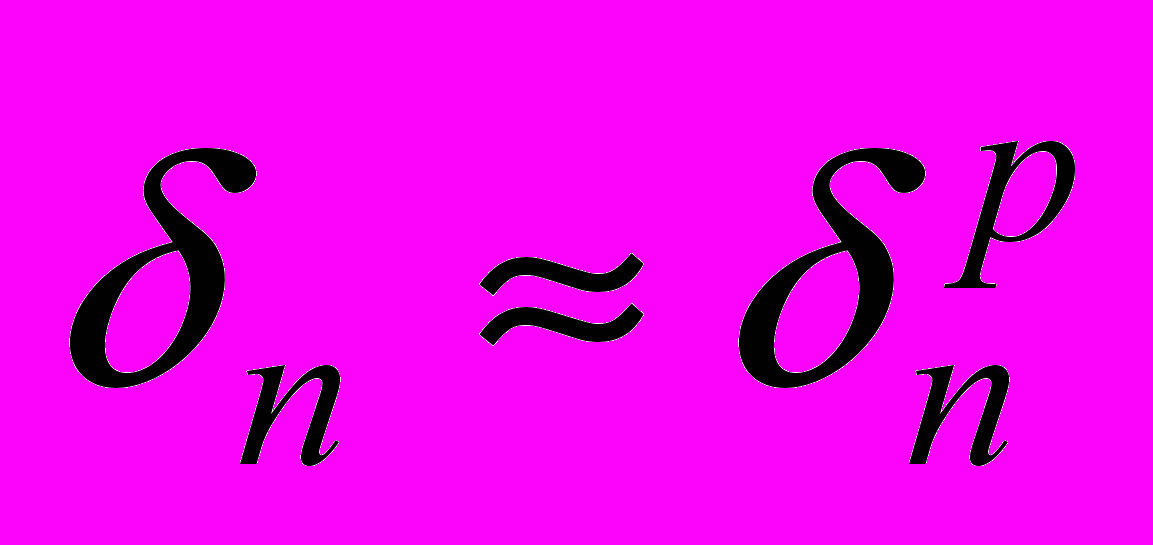. Таким образом, для практики возникает следующая проблема: определить такую (расчетную) погрешность 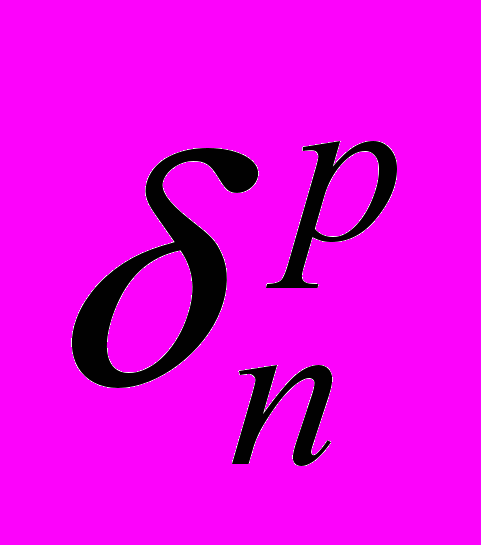, что

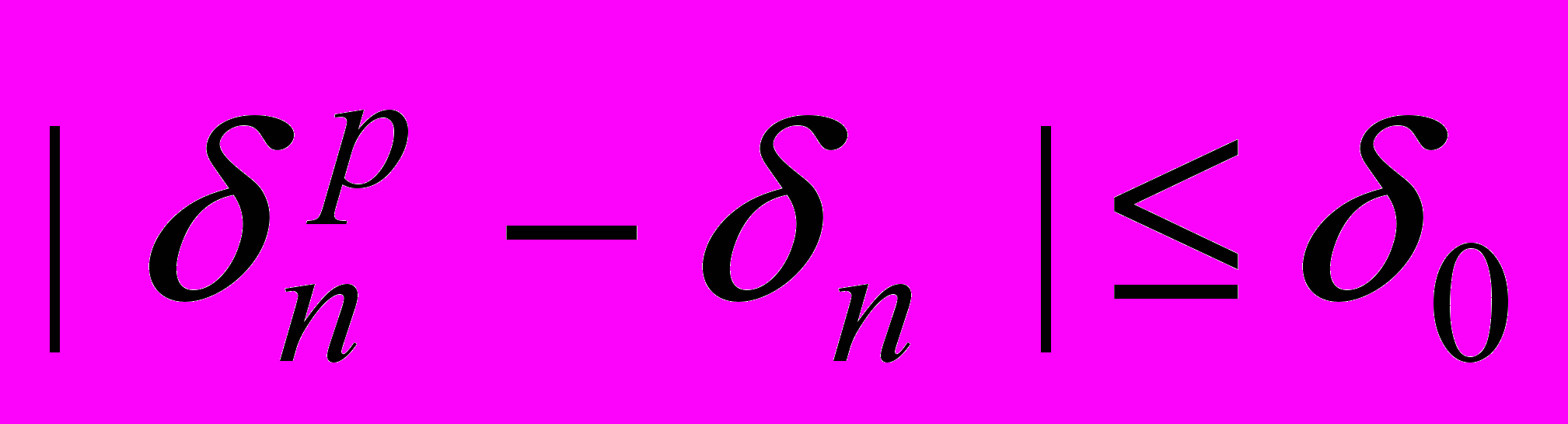, (1)

где 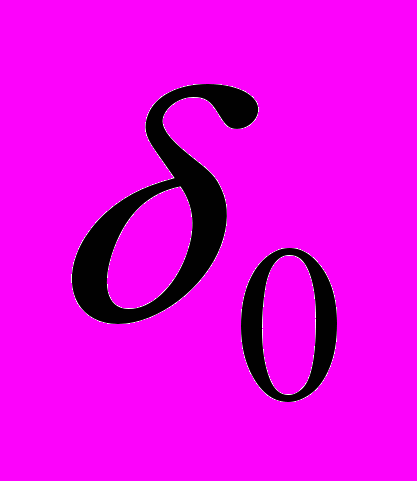- заданная малая величина.

Отметим, что на практике верхние (нижние) оценки используют для определения расчетной погрешности 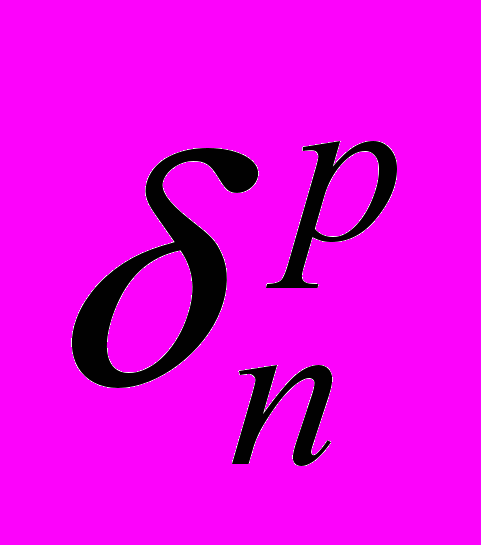. Для погрешности 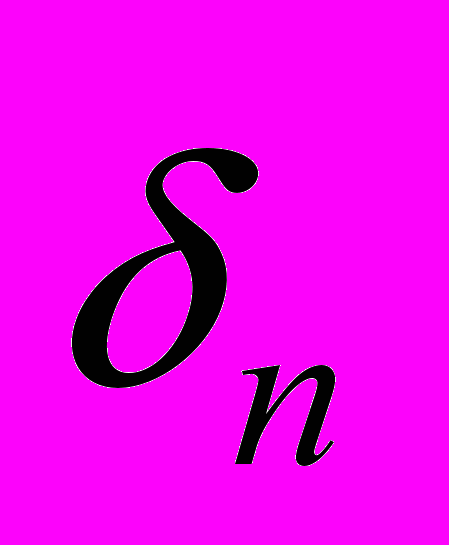широко используют оценку вида

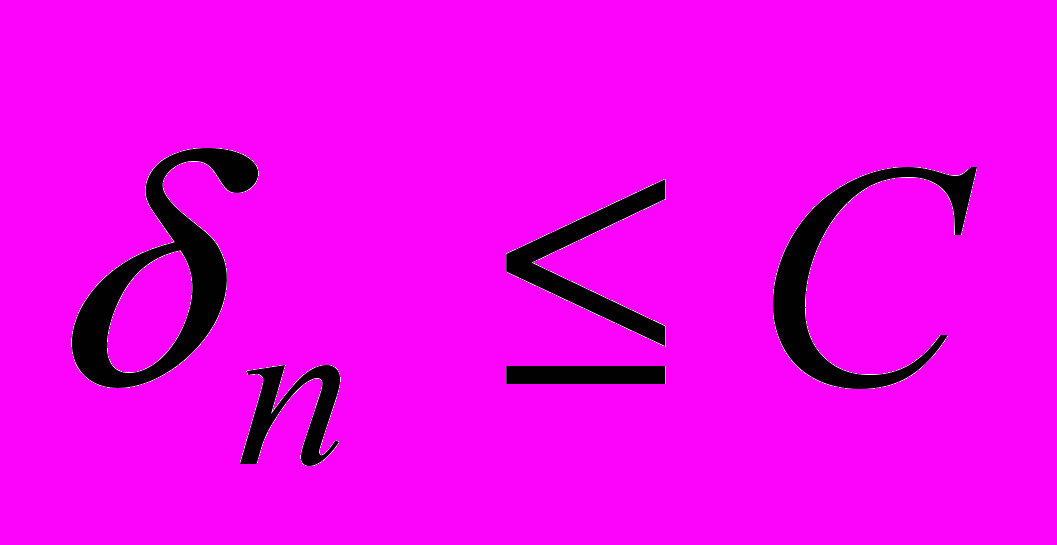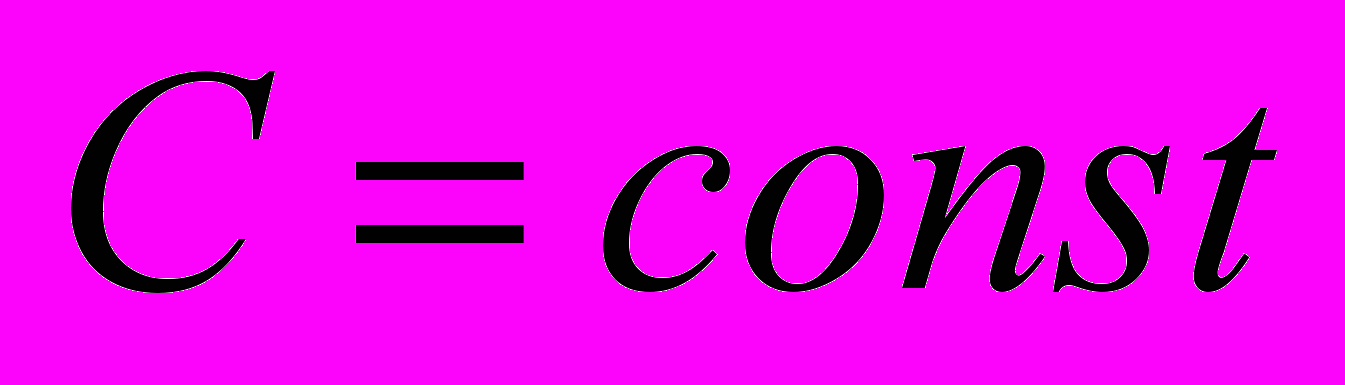, . (2)

Для оценки (2) считают, что 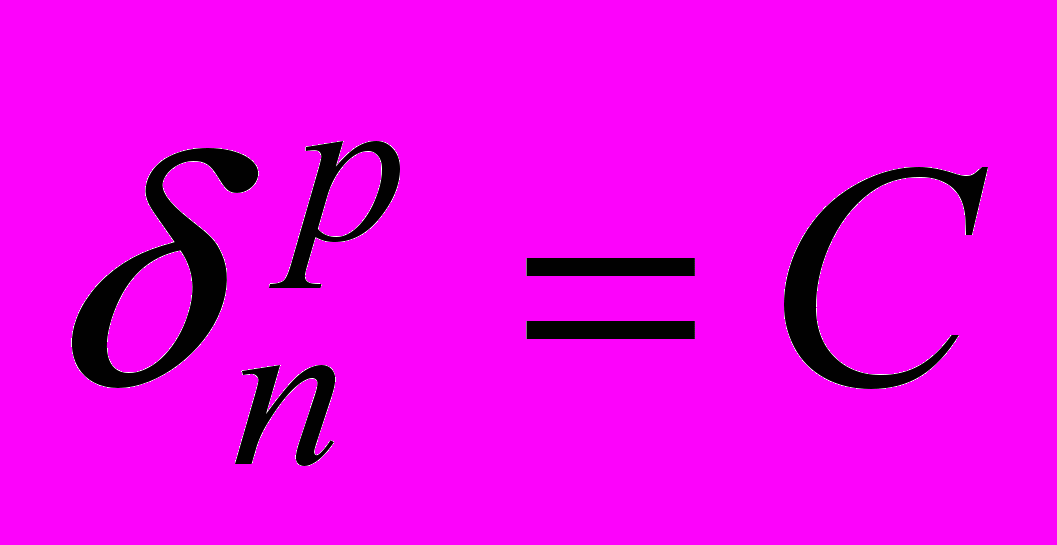. Однако, при 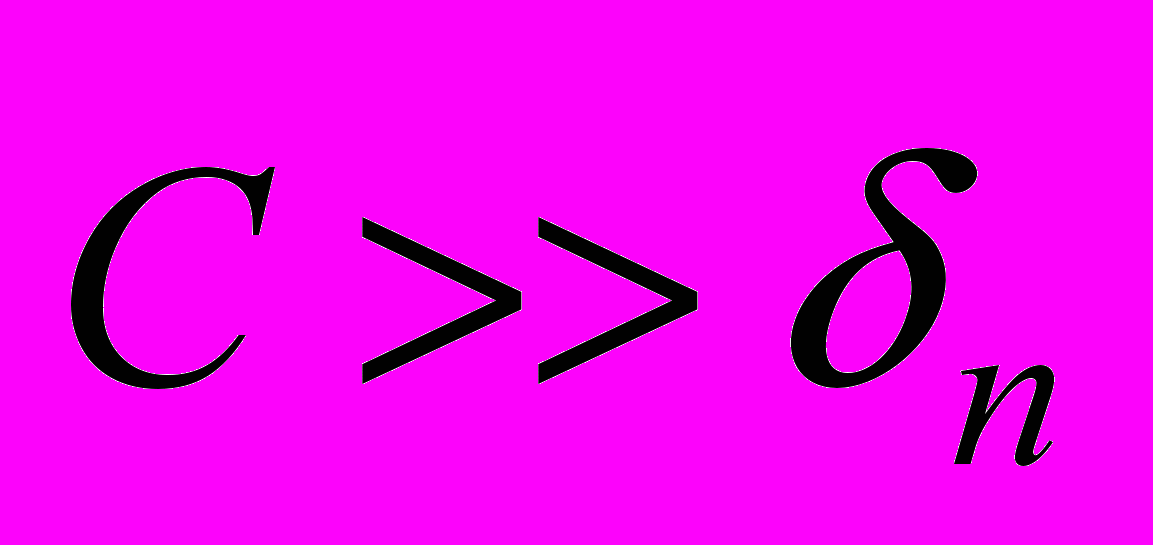имеем 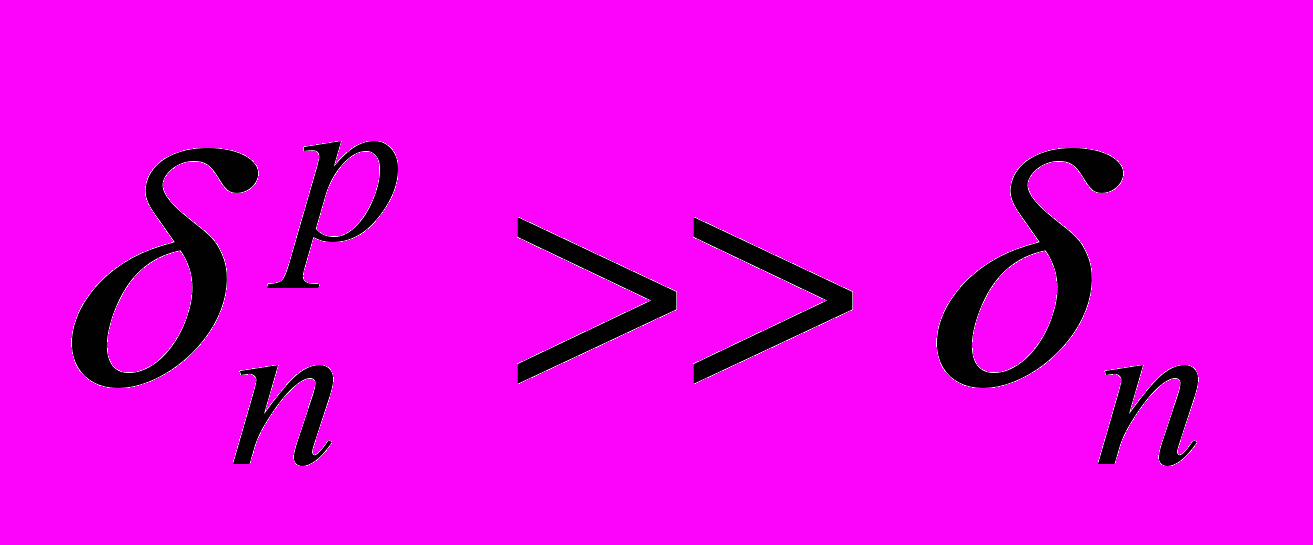. В этом случае применять 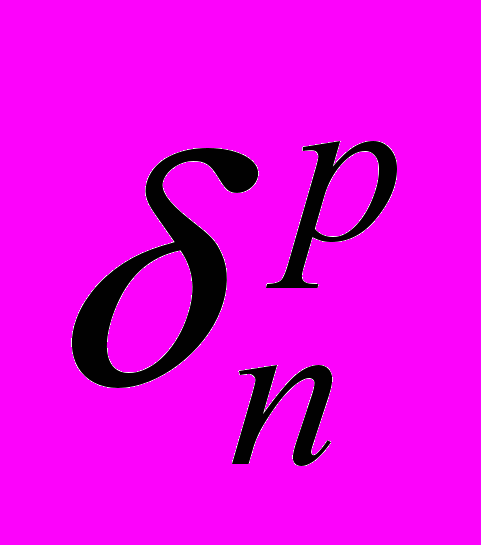в расчетах затруднительно, так как возможно, что .

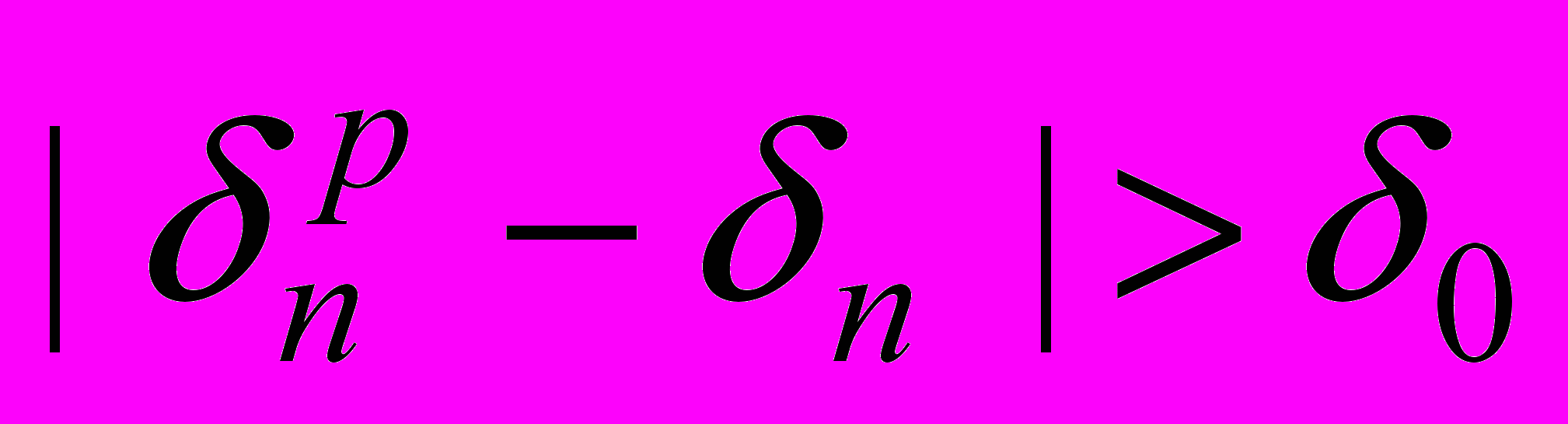В данной работе предложена численная процедура построения относительных погрешностей для максимальных узловых перемещений конечно-элементных моделей упругих двумерных композитов регулярной структуры заданного вида, которые испытывают плоское напряженное состояние (имеют гладкие границы и для которых задан характер нагружения). Процедура построения двусторонних оценок для относительных погрешностей узловых перемещений дискретных моделей однородных тел изложена в [3,4]. В основе предлагаемой процедуры лежит следующее утверждение. Для определенного класса решений 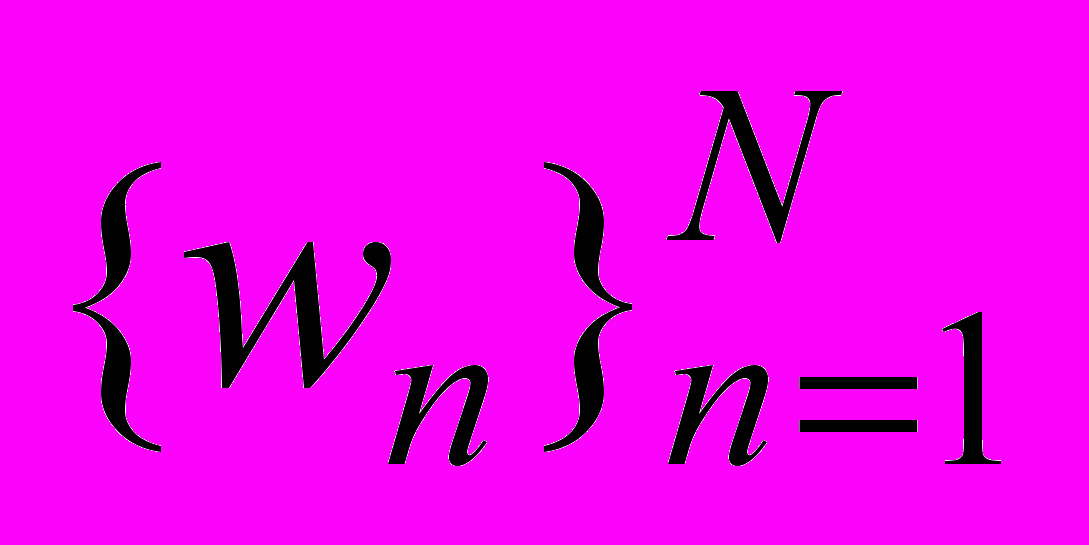плоской задачи упругости, построенных (по микроподходу) с помощью МКЭ для двумерного композита, существуют такие непрерывные функции 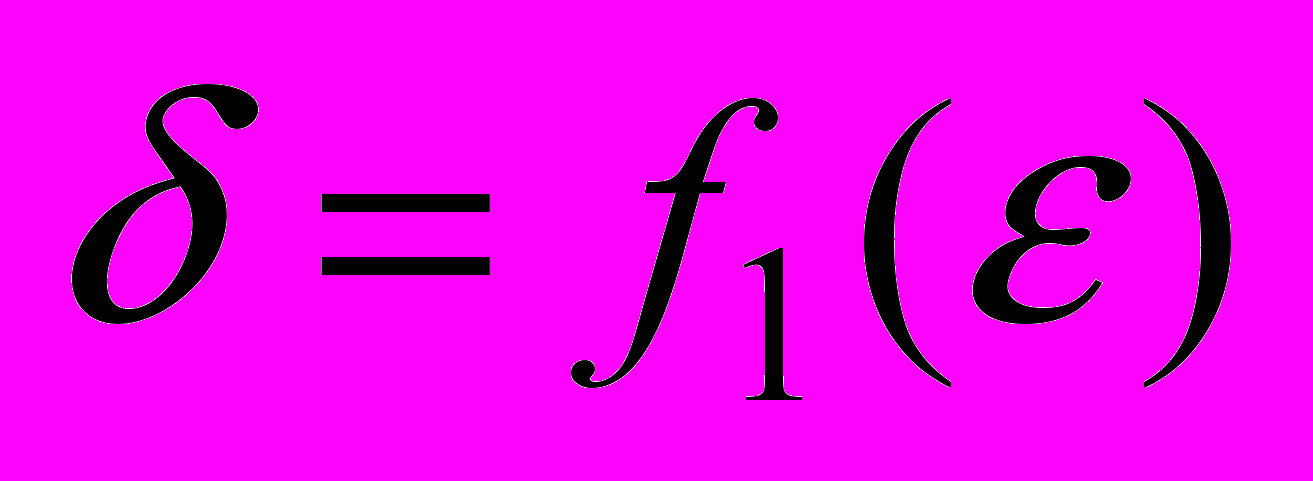, , 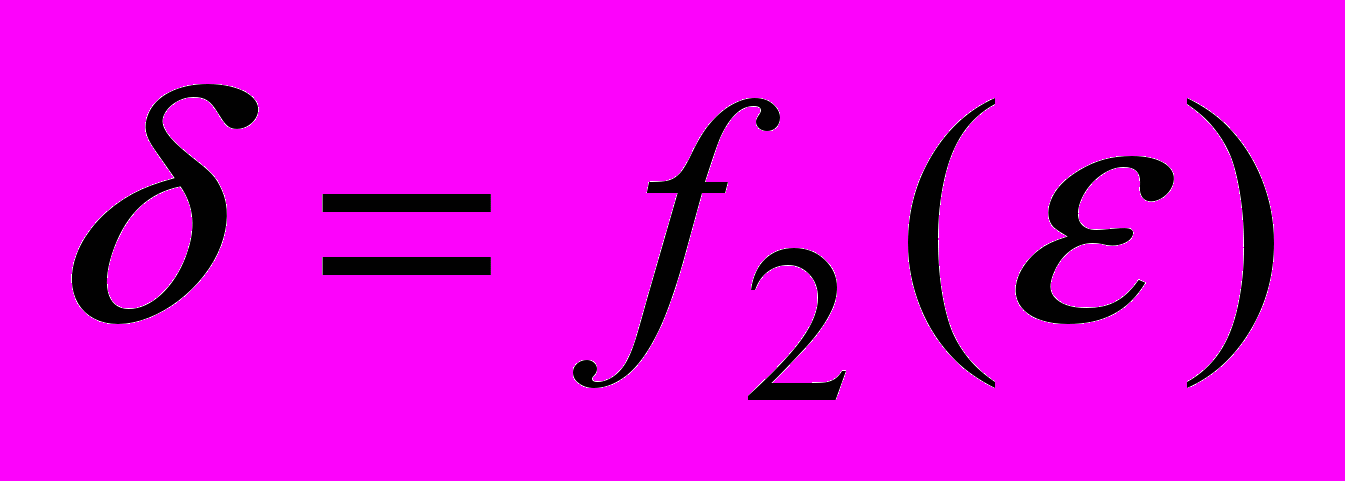что для погрешности 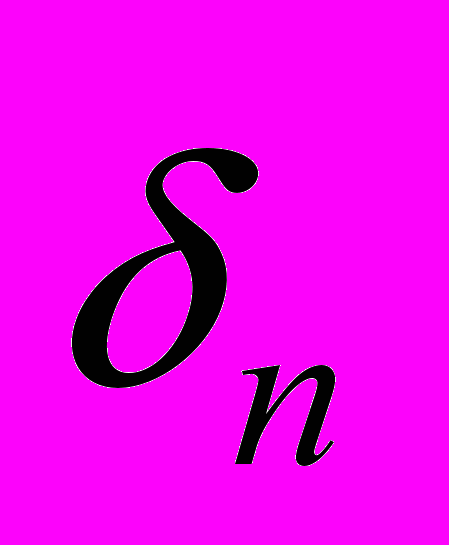всякого решения 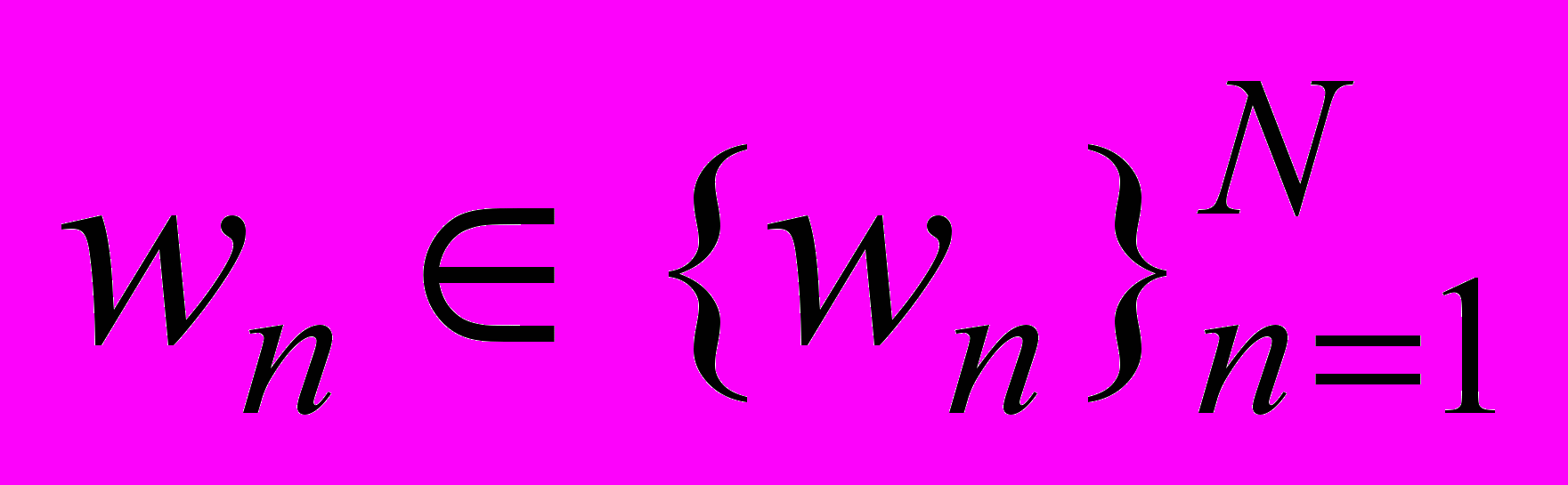при 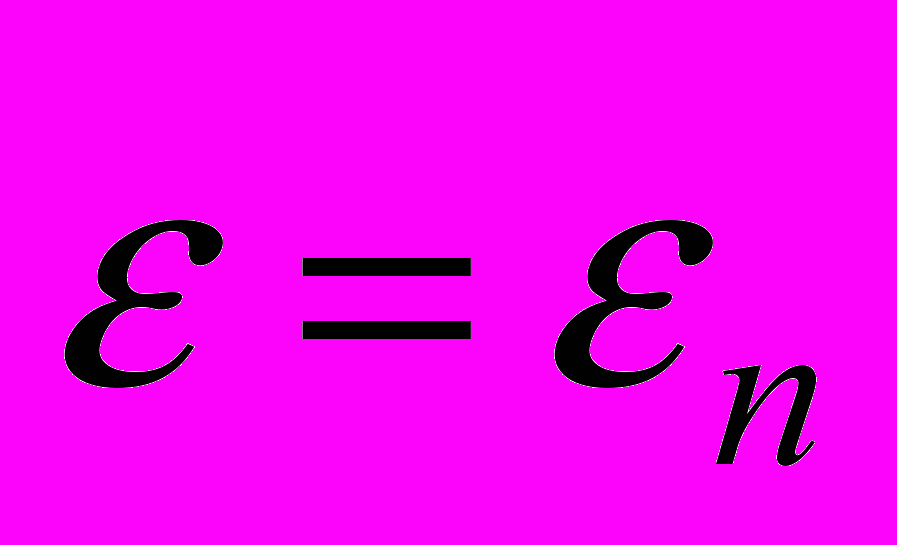выполняются неравенства

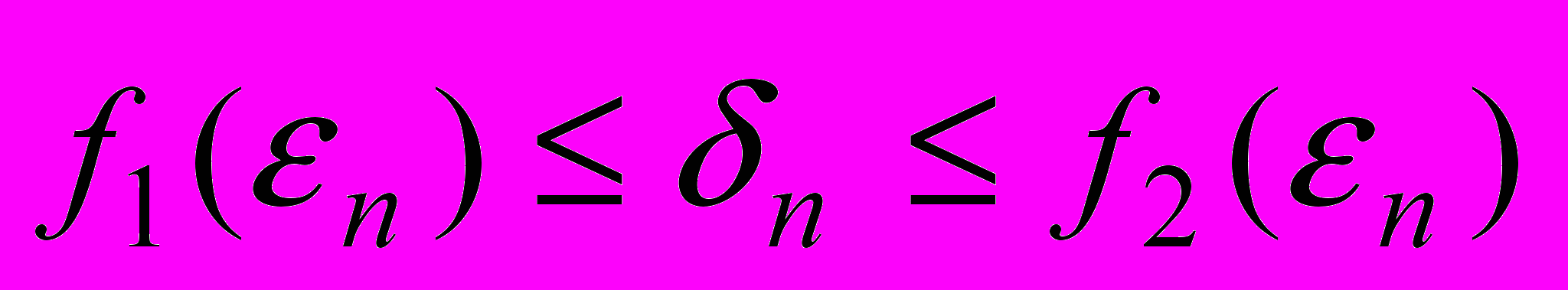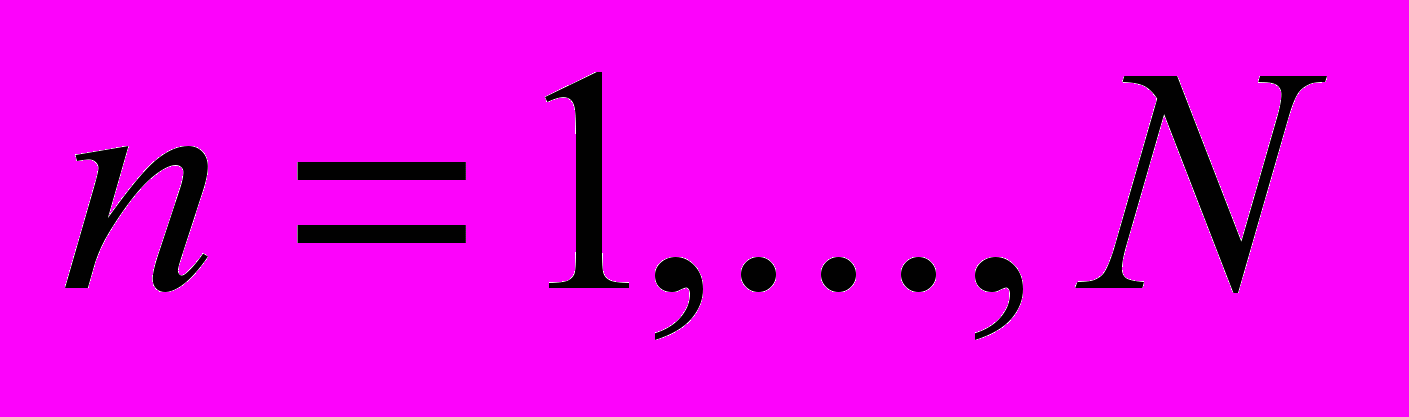, , (3)

где 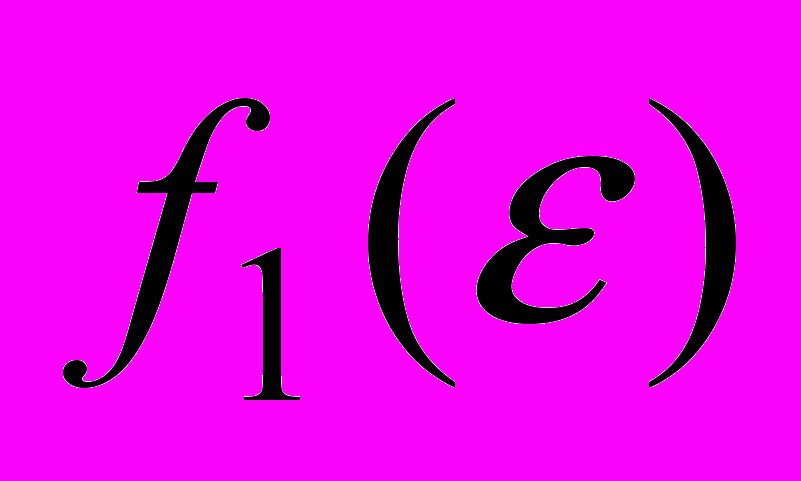, 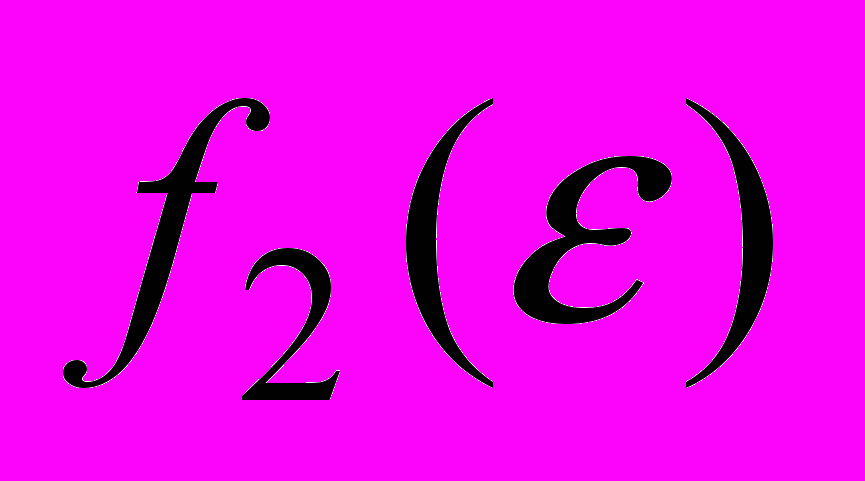- функции соответственно нижних и верхних оценок для погрешностей 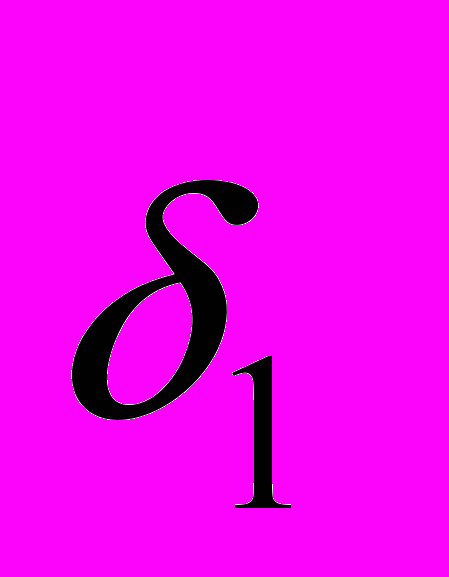, …,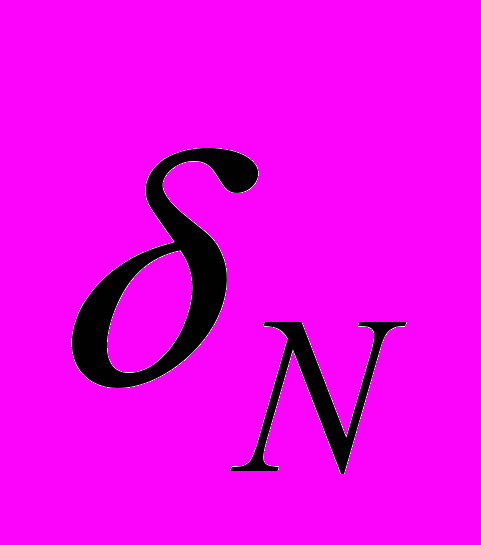; параметр 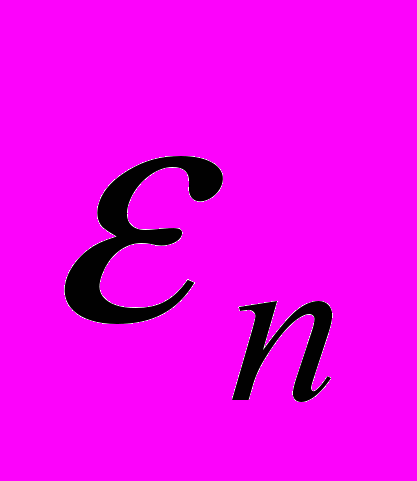определяется по формуле

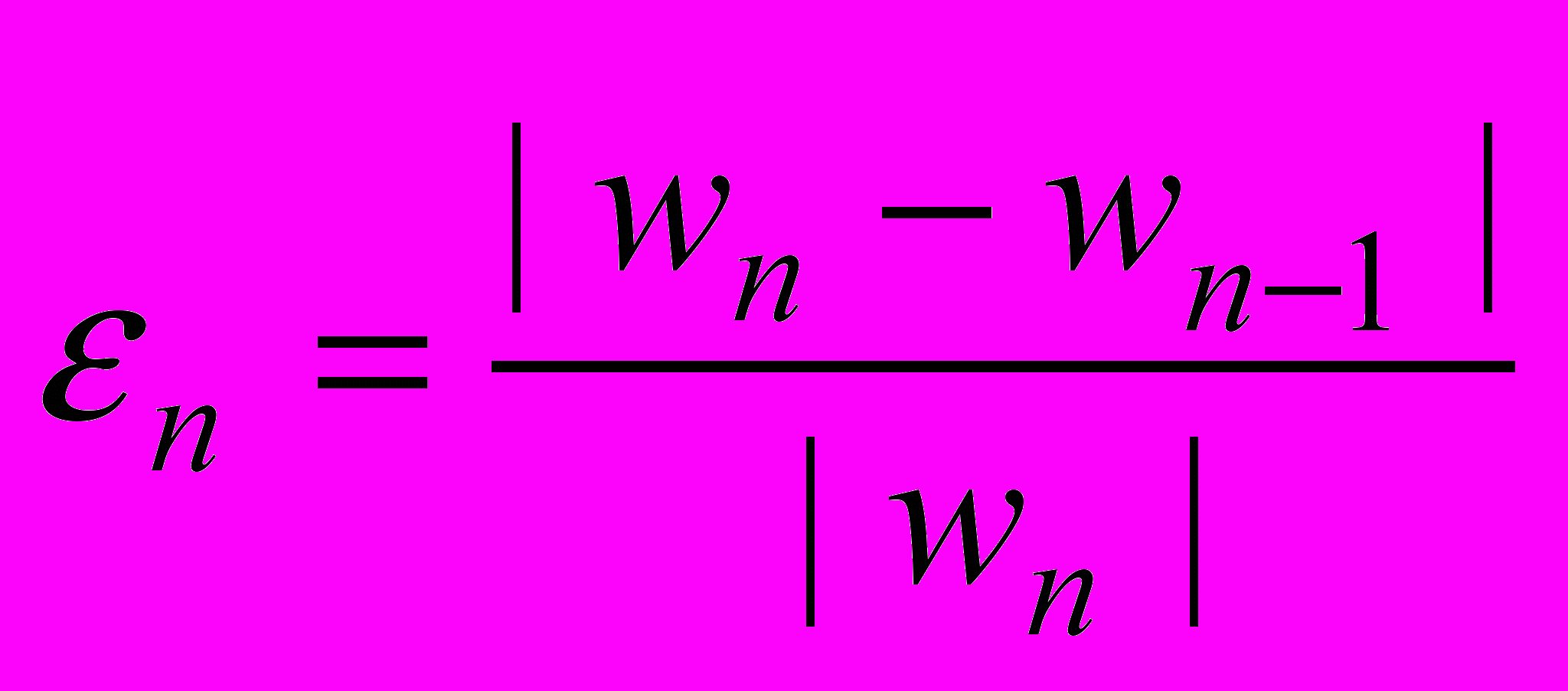. (4)

Процедура сводится к построению (с помощью численных экспериментов) в декартовой системе координат 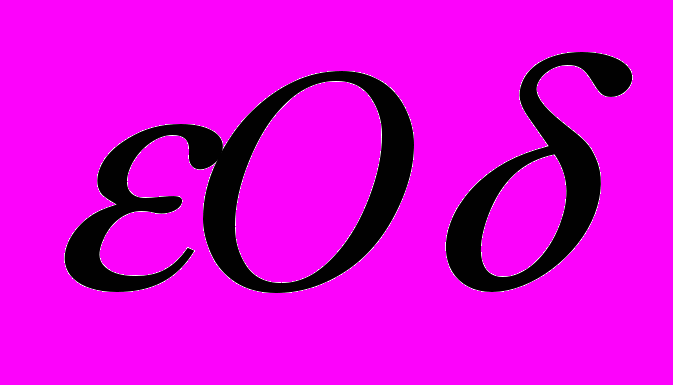графиков функций 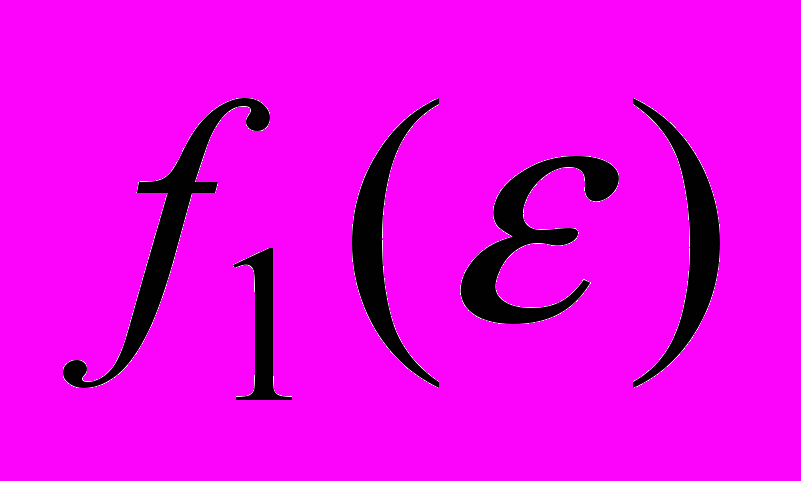, , 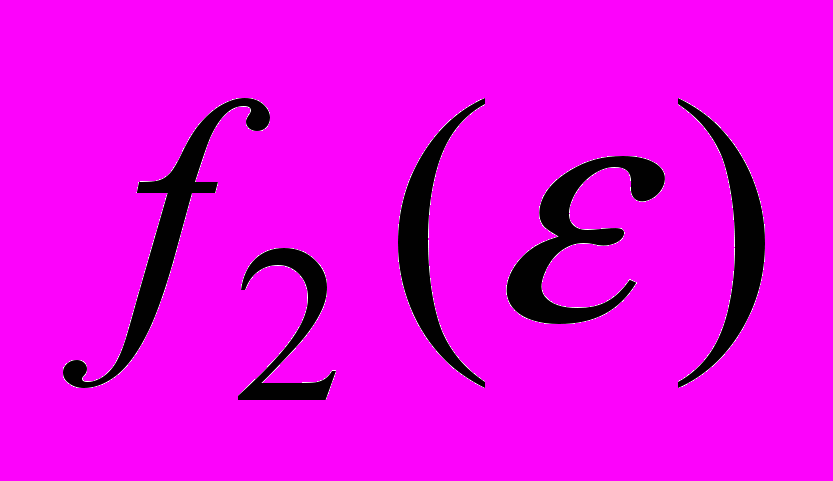которые отвечают выбранному закону измельчения регулярных исходных разбиений и заданному характеру нагружений двумерных композитов (с гладкими границами). Суть применения графиков функций 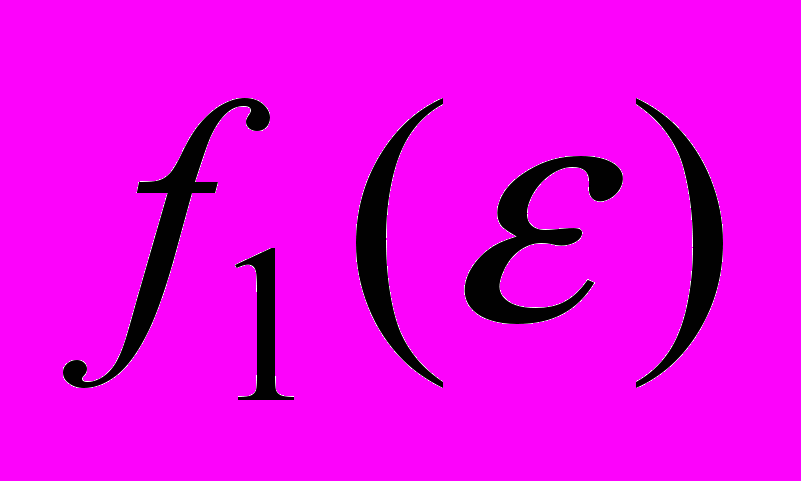, 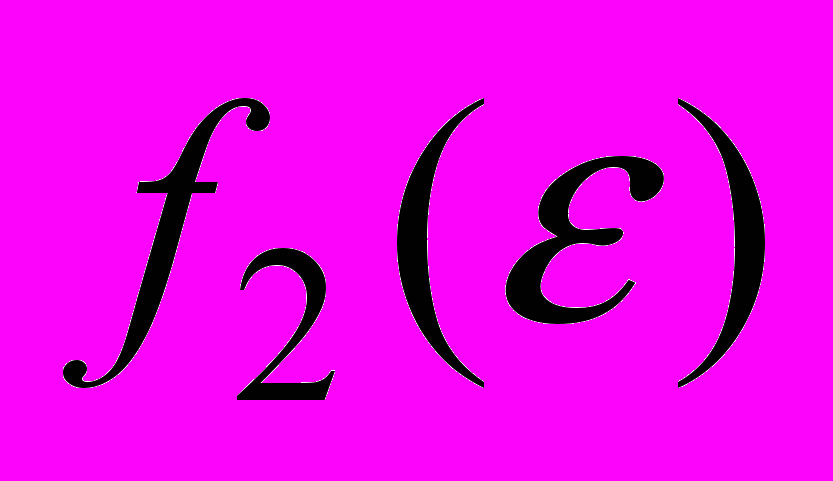для определения верхних и нижних оценок для относительных погрешностей максимальных узловых перемещений дискретных моделей композитов состоит в следующем. Пусть для упругого двумерного композита регулярной структуры заданного вида построены (по микроподходу) с помощью МКЭ решения 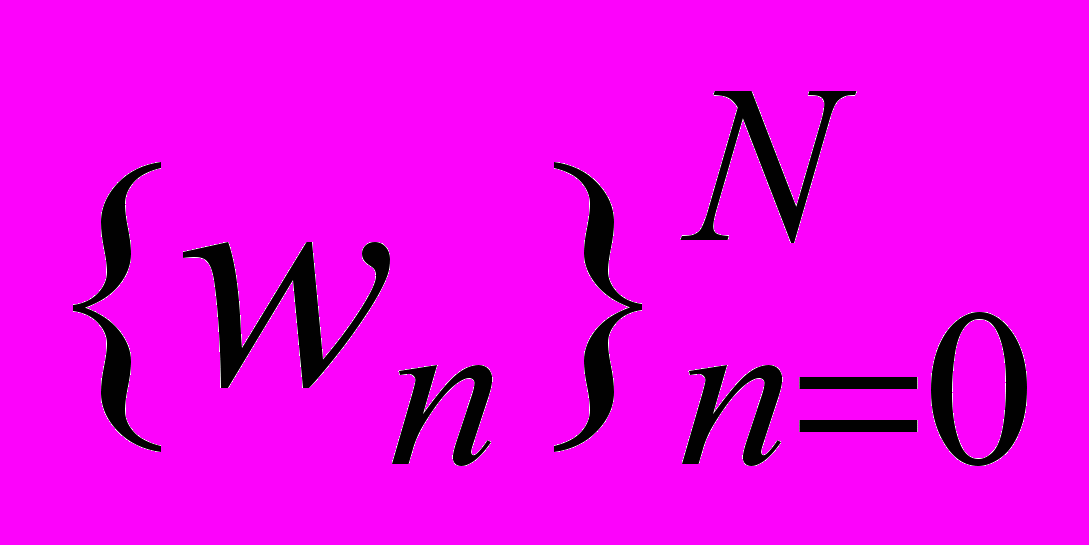плоской задачи упругости при использовании выбранного закона измельчения регулярных разбиений 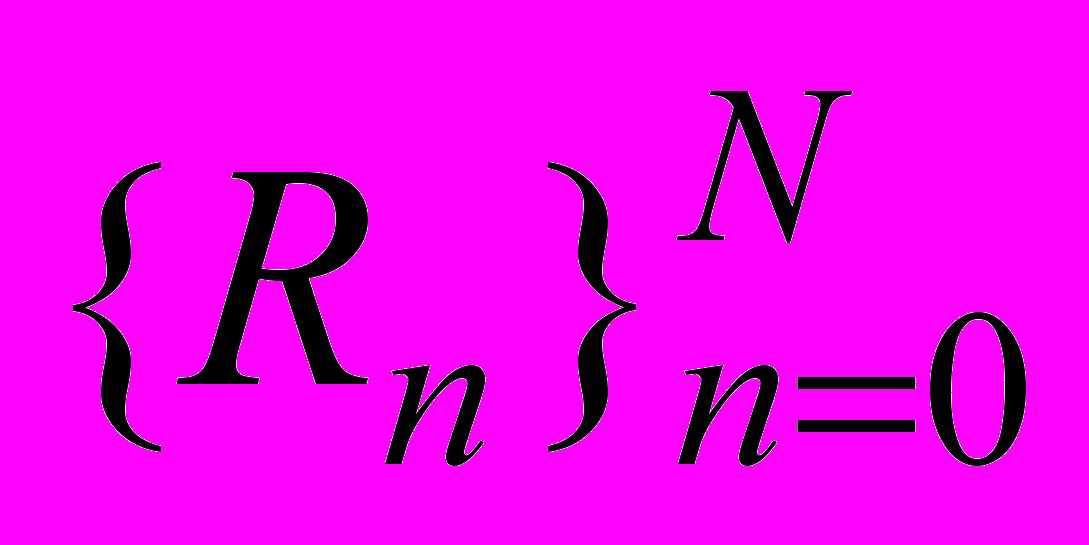и заданного вида нагружений, для которых были построены функци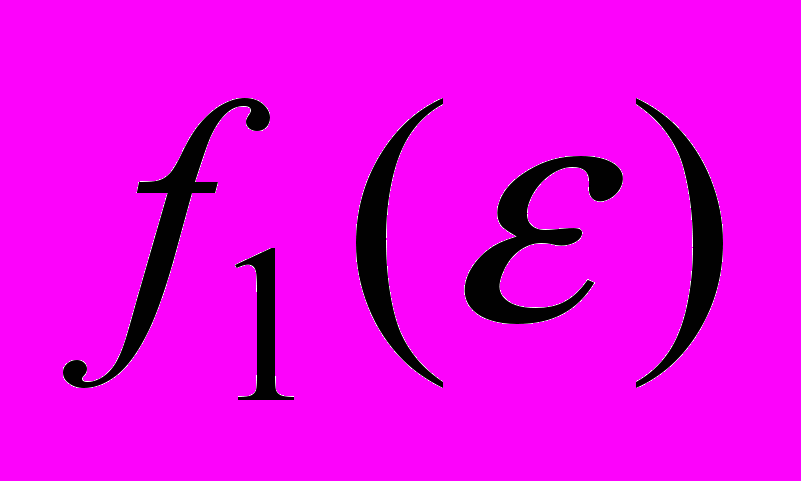и и 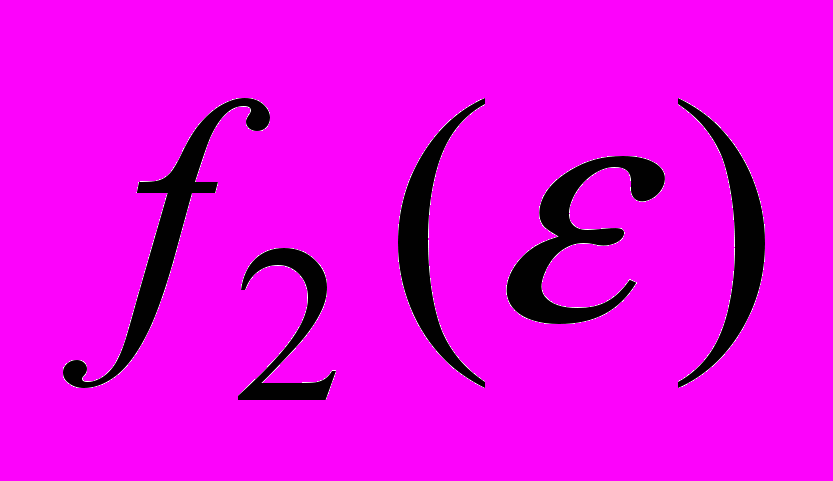. Для выбранного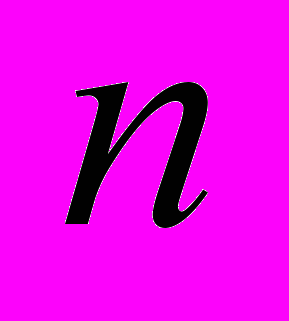 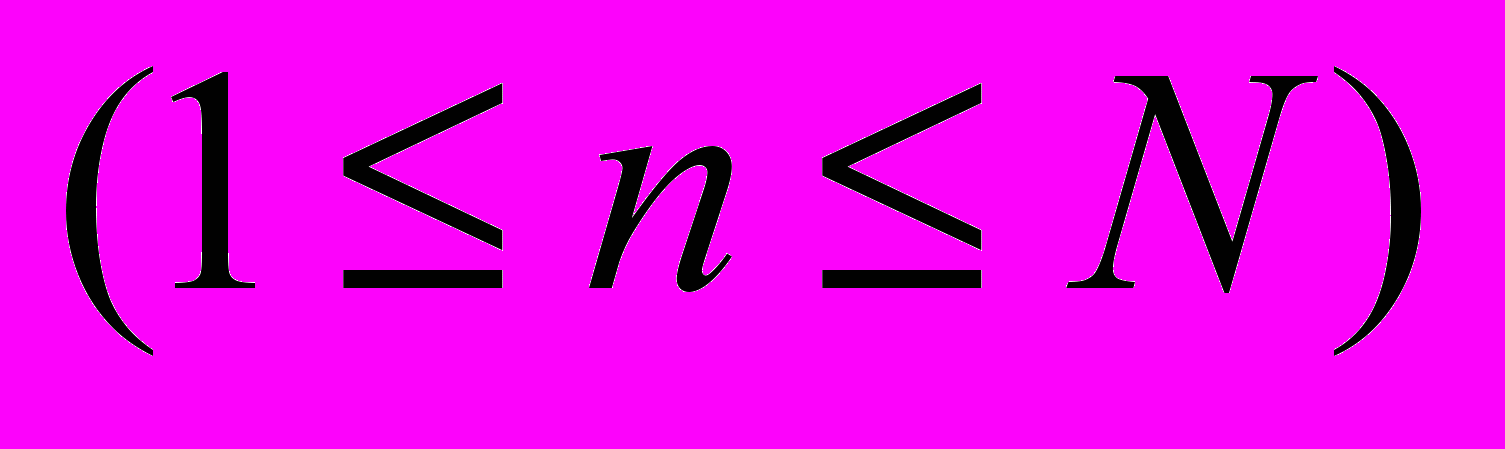определяем параметр 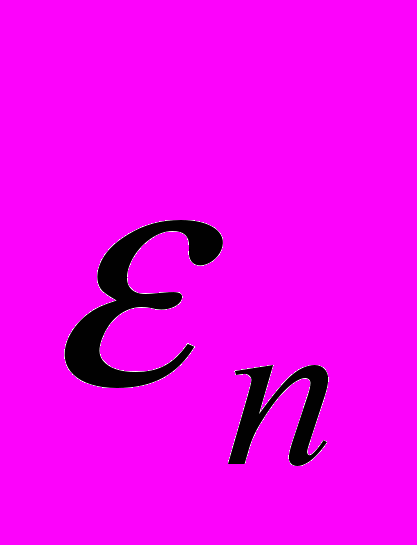по формуле (4). Затем на плоскости 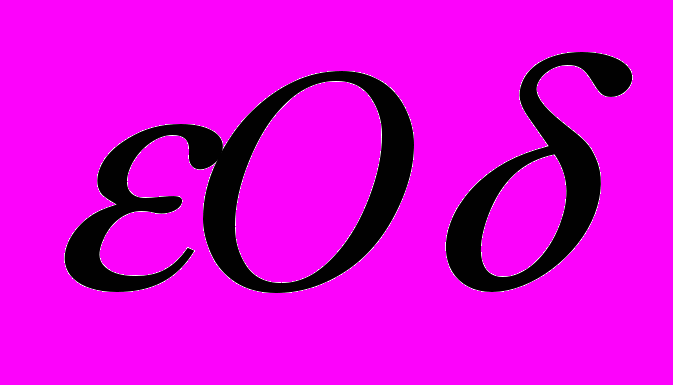из точки с координатами 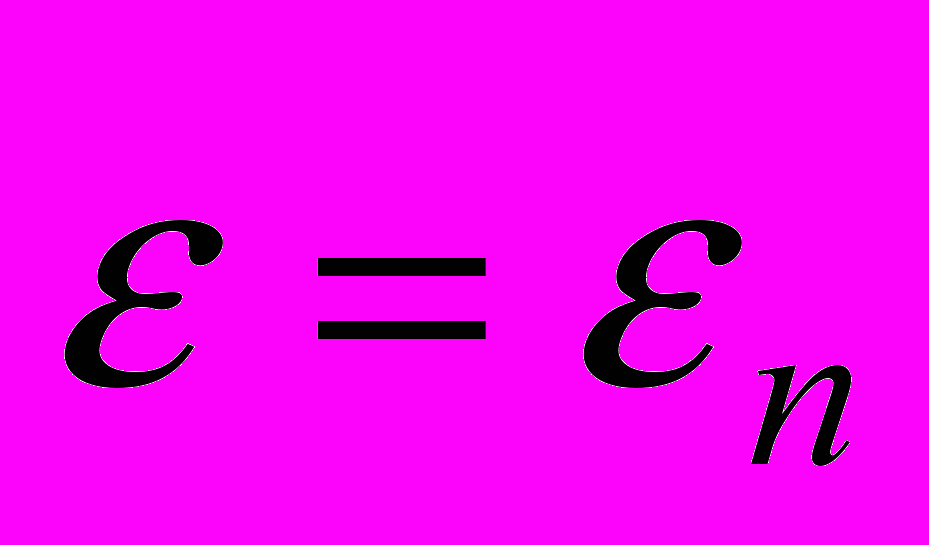, 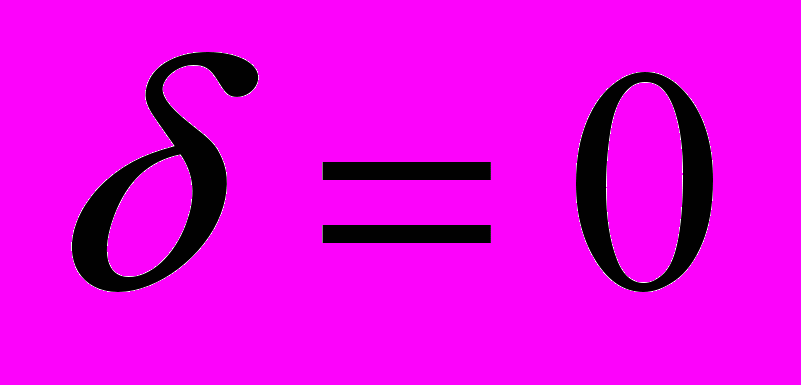восстанавливаем перпендикуляр к оси 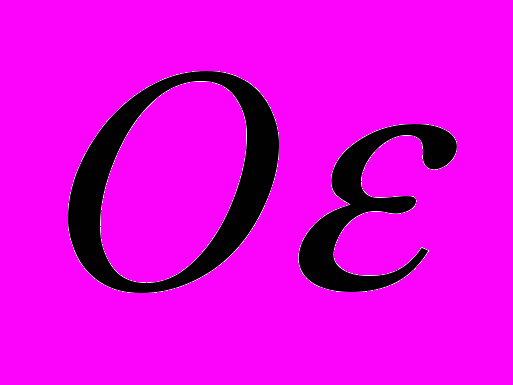до пересечения с графиками функций 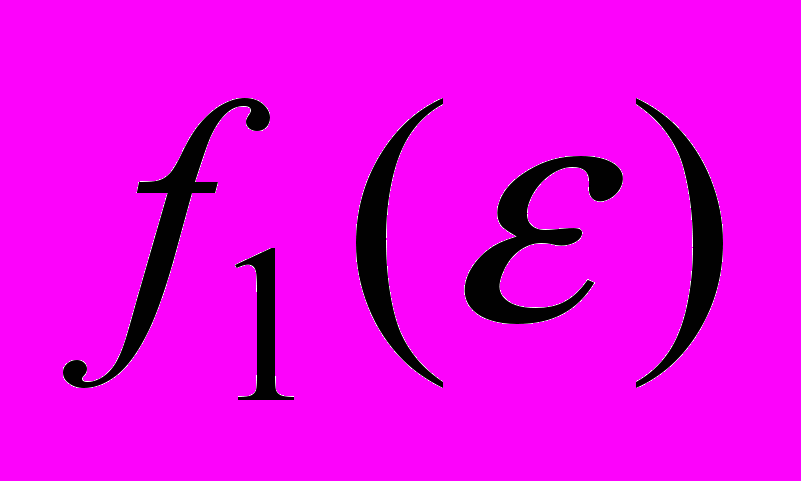, 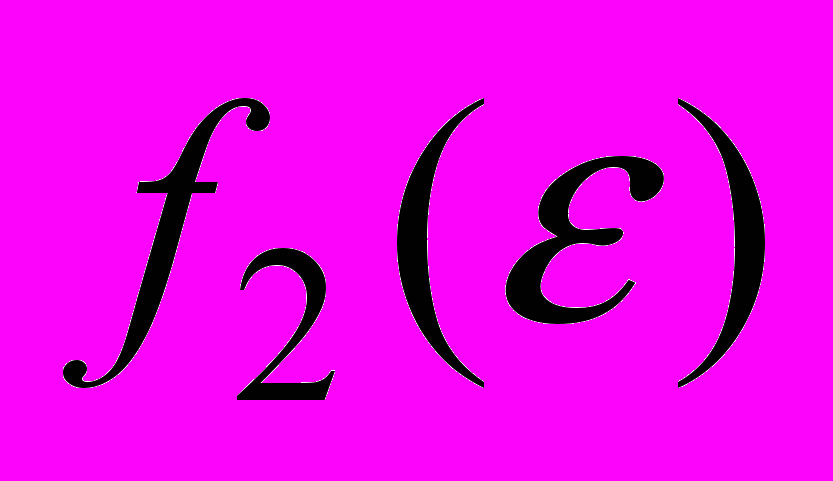и графически определяем значения функций 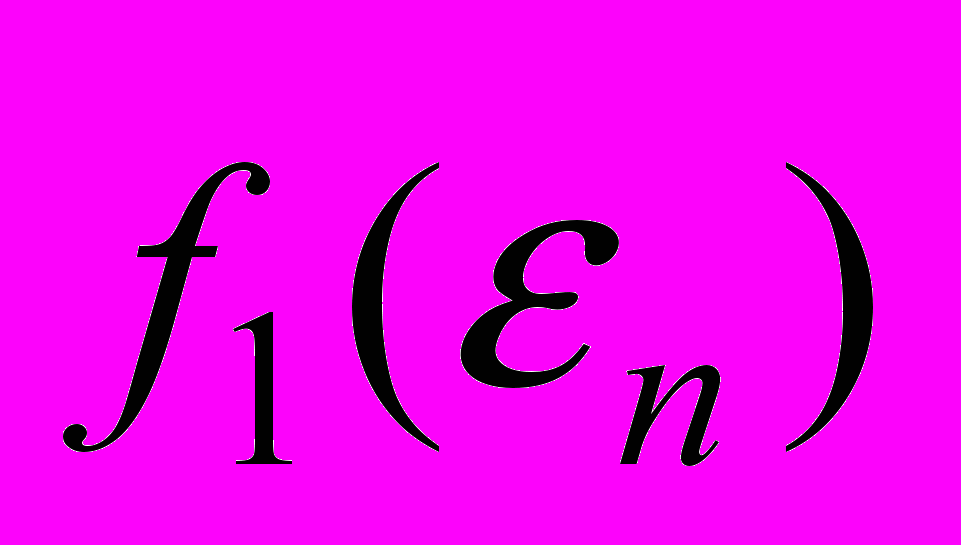, 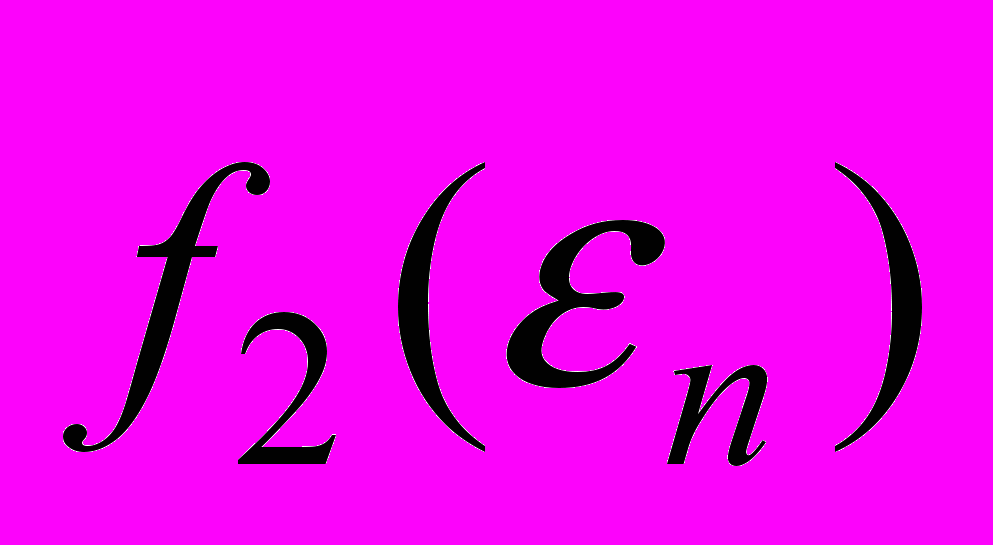. Тогда для погрешности 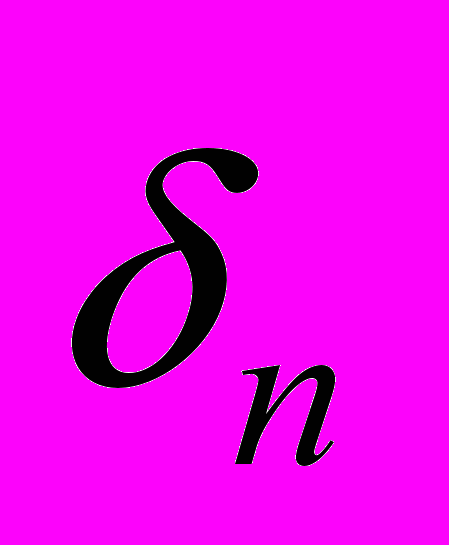решения 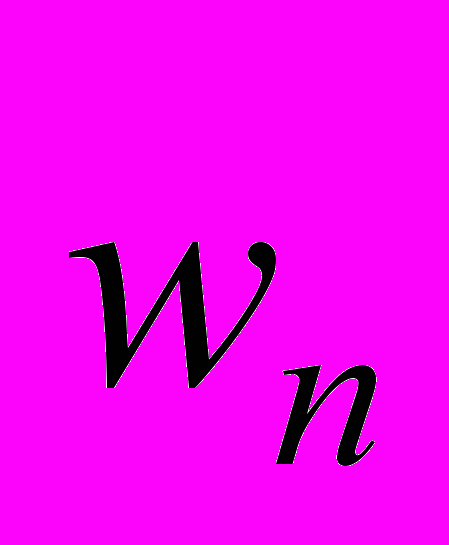выполняются двусторонние оценки (3).

Достоинство предлагаемой процедуры состоит в следующем. За счет выбора закона измельчения исходных регулярных разбиений композитов, порядка конечных элементов, которые представляют регулярные разбиения 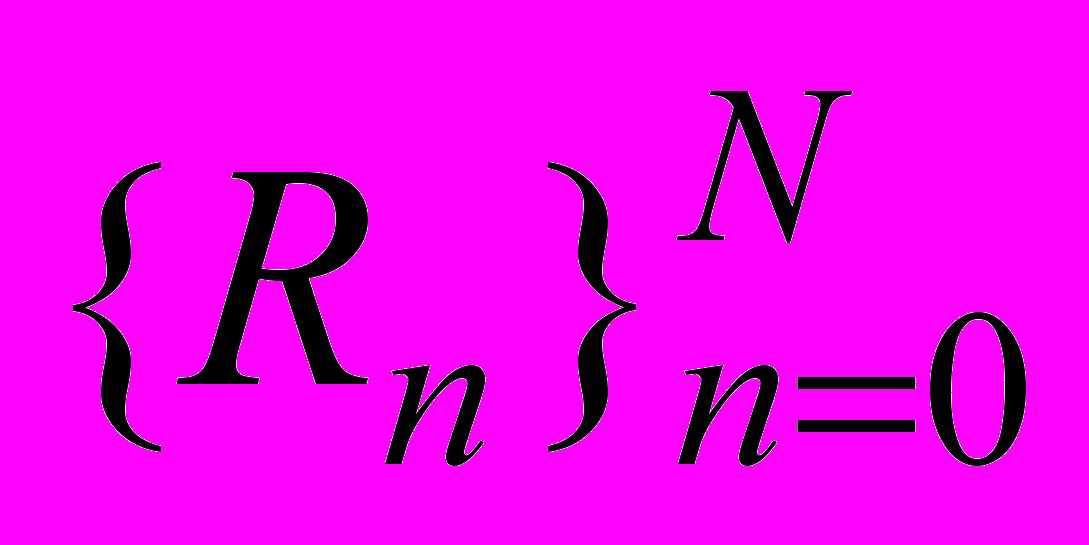(при заданном характере нагружения композитов), представляется возможным построить такие функции 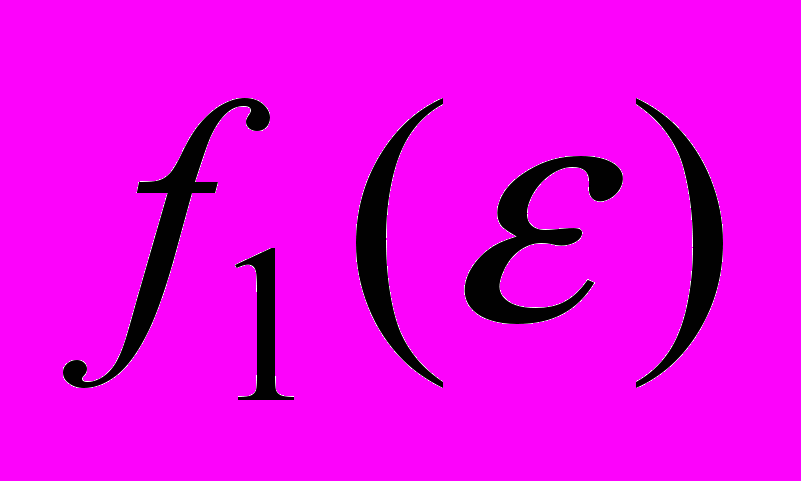, , 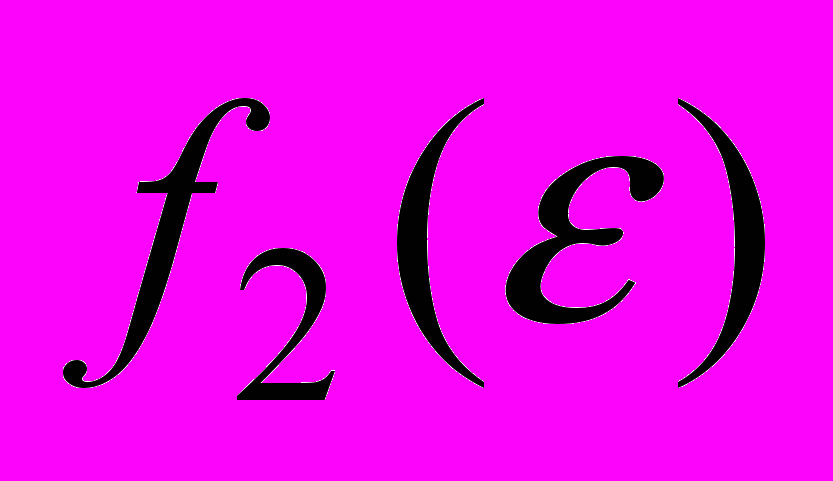что

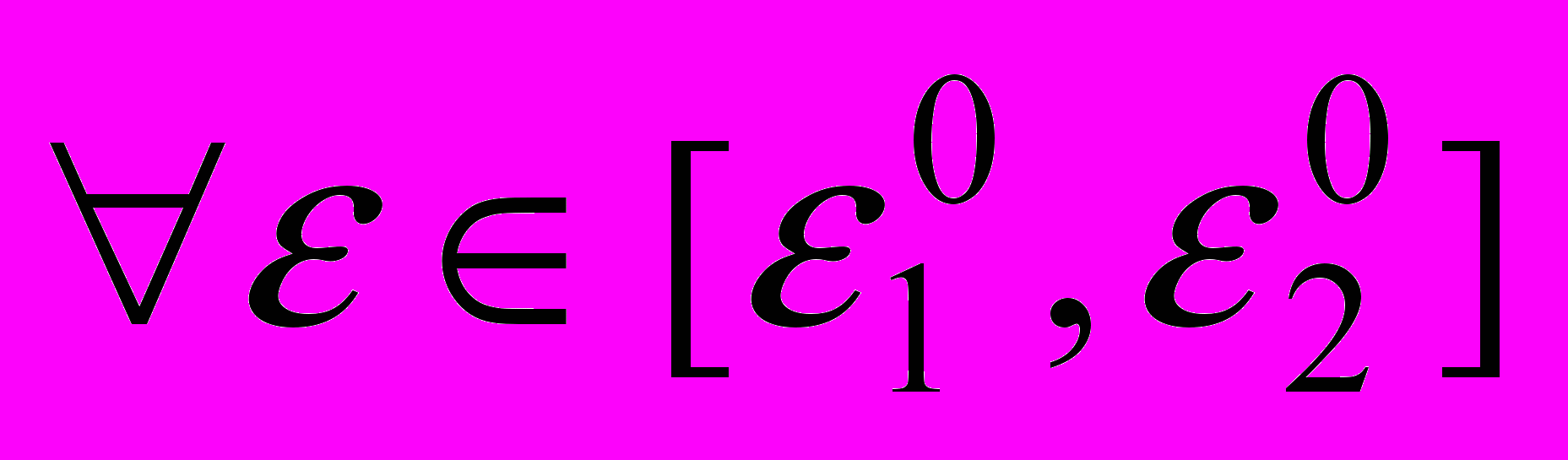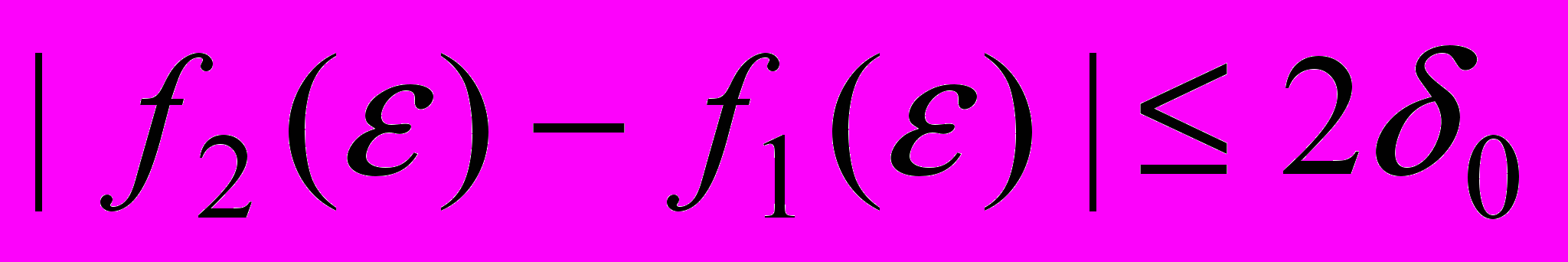: , (5)

где 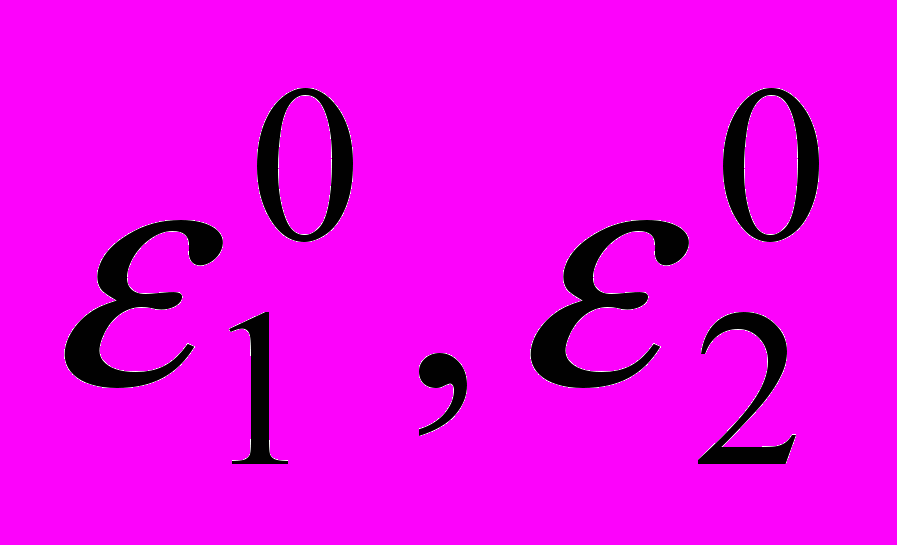- заданы, 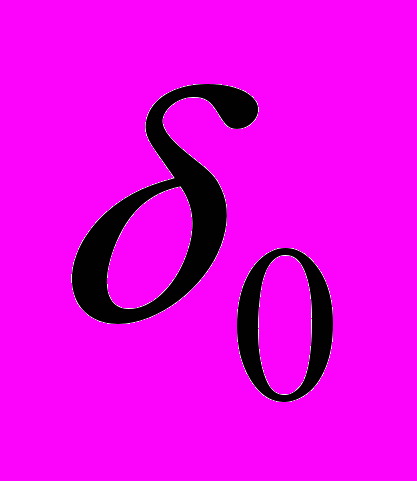- заданная малая величина.

В силу малости 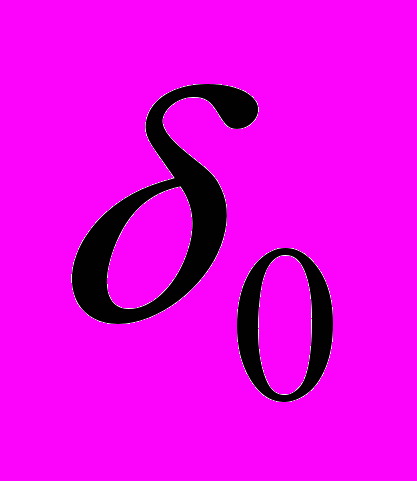согласно (5) функцию относительных погрешностей 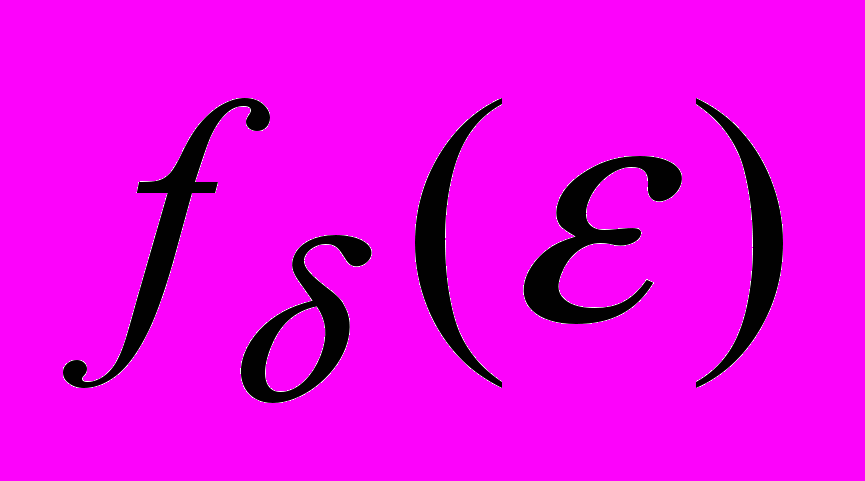для решений 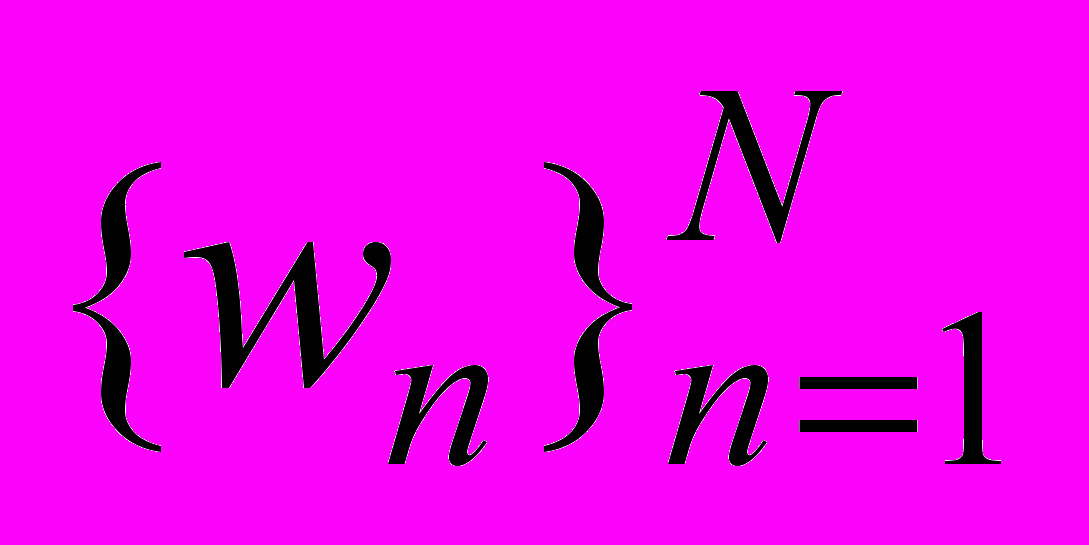на отрезке 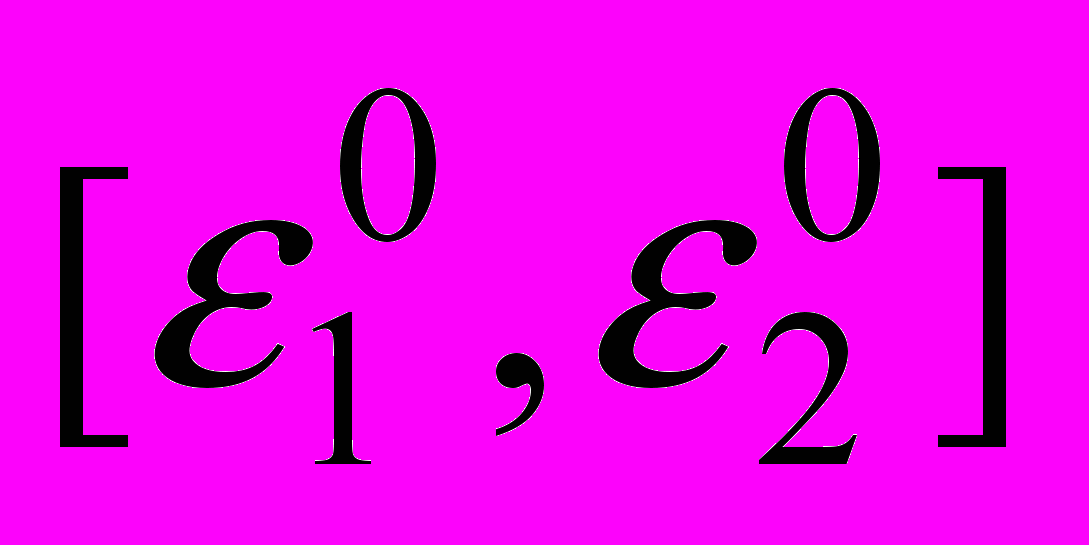приближенно можно представить в виде

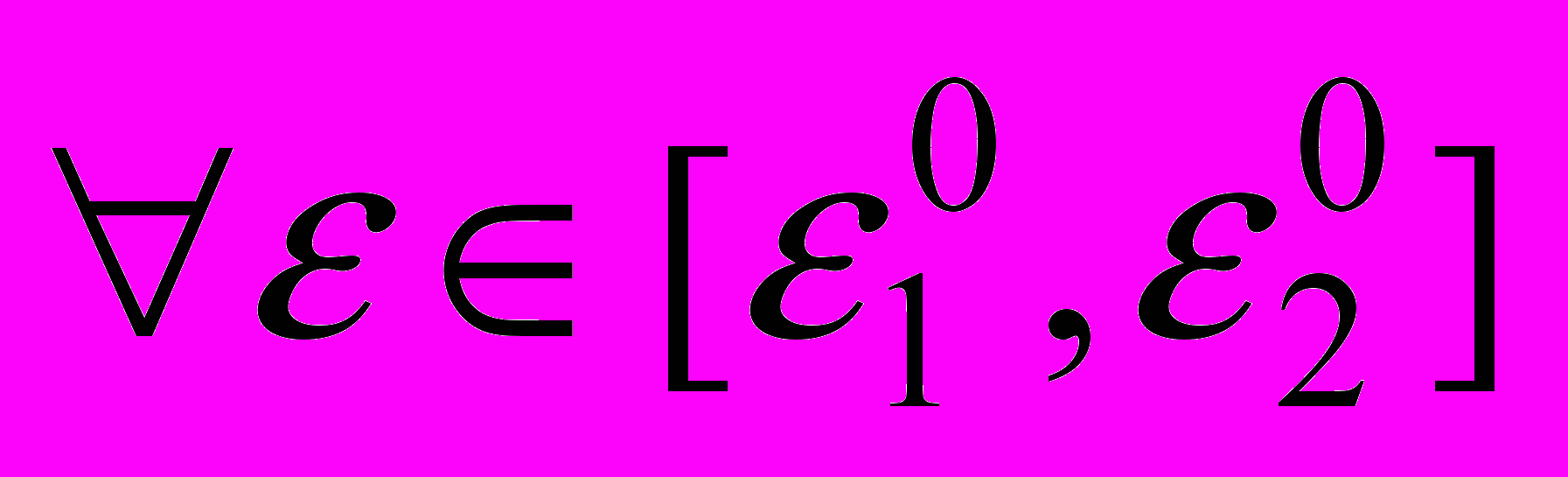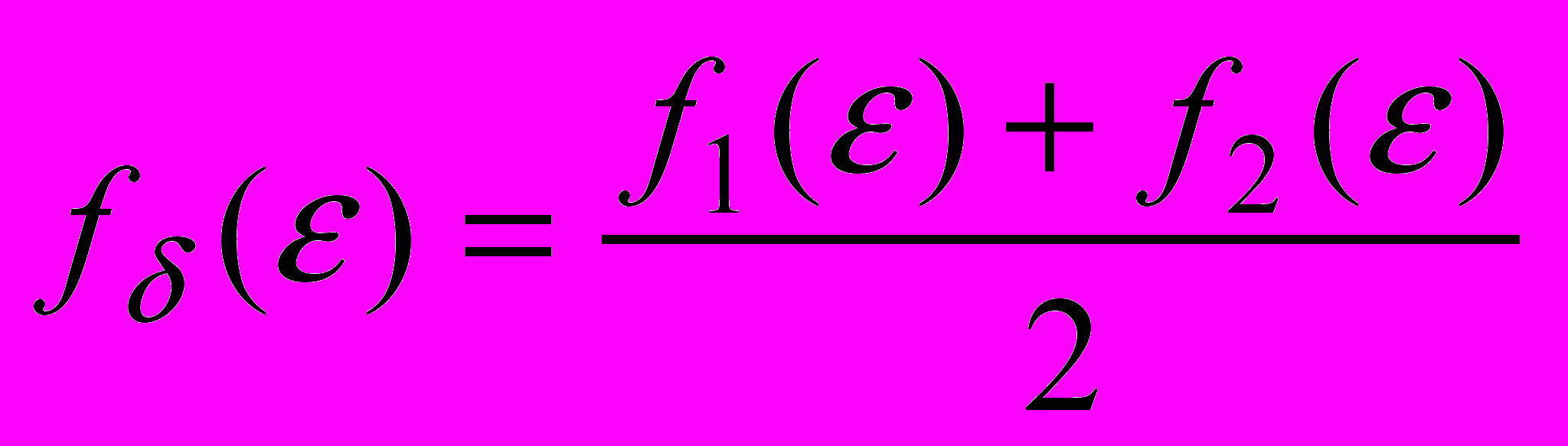: . (6)

Отметим, что в силу (5) для нижней 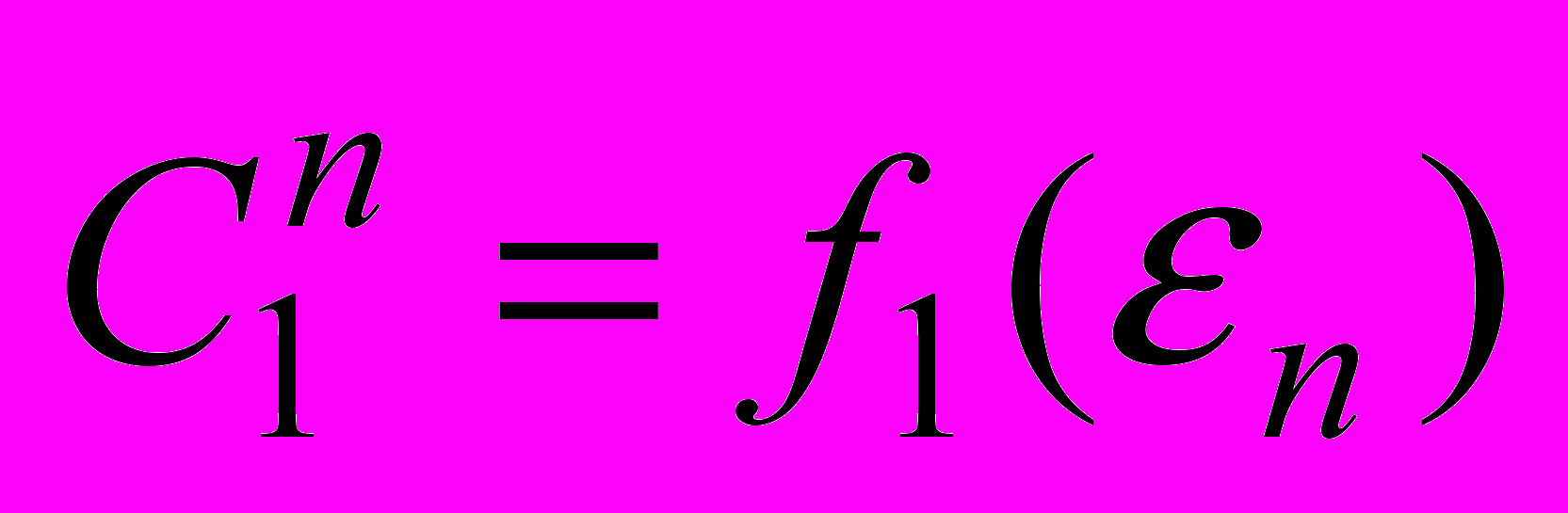и верхней 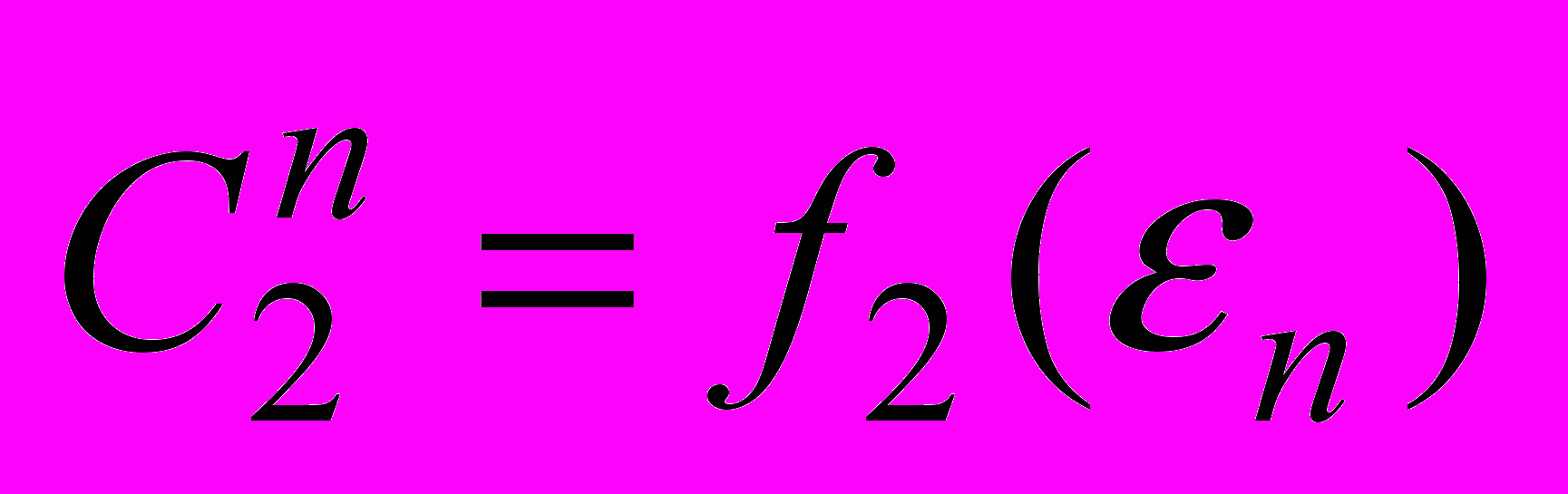оценок выполняется неравенство 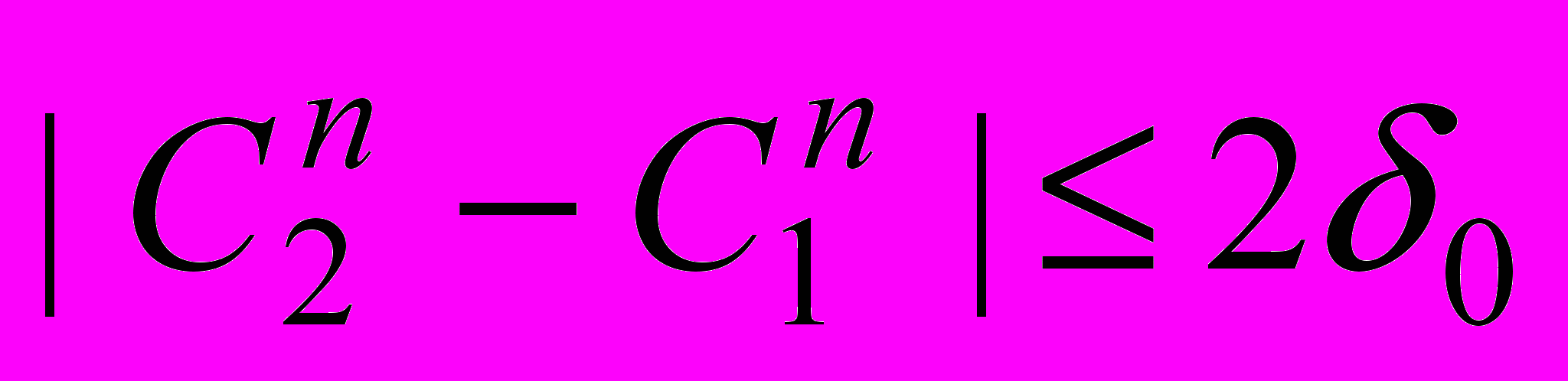, т. е. погрешность 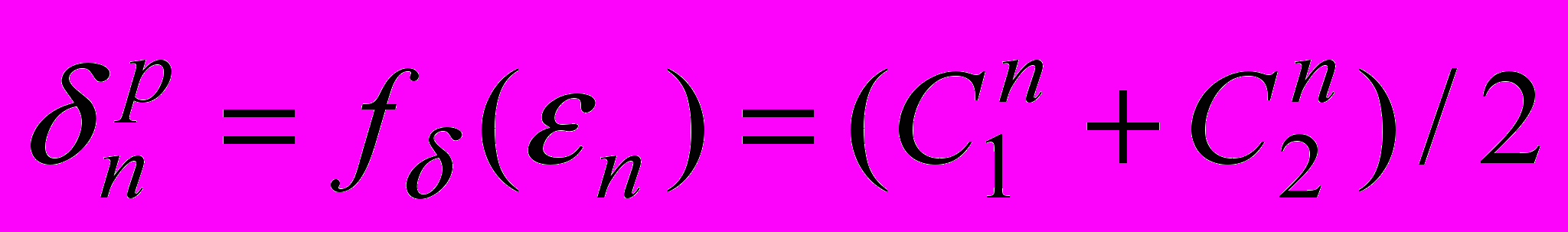удовлетворяет условию (1), 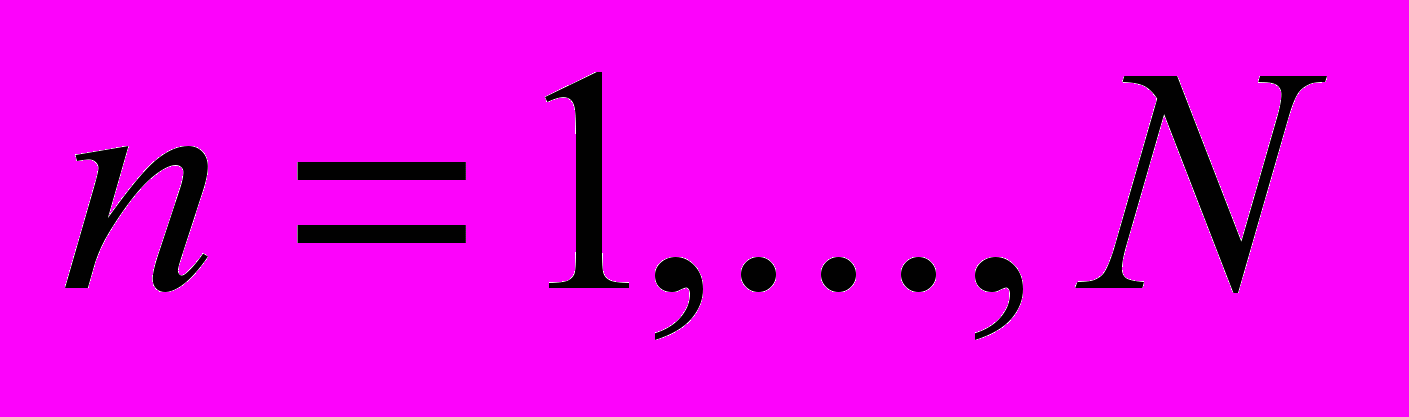. Процедура построения относительных погрешностей для максимальных эквивалентных напряжений конечно-элементных моделей двумерных упругих композитов регулярной структуры заданного вида аналогична процедуре, описанной в данной работе. Работа выполнена при финансовой поддержке РФФИ (код проекта 11-01-00053).


СПИСОК ЛИТЕРАТУРЫ

1. Постнов В.А. Численные методы расчета судовых конструкций. Л.: Судостроение, 1977. 279 с.

2. Норри Д., де-Фриз Ж. Введение в метод конечных элементов. М.: Мир, 1981. 304 с.

3. Матвеев А.Д. Численное моделирование двусторонних оценок для относительных погрешностей конечно-элементных решений плоской задачи упругости // Деп. в ВИНИТИ РАН, №1033 – B2008, - 21с.

4. Матвеев А.Д. Процедура построения двусторонних оценок погрешностей конечноэлементных решений плоской задачи упругости // Вестник КрасГАУ. 2009. №4. С. 21-29