От лат evaporo испаряю и греч grapho пи­шу), метод получения изображений объектов в их собственном (обычно ик) тепловом излучении. Предложен нем

Вид материала

Документы

Содержание Эллиптическая поляриза­ция Эмиссионная спектроскопия Эмиссионная электроника Энергетическая освещённость Энергетическая сила света Энергетические фотометри­ческие величины Энергии сохранения закон Г. Я. Мякишев. Относительности теория Энергия ионизации Энергия покоя Энергия химической связи V — объём системы. Полный диф­ференциал Э. (при неизменных N Д. Н. Зубарев. S, назв. «Э.» (дифф. определение Э.). Разность Э. системы в двух произвольных состоя­ниях А Клаузиуса неравенство. Д. Н. Зубарев. Оптич. схема эпидиаскопа. Проекционный аппарат.

Подобный материал:

• Реферат по русскому языку на тему: «Типы словарей», 284.65kb.
• Метод распознавания изображений гистологических препаратов в задачах медицинской диагностики, 31.25kb.
• Конспект лекций для 16-и часового курса начертальная геометрия издание 2-ое, 578.52kb.
• Обработка и передача изображений, 243.48kb.
• Социоло́гия (от лат socius общественный; др греч. λόγος мысль, причина) наука о закономерностях, 85.75kb.
• Isbn 5-7262-0634 нейроинформатика 2006, 165.42kb.
• М. В. Лычагин Зав кафедрой д э. н., профессор, 986.65kb.
• Предложен метод неразрушающего акустического контроля многофазных макрооднородных композитных, 14.58kb.
• От греч autos -сам, bios жизнь, grapho пишу, лит прозаический жанр; как правило, последовательное, 2051.5kb.
• М. В. Корытова научный руководитель Р. Т. Файзуллин, д т. н., профессор Омский государственный, 26.14kb.

ЭЛЛИПТИЧЕСКАЯ ПОЛЯРИЗА­ЦИЯ, см. Поляризация света.

ЭМАН (от лат. emano — вытекаю, рас­пространяюсь) (Е), редко применя­емая внесистемная ед. концентрации (уд. активности) радиоакт. нуклидов в жидкостях или газах. 1 Э. равен концентрации радиоакт. нуклида, име­ющего активность 10^-10 кюри на 1 л р-ра или газовой смеси. 1 Э.=10^-10 Ки/л=3,7•10^-3 Бк/м³.

ЭМИССИОННАЯ СПЕКТРОСКОПИЯ, изучение структуры и св-в квантовых систем по их спектрам испускания. Спектры испускания атомов, молекул и тв. тел получают в спектральных приборах; их возбуждают разл. спо­собами: облучая светом, помещая ис­следуемое в-во в пламя горелки, воз­буждая атомы в-ва электрич. разрядом и т. д. Э. с. лежит в основе эмис­сионного спектрального анализа. См. также Спектроскопия.

ЭМИССИОННАЯ ЭЛЕКТРОНИКА, область физики, охватывающая ис­следования и использование явлений, связанных с эмиссией эл-нов и ионов из тв. тела или жидкости в вакуум или др. среду, а также с др. про­цессами на поверхности тв. тел при бомбардировке её ч-цами.

ЭНАНТИОМОРФИЗМ (от греч.enantios — находящийся напротив, про­тивоположный и morphe — форма), свойство нек-рых объектов обра­зовывать зеркально равные друг другу по строению модификации. Один из таких объектов условно наз. «правым», а другой — «левым». Энантиоморфные объекты могут опи­сываться только точечной группой симметрии, содержащей лишь оси симметрии, в частном случае могут быть асимметричными. Примеры энантиоморфных объектов — кристаллы винной кислоты, кварца, многие ор­ганич. молекулы, напр. аминокис­лоты. Др. термин, эквивалентный Э.,— хиральность. См. Симметрия кристаллов, Изомерия молекул.

В. К. Вайнштейн

ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ (облучённость), поверхност­ная плотность лучистого потока; рав­на отношению потока излучения к площади облучаемой поверхности. Единица измерения Э. о.— Вт/м². В си­стеме световых величин аналогом Э. о. явл. освещённость.

ЭНЕРГЕТИЧЕСКАЯ СИЛА СВЕТА, то же, что сила излучения.

ЭНЕРГЕТИЧЕСКАЯ ЭКСПОЗИЦИЯ (количество облучения, доза Н_е), отношение энергии dQ_e падающего на элемент поверхности излучения к площади dA этого элемента. Экви­валентное определение: Э. э. есть произведение энергетической освещён­ности Е_е на длительность облучения dt.

H_e=dQ_e/dA=∫E_edt. Ед. измерения Э. э.— Дж•м^-2. В системе световых величин аналогичная Э. э. величина наз. экспозицией. Понятием Э. э. широко пользуются также при работе с корпускулярным излучением.

Д. Н. Лазарев.

ЭНЕРГЕТИЧЕСКИЕ ФОТОМЕТРИ­ЧЕСКИЕ ВЕЛИЧИНЫ, величины, характеризующие энергетич. парамет­ры оптического излучения безотно­сительно к его действию на приёмники излучения. В таблице приведены наиб. употребительные Э. ф. в. и единицы



их измерения. Соотношения между Э. ф. в. те же, что и между соответ­ствующими световыми величинами.

Д. Н. Лазарев.

ЭНЕРГИИ СОХРАНЕНИЯ ЗАКОН, один из наиб. фундам. законов при­роды, согласно к-рому важнейшая физ. величина — энергия сохраняется в изолиров. системе. В изолиров. системе энергия может переходить из одной формы в другую, но её кол-во остаётся постоянным. Если система не изолирована, то её энергия может изменяться либо при одноврем. изменении энергии окружающих тел на такую же величину, либо за счёт изменения энергии вз-ствия тела с

902


окружающими телами. При переходе системы из одного состояния в другое изменение энергии не зависит от того, каким способом (в результате каких вз-ствий) происходит переход, т. е. энергия — однозначная ф-ция состоя­ния системы.

Э. с. з. явл. строгим законом природы, справедливым для всех из­вестных вз-ствий, он связан с однородностью времени, т. е. с тем фак­том, что все моменты времени экви­валентны и физ. законы не меняются со временем (см. Симметрия в физике). Э. с. з. для механич. процессов уста­новлен Г. В. Лейбницем (1686), для немеханич. явлений — Ю. Р. Майером (1845), Дж. П. Джоулем (1843 — 1850) и Г. Л. Гельмгольцем (1847). В термодинамике Э. с. з. наз. первым началом термодинамики.

До создания А. Эйнштейном спец. теории относительности (1905) за­коны сохранения массы и энергии существовали как два независимых закона. В теории относительности они были слиты воедино (см. также Со­хранения законы).

• Энгельс Ф., Диалектика природы, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20; Ленин В. И., Материализм и эмпириокритицизм, Полн. собр. соч., 5 изд., т. 18; М а й е р Р., Закон сохране­ния и превращения энергии. Четыре исследо­вания. 1841—1851, М.—Л., 1933; Гельм­гольц Г., О сохранении силы, пер. с нем., 2 изд., М.— Л., 1934; Планк М., Принцип сохранения энергии, пер. с нем., М.— Л., 1938; Л а у э М., История фи­зики, пер. с нем., М., 1956; В и г н е р Е., Этюды о симметрии, пер. с англ., М., 1971.

Г. Я. Мякишев.

ЭНЕРГИЯ (от греч. energeia — дей­ствие, деятельность), общая количеств. мера движения и вз-ствия всех видов материи. Э. не возникает из ничего и не исчезает, она может только пере­ходить из одной формы в другую (см. Энергии сохранения закон). Понятие Э. связывает воедино все явления природы.

В соответствии с разл. формами движения материи рассматривают раз­ные формы Э.: механич., внутр., эл.-магн., хим., ядерную и др. Это де­ление до известной степени условно. Так, хим. Э. складывается из кине­тич. Э. движения эл-нов и электрич. Э. вз-ствия эл-нов друг с другом и с ат. ядрами. Внутр. Э. равна сумме кинетич. Э. хаотич. движения молекул относительно центра масс тел и потенц. Э. вз-ствия молекул друг с другом. Э. системы однозначно зависит от параметров, характеризующих со­стояние системы. В случае непрерыв­ной среды или поля вводятся понятия плотности Э., т. е. Э. в ед. объёма, и плотности потока Э., равной про­изведению плотности Э. на скорость её перемещения.

Относительности теория показала, что Э. тела неразрывно связана с его массой т соотношением ξ= mc². Лю­бое тело обладает Э.; если масса по­коящегося тела m₀, то его Э. покоя ξ₀=m₀c²', эта Э, может переходить в др. виды Э. при превращениях частиц (распадах, яд. реакциях и т. п.).

Согласно классич. физике, Э. любой системы меняется непрерывно и может принимать любые значения. Квант. теория утверждает, что Э. микроча­стиц, движение к-рых происходит в огранич. объёме пр-ва (напр., эл-нов в атоме), принимает дискр. ряд зна­чений. Так, атомы испускают эл.-магн. Э. в виде дискр. порций — све­товых квантов, или фотонов.

Э. измеряется в тех же ед., что и работа: в системе СГС — в эргах, в СИ — в джоулях; в ат. и яд. физике и физике элем. ч-ц обычно применя­ется внесистемная ед.— электрон-вольт.

• См. лит. при ст. Энергии сохранения закон.

Г. Я. Мякишев.

ЭНЕРГИЯ ИОНИЗАЦИИ, равна работе, затрачиваемой на удаление одного внеш. эл-на из атома (на иони­зацию атома), находящегося в осн. энергетич. состоянии. Численно равна ионизационному потенциалу.

ЭНЕРГИЯ ПОКОЯ частицы (тела), энергия ч-цы в системе отсчёта, в к-рой она покоится: ξ₀=m₀c², где m₀ — масса покоя ч-цы.

ЭНЕРГИЯ СВЯЗИ, энергия связ. системы к.-л. ч-ц (напр., атома как системы из ядра и эл-нов), равная работе, к-рую необходимо затратить, чтобы разделить эту систему на со­ставляющие её ч-цы и удалить их друг от друга на такое расстояние, на к-ром их вз-ствием можно пренеб­речь. Э. с. определяется вз-ствием ч-ц и явл. отрицат. величиной, т. к. при образовании связ. системы энергия выделяется. Абс. величина Э. с. ха­рактеризует прочность связи и устой­чивость системы. Напр., для ат. ядра Э. с. определяется сильным взаимодей­ствием нуклонов в ядре и, согласно соотношению Эйнштейна, пропорц. де­фекту масс m:ξ=mc². Для наиб. устойчивых ядер Э. с. составляет ок. 8•10⁶ эВ/нуклон (удельная Э. с.). Эта энергия может выделиться при слиянии лёгких ядер в более тяжёлое ядро (см. Термоядерные реакции), a также при спонтанном делении тяжё­лых ядер, объясняемом уменьшением уд. Э. с. с ростом ат. номера (см. Радиоактивность). Э. с. эл-нов в атоме или молекуле определяется электромагнитными взаимодействия­ми и для каждого эл-на пропорц. ионизац. потенциалу; напр., для атома Н в осн. состоянии она равна 13,6 эВ. Этим же вз-ствием обусловлена Э. с. атомов в молекуле и кристалле (см. Межатомное взаимодействие). Э. с., обусловленная гравитационным взаи­модействием, обычно мала и имеет значение лишь для нек-рых косм. объектов (см., напр., Чёрная дыра).

ЭНЕРГИЯ ХИМИЧЕСКОЙ СВЯЗИ, для двухат. молекул — энергия уда­ления атомов на бесконечно большое расстояние друг от друга; для многоат. молекул, радикалов, ионов — энергия диссоциации. Суммарная энергия удаления всех атомов многоат. молекулы друг от друга на беско­нечно большое расстояние, наз. энер­гией образования молекулы, равна приближённо сумме Э. х. с. Энергию образования молекулы обычно разби­вают на вклады Э. х. с., оценивая их с помощью различных аддитивных схем. Экспериментально измеряют ли­бо энергию образования молекул, сжигая соединения в калориметрич. бомбах, либо определяют энергию диссоциации молекул с помощью элект­ронного удара и др. методов. Теор. расчёт Э. х. с.— одна из осн. задач квантовой химии.

ЭНТАЛЬПИЯ (от греч. enthalpo — нагреваю) (теплосодержание, тепло­вая функция Гиббса), потенциал тер­модинамический, характеризующий состояние макроскопич. системы в термодинамич. равновесии при выборе в кач-ве основных независимых пе­ременных энтропии S и давления р. Обозначается H(S, p, N, х_i), где N — число ч-ц системы, x_i — др. макроско­пич. параметры системы. Э.— адди­тивная ф-ция (т. е. Э. всей системы равна сумме Э. составляющих её частей), с внутренней энергией U системы Э. связана соотношением:

H=U+pV, (1)

где V — объём системы. Полный диф­ференциал Э. (при неизменных N и x_i) имеет вид:

dH = TdS + Vdp. (2)

Из ф-лы (2) можно определить темп-ру Т и объём V системы: Т=(дН/дS)_р, V=(дН/др)_S. При пост. давлении теп­лоёмкость системы с_р= (дН!дТ)_р. Эти св-ва Э. при пост. р аналогичны св-вам внутр. энергии при пост. V:

T=(дU/дS)_v, р=-(дU/дV)_S, c_V =(дU/дT)_V.

Равновесному состоянию системы при пост. S и p соответствует мин. значение Э. Изменение Э. (ЛЯ) равно кол-ву теплоты, к-рое сообщают системе или отводят от неё при пост. давлении, поэтому значения H характеризуют тепловые эффекты фазовых переходов (плавления, кипения и т. д.), хим. реакций и др. процессов, протекаю­щих при пост. давлении. При тепловой изоляции тел (и пост. р) Э. сохра­няется, поэтому её называют иногда теплосодержанием или тепловой ф-ци­ей. Условие сохранения Э. лежит, в частности, в основе теории Джоуля — Томсона эффекта, нашедшего важное практич. применение при сжижении газов. Термин Э. был предложен голл. физиком X. Камерлинг-Оннесом.

Д. Н. Зубарев.

ЭНТРОПИЯ (от греч. entropia — поворот, превращение), понятие, впер­вые введённое в термодинамике для определения меры необратимого рас-

903


сеяния энергии. Э. широко применя­ется и в др. областях науки: в ста­тистической физике как мера веро­ятности осуществления к.-л. макро­скопич. состояния; в теории инфор­мации как мера неопределённости к.-л. опыта (испытания), к-рый может иметь разные исходы. Эти трактовки Э. имеют глубокую внутр. связь. Напр., на основе представлений об информац. Э. можно вывести все важнейшие положения статистич. фи­зики.

В термодинамике понятие «Э.» было введено нем. физиком Р. Клаузиусом (1865), к-рый показал, что процесс превращения теплоты в работу под­чиняется определ. физ. закономер­ности — второму началу термоди­намики, к-рое можно сформулировать строго математически, если ввести особую ф-цию состояния —Э. Так, для термодинамич. системы, совершающей квазистатически (бесконечно медлен­но) циклич. процесс, в к-ром система последовательно получает малые кол-ва теплоты Q при соответствующих значениях абс. темп-ры Т, интеграл от «приведённого» кол-ва теплоты Q/T

по всему циклу равен нулю



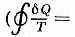
=0 — т. н. равенство Клаузиуса). Это равенство, эквивалентное второму на­чалу термодинамики для равновесных процессов, Клаузиус получил, рассмат­ривая произвольный циклич. процесс как сумму очень большого (в пределе бесконечно большого) числа элемен­тарных Карно циклов. Математичес­ки равенство Клаузиуса необходимо и достаточно для того, чтобы выражение

dS=Q/T (1)

представляло собой полный дифферен­циал ф-ции состояния S, назв. «Э.» (дифф. определение Э.). Разность Э. системы в двух произвольных состоя­ниях А и В (заданных, напр., значе­ниями темп-р и объёмов) равна:S_B-S_A=∫^B_AQ/T (2)

(интегр. определение Э.). Интегриро­вание здесь ведётся вдоль пути лю­бого квазистатич. процесса, связываю­щего состояния А и В, при этом, сог­ласно равенству Клаузиуса, прираще­ние Э. S=S_B-S_A не зависит от пути интегрирования. Т. о., из второго начала термодинамики следует, что существует однозначная ф-ция состоя­ния S, к-рая при квазистатич. адиабатич. процессах (Q=0) остаётся постоянной. Процессы, в к-рых Э. оста­ётся постоянной, наз. изоэнтропийными. Примером может служить про­цесс, широко используемый для по­лучения низких темп-р,— адиабатич. размагничивание (см. Магнитное ох­лаждение). При изотермич. процессах изменение Э. равно отношению сооб­щённой системе теплоты к абс. темп-

ре. Напр., изменение Э. при испаре­нии жидкости равно отношению теп­лоты испарения к темп-ре испарения при условии равновесия жидкости с её насыщ. паром.

Согласно первому началу термоди­намики, Q=dU+pdV, т. е. сообща­емое системе кол-во теплоты равно сумме приращения внутренней энер­гии dU и совершаемой системой элем. работы pdV, где р — давление, V -объём системы. С учётом первого на­чала термодинамики дифф. определе­ние Э. принимает вид:

dS =1/T(dU+pdV), (3)

откуда следует, что Э. представляет собой потенциал термодинамический при выборе в кач-ве независимых пе­ременных внутр. энергии U и объёма V. Частные производные Э. связаны с Т и р соотношениями:

1/T=(дS/дU (4) и p/T-=(дS/дV)_U (5) к-рые определяют уравнения состоя­ния системы (первое — калорическое, второе — термическое). Ур-ние (4) ле­жит в основе определения абсолютной температуры (см. также Температура, Температурные шкалы).

Ф-ла (2) определяет Э. лишь с точ­ностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. про­извольным). Абс. значение Э. можно установить с помощью третьего на­чала термодинамики, основываясь на к-ром, за нач. точку отсчёта Э. при­нимают S₀=0 при Т=0.

Важность понятия Э. для анализа необратимых (неравновесных) про­цессов также была показана впервые Клаузиусом. Для необратимых про­цессов интеграл от приведённой теплоты Q/T по замкнутому пути всегда отрицателен

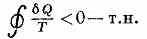
Клаузиуса неравенство. Это неравен­ство — следствие теоремы Карно: кпд частично или полностью необратимого циклич. процесса всегда меньше, чем кпд обратимого цикла. Из неравенст­ва Клаузиуса вытекает, что



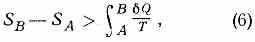
поэтому Э. адиабатически изолирован­ной системы при необратимых про­цессах может только возрастать.

Т. о., О. определяет хар-р процес­сов в адиабатич. условиях: возможны только такие процессы, при к-рых Э. либо остаётся неизменной (обратимые процессы), либо возрастает (необра­тимые процессы). При этом не обяза­тельно, чтобы возрастала Э. каждого из тел, участвующих в процессе. Уве­личивается общая сумма Э. тел, в к-рых процесс вызвал изменения.

Термодинамич. равновесию адиаба­тич. системы соответствует состояние с максимумом Э. Энтропия может иметь не один, а неск. максимумов, при этом система будет иметь неск. состояний равновесия. Равновесие,

к-рому соответствует наибольший мак­симум Э., наз. абсолютно устойчивым (стабильным). Из условия максималь­ности Э. адиабатич. системы в состоя­нии равновесия вытекает важное след­ствие: темп-ра всех частей системы в состоянии равновесия одинакова.

Понятие Э. применимо и к термоди­намически неравновесным состояниям, если отклонения от термодинамики рав­новесия невелики и можно ввести представление о локальном термоди­намическом равновесии в малых, но ещё макроскопич. объёмах. В целом Э. неравновесной системы равна сум­ме Э. её частей, находящихся в ло­кальном равновесии.

Термодинамика неравновесных про­цессов позволяет более детально ис­следовать процесс возрастания Э. и вычислить кол-во Э., образующейся в ед. объёма в ед. времени вследствие отклонения от термодинамич. равно­весия,— производство энтропии.

Статистич. физика связывает Э. с вероятностью осуществления данного макроскопич. состояния системы. Э. определяется через логарифм ста­тистического веса  данного равновес­ного состояния:

S=kln(ξ, N), (7)

где (ξ, N)—число квантовомеханич. уровней в узком интервале энергии ξ вблизи значения энергии £ системы из N ч-ц, в классич. статистич. физике  — величина объёма в фазовом про­странстве системы при заданных ξ и N. Впервые связь Э. с вероятностью состояния системы была установлена австр. физиком Л. Больцманом в 1872: возрастание Э. системы обусловлено её переходом из менее вероятного со­стояния в более вероятное. Иными сло­вами, эволюция замкнутой системы осуществляется в направлении наибо­лее вероятного распределения энергии по отд. подсистемам.

В отличие от термодинамики, ста­тистич. физика рассматривает особый класс процессов — флуктуации, при к-рых система переходит из более ве­роятного состояния в менее вероятное, и её Э. уменьшается. Наличие флук­туации показывает, что закон возра­стания Э. выполняется только в ср. для большого промежутка времени.

Э. в статистич. физике тесно связа­на с информац. Э., к-рая служит ме­рой неопределённости сообщений (со­общения описываются множеством ве­личин x₁, х₂, . . ., х_n и вероятностей Р₁, Р₂,. . .,Р_n появления этих вели­чин в сообщении). Для определённого (дискретного) статистич. распределе­ния вероятностей Р_k информац. Э. на­зывают величину

H_и=-ⁿ_k=1Р_kInP_k при ⁿ_k=1P_k=1.(8)

Н_и=0, если к.-л. из Р_k равно 1, а ост.— нулю, т. е. информация достоверна, неопределённость отсутствует. Э. при­нимает наибольшее значение, когда все P_k одинаковы (неопределённость в информации максимальна). Информац.

904


Э., как и термодинамическая, обла­дает св-вом аддитивности (Э. неск. со­общений равна сумме Э. отд. сообще­ний). Из вероятностной трактовки информац. Э. могут быть выведены осн. распределения статистич. физики: ка­ноническое Гиббса распределение, к-рое соответствует макс. значению информац. Э. при заданной ср. энергии, и большое канонич. распределение Гиббса — при заданных ср. энергии и числе ч-ц в системе.

• См. лит. при ст. Термодинамика.

Д. Н. Зубарев.

ЭПИДИАСКОП (от греч. epi — на, dia — через и skopeo — смотрю) (эпидиапроектор), комбинированный про­екционный аппарат, позволяющий по­лучать на экране изображения как прозрачных, так и непрозрачных ори­гиналов. Совмещает в себе эпипроектор и диапроектор. Оптич. схема про­стейшего эпидиаскопа в двух режи­мах его работы представлена на ри­сунке: а) эпископическая проекция,



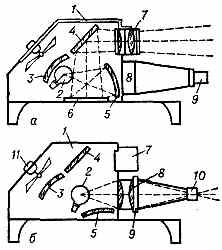
Оптич. схема эпидиаскопа.


б) диаскопическая проекция. В пер­вом случае лучи от источника све­та 2 с помощью сферических зеркал 3 и 5 освещают непрозрачный объ­ект 6, от которого диффузно рассеян­ные лучи попадают в светосильный проекц. объектив 7, отражаясь от зеркала 4; 1 — кожух, 11 — система охлаждения. При диаскопич. проек­ции зеркало 5 отклоняется, открывая доступ лучам от источника 2 в кон­денсор 8. Последний, равномерно ос­вещая диапозитив, вставленный в рам­ку 9, направляет лучи в объектив 10, проецирующий изображение на экран.

• См. лит. при ст. Проекционный аппарат.