Управление образования администрации городского округа «Город Йошкар-Ола» моу «Средняя общеобразовательная школа №20 г. Йошкар-Олы» Тайны «Золотого сечения» (реферат)
| Вид материала | Реферат |
Содержание14. Источники информации I. Построим пятиугольник. Приближенно 0,6. Ас:вс = вс:ав=0,6 II. Существует такое понятие - золотой прямоугольник Освещенная солнцем сосна. |
- Постановление мэра города Йошкар-Олы, 281.53kb.
- Публичный доклад моу гимназия №14, 460.05kb.
- Постановление мэра города Йошкар-Олы, 265.13kb.
- Отчет о результатах деятельности главы администрации городского округа «Город Йошкар-Ола», 1507.08kb.
- Постановление мэра города Йошкар-Олы, 220.5kb.
- Финансирование мероприятий программы предусматривать при разработке проектов бюджетов, 281.6kb.
- Ведомственная целевая программа функционирования администрации городского округа «Город, 2843.64kb.
- Постановление мэра города Йошкар-Олы, 239.53kb.
- О. П. Войнов решение собрания депутатов городского округа «Город Йошкар-Ола» пятого, 34.67kb.
- Исполнителем мероприятий Программы является Министерство внутренних дел Место нахождения, 77.66kb.
Заключение
Рациональные и иррациональные числа являются своеобразными противоположностями. Но природа едина, и ее противоположности не только находятся в противодействии, борьбе, но и в единстве. И не удивительно, что многие иррациональные числа выражаются через совокупность целых чисел. Все три числа:p, e и Ф – связаны между собой простыми отношениями и могут быть выражены в виде пределов бесконечных дробей. Кроме того, на примере золотой пропорции показано, что целые числа натурального ряда : 1, 2, 3, … могут быть выражены через иррациональное число Ф. Кроме того, число Ф с любой степенью точности может быть выражено через отношение целых чисел. Разве эти примеры не свидетельствуют о единстве рационального и иррационального в природе?!
Мы так часто говорим о единстве и борьбе противоположностей, что это понятие стало тривиальным, само собой разумеющимся и не требующим исследования. Может быть, поэтому этот фундаментальный закон природы так мало исследован и углублен и, что характерно, почти совершенно не математизирован. А между тем он достоин самого пристального изучения и развития – ведь это один из основных, наиболее общих законов мироздания.
14.
Источники информации
- www.abc-people.com Ковалев Ф.В. Золотое сечение в живописи.
К.: Вища школа, 1989.
- Кеплер И. О шестиугольных снежинках. – М., 1982.
- Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
- Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
- Стахов А. Коды золотой пропорции.
- А.В. Волошинов Пифагор.- М: Просвещение, 1993 г.
- Г.И. Глейзер История математики в школе VII-VIII кл. Пособие для
учителей.- М: Просвещение, 1982 г.
- Энциклопедия для детей. Т.11. Математика /Глав. ред. М.Д. Аксенова.
М.: Аванта +, 1999. – 688 с.
- Леонардо да Винчи: жизнь, творчество, произведения. ИДДК, DISC-0521,
ООО “Бизнессофт”, Россия, 2004.
10. www.abc-people.com
15.

С давних пор ученые занимались поисками гармонии и совершенства. Одним из таких вопросов был деление отрезка таким образом, чтобы отношение частей было совершенным. Задолго до нашей эры, в различных точках мира, разные ученые, независимо друг от друга, находили это отношение, и у всех это отношение было одним и тем же. И сейчас мы с вами найдем такое деление отрезка, таким способом, каким его нашел знаменитый ученый Пифагор.
I. Построим пятиугольник.
И с помощью пятиугольника мы найдем это совершенное отношение.
Построим две диагонали пятиугольника, как показано на экране

И расставим буквы, как показано на экране. Измерим отрезки АС и ВС и найдем отношение этих отрезков – меньшего к большему. Чему равно это отношение?
- Приближенно 0,6.
А теперь, найдем отношение длин отрезков ВС и АВ. Чему равно это отношение?
- Приближенно 0,6.
Что же получается? Отношение АС к ВС и отношение ВС к АВ приближенно равны 0,6!
- АС:ВС = ВС:АВ=0,6
Такую пропорцию, где меньшее так относится к большему, как большее к целому, назвали золотой пропорцией. А деление отрезка в таком отношении – золотым сечением
Что означает слово сечение?
- Отсечь, рассечь, разделить.
Деление – сечение. А почему его назвали золотым, мы с вами выясним позже.
Проведем остальные диагонали пятиугольника. Какую фигуру мы получили?
- Звезду.
Какая фигура расположена внутри звезды?
- Пятиугольник.
И в этом пятиугольнике можно провести диагонали и получить звезду, и продолжать процесс можно бесконечно!
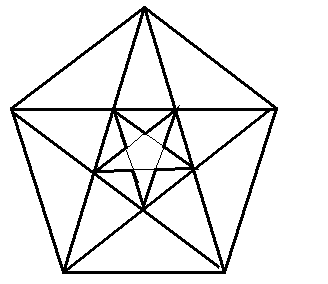
Этот пятиугольник называется пентаграммой, знак школы Пифагора. Во времена Пифагора он считался магическим. Отношение частей его диагоналей, названное золотым сечением, и приближенно равное 0,6, а более точно 0,618, считалось идеальным. Недаром пятиконечная звезда всегда привлекала человека своей формой.
Вы часто рисовали эту звезду, не задумываясь о ее совершенной форме. А мы с вами обосновали красоту этой фигуры с помощью математики!
II. Существует такое понятие - золотой прямоугольник.
- Отношение ширины прямоугольника к его длине приближенно равно 0,6.
Золотой прямоугольник обладает замечательным свойством: если от золотого прямоугольника отрезать квадрат со стороной равной ширине, то оставшийся прямоугольник также будет золотым.
Психологи утверждают, что человек, живущий в комнате, имеющей форму золотого прямоугольника, более спокойный, уравновешенный.
Итак, мы с вами добрались до первой станции – Живописная.
Перед вами репродукция картины Ивана Шишкина “Корабельная роща”
Назовите самую яркую деталь на этой картине.
- Освещенная солнцем сосна.
Что вы можете сказать о месте расположения этой сосны?
- Она делит картину в отношении золотого сечения.
Проверим это!
Ярко освещенная солнцем сосна, стоящая на переднем плане, делит длину картины по горизонтали в золотом отношении.
Справа от сосны, освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по вертикали. Так же можно найти мотивы золотого сечения и в других частях картины.
Наличие в картине ярких деталей, делящих ее по золотому сечению, придает картине уравновешенность, чувство спокойствия и гармонии.
Картины великих художников, вызывающие непонятную, притягательную силу, запоминающиеся, написаны с применением золотого сечения. Чтобы создать шедевр, даже в искусстве необходима математика!
Следующая станция – Архитектурная
- Перед Вами здание - Парфенон, находится в Греции.
Это здание построено в 5 веке до н.э. зодчим Иктином, в честь богини Афины. Это здание – символ Греции, тоже построено по принципу золотого сечения. Оно считается совершеннейшим из архитектурных сооружений. Отношений высоты здания к его длине равно приближенно 0, 618. По вертикали здание также делится по золотому сечению с точностью до тысячных!!!
Золотое сечение очень часто используется в строительстве, пример тому Дом Пашкова, считавшийся одним из самых красивых зданий в Москве в 19 веке (с него началось развитие библиотеки им. Ленина), Храм Василия Блаженного (Покровский собор) на Красной площади.
Беседуя об архитектуре, мы с вами незаметно добрались до станции – Растительная.
На этой станции мы с вами узнаем о том, что и в природе золотое сечение не редкость. Обратите внимание на цветок.
Кто-нибудь прослеживает мотивы золотого сечения? Листья располагаются на стебле таким образом, что между двумя парами листьев третья расположена в месте золотого сечения. Измерив расстояние от нижнего листа до среднего, затем от среднего до верхнего, найдем отношение этих длин. - Приближенное значение равно 0,6
При таком расположении листьев, как утверждают биологи, достигается максимальное восприятие солнечных лучей. Сама природа определила отношение золотого сечения – человек это заметил и использовал это знание!
Мы добрались до последней станции – Анатомической.
На этой станции мы выясним, почему такое отношение назвали золотым. Перед вами изображение человеческого тела. Что можно сказать о нем?
- Линия пояса делит тело человека в золотом отношении.
А какие части человеческого тела также построены по принципу золотого сечения?
- Лицо, рука, кисть
Золотое сечение повсеместно присутствует в теле человека. И изначально золотое сечение, золотую пропорцию называли божественной пропорцией. Как вы думаете, почему?
- В Библии сказано, что Бог создал человека по образу и подобию своему.
И, когда человек узнал, что его тело делится в таком отношении, он назвал это отношение “божественным”, а Леонардо да Винчи назвал его золотым, в смысле “идеальным”. Золотое сечение дано человеку самой природой в пропорциях своего тела, поэтому золотое сечение стало для человека эталоном красоты.
Когда вы слушаете собеседника, куда вы смотрите?
- В глаза.
А почему не на рот? Как вы думаете?
- Линия глаз делит лицо человека в золотом сечении.
Линия пояса делит тело человека по золотому сечению. Но пропорции тел мужчины и женщины отличаются друг от друга. У одних отношение верхней части тела к нижней более приближенно к значению золотого сечения, как вы думаете, чьи пропорции идеальней – мужчины или женщины? Чье тело более совершенно?
- Женщины
Неправильно! Мужчины. У женщины ноги по отношению к телу короче, чем у мужчины. Но женщины исправили этот несправедливость. Как вы думаете как?
- Каблуки.
Правильно! Женщины носят туфли на каблуках не для того, чтобы увеличить свой рост, а для того, чтобы увеличить, пусть зрительно, длину ног.
А с золотым прямоугольником мы с вами встречаемся в жизни очень часто! Возьмите в руки ваш билет – шоколадку и выясните, является ли она золотым прямоугольником!
- Отношение ширины к длине приближенно равно 0,6.
И лист бумаги, и почтовая открытка, и карманный календарь, и проездной билет, и, как вы убедились, даже шоколадка, являются золотым прямоугольником.
Как вы думаете, почему эти знакомые и привычные для нас вещи выполнены в форме золотого прямоугольника?
- Потому что это приятная для человеческого глаза форма!
А золотое сечение встречается в жизни в самых неожиданных местах. Это и окрас шкуры некоторых животных, и размер ящерицы, и даже куриное яйцо. В старших классах мы узнаем, что золотое сечение присутствует в паутине, в раковине улитке, в расположении семян подсолнуха, и даже в нашей галактике!
Математика вокруг нас. Ее законам подчинена и природа, и деятельность человека, и строение самого человека подчиняется математическим законам.
