2. Модели перехода к рыночной экономике и их особенности
| Вид материала | Документы |
- План реферата Фармацевтический рынок в России в условиях перехода к рыночной экономике., 187.83kb.
- Темы курсовых работ по дисциплине «Макроэкономика» Сущность и основные черты рыночной, 37.01kb.
- Программа «общественное мнение» работники вузов и студенты на этапе перехода к рыночной, 3742.16kb.
- Тематика курсовых работ по дисциплине Экономическая теория Муниципальная собственность, 138.43kb.
- Период перехода от социалистической к рыночной экономике не имеет аналогов в мировой, 105.95kb.
- Опорный конспект Особенности развития финансово-кредитного механизма во многом определяются, 39.89kb.
- План счетов и особенности организации бухгалтерского учета в коммерческих банках Горелый, 33.01kb.
- Подготовки специалиста в рамках национальной модели, 135.8kb.
- План: Понятие рыночной экономики Необходимость и сферы государственного вмешательства, 81.36kb.
- Орлянский Евгений Анатольевич кандидат экономических наук, доцент, профессор кафедры, 529.36kb.
Раздел III.
1.Статистические методы и их применение для решения экономических задач
При статистическом исследовании финансово-экономических показателей в ходе анализа, осуществляемого вручную или посредством ПЭВМ, вычисляют простейшие
характеристики динамики их развития, выявляют закономерности прошлого развития и оценивают возможность их перенесения а будущее. Для успешного решения этого необходимо:
1) иметь достаточный для проявления статистических закономерностей объем данных (для годовых наблюдений —- не менее пяти уровней, для сезонных процессов — не менее трех периодов сезонности);
2) обеспечить методологическую сопоставимость данных;
3) на основе содержательного анализа исследуемого показателя обосновать возможность переноса закономерностей прошлого на выбранный период прогнозирования;
4) получить адекватную математическую модель и на ее основе построить точечные и интервальные прогнозы.
Основной формой представления статистической информации являются временные ряды (ВР) наблюдений. Цель статистического анализа ВР — изучение соотношения между закономерностью и случайностью формирования значений уровней ряда и оценка количественной меры их влияния.
Статистические методы исследования исходят из представления уровней ряда в виде суммы нескольких компонент, отражающих закономерность и случайность развития, в частности, в виде суммы нескольких компонент:
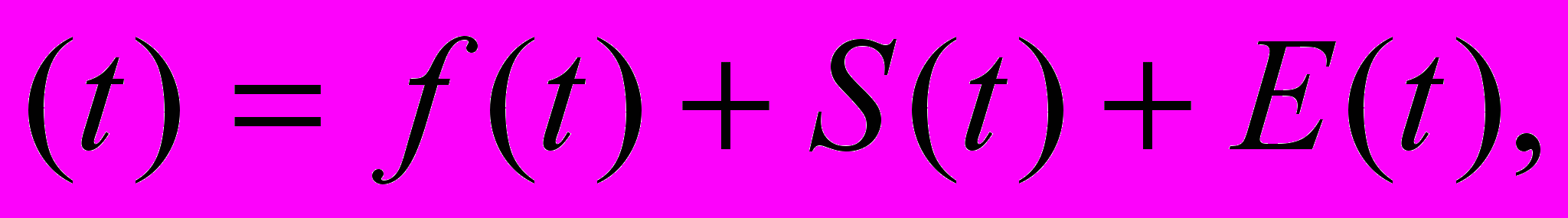
где f(t) — тренд, представляющий собой устойчивое изменение показателя в течение длительного времени, являющийся детерминированной компонентой, выражает аналитическую функцию, на которой формируются прогнозные оценки; S(t) — сезонная компонента, характеризующая устойчивые внутригодичные колебания уровней, представляемая квартальными или месячными данными (наличие устойчивых колебаний в суточных или недельных данных может рассматриваться как циклическое явление и может отображаться сезонной компонентой);
E(t) - остаточная компонента, представляющая собой расхождение между фактическими и расчетными значениями (если построена адекватная (хорошая) модель, то Е(t) является близкой к 0, случайной, независимой, подчиняющейся нормальному закону распределения компонентой, в противном случае модель является плохой).
Формирование уровней ряда определяется закономерностями трех основных типов:
инерцией тенденции,
инерцией взаимосвязи между последовательными уровнями ряда
инерцией взаимосвязи между исследуемым показателем и показателями-факторами, оказывающими на него причинное воздействие. Соответственно различают задачи анализа и моделирования тенденций, взаимосвязи между последовательными уровнями ряда; причинных взаимодействий между исследуемым показателем и показателями-факторами. Первая задача решается с помощью методов компонентного анализа, вторая — адаптивных методов и моделей, третья — эконометрического моделирования, базирующегося на методах корреляционно-регрессионного анализа.
Алгоритм статистического компонентного анализа обычно связан со следующими процедурами:
постановкой задачи и подбором исходной информации; предварительным анализом исходных временных рядов и формированием набора моделей прогнозирования; численным оцениванием параметров моделей;
определением качества моделей (адекватности и точности); выбором одной лучшей или построением обобщенной модели; получением точечного и интервального прогнозов.
При формулировании цели исследования осуществляется содержательный (логический и экономический) анализ исследуемого процесса; решается вопрос о выборе показателя, характеризующего его наиболее полно; определяются показатели, оказывающие влияние на ход развития; определяются наиболее разумный период упреждения прогноза, оптимальный горизонт прогнозирования.
4.Производственные функции и их применение для решения экономических задач
При изучении экономических процессов в современном крупномасштабном производстве бывает чрезвычайно трудно или невозможно, собрать необходимую статистику для практического построения модели, скажем типа модели Неймана, учитывающей внутреннюю структуру производства. С другой стороны, зачастую гораздо проще получить отчетные данные о поведении и взаимосвязи укрупненных экономических показателей, таких, как стоимость произведенного продукта, объем основных фондов, численность работников и т. п. Оказывается, что, оперируя даже такими укрупненными показателями и рассматривая производственный объект как «черный ящик» (т. е. изучая лишь связь между затраченными средствами и произведенным продуктом), можно получать определенные содержательные выводы.
Высказанные соображения лежат в основе теории производственных функций. Возникновение теории производственных функций принято относить к !928 г., когда появилась статья американских ученых экономиста П. Дугласа и математика Д. Кобба «Теория производства». В этой статье была предпринята попытка определить эмпирическим путем влияние величины затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США. Были использованы статистические данные за 1899—1922 гг. и поставлены следующие задачи:
1. Определить параметрический класс функций, наиболее точно приближающий количественные соотношения между тремя выбранными характеристиками производственной деятельности.
2. Найти числовые параметры, задающие конкретную функцию этого класса,
3. Сравнить результаты, получаемые как значения функций,
с фактическими данными.
Д. Коббом была предложена функция вида
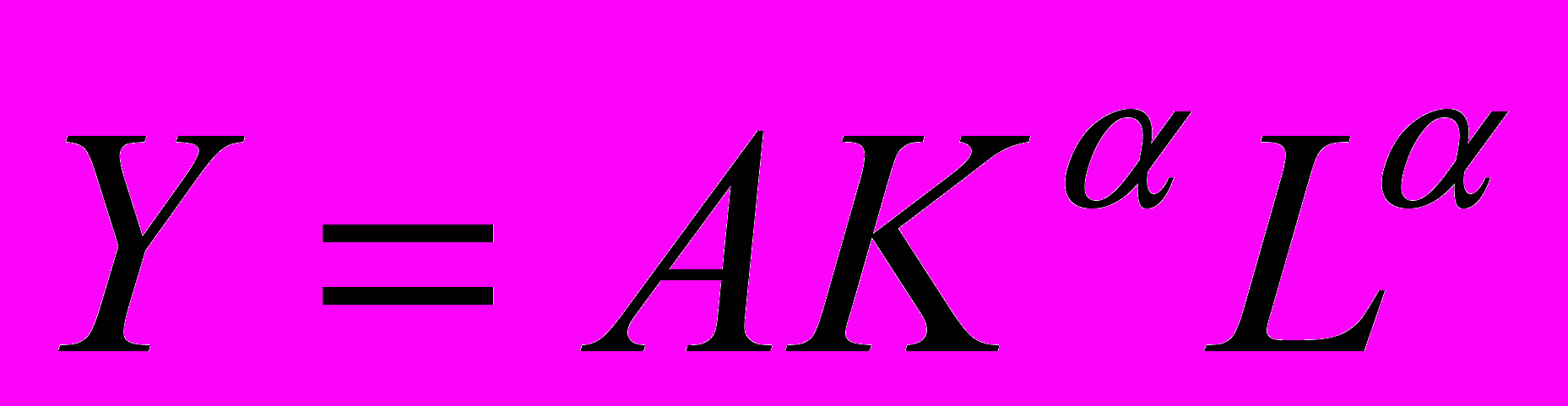 , где Y - объем выпущенной продукции, K—объем основного капитала, L —затраты труда, А, α, β—числовые параметры. Заранее накладывались условия A<0, α,β≥0, α+β=1.
, где Y - объем выпущенной продукции, K—объем основного капитала, L —затраты труда, А, α, β—числовые параметры. Заранее накладывались условия A<0, α,β≥0, α+β=1.Была составлена система уравнений
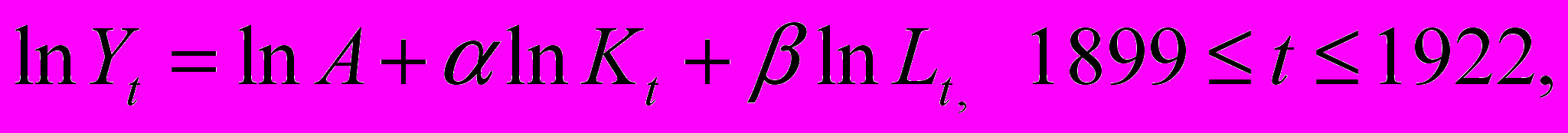
где Y,K,L -фактическое значение соответствующих величин в год t. Методом наименьших квадратов отыскивались значения А, α, β, минимизирующие выражение
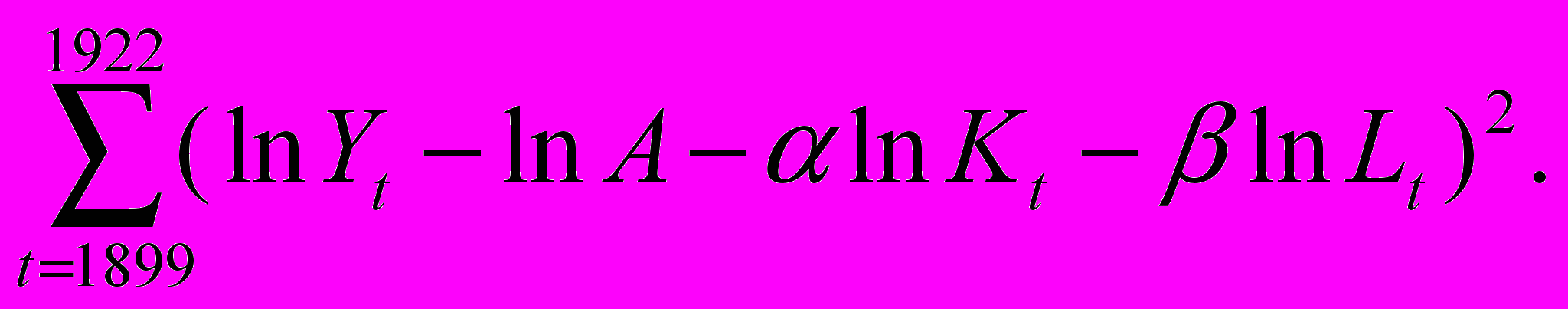
При этом оказалось, что А=1,01, α = 0,25, β = 0,75, а сравнение величины
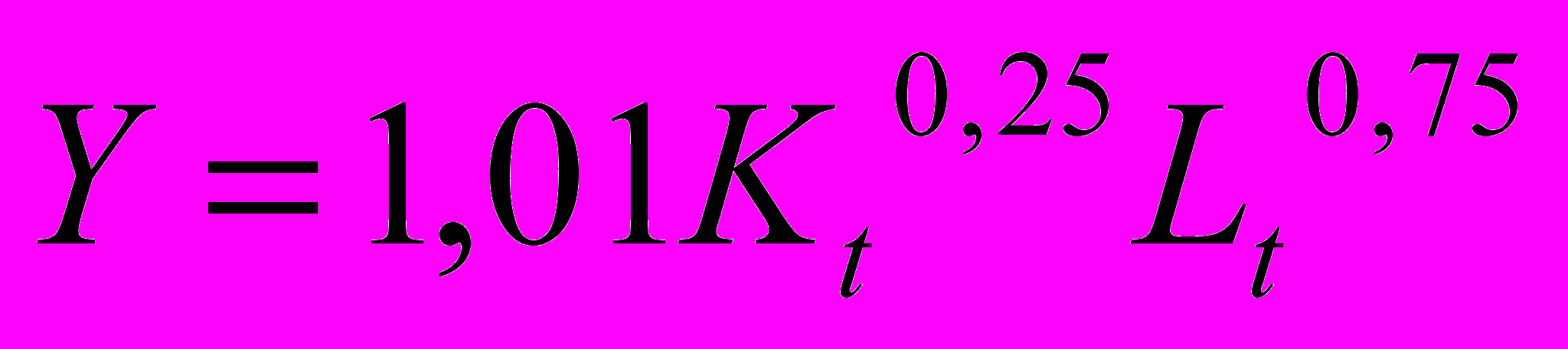 дает хорошее приближение к действительности.
дает хорошее приближение к действительности. 5. Модель межотраслевого баланса (модель Леонтьева)
№10.Модель ‘затраты-выпуск’ В.Леонтьева. Эта модель является межотраслевым балансом. В каждой стране экономика есть большая система взаимосвязанных отраслей, производящих продукты и передающих другим отраслям. Чтобы надежно прогнозировать состояние экономики надо брать 600-800 отраслей. При сопоставлении различных производственных затрат и предполагаемого выпуска продукции в каждой отрасли появляется возможность выбрать наилучший вариант. Анализ взаимосвязи отраслей материального произ-ва был осуществлен в моделе межотраслевого баланса в 30-е гг 20 века Леонтьевым и получил название: метод “затраты-выпуск”. В моделе описываются количественные соотношения (коэф) между затратами ресурсов и выпуском продукции каждой отрасли. Она выполнена в форме таблицы и похожа на шахмат. доску, где отображены потоки товаров и услуг из отрасли в отрасль материального произ-ва. По гориз: показано распределение продукции отдельных отраслей между другими отраслями. По верт: записаны затраты других отраслей на продукцию данной отрасли. Разделив каждый из этих показателей на объем годового продукта получается набор коэф-ов затрат на единицу любой продукции. Взятые все вместе эти коэф-ты образуют жесткий каркас систем урав-ний общественноэконом-ого равновесия. Что помогает точно прогнозировать величину конечного обществ-ого продукта (ВНП). При этом выполняется требование сбалансированности между суммарным спросом и суммарного объема его выпуска. Особенно применима эта модель при эволюционном развитии экономики, при устоявшейся эконом-ой структуре.
Модель Л. была использована для того, чтобы предсказать, как всеобщая занятость и занятость по секторам будет изменяться по мере того, как экономика переходит от мира к войне и обратно. Экономика разоружения также впоследствии стала одним из предметов исследовательской деятельности Л., глубоко интересовавших его всю жизнь. Менее чем за 10-летие после работы, проведенной Бюро статистики труда, метод Л. стал главной составной частью систем национальных счетов большинства стран мира, как капиталистических, так и социалистических. Он применяется и совершенствуется до сих пор правительственными и международными организациями и исследовательскими институтами во всем мире. Анализ по методу «затраты – выпуск» относится к той области экономики, создателем которой был французский экономист XIX в. Леон Вальрас и которая известна как теория всеобщего равновесия. Она ставит в центр внимания взаимозависимость экономических отношений, представленную системой уравнений, выражающих экономику как единое целое. С самого начала своей работы Л. признавал систему взаимозависимостей Вальраса. Но до систематического применения Л. этих взаимозависимостей на практике анализ всеобщего равновесия не использовался как инструментарий в процессе формирования экономической политики. До нововведений Л. главным методом в основном потоке экономической науки был анализ частичного равновесия, ставящий в центр внимания небольшое число изменяющихся переменных. Так, например, экономист мог рассчитать, как налог на импортную нефть мог отразиться на спросе на автомобильный бензин, игнорируя при этом любые отдаленные последствия, которые этот налог мог вызвать в сталелитейной промышленности. Экономисты в течение длительного времени сознавали тот факт, что анализ частичного равновесия серьезно искажает реальность, если масштабы промышленности или степень изменений, которые подвергаются изучению, достаточно велики. Применение Л. системы Вальраса для решения этой проблемы и анализ Л. по методу «затраты – выпуск» связаны с составлением шахматных таблиц (шахматных балансов). Такая таблица делит хозяйство на большое число отраслей (секторов) – первоначально на 44 сектора. Продажи промежуточных продуктов и готовых товаров секторами, перечисленными в левой стороне таблицы, вписываются в вертикальные колонки под наименованиями соответствующих секторов, записанными в том же порядке в верхнем горизонтальном ряду. Вторая таблица, или сетка, составленная из «технических коэффициентов», выводится из закрытой модели шахматной таблицы Когда эти коэффициенты расставляются в системе уравнений, которые решаются одновременно, составляется третья таблица, называемая «инверсией Л.», которая показывает, что требуется от каждого сектора для приращения общего выпуска на один доллар. Значение инверсии Л. определяется тремя обстоятельствами. Во-первых, ее использование привело к улучшению положения при сборе международных экономических и статистических данных, невероятно выросших количественно в последние десятилетия. Во-вторых, инверсия в деталях раскрывает работу внутреннего механизма хозяйства, причем ограничителем выступает только громоздкость расчетов. В-третьих, после оценки спроса на готовые товары или определения его перспективы инверсия может быть использована для проведения анализа экономической политики, поскольку она показывает – и прямо, и косвенно, – что требуется от каждого сектора в виде затрат для увеличения выпуска данных товаров. Л. совершенствовал свою систему на протяжении 50-х и 60-х гг. С появлением более сложных компьютеров он увеличивал количество секторов и освобождался от некоторых упрощающих предположений, прежде всего от условия, что технические коэффициенты остаются неизменными, несмотря на изменение цен и технический прогресс. Чтобы исследовать проблемы экономического роста и развития, Л. разработал динамический вариант прежде статичной модели анализа «затраты – выпуск», добавив в нее показатели потребностей в капитале к списку так называемого конечного спроса, или конечных продаж. Поскольку метод «затраты – выпуск» доказал свою полезность в качестве аналитического инструмента в новой сфере региональной экономики, шахматные балансы начали составляться и для хозяйства некоторых американских городов.
Схема межотраслевого баланса (модель Леонтьева)
В основе модели лежат следующие предположения:
- В экономической модели производятся, покупаются, потребляются и инвестируются n продуктов.
- Каждая отрасль является чистой, т.е. производит только один продукт; совместное производство различных продуктов исключается. Различные отрасли выпускают различные продукты.
- Под производственным процессом каждой отрасли понимается преобразование некоторых типов продуктов в определенный продукт. При этом соотношение затраченного продукта и впускаемого предполагается постоянным.
Пусть весь производственный сектор народного хозяйства разбит на n чистых отраслей, т.е. их продукция предполагается однородной. Чистая отрасль есть некая экономическая абстракция, не обязательно существующая реально в виде каких-то организационных форм типа министерства, треста, объединения. Несомненно, что включение в схему межотраслевого баланса только чистых отраслей затрудняет ее непосредственное применение, поскольку на практике планирование и отчетность осуществляются в рамках существующих организационных структур. Однако подобная идеализация оправдана, с одной стороны, тем, что она позволяет провести детальный анализ сложившейся технологической структуры общественного производства и распределения, а с другой — тем, что опыт, накопленный при изучении данной упрощенной схемы, привел к построению более содержательных моделей.
Возвращаясь к описанию схемы межотраслевого баланса, предположим, что каждая отрасль выпускает продукт только одного типа и разные отрасли выпускают разные продукты. Таким образом, в рассматриваемой нами производственно-экономической системе выпускается п видов продуктов. В процессе производства своего вида продукта каждая отрасль нуждается в продукции других отраслей.
Допустим теперь, что на производство единицы j–того продукта в некоторой отрасли необходимо затратить aij единиц продукта i. Валовый выпуск xi продукта i за год распадается на две части: на производственное потребление во всех отраслях и на конечное непроизводственное потребление. В предположениях 1-3 производственное потребление продукта i всеми отраслями равно
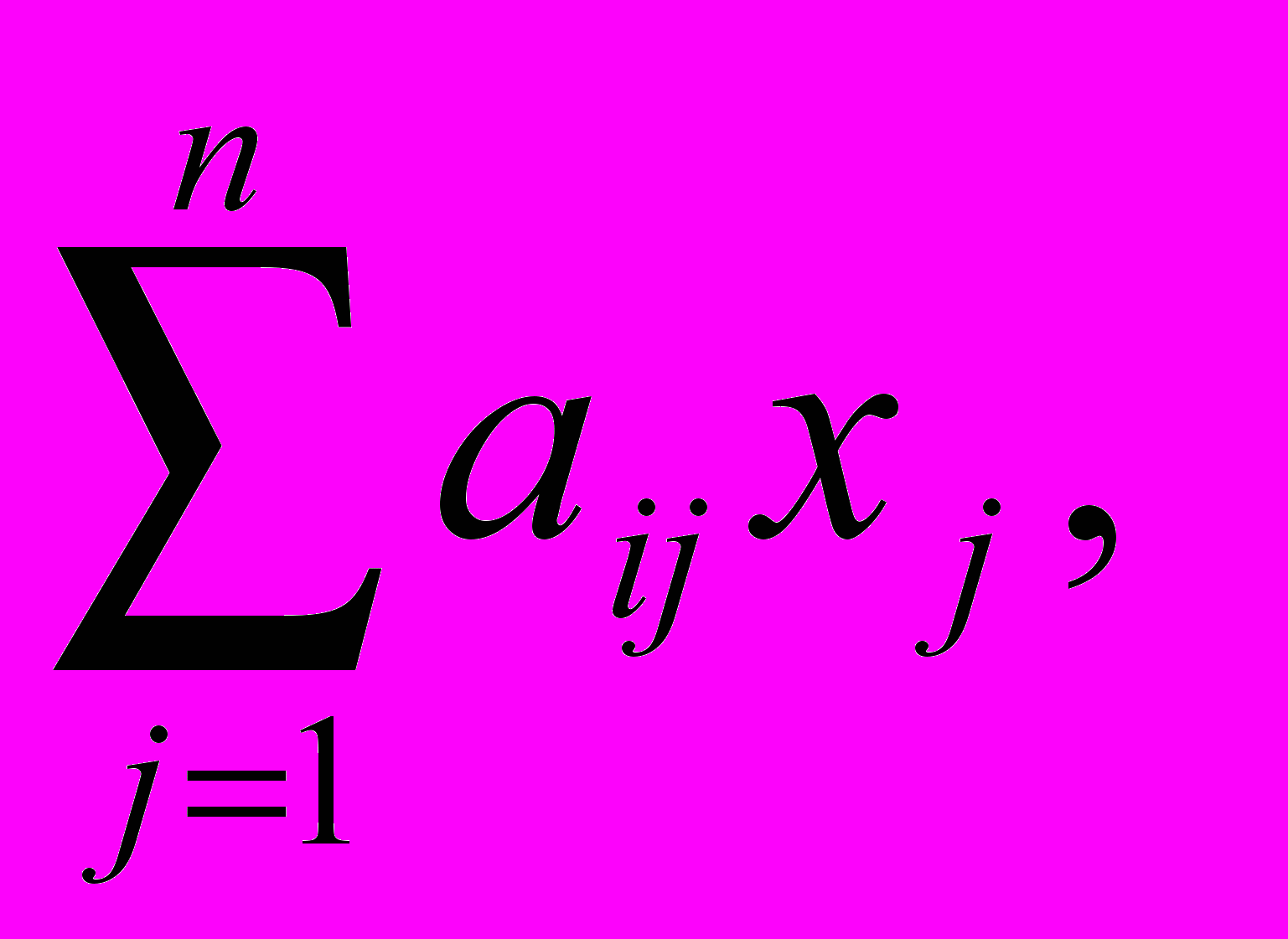 поэтому чистый выпуск продукта I за фиксированный период времени (например, за прошедший год) составит:
поэтому чистый выпуск продукта I за фиксированный период времени (например, за прошедший год) составит: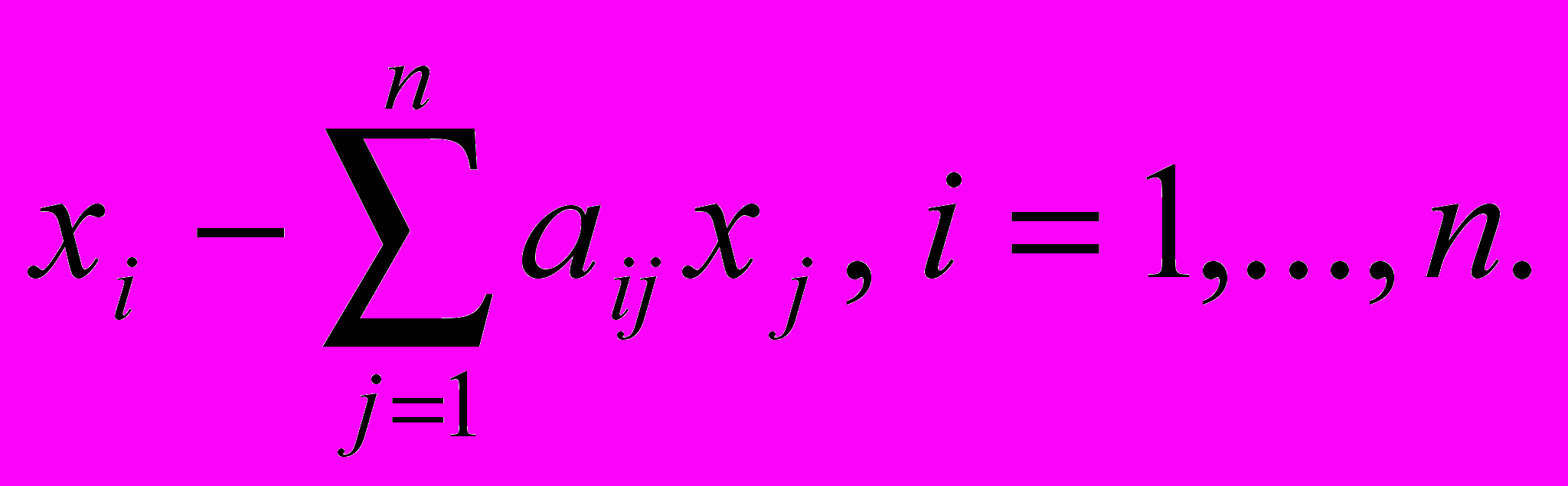
Если приравнять чистый выпуск каждого i-того продукта и конечный спрос на него yi , то образуется система уравнений:
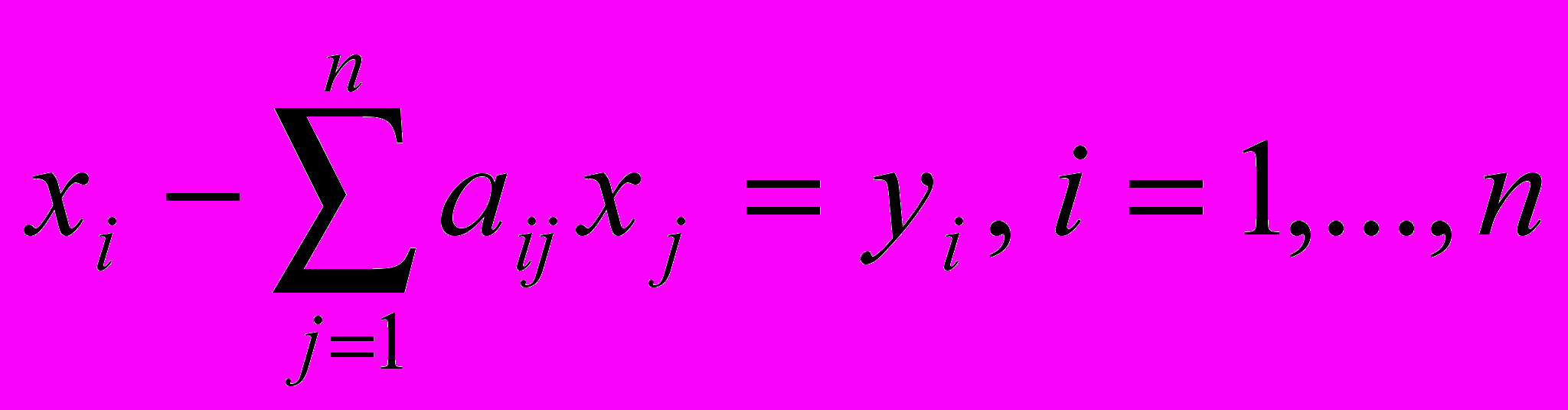 ,(1.1)
,(1.1)которая и составляет модель Леонтьева.
Единицы измерения всех указанных величин могут быть либо натуральными (тонны, штуки, киловатт-часы и т. д.), либо стоимостными, в зависимости от чего различают натуральный и стоимостный межотраслевой баланс. Для определенности мы в дальнейшем будем иметь в виду натуральный баланс.
Числа aij в некотором смысле полностью характеризуют технологию j-й отрасли в отчетный период: при данной структуре затрат и их объеме оказался возможным выпуск единицы продукции i. Числа aij носят название коэффициентов прямых затрат отрасли с номером j.
Матрица A=aij несет много информации о сложившейся структуре межотраслевых связей, о существующей технологии общественного производства. Сравнивая такие матрицы, составленные в достаточно разнесенные моменты времени, можно проследить направления изменения и развития технологии. Однако еще более интересные возможности открываются в связи с идеей использования матрицы А для текущего и долгосрочного планирования и прогнозирования производства.
Сделаем два важных предположения. Первое из них состоит в том, что мы будем считать сложившуюся технологию производства неизменной в течение некоторого промежутка времени. В зависимости от постановки задачи промежуток времени может быть равен одному календарному периоду (скажем, году) или нескольким.
Второе предположение состоит в постулировании свойства линейности существующей технологии. Именно, будем считать, что для осуществления объема xj валового выпуска продукции отрасли j необходимо и достаточно произвести затраты в объемах xjaij продукции всех отраслей. Конечно, каждое из этих предположений является очередной идеализацией реального положения вещей. Так, требование линейности означает, что каждая отрасль способна произвести любой объем своей продукции при условии, что ей будет обеспечено сырье в необходимом количестве. На самом деле, конечно, это не так, ибо производственные возможности всякой отрасли ограничены имеющимся объемом трудовых ресурсов и основных фондов. Будем говорить, что матрица A=aij описывает технологию при единичной интенсивности работы всех отраслей. Допустим, что в рассматриваемый промежуток времени все отрасли будут работать таким образом, что отрасль с номером j произведет объем xj валового выпуска своей продукции. Скажем, что j-я отрасль при этом работает с интенсивностью хj. Обозначим через х вектор валового выпуска (интенсивностей), х=(х1,х2,.......хn). Воспользовавшись предположением о линейности, нетрудно подсчитать часть общего валового выпуска, израсходованную на производственные нужды в процессе выпуска. Переходя к матричным обозначениям, видим, что вектор производственных затрат равен Ах. Тогда свободный остаток, равный yi будет использован на непроизводственные цели и накопление.
Уравнение (1.1) вместе с изложенной интерпретацией матрицы А и векторов х, y называется моделью Леонтьева. В том случае, когда решение системы (1.1) существует для любого неотрицательного вектора y конечного спроса, говорят, что модель Леонтьева (и матрица А) продуктивна. Таким образом, сущность леонтьевского метода состоит в определении валового выпуска отраслей по заданному экзогенно конечному спросу на основе данных о технологических возможностях, воплощенных в расходных коэффициентах aij. Разумеется, может быть решена и обратная задача нахождения вектора y.
Если модель Леонтьева продуктивна, то для любого вектора конечного спроса y<0 однозначно определяется неотрицательный вектор валового выпуска по формуле
x=y+Ay+A2y+......
Матрица А*=(1-А)-1>0 называется матрицей полных затрат, поскольку каждый ее коэффициент
 показывает, сколько надо произвести единиц i-го продукта на единицу j-го конечного продукта.
показывает, сколько надо произвести единиц i-го продукта на единицу j-го конечного продукта.7. Модель задачи по оптимизации запасов и ее ЭОС.
В структуре оборотных производственных фондов большой удельный вес занимают производственные запасы сырья, материалов и других материальных ценностей. На их долю приходится более половины суммы оборотных средств, а в пищевой промышленности эта доля порой достигает 80% и более.
Поэтому очень важно определить оптимальную величину расходов на создание производственных запасов, которая обеспечивала бы эффективное функционирование производства при минимальном объеме затрат на его материально-техническое обеспечение.
Расходы на создание и хранение запасов зависят от величины производственного запаса, налога на капитал, вложенный в запасы, страхование стоимости содержания складов, затрат, связанных с потерями (порча, устаревание и т.д.).
Но в то же время при создании и хранении запасов надо принимать во внимание и нестоимостные факторы. Здесь надо иметь в виду гарантии в отношении качества, опыт поставщика, уверенность в поставке и желательную перспективу взаимоотношений между поставщиком и производителем.
Важным является также транспортный фактор, который в ряде случаев играет более важное значение, чем цена ресурса. Ведь может сложиться такое положение, когда заявленная поставщиком высокая цена при перевозке в 10 км окажется выгоднее низкой цены, названной поставщиком, находящимся за 200 км.
Регулированию запасов посвящено много исследований, и на это имеется достаточно оснований. Это и понятно: выгода в результате рационального подхода к регулированию запасов достигает, как показывает практика, существенных размеров. Это особенно важно для предприятий, нуждающихся в больших запасах.
Важным моментом в расчете запасов является знание издержек, связанных с ними. Наиболее существенными из них являются:
Стоимость оформления заказа. Здесь возникают как постоянные, так и переменные затраты. Постоянные расходы - это заработная плата работников отделов снабжения, вложения в оборудование и накладные расходы, рассчитанные на определенный объем сырья. Переменные расходы зависят от способа оформления заказа, стоимости пересылки документов, увеличения числа заказов и т.д.
- Издержки на текущие запасы. Известно, что каждое предприятие с целью бесперебойного функционирования должно поддерживать минимальные запасы. И в этом случае запасы становятся в известной степени формой капиталовложений. В данном случае капитал связан в материалах, сырье и товарах. И естественно, если бы он был свободен, то он бы нашел свое применение: даже поместив его в банк, можно было бы получать процент. Иными словами, сточки зрения экономической науки создание даже минимальных запасов вызывает издержки в форме неиспользованных возможностей.
Текущие расходы на запасы должны также включать складские издержки. Они возникают с увеличением запасов по сравнению с нормируемым объемом, так как в этом случае требуется расширение складов и т.д. В текущие расходы также следует включить издержки на страхование, порчу товаров, хищения и др.
Теперь посмотрим, каким образом перечисленные выше расходы проявляют себя и что можно сделать, чтобы добиться их оптимальной величины. В решении этой задачи необходимо прежде всего установить связь между размером заказа (число единиц, закупленных один раз) с общей стоимостью оформления заказа и с общей суммой текущих расходов на содержание запасов.
Допустим, мы имеем число единиц, закупаемых в результате одного заказа - "х". По мере того, как число единиц (х), закупаемых за один раз, возрастает, текущие расходы на содержание запасов также увеличиваются. Но вместе с тем, если число единиц в одном заказе увеличивается, очевидно, количество заказов при постоянных объемах производства уменьшится, что приведет, естественно, к уменьшению расходов на оформление заказа. Эти изменения можно видеть на рис. 1.
Допустим, что потребность в определенных видах сырья или полуфабрикатов составляет 500 условных единиц в год и мы заказываем это число за один раз, т.е. в течение года мы делаем один заказ.
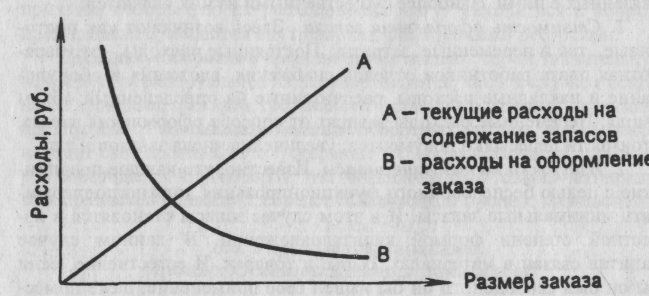
Рис. 1. Изменение суммы расходов на оформление заказа и расходов на содержание запасов
В процессе производства число заказанных единиц уменьшается до нуля, а средние запасы в этом случае равны 250 единицам.
Текущие расходы на содержание запасов определяются в расчете на среднюю стоимость в рублях 250 единиц. Расходы на оформление заказа в этом случае возникают всего один раз в год.
Ну а если бы заказы делались два раза в год, то тогда первоначальный заказ падает до нуля и снова возрастает до 250 единиц.
Средний уровень запасов в данном случае составляет 125 единиц, расходы на оформление заказа возникают дважды, а расходы на содержание запасов сокращаются вдвое.
Таким образом, из изложенного следует, что различие в образе действий в отношении запасов приводит к различным затратам. На рис. 2 показан график общей суммы расходов.
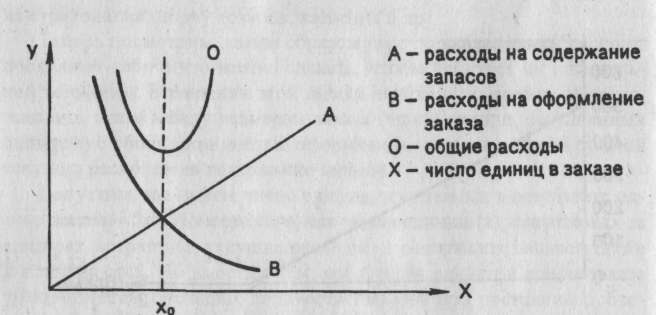
Рис. 2. Изменение общей суммы расходов
Из рисунка следует, что минимальные расходы будут получены при X = Хо.
Составим уравнение, определяющее общую сумму затрат:
Среднее число единиц, составляющих запасы, равняется X, где X - число единиц, соответствующих одному заказу.
- Средний запас в денежном выражении составляет СХ, где С - стоимость единицы изделий данного наименования.
3. Общая сумма затрат на содержание запасов составляет (СХ /2) Сс, где Сс - годовая ставка начислении на содержание запасов, выраженная в процентах к стоимости последних.
Число заказов за год равно Z.
- Общая сумма затрат на оформление заказов за год составляет CpZ, где Ср - переменные расходы при оформлении одного заказа.
В итоге общую сумму затрат (ТС) можно выразить с помощью следующего уравнения:
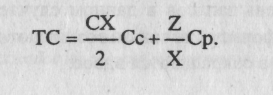
В соответствии с теорией запасов существует несколько способов минимизации общей суммы расходов (ТС).
Можно взять первую производную по X от общей суммы затрат и приравнять полученную величину к нулю, т.е. dTC : dx = О, имея в виду определить точку, соответствующую нулевому наклону
кривой и минимуму ТС.
- Можно использовать графический метод. Для этого надо нанести кривые, соответствующие каждому из слагаемых затрат, а затем получить общую их сумму, как это показано на рис. 4.
- Можно подставлять различные значения X в уравнение общей суммы затрат до достижения минимума этой величины.
В соответствии с моделью Улкинсона (Баумоля) запасы на предстоящий период определяются в следующих размерах:
а) минимальный остаток принимается нулевым;
б) оптимальный (он же максимальный) остаток рассчитывается по формуле:
Q=
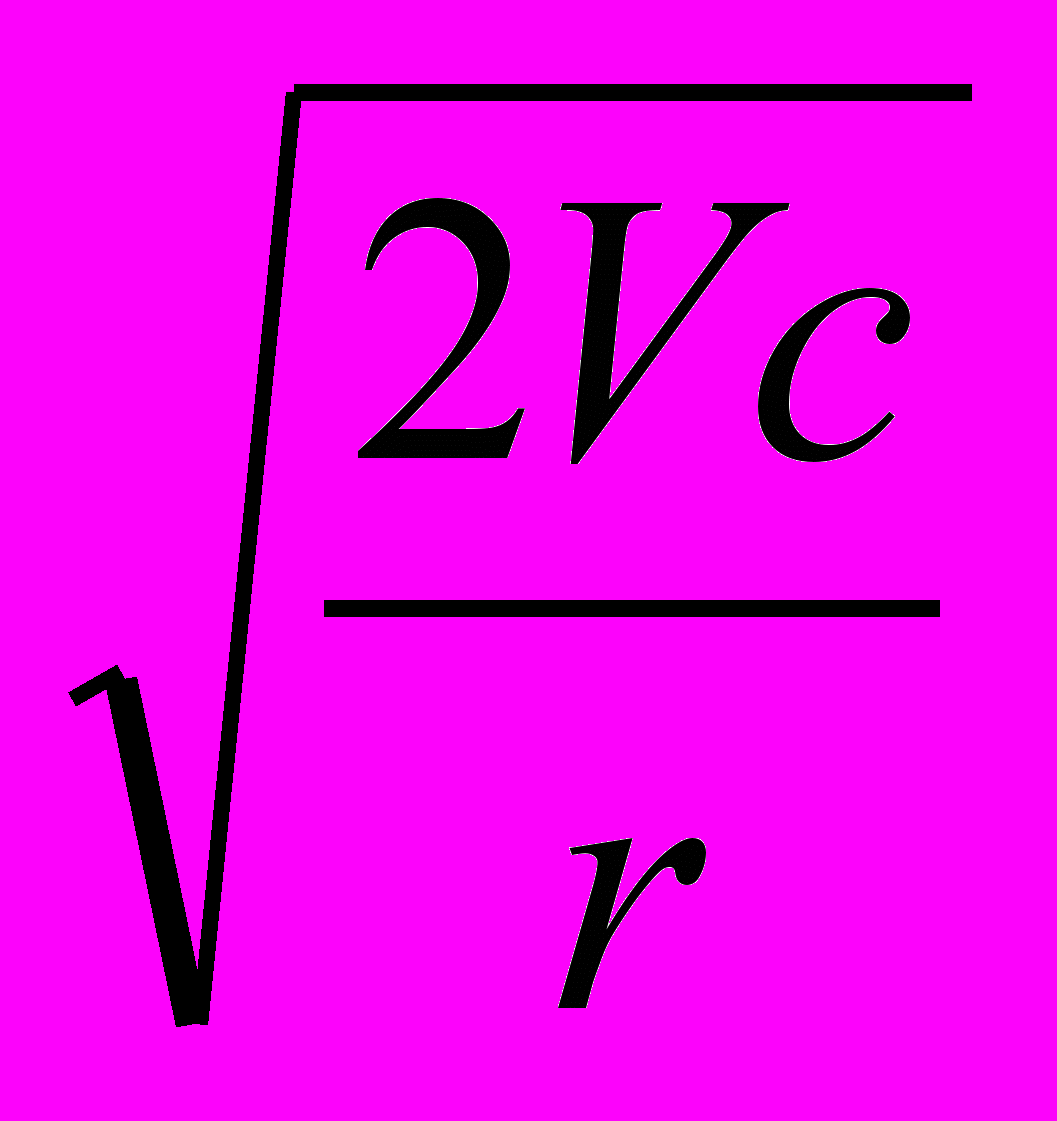 ,
, где Q - запасы в планируемом периоде;
c — средняя сумма расходов по обслуживанию одной поставки;
V — общий расход материала в предстоящем периоде;
r —затраты на хранение единицы запаса.
Средний размер запаса в соответствии с этой моделью планируется как половина оптимального (максимального) их размера.
9. Модель задачи выбора кратчайшего пути
Одним из универсальных средств представления информации о специфике протекания различного рода технических, экономических, организационных процессов и функционирования систем являются графовые модели. Под графом понимают совокупность вершин, отображаемых кружочками, точками и др., и ребер (дуг), взвешенных каким-либо образом и соединяющих вершины графа. Граф, в котором связь между вершинами имеет направление, отображаясь с помощью дуг, называется сетью. С помощью сетей решаются различные оптимизационные задачи, связанные с пространственным перемещением объектов, временным исполнением работ субъектами и др.
Рассмотрим некоторые наиболее распространенные на практике сетевые модели и задачи.
Задача коммивояжера. В нашей жизни часто встречаются ситуации, которые связаны с перемещением («из пункта А в пункт Б») и разнообразным поведением j-го субъекта или функционированием i-го объекта. К числу таких задач относится задача коммивояжера, связанная с минимизацией пути при посещении ряда объектов.
Для составления математической модели задачи обычно вводят следующие обозначения: i и j — номера пунктов выезда и заезда; tij —время переезда из пункта i в пункт j (в общем случае tij не равняется tji , например, если один пункт находится на возвышенности, а другой —в долине). Кроме этого, вводятся булевые переменные, причем принимают, что δij= 1, если из пункта i мы едем в пункт j, δij = 0 — в противном случае. Например, если из пункта i выехать (въехать) только один раз в каком-то определенном направлении в (из) любой(го) другой(го) пункт(а) j из п имеющихся либо оставаться в пункте i, то данное условие можно записать так:
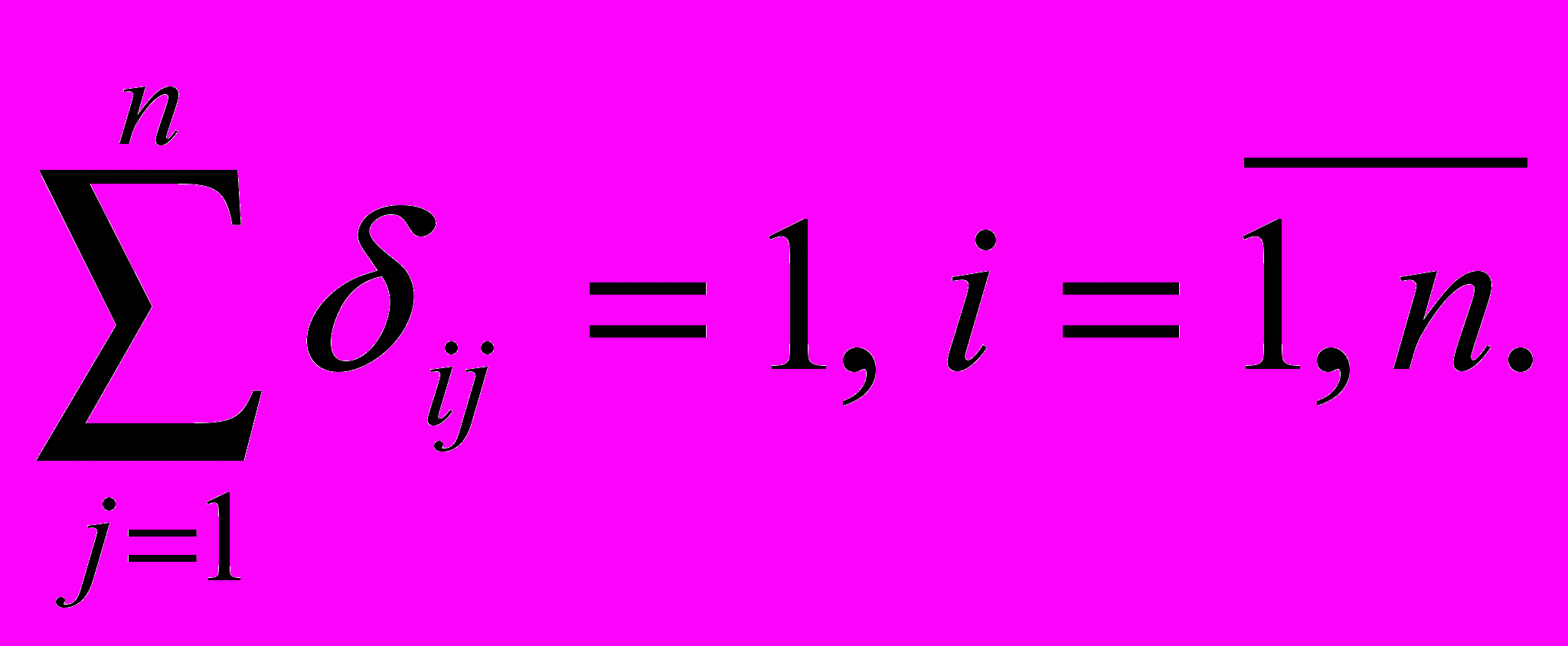
Общая постановка данной задачи, включающей объезд п пунктов, записывается в следующем виде:
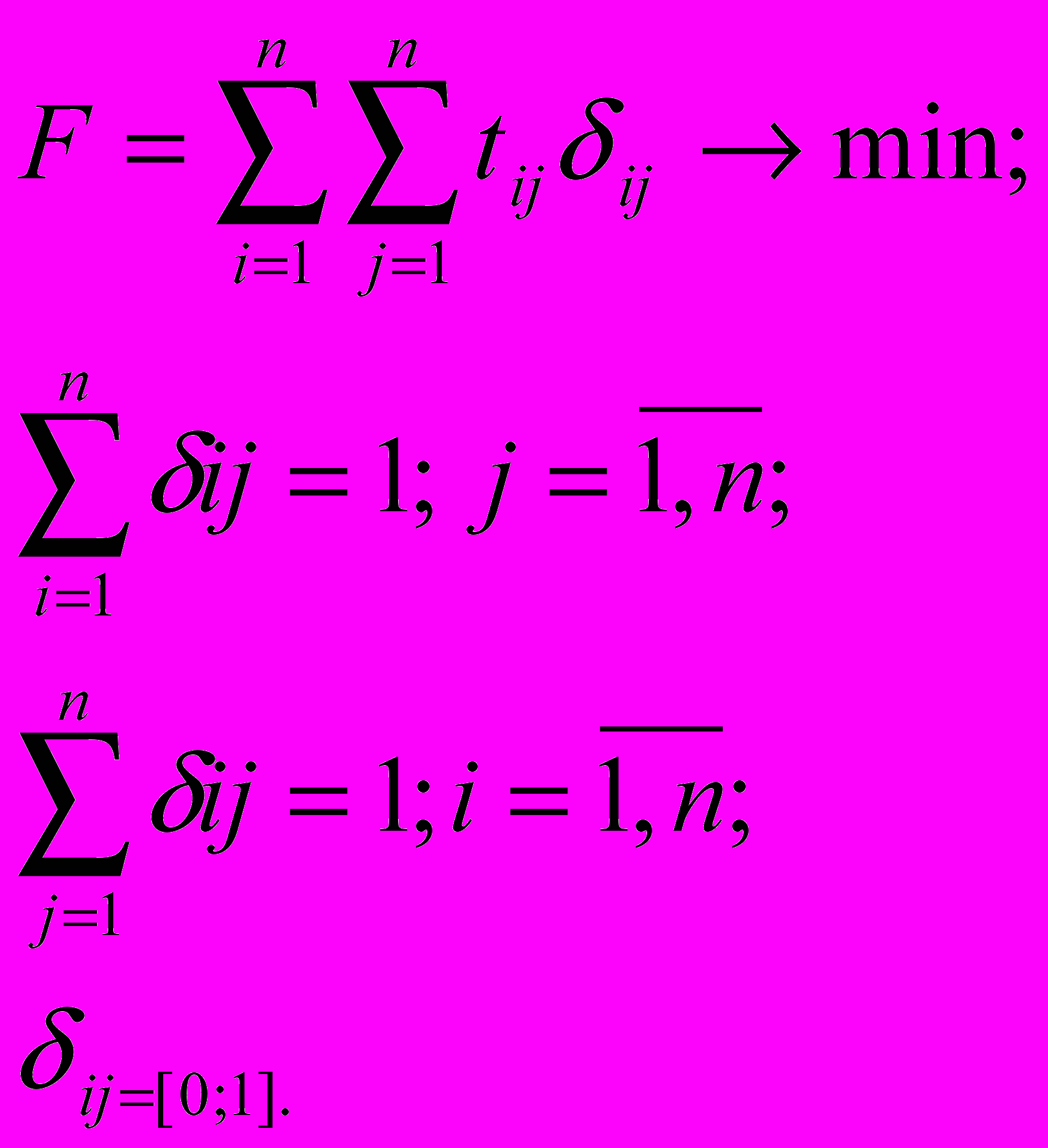
Заметим, что данная система включает условия, являющиеся необходимыми, но этого недостаточно. Требование непрерывности маршрута обеспечивается введением дополнительных переменных, исключающих создание подциклов.
К задаче коммивояжера сводятся задачи выбора маршрута при развозке грузов, последовательности обработки различных деталей на одном станке, проектирования технологических процессов и т.д.
Задача поиска кратчайшего пути. Пусть данная задача формулируется следующим образом: из пункта i в пункт j ведет много дорог, на одних из которых движение одностороннее, а на других — двустороннее (длина пути между пунктами указывается на каждой дуге). Требуется найти кратчайший путь из пункта i в в пункт j.
При составлении математической модели задачи должно соблюдаться условие непрерывности маршрута и одноразовости посещения пунктов (в каждый пункт должна входить и выходить только одна дуга). Это требование выполняется, если соблюдаются условия:
а) для дуг, входящих в пункт,
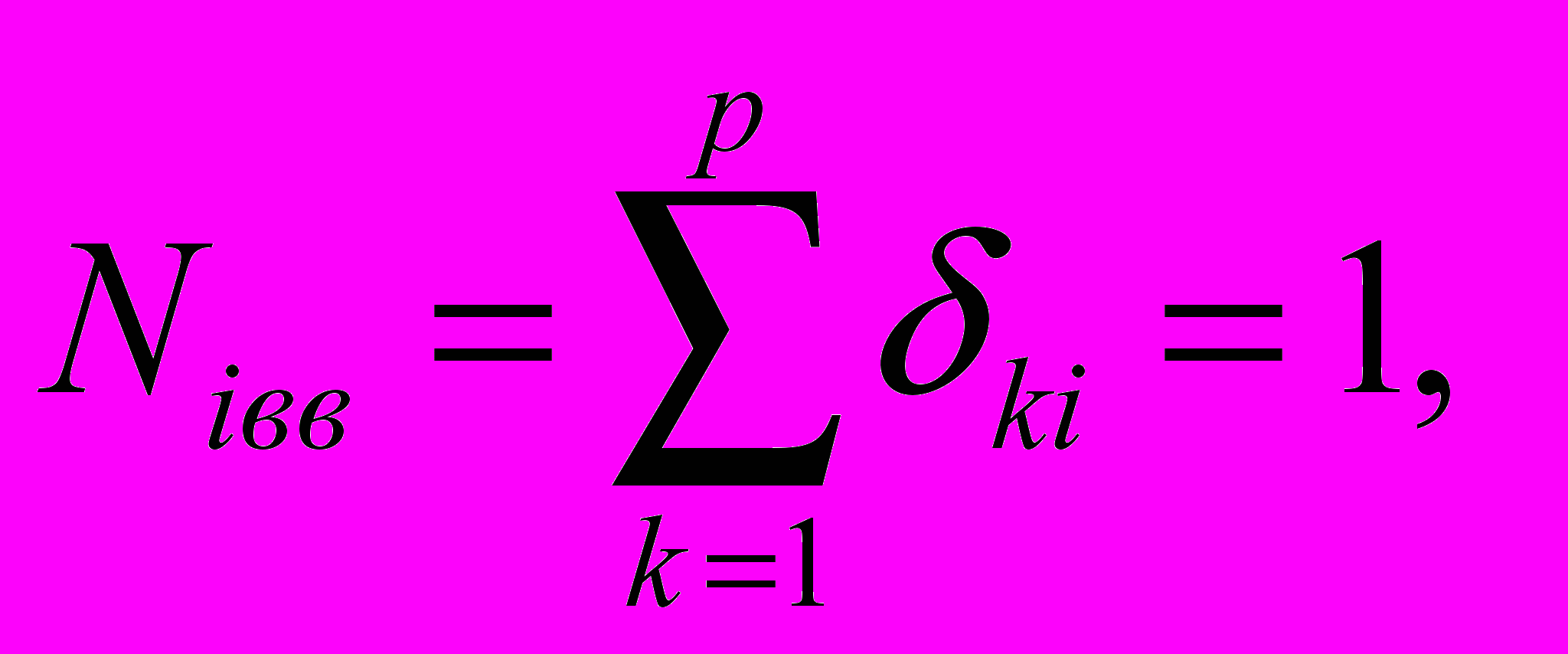
где δki соответствует дуге, выходящей из пункта k и входящей в пункт i;
δki = 1, если дуга k—i входит в маршрут; δki = 0 — в противном случае;
б) для дуг, выходящих из пункта,
Njвых =
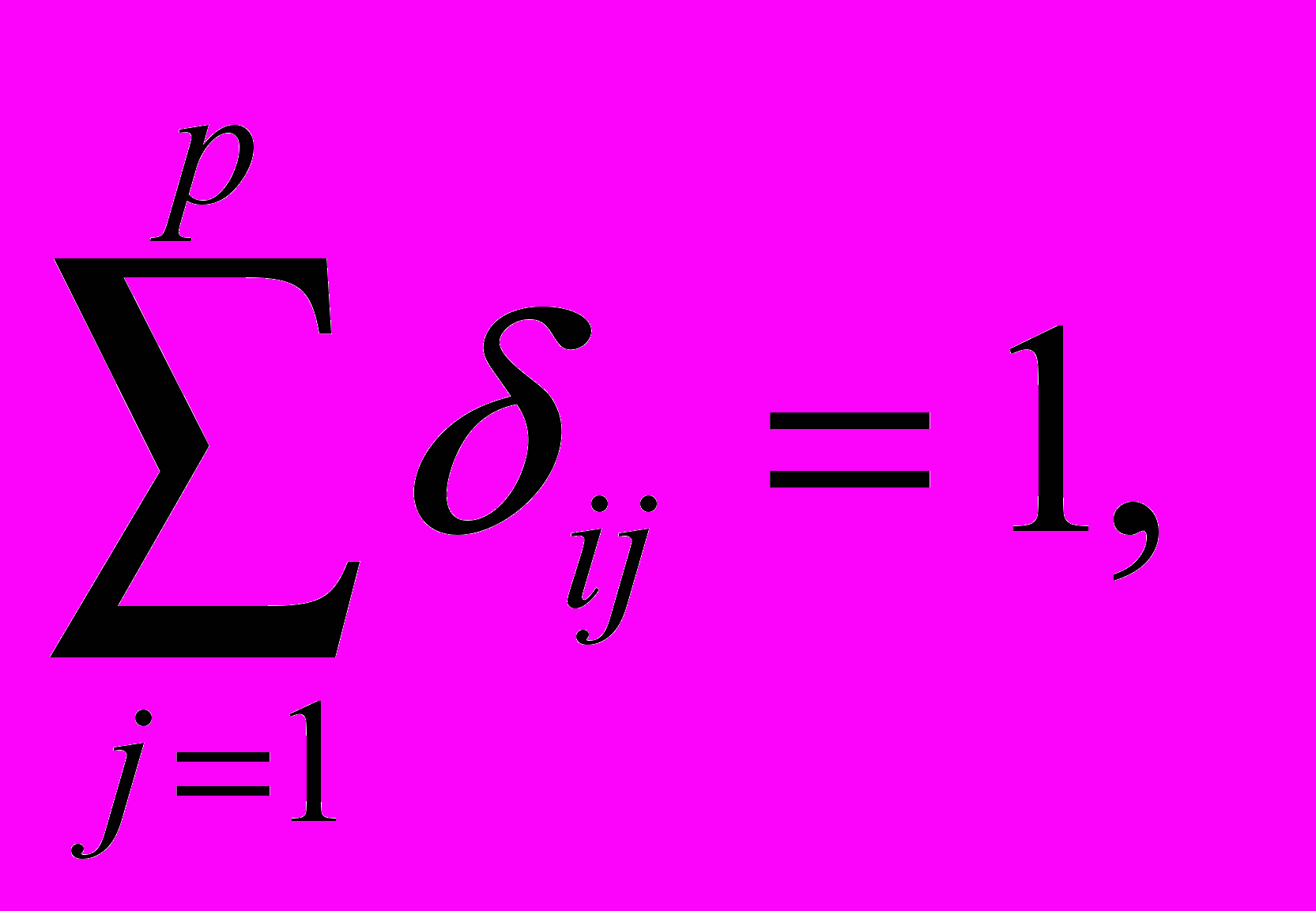
где δij соответствует дуге, выходящей из пункта i и входящей в пункт j; δij = 1, если дуга i-j входит в маршрут; δij = 0 — в противном случае.
В
 се пункты маршрута подразделяются на начальный, промежуточный и конечный, и для них должно выполняться условие:
се пункты маршрута подразделяются на начальный, промежуточный и конечный, и для них должно выполняться условие:1- для начального пункта;
Niвх-Niвых= 0- для промежуточного пункта;
1 – для конечного пункта.
Если необходимо, чтобы маршрут имел при этом и кратчайшую длину, необходимо добавить следующую целевую функцию:
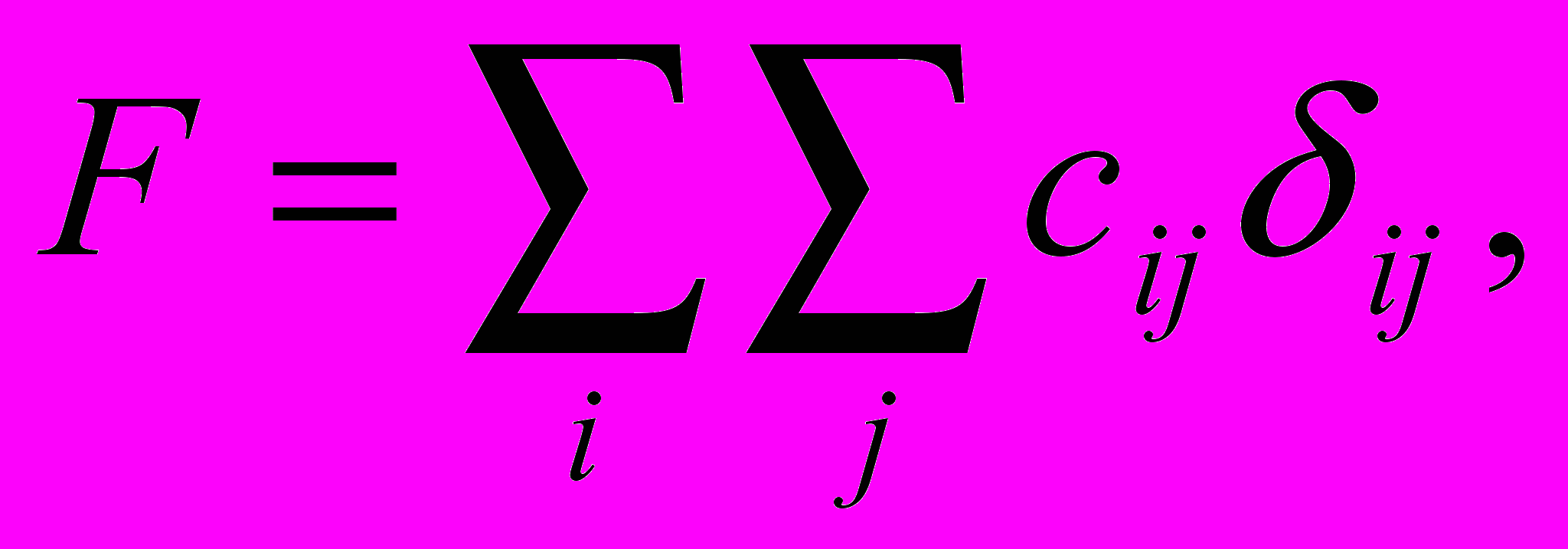
где cij —длина пути, а суммирование производится по всем дугам. Объединяя ограничения и целевую функцию, запишем систему:

На переменные δij здесь достаточно наложить только требование неотрицательности. Требование же, чтобы δij = 0 или δij = 1, можно не накладывать, так как такая задача из-за ограничений обеспечивает получение в решении для δij только либо нуля, либо единицы. Таким образом, приведенная система является обычной задачей линейного программирования, которую можно реализовать без наложения требований целочисленности.
Реально существующие длинные маршруты трудно обозримы, сплошной же перебор всевозможных вариантов —весьма трудоемкая процедура, поэтому для нахождения кратчайшего пути необходимо решение задачи линейного программирования. В общем случае характеристика дуги i—j может иметь самый различный смысл: продолжительность, стоимость, трудоемкость и т.д. в целом к задаче выбора кратчайшего пути или маршрута сводятся самые разнообразные задачи, включая задачу выбора оптимального маршрута при разработке технологических процессов.
