Ікурс (ІІ семестр) Укладач: доц. Комаров Ю. А. Затверджено
| Вид материала | Документы |
- Робоча навчальна програма для студентів спеціальності 030301-журналістика Затверджено, 233.63kb.
- Ікурс Ікурс Ікурс Ікурс Котенко, 53.21kb.
- Робоча навчальна програма з дисципліни «Політичні комунікації» Укладач: к філол н.,, 310.09kb.
- Методические рекомендации Издание второе, переработанное и дополненное Минск 2006 удк, 270.38kb.
- Университетский образовательный стандарт высшего профессионального образования 010100, 1014.31kb.
- Ежегодная Международная научно-практическая конференция LXIV герценовские чтения, 132.21kb.
- Методичні рекомендації Історія зарубіжної літератури ІІI курс, 5 семестр Укладач: доц., 295.51kb.
- Дополнительная программа кандидатского экзамена по специальности 08. 00. 13 «Математические, 276.2kb.
- Методичні рекомендації Історія зарубіжної літератури ІІ курс, 4 семестр Укладач: доц., 349.7kb.
- Программа и тезисы докладов 59-й студенческой научной конференции физического факультета, 1256.84kb.
міністерство освіти і науки україни
Київський національний лінгвістичний університет
к о н т р о л ь н а р о б о т а
З математичного програмування
Для студентів факультету заочного та вечірнього навчання
І курс (ІІ семестр)
Укладач: доц. Комаров Ю.А.
Затверджено
на засіданні кафедри інформатики
та комп’ютерних технологій
протокол № 11 від 08.06.2006
Зав. кафедри
доц. Коваль Т.І.
Київ - 2006
Загальні положення.
Завдання з контрольної роботи з математичного програмування складається з 3-х частин, що відповідає 3-м розділам навчальної дисципліни.
Кожний студент має виконати усі завдання з кожного розділу.
Розв’язання завдань має бути виконано з необхідним поясненням і обгрунтуванням виконуваних дій.
Контрольна робота має бути акуратно оформлена; порядок запису виконаних завдань має відповідати їх нумерації.
Студент, який не виконав усіх завдань і не оформив належним чином контрольну роботу, не допускається до захисту контрольної роботи з виставленням оцінки “не зараховано”.
Захист контрольної роботи здійснюється за таким порядком: студент отримує індивідуальний варіант завдань, аналогічних завданням з контрольної роботи і протягом обмеженого часу демонструє володіння методами розв´язання відповідних задач. Подальше уточнення степеня володіння необхідними методами та навичками здійснюється на співбесіді. По ходу співбесіди викладач має право задавати питання щодо застосованих термінів, понять, формул, теорем.
Успішний захист контрольної роботи може бути врахований при виставленні екзаменаційної оцінки.
Факультет заочного та
вечірнього навчання КНЛУ
2006/2007 н.р.
Контрольна робота з математичного програмування
Розділ І
1. Задача про інвестування. Розв’язати методом динамічного програмування.
 | 0 | 1 | 2 | 3 | 4 | 5 |
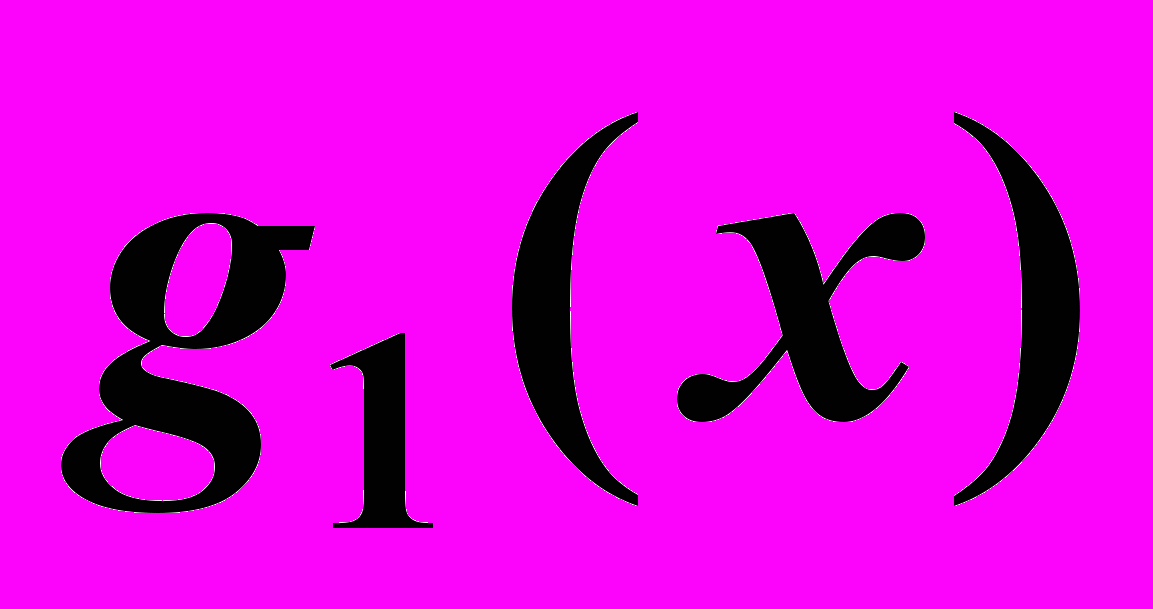 | 0 | 5 | 15 | 40 | 80 | 90 |
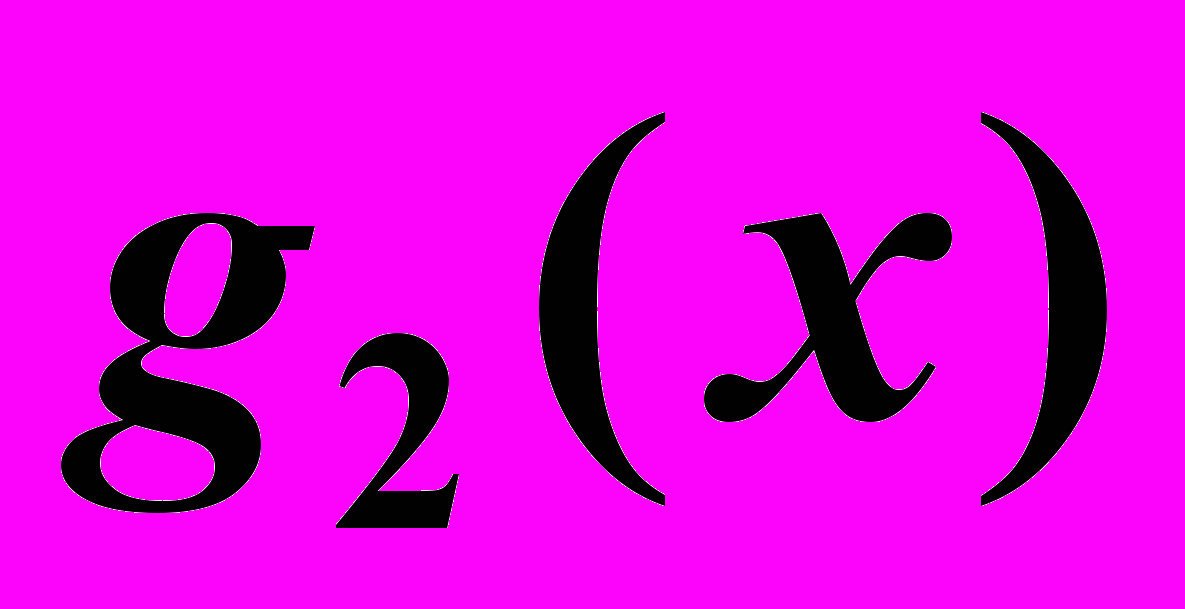 | 0 | 5 | 15 | 50 | 70 | 80 |
 | 0 | 4 | 26 | 55 | 70 | 75 |
2. Задача про призначення. Розв’язати угорським методом:
2.1. Задачу про мінімально-витратне призначення;
2.2. Задачу про максимально-ефективне призначення,
інтерпретуючи матрицю відповідно як матрицю витрат та як матрицю ефективностей
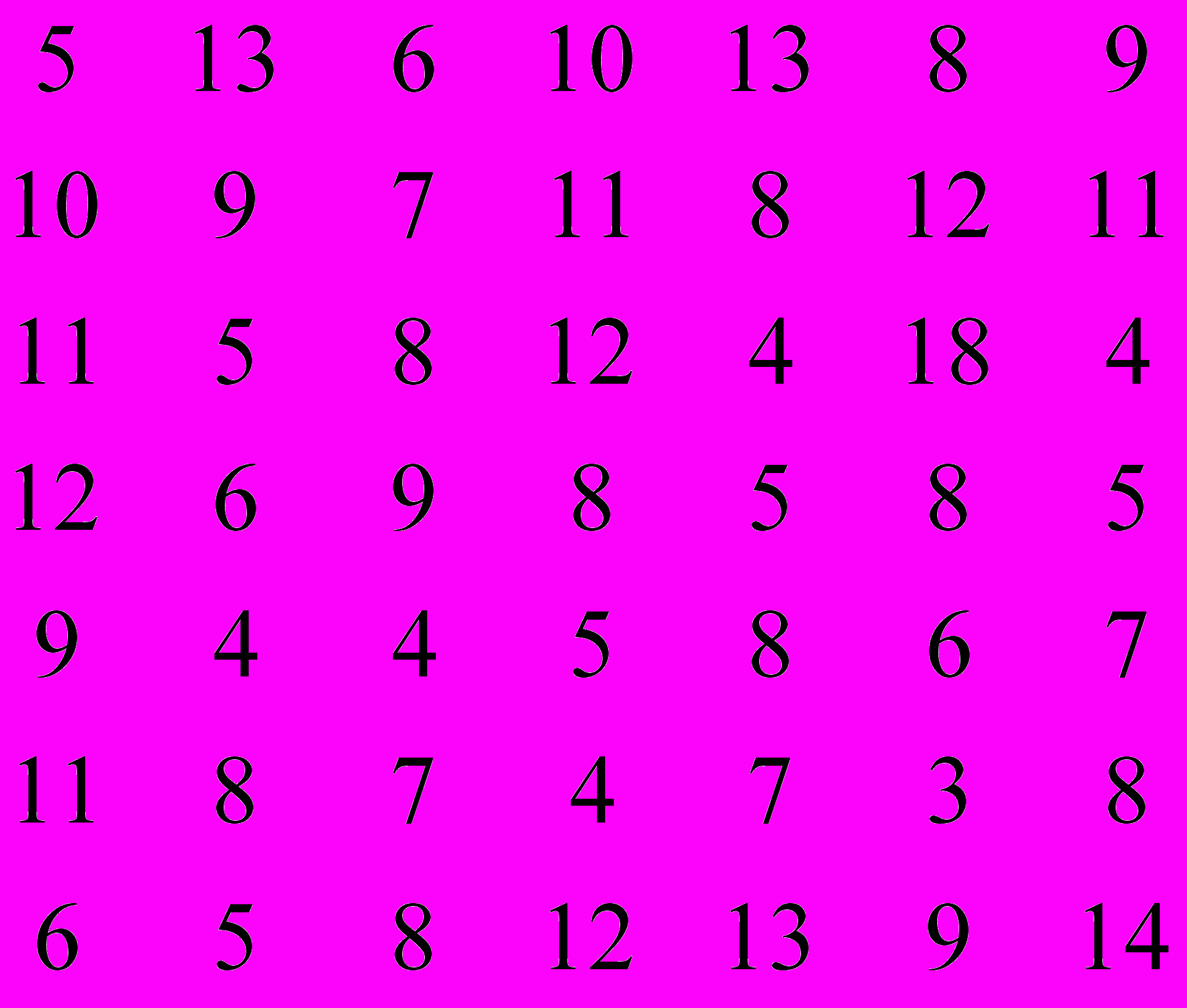
3. Транспортна задача без обмежень на пропускні спроможності.
Двома способами (методом з північно-західного кута та методом мінімального елемента) знайти початковий допустимий план перевезень (дпп). Для кожного дпп обчислити сумарні транспортні витрати. Зробити один крок методу потенціалів (виділення базисних клітин в транспортній таблиці; долучення при потребі до множини базисних клітин умовно базисних клітин; обчислення потенціалів; обчислення оцінок; перевірка виконання чи невиконання критерію оптимальності; вибір клітини з найбільшим порушенням критерію оптимальності; побудова компенсаторного циклу з допомогою методу викреслювання; вибір величини перевезення для циклічного перекидання по компенсаторному циклу; покращення поточного дпп). Виписати оптимальний дпп. Числові дані – перша таблиця з завдання 4.
4. Транспортна задача з обмеженнями (ТЗО).
Виконати таке саме завдання, що й для ТЗ без обмежень на пропускні спроможності.
-
15
30
65
20
10
50
14
10
2
5
10
20
11
5
4
11
3
30
9
8
12
1
18
40
1
4
9
17
18
-
15
35
14
10
5
8
4
20
12
18
10
7
32
20
14
11
15
25
14
12
5. Задача знаходження найкоротшого шляху на мережі.
Знайти найкоротший шлях на мережі методом Мінті.

6. Задача знаходження допустимого транспортного потоку на транспортній мережі.
Розширити траспортну мережу допоміжним джерелом і допоміжним стоком та відповідними комунікаціями. Звести задачу про знаходження допустимого транспортного потоку до задачі про знаходження максимального потоку. Зробити 3 кроки методу Форда-Фалкерсона (виписати 3 ланцюжки, по яких здійснювалось збільшення потоку). Виписати максимальний потік на розширеній мережі та вказати, як по ньому визначити шуканий допустимий транспортний потік. На мережі залишити позначки, які доводять максимальність потоку (неможливість його збільшення).
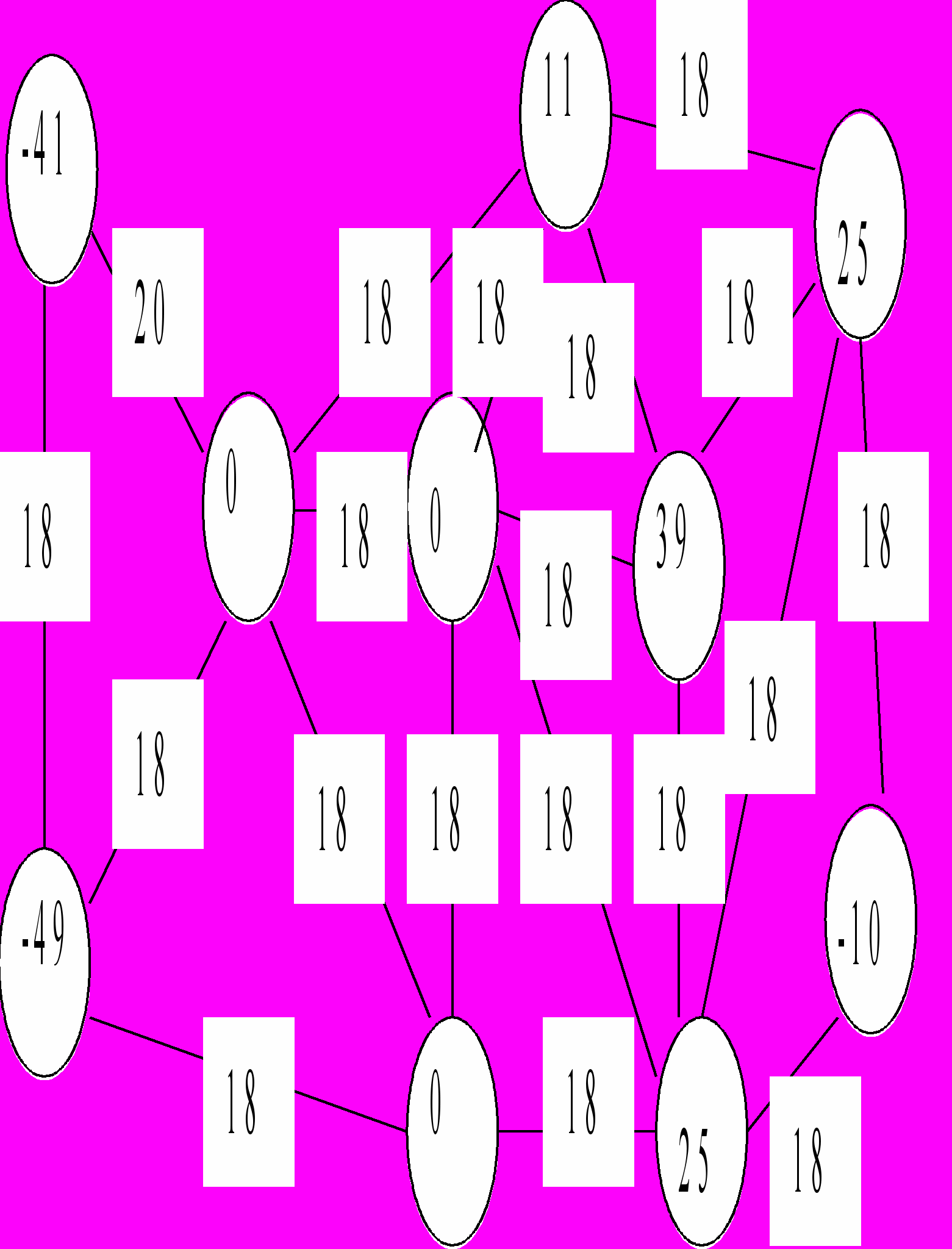
7. Задача про рюкзак.
Розв’язати задачу про рюкзак методом віток і границь.
 | 1 | 2 | 3 | 4 | 5 |
 | 5 | 4 | 5 | 4 | 4 |
 | 15 | 12 | 10 | 8 | 8 |
Факультет заочного та
вечірнього навчання КНЛУ
2006/2007 н.р.
Контрольна робота з математичного програмування
Розділ ІІ
Завдання.
1. Розв’язати дану задачу лінійного програмування
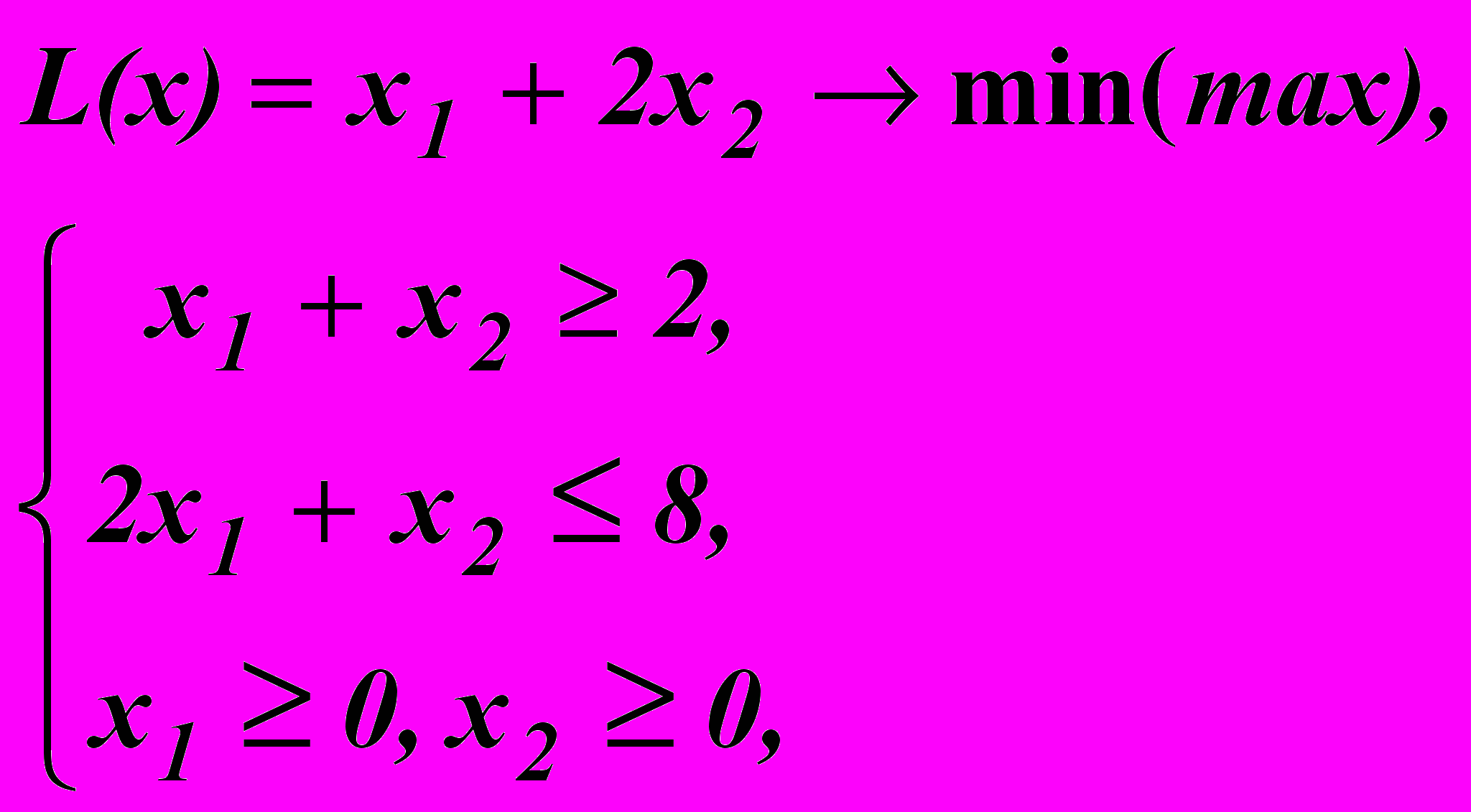
графічним методом. Зробити малюнок допустимої множини, лінії рівня цільової функції з вказанням напрямків зростання і спадання; точно обчислити координати кутових точок допустимої множини.
2.Розв’язати задачі лінійного програмування з п.1 (окремо: задачу мінімізації та задачу максимізації) симплексним методом, початковий опорний план знайти методом штучного базису.
3.Отримані розв’язки порівняти.
Факультет заочного та
вечірнього навчання КНЛУ
2006/2007 н.р.
Контрольна робота з математичного програмування
Розділ ІІІ
Завдання.
Для даної задачі нелінійного програмування (ЗНЛП)
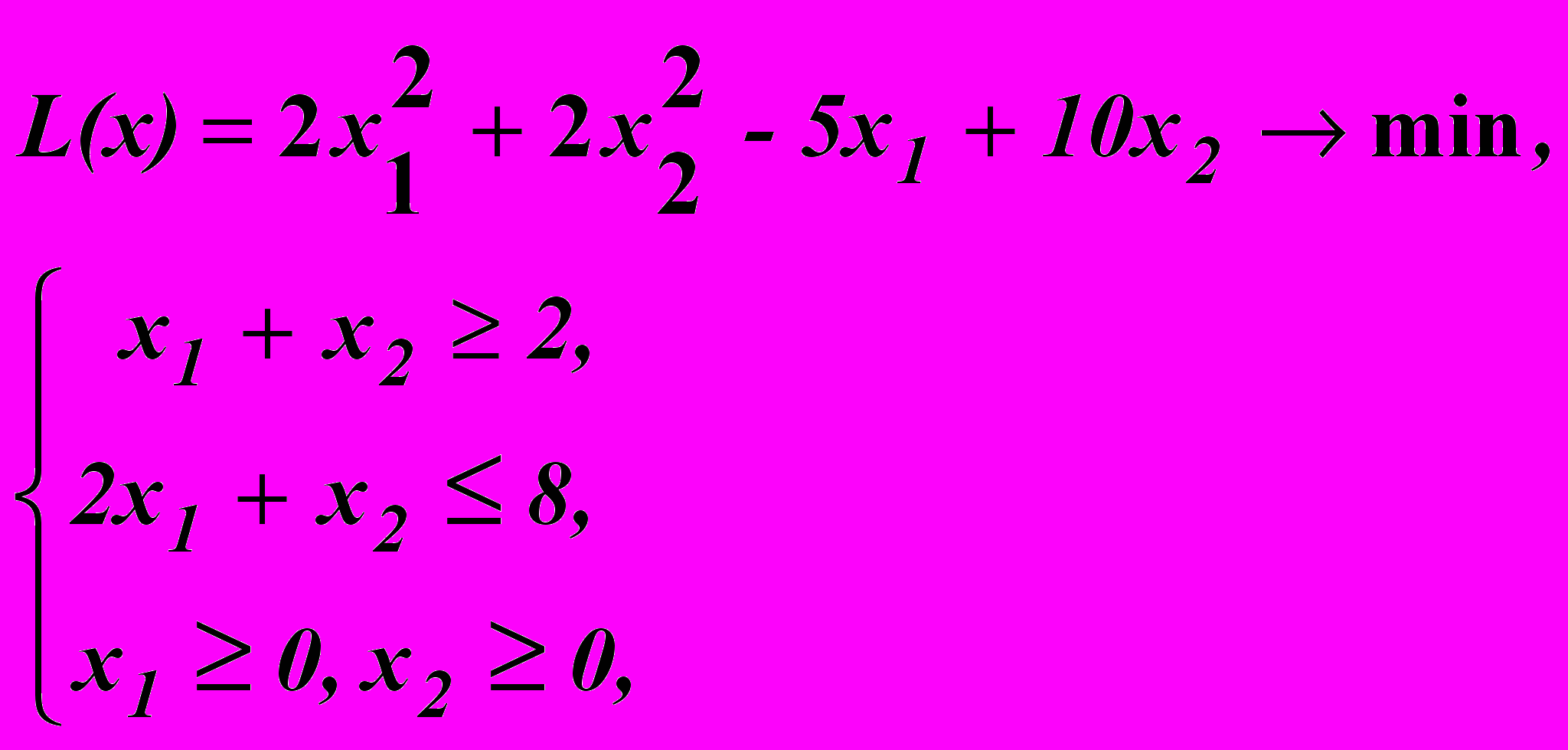
1. Дати геометричну iнтерпретацiю даної ЗНЛП:
зробити малюнок допустимої множини, ліній рівня цільової функції з вказанням точки глобального екстремуму; точно обчислити координати кутових точок допустимої множини; наближено, з геометричних міркувань, відшукати точку мінімуму цільової функції на допустимій області.
2. Знайти розв’язок задачі безумовної оптимізації (точку глобального екстремуму цільової функції) за теоремою Ферма.
3. Знайти розв’язок задачі безумовної оптимізації методом найскорiшого спуску.
3.1. Першу iтерацю зробити з використанням методу золотого
перерiзу.
3.2. Другу iтерацю зробити з використанням методу
половинного дiлення (дiхотомiї).
4. Розв’язати дану ЗНЛП методом множників Лагранжа.
