1 Постановка задачи
| Вид материала | Документы |
- Задачи оптимизации с ограничениями в виде неравенств. Постановка задачи. Геометрические, 42.48kb.
- Курсовой проект по дисциплине «Теория информационных процессов и систем» тема: Задачи, 258.87kb.
- И. Д. Салмин московский инженерно-физический институт (государственный университет), 27.33kb.
- Сопротивление композиционных материалов, 28.35kb.
- Удк 532 0727. 12 Физическое моделирование гидравлических явлений, 105.2kb.
- Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 24.28kb.
- Дисциплина: Инженерия знаний Доклад Генетические алгоритмы, 371.21kb.
- Титул Напротив фамилии оставить автограф автора. Задание, 11.99kb.
- План урока Вступительное слово учителя. «Золотое сечение» в математике постановка задачи,, 118.33kb.
- Исследование операций, 82.88kb.
4.2Описание модели, состоящей из дифференциальных уравнений, решаемых методами Рунге-Кутты, на примере ”модели экскаватора”
“Модель экскаватора” состоит из одного сервера, обслуживающего N клиентов, причём скорость обслуживания одинакова и клиенты возвращаются к северу за равные промежутки времени. Можно представить, что сервер является экскаватором, нагружающим грузовые машины.
Параметрами модели являются скорость обслуживания машин экскаватором μ и скорость передвижения машин ν. Искомыми величинами являются вероятности
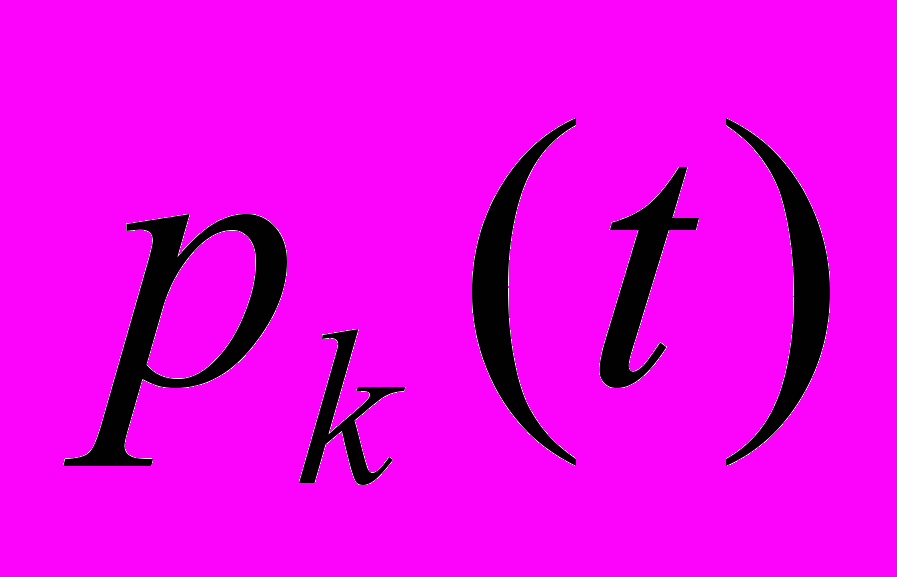, k=0,...,N того, что в данный момент времени k клиентов стоят перед экскаватором в очереди. Получается система, состоящая из N дифференциальных уравнений:
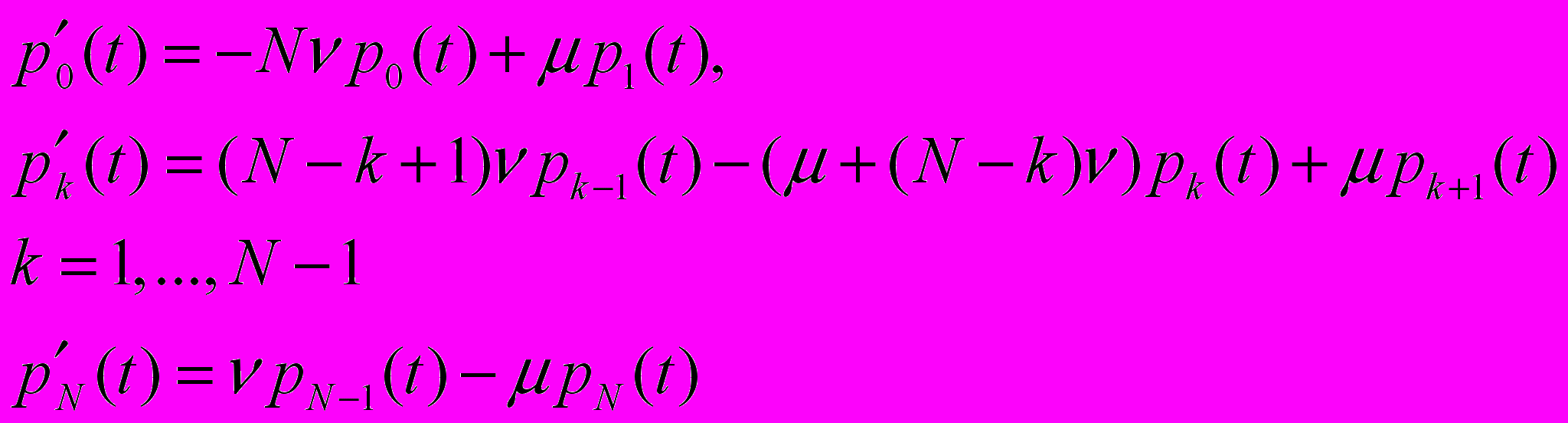(1)4.2.1Общая структура и системы уравнений модели
……………………………………
……
……
…..
…..
…………………………….
После тега < Model> следует элемент EquationSet,
описывающий систему уравнений (1). Эта система уравнений разбита на три части, каждая из которых описывается в отдельном теге <MathBlock>. Первый элемент MathBlock описывает первое уравнений системы, третий MathBlock – последнее уравнение. Второй MathBlock с помощью цикла описывает оставшиеся (N-1) уравнений.
Затем идёт элемент NumericalMethod , описывающий каким численным методом решается данная система уравнений. Эта система решается с помощью метода Рунге-Кутта.
Далее в теге <ModelParametres> описываются параметры модели, передаваемые численным методам. На этом описание вычислительной модели с помощью SimulML заканчивается
4.2.2Численный метод, решающий систему уравнений модели
Элемент RungeKuttaMethod определяет, каким именно численным методом будет решаться система уравнений.
vector
vector
fn
vector
Далее следуют типы данных, используемые в данном численном методе. Мы видим,
что метод Рунге-Кутта использует входной параметр вектор-функцию f , промежуточный параметр вектор r и выдаёт на выходе вектор v
С элемента MathBlock идет Xlink на xml-документ RungeKuttaMethod.xml, в котором описываются математические формулы, используемые в методе Рунге-Кутты. Этот xml-документ выглядит следующим образом:
……
В конце описания численного метода задаются типы данных параметров, используемых в таблице Бутчера:
vector
vector
matrix
4.2.3 Параметры модели
В элементе ModelParametres перечисляются параметры модели, передаваемые численному методу или его составной части.
cycle determining vector components-->
………….
Вектор p – это выходной параметр метода Рунге-Кутты (в описании самого метода этот параметр назывался v, поэтому нам пришлось переопределить его название с помощью атрибута overdetermined_name). Компоненты вектора задаются с помощью цикла.
first vector-function component-->
..................
middle vector-function components (determined by cycle)-->
…………………..
vector-function component-->
..................
Вектор-функция f , передаваемая методу Рунге-Кутта, задаётся по частям : определяется первый компонент вектор функции, затем с помощью цикла последующие (N-1) компонентов и отдельно последний компонент вектор-функции
value of this variable may be determined by user -->
value of this variable may be determined by user -->
value of this variable may be determined by user -->
Параметры N, ν, μ также передаются методу Рунге-Кутта. Их значения могут варьироваться пользователем, работающим с программным приложением, использующим SimulML .
В конце описания модели задаются параметры a, c и B , задающие таблицу Бутчера.
5Заключение
В данной работе решена задача создания XML-ориентированного языка описания вычислительных моделей. Язык SimulML описывает модель как на теоретическом уровне (структура модели, параметры модели и зависимости между ними), так и на уровне математических вычислений (численных методов, решающих системы уравнений модели). Связующим звеном между этими описаниями является набор тегов, отвечающих за передачу параметров модели численным методам.
Полноту и гибкость созданного языка подтвердила реализация на SimulML двух конкретных вычислительных моделей: в модели кровообращения упор делался на описание структуры системы моделей и связи различных параметров внутри этой системы, в модели экскаватора была наглядным образом показана связь внутренних параметров модели с численными методами.
Общим направлением работы являлось повышение уровня воспроизводимости результатов научных исследований в области численного моделирования. В дальнейшем можно решать следующие задачи в этом направлении: импорт/экспорт тегов SimulML в конкретный программный комплекс для моделирования, создание механизма генерации из SimulML исходного кода на языках программирования.