Исследование операций

Вид материала

Исследование

Содержание 2. Теоретическое описание 2.2 Симплекс метод 3. Общее описание реализуемой программы 4. Листинги программы

Подобный материал:

• Исследование операций " для подготовки специалиста по cпециальности 030100, 77.09kb.
• Журналы российской академии наук, 50.22kb.
• Журналы Российской академии наук, 48.74kb.
• Рабочей программы дисциплины Исследование операций по направлению подготовки 230700, 16.33kb.
• Формирование исследования операций как самостоятельной ветви прикладной математики, 99.74kb.
• Программа дисциплины Исследование операций для направления080200. 62 Менеджмент подготовки, 206.74kb.
• Исследование операций, 176.07kb.
• Программа учебной дисциплины «Математические модели в теории управления и исследование, 114.92kb.
• Учебной дисциплины «Теория игр и исследование операций» для направления 010100., 42.57kb.
• Зированные системы управления, исследование операций, системный анализ, математическое, 136.69kb.

АКАДЕМИЯ УПРАВЛЕНИЯ ТИСБИ

ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ

на тему:

«Симплекс метод»

по предмету:

Исследование операций


Выполнил:

Студент гр. И-211

Бикмаметов Артем

Принял:

к.тех.н., доцент

Печеный Е А.


Казань, 2005

Оглавление

1. Постановка задачи. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .стр. 3

2. Теоретическое описание ………………………….………………... . . . .стр. 4

2.1 Безградиентные методы.……………………………………………….. . . . . . . . . стр. 4

2.2 Симплекс метод..…………………………….... . . . . . . . . . . . . . . . . . . . . . . . . . . . .стр. 5

3. Общее описание реализуемой программы. . . . . . . . . . . . . . . . . . . . . . . стр. 8

4. Листинги программы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .стр. 11

5. Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . … . стр. 18

1. Постановка задачи


На основе изученного алгоритма симплекс-метода создать работающее программное приложение в виде компонента для решения задач по отысканию максимума или минимума функции двух переменных.

2. Теоретическое описание

2.1 Безградиентные методы


При использовании градиентных методов для определения величины и направления шага поиска требовался предварительный анализ производных оптимизируемой функции по всем независимым переменным. Для сложной целевой функции это связано с выполнением большого объема вычислений, особенно при большом числе переменных.

Безградиентные методы основаны на использовании в процессе поиска информации, получаемой от сравнительной оценки значений целевой функции в результате выполнения очередного шага.

С использованием безградиентных методов может быть реализован как одномерный поиск (для случая, когда целевая функция зависит от одной независимой переменной), так и многомерный поиск. При одномерном поиске используются следующие методы: одномерного сканирования, локализации экстремума функции, "золотого сечения" и др. Методы многомерного поиска - покоординатного спуска, многомерного сканирования, Хука-Дживса, симплексный - могут использовать методы одномерного поиска как вспомогательные.

2.2 Симплекс метод


Основная идея этого метода заключается в том, что по известным значениям целевой функции в вершинах выпуклого многогранника, называемого симплексом, находится направление, в котором требуется сделать следующий шаг, чтобы получить наибольшее уменьшение (увеличение) значения целевой функции. При этом под симплексом в n-мерном пространстве понимается многогранник, имеющий n+1 вершину. Примером симплекса в двумерном пространстве, т.е. на плоскости, является треугольник. В трехмерном пространстве - тетраэдр.

Симплекс обладает следующим свойством - против любой из его вершин S_j расположена только одна грань, на которой можно построить новый симплекс, отличающийся от прежнего расположением новой вершины S_j , тогда как остальные вершины обоих симплексов совпадают. Вершина нового симплекса S_j , вообще говоря, может находиться и по другую сторону грани от вершины S_j . Это свойство симплекса и обусловило возможность его применения при решении задач оптимизации.

Рассмотрим простейший случай - поиск минимума целевой функции двух переменных R(U₁ ,U₂ ).


Алгоритм поиска следующий:
1. Рассчитываются значения целевой функции в вершинах выбранного вами симплекса S₁₀ ,S₂₀ ,S₃₀



2. Выбирается вершина, где значение R(U₁ ,U₂) наибольшее - S₁₀ .

3. Новый симплекс S₁₁ ,S₂₀ ,S₃₀ строится следующим образом: - находится середина противолежащей грани S₂₀ ,S₃₀ - точка А - через точки S₁₀ и А проводится прямая. На этой прямой от точки А откладывается отрезок АS₁₁ , равный по величине отрезку S₁₀ А.

4. В новой вершине вычисляется значение целевой функции.

5. Из вершин нового симплекса S₁₁ ,S₂₀ ,S₃₀ выбирается та, где значение целевой функции максимально.

6. Аналогично п.3 строится новый симплекс S₁₁ ,S₂₀ ,S₃₁ , т.е. исключается вершина S₃₀ , имевшая наибольшее значение целевой функции и т.д.

В результате применения рассмотренной процедуры исключения вершин симплексов с наибольшим значением целевой функции процесс поиска сходится к минимальному значению R(U₁ ,U₂ ). При возникновении зацикливания в окрестностях точки экстремума необходимо уменьшать размеры симплекса.

Критерием окончания поиска могут служить размеры симплекса. Например, если все ребра симплекса станут меньше d, то поиск можно прекращать.

Рассмотрим алгоритм симплексного метода для задач произвольной размерности.

Пусть вершинам исходного симплекса S_i (i=1,2,...,n+1) отвечают координаты U^-(i) =(U⁽ⁱ⁾₁ ,U⁽ⁱ⁾₂ ,..., U⁽ⁱ⁾_n), (i=1,2,...,n+1). И пусть наибольшее значение целевой функции соответствует вершине S_j. Определим координаты вершины S_j нового симплекса.

Вершина S_j располагается симметрично вершине S_j относительно середины грани, находящейся против вершины S_j. Координаты центра этой грани U^-(i) определяются по формуле:





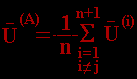
причем суммирование ведется только по тем векторам U⁽ⁱ⁾ , которые отвечают вершинам S_i , образующим эту грань. Вектор , характеризующий расстояние от вершины S_j до центра противолежащей грани, будет равен: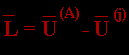





Координаты вершины S_j определяются по формуле





Подставив выражение для U, получим:





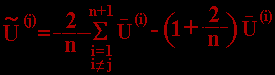
Эта формула определяет координаты вершины S_j нового симплекса.


При необходимости можно уменьшить размеры симплекса (в случае зацикливания в окрестности точки оптимума), можно пользоваться следующим выражением:





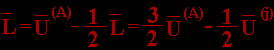
Наиболее эффективно симплексный метод сходится при использовании правильных симплексов - равностороннего треугольника или тетраэдра, образованного равносторонними треугольниками. В этом случае направление поиска совпадает с направлением градиента (если симплекс достаточно мал).

Симплексный метод обладает еще одним важным достоинством - при увеличении размерности задачи вычислительные затраты возрастают незначительно, т.к. на каждом шаге считается только одно значение целевой функции.

3. Общее описание реализуемой программы


Программа написана на языке высокого уровня Delphi Pascal. Она использует четыре основные подпрограммы, отвечающие за ввод/вывод данных, операции над входными данными и прорисовку графических компонентов.

Для правильной работы приложения надо ввести исходные данные, это:

- уравнение двух переменных вида min/max 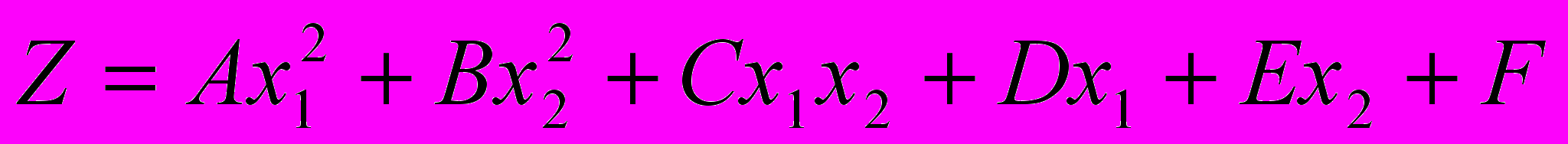, причем если не ввести константы A,B,C,D,E,F то программа примет их за ноль.

- Координаты одной вершины и длину стороны равностороннего треугольника.

После ввода начальных данных программа вычислит координаты двух других вершин и построит равносторонний треугольник.





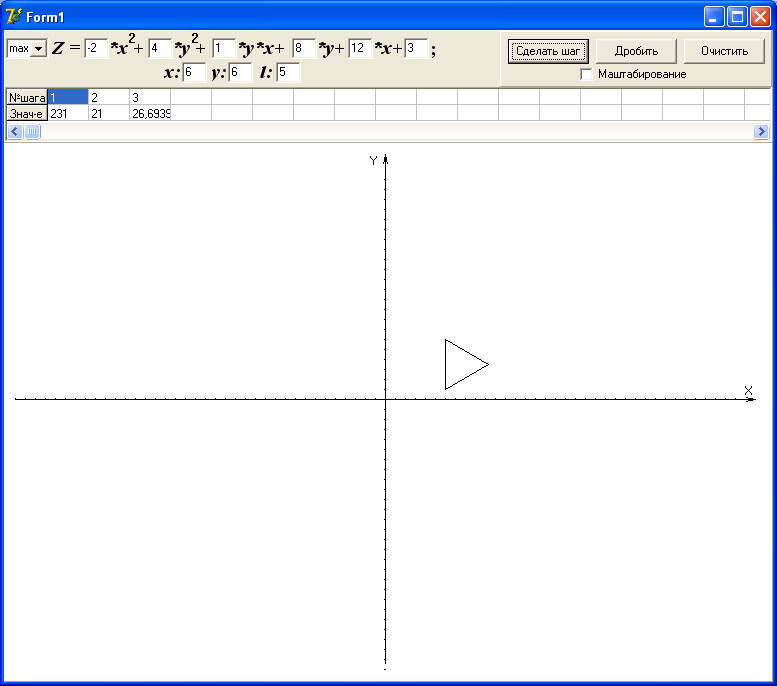
При каждом следующим шаге к имеющейся фигуре будет достраиваться одна вершина.

В случае зацикливания в окрестности точки оптимума, можно уменьшить размеры симплекса (шага) в два раза, для этого нужно нажать кнопку “дробить”, если поставить галочку напротив “масштабирование” то при дроблении останутся только два последних треугольника. Это более наглядно, чем без масштабирования






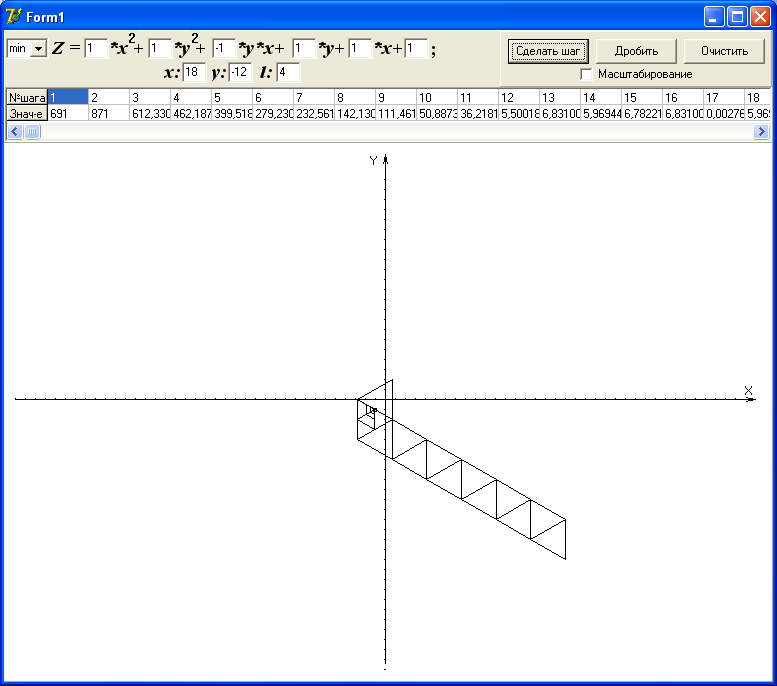
4. Листинги программы


unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, ExtCtrls, Grids, StdCtrls;

type

TForm1 = class(TForm)

Panel1: TPanel; StringGrid1: TStringGrid; Panel2: TPanel; Button1: TButton; Edit2: TEdit;

Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; Edit6: TEdit; Edit1: TEdit; Label1: TLabel; Label2: TLabel; Label3: TLabel; Label4: TLabel; Label5: TLabel; Label6: TLabel; Label7: TLabel; Label8: TLabel; Panel3: TPanel; Image1: TImage; Button3: TButton; Label9: TLabel; Label10: TLabel; Label11: TLabel; Edit8: TEdit; Edit9: TEdit; Edit10: TEdit;

Label12: TLabel; ComboBox1: TComboBox; Button2: TButton; CheckBox1: TCheckBox;

procedure Button1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

Procedure ZanosRez;

Procedure First;

Procedure Pl1;

Procedure Pl2;

Procedure Pl3;

procedure Button3Click(Sender: TObject);

procedure Button2Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;


var

Form1: TForm1;

x1,y1,x2,y2,x3,y3,x,y:variant;

Zn1,Zn2,Zn3: real;

i,j,k:integer;

a,b,c,d,e,f:real;


implementation


{$R *.dfm}


Procedure TForm1.ZanosRez;

begin

if ((Edit8.Text='')or(Edit9.Text='')or(Edit10.Text=''))then showmessage(‘Введите координаты и/или длину стороны!’);

x1:=strtoint(Edit8.Text);

y1:=strtoint(Edit9.Text);

j:=random(4);

case j of

0:begin

x2:=x1+strtoint(edit10.Text);

y2:=y1;

j:=random(2);

case j of

0:begin

x3:=(x1+x2)/2;

y3:=sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)))+y1;

end;

1:begin

x3:=(x1+x2)/2;

y3:=y1-sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)));

end;

end;

end;

1:begin

x2:=x1-strtoint(edit10.Text);

y2:=y1;

j:=random(2);

case j of

0:begin

x3:=(x1+x2)/2;

y3:=sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)))+y1;

end;

1:begin

x3:=(x1+x2)/2;

y3:=y1-sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)));

end;

end;

end;

2:begin

y2:=y1+strtoint(edit10.Text);

x2:=x1;

j:=random(2);

case j of

0:begin

y3:=(y1+y2)/2;

x3:=sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)))+x1;

end;

1:begin

y3:=(y1+y2)/2;

x3:=x1-sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)));

end;

end;

end;

3:begin

y2:=y1-strtoint(edit10.Text);

x2:=x1;

j:=random(2);

case j of

0:begin

y3:=(y1+y2)/2;

x3:=sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)))+x1;

end;

1:begin

y3:=(y1+y2)/2;

x3:=x1-sqrt((strtoint(Edit10.Text))*(strtoint(Edit10.Text))-(((strtoint(Edit10.Text))/2)*((strtoint(Edit10.Text))/2)));

end;

end;

end;

end;

if Edit1.Text=''then a:=0 else a:=strtofloat(Form1.Edit1.Text);

if Edit2.Text=''then b:=0 else b:=strtofloat(Form1.Edit2.Text);

if Edit3.Text=''then c:=0 else c:=strtofloat(Form1.Edit3.Text);

if Edit4.Text=''then d:=0 else d:=strtofloat(Form1.Edit4.Text);

if Edit5.Text=''then e:=0 else e:=strtofloat(Form1.Edit5.Text);

if Edit6.Text=''then f:=0 else f:=strtofloat(Form1.Edit6.Text);

image1.Canvas.MoveTo(380+10*x1,255-10*y1);

image1.Canvas.LineTo(380+10*x2,255-10*y2);

image1.Canvas.LineTo(380+10*x3,255-10*y3);

image1.Canvas.LineTo(380+10*x1,255-10*y1);

end;

Procedure TForm1.First;

begin

Zn1:=a*x1*x1+b*y1*y1+c*y1*x1+d*y1+e*x1+f;

Zn2:=a*x2*x2+b*y2*y2+c*y2*x2+d*y2+e*x2+f;

Zn3:=a*x3*x3+b*y3*y3+c*y3*x3+d*y3+e*x3+f;

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn1);

inc(i);

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn2);

inc(i);

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn3);

inc(i);

end;

Procedure TForm1.Pl1;

begin

x:=x1+x2+x3-2*x1;

y:=y1+y2+y3-2*y1;

x1:=x;

y1:=y;

Zn1:=a*x1*x1+b*y1*y1+c*y1*x1+d*y1+e*x1+f;

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn1);

image1.Canvas.MoveTo(380+10*x1,255-10*y1);

image1.Canvas.LineTo(380+10*x2,255-10*y2);

image1.Canvas.LineTo(380+10*x3,255-10*y3);

image1.Canvas.LineTo(380+10*x1,255-10*y1);

inc(i);

end;

Procedure TForm1.Pl2;

begin

x:=x1+x2+x3-2*x2;

y:=y1+y2+y3-2*y2;

x2:=x;

y2:=y;

Zn2:=a*x2*x2+b*y2*y2+c*y2*x2+d*y2+e*x2+f;

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn2);

image1.Canvas.MoveTo(380+10*x1,255-10*y1);

image1.Canvas.LineTo(380+10*x2,255-10*y2);

image1.Canvas.LineTo(380+10*x3,255-10*y3);

image1.Canvas.LineTo(380+10*x1,255-10*y1);

inc(i);

end;

Procedure TForm1.Pl3;

begin

x:=x1+x2+x3-2*x3;

y:=y1+y2+y3-2*y3;

x3:=x;

y3:=y;

Zn3:=a*x3*x3+b*y3*y3+c*y3*x3+d*y3+e*x3+f;

StringGrid1.Cells[i,0]:=inttostr(i);

StringGrid1.Cells[i,1]:=floattostr(zn3);

image1.Canvas.MoveTo(380+10*x1,255-10*y1);

image1.Canvas.LineTo(380+10*x2,255-10*y2);

image1.Canvas.LineTo(380+10*x3,255-10*y3);

image1.Canvas.LineTo(380+10*x1,255-10*y1);

inc(i);

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

if i=1 then zanosRez;

if CheckBox1.Checked=true then begin

if ComboBox1.Text='max'then begin

if i=1 then First else begin

If (zn1<=zn2)and(zn1
If (zn2
If (zn3
end;

end else If ComboBox1.Text='min'then begin

if i=1 then First else begin

If (zn1>=zn2)and(zn1>zn3)then Pl1 else

If (zn2>zn1)and(zn2>=zn3)then Pl2 else

If (zn3>zn1)and(zn3>=zn2)then Pl3

end;

end;

end else begin

if CheckBox1.Checked=false then begin

if ComboBox1.Text='max'then begin

if i=1 then First else begin

If (zn1<=zn2)and(zn1
If (zn2
If (zn3
end;

end else If ComboBox1.Text='min'then begin

if i=1 then First else begin

If (zn1>=zn2)and(zn1>zn3)then Pl1 else

If (zn2>zn1)and(zn2>=zn3)then Pl2 else

If (zn3>zn1)and(zn3>=zn2)then Pl3

end;

end;

end;

end;

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

randomize;

for i:=1 to 73 do begin

image1.Canvas.MoveTo(10*i,254);

image1.Canvas.LineTo(10*i,256);

end;

for i:=3 to 52 do begin

image1.Canvas.MoveTo(379,10*i+5);

image1.Canvas.LineTo(381,10*i+5);

end;

i:=1;

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(380,520);

image1.Canvas.MoveTo(10,255);

image1.Canvas.LineTo(750,255);

image1.Canvas.TextOut(365,10,'Y');

image1.Canvas.TextOut(740,240,'X');

stringGrid1.Cols[0].Text:='¹øàãà';

stringGrid1.Rows[1].Text:='Çíà÷-å';

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(382,20);

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(378,20);

image1.Canvas.MoveTo(750,255);

image1.Canvas.LineTo(740,257);

image1.Canvas.MoveTo(750,255);

image1.Canvas.LineTo(740,253);

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

if CheckBox1.Checked=true then begin

For k:=0 to 767 do begin

for j:=0 to 537 do begin

image1.Canvas.Pixels[k,j]:=clwhite;

end;

end;

image1.Canvas.MoveTo(380,0);

image1.Canvas.LineTo(380,540);

image1.Canvas.MoveTo(0,255);

image1.Canvas.LineTo(790,255);

for k:=1 to 77 do begin

image1.Canvas.MoveTo(10*k,254);

image1.Canvas.LineTo(10*k,256);

image1.Canvas.MoveTo(379,10*k+5);

image1.Canvas.LineTo(381,10*k+5);

end;

image1.Canvas.MoveTo(380+10*x1,255-10*y1);

image1.Canvas.LineTo(380+10*x2,255-10*y2);

image1.Canvas.LineTo(380+10*x3,255-10*y3);

image1.Canvas.LineTo(380+10*x1,255-10*y1);

if ComboBox1.Text='max'then begin

If (zn1<=zn2)and(zn1<=zn3)then Pl1 else

If (zn2
If (zn3
end else If ComboBox1.Text='min'then begin

If (zn1>=zn2)and(zn1>=zn3)then Pl1 else

If (zn2>zn1)and(zn2>=zn3)then Pl2 else

If (zn3>zn1)and(zn3>zn2)then Pl3

end;

x:=(x1+x2)/2;

y:=(y1+y2)/2;

x1:=x;

y1:=y;

x:=(x3+x2)/2;

y:=(y3+y2)/2;

x3:=x;

y3:=y;

Zn1:=a*x1*x1+b*y1*y1+c*y1*x1+d*y1+e*x1+f;

Zn2:=a*x2*x2+b*y2*y2+c*y2*x2+d*y2+e*x2+f;

Zn3:=a*x3*x3+b*y3*y3+c*y3*x3+d*y3+e*x3+f;

end else begin

x:=(x1+x2)/2;

y:=(y1+y2)/2;

x1:=x;

y1:=y;

x:=(x3+x2)/2;

y:=(y3+y2)/2;

x3:=x;

y3:=y;

Zn1:=a*x1*x1+b*y1*y1+c*y1*x1+d*y1+e*x1+f;

Zn2:=a*x2*x2+b*y2*y2+c*y2*x2+d*y2+e*x2+f;

Zn3:=a*x3*x3+b*y3*y3+c*y3*x3+d*y3+e*x3+f;

end;

end;


procedure TForm1.Button2Click(Sender: TObject);

begin

For k:=0 to 767 do begin

for j:=0 to 537 do begin

image1.Canvas.Pixels[k,j]:=clwhite;

end;

end;

For k:=0 to 1 do begin

for j:=1 to 50 do begin

stringGrid1.Cells[j,k]:='';

end;

end;

for k:=1 to 73 do begin

image1.Canvas.MoveTo(10*k,254);

image1.Canvas.LineTo(10*k,256);

end;

for k:=3 to 52 do begin

image1.Canvas.MoveTo(379,10*k+5);

image1.Canvas.LineTo(381,10*k+5);

end;

i:=1;

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(380,520);

image1.Canvas.MoveTo(10,255);

image1.Canvas.LineTo(750,255);

image1.Canvas.TextOut(365,10,'Y');

image1.Canvas.TextOut(740,240,'X');

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(382,20);

image1.Canvas.MoveTo(380,10);

image1.Canvas.LineTo(378,20);

image1.Canvas.MoveTo(750,255);

image1.Canvas.LineTo(740,257);

image1.Canvas.MoveTo(750,255);

image1.Canvas.LineTo(740,253);

end;


end.

5. Список использованной литературы

1.

2. Мищенко А.В., Косоруков О.А. “Исследование операций. Учебник для ВУЗов.”, изд. Экзамен, 2003 г.