1 Постановка задачи
| Вид материала | Документы |
Содержание3.4Расширение возможностей MathML 3.4.2Вспомогательные теги 4Реализация языка и полученные результаты 4.1.1Теоретическая модель Значение переменной |
- Задачи оптимизации с ограничениями в виде неравенств. Постановка задачи. Геометрические, 42.48kb.
- Курсовой проект по дисциплине «Теория информационных процессов и систем» тема: Задачи, 258.87kb.
- И. Д. Салмин московский инженерно-физический институт (государственный университет), 27.33kb.
- Сопротивление композиционных материалов, 28.35kb.
- Удк 532 0727. 12 Физическое моделирование гидравлических явлений, 105.2kb.
- Задачи нелинейной и дискретной оптимизации. Методы решения. Постановка и экономико-математическая, 24.28kb.
- Дисциплина: Инженерия знаний Доклад Генетические алгоритмы, 371.21kb.
- Титул Напротив фамилии оставить автограф автора. Задание, 11.99kb.
- План урока Вступительное слово учителя. «Золотое сечение» в математике постановка задачи,, 118.33kb.
- Исследование операций, 82.88kb.
3.4Расширение возможностей MathML
3.4.1Новые типы данных
В численных методах фигурируют такие параметры как вектор-функция, матрица, элементами которой является функции и т.п. Возможности MathML ограничены и подобные типы данных отсутствуют в этом языке, поэтому приходится доопределять такие переменные с помощью элемента Datatype, уже встречавшегося в пункте 3.2.
Опишем этот элемент в DTD:
DataType
type CDATA (in|out|calculated|regulated|constant) "in"
>
ParamType (vector | fn | matrix | set | int | real | bool)>
Параметр type элемента Datatype может принимать значения, описанные в пункте Error: Reference source not found для элемента ModelVariables. По умолчанию type принимает значение ”in”, то есть параметр считается входным.
Элементы ParamType определяют тип данных параметра и могут принимать значения
”вектор”, ”функция”, ”матрица”, ”множество”, ”целое число”, ”действительное число”, ”булиновская переменная”.
Сложные типы данных образуются с помощью комбинации элементов ParamType, причём важна последовательность, в которой эти элементы расположены.
Допустим, код
f
fn
vector
указывает на то, что f является вектор-функцией, а код
f
vector
fn
определяет f как функцию многих переменных.
3.4.2Вспомогательные теги
В MathML отсутствуют теги, направленные на описание логики математических вычислений. С целью элементарного структурирования формул в численных методах мы ввели элемент MathBlock , но его оказалось недостаточно для адекватного описания логики вычислений.
Наиболее остро чувствуется невозможность создания циклических построений для более-менее точного описания численных методов и систем уравнений. Эту проблему можно решить с помощью определения в MathML дополнительного элемента
for (ci,(apply|ci|cn),(apply|ci|cn),cn,(apply|for))>
Как видим, for включает в себя пять элементов. Первый элемент содержит переменную цикла. Очевидно, что только ci может быть таким элементом.
Второй и третий элементы задают нижний и верхний предел цикла соответственно. Эти пределы могут быть числом, переменной или формулой. Четвертый элемент в теге
Элемент
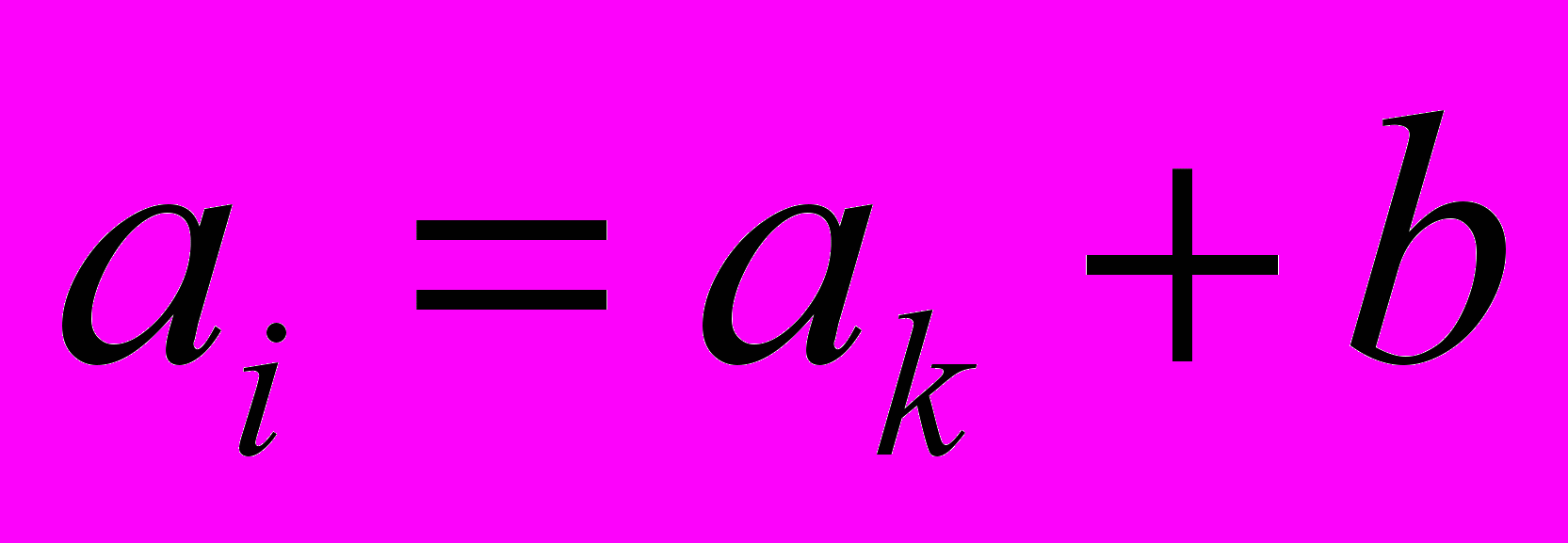, где i=1…n; k=0..i-1. Этот цикл будет выглядеть следующим образом:
4Реализация языка и полученные результаты
4.1Описание структуры системы моделей, состоящих из алгебраических уравнений, и взаимосвязи параметров внутри неё на примере модели сердца
4.1.1Теоретическая модель
В этом пункте будет описание теоретической модели на основе DTD, изложенного в Error: Reference source not found
Модель кровообращения имеет некоторые параметры и включает в себя другие модели:
Модель 1 — Кровообращение
| Значение переменной | Тип | Имя | Величина | Единицы измерения | Размерность |
| Системный кровоток | расчетный | Q | 70 | мл/с | Поток |
| Давление на выходе из большого круга | расчетный | 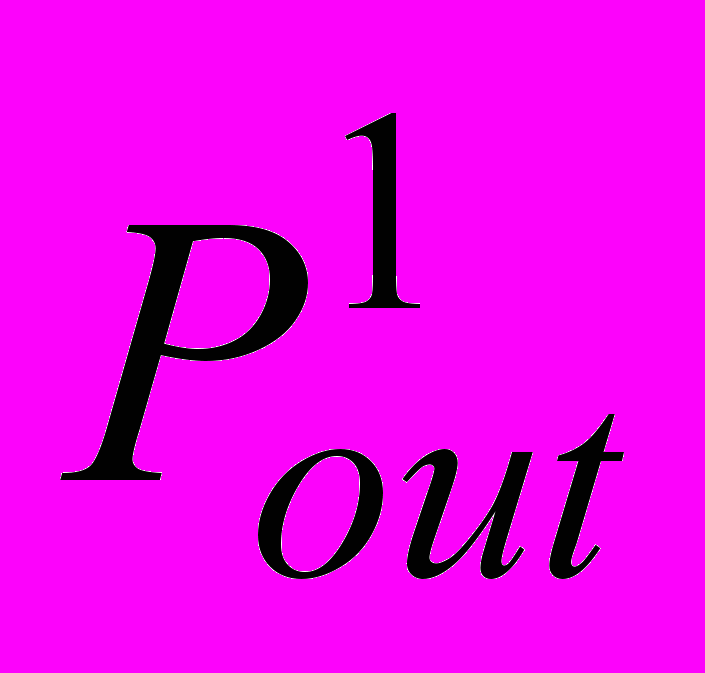 | 3 | мм.рт.ст | Давление |
| Давление на входе в малый круг | расчетный | 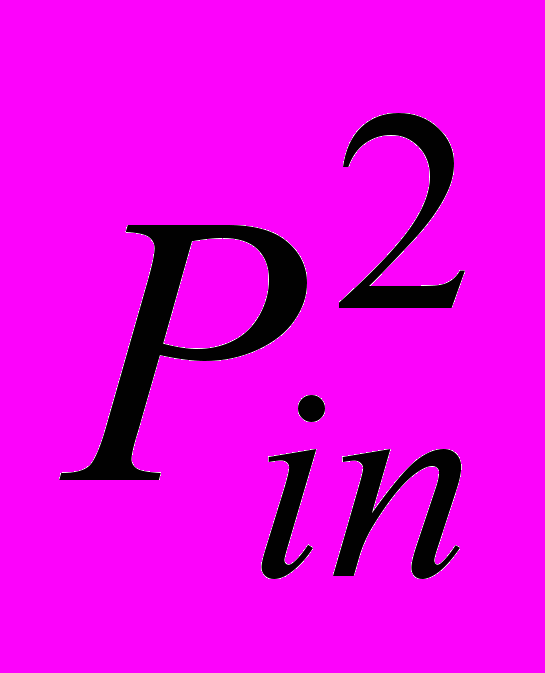 | 13 | мм.рт.ст | Давление |
| Давление на выходе из малого круга | расчетный | 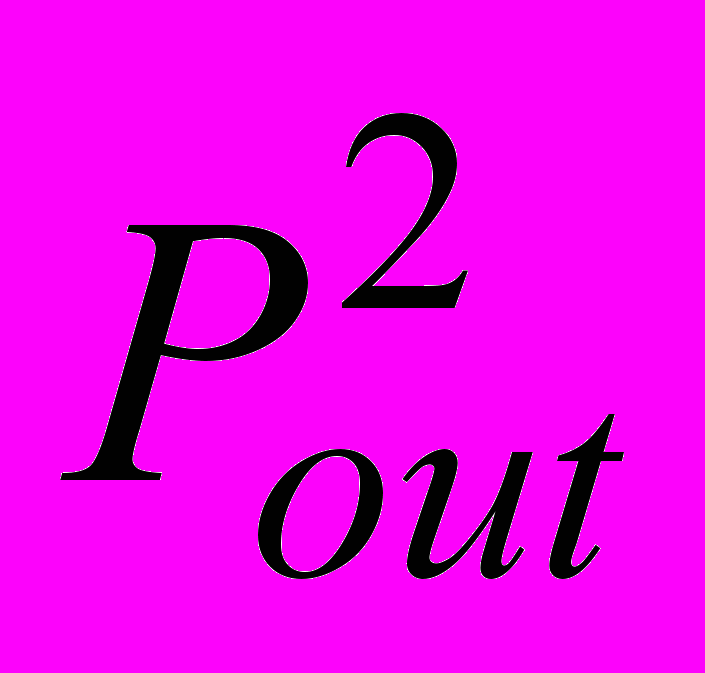 | 6 | мм.рт.ст | Давление |
| Давление на входе в большой круг | расчетный | 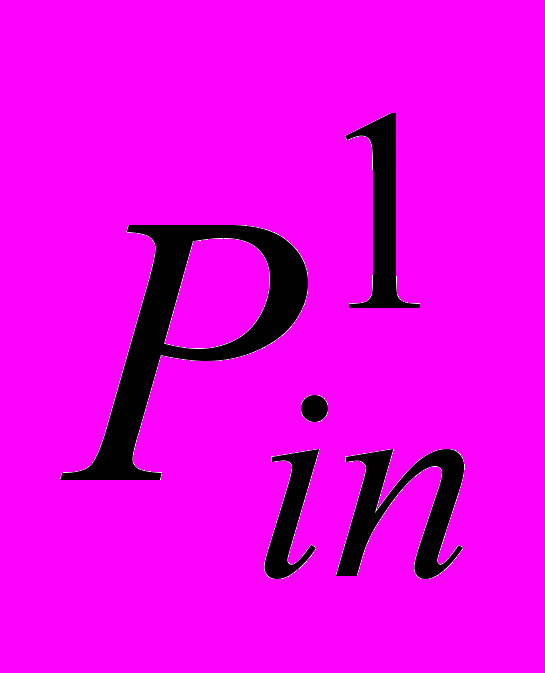 | 100 | мм.рт.ст | Давление |
Модель 1.1 — Сосудистая система
Модель 1.1.1 — Большой круг
| Общее сопротивление | константа | R1 | 1.4 | мм.рт.ст/(мл/с) | Сопротивление |
| Жесткость (артерий) | константа | E1 | 0.8 | мм.рт.ст/мл | Жесткость |
Модель 1.1.2 — Малый круг
| Общее сопротивление | константа | R2 | 0.115 | мм.рт.ст/(мл/с) | Сопротивление |
Модель 1.2 — Сердце
| Частота сердечных сокращений | константа | ν | 65 | уд/мин | Частота |
| Длительность систолы | константа | τs | 0.28 | с | Время |
Модель 1.2.1 — Правый желудочек
| Сопротивление («ЭДС») | константа | Rж | | мм.рт.ст/(мл/с) | Сопротивление |
Модель 1.2.2 — Левый желудочек
| Жесткость желудочка | константа | K | 0.54 | мм.рт.ст/мл | Жесткость |
| Выходная жесткость | входной | E | 0.8 | мм.рт.ст/мл | Жесткость |
| Выходное сопротивление | входной | R | 1.4 | мм.рт.ст/ (мл/с) | Сопротивление |
| Диастолическое давление | входной | Pd | 6 | мм.рт.ст | Давление |
| Нижнее артериальное давление | выходной | Pa | 80 | мм.рт.ст | Давление |
| Систолическое давление | расчетный | Ps | 120 | мм.рт.ст | Давление |
| Максимальное систолическое давление | регулиру-емый | Pm | 280 | мм.рт.ст | Давление |
| Систолический объем | расчетный | Vs | 70 | мл | Объем |
| Минимальный систолический объем | регулиру-емый | Vm | 40 | мл | Объем |
| Диастолический объем | регулиру-емый | Vd | 130 | мл | Объем |
| Ударный объем | расчетный | ΔV | 60 | мл | Объем |
Формулизуем эту иерархическую структуру модели на SimulML:
δV
δV
.......
Параметры модели в этой системе связаны между собой и мы можем указать эти
связи в элементах Connection. Напомним, что теоретическая модель не содержит уравнений и связи переменных просто указаны качественно. В данной модели подобных связей
очень много – опишем одну для примера. Так выглядит связь системного кровотока Q
с диастолическим давлением Pd :