И. Лакатос Доказательства и опровержения. Как доказываются теоремы

Вид материала

Задача

Содержание 7. Проблема пересмотра содержания а) «Наивность» наивной догадки б) Индукция как основа метода доказательств и опровержений

Подобный материал:

• Правила и ошибки возможные при определении. Деление как логическая операция. Виды деления, 23.4kb.
• Тема 1 курс, 30.71kb.
• Содержание: Введение, 134.15kb.
• Программа вступительного экзамена в магистратуру математического факультета, 107.92kb.
• Брянский городской лицей №1 имени А. С. Пушкина Визитная карточка учебного проекта, 50.66kb.
• Программа для поступающих в аспирантуру по специальности 05. 13. 18 Математическое, 37.95kb.
• Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пи­фагора, 42.5kb.
• Применима ли теорема Пифагора к сферическому треугольнику?, 116.8kb.
• Математические утверждения и теоремы, их виды, работа с теоремами. Обоснования и доказательства., 63.84kb.
• Вопросы философии, 2006, №6 Парадигмы, исследовательские программы и ядро раздела науки, 437.91kb.

7. Проблема пересмотра содержания

а) «Наивность» наивной догадки

Дзета. Я согласен с Омегой и также оплакиваю факт, что устранители монстров, исключений и инкорпораторы лемм все стремятся к некоторой истине за счет содержа­ния. Но его Правило 4 ¹¹⁵, требующее более глубоких доказательств той же самой наивной догадки, не будет до­статочным. Почему наши поиски содержания должны быть ограничены первой наивной догадкой, на которую мы на­пали? Почему целью нашего исследования должна быть «область наивной догадки»?

Омега. Я не понимаю вас. Конечно, нашей задачей было найти область истинности отношения V—E+F=2?

Дзета. Нет! Нашей задачей было найти связь V, Е и F для любого многогранника. Ведь только по чистой слу­чайности мы сначала познакомились с многогранниками, для которых F—E+F=2. Но критическое исследование этих «эйлеровых» многогранников показало нам, что не­эйлеровых многогранников существует гораздо больше, чем эйлеровых. Почему же нам не обратить внимания на область истинности V—E+F= -6, V—E+F=28 или V—E+F=0? Разве они не так же интересны?

Сигма. Вы правы. Мы обратили так много внимания на V—E+F=2 только по той причине, что первоначаль­но считали это истинным. Теперь же мы знаем, что это не так,— нам нужно найти новую, более глубокую наивную догадку...

Дзета ..., которая будет менее наивной...

Сигма ..., которая даст соотношение между V, Е и F для любого многогранника.

Омега. Зачем спешить? Решим сначала более скром­ную задачу, которую мы поставили перед собой: объяс­нить, почему некоторые многогранники являются эйлеро­выми. До сих пор мы пришли только к частичным объяс­нениям. Например, ни одно из найденных доказательств не объяснило, почему картинная рама с кольцеобразными гранями спереди и сзади будет эйлеровой (рис. 16). Она имеет 16 вершин, 24 ребра и 10 граней...





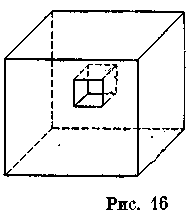
Тета. Она, конечно, не будет многогранником Коши: у нее есть туннель, кольцеобразные грани...

Бета. И все-таки она эйлерова! Как неразумно! Если многогранник провинился один раз — туннель без кольце­образных граней (рис. 9), — то его отбрасывают к козли­щам, а тот, который сделал вдвое больше преступлений — имеет кольцеобразные грани (рис. 16), — допущен к ов­цам¹¹⁶.

Омега. Вы видите, Дзета, у нас достаточно загадок и для эйлеровых многогранников. Решим же их, прежде чем заняться более общей задачей.

Дзета. Нет, Омега. «На много вопросов иногда бывает легче отве­тить, чем только на один. Новая бо­лее претенциозная проблема может оказаться более легкой, чем первона­чальная»¹¹⁷ 108. В самом деле, я покажу, что ваша узкая случайная задача мо­жет быть решена только после реше­ния более широкой, существенной.

Омега. Но я хочу раскрыть сек­рет эйлеровости!

Дзета. Я понимаю ваше упорство: вы поставили за­дачу определить, где Бог поместил твердь, отделяющую эйлеровы многогранники от неэйлеровых. Но нет основа­ния думать, что слово «эйлеров» вообще встречалось у Бо­га в плане вселенной. А что если эйлеровость только слу­чайное свойство некоторых многогранников? В этом случае будет неинтересно, или даже невозможно, найти случай­ные зигзаги в демаркационной линии между эйлеровыми и неэйлеровыми многогранниками. Тем более это допуще­ние оставит незапятнанным рационализм, потому что эй­леровость не будет тогда частью рационального плана вселенной. Поэтому забудем об этом. Один из основных пунктов критического рационализма заключается в том, что надо быть всегда готовым во время решения оставить свою первоначальную задачу и заменить ее другой.

б) Индукция как основа метода доказательств и опровержений

Сигма. Дзета прав. Какое несчастье!

Дзета. Несчастье?

Сигма. Да. Вы теперь хотите ввести новую «наив­ную догадку» о соотношении между V, Е и F для любо­го многогранника, не правда ли? Невозможно! Взгляните на большую толпу контрапримеров. Многогранники с по­лостями, многогранники с кольцеобразными гранями, с туннелями, сросшиеся друг с другом в ребрах, в верши­нах... V—E+F может принять вообще любое значение. Вы, пожалуй, не сумеете разглядеть в этом хаосе какой-нибудь порядок! Твердую почву эйлеровых многогран­ников мы покинули для болота! Мы невозвратно потеряли наивную догадку и не имеем надежды получить другую!

Дзета. Но...

Бета. А почему нет? Вспомните кажущийся безна­дежным хаос в нашей таблице чисел вершин, ребер и гра­ней даже у самых обыкновенных многогранников.

	Многогранники	F	V	E
1.	Куб	6	8	12
2.	Треугольная призма	5	6	9
3.	Пятиугольная призма	7	10	15
4.	Четырехугольная пирамида	5	5	8
5.	Треугольная пирамида	4	4	6
6.	Пятиугольная пирамида	6	6	10
7.	Октаэдр	8	8	12
8.	«Башня»	9	9	16
9.	Усеченный куб	7	10	15

Мы столько раз не могли .подобрать для них формулу¹¹⁸.Но потом внезапно нас поразил настоящий закон, управ­ляющий ими:


V-E+F = 2.


Каппа (в сторону). «Настоящий закон»? Странное название для полнейшей ложности.

Бета. Все, что мы должны теперь сделать, это допол­нить нашу таблицу новыми данными для неэйлеровых многогранников и поискать новую формулу: при наличии терпеливого прилежного наблюдения и некоторого сча­стья мы попадем на правильную формулу; затем мы мо­жем снова ее улучшить, применяя метод доказательств и опровержений!

Дзета. Терпеливое, прилежное наблюдение? Пробо­вать одну формулу за другой? Может быть, вы придумаете гадательную машину, которая будет давать вам случайные формулы и пробовать их на вашей таблице? Неужели вы так думаете о прогрессе науки?

Бета. Не понимаю вашего гнева. Ведь вы, конечно, согласитесь, что начало нашего знания, наши наивные догадки могут прийти только после прилежного наблюде­ния и внезапного прозрения, как бы много ни взял на себя наш критический метод «доказательств и опровержений», после того как мы найдем наивную догадку? Любой дедуктивный метод должен начинаться с индуктивного основания!

Сигма. Ваш индуктивный метод никогда не принесет удачи. Мы пришли к F-E + F=2 только потому, что в нашей первоначальной таблице не было ни картинной рамы, ни морского ежа. Теперь же, когда этот историче­ский инцидент...

Каппа (в сторону) ... или благосклонное божествен­ное руководство...

Сигма... более уже не существует, вы никогда не смо­жете из хаоса «индуцировать» порядок. Мы начали с дол­гого наблюдения и со счастливым прозрением — и потер­пели поражение. Теперь вы предлагаете начать снова с еще более долгим наблюдением и с более счастливым про­зрением. Даже если бы мы пришли к какой-нибудь новой наивной догадке — в чем я сомневаюсь — мы кончили бы только такой же путаницей.

Бета. Может быть, вы хотите совсем отказаться от исследования? Нам нужно начать снова — прежде всего с некоторой новой наивной догадки, а затем снова пройти через метод доказательств и опровержений.

Дзета. Нет, Бета. Я согласен с Сигмой, поэтому и не начну опять с новой наивной догадки.

Бета. Тогда с чего же вы хотите начать, если не с индуктивного обобщения на низшем уровне в качестве наивной догадки? Или у вас есть какой-нибудь другой ме­тод для начала?