Курс лекций для специальности «Прикладная математика» Первый семестр
| Вид материала | Курс лекций |
- Курс лекций для специальности Прикладная математика и информатика, 774.04kb.
- Календарный план лекций по курсу «математический анализ» Для специальности «Математика», 39.98kb.
- Рабочая программа, 160.99kb.
- Рабочая программа, 182.62kb.
- Цифровая обработка сигналов, 137.86kb.
- Курс лекций (28 часов) канд филос наук О. В. Аронсон Курс лекций «Математика и современная, 27.49kb.
- Урс «Численное решение обыкновенных дифференциальных уравнений» читает кафедра фн-2, 24.78kb.
- Курс IV семестр 8 Всего аудиторных занятий 52 Лекций, 117.53kb.
- Курс лекций в электронной форме содержит все лекции предусмотренные программой дисциплины, 32.88kb.
- Календарный план учебных занятий по обязательной дисциплине «Дискретная математика, 109.62kb.
Государственноеобразоватеьное учреждение
Высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЛЕСА»
А.В. Корольков
Программирование и алгоритмические языки
Курс лекций для специальности
«Прикладная математика»
Первый семестр
Москва
Издательство Московского государственного университета леса
2006
Содержание
Общие сведения.
Название курса: «Программирование и алгоритмические языки»
| Вид занятий | часов в 1 семестре | часов во 2 семестре |
| Лекций | 34 (2 час/нед) | 34 (2 час/нед) |
| Практических | 34 (2 час/нед) | 17 (1 час/нед) |
| Лаборат | 34 (2 час/нед) | 34+17 (3 час/нед) |
Отчетность
| I семестр Программы на 20 баллов Контрольная Коллоквиум Зачет Экзамен | II семестр Программы на 10 баллов (до 1 апреля) Контрольная Курсовая работы Экзамен |
Содержание курса
| I семестр | лек. 1- 7 лек. 8-12 лек.13-17 | Основы алгоритмизации, структурное программирование. Технологии программирования, реализация на ТР Модули, стандартные модули. |
| II семестр | лек.1-7 лек. 8- 14 лек. 15-17 | Абстрактные Структуры Данных (АСД), реализация на ТР. Технологии программирования, реализация на языке Fortran Общие вопросы программирования |
Дальнейшее обучение программированию (по семестрам)
Математическое обеспечение ЭВМ (3,4)
Методы разработки ПО (Объектно-ориентированное программирование ОП) (4)
Машинно ориентированные языки (4,5)
Компьютерная графика (5,6)
Проектирование трансляторов (6,7-кр)
Системное программное обеспечение (ПО) (6,7,8-кр)
Базы данных и экспертные системы (7,8)
ПО современных коммуникаций (9 каф ЭМТ)
Рекомендуемая литература
- Фигурнов. IBM PC для пользователей. "Ф и С", 1995.
- Йенсен К., Вирт Н. Паскаль: руководство для пользователя. – М.: Финансы и статистика, 1989.
- Фаронов В.В. Турбо-Паскаль 7.0. Начальный курс. Учебное пособие. М. 1997.
- Ван Тассел Д. Стиль, разработка, эффективность и испытания программ. -М.: Мир. 1985.
- Дал У., Дейкстра Э., Хоар К. Структурное программирование. - М.: Мир, 1975.
- Горелик А.М., Ушакова В.Л., Шура-Бура М.Р. Мобильность программ на Фортране. "Ф и С", 1984.
- Боровин Г.К., Комаров М.М., Ярошевский В.С. Ошибки-ловушки при программировании на Фортране. Статистика, 1989.
- Вирт Н. Алгоритмы и структуры данных. – С-П, 2001.
- Дал У., Дейкстра Э., Хоар К. Структурное программирование. - М.: Мир, 1975.
- Программирование на языке Паскаль. Задачник. Под ред. О.Ф.Кусковой. Питер, 2002.
I семестр
Лекция 1
1.1 Алгоритм. Понятие алгоритма
Алгоритм – одно из фундаментальных, неопределяемых понятий математики. Под алгоритмом следует понимать некое предписание, которое указывает, как исходные данные можно переработать в результат. Алгоритм предназначен конкретному исполнителю, который умеет выполнять некоторый (фиксированный) набор элементарных операций. Алгоритм регламентирует последовательность выполнения элементарных операций, поэтому он должен быть записан на языке, понятном исполнителю.
Например, алгоритмом можно считать рецепт приготовления пирога в кулинарной книге. Исполнителем этого алгоритма может быть кулинар, или другой человек, умеющий готовить. Рецепты записываются на обычном бытовом языке в терминах простейших кулинарных операций. В качестве исходных данных к рецепту прилагается список продуктов. Действуя по рецепту, используя продукты, указанные в списке, кулинар в качестве результата получит готовое блюдо.
1.2 Алгоритмические языки
Записать алгоритм можно на любом языке (на русском, на китайском, на языке условных знаков). Однако, для записи алгоритма для такого строгого исполнителя, как вычислительная машина, не все языки годятся. Вычислительная машина «умеет» выполнять лишь определенный набор машинных команд. Именно в терминах машинных команд должен быть сформулирован для нее алгоритм.
Записывать алгоритмы для вычислительной машины в кодах очень непроизводительно. Поэтому для записи алгоритмов для ЭВМ разработаны специальные строгие математические языки, называемые алгоритмическими языками. В настоящее время существует много алгоритмических языков. Они отличаются друг от друга различными выразительными средствами записи алгоритмов и различными возможностями. Но всех их объединяет одно – для каждого из них разработаны специальные программы, называемые трансляторами, с помощью которых текст, написанный на алгоритмическом языке, превращается в алгоритм, записанный на языке машинных кодов.
Разработчики алгоритмических языков вынуждены искать компромисс между простотой транслятора и простотой использования алгоритмического языка. Чем ближе выразительные средства алгоритмического языка к машинным кодам, тем проще сам транслятор, тем более эффективен алгоритм, записанный в машинных кодах. Чем ближе выразительные средства алгоритмического языка к бытовому разговорному языку, тем легче программисту записать на нем алгоритм. Однако за простоту нужно платить. В результате, алгоритм, записанный в кодах машины, полученный транслятором с такого языка, менее эффективен, а сам транслятор более сложен. Языки, близкие к разговорному по своим выразительным средствам, принято называть языками высокого уровня, тогда как языки, близкие к кодам машины по своим выразительным средствам, называют языками низкого уровня, или машинно-ориентированными языками.
Алгоритмические языки служат для записи алгоритмов. При разработке алгоритма не следует ограничиваться средствами, предоставляемыми конкретным алгоритмическим языком. Более естественно для уже разработанного алгоритма выбрать алгоритмический язык, выразительные средства которого наиболее подходят для его записи. В связи с этим, разработку алгоритмов целесообразно вести не зависимо от имеющихся в арсенале алгоритмических языков, а на специальном строгом математическом (не допускающем двусмысленности) языке максимально высокого уровня. Таким языком может служить язык схем алгоритма.
Мышление у человека устроено так, что решение задачи может быть получено на абстрактном понятийном уровне, вообще без привлечения языков. Такое решение может быть сформулировано и обсуждаться с коллегами на бытовом языке, однако, для реализации на компьютере необходимо полученное решение формализовать. Если формализацию провести с использованием языка схем алгоритма по определенным правилам, то можно перевод решения задачи на реальный алгоритмический язык свести к некоей формальной процедуре. Такой подход позволяет программисту максимальным образом сконцентрироваться на получении решения поставленной задачи на абстрактном понятийном уровне и на записи этого решения на языке очень близком к разговорному. Этапы создания программы решения задачи можно изобразить с помощью следующей диаграммы:
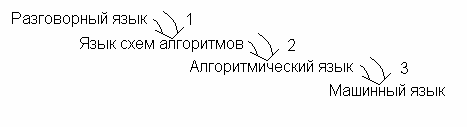
Здесь этап 1 – творческие усилия составителя алгоритма, этап 2 – формализованный перевод алгоритма в текст на алгоритмическом языке, этап 3 – трансляция текста с алгоритмического языка в коды машины.
1.3 Запись алгоритма
Условимся записывать алгоритм с помощью следующих обозначений:
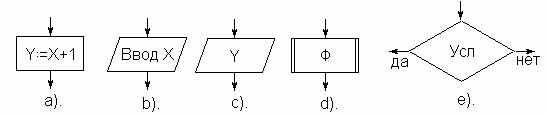
a). Элементарная операция присваивания. В прямоугольнике записывается сама операция.
b). Элементарная операция ввода. В параллелограмме записывается ключевое слово «Ввод» и список переменных через запятую, значения которых должны быть введены. В данном случае вводится значение единственной переменной X.
c). Элементарная операция вывода. В параллелограмме записывается список переменных и констант, значения которых должны быть выведены. В данном случае выводится значение единственной переменной Y.
Будем считать, если это не оговорено особо, что ввод данных осуществляется с клавиатуры, а вывод – на экран монитора.
d). Подалгоритм, требующий дальнейшей детализации. В прямоугольнике с двойными боковыми ребрами записывается имя подалгоритма. В данном случае имя подалгоритма «Ф».
e). Решение. С помощь этой конструкции можно осуществлять ветвление алгоритма в зависимости от значения логического выражения Усл внутри ромбика. Если значение логического выражения «истина», то осуществляется переход по стрелке «да», в противном случае по стрелке «нет». Условимся всегда стрелку «да» рисовать влево, стрелку «нет» - вправо.
Линиями со стрелками будем показывать последовательность выполнения перечисленных операций.
1.4 Элементарные структуры
Любое, даже очень сложное решение задачи, может быть выражено алгоритмом, представляющим собой композицию следующих трех простых структур:
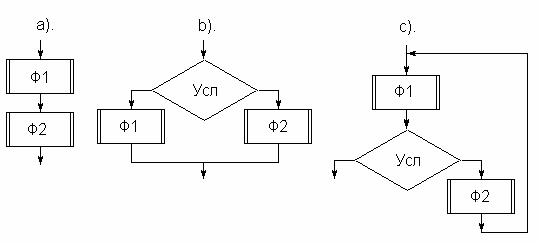
Структура a) – линейная. Действия выполняются последовательно – сначала выполняется фрагмент Ф1, затем фрагмент Ф2. Структура b) – выбор. В зависимости от истинностного значения логического выражения Усл выполняется либо фрагмент Ф1, либо фрагмент Ф2. Структура с) – цикл. Многократно повторяется фрагмент Ф1 – тело цикла, перед каждым последующим выполнением тела цикла выполняется фрагмент Ф2 – модификатор. Логическое выражение Усл является условием выхода из цикла.
Если Вы хотите записать решение задачи с помощью перечисленных схем, попробуйте изложить решение задачи на бытовом, разговорном языке. В изложении решения неминуемо будут использоваться такие конструкции, как «сначала … затем», «если … то … иначе …», «повторяем … пока …», или на них похожие. Эти конструкции определяют соответствующие элементарные структуры. Попробуйте определить самую внешнюю структуру Вашего алгоритма. Если это удастся, то алгоритм разобьется на два подалгоритма (Ф1 и Ф2), которые можно записывать независимо, как решение двух более простых задач.
Заметим, что элементарные структуры имеют единственный вход и единственный выход. Таким образом, элементарные структуры топологически совместимы, то есть, вместо любого фрагмента можно поместить любую структуру. Поэтому, записав подалгоритмы Ф1 и Ф2, мы можем записать и сам алгоритм, связав решения соответствующей структурой.
Построение алгоритма последовательным выделением самой внешней структуры лежит в основе методики нисходящего метода проектирования алгоритмов (детализация сверху вниз). Используя описанный выше подход, мы получаем решение задачи в виде композиции трех элементарных структур. Если иметь таблицу перевода каждой элементарной структуры на какой-нибудь алгоритмический язык, то легко получить запись всего алгоритма на этом алгоритмическом языке.
