Курс лекций для специальности «Прикладная математика» Первый семестр

Вид материала

Содержание

3.1 Проект программы
3.2. Частные случаи для структуры цикла
Цикл с постусловием
WHILE i>=1 DO BEGIN
Цикл с параметром

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 13

Лекция 3

3.1 Проект программы

В профессиональные обязанности прикладного математика входит создание проекта программы. В самом общем случае проект программы включает в себя следующие позиции:

Точная формулировка задачи, включая разработку будущего интерфейса пользователя, с описанием входных и выходных данных.
Выбор типов данных, соответствующих параметрам объекта исследования, выбор имен констант, переменных, процедур и функций, соответствующих этим параметрам и описывающих функционирование объекта исследования.
Создание структур данных, моделирующих взаимосвязь параметров объекта исследования.
Разработка иерархии алгоритмов и подалгоритмов (процедур и функций), обрабатывающих созданные структуры данных.
Разработка алгоритма решения задачи.

Каждый из перечисленных пунктов требует глубокого осмысления и будет уточняться по мере изложения материала текущего курса. Попробуйте на базе материала 1 и 2 лекций при выполнении лабораторных работ максимально проработать позиции проекта программы.

3.2. Частные случаи для структуры цикла

Полный цикл с) пункта 1.4 редко используется при разработке алгоритмов. При решении конкретных задач используются частные случаи этого цикла, в которых отсутствует один из блоков – либо Ф1, либо Ф2. Можно строго математически доказать, что этих двух частных случаев цикла достаточно для организации любого цикла.

Решим такую задачу: написать программу, вычисляющую сумму

S=1-1/2+1/3-1/4+1/5-1/6-...+1/999-1/n.

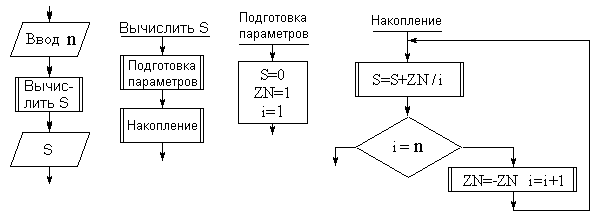
В этом решении использован полный цикл. Однако, нетрудно видеть, что подалгоритм «Накопление» можно реализовать по-другому. Сравните представленные ниже реализации:

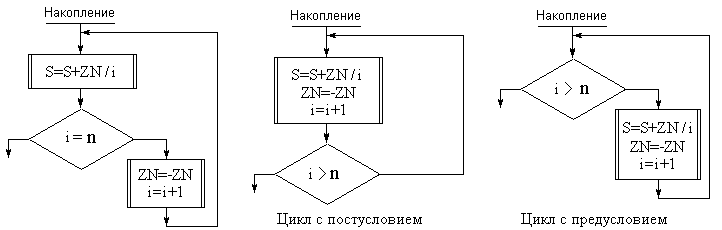
Обратите внимание на то, что тело цикла с постусловием обязательно будет выполнено хотя бы один раз при любом значении n и начальном значении параметра цикла i, тогда как при начальном значении параметра цикла i > n тело цикла с предусловием не будет выполнено ни разу.

Для реализации цикла с предусловием на языке ТР (как и на многих других языках) удобнее вместо условия выхода из цикла использовать условие продолжения цикла (напоминаю, в блоке решения стрелка влево всегда помечается значением «истина», стрелка вправо – значением «ложь»):

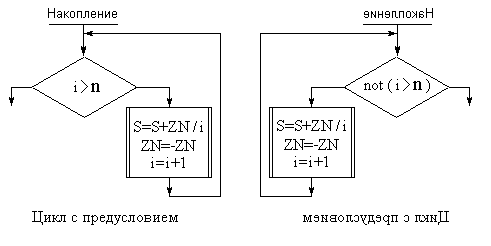
Можно доказать эквивалентность полного цикла и цикла с постусловием. Действительно, каждый цикл с постусловием является частным случаем полного цикла. Вот иллюстрация к доказательству факта, что любой полный цикл может быть организован как цикл с постусловием:

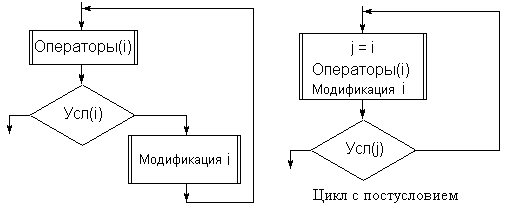
Приведем решения поставленной задачи с использованием частных случаев полного цикла:

Цикл с постусловием	Цикл с предусловием
readln(n); S=0; Zn=1; I=1; repeat S=S+Zn/I; Zn=-Zn; I=I+1 until I>n; writeln(S)	readln(n); S=0; Zn=1; I=1; while not(I>n) do begin S=S+Zn/I; Zn=-Zn; I=I+1; end; writeln(S)

Если в решении задачи заранее известно количество повторений тела цикла (в нашей задаче n), можно упростить изображение структуры, указав лишь операции в теле цикла и границы изменения параметра цикла – начальное значение, конечное значение и шаг. Такой цикл называется циклом с параметром. На языке ТР имеется оператор цикла с параметром.

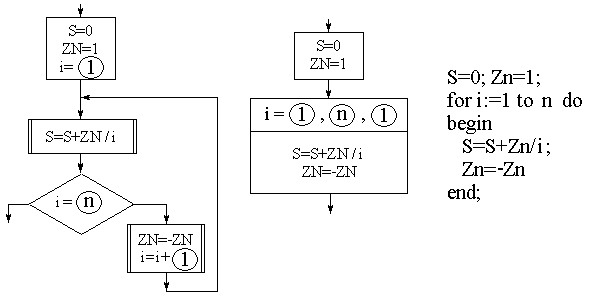
В решении задачи параметром цикла может оказаться любая переменная, соответствующая какому-либо параметру объекта исследования. Однако, решение можно всегда переформулировать так, что параметром цикла будет служить номер итерации (повторения выполнения тела цикла). В этом случае параметр цикла будет изменяться всегда от 1 до максимального номера итерации с шагом 1.

3.3 Массивы

Массивом называют структуру данных, которая содержит упорядоченное множество однотипных переменных (элементов) с одним и тем же именем (именем массива). Для обращения к конкретным элементам массива используется индекс (условный номер элемента).

x₁,x₂,...x₁₀ – обозначения, принятые в математике, x[1],x[2],...x[10] – в ТР.

Индексами могут служить выражения.

Объявление массива в программе:

VAR <Имя>: ARRAY[<Нач_индекс>..<Кон_индекс>] of <Тип>;

где

<Имя> - имя переменной-массива;
ARRAY, of - ключевые слова;
<Нач_индекс> и <Кон_индекс> - целые числа (пока), определяющие диапазон изменения индексов (номеров) элементов массива;
<Тип> - тип элементов массива.

Таким образом, при объявлении массива необходимо указать его идентификатор (имя), тип данных элементов массива и размер. В квадратных скобках указываются величины, соответствующие начальному и конечному индексам, разделенные двумя точками.

Например,

VAR

Matrix : ARRAY [1 .. 10] OF REAL;

Koef : ARRAY [1 .. 3] OF INTEGER;

Пример

Ввести несколько чисел и распечатать их в обратном порядке.

Массив Х, содержащий 100 элементов.

Ввести n (n<=100).

(Нарисовать схемы и записать тексты)

i:=1;

WHILE i<=n DO BEGIN

READLN(Х[i]);

i:=i+1

END;

i:=n;

WHILE i>=1 DO BEGIN

WRITELN(X[i]);

i:=i-1

END;

i:=1;

REPEAT

READLN(X[i]);

i:=i+1

UNTIL i>n;

i:=n;

REPEAT

WRITELN(X[i]);

i:=i-1

UNTIL i<1;

Цикл с параметром:

For i:=1 to n do readln(X[i]);

For i:=n downto 1 do writeln(X[i]);

For i:=1 to n do writeln(X[n-i+1]);