В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www diplomant-spb

Вид материала

Курсовая

Подобный материал:

• В представленной на сайте версии работы изменены числовые данные. Для получения работы, 452.38kb.
• В представленной на сайте версии работы изменены числовые данные. Для получения работы, 993.9kb.
• В представленной на сайте версии работы изменены числовые данные. Для получения работы, 443.94kb.
• Реферат Введение, 277.44kb.
• Литература Исходные данные, 156.35kb.
• Решение краевой задачи, 126.35kb.
• Курсовой проект Расчет усилительного каскада на транзисторе, 76.26kb.
• Курсовой проект изложен на 26 страницах, содержит 3 рисунка, 3 таблицы, 237.8kb.
• Контрольная работа по экономике, 00 стр. Задача, 219.54kb.
• «Проектирование технологического процесса механической обработки детали «Полумуфта», 370.42kb.

H_B/Н_н=64/114=,561<,6 и N_н/N_B=2542,8/277,6=11,2 > 3, следова­тель­но ₁=2, ₂=3; l_x1=₁l₁=21485=297 см, для верхней части колонны l_x2= =3615=1845 см. Расчетные длины из плоскости рамы для нижней и верхней час­тей соответственно l_y1=H_н=1485 см; l_y2=H_B-h_б=615-16=455 см.

5.3 Подбор сечений верхней части колонны.

Сечение верхней части колонны принимаем в виде сварного двутавра высотой h_в=7 мм. Требуемая площадь сечения:

- для симметричного двутавра i_x,42h_в=,427=29,4 см; _x,35h_в= =,357=24,5 см. Приведенная гибкость:

_x’=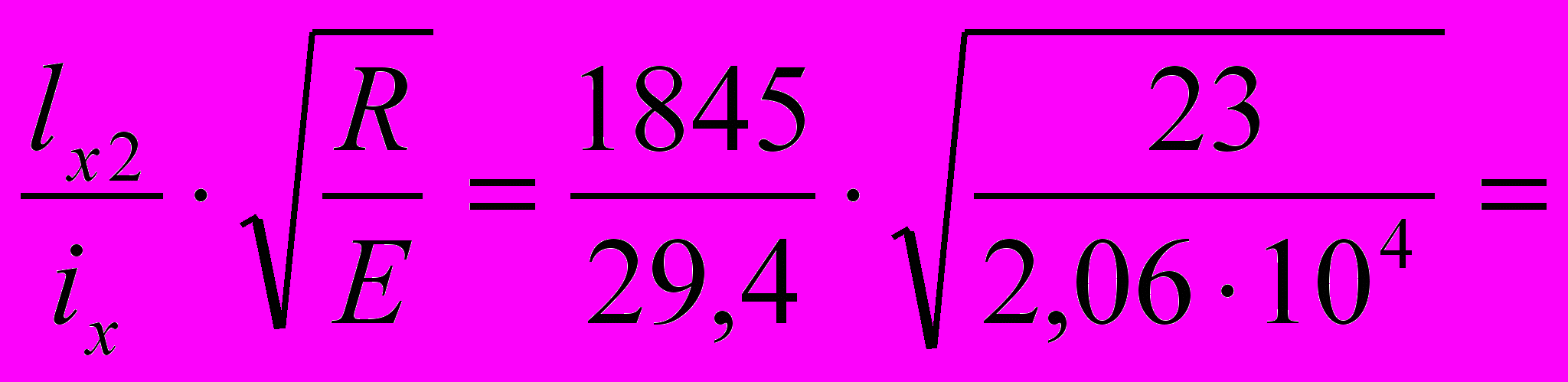2,731

m_x=e_x/_x=M/(N,35h_в)=15 /24,5=6,11. Принимаем в первом приб­ли­же­нии A_п/А_ст=1. =1,4-,2=1,4-,2*2,9

=1,358; m_1x=m_x=1,3586,11=8,3. По _x’=2,9, m_1x=8,3 прини­ма­ем _вн=,154; А_тр=564,69/(,15423)=159 см².

5.3.1 Компоновка сечения.

Высота стенки h_ст=h_в-2t_п= ( принимаем предварительно толщину по­лок t_п=1,4 см )=7-21,4=67,2 см.

При m>1 и ‘>,8 из условия местной устой­чивости:




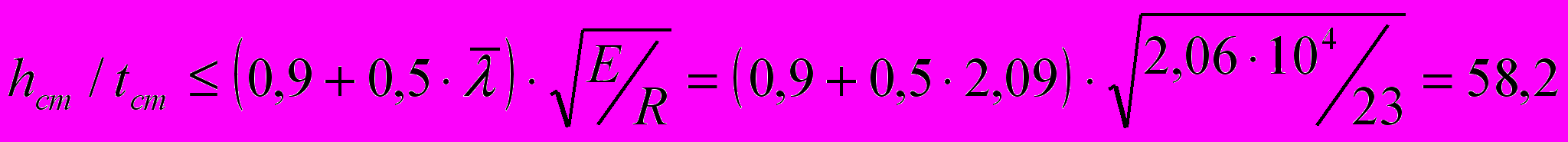
t_ст>67,2/58,2=1,18 см; с целью экономии стали использу­ем закрити­чес­кую работу стенки и принимаем t_ст=,8. Включаем в расчетную площадь сечения колонны два крайних учас­т­ка стенки шириной по ,85t_ст(E/R)^1/2=,85,8(2,61⁴/23)^1/2=14,94 см. Тре­буемая площадь полки:

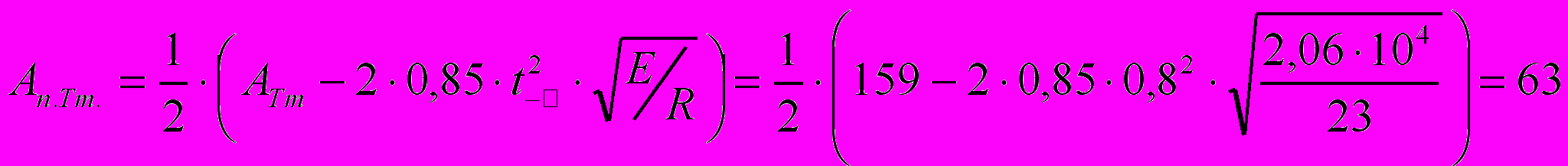см²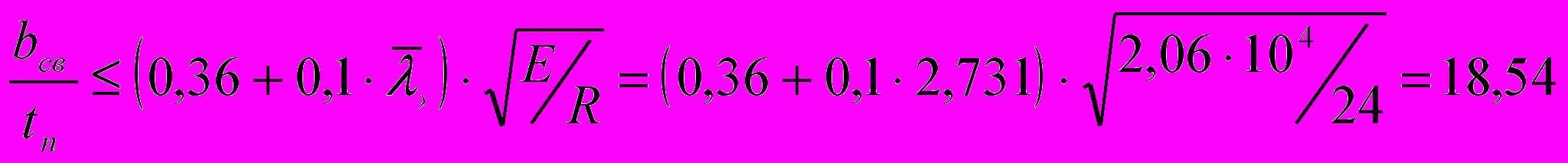



Принимаем b_п=4 см; t_п=1,6 см. Тогда А_п=41,6=72 см²;

b_п=4 см = l_y2/2=455/2=24 см; b_св/t_п=(4-,8)/(21,6)=1,8<17.

5.3.2 Геометрические характеристики сечения.





Полная площадь сечения А=2х х41,6+99,8,8=181, см². Расчетная площадь сечения с учетом только устойчивой части стенки А=241,6+ +2,85,8²(26/23)^1/2=176,56 см².

I_x=,866,8³/12+241,6((7,-1,6)/2)²= =17428, см⁴;

I_y=21,64³/12=192, см⁴; ­

W_x=17428/66,8/2=5184 см³;






8


4







16 672 16


7


i_x=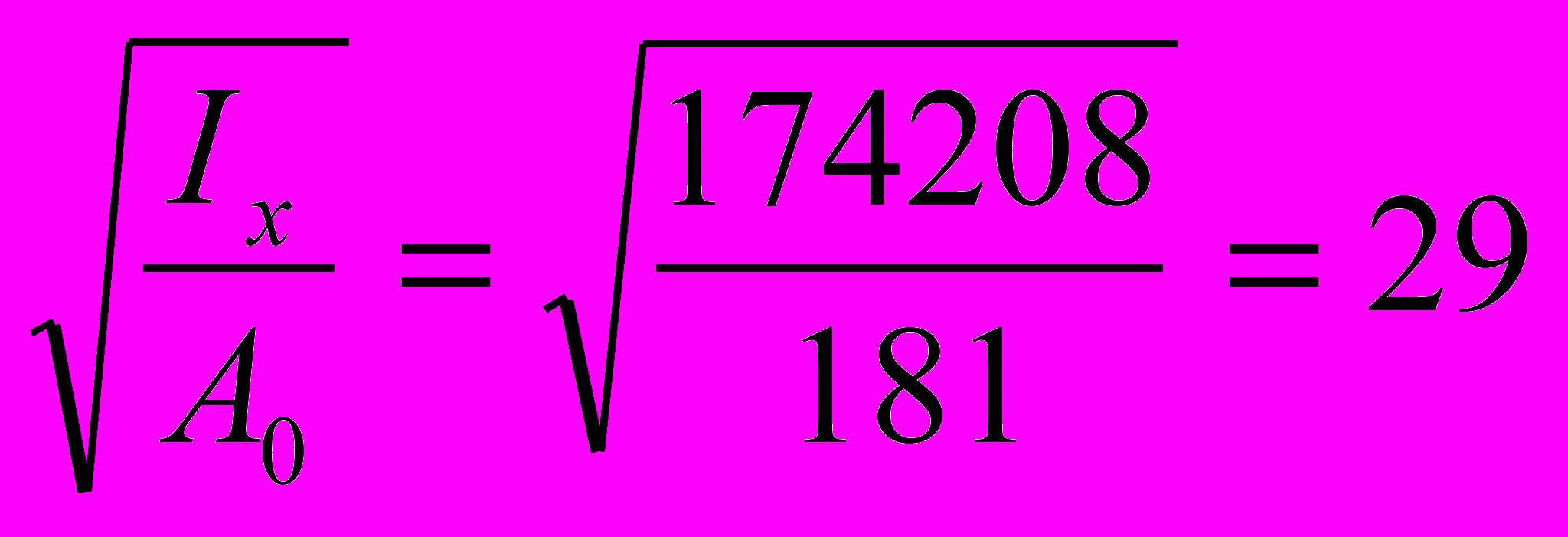см; i_y= 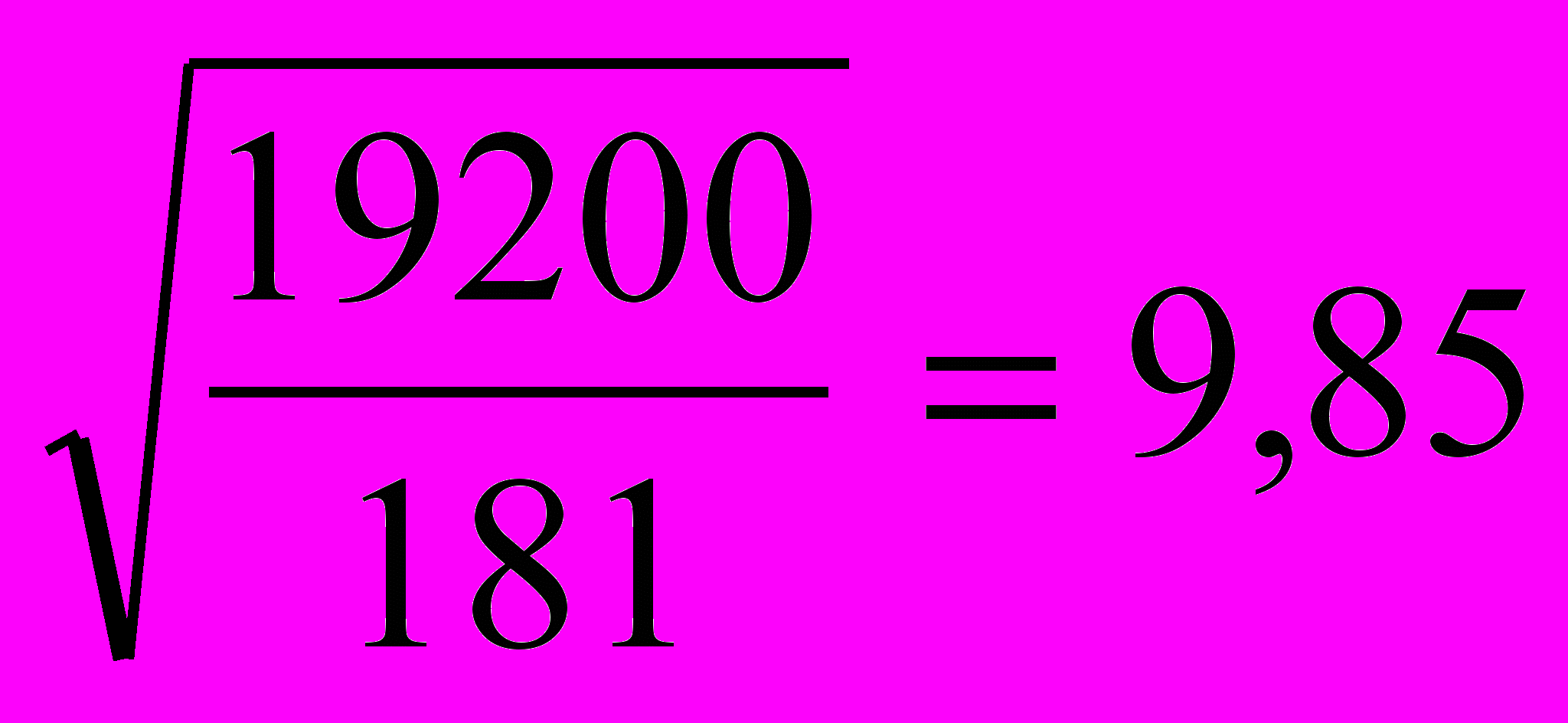см


_x=W_x/A=5184/181=26,2 см


5.3.3 Проверка устойчивости верхней части колонны

в плоскости действия момента.


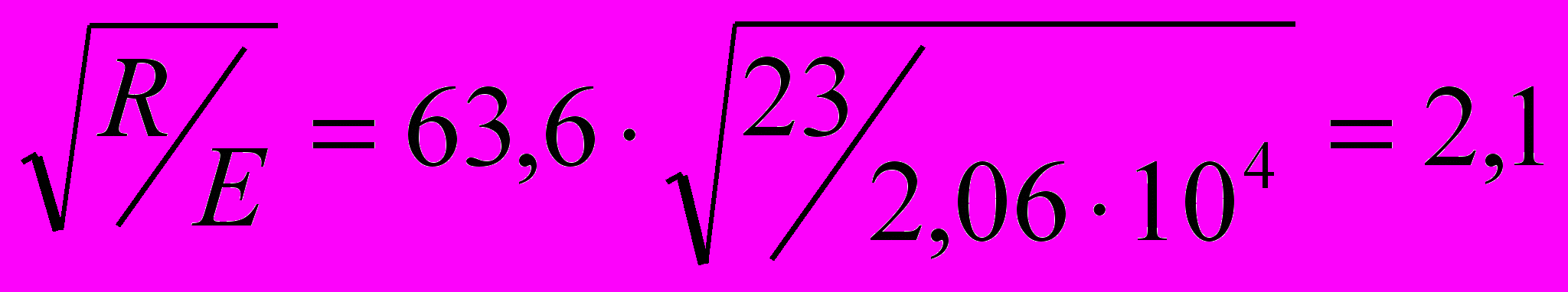_x=1845/29=63,6; _x’=_x; m_x=M_x/(Nх х_x)= 15/26,2=5,73; A_п/А_ст=1,64/(,866,8)=1,3;

Значение коэффициента  при А_п/А_ст=1,3: =1,358; m_1x=m_x=1,3585,73=7,78. По вы­численным _х’=2,1 и m_1x=7,78 принимаем _вн=,145.


=564,69/(,145181)=21,9 кН/см² < R=23 кН/см².


Недонапряжение (23-21,9)/231%4%.


5.3.4 Проверка устойчивости верхней части колонны

из плоскости действия момента.


M_1-1=-846,29 кНм; M_2-2=2,2 кНм .Наибольший момент в пределах средней трети расчетной длины стерж­ня l_yв:





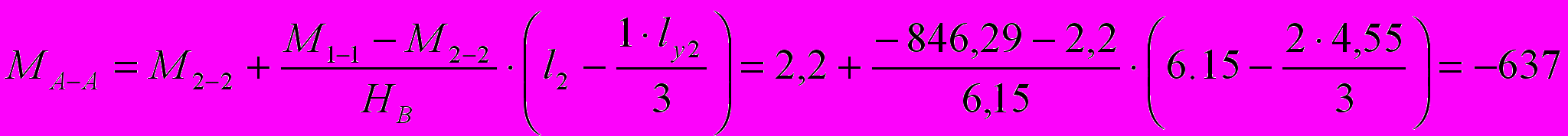
m_x=M_A-A/(N_x)=637/(564,6926,2)=3,94.

При m_x=3,94<5, c=/(1+m_x); при _y=455/9,85=46,, _y=,85. Коэф­фициенты  и : =1 при 1_x<5; =,65+,5m_x=,65+,53,94=,847.

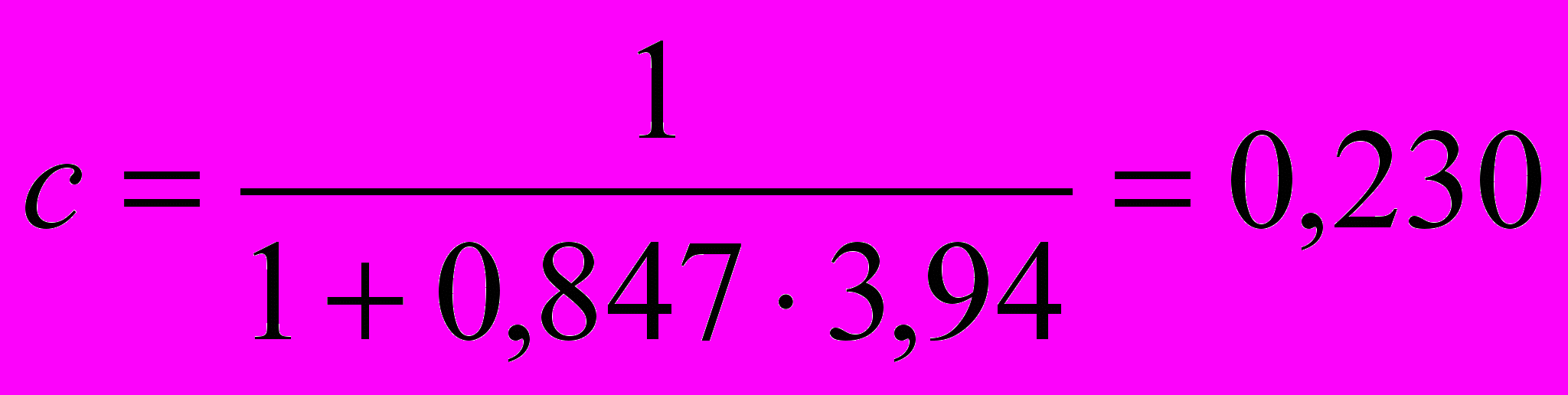; Т.к.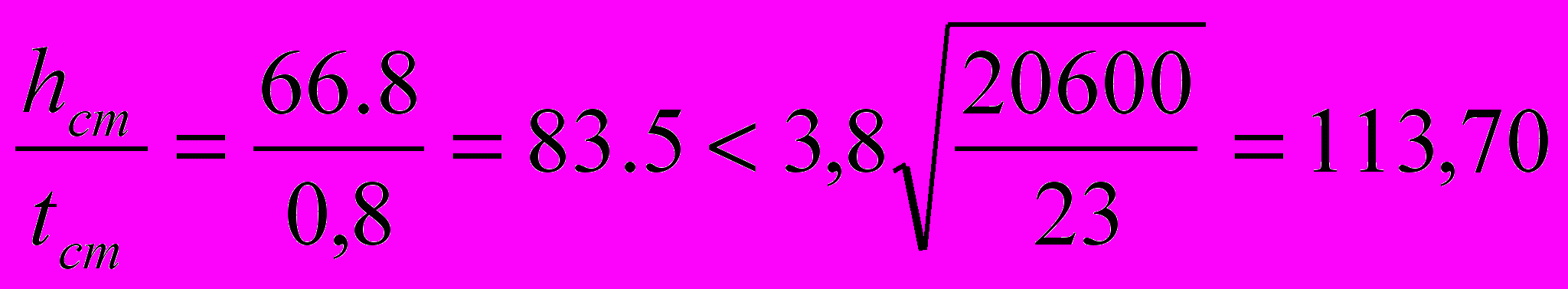 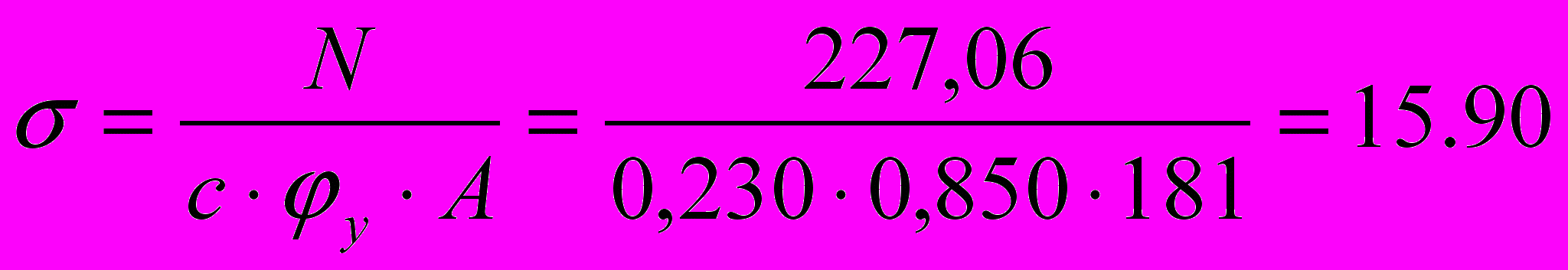<24 кН/см²


5.4 Подбор сечений нижней части колонны.


Сечение нижней части колонны - сквозное, состоящее из двух ветвей, соединенных решеткой. Высота сечения h_н=125 мм. Подкрановую ветвь ко­лон­ны принимаем из широкополочного двутавра, наружнюю - составного сечения из трех листов.

Определяем ориентировочное положение центра тяжести. Принима­ем z=5 см; h=h-z=125-5=125 см.


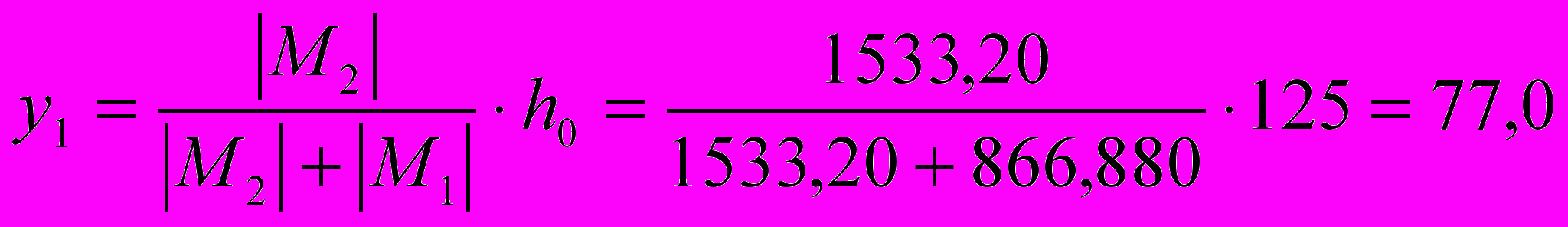; y₂=h-y₁=12-77=43 см.


Усилия в ветвях:

- в подкрановой ветви N_в1=24143/12+86688/12=1586 кН;

- в наружней ветви N_в2=2741,377/12+15332/12=337 кН.

Определяем требуемую площадь ветвей и назначаем сечение:

- для подкрановой ветви А_в1=N_в1/(R); задаемся =,8; R=23 кН/см².

A_в1=1586/(,823)=86,12 см².

по сортаменту принимаем двутавр 5Б1, А_в1=93 см²; i_x=4,2 см; i_y=2 cм;

- для наружней ветви А_в2=N_в2/(R)=337, /(,823)=165, см², где R=23 кН/см² для листового проката из стали С245 c <2 мм. Для удобства прикрепления элементов решетки просвет между внутренними гранями по­лок принимаем таким же, как в подкрановой ветви (53 мм). Толщина стенки швелера для удобства соединения встык с полкой надкра­но­вой части колонны t_ст=16 мм. Высота стенки из условия размещения сварных швов h_cт=53мм, А_cт=84,8 см².

Требуемая площадь полок А_п.тр.=(А_в2-t_стh_ст)/2=(165, -1,653)/2= 4,1 см². Из условия местной устойчивости полки швеллера b_п/t_п<(,38+ +,8‘)(E/R)^1/216. Принимаем: t_п=2, см, b_п=21 см, А_п=42 см².

Геометрические характеристики ветви:

A_в2=1,653+42,2=168,8 см²; z=(1,653,8+42211,3)/168,86 см; I_x2= =1,6535,2²+2221³/12+426,1²2=856; I_y2=1,653³/12+42224,7²=7198;


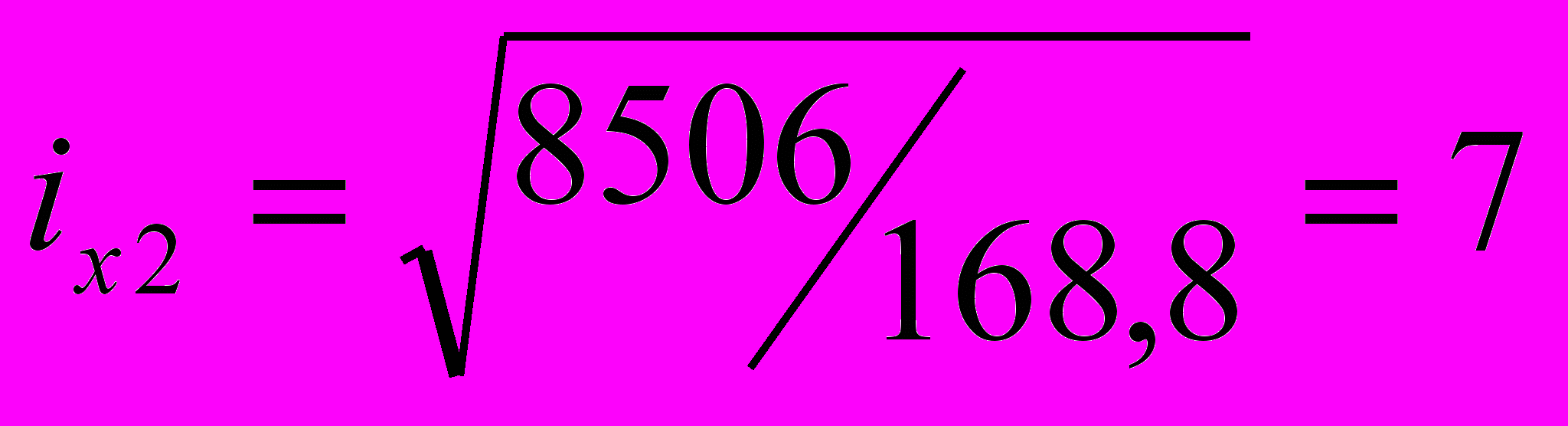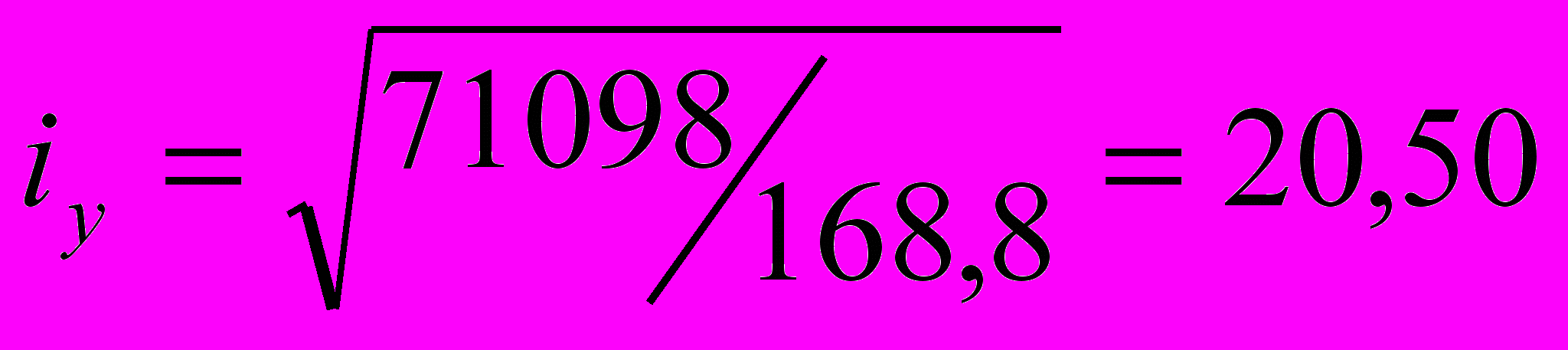см; см;

Уточняем положение центра тяжести сечения колонны h=h_н-z= 125-6,=119 мм=119, см; y₁=A_в2h/(А_в2+А_в1)=168,8119/(93,+168,8)= 77 см; y₂=119,-77=42 см. Отличие от первоначально принятых разме­ров мало, поэтому усилия в ветвях не пересчитываем.


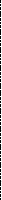
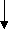
16 21

2




594

53 468


14 6 у₂=42 у₁=77



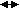
h=119

h_н=125


5.4.1 Проверка устойчивости ветвей.


Из плоскости рамы (относительно оси y-y) l_y=1485 см. Подкрановая ветвь: _y=l_y/i_y=1485/2,=74,25, следовательно _y=,747.


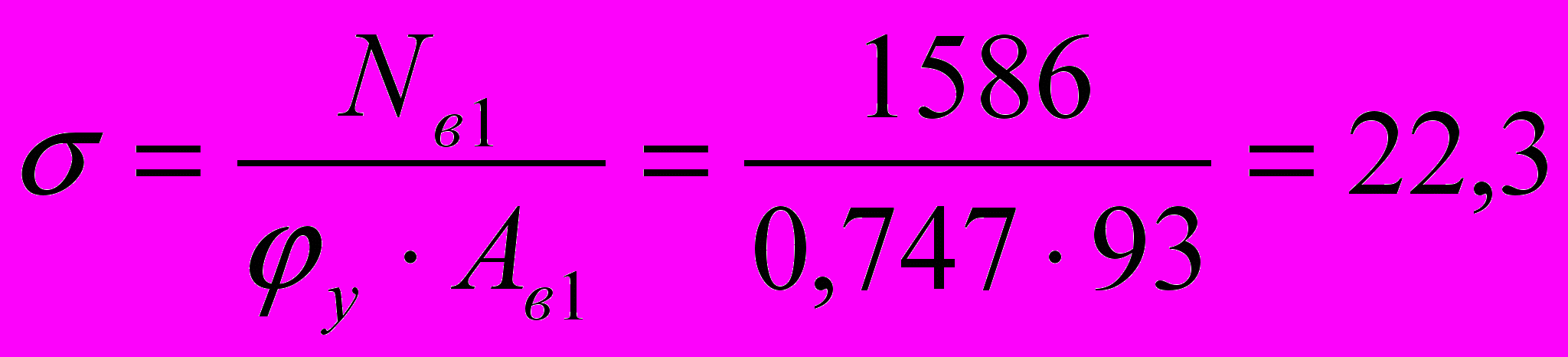кН/см² < R=23 кН/см².


Наружняя ветвь: _y=l_y/i_y=1485/2,5=72,1 следовательно _y=,75. =N_в2/(_yA_в2)=337/(,75168,8)=22,8 кН/см² < R=23 кН/см².

Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы олределяем требуемое расстояние между узлами решетки: _x1=l_в1/i_x1=_y=74,25; отсюда l_в1=74,25i_x1=61,734,2=31, см, принимаем l_в1=281 см, раз­делив нижнюю часть колонны на целое число панелей n=5. (1485-7-1=145; 145/5=281)

Проверяем устойчивость ветвей в плоскости рамы (относительно осей x₁-x₁ и х₂-х₂):

- для подкрановой ветви _х1=281/4,2=66,9, следовательно _х=,78.


=N_в1/(A_в1)=1579/(,7893)=21,8 кН/см² < R=23 кН/см².


- для наружней ветви _х2=281/7=4, следовательно _х=,89.


=N_в2/(A_в2)=337/(,89168,8)=2,3 кН/см² < R=23 кН/см².


5.4.2 Расчет решетки подкрановой части колонны.


Поперечная сила в сечении колонны Q_max=177,32 кН; Q_усл=,2А=,2х х(93+168,8)=52,3 кН < Q_max, расчет решетки проводим на Q_max.

Усилия сжатия в раскосе: N_R=Q_max/2sin=177,32/2,665=134, кН, где sin=h_н/l_р=125/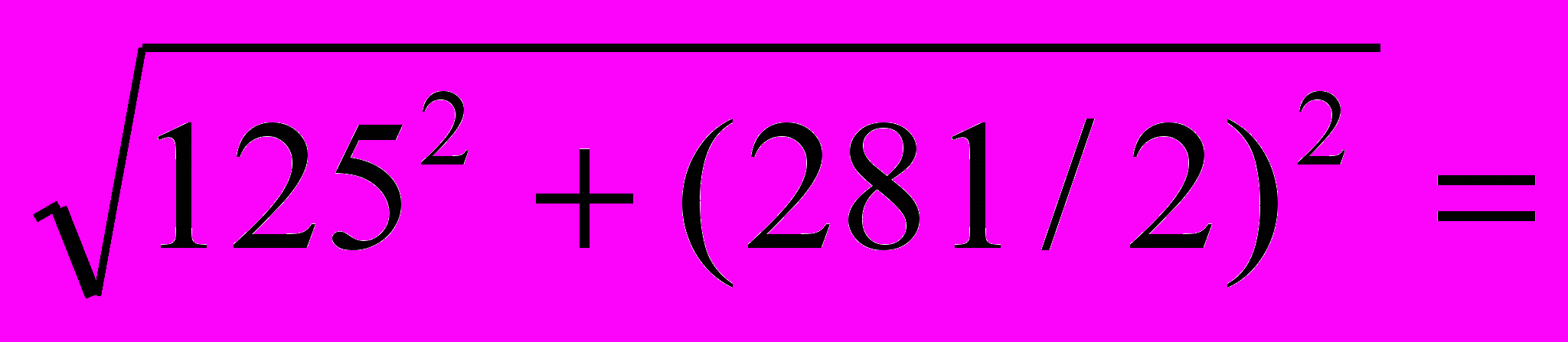,665, 41 - угол наклона раскоса. За­да­ем­ся _р=1 следовательно =,55.

Требуемая площадь раскоса: A_р.тр.=N_R/R=134,/(,5523,75)= =14,1 см². По сортаменту принимаем равнополочный уголок 9х9 с А_р= =15,6 см², i_min=1,77 см.

Проверка напряжения в раскосе: _max=l_р/i_min=189/1,77=16, следова­тель­но =,52, где l_р=h_н/sin=125/,665=189 см.


