Конспект лекций для 16-и часового курса начертальная геометрия издание 2-ое
| Вид материала | Конспект |
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
- Конспект лекций по курсу Начертательная геометрия (для студентов заочной формы обучения, 1032.28kb.
- Конспект лекций 2010 г. Батычко Вл. Т. Муниципальное право. Конспект лекций. 2010, 2365.6kb.
- Конспект лекций 2008 г. Батычко В. Т. Административное право. Конспект лекций. 2008, 1389.57kb.
- Конспект лекций 2011 г. Батычко В. Т. Семейное право. Конспект лекций. 2011, 1718.16kb.
- Конспект лекций 2011 г. Батычко Вл. Т. Конституционное право зарубежных стран. Конспект, 2667.54kb.
- Конспект лекций 2010 г. Батычко В. Т. Уголовное право. Общая часть. Конспект лекций., 3144.81kb.
- Программа курса Конспект лекций > Тесты Задачи > Вопросы к экзамену Методические рекомендации, 1693.2kb.
- Конспект лекций Батычко Вик. Т таганрог 2011, 2102.18kb.
- Конспект лекций организация производства и маркетинг для студентов 3 курса специальностей, 2989.73kb.
6.ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕСКИХ ФИГУР
6.1.Параллельность прямых и плоскостей
Прямая параллельна плоскости, если она параллельна какой-либо прямой этой плоскости.
 |
| |
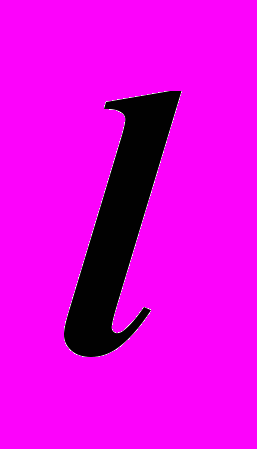 параллельна плоскости
параллельна плоскости  , так как она параллельна прямой
, так как она параллельна прямой 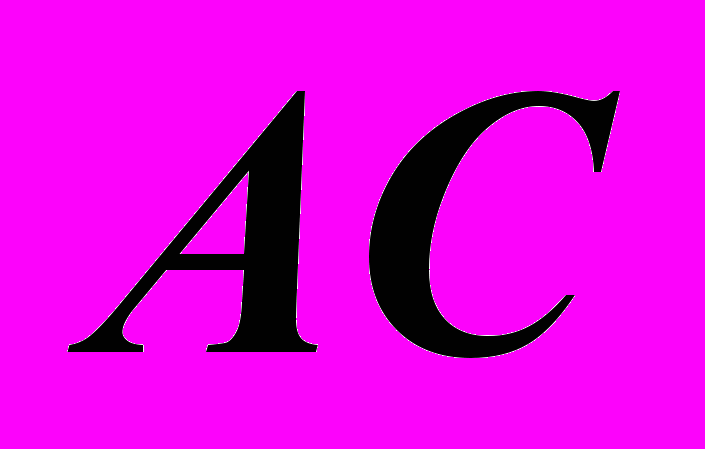 , принадлежащей этой плоскости.
, принадлежащей этой плоскости.Две плоскости параллельны, если две не параллельные прямые одной плоскости параллельны, соответственно, двум прямым другой плоскости.
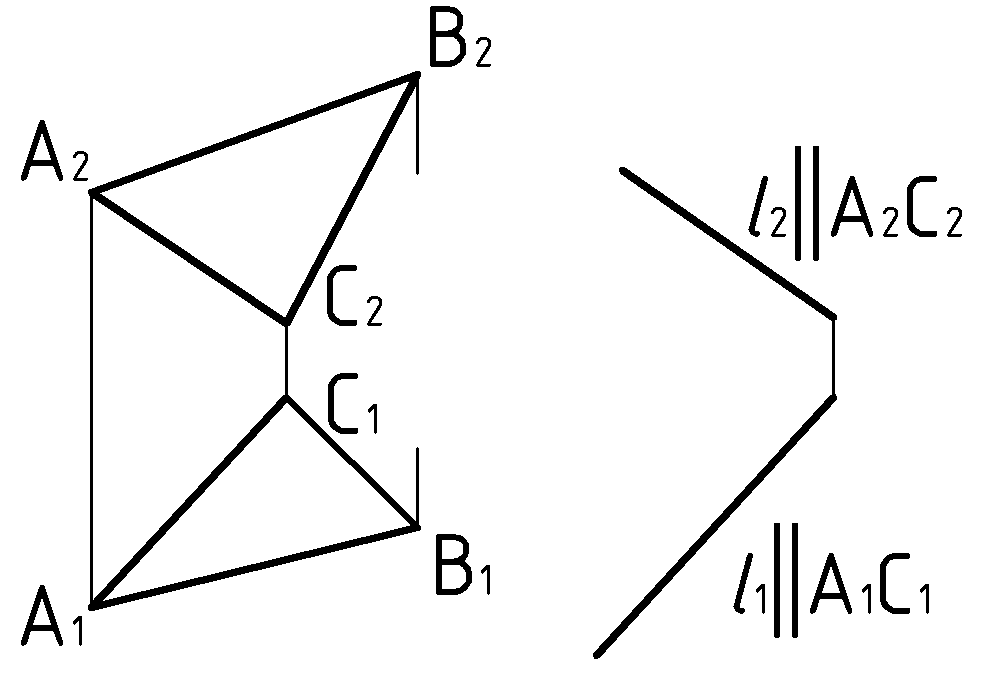
Пример (Рис.61). Задать плоскость
 , параллельную плоскости
, параллельную плоскости 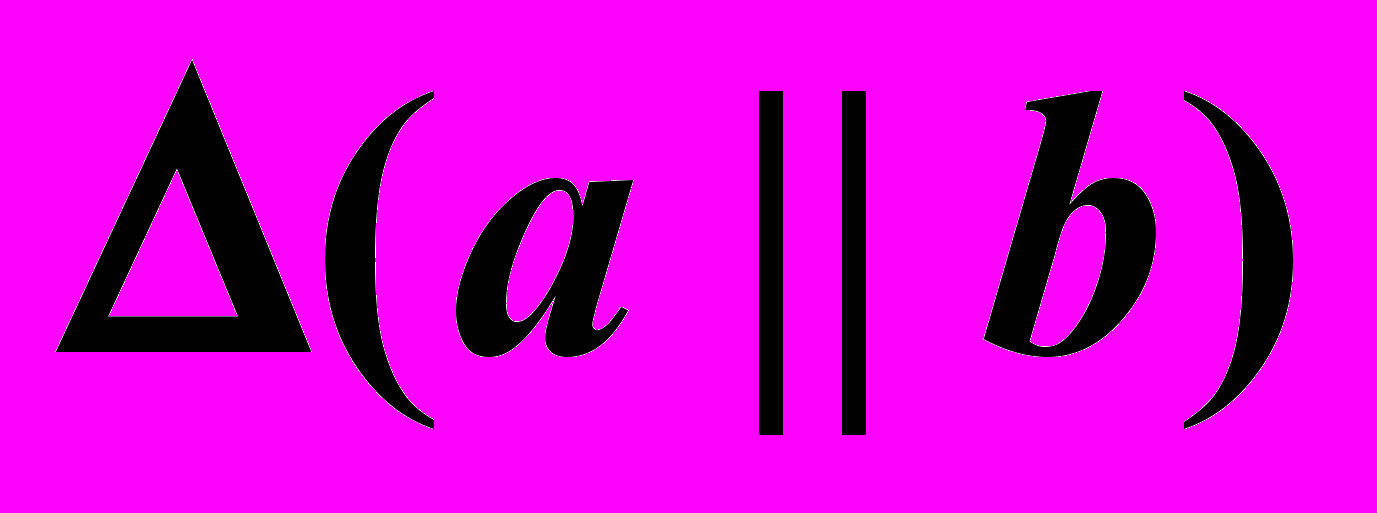 .
. Искомую плоскость зададим двумя пересекающимися прямыми, которые параллельны, соответственно, прямым, задающим плоскость
 и дополительной прямой “
и дополительной прямой “ ” на этой же плоскости.
” на этой же плоскости. 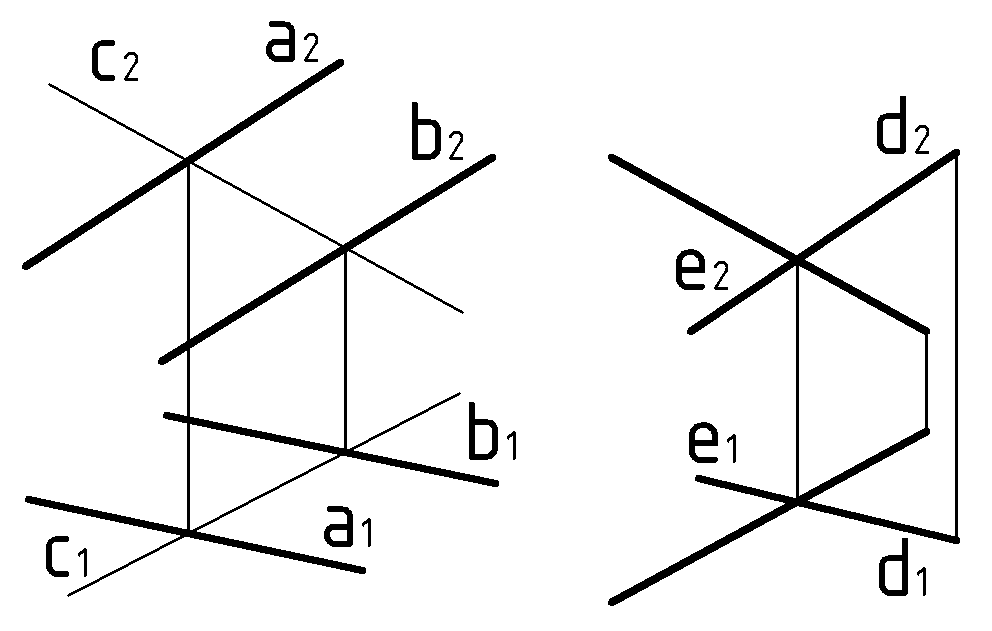 |
| |
| Дано: 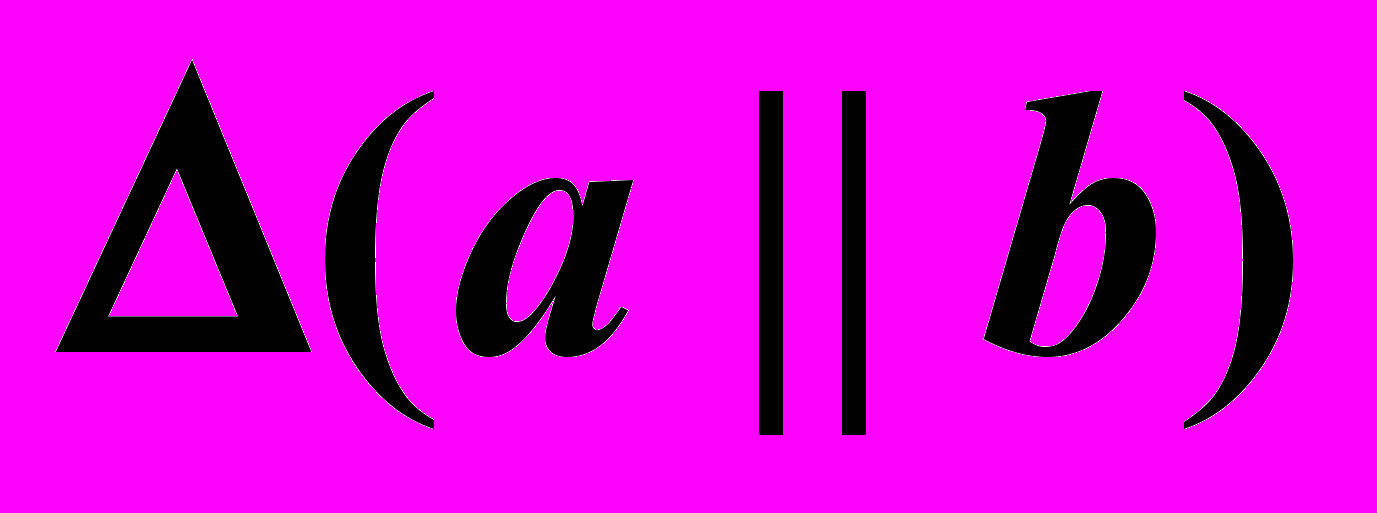 . . | Решение: 1). 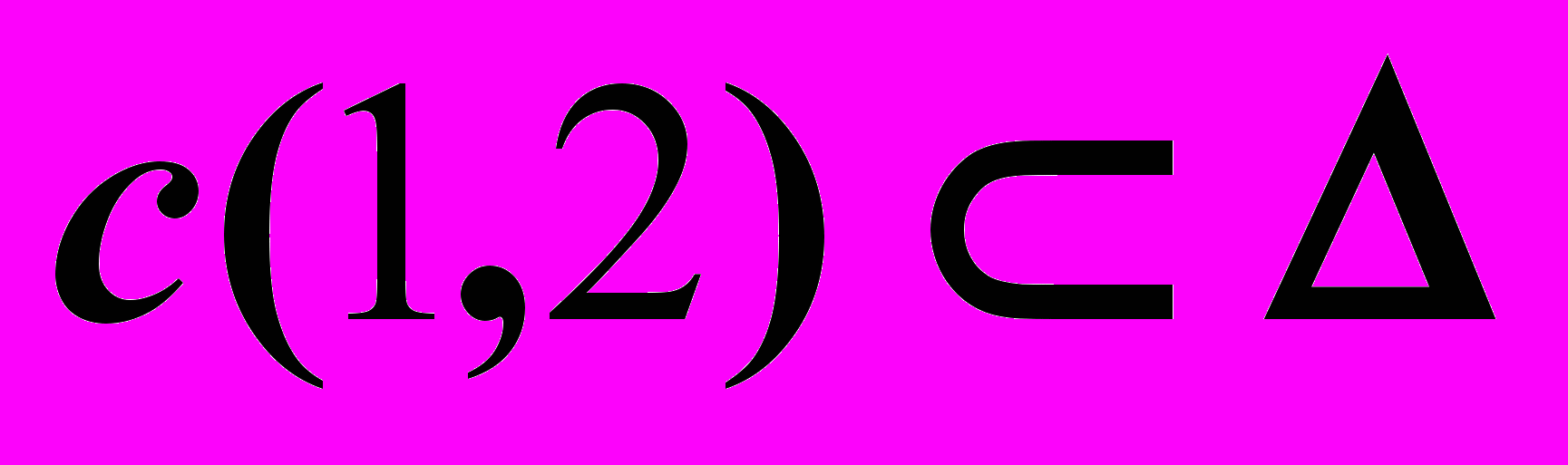 . .2). 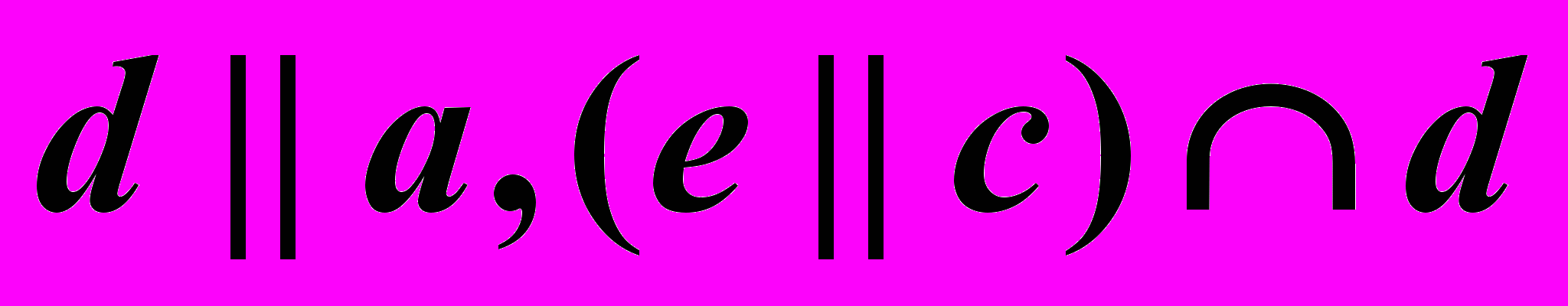 3).  . . |
| ?: 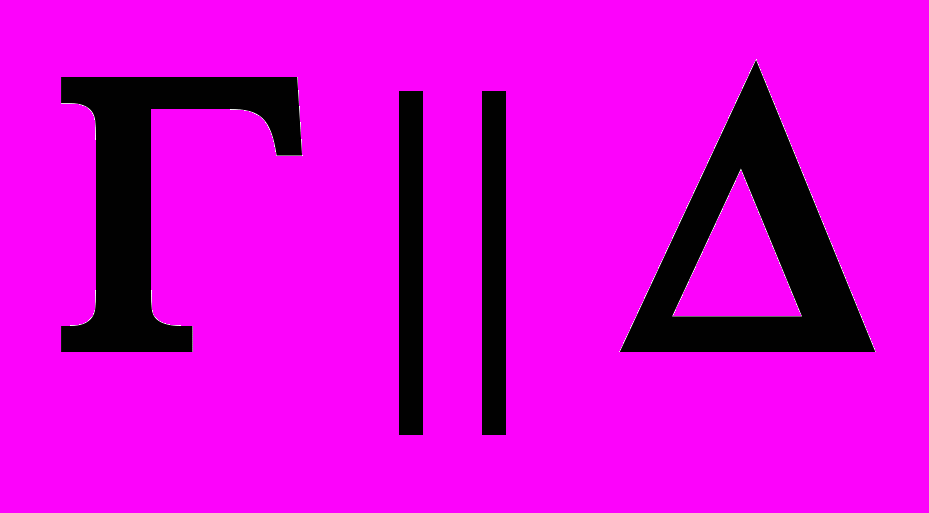 . . |
6.2.Общие понятия перпендикулярности.
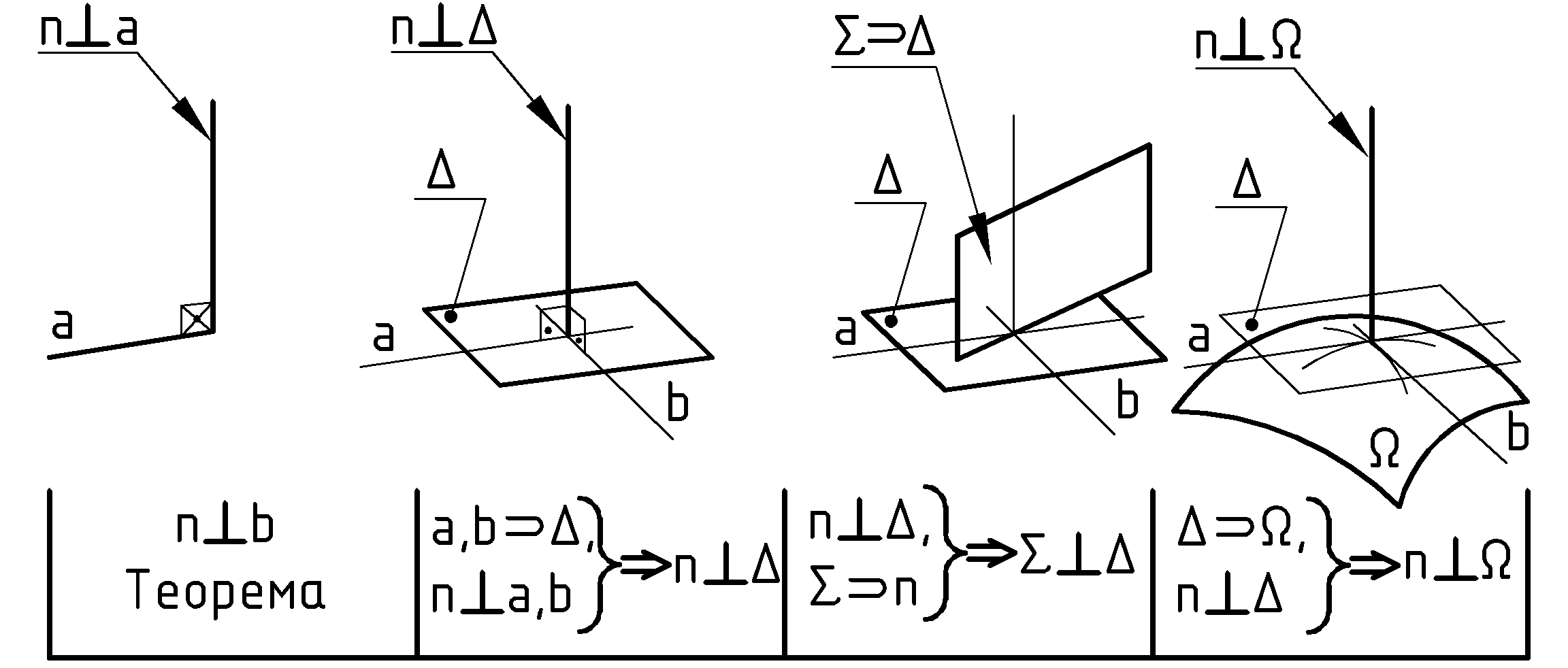
Задачи на перпендикулярность – логически взаимно связаны. От плоского прямого угла до нормали к криволинейной поверхности (Рис.62). Без теоремы о проецировании прямого угла не построить перпендикуляр к плоскости. Тем более – не решить задачу для взаимно перпендикулярных плоскостей и не построить на чертеже нормаль к криволинейной поверхности.
 |
| |
По теореме о проецировании прямого угла следует, что прямой угол проецируется без искажения, если одна сторона параллельна плоскости проекций, а вторая – не перпендикулярна к ней.
 |
| |
 ,
, 
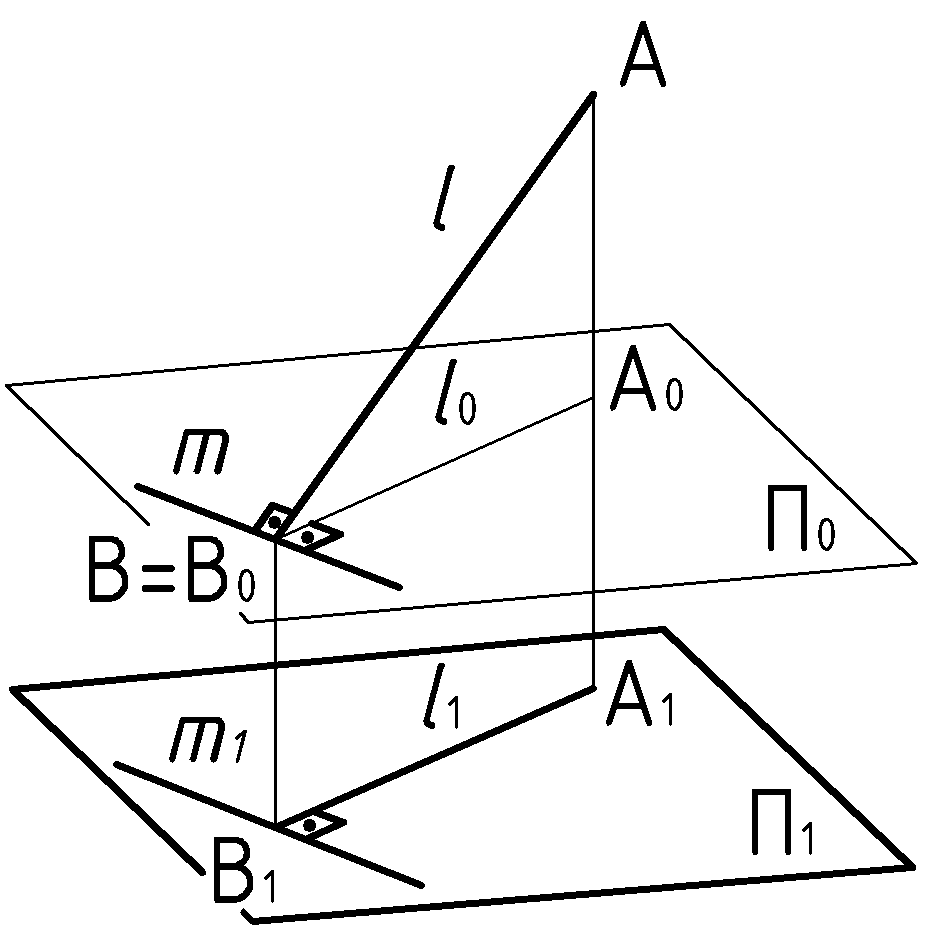
Введем на рисунке плоскость проекций П1, параллельную П0 и доказательство теоремы о проецировании прямого угла станет очевидным:
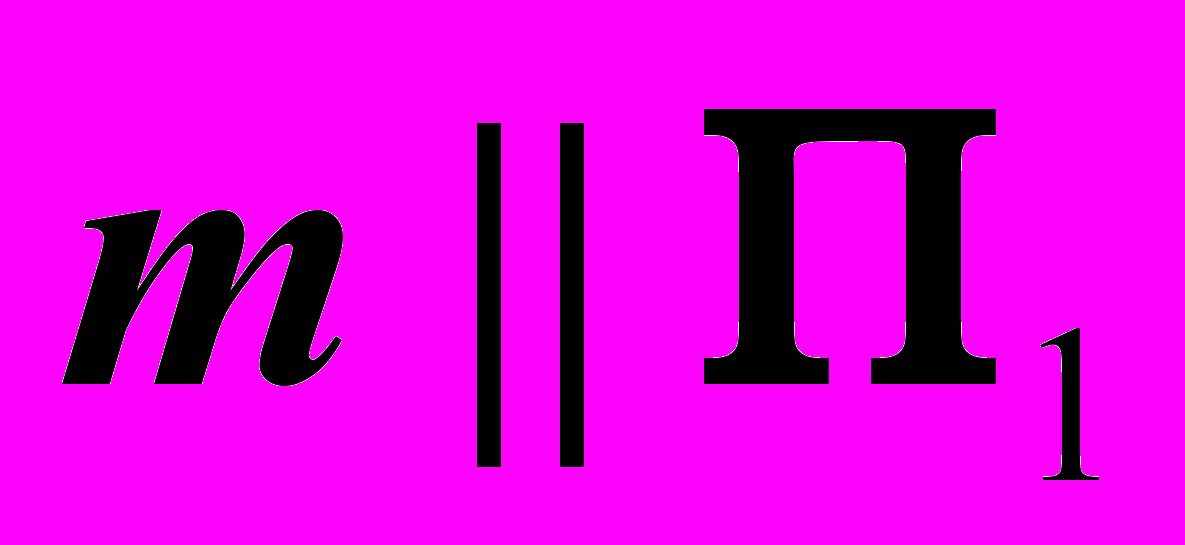 ,
, 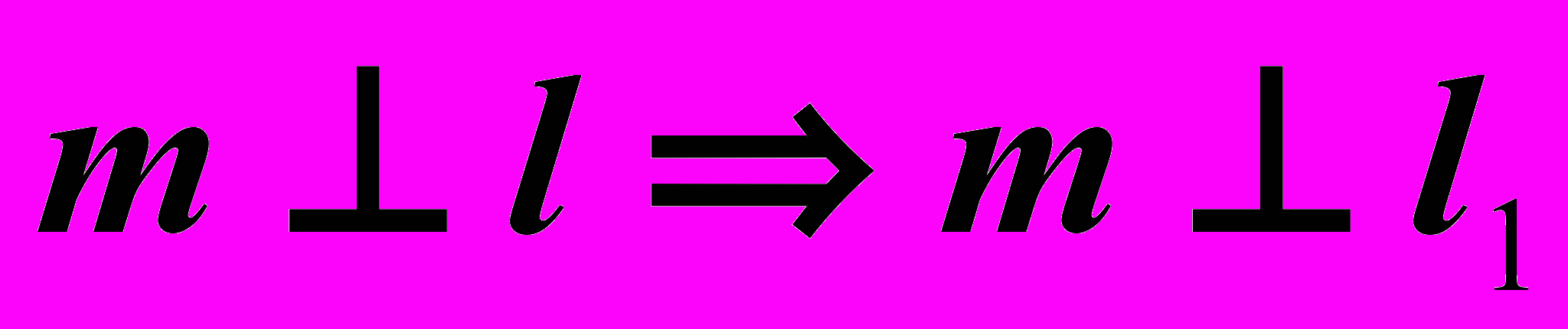
6.3.Перпендикулярность прямых и плоскостей.
 |
| |
 и
и  . И провести перпендикуляры к линии
. И провести перпендикуляры к линии 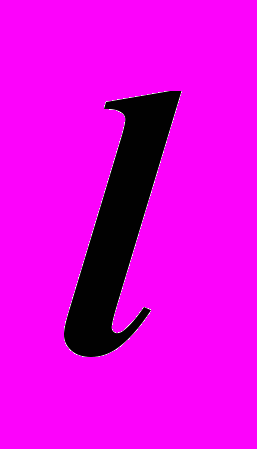 .
.Через любую точку в пространстве можно провести бесконечное число прямых, пересекающих линию
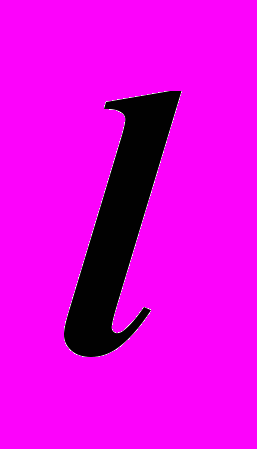 или скрещивающихся с ней под прямым углом. Но не все прямые, углы проецируются без искажения. Поэтому для проведения перпендикуляров предпочтительно задавать линии уровня.
или скрещивающихся с ней под прямым углом. Но не все прямые, углы проецируются без искажения. Поэтому для проведения перпендикуляров предпочтительно задавать линии уровня.| Решение: 1). 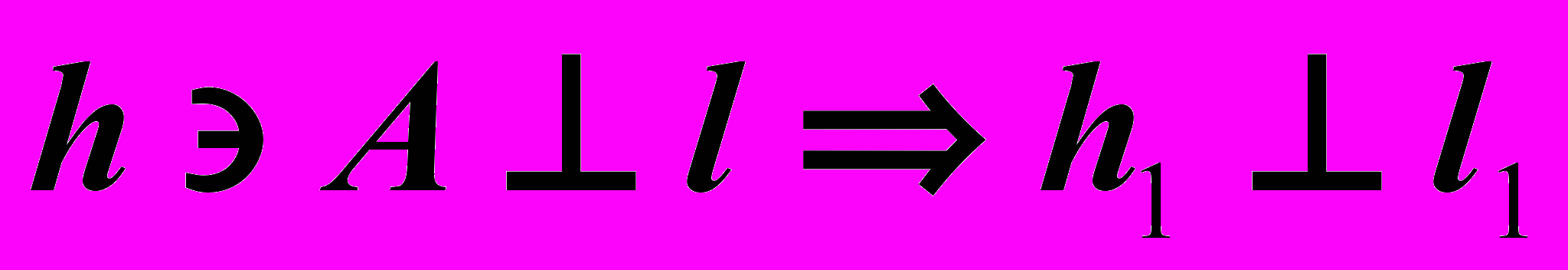 , , | 2). (f  B) B)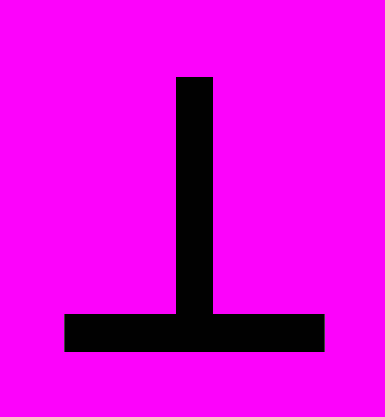 l l f2 f2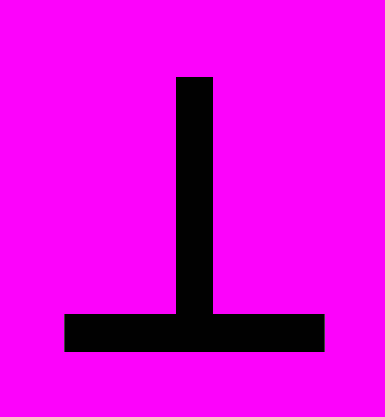 l2 l2 |
Для прямой, перпендикулярной к плоскости, дадим поэтапно три определения: общее для пространства, в принципе применимое для комплексного чертежа и практически применимое для выполнения графических построений:
1) Прямая перпендикулярна к плоскости, если она перпендикулярна к двум не параллельным прямым этой плоскости.
2) Прямая перпендикулярна к плоскости, если она перпендикулярна (в частности) к двум линиям уровня на этой плоскости.
3) Прямая перпендикулярна к плоскости, если горизонтальная проекция прямой перпендикулярна к горизонтальной проекции горизонтали этой плоскости, а фронтальная проекция прямой- перпендикулярна к фронтальной проекцией фронтали. (Используются любые пары изображения перпендикуляра и с профильной проекцией. Тогда профильная проекция прямой перпендикулярна к профильной прямой плоскости).
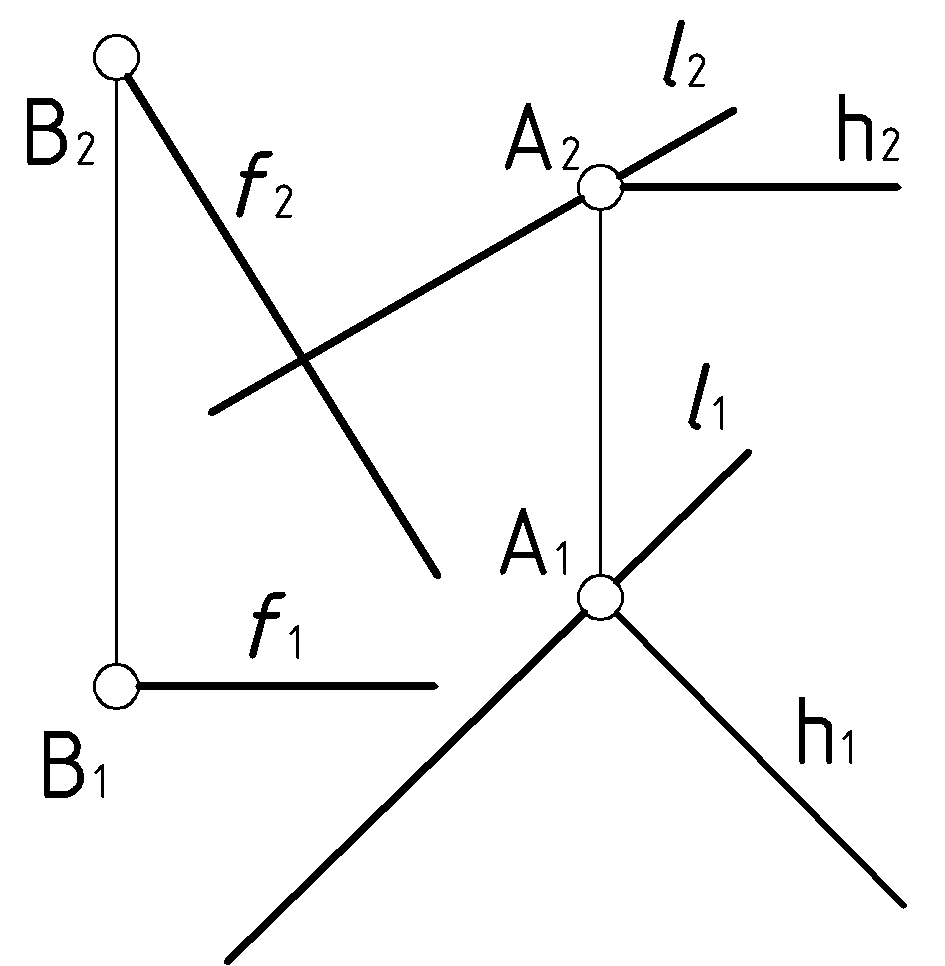
Пример 2 (Рис.65). Через точку
 провести перпендикулярную к плоскости
провести перпендикулярную к плоскости 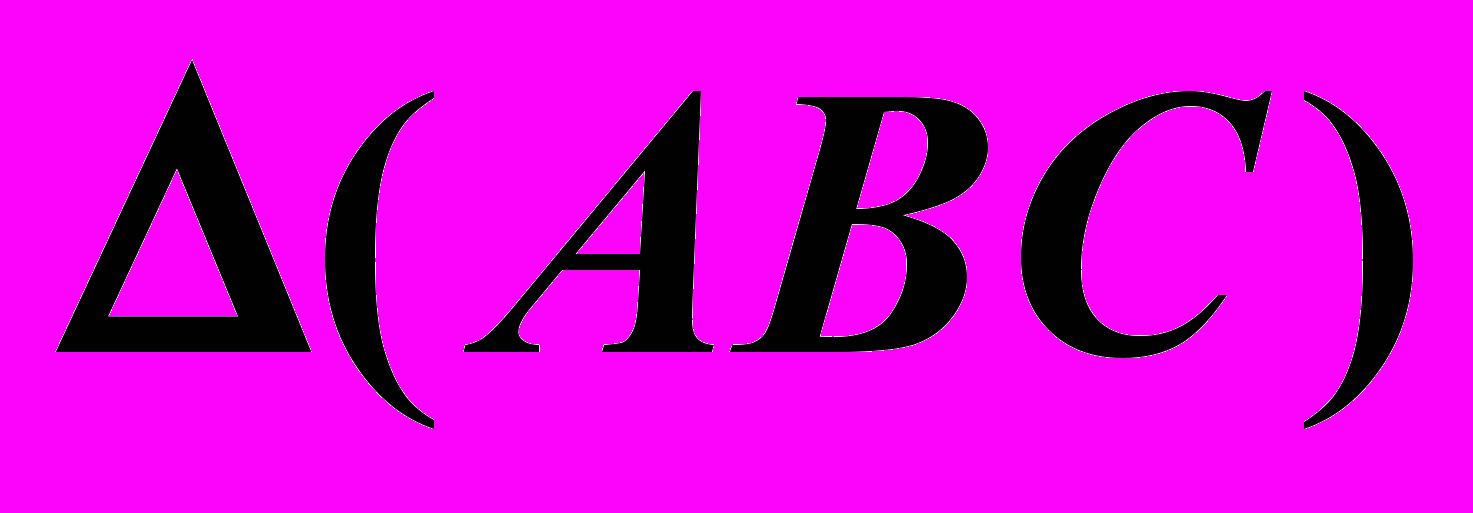 .
. 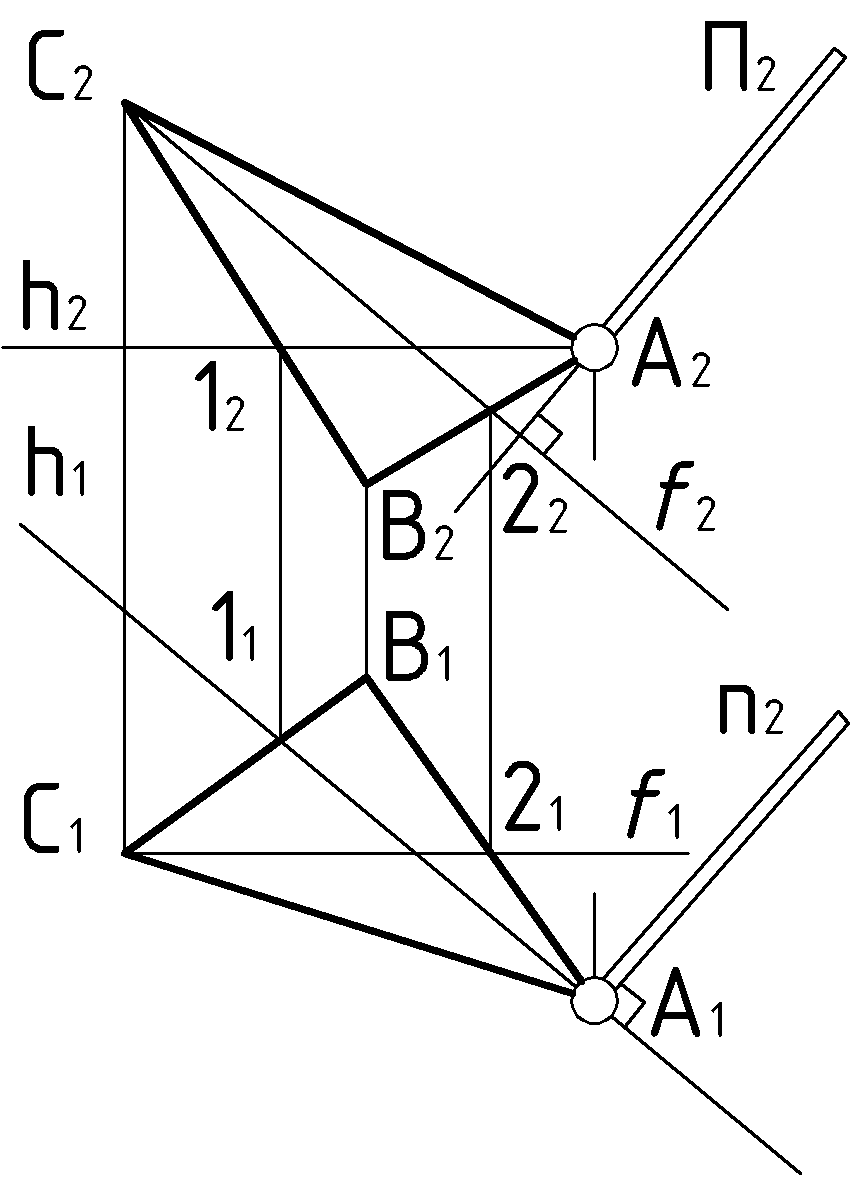 |
| |
| Дано: 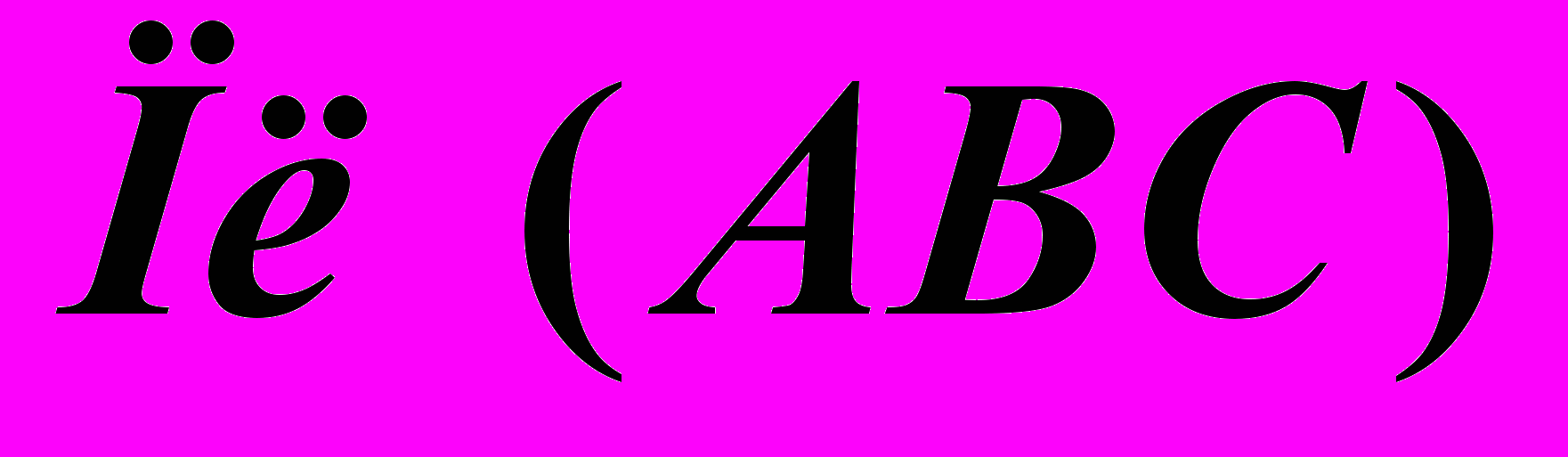 . . | Решение: 1).  , ,2). 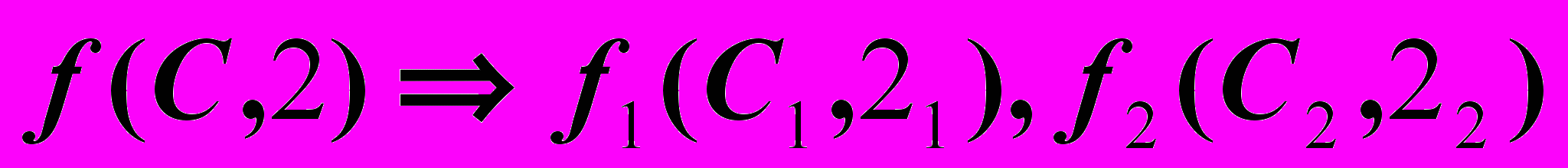 , ,3).  |
| ?: (n  A) A) 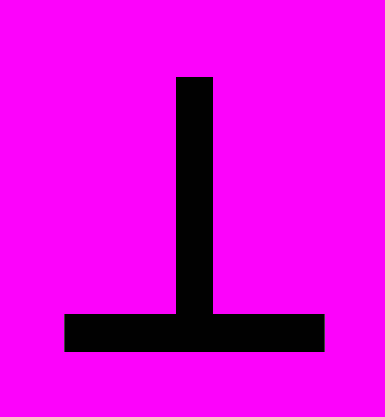 ∆. ∆. |
Пример 3 (Рис.66). Через точку
 провести плоскость, перпендикулярную к плоскости
провести плоскость, перпендикулярную к плоскости  .
. 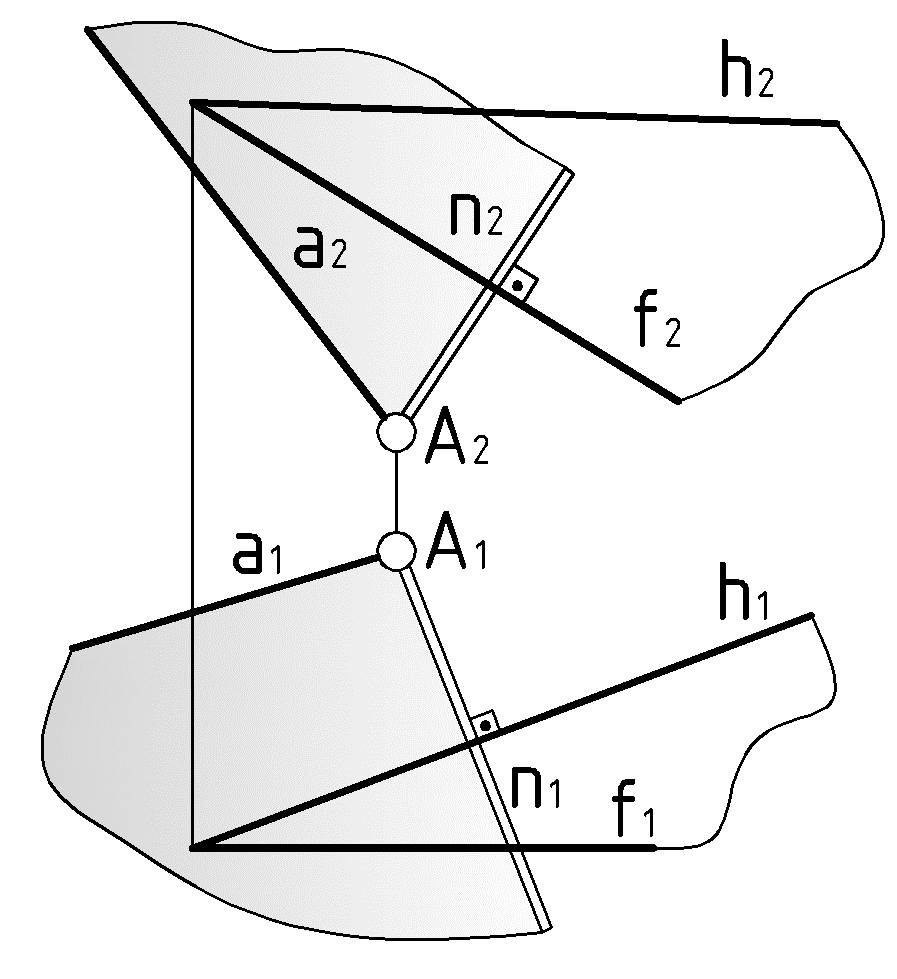 |
| |
| Дано:  | Решение: 1).  – произвольная прямая, – произвольная прямая,2).  , ,3).  . . |
| ?: 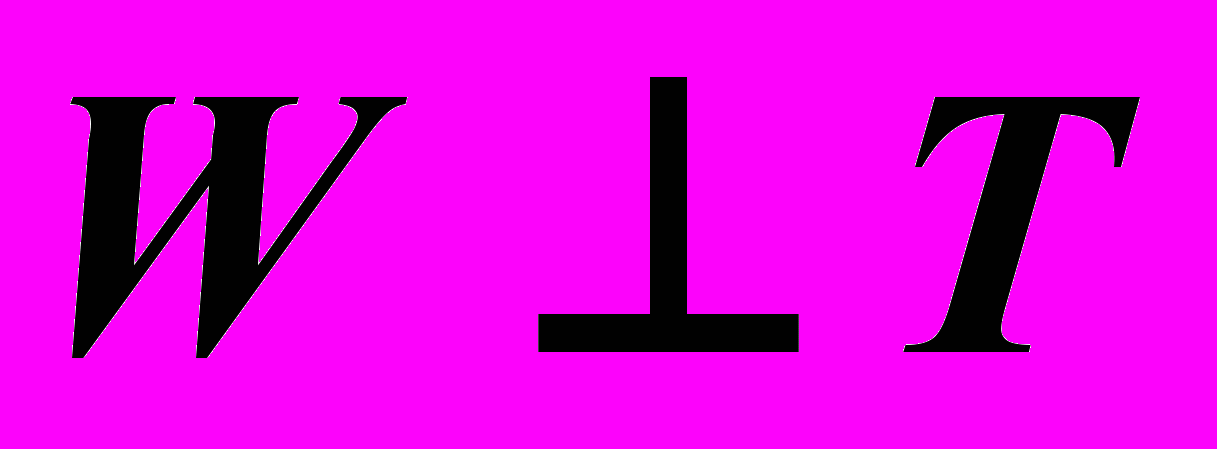 . . |
