Конспект лекций для 16-и часового курса начертальная геометрия издание 2-ое
| Вид материала | Конспект |
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
- Конспект лекций по курсу Начертательная геометрия (для студентов заочной формы обучения, 1032.28kb.
- Конспект лекций 2010 г. Батычко Вл. Т. Муниципальное право. Конспект лекций. 2010, 2365.6kb.
- Конспект лекций 2008 г. Батычко В. Т. Административное право. Конспект лекций. 2008, 1389.57kb.
- Конспект лекций 2011 г. Батычко В. Т. Семейное право. Конспект лекций. 2011, 1718.16kb.
- Конспект лекций 2011 г. Батычко Вл. Т. Конституционное право зарубежных стран. Конспект, 2667.54kb.
- Конспект лекций 2010 г. Батычко В. Т. Уголовное право. Общая часть. Конспект лекций., 3144.81kb.
- Программа курса Конспект лекций > Тесты Задачи > Вопросы к экзамену Методические рекомендации, 1693.2kb.
- Конспект лекций Батычко Вик. Т таганрог 2011, 2102.18kb.
- Конспект лекций организация производства и маркетинг для студентов 3 курса специальностей, 2989.73kb.
4.3.Конические сечения
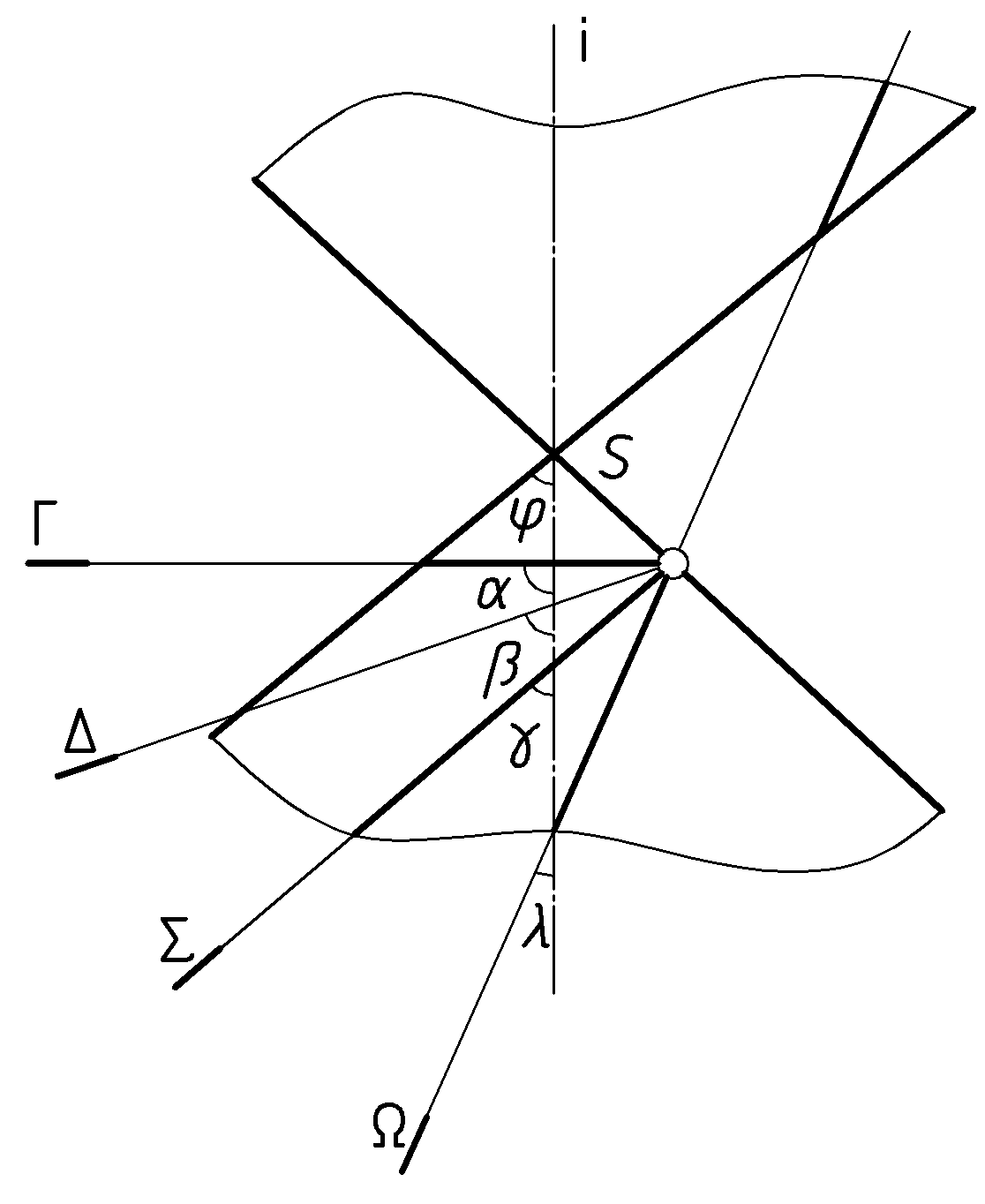 |
| |
Если
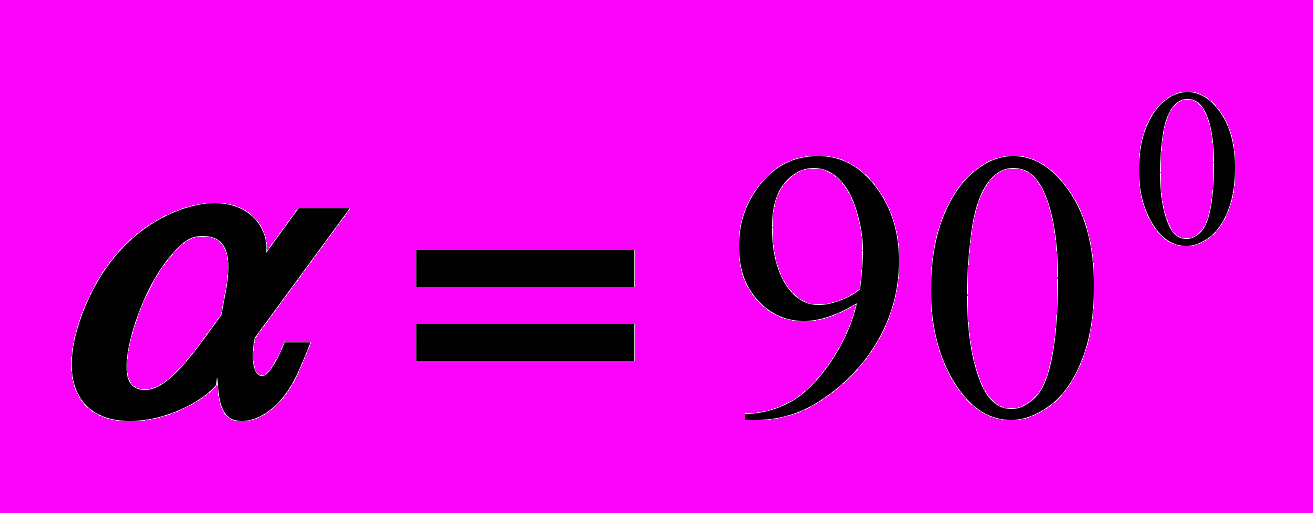 , то – окружность,
, то – окружность, Если
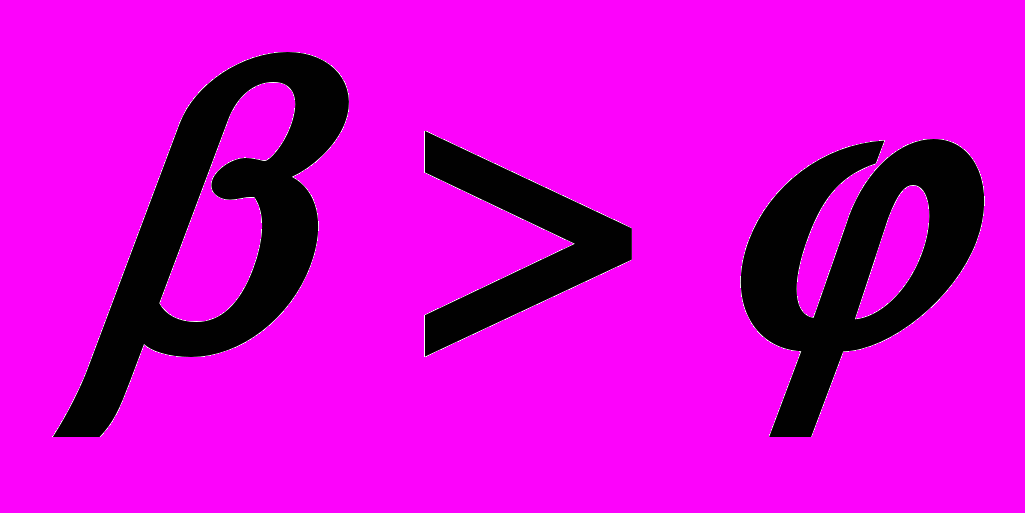 , то – эллипс,
, то – эллипс,Если
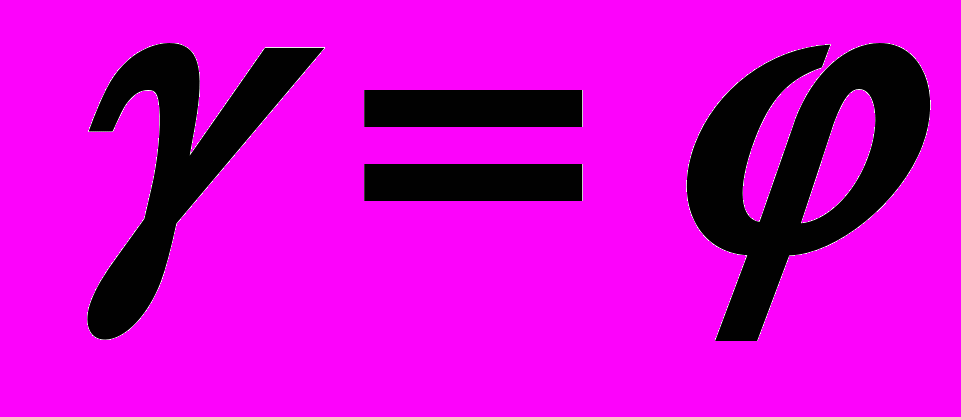 , то – парабола,
, то – парабола,Если
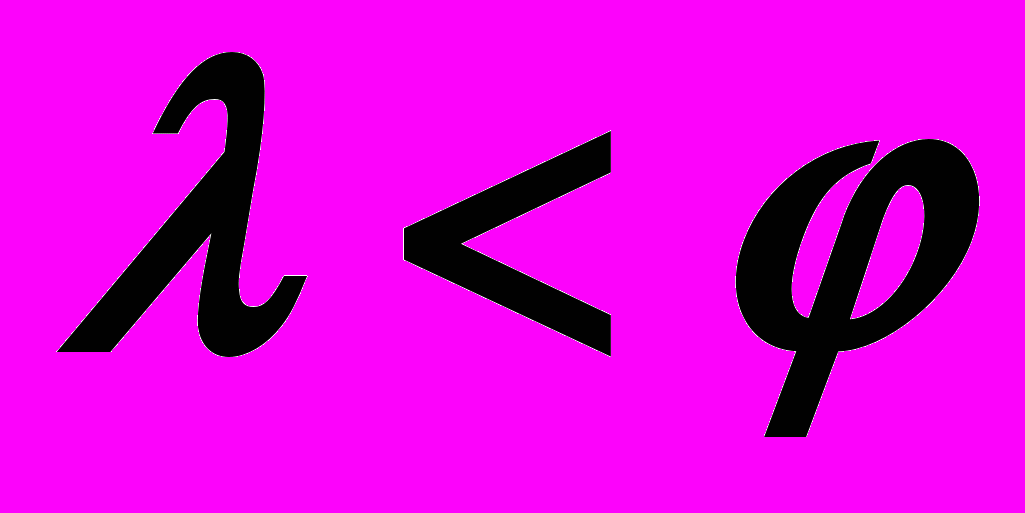 , то – гипербола.
, то – гипербола.4.4.Пересечение геометрических фигур с привлечением посредников
Сложнее решаются задачи на пересечение геометрических фигур, если ни одна из них не является проецирующей. В таких случаях трудно обойтись без привлечения третьих участников пересечения – так называемых посредников. В виде проецирующих секущих плоскостей или секущих сфер, соосных с заданными поверхностями вращения. При этом, все разнообразие подобных задач решается на основе единого алгоритма, необходимый объем которого может быть максимально полным или практически доведенным до нуля.
Рассмотрим наиболее общий случай: пересечение криволинейных поверхностей, например,
 и
и  . ( Рис.41):
. ( Рис.41): 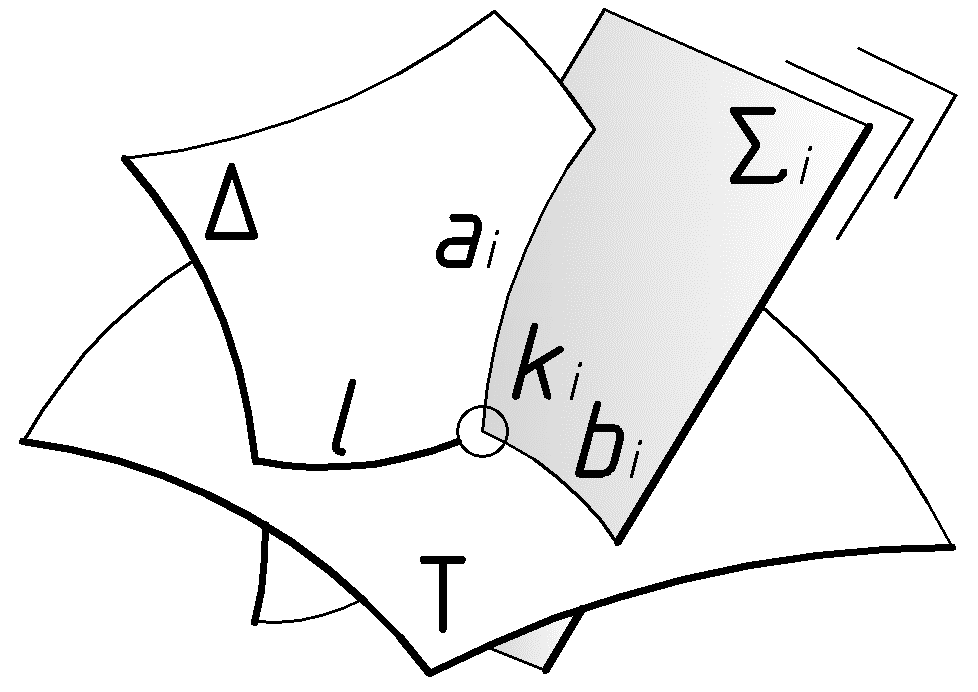 |
| |
 и
и  пересекаются по некоторой линии:
пересекаются по некоторой линии: 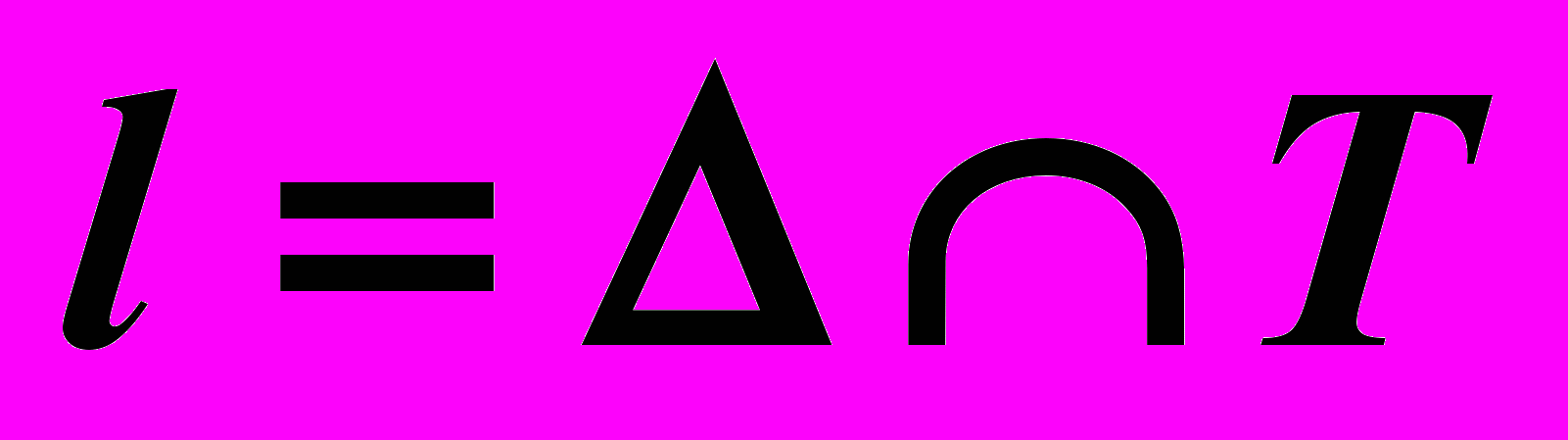 .
. 2). Всякая линия задается точками. Зададим линию ℓ в виде объединения n-ого количества текущих точек
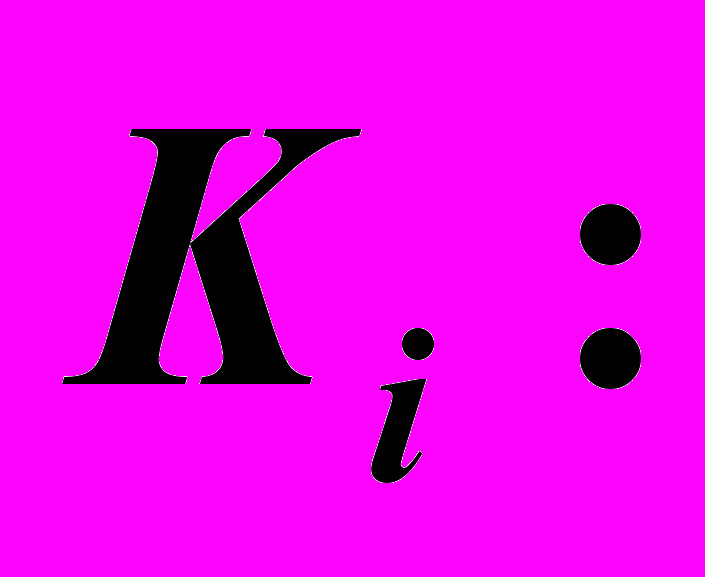
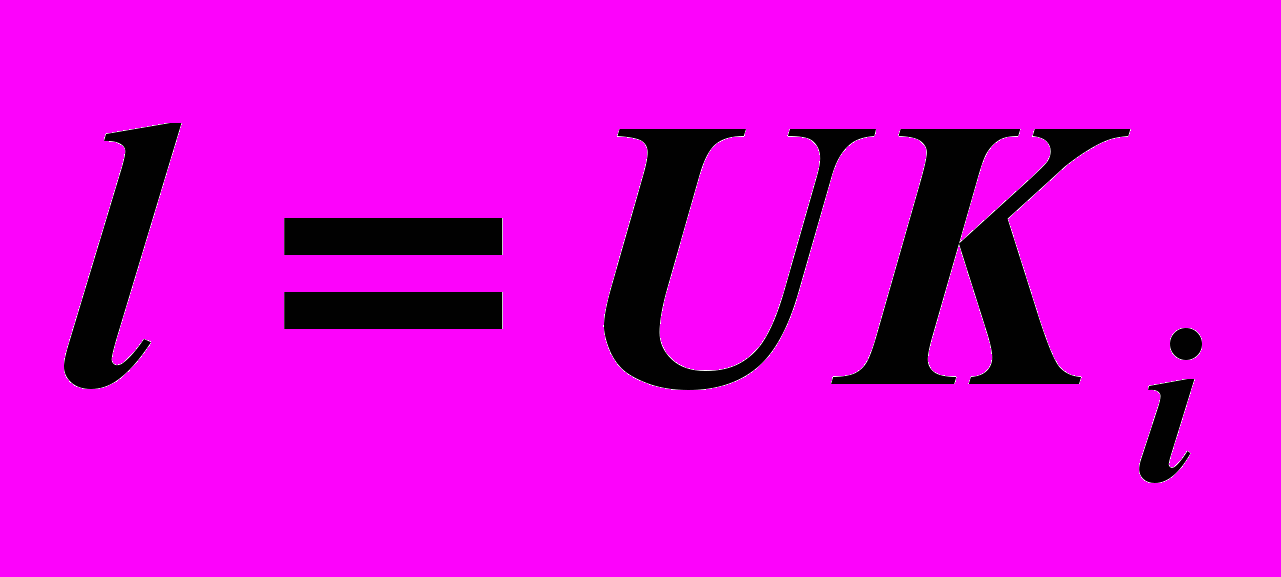 .
.3). Любая точка на чертеже должна быть задана двумя пересекающимися линиями. Пусть для текущей точки
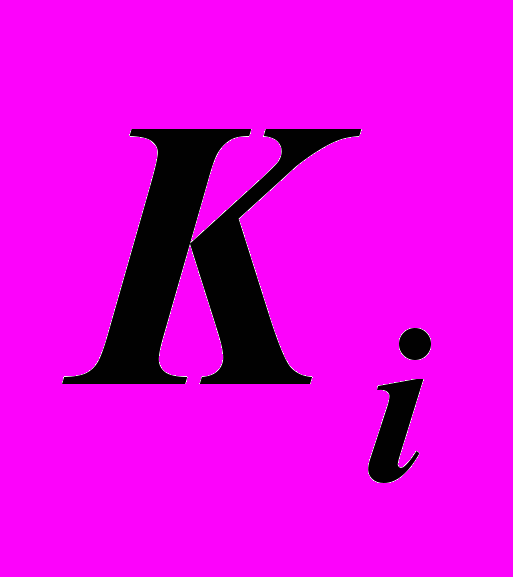 это будут две линии: одна на поверхности Δ, другая – на поверхности
это будут две линии: одна на поверхности Δ, другая – на поверхности 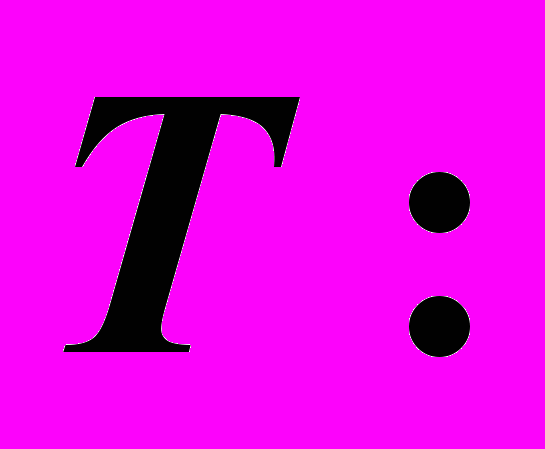
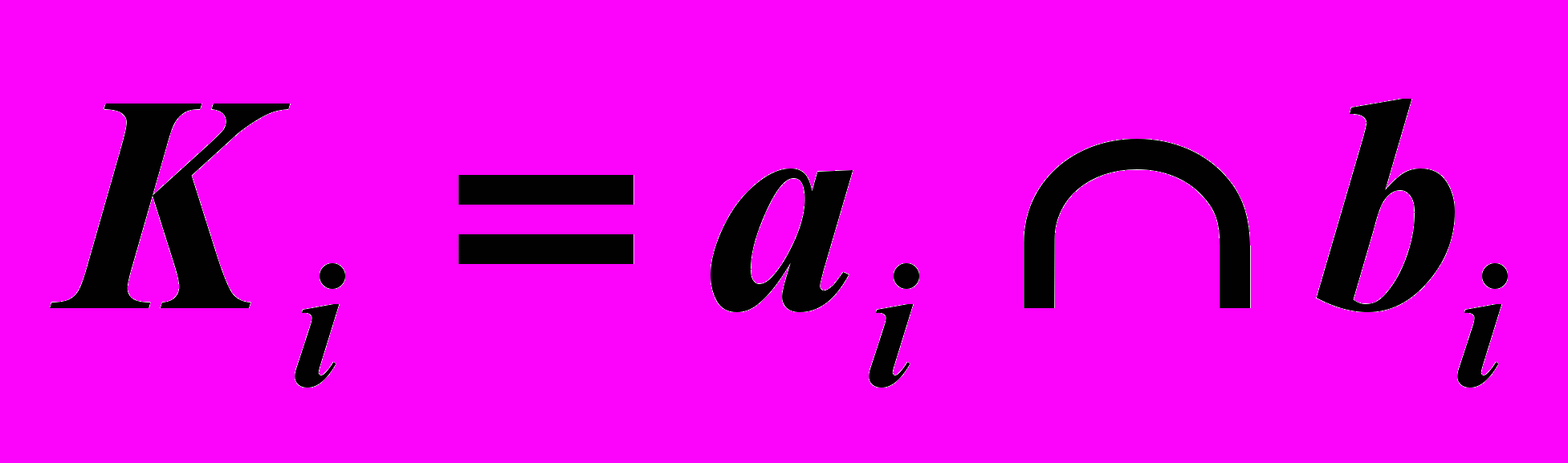
4). Посредник пересекает заданные поверхности по двум линиям, а линии пересекаются в точке, принадлежащей искомой линии пересечения поверхностей. То есть:
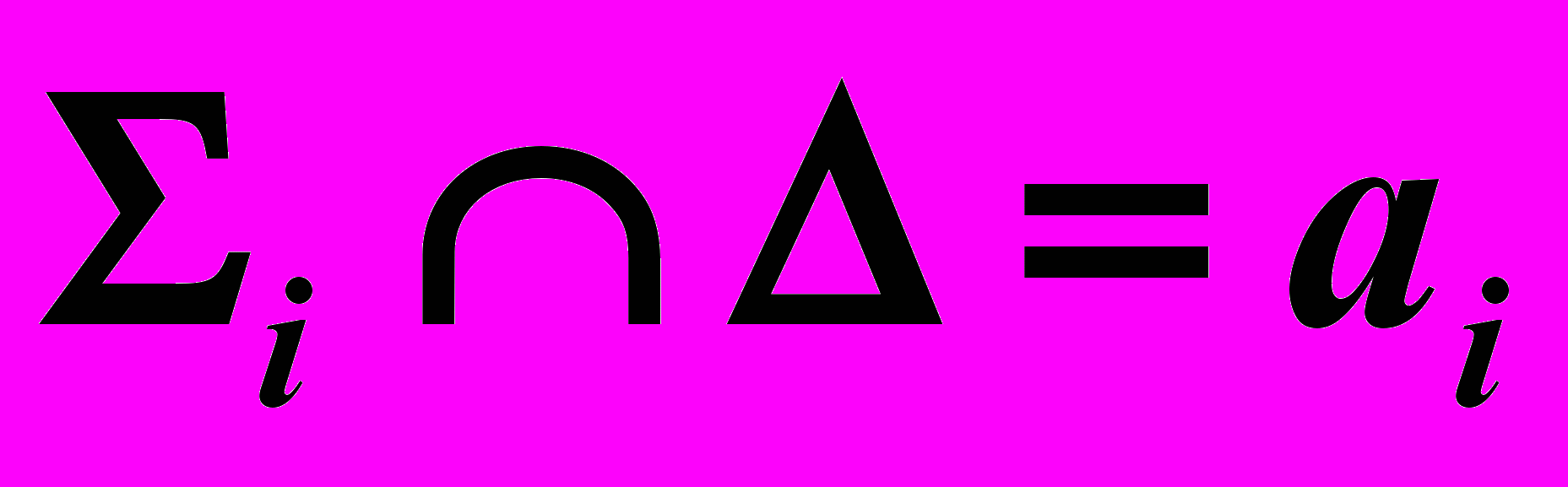 и
и 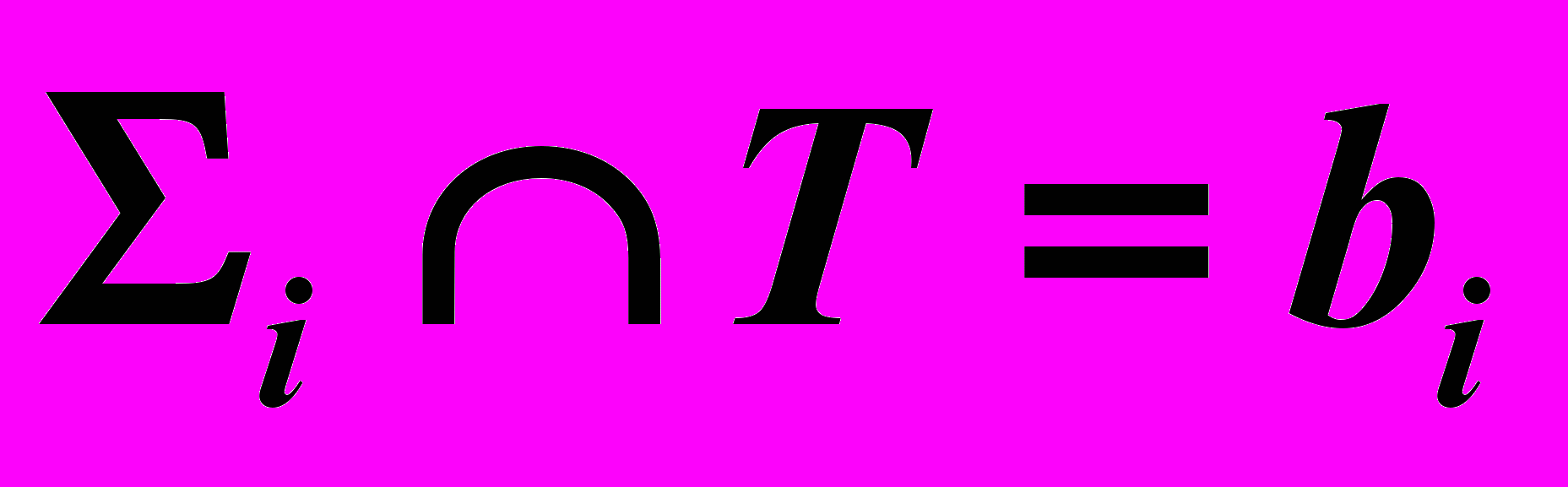 ,
, 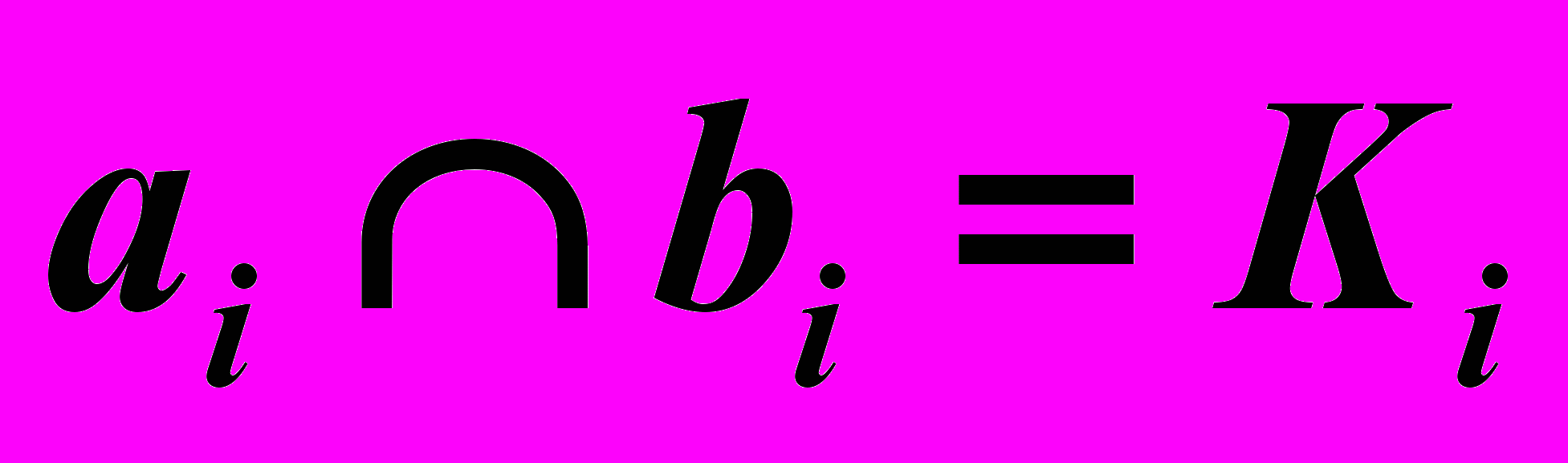 ,
, 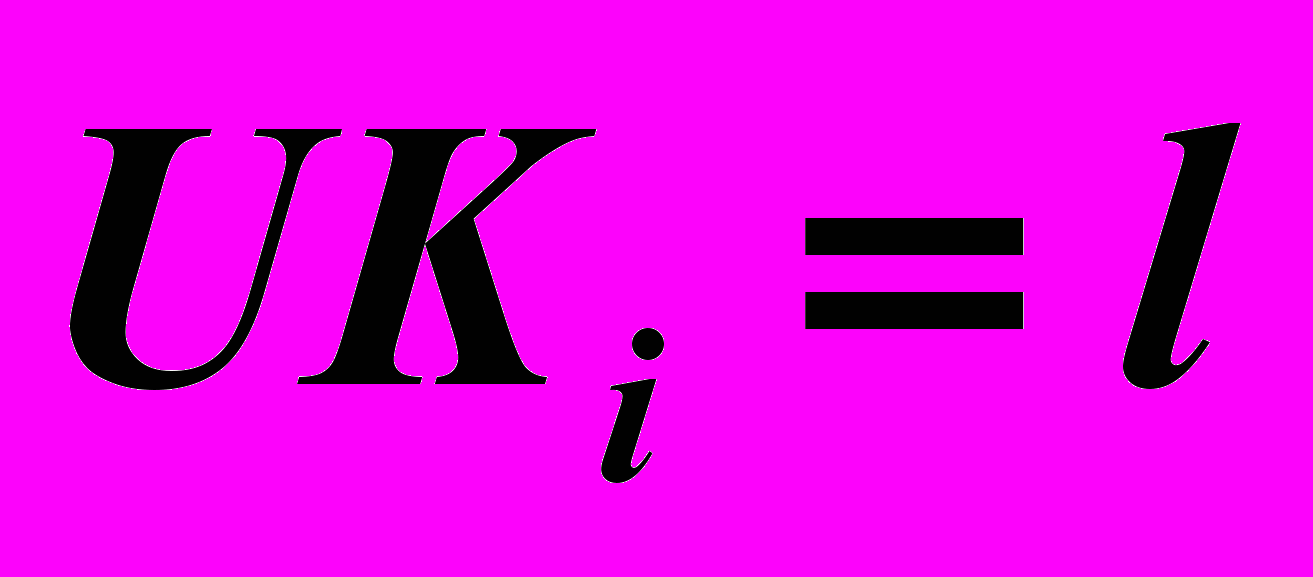 .
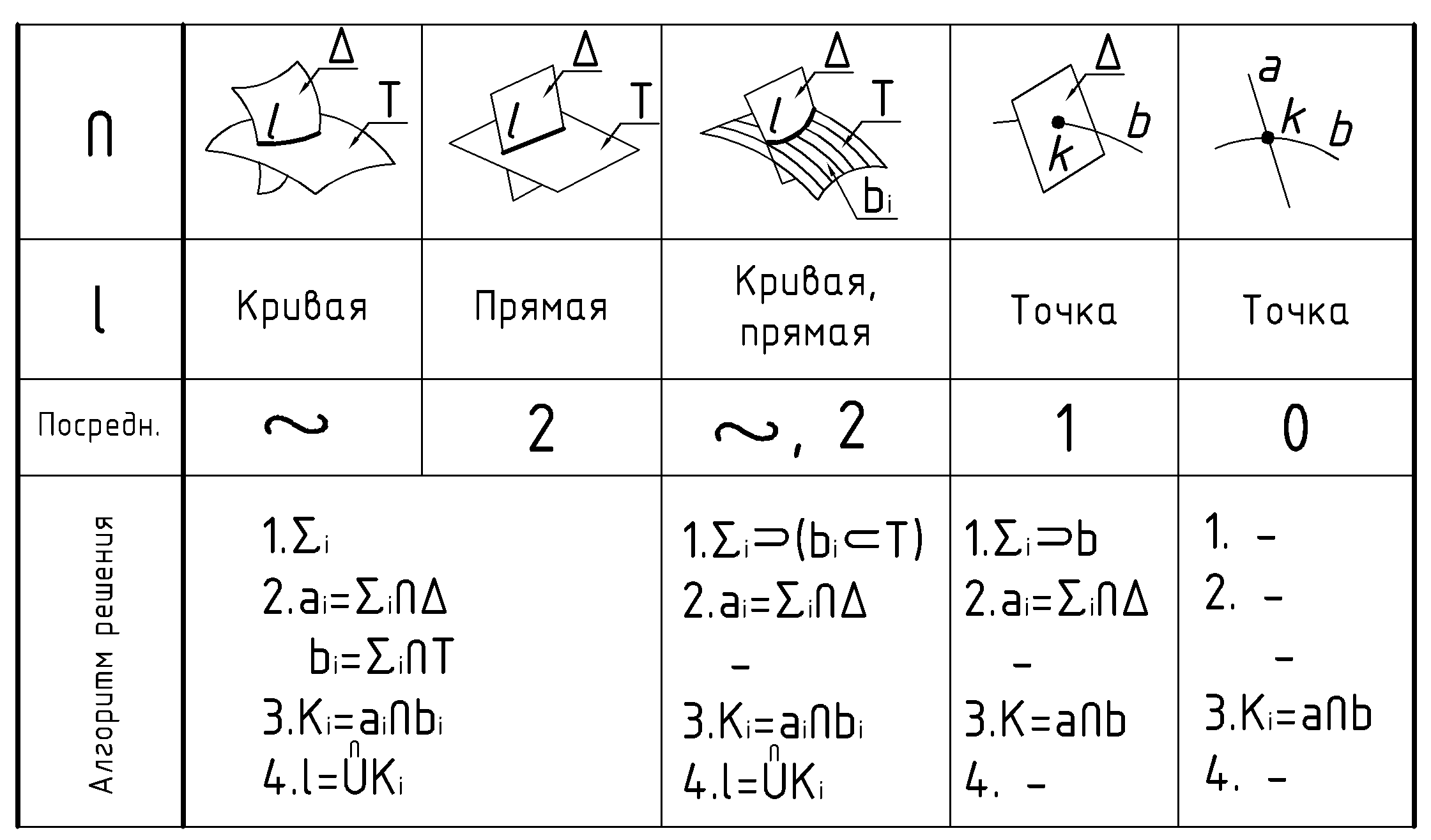
.Последняя череда рассуждений и отражает содержание алгоритма решения задач на пересечение геометрических фигур с привлечением посредников в полном объеме. От чего зависит объем алгоритма, показано на Рис.42.
Для плоскостей необходимо меньшее число посредников, чем для пересечения криволинейных поверхностей.
Если одна из фигур задается каркасом, то посредники следует проводить через его элементы. В этом случае алгоритм решения сокращается на одну позицию. Поскольку каждый элемент каркаса используется в качестве одной из двух вспомогательных линий.
При вырождении одной из поверхностей в линию алгоритм сокращается еще на одну строчку. Единственный посредник проводится через эту линию, которая играет теперь роль одной из двух вспомогательных линий. И еще. Поскольку результат пересечения – точка, то отпадает позиция объединения точек.
И, наконец, пересечение 2-х линий вообще не требует применения посредников. Роль вспомогательных линий играют сами пересекающиеся линии.
 |
| |
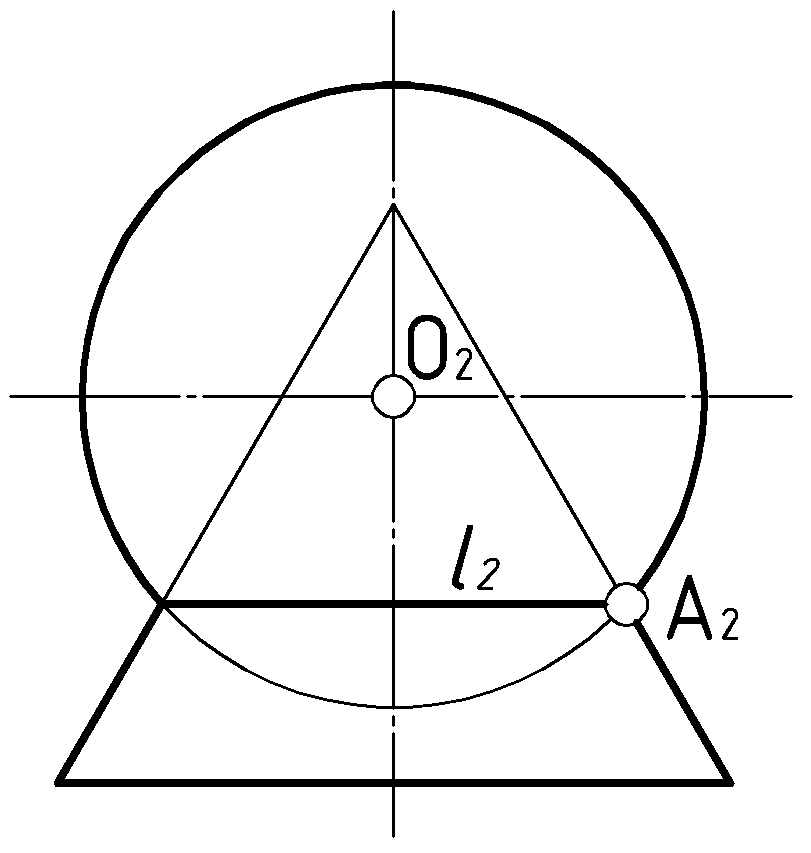
Каковы же требования к самим посредникам? Посредники выбираются из таких сообщений, чтобы они пересекали заданные поверхности с минимальным объемом графических построений. То есть пересекали поверхность по линиям с простыми проекциями:
 |
| |
Справедливость такого утверждения основана на теореме о пересечении соосных поверхностей вращения(Рис.43): “Соосные поверхности вращения пересекаются по окружности, поскольку любая общая для них точка
 при вращении образует общую для этих поверхностей окружность”. В частном положении окружность проецируется в простые линии.
при вращении образует общую для этих поверхностей окружность”. В частном положении окружность проецируется в простые линии.4.4.1.Метод проецирующих секущих плоскостей
Пример 1 (Рис.44). Построить точку пересечения прямой
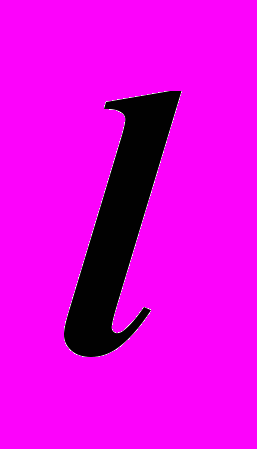 плоскостью
плоскостью 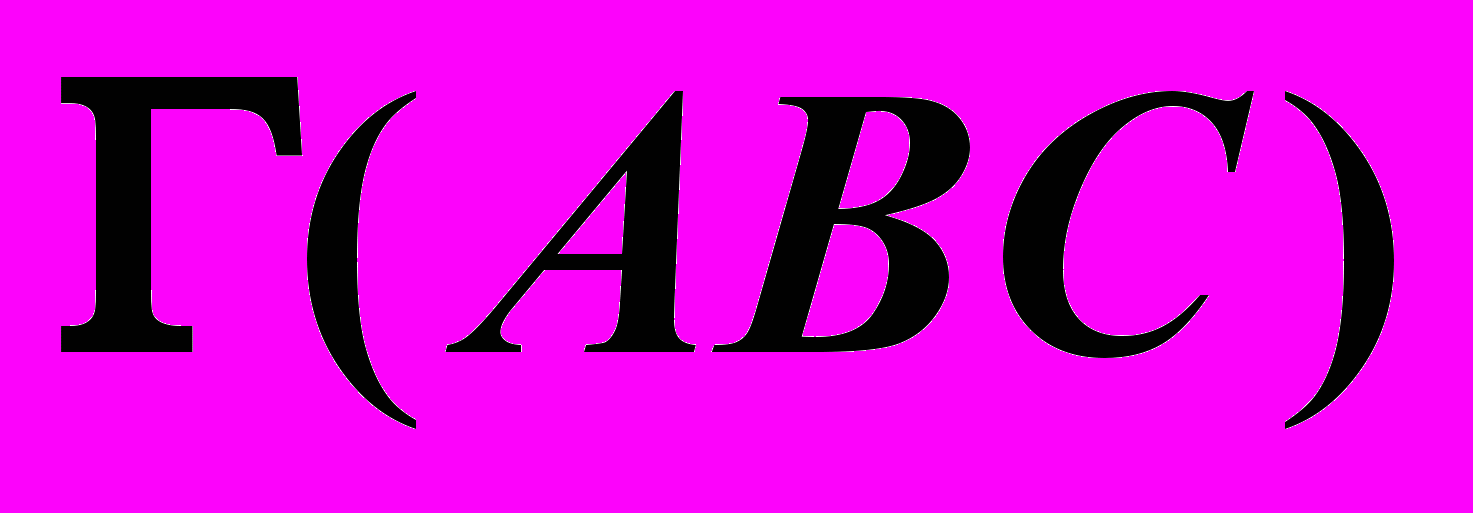 .
. 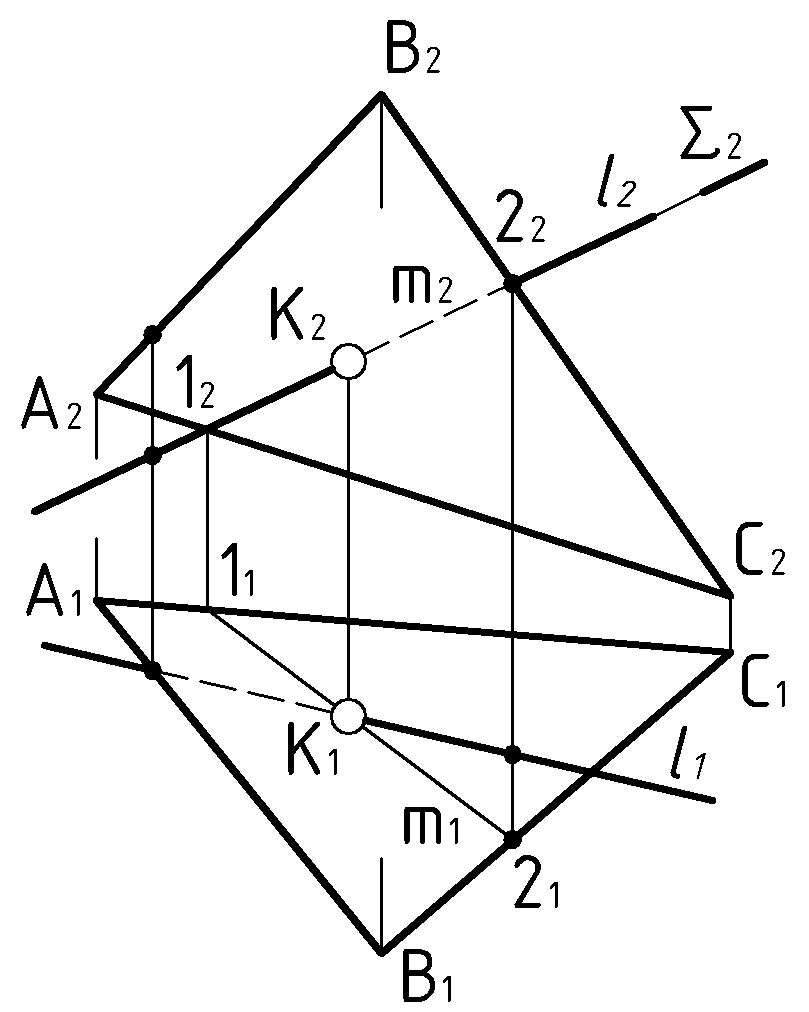 |
| |
| Дано: Прям. 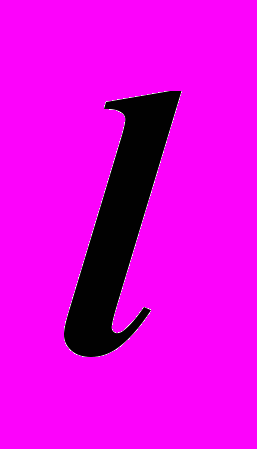 Пл. 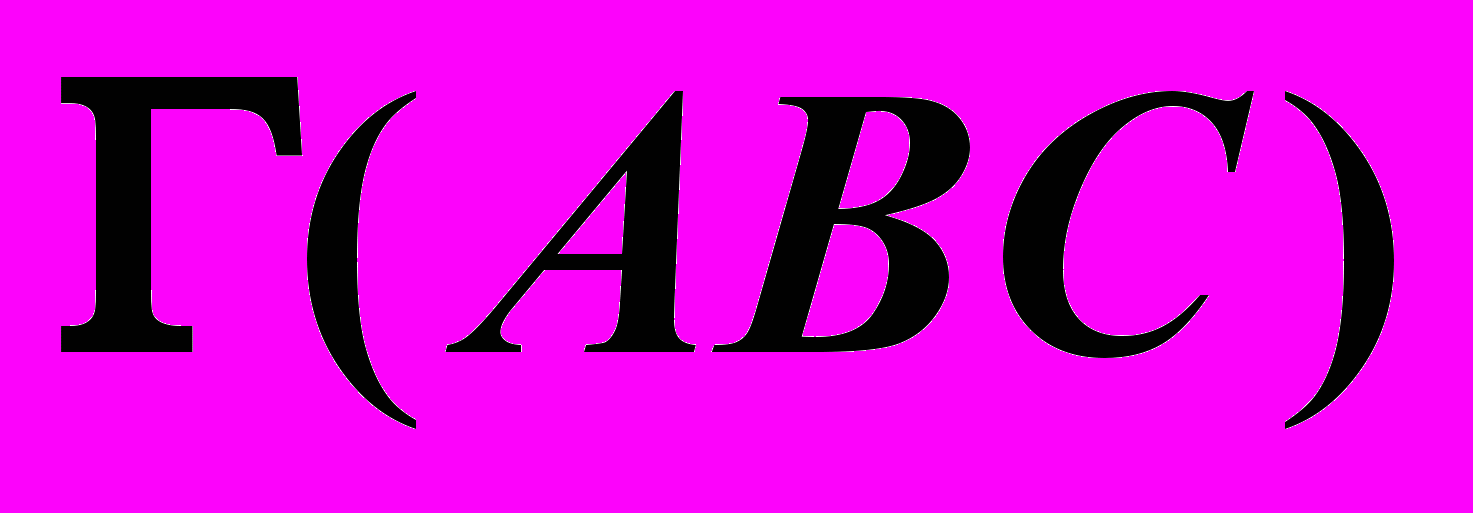 | Решение: 1) 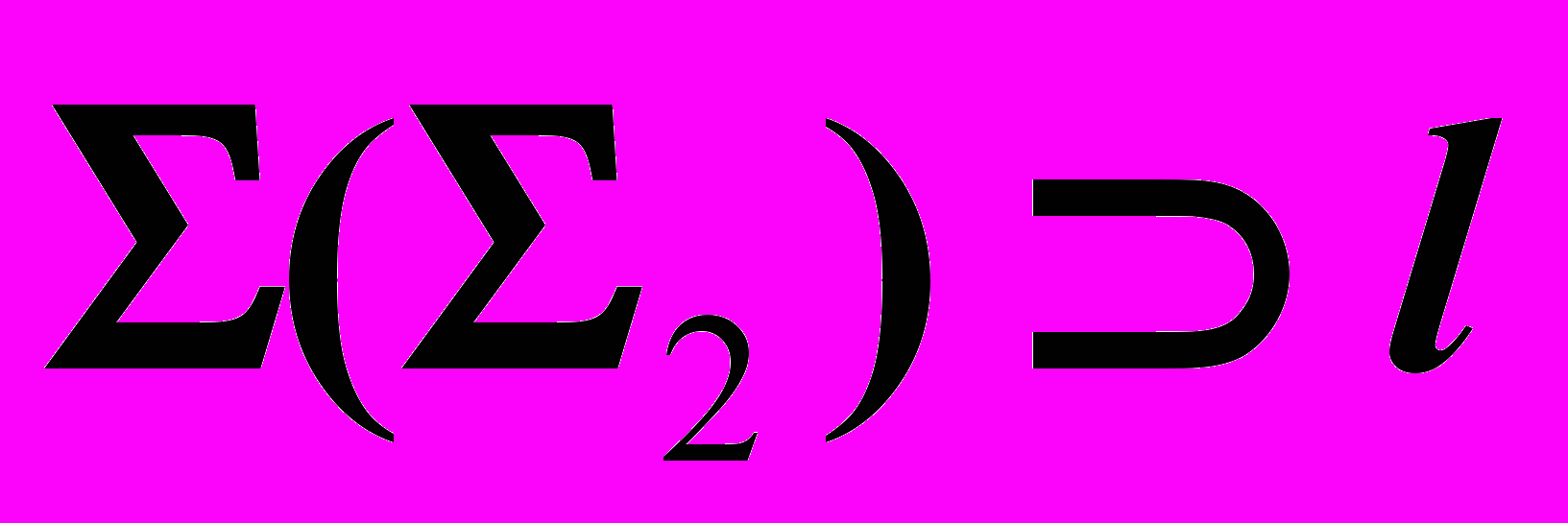 , ,2) 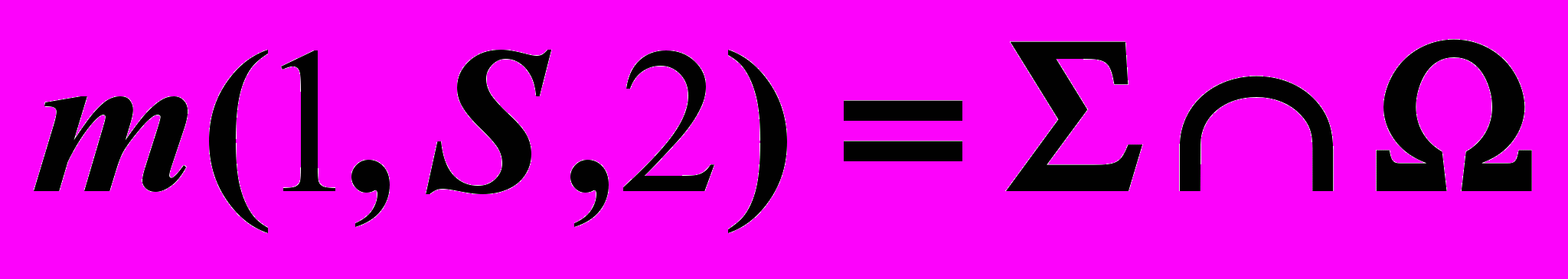 , ,3) 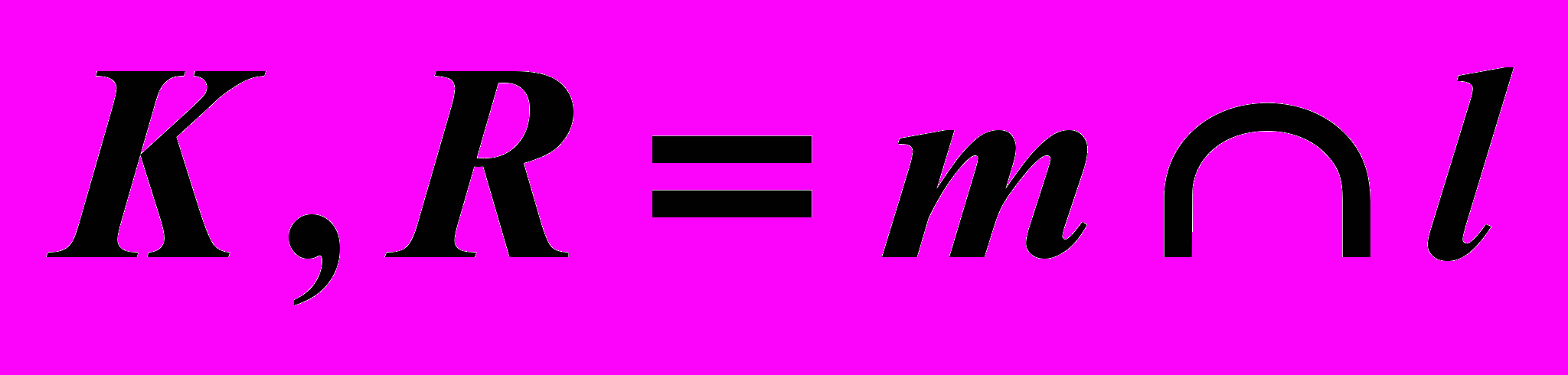 , ,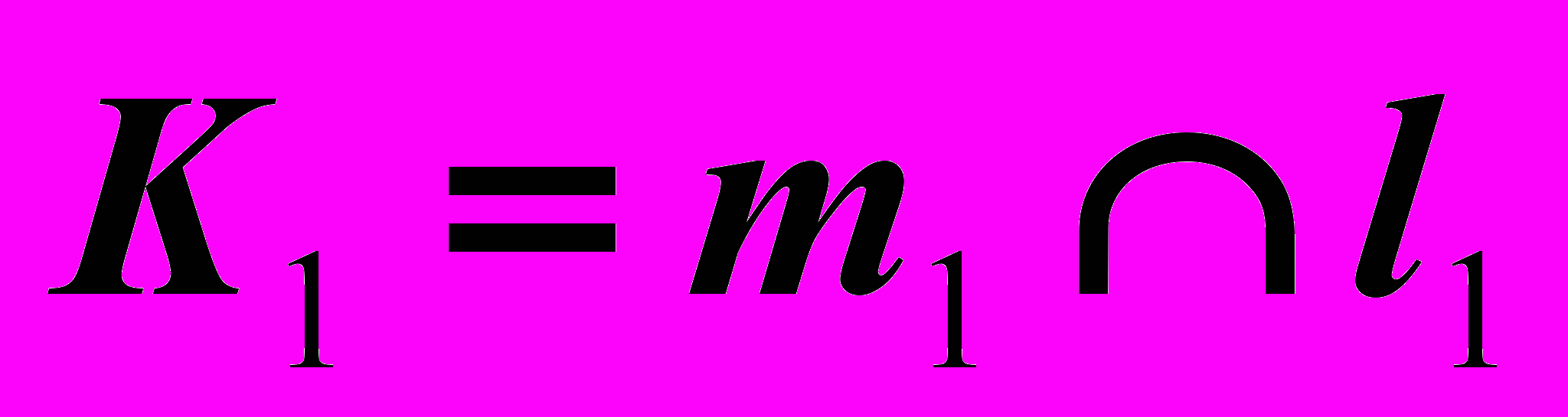 , , . .4) Видимость. |
| ?: 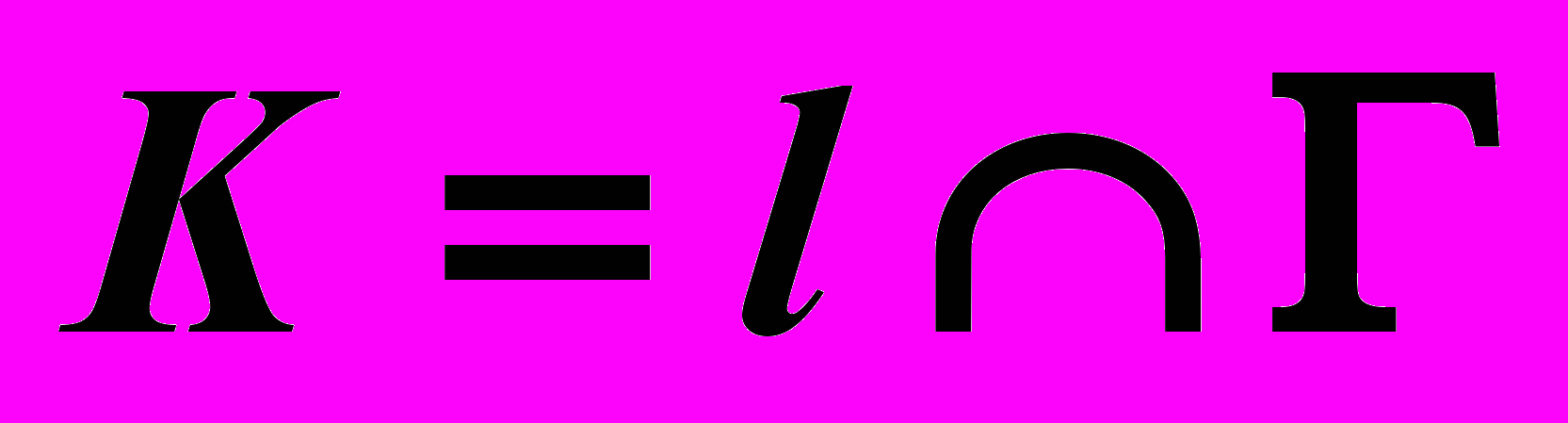 . . |
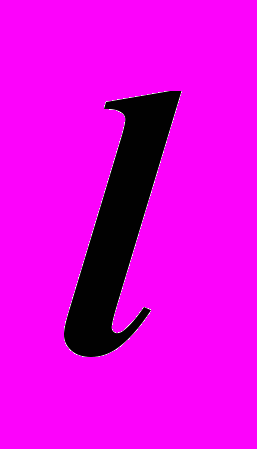 посредник
посредник 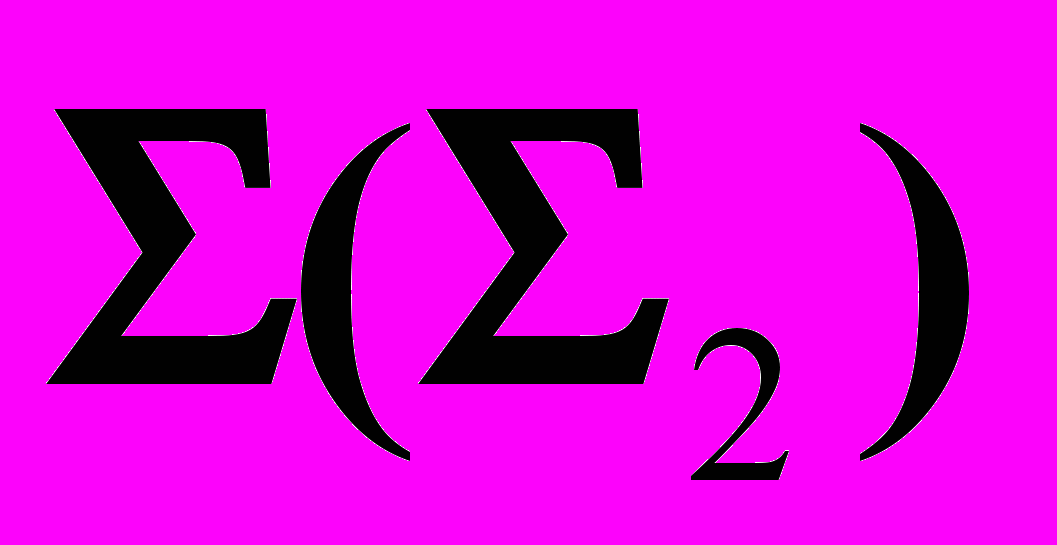 определяем его пересечение с плоскостью
определяем его пересечение с плоскостью  по прямой
по прямой 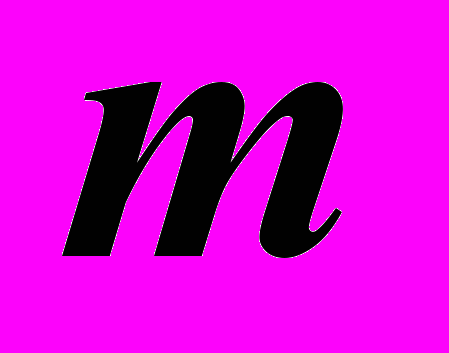 . Для нахождения искомой точки K пересекаем вспомогательную линию
. Для нахождения искомой точки K пересекаем вспомогательную линию 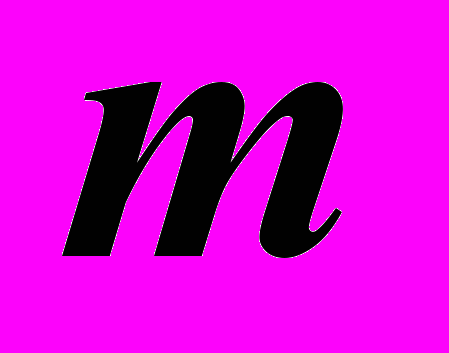
 с заданной -
с заданной - 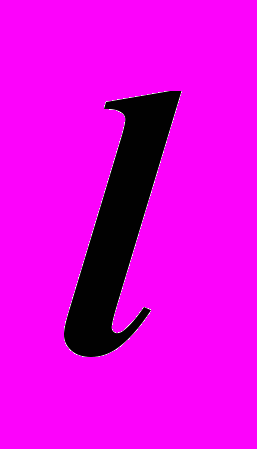 . Построение точки K начинается с горизонтальной проекции.
. Построение точки K начинается с горизонтальной проекции.Видимость проекций прямой
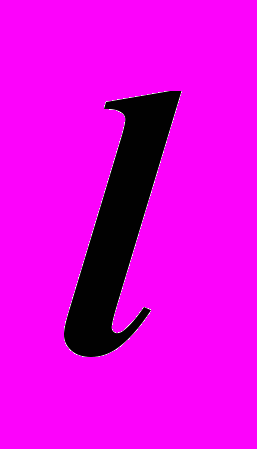 определяется по отмеченным на чертеже конкурирующим точкам.
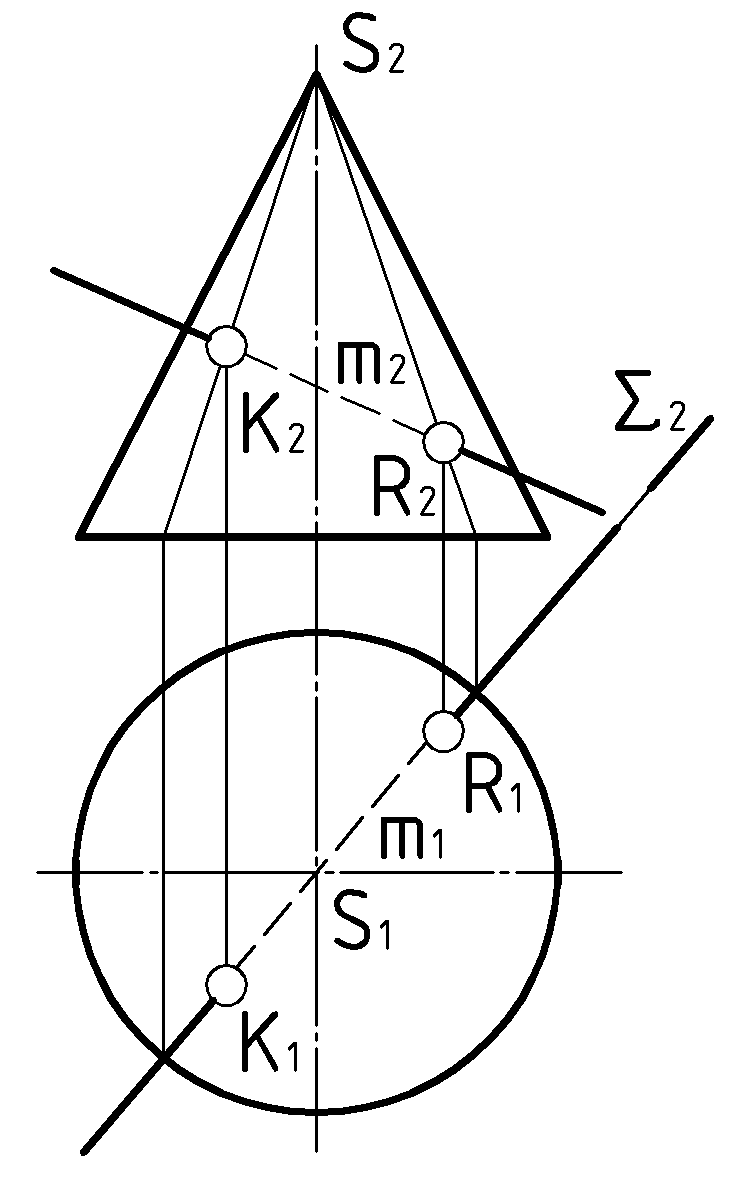
определяется по отмеченным на чертеже конкурирующим точкам.| Дано: Кон. 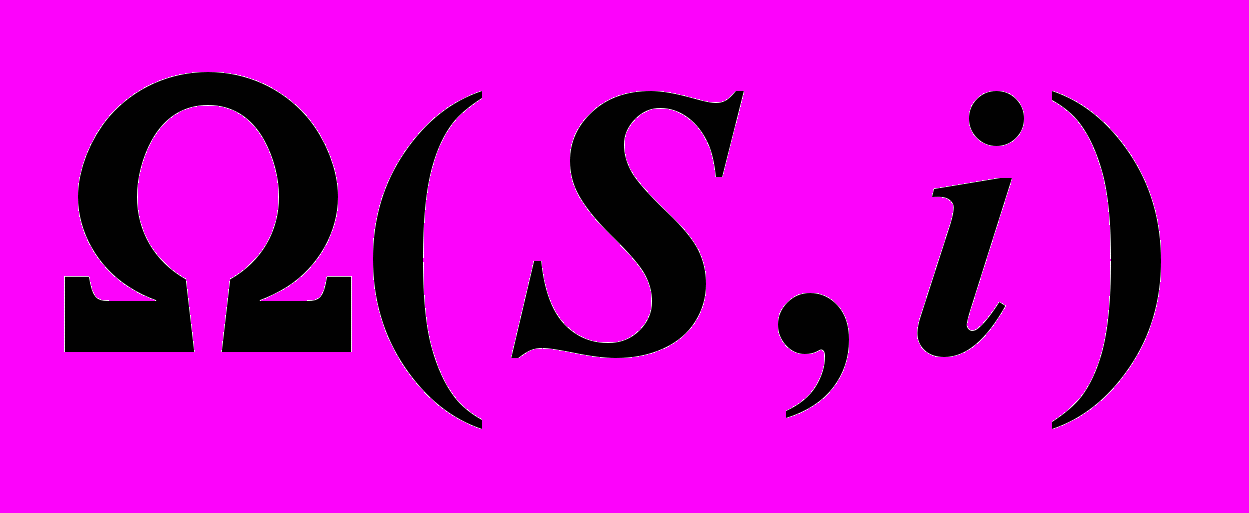 , ,Пр. 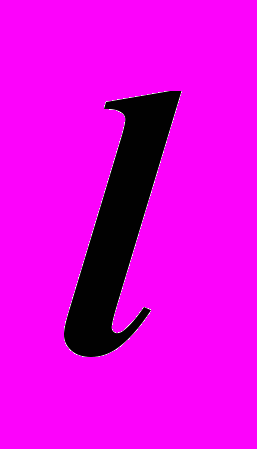 | Решение: 1) 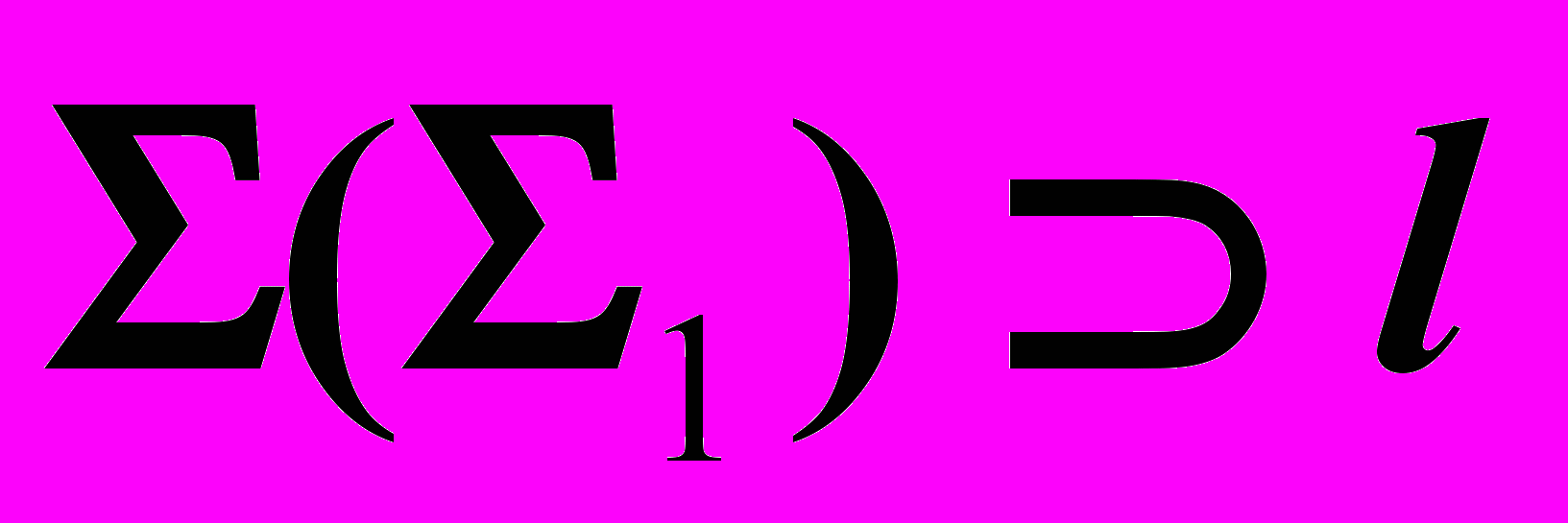 , ,2) 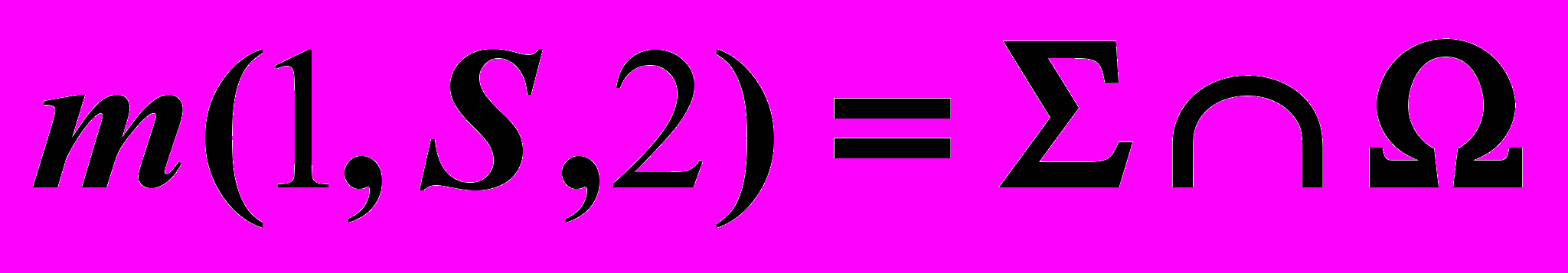 , ,3) 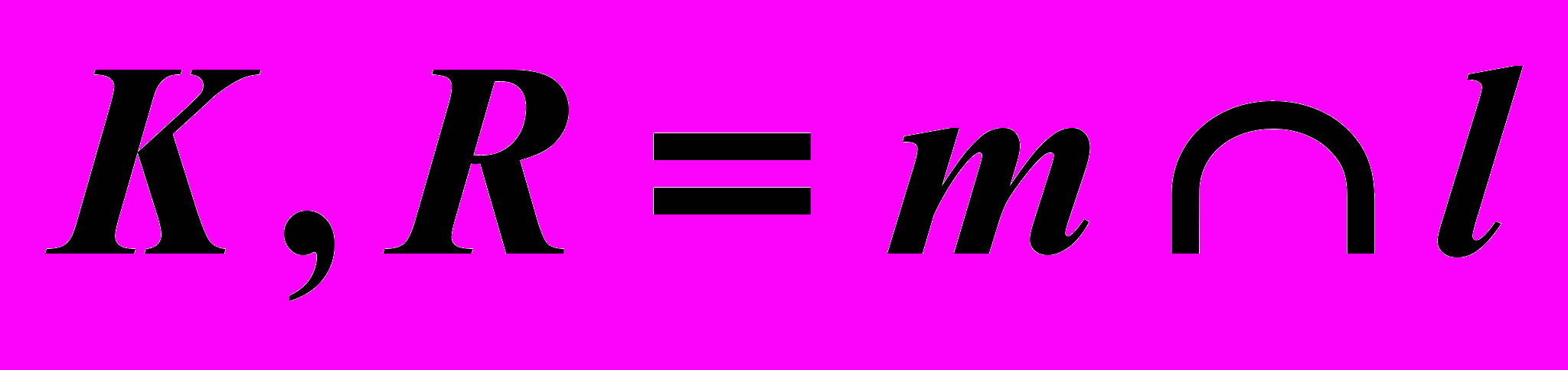 : :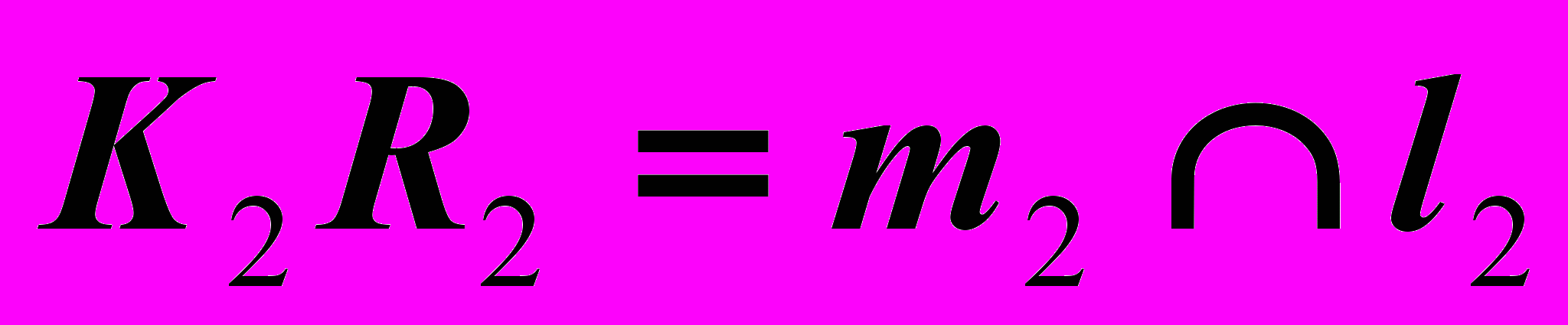 , , , ,4) Видимость. |
| ?: 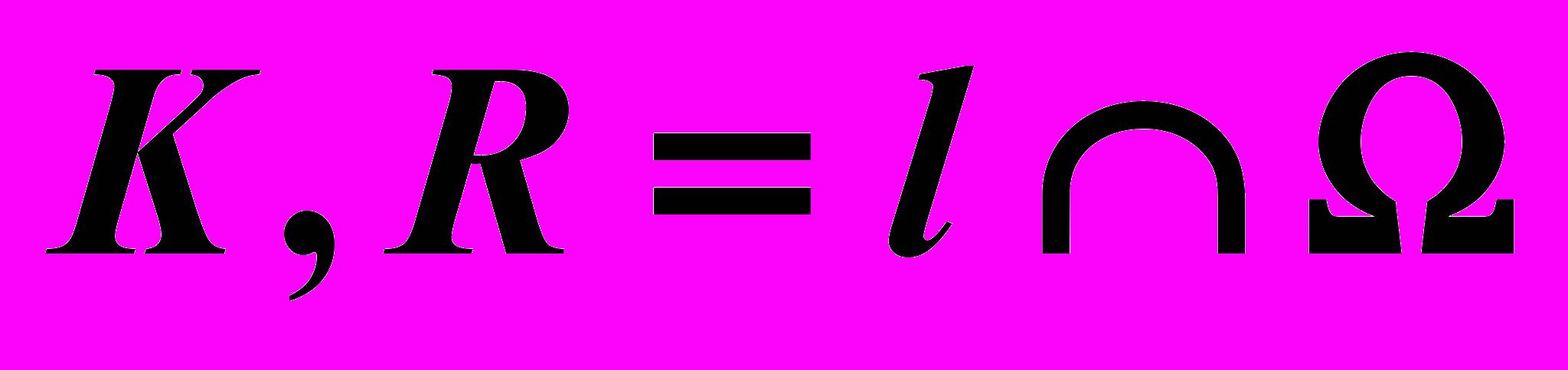 . . |
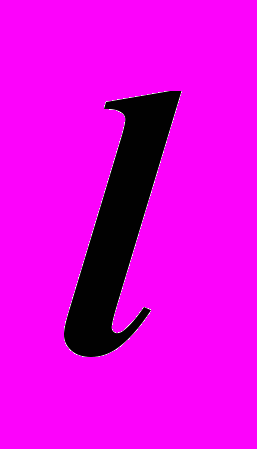 с конусом вращения
с конусом вращения 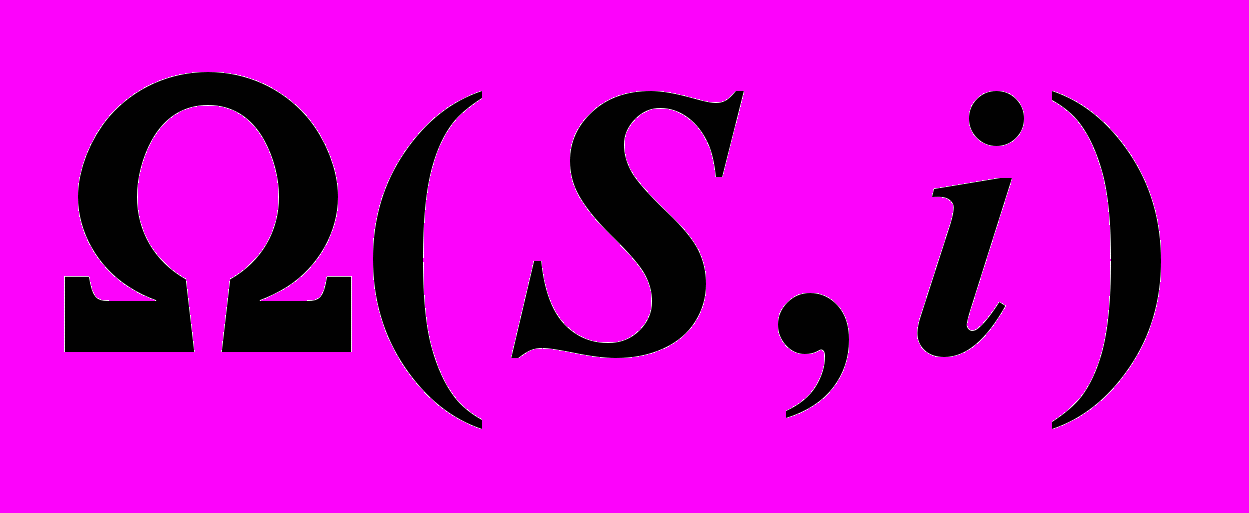 .
.  |
| |
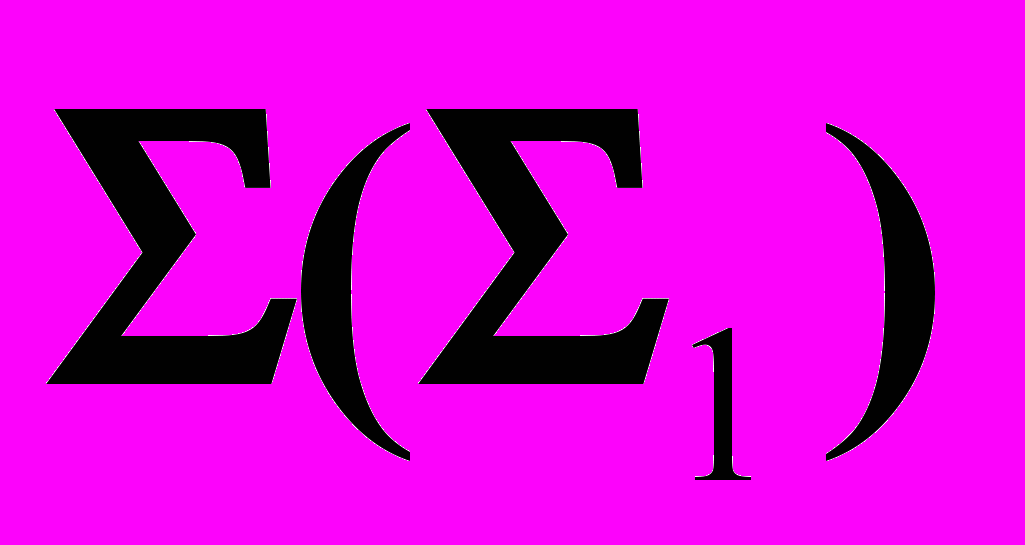 , проведенный через заданную прямую
, проведенный через заданную прямую 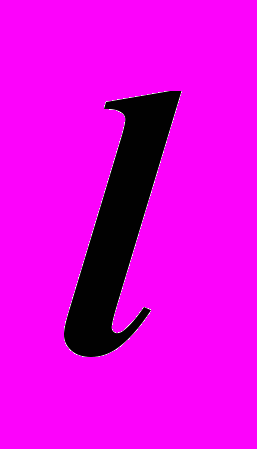 , пересекает конус по ломаной линии
, пересекает конус по ломаной линии 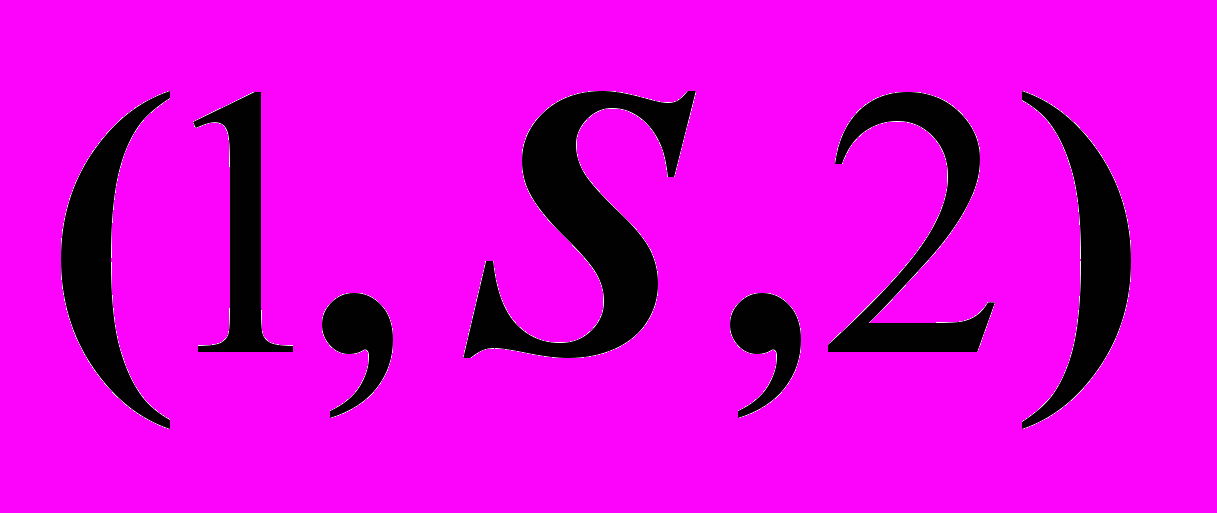 . Места пересечения прямой
. Места пересечения прямой 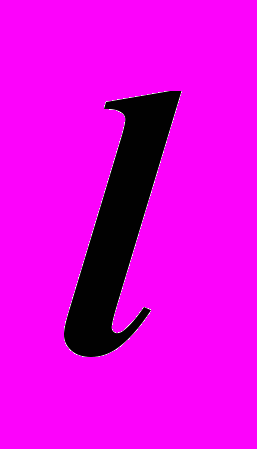 с полученным сечением конуса определяют искомые точки
с полученным сечением конуса определяют искомые точки 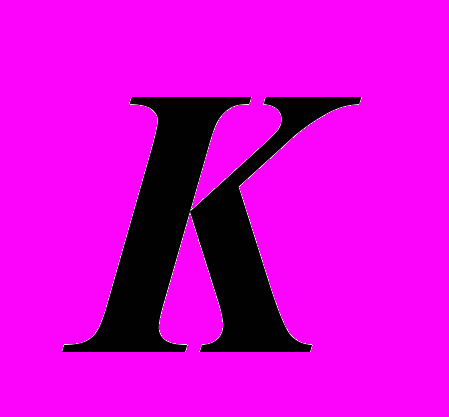 и
и  . Построение этих точек на чертеже начинается с фронтальных проекций.
. Построение этих точек на чертеже начинается с фронтальных проекций.Видимость горизонтальной проекции линии
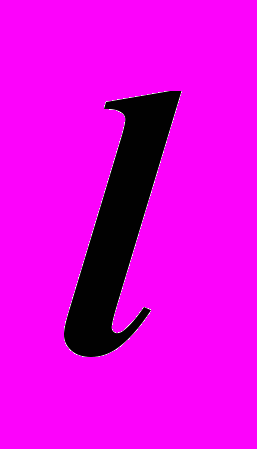 - очевидна. Видимость на фронтальной плоскости проекций определяется видимостью проекций искомых точек пересечения
- очевидна. Видимость на фронтальной плоскости проекций определяется видимостью проекций искомых точек пересечения 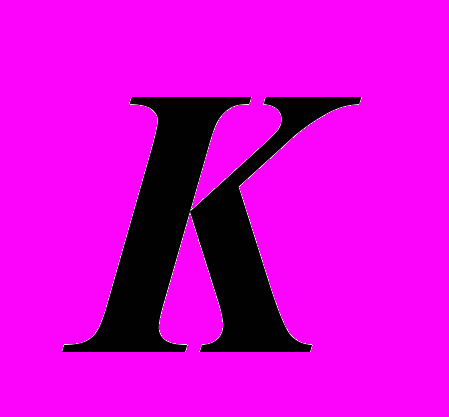 и
и  .
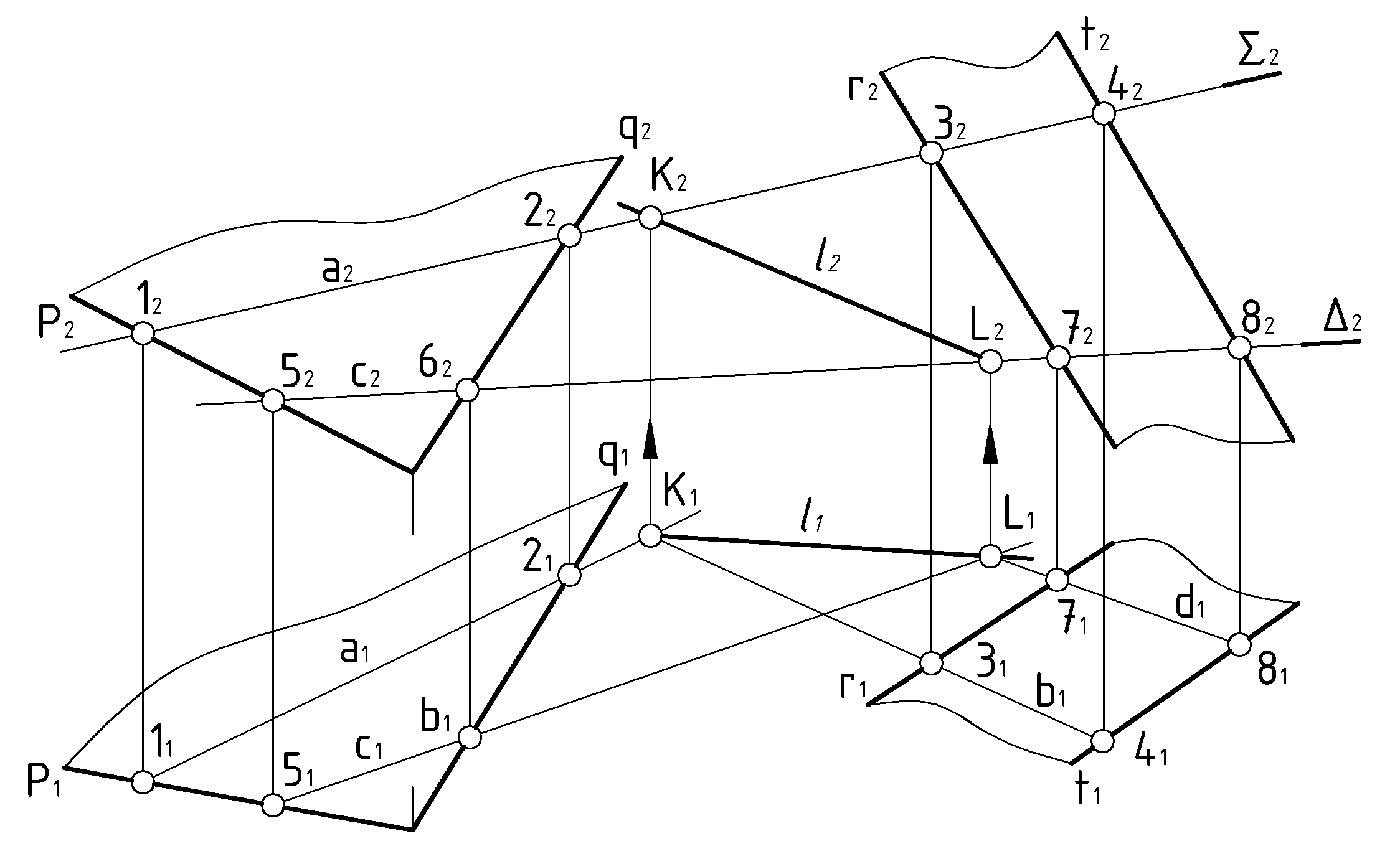
.Пример 3 (Рис.46). Построить линию пересечения плоскостей
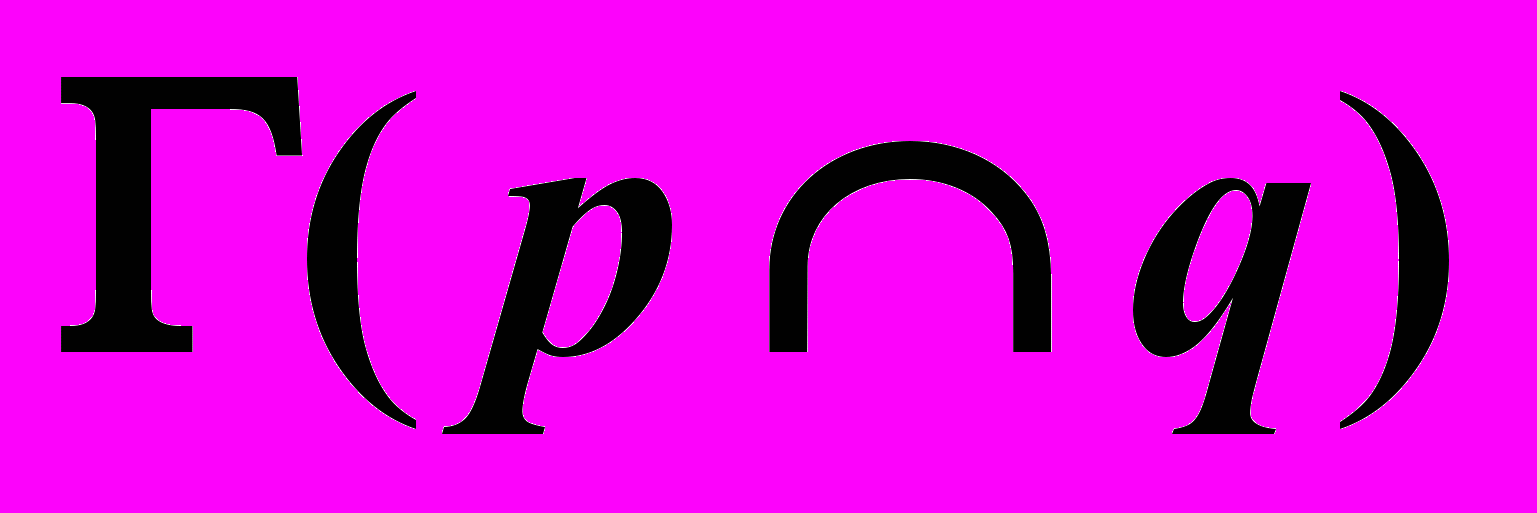 и
и 
 .
.| Дано: Пл. 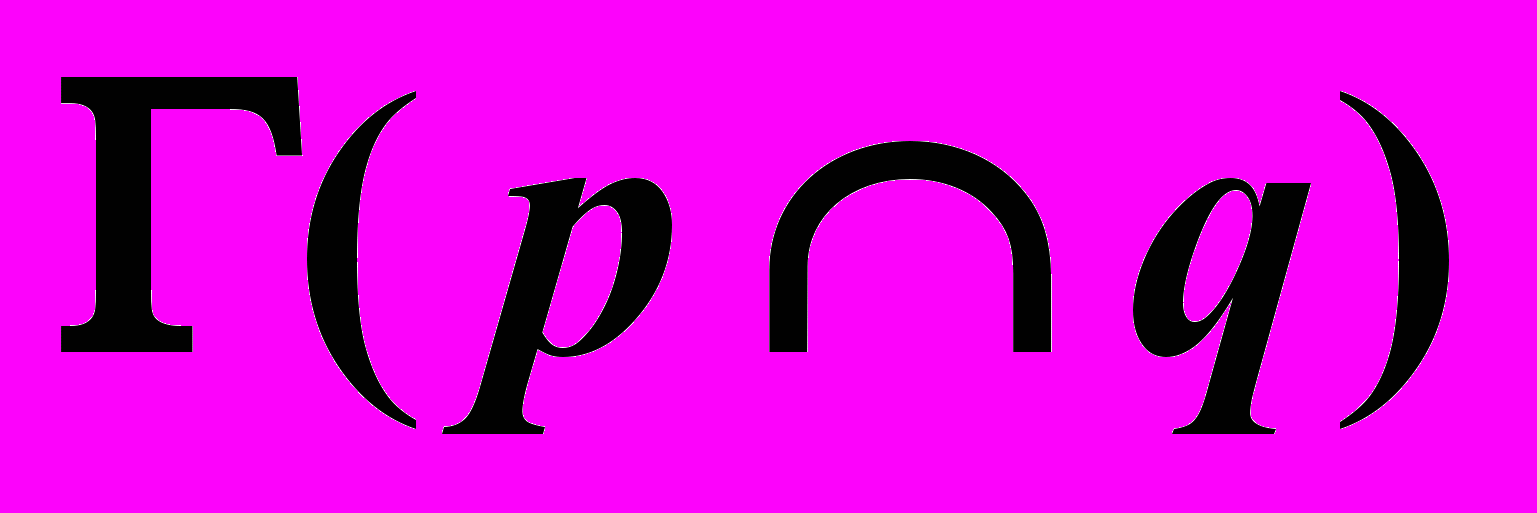 Пл.  ?: 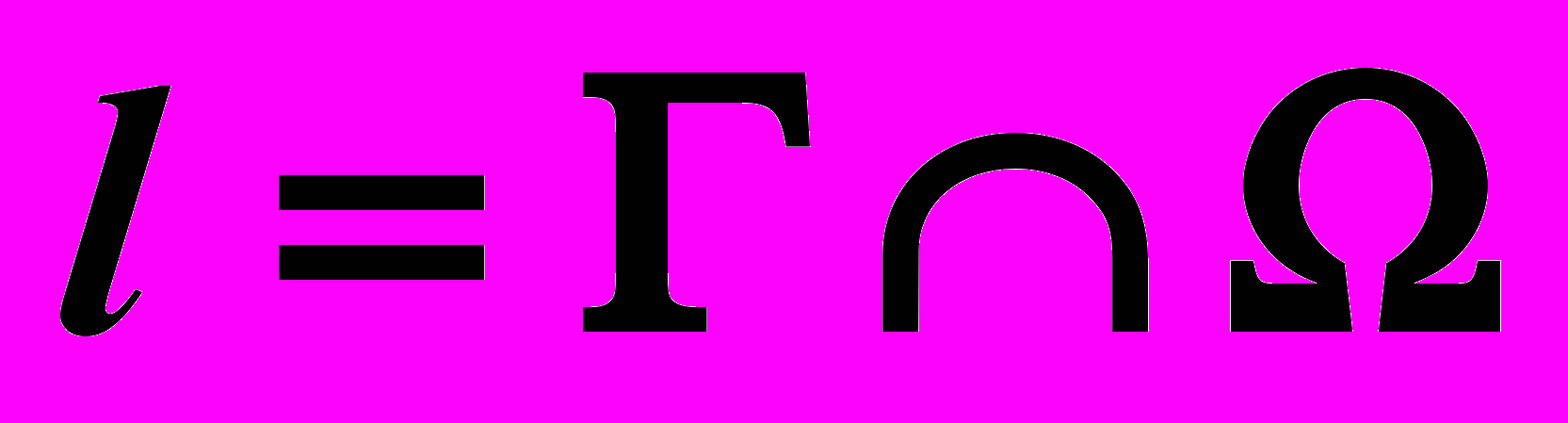 | Решение: | |
| 1). 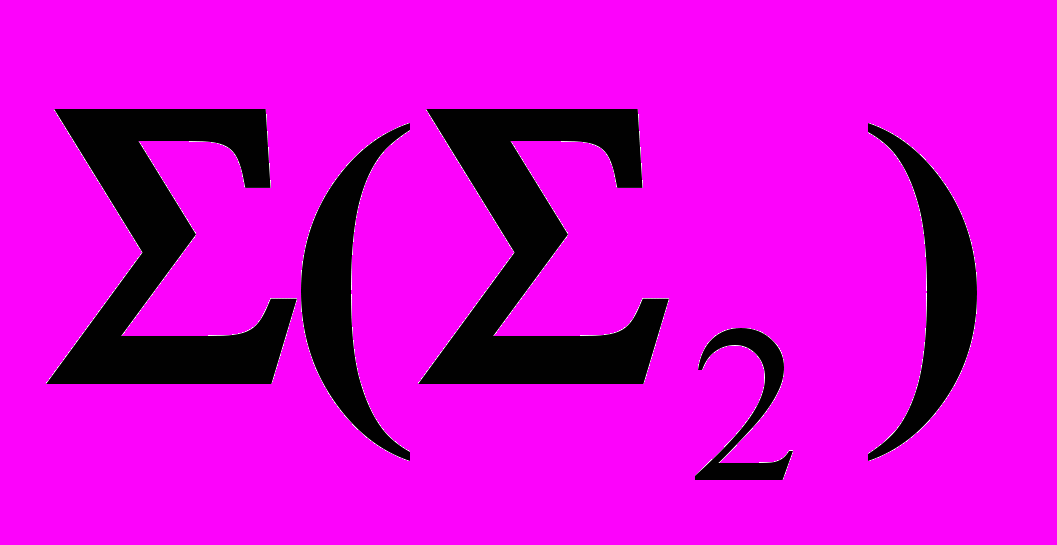 , , | 4). 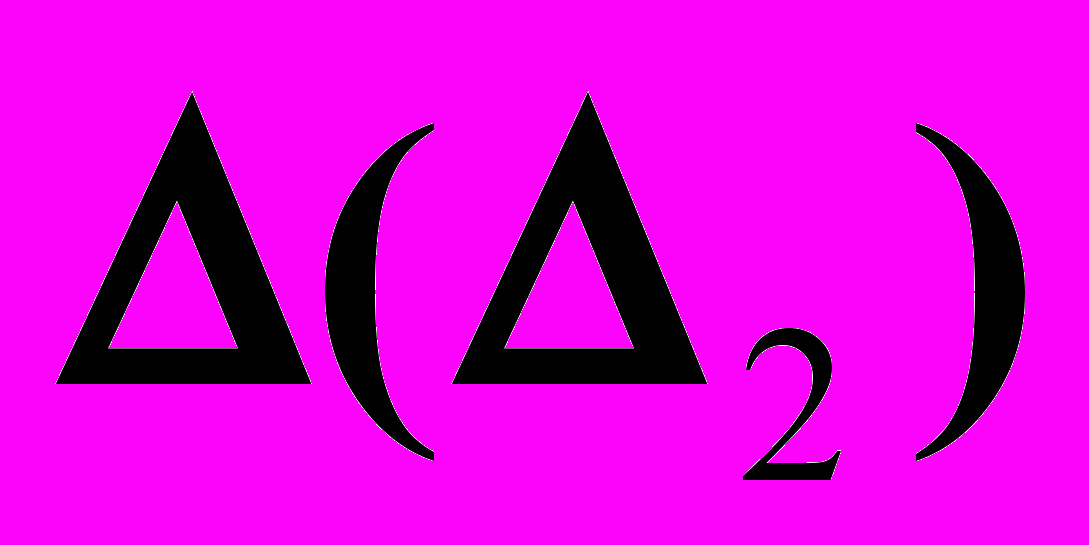 , , | – посредник. |
| 2).  , , , , | 5). 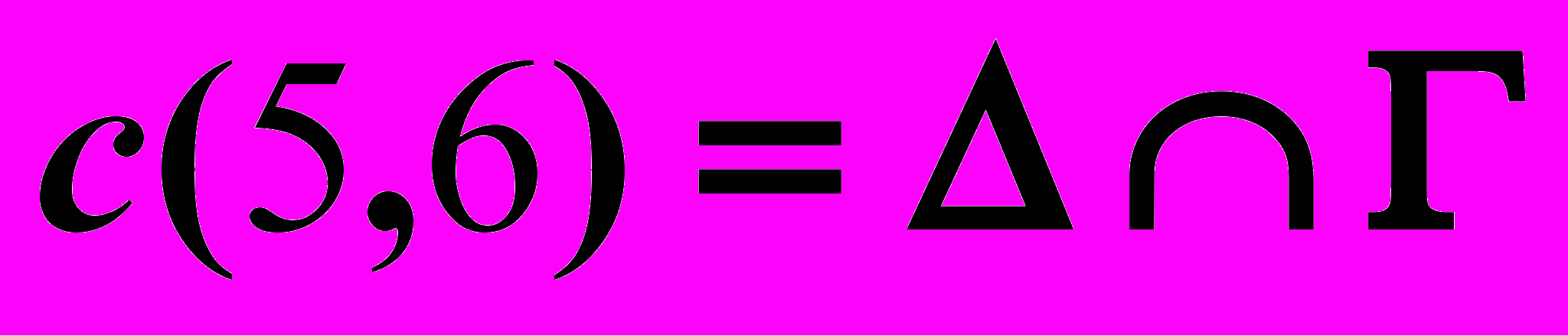 , ,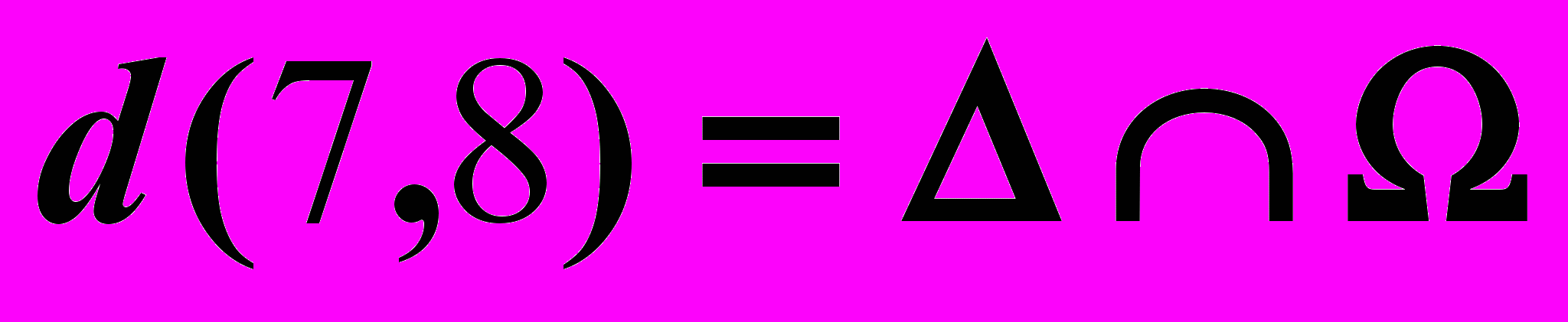 , , | – вспомогательные прямые. |
| 3). 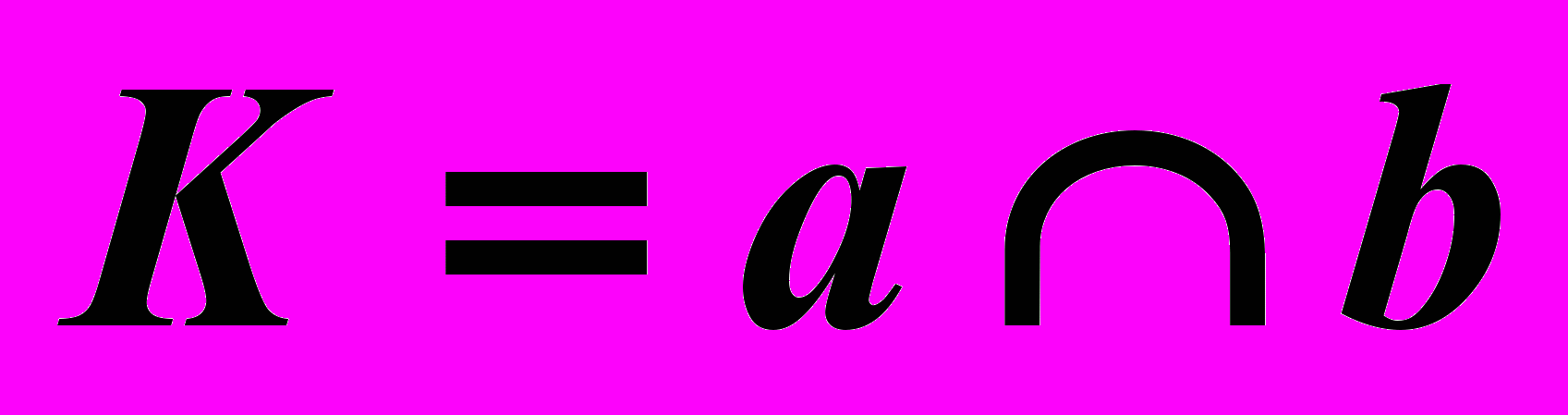 , , | 6). 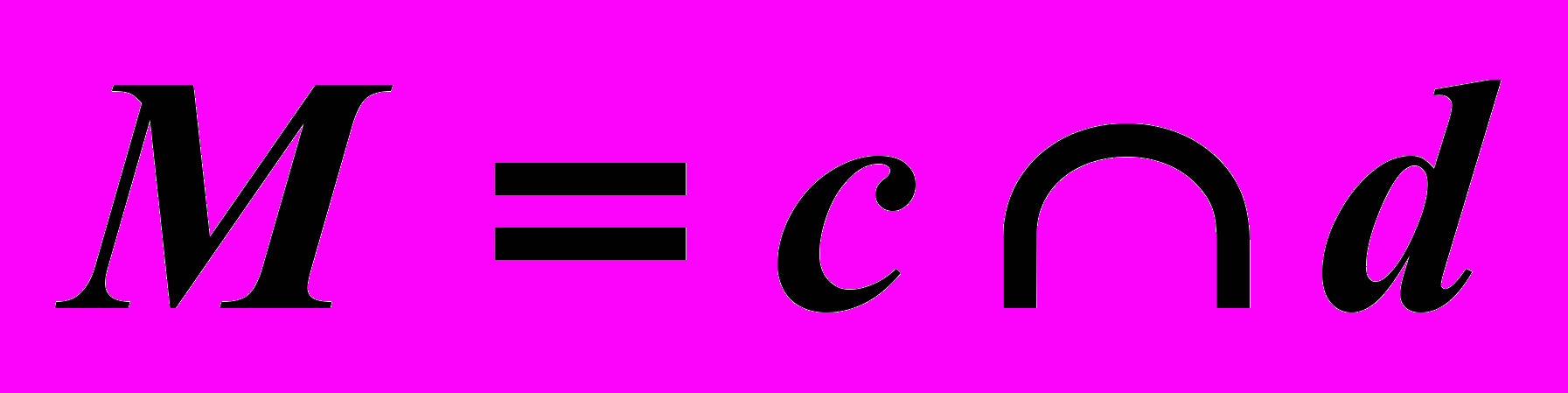 , , | – точка линии пересечения. |
| 7)  . . | – линия пересечения. |
 |
| |
| № | Посредники | Линии | Точки |
| 1 | Произвольно расположенные | 4 | 8 |
| 2 | Параллельные | 4 | 6 |
| 3 | Параллельные и использующие заданные каркасы плоскостей | 2 | 3 |
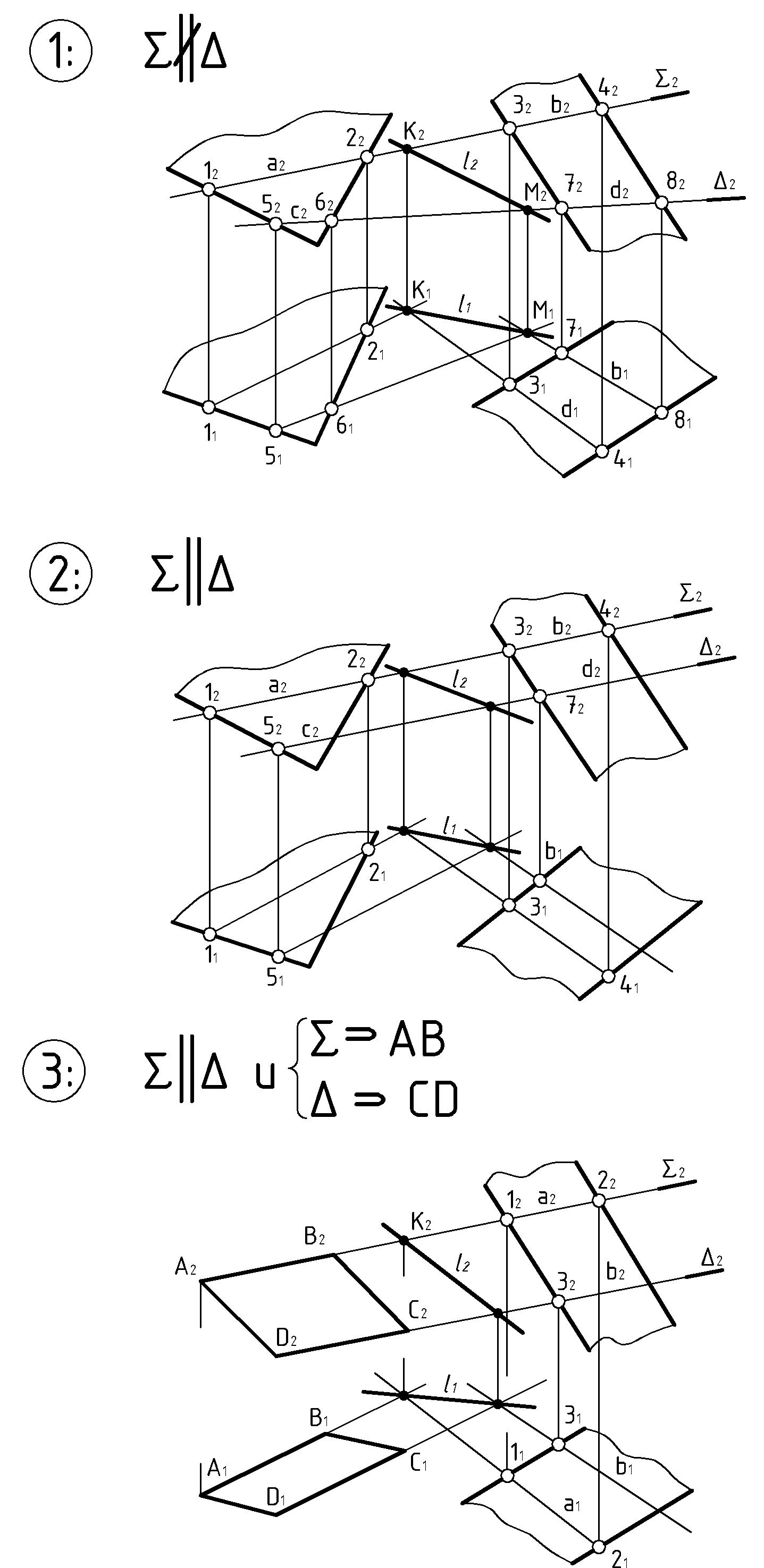
Те же результаты можно видеть на Рис.47/
 |
| |
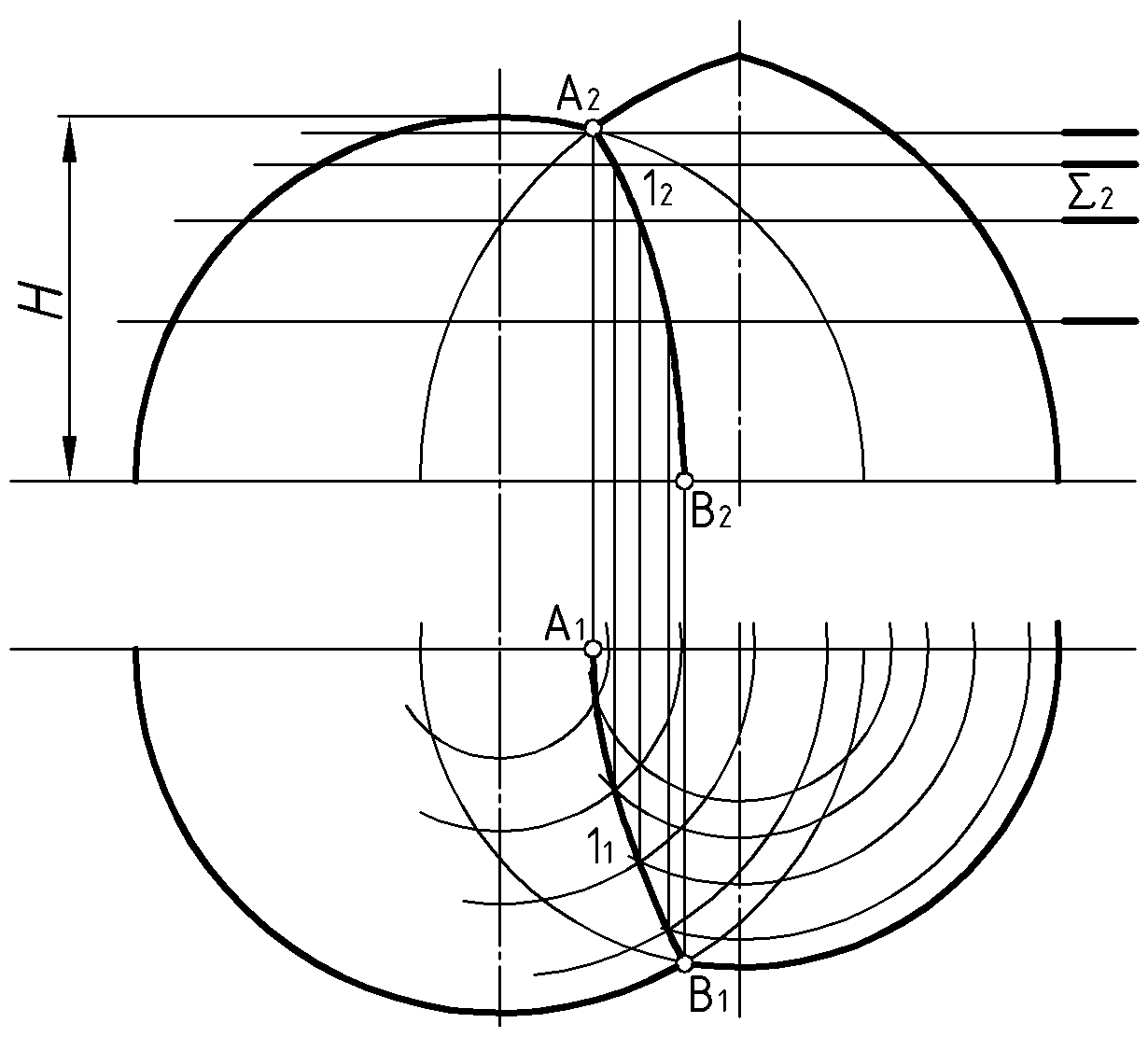
Пример 4 (Рис.48). Построить линию пересечения закрытого тора и полусферы.
 |
| |
1) Выбрать способ решения задачи.
2) Построить опорные точки линии пересечения любым способом и обозначить их буквами. (В данном случае – это самая высокая точка
 и точка
и точка 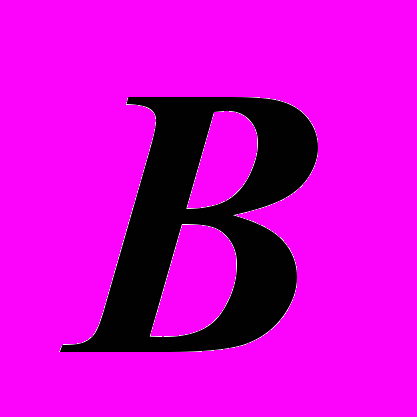 на основании поверхностей).
на основании поверхностей).3) Ограничить опорными точками область применения посредников (размер
 в данной задаче).
в данной задаче).4) Построить необходимое число промежуточных точек линии пересечения выбранным методом и при необходимости обозначить их цифрами.
5) Построить линию пересечения.
6) Обвести чертеж в целом с учетом видимости.
4.4.2.Метод концентрических сфер
Метод концентрических сфер применяется для пересечения поверхностей вращения, у которых общая плоскость симметрии параллельна плоскости проекций. В этом случае сфера с центром в точке пересечения осей вращения соосна с поверхностями и пересекает их по окружностям. Которые, в свою очередь, пересекаются в двух точках, принадлежащих искомой линии пересечения. На чертеже – это совпадающие между собой проекции двух конкурирующих точек в месте пересечения вырожденных проекций вспомогательных окружностей. В таких случаях пояснения и обозначения на чертеже ведутся, как правило, только для видимых проекций конкурирующих точек и, соответственно, для видимых проекций конкурирующих частей линии.
В целом решение задач методом концентрических сфер ведется в обычной, принятой ранее последовательности. За исключением того, что после выбора метода необходимо ограничить область применения посредников минимальной и максимальной сферами.
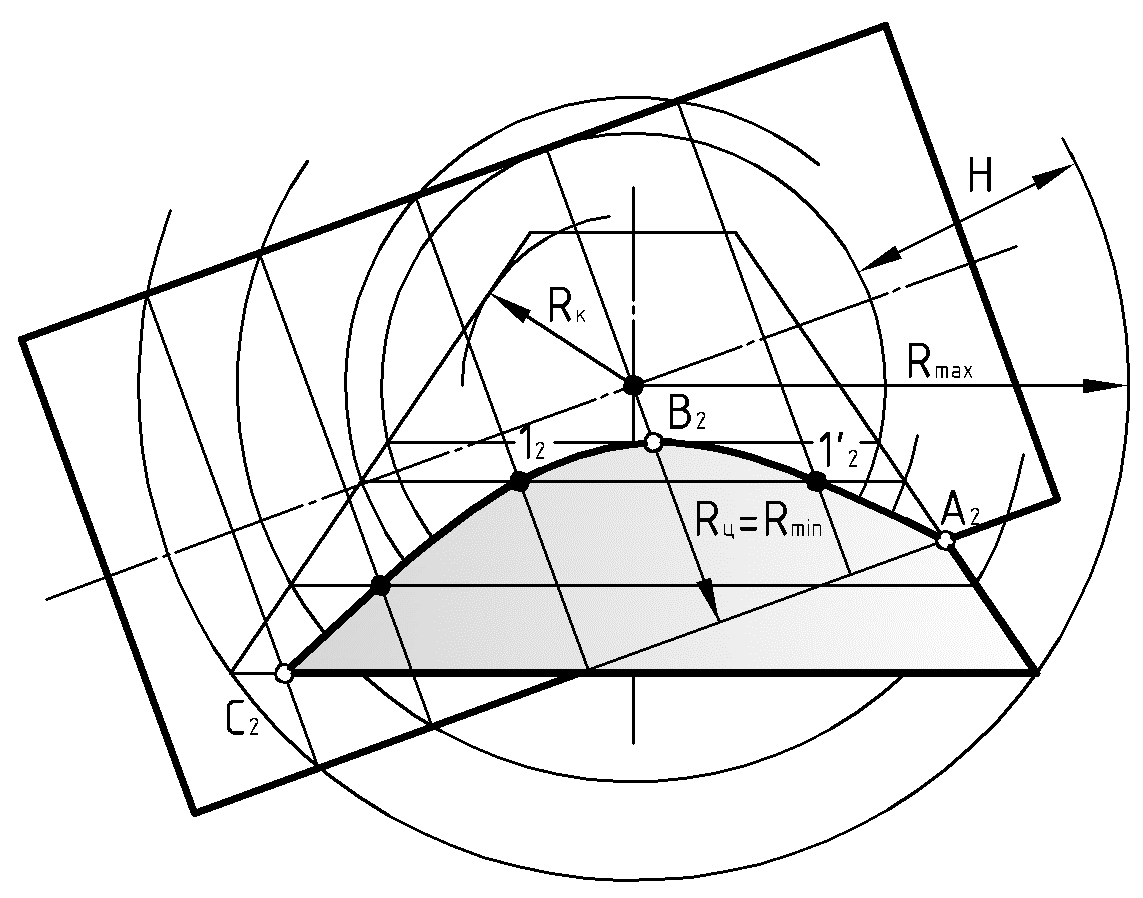
Пример (Рис.49). Построить линию пересечения поверхностей вращения цилиндра и конуса с общей фронтальной плоскостью симметрии.
 |
| |
1) Условия задачи позволяют использовать способ концентрических сфер.
2) Определяем область применения посредников.
Радиус минимальной сферы (
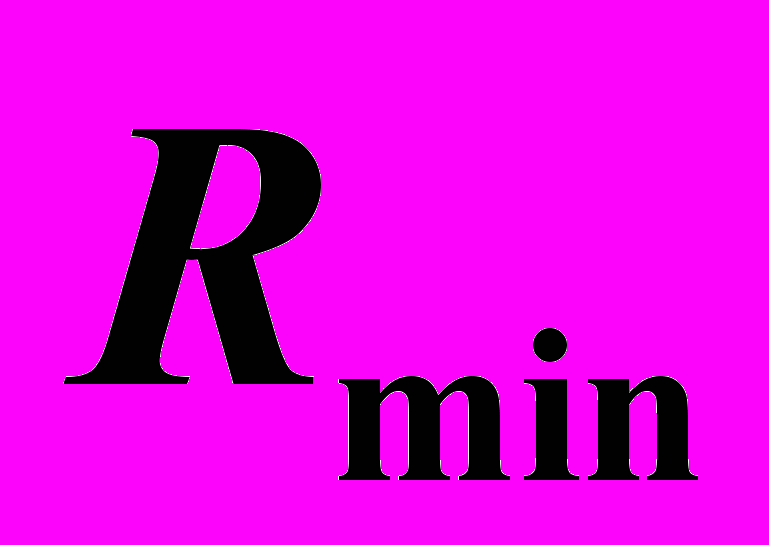 ) определяем сравнением сфер, вписанных в заданные поверхности (
) определяем сравнением сфер, вписанных в заданные поверхности (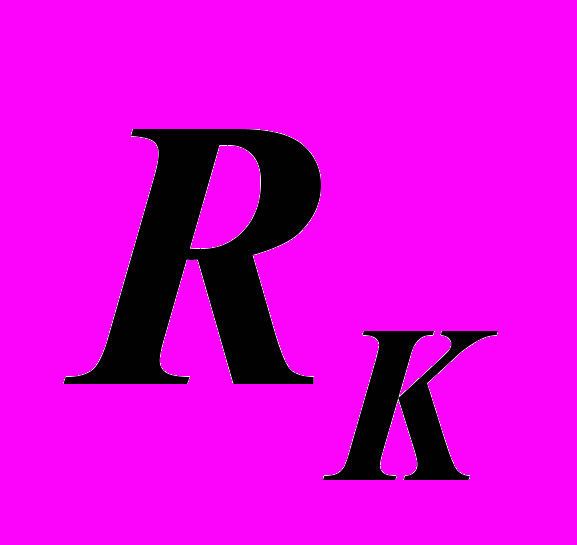 и
и 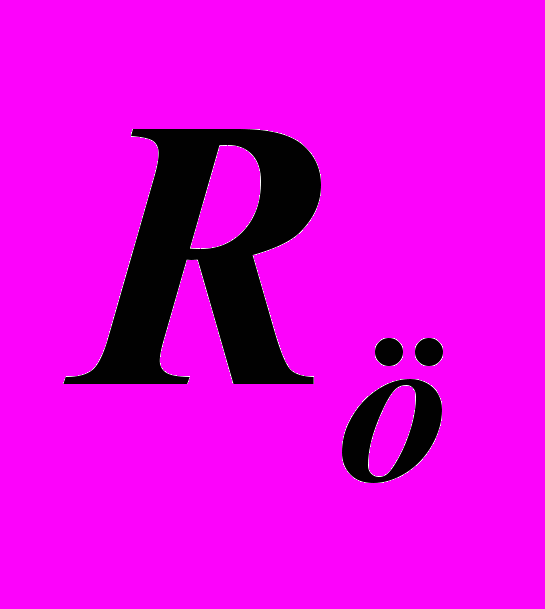 ). Выбор падает на больший радиус, радиус сферы, вписанной в цилиндр (
). Выбор падает на больший радиус, радиус сферы, вписанной в цилиндр (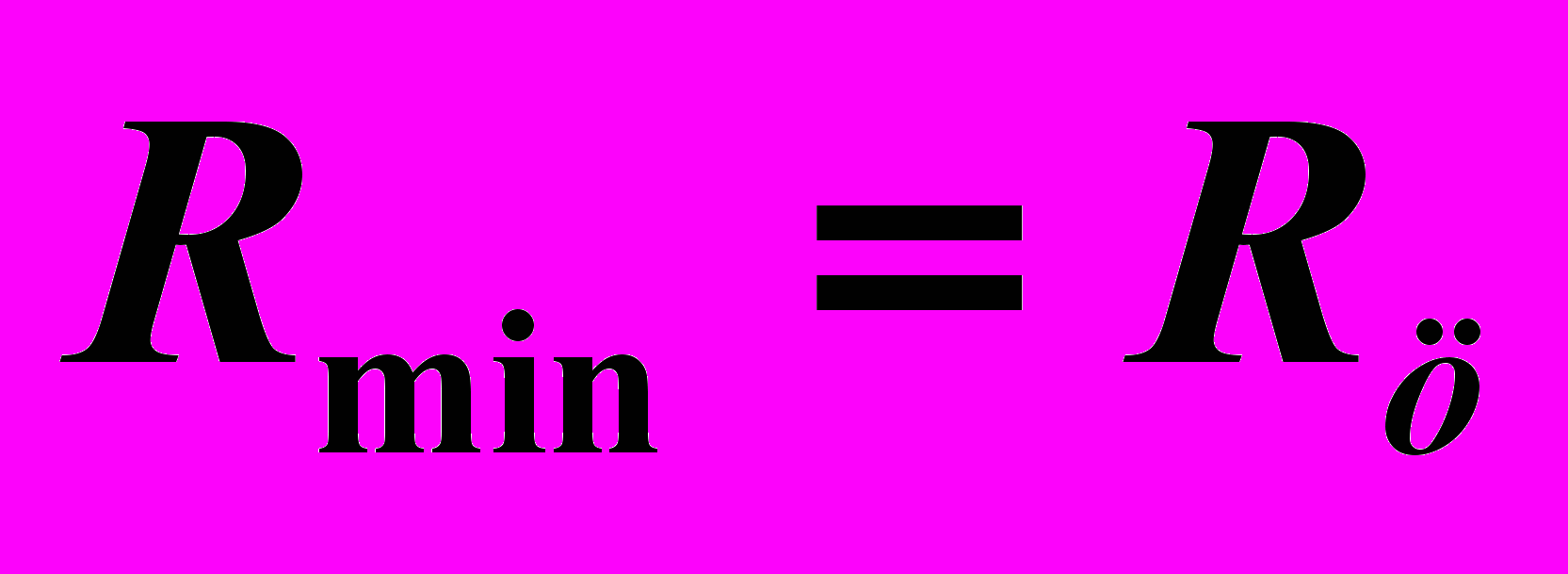 ). Воспользуемся тем, что минимальная сфера дает возможность построить одну из опорных точек
). Воспользуемся тем, что минимальная сфера дает возможность построить одну из опорных точек 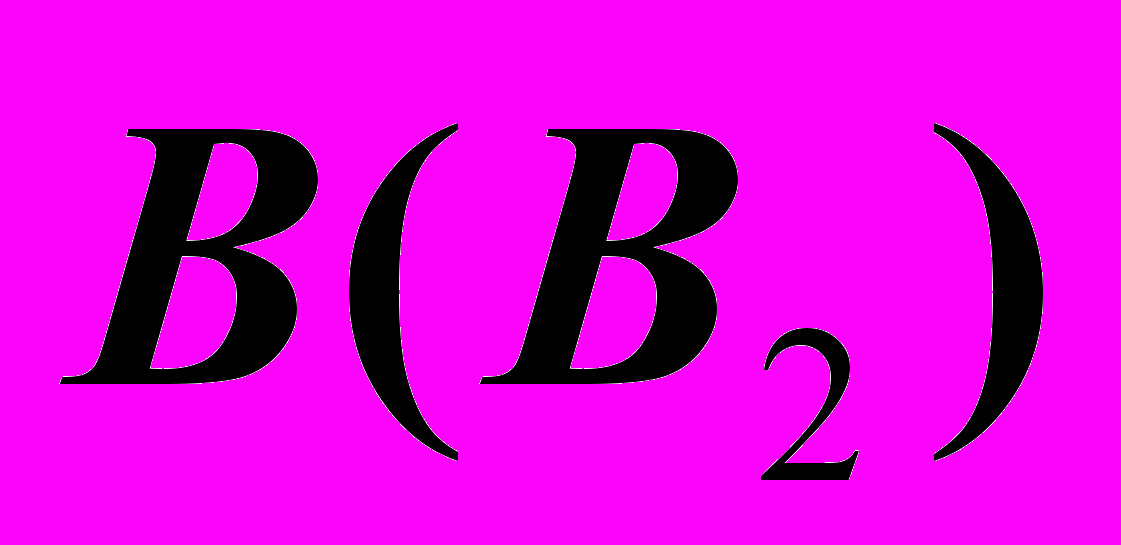 как место пересечения проекций линий касания сферы с цилиндром и линии пересечения её с конусом.
как место пересечения проекций линий касания сферы с цилиндром и линии пересечения её с конусом.Максимальная сфера должна пройти через самую удаленную от центра точку, принадлежащую искомой линии. В данном случае это сфера, которая проходит через основание конуса и пересекает цилиндр (
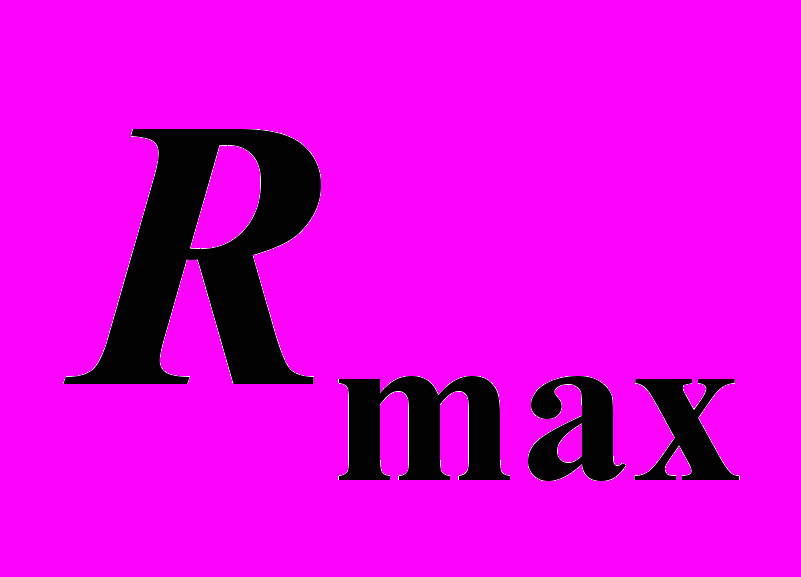 ). И вот – проекция еще одной опорной точки:
). И вот – проекция еще одной опорной точки: 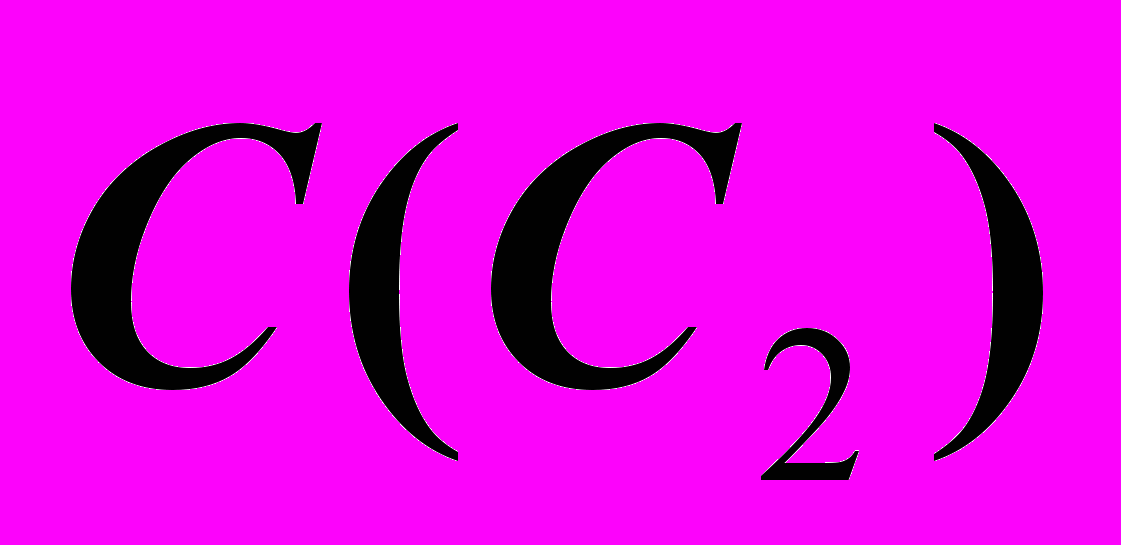 .
.3) На этом этапе определяют опорные точки. В нашем случае осталось не строить, а просто обозначить очерковую проекцию точки
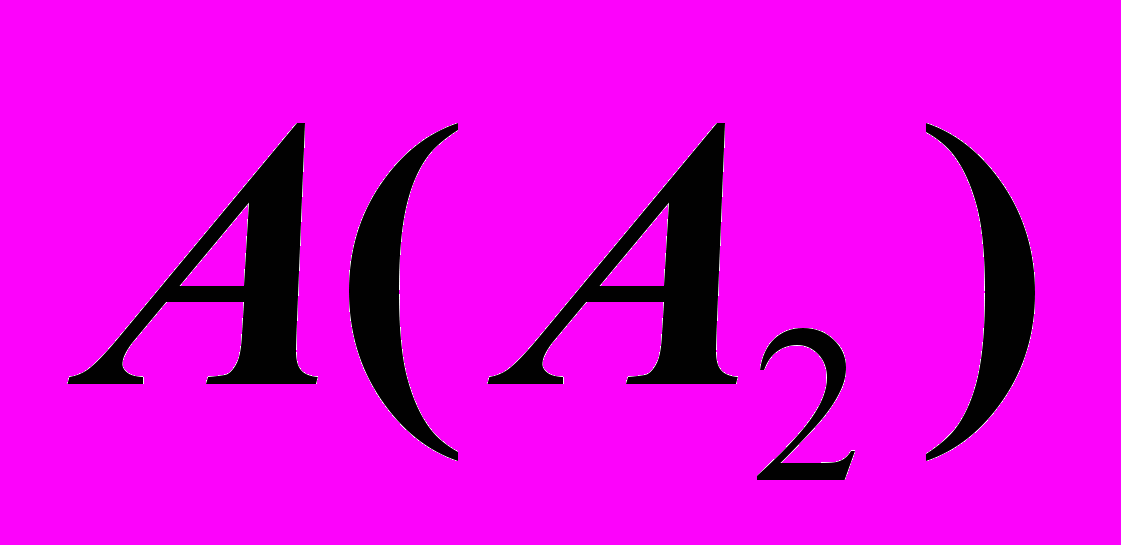 пересекающей главные меридианы поверхностей. В итоге имеем три опорные точки проекции начала и конца линии и степени ее перегиба.
пересекающей главные меридианы поверхностей. В итоге имеем три опорные точки проекции начала и конца линии и степени ее перегиба.4) При помощи промежуточных сфер определяем проекции необходимого числа текущих точек.
5) Строим изображение искомой линии пересечения.
6) Обводим чертеж с учетом видимости.
Особый интерес вызывает частный случай метода концентрических сфер, когда поверхности вращения описаны вокруг одной и той же сферы. Это приводит к резкому сокращению трудоемкости построений благодаря теореме Г. Монжа.
4.4.3.Частный случай теоремы Г.Монжа
(без доказательства)
Если две поверхности вращения 2-го порядка(конусы и цилиндры)описаны вокруг общей сферы, то они пересекаются по двум линиям того же порядка. Это могут быть эллипсы или параболы. Плоскости которые пересекаются по прямой, проходящей через точки пересечения линий касания сферы с заданными поверхностями.
В этом случае вырожденные прямолинейная проекция каждой из линий пересечения строится по двум из трёх возможных точкам. Это проекция двух точек пересечения очерковых образующих и совмещенная проекция конкурирующих точек пересечения искомых линий пересечения.
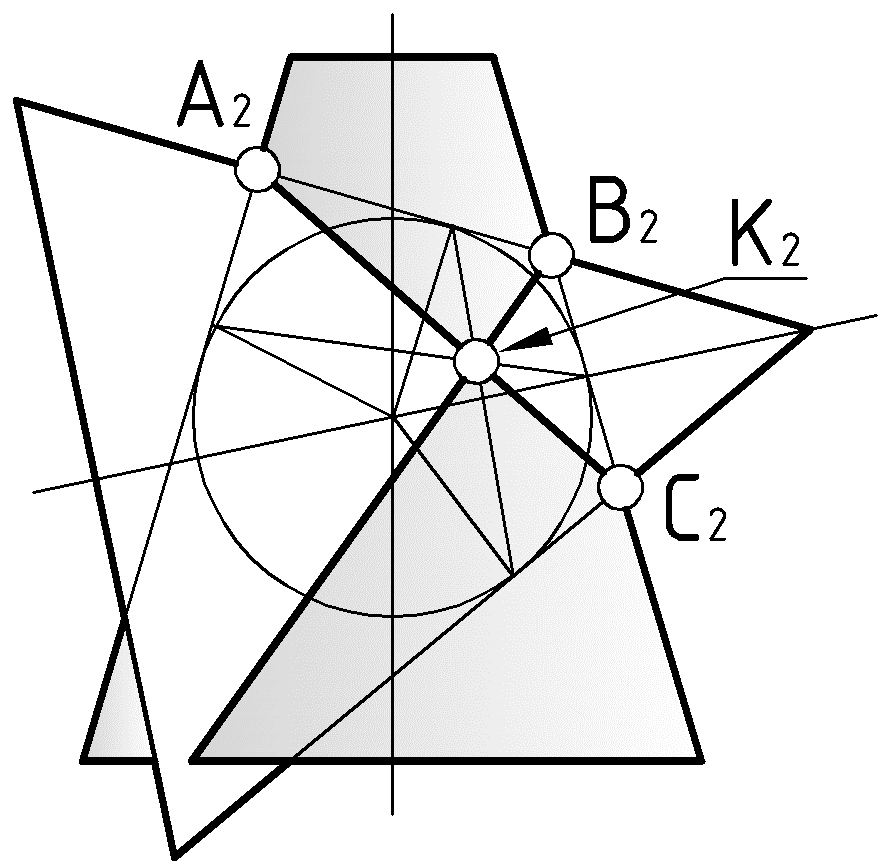
Пример (Рис.50). Построить результат пересечения цилиндра и конуса вращения, если они описаны вокруг одной и той же сферы.
 |
| |
1). Обозначим проекции всех очерковых точек:
 ,
, 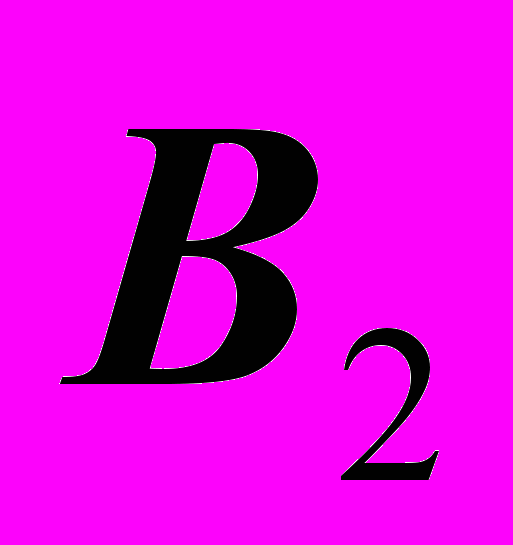 и
и 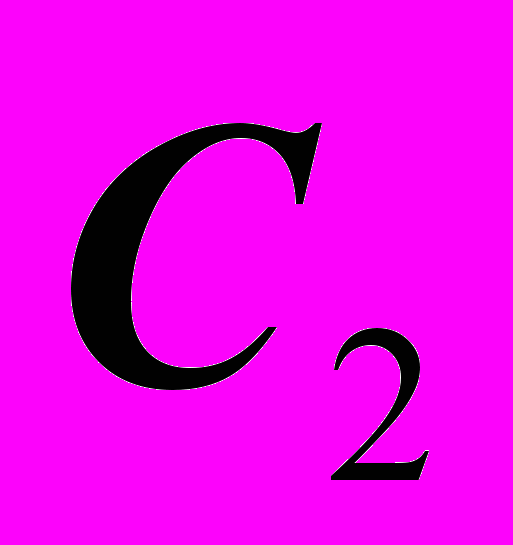 .
.2). Строим проекцию одного из эллипсов:
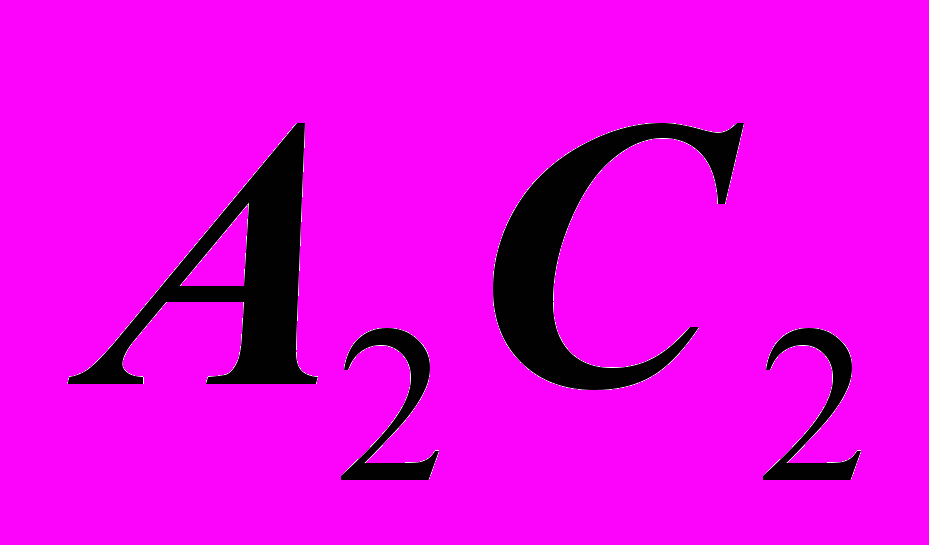 .
.3). Строим проекцию 2-ого эллипса:
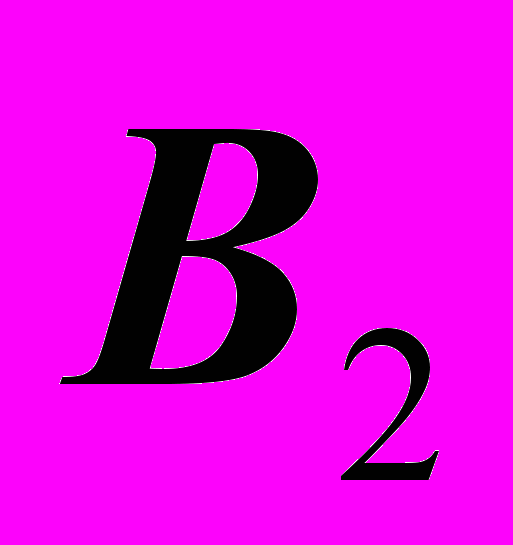 ,
, 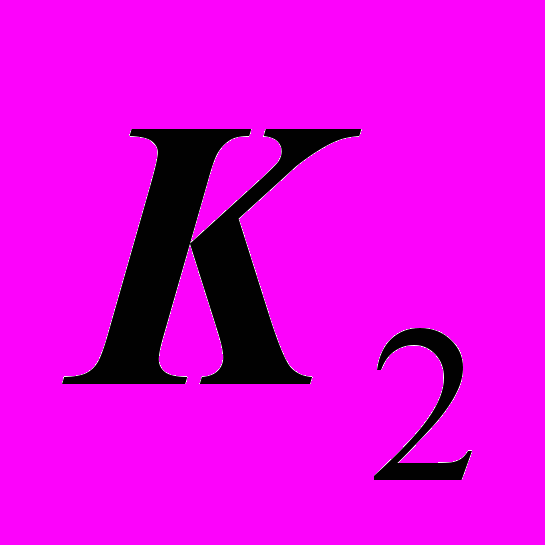 , где
, где 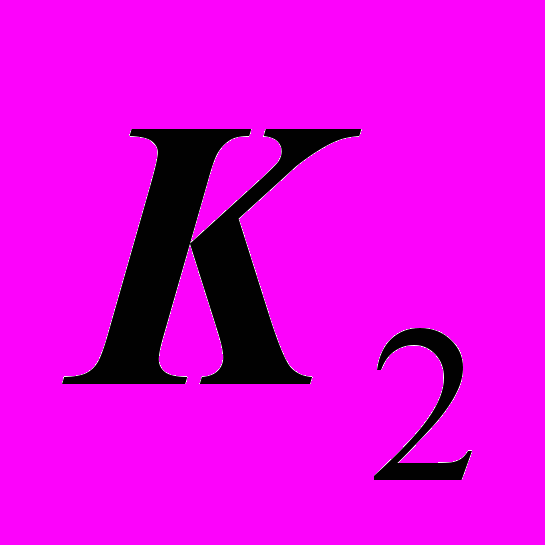 – результат пересечения проекций линий по которым сфера касается с заданными поверхностями.
– результат пересечения проекций линий по которым сфера касается с заданными поверхностями.