1 Общее описание моделей дс потоков

Вид материала

Содержание

2.5 Стратификация данных.
2.6 Нейронные сети.
2.7 Перспективы дальнейших исследований.
Список литературы.
Приложение. Исходные коды.

Подобный материал:

1 2 3 4 5 6

2.5 Стратификация данных.

Одним из наиболее простых и эффективных статистических методов анализа данных является метод стратификации (очень широко используется в социологии). В соответствии с этим методом производят стратификацию статистических данных, то есть группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности. Данные, разделенные на группы в соответствии с их особенностями, называют стратами (классами), а сам процесс разделения на страты – стратификацией.

Метод стратификации вполне можно использовать для выявления аномальной активности трафика. Если разбить данные на группы (страты) по значениям всех трех оценок λ, α₁, α₂ (рис. 5), то становится возможным отнести вновь полученные данные к какой-то из групп, что будет характеризовать нормальную активность трафика или же если данные не попадают ни в одну из групп, то имеет место быть аномальная активность.

Метод стратификации очень широко используется и имеет уже сложившийся инструментарий для работы с ним. Он требует более детального изучения, для возможности его эффективного использования.

2.6 Нейронные сети.

Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети Маккалока и Питтса [18]. Впоследствии, после разработки алгоритмов обучения, получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.

ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.

Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что, в случае успешного обучения, сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке, а также неполных и/или «зашумленных», частично искаженных данных. Схема простой нейросети представлена на рисунке 13.

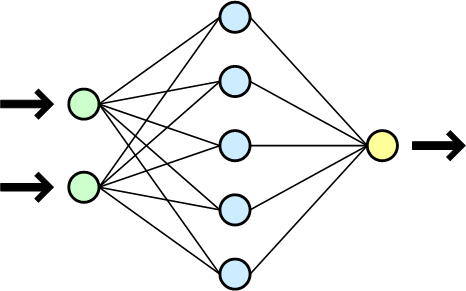
Рис. 13. Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым — выходной элемент.

Нейросети широко используются для поиска зависимостей в данных и кластеризации. Например, нейросеть на основе методики МГУА (метод группового учета аргументов) позволяет на основе обучающей выборки построить зависимость одного параметра от других в виде полинома. Такая сеть может найти сложные скрытые зависимости в данных, которые не обнаруживаются стандартными статистическими методами. Это открывает интересную перспективу использования нейросетей для выявления аномальной активности трафика. К тому же задача кластеризация очень схожа с задачей стратификации, о которой говорилось в пункте 2.5. Нейросети – довольно сложная тема и в данной работе рассмотрена очень поверхностно. Но уже по имеющимся данным можно утверждать, что нейронные сети можно использовать для создания алгоритма выявления аномальной активности сетевого трафика, но тем не менее этот вопрос требует более детального изучения.

2.7 Перспективы дальнейших исследований.

Несмотря, на то, что сформулирована общая идея алгоритма, остается большой простор для исследования, так как только были выдвинуты возможные методы обнаружения аномальной активности сетевого трафика, но не применены на практике. К тому же помимо предложенных методов: разбивания на области (страты) и определения характера сетевой активности на основании зависимостей характерных оценок альтернирующего потока, вполне вероятно, что существуют и другие методы. Существуют такие области научной деятельности, как нейронные сети и теория выбросов в прикладной статистике, которые вполне могут быть использованы для дальнейшей исследовательской области по тематике дипломного проекта.

Заключение.

При работе над дипломным проектом были достигнуты следующие цели:

Были изучены модели дважды стохастических потоков.
Разработана общая идея алгоритма.
Написано программное обеспечение для сбора и анализа статистики.
Собраны статистические данные.
Проанализированы полученные данные, построены оценки потока.
Предложены возможные методы выявления аномальной активности в сети.

Задача построения адаптивного алгоритма выявления аномального поведения трафика сети на основании характерных изменений оценок параметров, эффективно работающего в любой компьютерной сети, является очень обширной и полностью рассмотреть ее в рамках одной работы не представляется возможным. Несмотря на то, что в работе представлены несколько возможных методов выявления аномальной активности сетевого трафика, остается большой простор для исследовательской деятельности по данной тематике. Большой научный интерес к задаче обусловлен обширностью темы и отсутствием подобных алгоритмов. Для дальнейшей работы в этой области потребуются исследования и наработки других научных областей, например, таких, как нейронные сети и теория выбросов в прикладной статистике.

Список литературы.

[1] Erlang A. K. – The Theory of Probabilities and Telephone Conversations // Nyt Tidsskrift for Matematik – 1909. – Vol. 20. – pp 33–39.

[2] Головко Н.И., Каретник В.О., Танин В.Е., Сафонюк И.И. – Исследование моделей систем массового обслуживания в информационных сетях // Сибирский журнал индустриальной математики. – 2008. – T.XI -№ 2(34). – стр.. 50-58.

[3] Кендалл Д. – Стохастические процессы, встречающиеся в теории очередей, и их анализ методом вложенных цепей Маркова. // Сборник переводов "Математика" – 1959. – 3:6 – стр. 97 – 111.

[4] Хинчин А. Я. – Работы по математической теории массового обслуживания. – М.: Физматгиз. – 1963. – 235 с.

[5] Хинчин А. Я. – Математическая теория стационарной очереди. // Матем. сб. – 1932. – № 39. – стр. 73 – 84.

[6] В. В. Рыков – Управляемые системы массового обслуживания. // Итоги науки и техн. Сер. Теор. вероятн. Мат. стат. Теор. кибернет., т.12. – М.: ВИНИТИ. – 1975. – стр. 43 – 153.

[7] Дынкин Е.Б., Юшкевич А.А. – Управляемые марковские процессы и их приложения. – М.: НАУКА. – 1975. – 342 с.

[8] Васильева Л. А., Горцев А. М. – Оценивание параметров дважды стохастического потока событий в условиях его неполной наблюдаемости. // АиТ. – 2002. – № 3. – стр. 179 – 184.

[9] Горцев А. М., Ниссенбаум О. В. – Оптимальная оценка состояний асинхронного альтернирующего потока с инициированием лишних событий. // Вестн. ТюмГУ. – 2008. – № 6. – стр. 107 – 119.

[10] Горцев А. М., Шмырин И. С. – Оптимальная оценка состояний дважды стохастического потока событий при наличии ошибок в измерениях моментов времени. // АиТ. – 1999. – № 1. – стр. 52 – 66.

[11] Нежельская Л. А. – Алгоритм оценивания состояния синхронного МС-потока. // Тр. 11 Белорус. шк.-сем. по мас. обсл. – Минск. – 1995. – стр. 93 – 94.

[12] Никольский Н. Н – Адаптивный алгоритм контроля доступа вызовов в сетях пакетной телефонии для кодеков с переменной интенсивностью передачи информации // Автореферат диссертации на соискание ученой степени кандидата технических наук, Москва – 2007 – 168 c.

[13] Беккерман Е.Н., Катаев С.Г., Катаева С.С, Кузнецов Д.Ю. Аппроксимация МС-потоком реального потока событий // Вестник Томского гос. ун-та. — 2005. — № 14. Приложение. — С. 248-253.

[14] Ниссенбаум О. В., Пахомов И. Б. Аппроксимация сетевого трафика моделью альтернирующего потока событий // Прикладная дискретная математика. Приложение №1. – 2009. – стр. 78-79.

[15] Grossman A., Morlet J. – SIAM Journal Mathematics Analysis. – 1984. – Vol. 15. – p. 723.

[16] Добеши И. – Десять лекций по вейвлетам. – М.: Регулярная и хаотическая динамика. – 2001. – 464 c.

[17] Паниотто В. И. – Количественные методы в социологических исследованиях. – Киев: Наукова думка – 1982.

[18] Мак-Каллок У.С., Питтс В., Логическое исчисление идей, относящихся к нервной активности // В сб.: «Автоматы» под ред. К. Э. Шеннона и Дж. Маккарти. – М.: Изд-во иностр. лит. – 1956. – с.363

Приложение. Исходные коды.

Метод считает оценки параметров потока – λ, α₁ , α₂.

Параметры:

List< List > mainIntervalsList – список списков интервалов между пакетами за определенный промежуток времени.

List lambdaList, List alpha1List, List alpha2List, List lambdaWave – списки, которые в конце работы метода будет заполненs значениями λ, α₁ , α₂и λ с волной, соответственно.

private void GetParamMarks (List< List > mainIntervalsList,

List lambdaList, List alpha1List,

List alpha2List, List lambdaWave)

{

try

{

alpha1List.Clear();

alpha2List.Clear();

lambdaList.Clear();

lambdaWave.Clear();

int statlen = mainIntervalsList.Count;

int[] val = new int[statlen];

double alp1mom = 0;

double alp2mom = 0;

double lammom = 0;

for (int count = 0; count < statlen; count++)

{

double C1 = 0;

double C2 = 0;

double C3 = 0;

for (int i = 0; i < mainIntervalsList[count].Count; i++)

{

double interval = mainIntervalsList[count][i];

C1 += interval;

C2 += Math.Pow(interval, 2);

C3 += Math.Pow(interval, 3);

}

C1 /= mainIntervalsList[count].Count;

C2 /= mainIntervalsList[count].Count;

C3 /= mainIntervalsList[count].Count;

double ksi = ((3 * C2 * C2) - (2 * C1 * C3));

double beta = (C3 - (3 * C1 * C2)) / ksi;

double ceta = 6 * ((2 * C1 * C1) - C2) / ksi;

double discrim = beta * beta - ceta;

if (beta <= 0 && ceta >= 0 && discrim >= 0)

{

double z1 = -beta + Math.Sqrt(discrim);

double z2 = -beta - Math.Sqrt(discrim);

double gamma = (z1 * z2 * (C1 - 1 / z2)) / (z2 - z1);

double lam = z2 - (z1 * z2 * (C1 - (1 / z2)));

double alp2 = (z1 * z2) / lam;

double alp1 = z1 + z2 - alp2 - lam;

if (lam < 0 || alp1 < 0 || alp2 < 0)

{

lam = 1 / C1;

alp2 = lam;

alp1 = 0;

}

alp1mom = alp1;

alp2mom = alp2;

lammom = lam;

}

lambdaList.Add(lammom);

alpha1List.Add(alp1mom);

alpha2List.Add(alp2mom);

lambdaWave.Add(1 / C1);

}

}

catch (Exception ex)

{

MessageBox.Show(ex.Message, "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);

}

}

Метод WaveletAnalyze делает разложение временного ряда (который подается в ксачестве параметра) вейвлет-преобразованием по базису Хаара и возвращает список разложений. CalcStep – вспомогательный метод.

public static List> WaveletAnalyze(List sourceList)

{

List> res =

new List>((int)Math.Log(sourceList.Count, 2) + 1);

int intervalLength = sourceList.Count;

for (int i = 0; i < Math.Log(sourceList.Count, 2); i++)

{

res.Add( CalcStep( sourceList, intervalLength ) );

intervalLength /= 2;

}

res.Add(sourceList);

return res;

}

private static List CalcStep(List sourceList, int length)

{

List result = new List();

int count = sourceList.Count / length;

for (int i = 0; i < count; i++)

{

double sum = 0;

for (int j = 0; j < length; j++)

sum += sourceList[i * length + j];

sum /= length;

for (int j = 0; j < length; j++)

sourceList[i * length + j] -= sum;

result.Add(sum);

}

return result;

}

Метод GetFreq возвращает конкретное разложение из всего списка разожений, полученных вейвлет-преобразованием.

private static List GetFreq(List> wave, int number)

{

int countOfWavelet = wave[wave.Count - 1].Count;

double[] res = new double[countOfWavelet];

int countPeriod = countOfWavelet / wave[number].Count;

int from = 0;

for (int i = 0; i < wave[number].Count; i++)

{

for (int j = from; j < from + countPeriod; j++)

res[j] = wave[number][i];

from += countPeriod;

}

return new List(res);

}

Метод GetSmoothNumbers строит сглаженный временной ряд по частотным разложениям, полученым вейвлет-преобразованием. Параметр count отвечает за то, сколько “верхних” разложений будет убрано, чтобы сгладить итоговый ряд.

private static List GetSmoothNumberst(List> wave,

int count)

{

int countOfWavelet = wave[wave.Count - 1].Count;

double[] res = new double[countOfWavelet];

for (int i = 0; i < wave.Count - count; i++)

{

for (int j = 0; j < wave[i].Count; j++)

{

int from = (countOfWavelet / (wave[i].Count)) * j;

int to = from + (countOfWavelet / (wave[i].Count));

for (int k = from; k < to; k++)

res[k] += wave[i][j];

}

}

return new List(res);

}

Blog