1 Общее описание моделей дс потоков

Вид материала

Содержание

2.4. Сглаживание оценок.
2.4.1. Подходы к сглаживанию данных.
2.4.2. Вейвлет-анализ и его применение.
Обработка экспериментальных данных
Обработка изображений
Сжатие данных.
Нейросети и другие механизмы анализа данных.
Системы передачи данных и цифровой обработки сигналов.
2.4.3. Сглаживание экспериментальных данных.

Подобный материал:

1 2 3 4 5 6

2.4. Сглаживание оценок.

При наличии временных рядов оценок параметров, можно приступать к непосредственно самой задаче анализа активности пользователя в сети. Как видно из рисунка 10, как правило графики оценок достаточно близки к графику кусочно-постоянной функции. Интервалы постоянства можно квалифицировать как интервалы, на которых характер трафика достаточно стабилен и однороден. Момент окончания такого интервала и начала следующего интервала постоянства есть момент, когда ситуация в сети изменяется, то есть характер трафика становится другим.

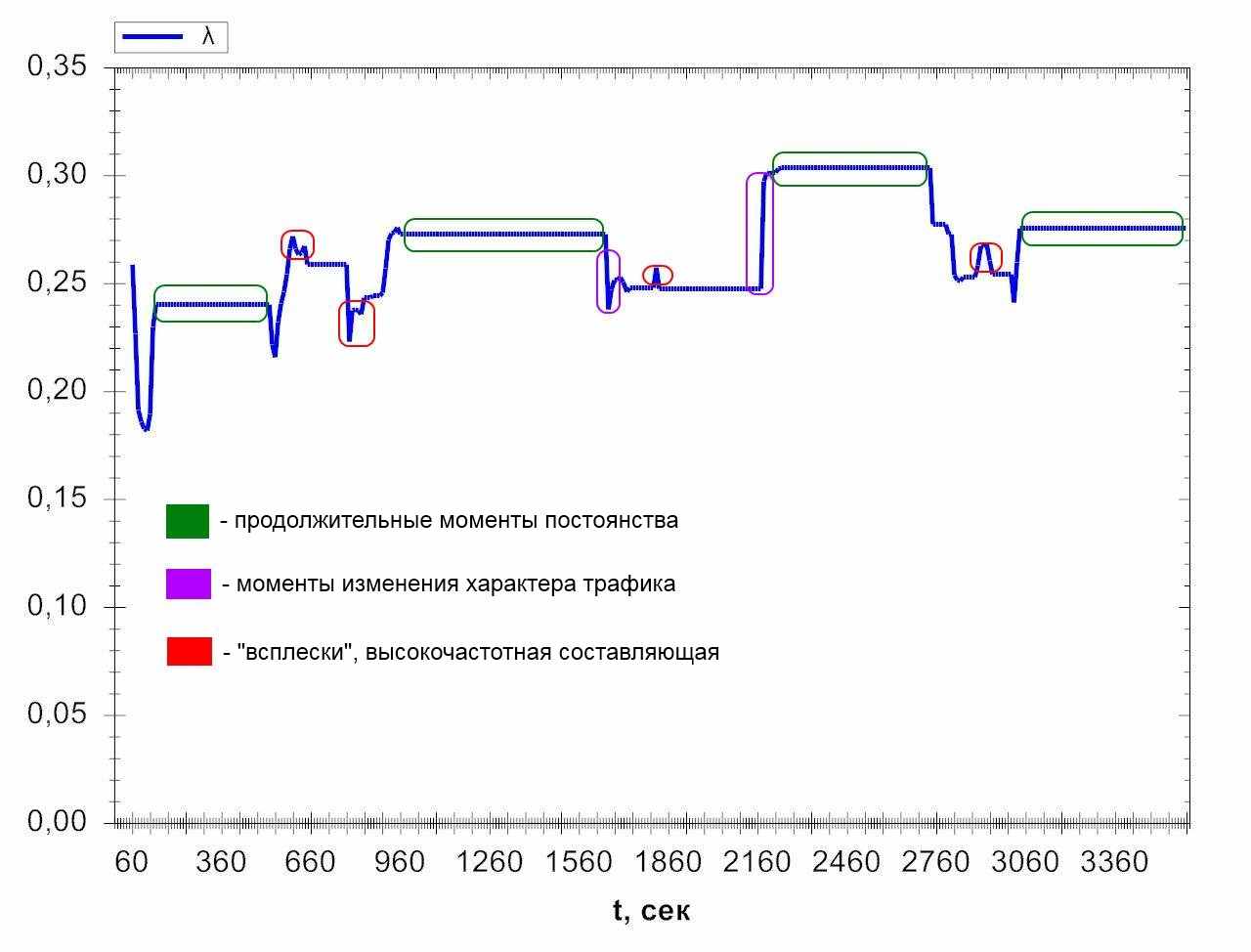
Рис. 10. Несглаженный временной ряд оценки λ.

Но также на графике присутствуют небольшие “всплески” – высокочастотная составляющая. Причиной таких высокочастотных колебаний является, во-первых, то, что математическая модель альтернирующего потока не в точности соответствует реальному трафику, как никакая идеальная модель не может соответствовать реальному явлению. Во-вторых, метод оценки параметров потока λ, α₁, α₂ имеет небольшую погрешность [8], которая также является причиной отклонений на графике. Такие колебания оценок могут затруднить определение моментов изменения характера трафика, маскируя их и затрудняя выделение интервалов постоянства на графике. Поэтому для упрощения последующей работы с временными рядами оценок, необходимо отфильтровать высокочастотные составляющие.

2.4.1. Подходы к сглаживанию данных.

На сегодняшний день наиболее используемыми способами фильтрации данных являются: преобразование Фурье и вейвлет-преобразование. Оба этих подхода можно применить для фильтрации данных в рассматриваемом случае, однако преобразование Фурье имеет несколько недостатков: во-первых: исходный сигнал заменяется на периодический, с периодом равным длительности исследуемого образца; во-вторых: преобразование Фурье плохо работает при изменении параметров процесса со временем (нестационарности), поскольку дает усредненные коэффициенты для всего исследуемого образца. Вейвлет-преобразование по базису Хаара лишено этих недостатков.

2.4.2. Вейвлет-анализ и его применение.

Основы вейвлет-анализа были разработаны в середине 80-х годов Гроссманом и Морле [15] как альтернатива преобразованию Фурье для исследования временных (пространственных) рядов с выраженной неоднородностью. В отличие от преобразования Фурье, локализующего частоты, но не дающего временного разрешения процесса, и от аппарата d-функций, локализующего моменты времени, но не имеющего частотного разрешения, вейвлет-преобразование, обладающее самонастраивающимся подвижным частотно-временным окном, одинаково хорошо выявляет как низко-частотные, так и высокочастотные характеристики сигнала на разных временных масштабах. По этой причине вейвлет-анализ часто сравнивают с "математическим микроскопом", вскрывающим внутреннюю структуру существенно неоднородных объектов.

Указанная универсальность обеспечила вейвлет-анализу широкое использование в самых различных областях знаний. Семейства анализирующих функций, называемых вейвлетами, применяются при анализе изображений различной природы, для изучения структуры турбулентных полей, для сжатия больших объемов информации, в задачах распознавания образов, при обработке и синтезе сигналов, например, речевых, для определения характеристик фрактальных объектов.

Подобно тому, как в основе аппарата преобразований Фурье лежит единственная функция w(t)=exp(it), порождающая ортонормированный базис пространства L2(0,2p) путем масштабного преобразования, так и вейвлет-преобразование строится на основе единственной базисной функции y(t), имеющей солитоноподобный характер и принадлежащей пространству L2(R), т.е. всей числовой оси.

В западной литературе за этой функцией закрепилось название "вейвлет", что означает "маленькая волна", в отечественной – иногда ее называют "всплеском".

Самый распространенный набор дискретных вейвлет-преобразований был сформулирован бельгийским математиком Ингрид Добеши (Ingrid Daubechies)[16] в 1988 году. Он основан на использовании рекуррентных соотношений для вычисления всё более точных выборок неявно заданной функции материнского вейвлета с удвоением разрешения при переходе к следующему уровню (масштабу). В своей основополагающей работе Добеши выводит семейство вейвлетов, первый из которых является вейвлетом Хаара.

Примеры часто используемых вейвлетов

HAAR - вейвлет:

FHAT - вейвлет ("Французская шляпа" - French hat):

Wave - вейвлет:

MHAT - вейвлет ("Мексиканская шляпа" - Mexican hat):

Вейвлет Морле (образует комплексный базис):

Применение вейвлет-преобразования:

Обработка экспериментальных данных. Поскольку вейвлеты появились именно как механизм обработки экспериментальных данных, их применение для решения подобных задач представляется весьма привлекательным до сих пор. Вейвлет-преобразование дает наиболее наглядную и информативную картину результатов эксперимента, позволяет очистить исходные данные от шумов и случайных искажений, и даже "на глаз" подметить некоторые особенности данных и направление их дальнейшей обработки и анализа. Кроме того, вейвлеты хорошо подходят для анализа нестационарных сигналов, возникающих в медицине, анализе фондовых рынков и других областях.

Обработка изображений. Наше зрение устроено так, что мы сосредотачиваем свое внимание на существенных деталях изображения, отсекая ненужное. Используя вейвлет-преобразование, мы можем сгладить или выделить некоторые детали изображения, увеличить или уменьшить его, выделить важные детали и даже повысить его качество!

Сжатие данных. Особенностью ортогонального многомасштабного анализа является то, что для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине к нулю и, следовательно, очень хорошо сжимаются обычными статистическими методами. Огромным достоинством вейвлет-преобразования является то, что оно не вносит дополнительной избыточности в исходные данные, и сигнал может быть полностью восстановлен с использованием тех же самых фильтров. Кроме того, отделение в результате преобразования деталей от основного сигнала позволяет очень просто реализовать сжатие с потерями – достаточно просто отбросить детали на тех масштабах, где они несущественны! Достаточно сказать, что изображение, обработанное вейвлетами, можно сжать в 3-10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!). В качестве примера отметим, что вейвлет-преобразование положено в основу стандарта сжатия данных MPEG4.

Нейросети и другие механизмы анализа данных. Большие трудности при обучении нейросетей (или настройке других механизмов анализа данных) создает сильная зашумленность данных или наличие большого числа "особых случаев" (случайные выбросы, пропуски, нелинейные искажения и т.п.). Такие помехи способны скрывать характерные особенности данных или выдавать себя за них и могут сильно ухудшить результаты обучения. Поэтому рекомендуется очистить данные, прежде чем анализировать их. По уже приведенным выше соображениям, а также благодаря наличию быстрых и эффективных алгоритмов реализации, вейвлеты представляются весьма удобным и перспективным механизмом очистки и предварительной обработки данных для использования их в статистических и бизнес-приложениях, системах искусственного интеллекта и т.п.

Системы передачи данных и цифровой обработки сигналов. Благодаря высокой эффективности алгоритмов и устойчивости к воздействию помех, вейвлет-преобразование является мощным инструментом в тех областях, где традиционно использовались другие методы анализа данных, например, преобразование Фурье. Возможность применения уже существующих методов обработки результатов преобразования, а также характерные особенности поведения вейвлет-преобразования в частотно-временной области позволяют существенно расширить и дополнить возможности подобных систем.

2.4.3. Сглаживание экспериментальных данных.

Для упрощения обработки данных необходимо произвести сглаживание, что позволит отфильтровать высокочастотную составляющую, которая ошибочно может быть принята, за изменения характера трафика. Алгоритм по сглаживанию временных рядов вейвлет-преобразованием по базису Хаара был успешно реализован, результат его действия представлен на рисунке 11.

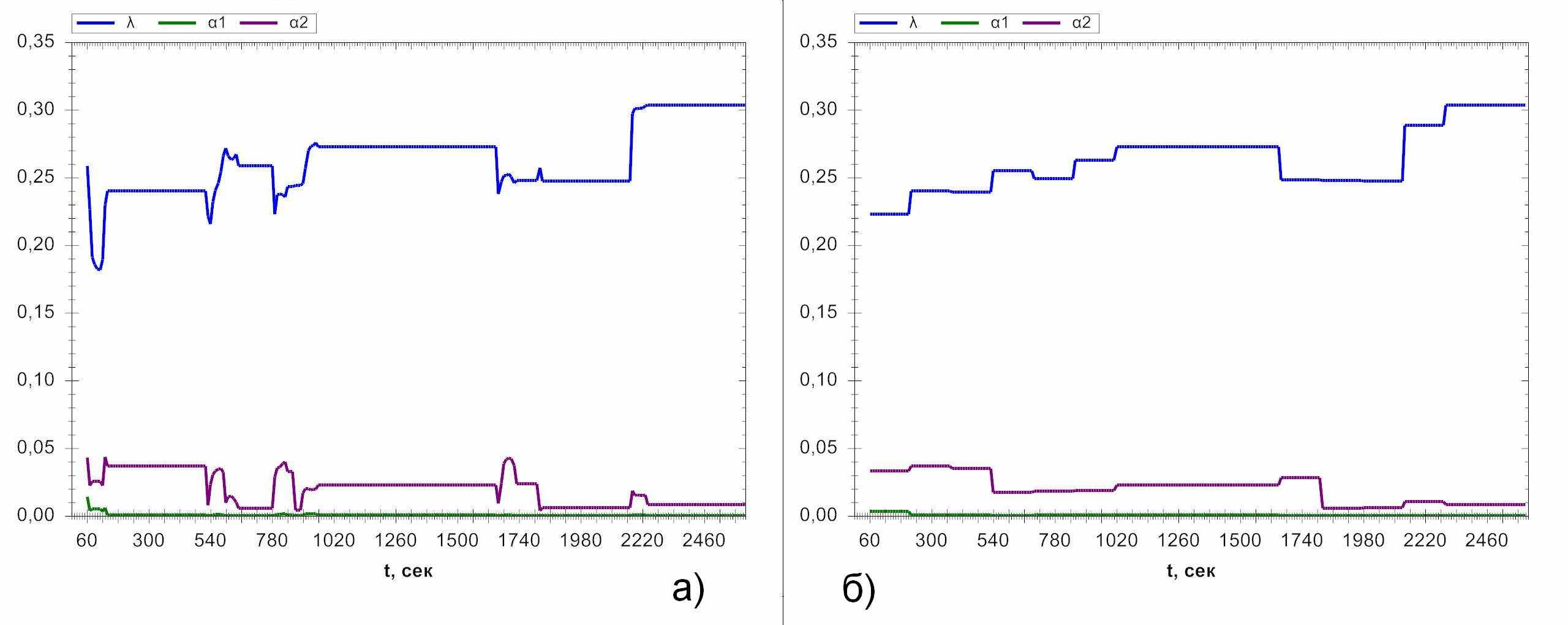
Рис 11. а) несглаженные временные ряды параметров.

б) сглаженные временные ряды параметров

Чтобы получить сглаженный временной ряд, при помощи вейвлет-преобразования производилось частотное разложение исходного временного ряда. Затем разложение, содержащее самую высокую частоту, удалялось и проводилась обратная сборка ряда. Результатом такой обработки временных рядов, изображенных на рисунке 11а, стали сглаженные ряды c более четкими моментами изменения характера трафика (рис. 11б). В ходе преобразования при разложении временного ряда значений λ, изображенном на рисунке 11а, вейвлет-преобразованием по базису Хаара были получены следующие разложения (рис. 12):