Geum.ru

1 Общее описание моделей дс потоков

Вид материалаДокументы

Содержание


Глава 1. Актуальные математические модели трафика компьютерной сети 1.1. Состояние проблемы.
Подобный материал:
1   2   3   4   5   6

Глава 1.

Актуальные математические модели трафика компьютерной сети




1.1. Состояние проблемы.


Развитие теории массового обслуживания, с помощью которой, возможно успешно описать модель сетевого трафика, насчитывает очень длительный период времени. Первые работы в этой области были опубликованы датским ученым А.К. Эрлангом в 1908-1922 годах [1]. Эти работы уже тогда определили основную область применения новой теории - обслуживание телетрафика.

Весомый вклад в развитие ТМО внесли такие ученые как В. Феллер, Д. Кенделл, А.Я. Хинчин и др. [3, 4]. В частности, один из основных методов теории - метод вложенных цепей Маркова - был разработан А.Я. Хинчиным [5] в начале 30-х гг.

Входящие потоки событий в системах массового обслуживания (СМО), рассмотренных в тот период времени, аппроксимировались одной из трех моделей: регулярный поток (системы с таким потоком относятся к детерминированным и рассматриваются в теории оптимизации как системы конвейерного типа), простейший (пуассоновский) поток и эрланговский (поток, полученный из пуассоновского путем разрежения) поток событий. При этом особое внимание уделяется системам с простейшим входящим потоком, тем более что СМО с входящим потоком Эрланга можно моделировать системой с входящим пуассоновским потоком.

В шестидесятые годы появились первые работы в области так называемых управляемых СМО [6, 7]. Исключительная актуальность оптимизационных задач, приведших к возникновению таких систем, объясняет дальнейшее бурное развитие этой тематики. Широта области применения управляемых систем и разнообразие задач, которые оказалось возможным решить с их помощью, повлекли более тщательную разработку этого направления. Ставились и решались все более частные задачи.

Несмотря на довольно широкую область применения ТМО, главными областями использования теории являются автоматизированные системы управления (АСУ) и сети связи, в том числе компьютерные сети. Наиболее сложные модели систем массового обслуживания создаются и исследуются именно для этих двух областей.

До середины 80-х годов относительная простота систем связи, изолированность разных видов связи друг от друга, низкая пропускная способность каналов, их дороговизна и, следовательно, высокая их загруженность приводили к тому, что для входящих потоков заявок использовались все те же относительно простые модели, что и во времена К.А. Эрланга - простейший поток. Реже - регулярный и эрланговский потоки. Усложнение структуры информационных систем, интеграция различных систем связи, разнообразие программного и аппаратного обеспечения, протоколов передачи информации приводят к тому, что теория, существовавшая до 80-х годов, во многом становится непригодной для анализа случайных процессов, существующих в современных сетях связи. В то же время, ТМО предлагает надежные, хорошо изученные общие математические методы теории вероятностей для детального анализа таких систем.

1.2. Общее описание моделей ДС потоков.


Модель пуассоновского потока соответствует реальному трафику компьютерной сети только на сравнительно небольших отрезках времени, так как интенсивность трафика, как правило, меняется со временем. Вообще, загрузка сетей связи зависит от многих факторов. Она может изменяться как циклически в течение суток (недели, года), так и в зависимости от того, какие компьютерные приложения в данный момент используют сеть. С одной стороны, локальная сеть организации загружена больше днем, чем ночью, с другой стороны сеть используется по-разному различными пользователями. В частности, можно различить сетевую активность делопроизводителя, который работает с электронными документами и пользуется сетью только для их отправки и получения данных, и системного администратора, на чей компьютер постоянно поступают данные о состоянии компьютеров и сетевых устройств офиса. Трафик первого пользователя представляет собой чередование долгих периодов "молчания" и кратковременных периодов, когда пакеты информации следуют один за другим. Трафик второго пользователя более равномерен. Однако, и в том и в другом случае имеется дело с потоками переменной интенсивности, причем изменения интенсивности таких потоков, как правило, носят стохастический характер. Такие потоки принято называть дважды стохастическими.

Такая случайная зависимость интенсивности входящих потоков от времени на практике встречается чаще, чем постоянная интенсивность, поэтому модели дважды стохастических потоков представляют определенный интерес с точки зрения практических приложений.

Интенсивность дважды стохастического потока является случайным процессом. В зависимости от характера этого процесса выделяют два больших класса таких потоков: 1) потоки, интенсивность которых является непрерывным (диффузионным) процессом; 2) потоки, интенсивность которых является кусочно-постоянным процессом.




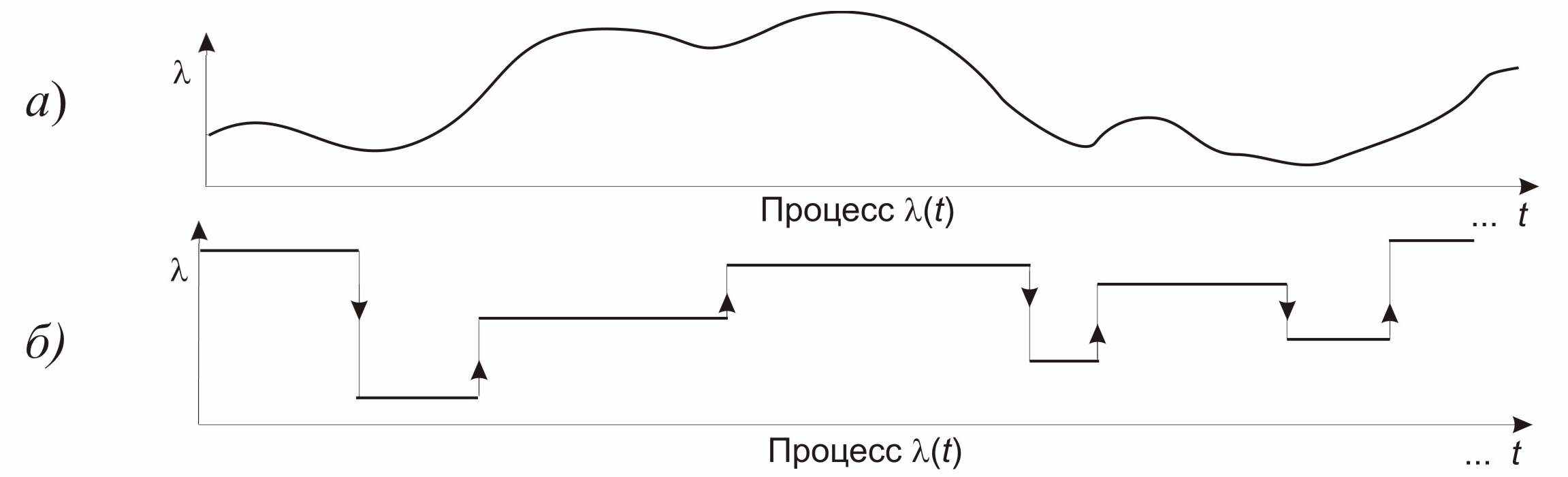
Рис.1. Изменение интенсивности дважды стохастического потока событий а) с непрерывно изменяемой интенсивностью; б) с кусочно-постоянной интенсивностью.

Потоки, интенсивность которых есть кусочно-постоянный процесс, в свою очередь, подразделяются на потоки с конечным числом состояний (с конечным числом значений, которое может принять процесс) и потоки со счетным числом состояний. Смена состояний происходит в случайные моменты времени, а на интервалах постоянства интенсивности поток ведет себя как простейший. Такие потоки наиболее пригодны для описания реальных потоков в сетях связи и цифровых сетях интегрального обслуживания. А также выделяют потоки с двумя состояниями, одно из которых соответствует нулевой интенсивности. Такие потоки называют альтернирующими.

Проводя наиболее общую классификацию альтернирующих потоков, выделяют следующие основные типы потоков: 1) асинхронные потоки событий, то есть потоки, изменение интенсивности которых происходит в случайные моменты времени, не связанные с моментами наступления событий; 2) полусинхронные потоки событий, то есть потоки, у которых переход из второго состояния в первое происходит в моменты наступления событий, а из первого во второе - независимо от моментов наступления событий.

Альтернирующие потоки, асинхронные и полусинхронные, могут являться моделями потоков, поступающих в общую сеть с одного источника. Например, источник может отправлять информацию на обслуживающий прибор порциями по мере ее накопления, что сформирует полусинхронный поток с двумя состояниями от источника (либо информация пересылается с максимальной интенсивностью, либо не пересылается вовсе, начало и конец окон передачи информации совпадают с моментами пересылки первого и последнего пакетов в "порции"). Если же интервалы времени, когда источник может проводить передачу, определяет обслуживающее или иное устройство, исходя из загруженности сети или сервера, то имеем асинхронный поток с двумя состояниями. В цифровых сетях, в частности, в компьютерных сетях, такими моделями может быть аппроксимирован трафик, исходящий от определенного порта компьютера (браузерный Интернет-трафик, трафик почтового сервиса, файловый трафик и т.п.). Для таких моделей были решены задачи оценивания состояний и параметров [8, 9, 10, 11].

Следует отметить, что характеристики потока, исходящего от одного источника, являются важными в свете некоторых практических задач. Например, поток исходящих информационных пакетов по какому-либо виду трафика в компьютерной сети характеризуется набором параметров потока, а значит, оценив эти параметры, можно составить определенный "портрет" источника, который, в свою очередь, может быть использован при анализе безопасности трафика на предмет выявления аномальной активности (вызванной, например, деятельностью сетевого вируса).

В то же время, не только в научной, но и в учебной и популярной литературе по информационным сетям всё чаще упоминаются вопросы разработки теоретических положений и необходимость научно обоснованных технических решений, обеспечивающих эффективность и повышение качества администрирования информационных сетей на основе исследования циркулирующих в них потоков.

На данный момент проведено достаточно большое количество исследований дважды стохастических потоков событий с точки зрения задач определения характеристик СМО, оценивания параметров и состояний потока. Также часто в литературе решается задача оптимального оценивания состояний дважды стохастического потока событий [8, 9, 10].

Таким образом, развитие телекоммуникационных сетей, информационных технологий, интегрирование различных видов связи, вычислительных систем и сетей породило множество задач по моделированию и анализу обслуживания информационных потоков, циркулирующих в сетях. В частности, такие информационные потоки достаточно адекватно описываются моделями дважды стохастических потоков событий [12, 13].