Краткий курс лекций по дисциплине «Электрические железные дороги» специальность 180700

Вид материала

Курс лекций

Содержание 20. Образование силы торможения. К – действительная сила нажатия на одну колодку; V Расчетный тормозной коэффициент 21. Сопротивления движению поезда. Сопротивление пути Сопротивление подвижного состава Сопротивление внешней среды От уклонов От кривых При низких температурах окружающего воздуха 22. Уравнение движения поезда. 23. Анализ уравнения движения поезда.

Подобный материал:

• Краткий курс лекций по дисциплине «Подвижной состав железнодорожного транспорта» специальность, 910.14kb.
• Открытое акционерное общество "российские железные дороги", 198.35kb.
• Методические указания: краткий курс лекций для студентов заочной формы обучения Санкт-Петербург, 1540.61kb.
• Краткий курс лекций, 182.24kb.
• Н. В. Рудаков Краткий курс лекций, 1552.23kb.
• Открытое акционерное общество "российские железные дороги", 1369.07kb.
• В. Б. Аксенов Краткий курс лекций, 1098.72kb.
• Краткий курс лекций по медицинской паразитологии Часть Клещи, 643.33kb.
• Краткий курс лекций по философии учебно-методическое пособие для студентов всех специальностей, 2261.57kb.
• Учебно-методический комплекс дисциплины История английской литературы Специальность, 473.74kb.

19. Влияние  изменения передаточного отношения зубчатой передачи

и изменения диаметра колес колесных пар

на тяговую и электротяговые характеристики.












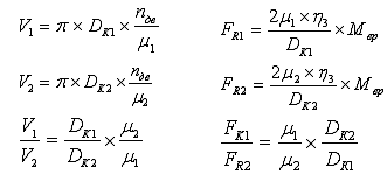
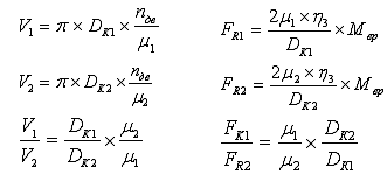
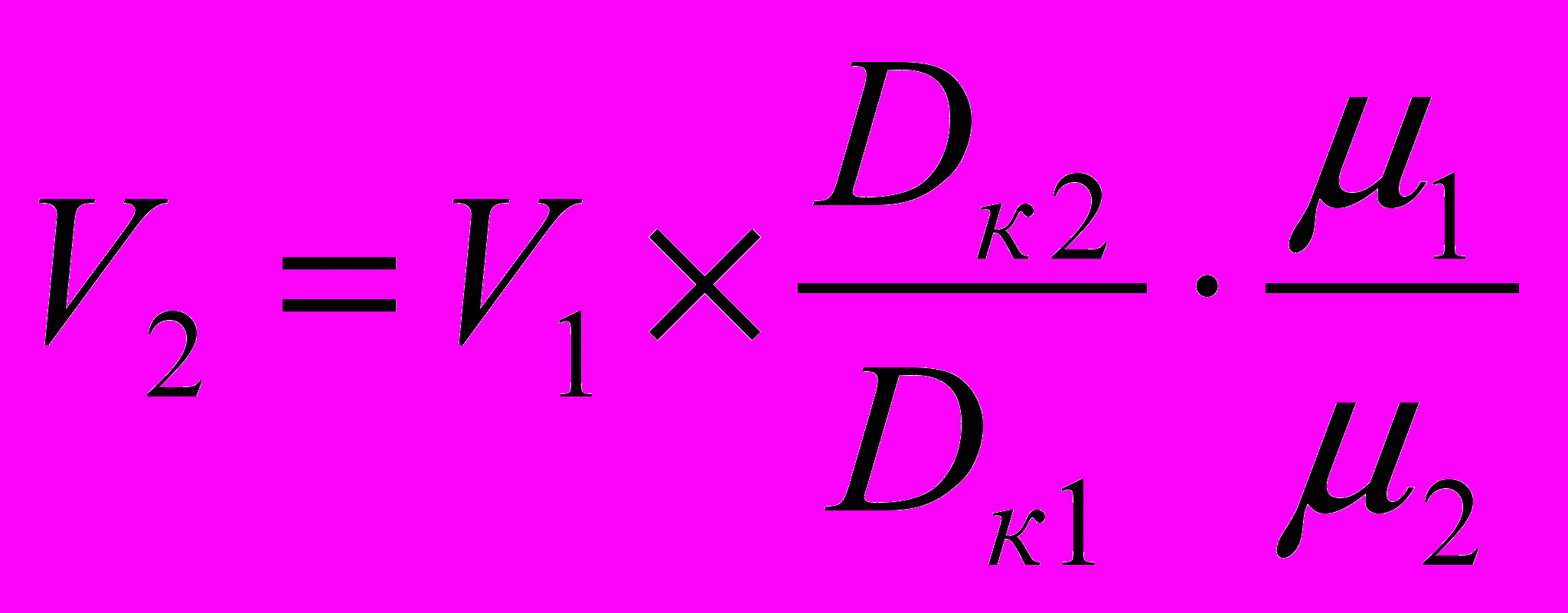
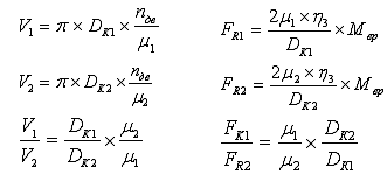
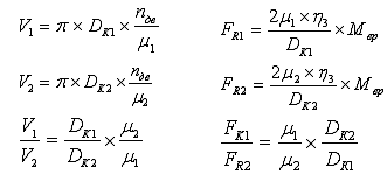
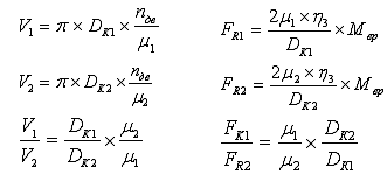
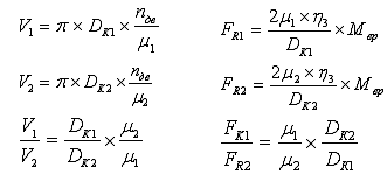
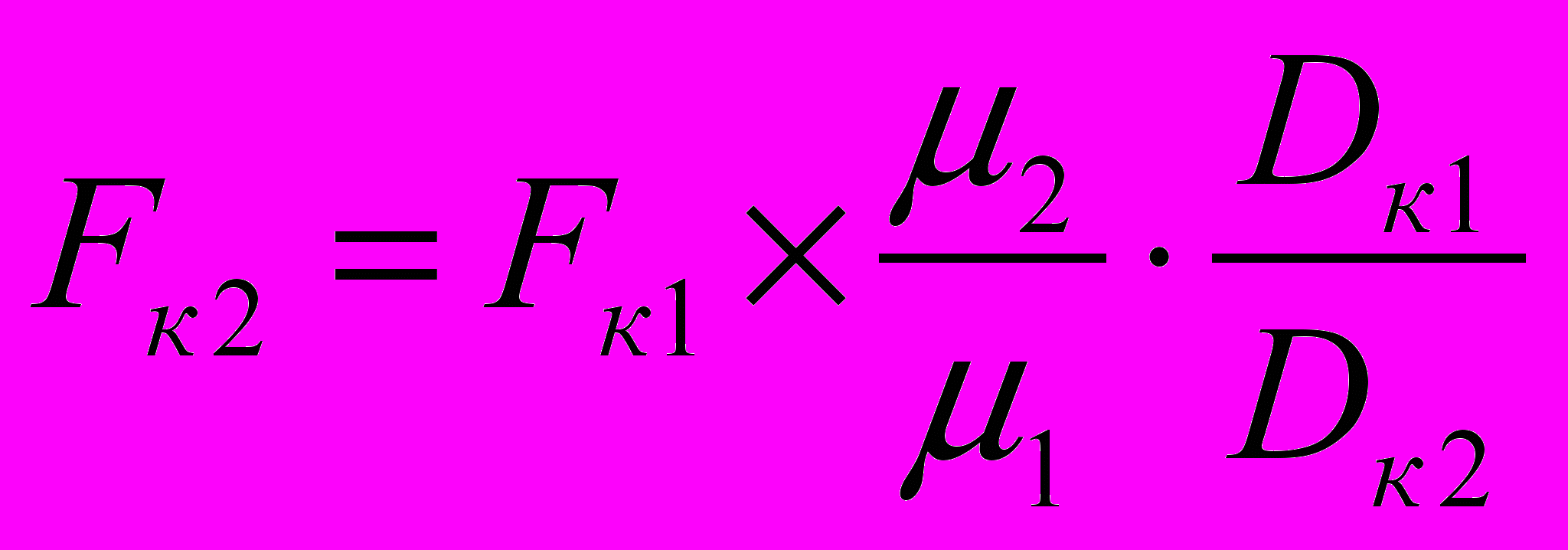
При неизменной частоте вращения якоря двигателя скорость движения будет больше при большем диаметре колес колесных пар и меньшем передаточном отношении зубчатой передачи.

При неизменном вращающемся моменте двигателя большая сила тяги будет при меньшем диаметре колес колесных пар и большем передаточном отношении зубчатой передачи.

Передаточное отношение у пассажирских локомотивов 1,5÷3,0, а у грузовых локомотивов - 3,5÷5,0.

20. Образование силы торможения.

П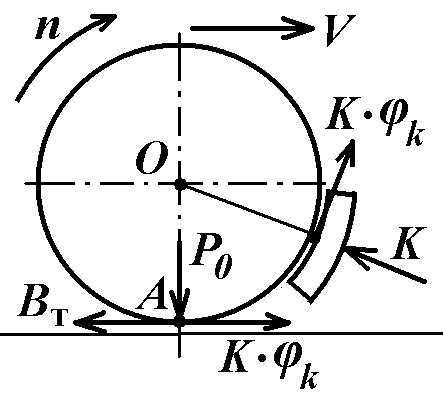ри механическом торможении подается сжатый воздух в тормозные цилиндры. Поршень в цилиндре перемещается, через шток, тяги  и рычаги прижимая тормозную колодку к колесу с усилением К. В месте контакта колеса с тормозной колодкой возникает сила трения K x φ_к, направленная навстречу вращению колеса. φ_к - это коэффициент трения колодки о колесо. Перенесем силу  силу трения

K x φ_к в точку А касания колеса с рельсом. Колесо прижато к рельсу силой Р₀. Обе эти силы внутренние по отношению к поезду и не могут повлиять на характер движения.

Если колесо прижато к рельсу с силой Р₀, то в результате сцепления колеса с рельсом сила 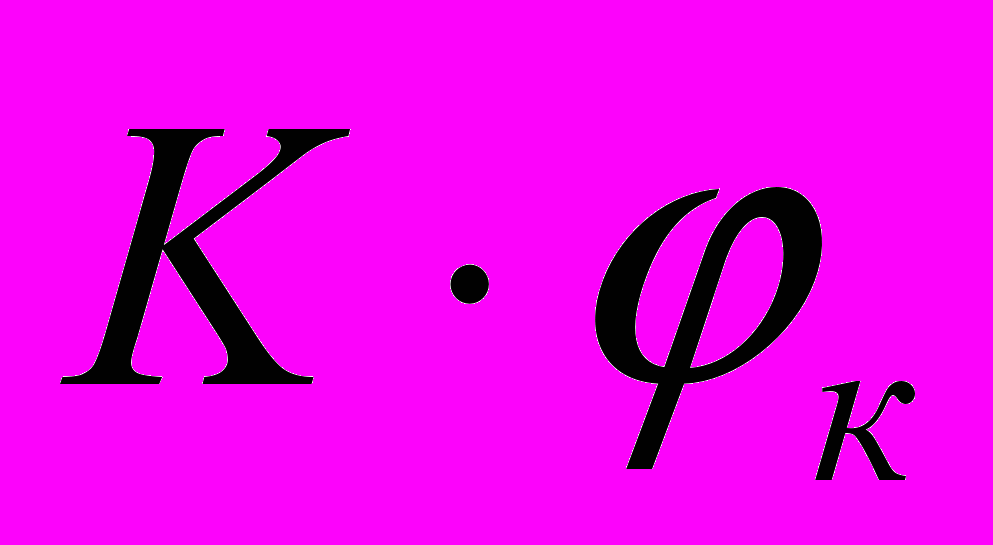 стремится сдвинуть рельс по направлению движения. Но рельс закреплен и вызывается реакция рельса по III закону Ньютона В_т, равная  K x φ_к и противоположно направленная. Эта сила по отношению к поезду является внешней и называется тормозной силой. Она действует против движения и создает колесу упор.

Тормозная сила одного колеса: B_т = K x φ_к

Сила «К» зависит от интенсивности торможения, от диаметра тормозного цилиндра, от давления воздуха в нем, от передаточного отношения рычажной передачи, от силы оттормаживающей пружины в тормозном цилиндре.

Коэффициент трения φ_к зависит от материала колодок, скорости движения и удельных сил нажатия колодок на колеса.

Применяются тормозные колодки: чугунные, чугунные с повышенным содержанием фосфора (до 1,0÷1,4%), и композиционные.

С увеличением скорости движения и удельного нажатия колодок коэффициент трения снижается, т.к. за счет тепла металл размягчается, в тонком слое может оплавиться. Для повышения коэффициента трения применяют двухстороннее нажатие колодок.

Коэффициент трения рассчитывают по эмпирическим формулам, например для чугунных накладок :

г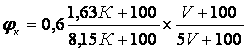де К – действительная сила нажатия на одну колодку; V – скорость движения.

Тормозная сила поезда определяется по формуле B_т = 1000 Σ K x φ_к , где В_т – тормозная сила в Н; К – сила нажатия на тормозную колодку в кН; 1000 – переводной коэффициент «кН» в «Н».

По этой формуле можно бы рассчитать тормозную силу, если бы вагоны были однотипными с одинаковыми силами нажатия колодок. А если вагоны разнотипные, то для каждой группы вагонов необходимо определять силу нажатия, рассчитывать коэффициент трения и суммировать.

Поэтому пользуются упрощенными методами. Применяются для расчета средние силы нажатия колодок четырехосного вагона при груженом и порожнем режимах для чугунных колодок К = 26,5 кН, для композиционных К = 15,7 кН. Подставив эти значения в эмпирические формулы коэффициента трения φ_к получаем так называемый расчетный коэффициент трения, который зависит только от скорости:

для чугунных колодок ,

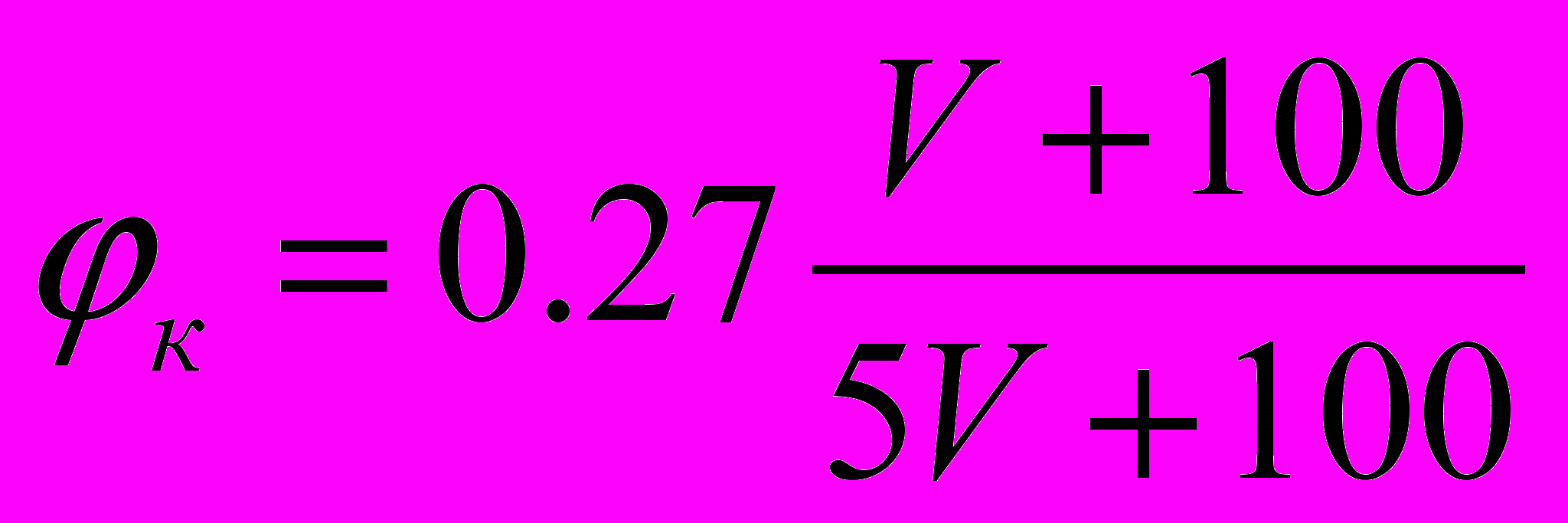для композиционных колодок .

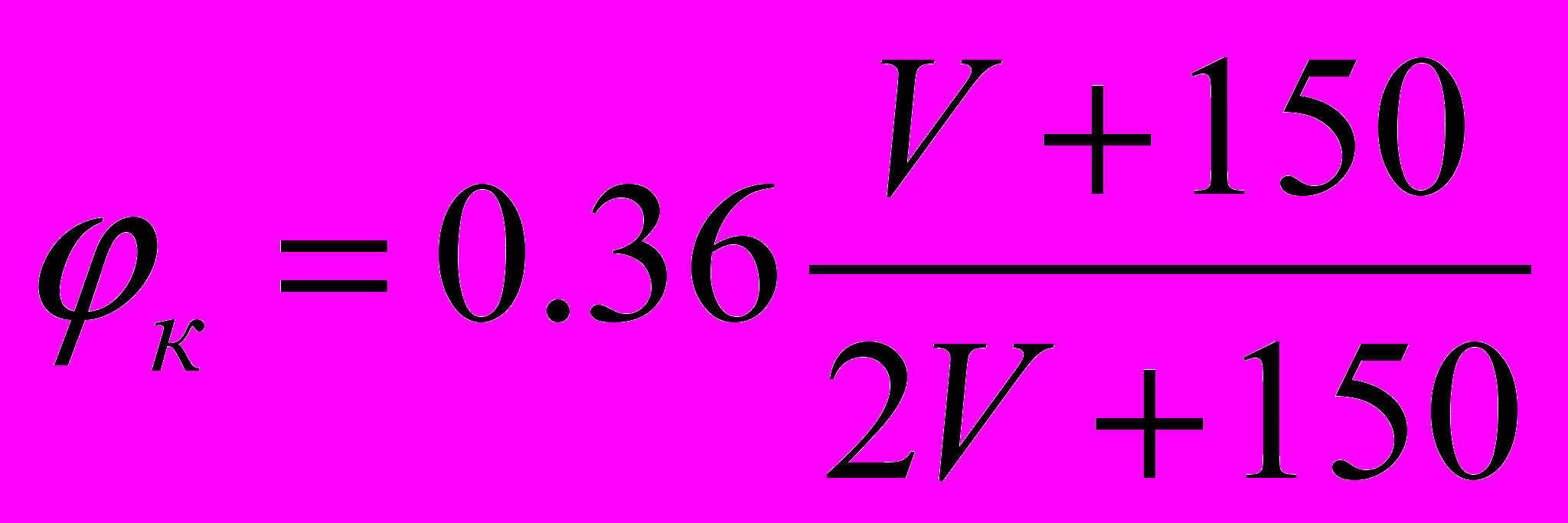Расчетные коэффициенты трения приводятся в таблице. Сравним эти величины: при V = 0→0,27 и 0,36; при V = 160→0,077  и 0,237. При сравнении заметно, что у чугунных колодок с увеличением скорости движения коэффициент трения резко снижается, да и чугунные колодки имеют больший износ. У композиционных колодок коэффициент трения выше. С увеличением скорости он в меньшей степени снижается. У чугунных колодок с повышенным содержанием фосфора коэффициент трения имеет промежуточное значение, но ближе к значениям чугунных колодок.

По величине тормозную силу желательно иметь большую. Но она не должна превышать силу сцепления колес с рельсами. В противном случае колесо прекращает вращение, начинается скольжение колеса по рельсу, образуется местный износ – ползун, который при дальнейшем движении по рельсам создает удары. K x φ_к ≤ P₀ x ψ . Отношение силы нажатия колодок на колесную пару К к нагрузке от колесной пары на рельсы Р₀ называют коэффициентом нажатия колодок 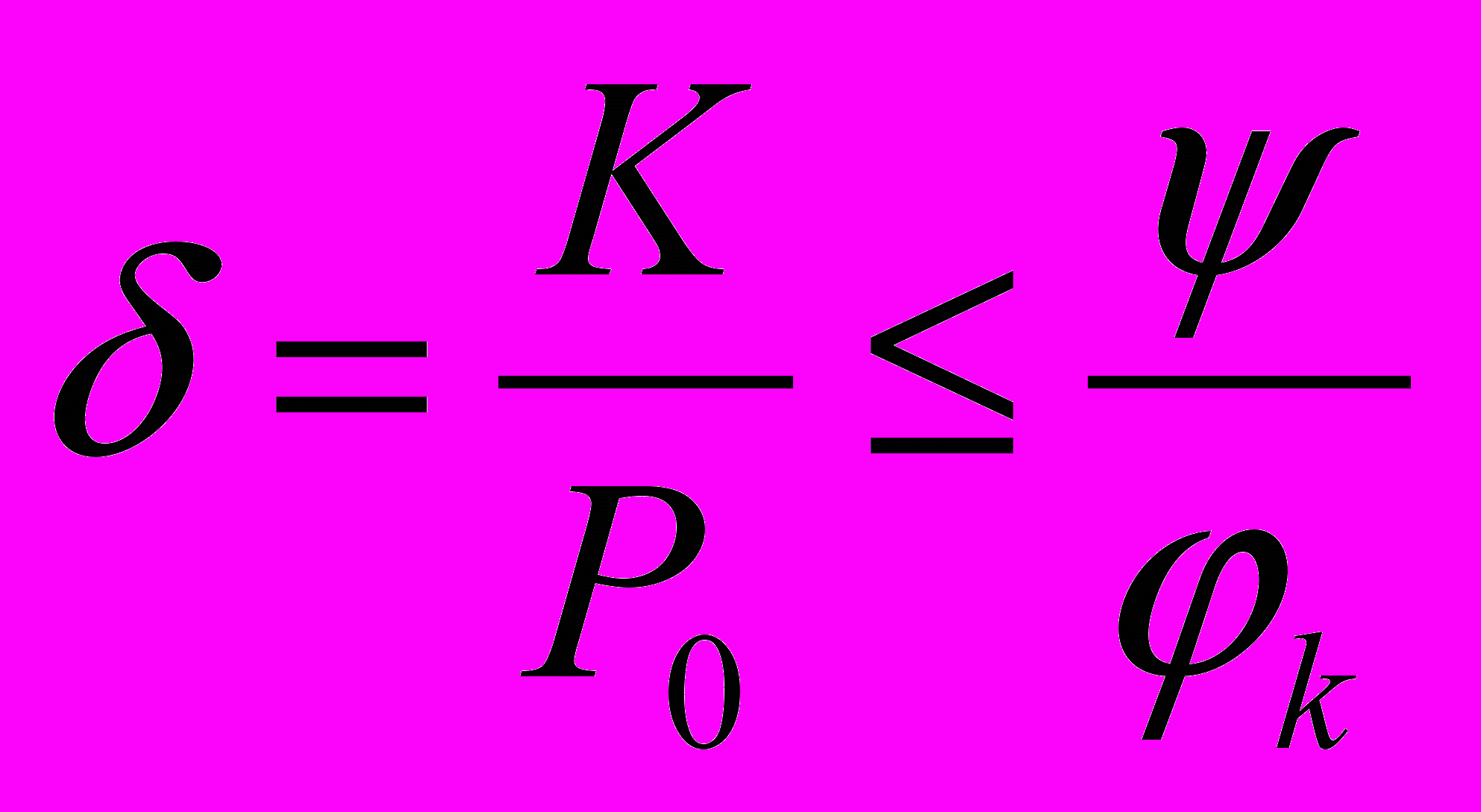. В расчетах принимают значения коэффициента нажатия колодок при чугунных колодках для локомотивов δ = 0,3÷0,5; для грузовых вагонов δ = 0,6÷0,7; для пассажирских вагонов δ = 0,7÷0,9; при композиционных колодках δ = 0,3. По заданному значению δ  определяют наибольшие силы нажатия колодок для каждой нагрузки Р₀.

Из этих формул видно, что при меньших значениях φ_к можно допускать наибольшие силы нажатия. Поэтому при использовании композиционных колодок, у которых φ_к выше, уменьшают силы нажатия изменением передаточного отношения в тормозной рычажной передаче или уменьшением давления в тормозных цилиндрах.

У грузовых вагонов от загрузки вагона значительно меняется Р₀. Чтобы получить меньшее значение коэффициента нажатия колодок δ  используются три режима работы воздухораспределителя. При загрузке меньше 3 т на колесную пару включается порожний режим с наименьшим нажатием и δ = 0,7, при загрузке от 3 т да 6 т включается средний режим, а при загрузке более 6 т включается воздухораспределитель на груженый режим и при К = 69 кН коэффициент нажатия колодок δ = 0,7. С композиционными колодками при загрузке до 6 т устанавливают порожний режим, более 6 т – средний режим.

Как отмечено выше, у чугунных колодок при высоких скоростях движения коэффициент трения имеет малые значения, и при неизменных К и δ тормозные силы получаются низкими. Для повышения тормозной силы при высоких скоростях у пассажирских вагонов с чугунными колодками увеличивают К и δ, а чтобы не получилось юза при низких скоростях движения устанавливают автоматические регуляторы , которые при скоростях 50÷60 км/ч снижают К и δ. Если же вагоны оборудованы композиционными колодками, то нет надобности вводить второй режим нажатия колодок.

Для сохранения величины тормозной силы необходимо действительную силу нажатия заменить на расчетную силу нажатия из равенства тормозных сил: K x φ_к = P_p x ψ, отсюда 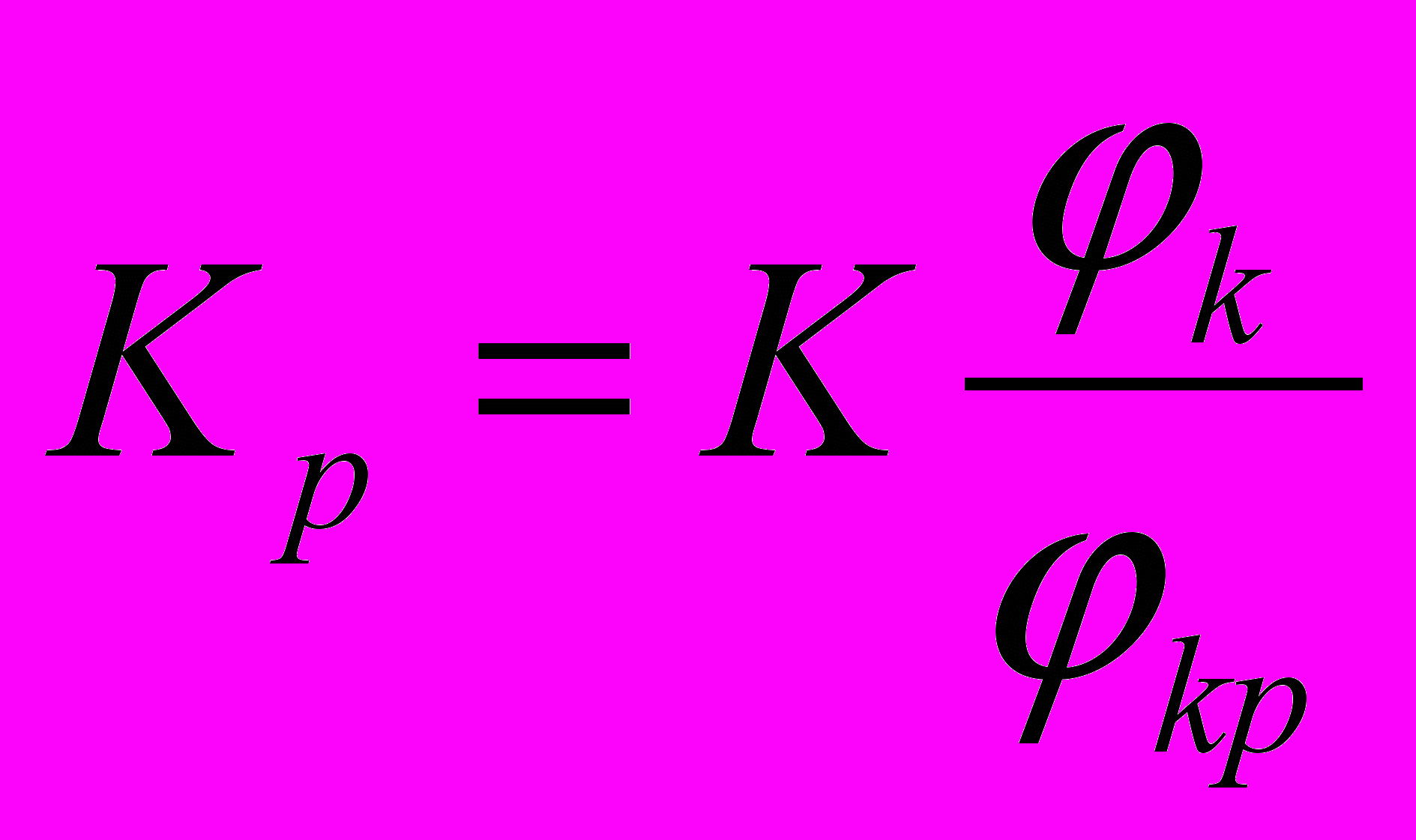, и  пользуясь эмпирическими формулами для φ_к и φ_кp получаем формулы для расчета расчетных сил нажатия:

для чугунных колодок ;

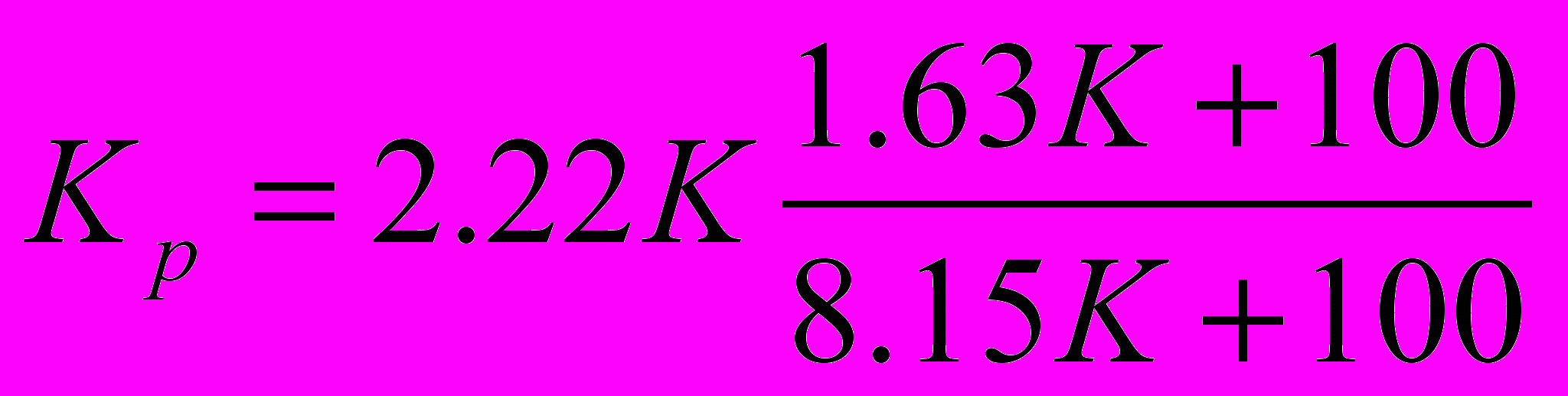для композиционных колодок .

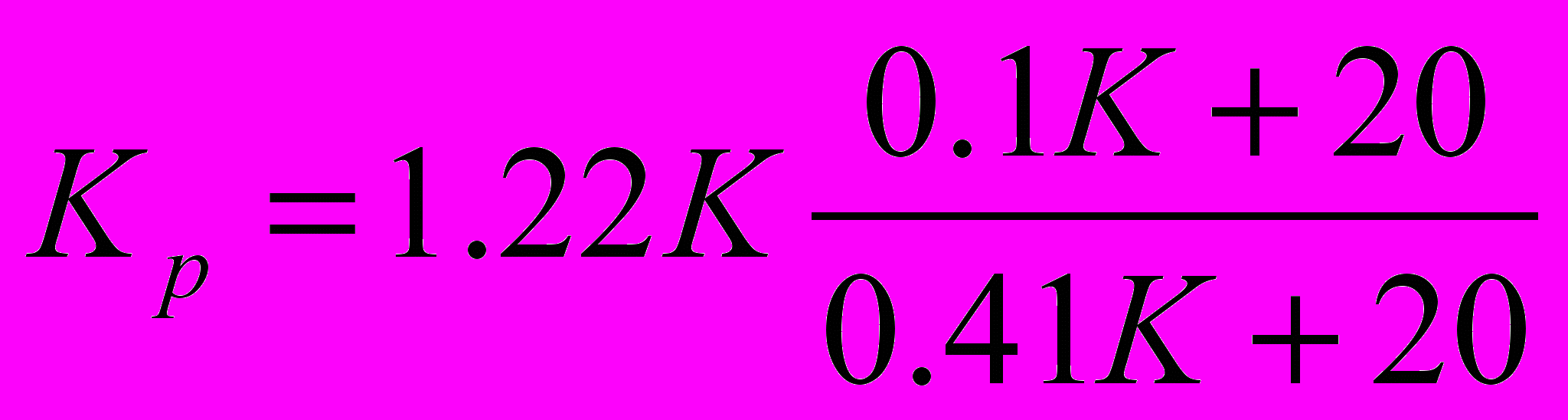Расчетные силы нажатия чугунных колодок для локомотивов и вагонов приводятся в таблицах. В ПТР указаны соотношения в зависимости от скорости движения расчетные нажатия композиционных колодок по отношению к чугунным.

С учетом расчетных величин К_р и φ_кp тормозная сила B_т = 1000 Σ K_p x φ_к , а так как φ_кp не зависит от величины К_р, то φ_кp выносям за знак суммы и B_т = 1000 Σ K_p x φ_кp.

Практически тормозную силу подсчитывают так: в зависимости от единицы подвижного состава по таблице определяют К_р, умножают на число осей однотипных единиц подвижного состава, по формулам или по таблице определяют φ_кp и определяют В_т.

Удельную тормозную силу (в Н/кН) находят поделив тормозную силу В_т на вес поезда m x g :   .

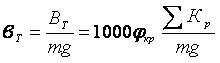Отношение суммарных сил расчетного нажатия колодок на колеса к весу поезда называется расчетным тормозным коэффициентом поезда. 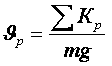, тогда .

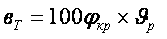Расчетный тормозной коэффициент характеризует степень обеспечения поезда тормозными средствами. Чем больше _p, тем больший тормозной коэффициент. Наименьшие значения _p  устанавливает МПС. Так например для грузовых и рефрижераторных составов при скорости до 90 км/ч _p = 0,33; для составов с порожними вагонами при скорости до100 км/ч _p = 0,58; для рефрижераторного поезда до 100 км/ч _p = 0,55, а до 120 км/ч _p = 0,6; для пассажирских составов до 120 км/ч _p = 0,6; до 140 км/ч _p = 0,78; до 160 км/ч _p = 0,8.

При работе грузового состава на участках со спусками до 20‰ тормозную силу локомотива и его массу не учитывают, тогда расчетный тормозной коэффициент  .

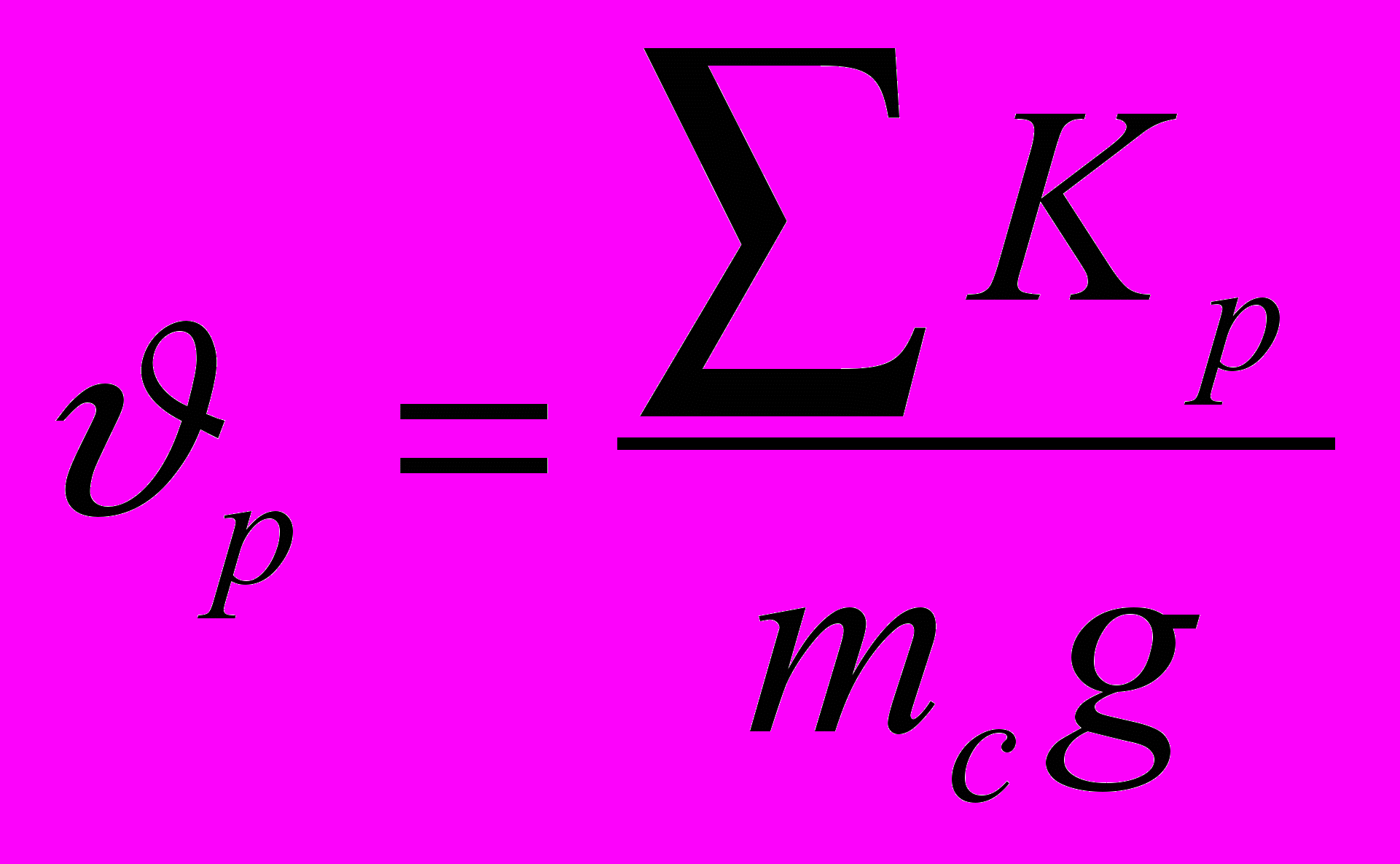Полное значение расчетного тормозного коэффициента и соответствующая ему тормозная сила реализуется только при экстренном торможении. Для остановки на станциях и раздельных пунктах или для снижения скорости перед заранее известным местом остановки  пользуются служебным торможением с расчетным тормозным коэффициентом x_p, для пассажирских поездов x_p, при этом и удельная тормозная сила 0,5 вт или 0,6 вт. При полном служебном торможении x_p.


21. Сопротивления движению поезда.


Силы, действующие вдоль оси пути по направлению движения поезда называются движущими силами, а силы встречного направления – силами сопротивления движения поезда.

Сопротивления движению поезда делятся на две составляющие:

I. Основное, действует при движении поезда всегда:

1). Сопротивление пути – трение качения колес по рельсам из-за деформации опорных поверхностей (сила обратно пропорциональна диаметру колес и зависит от твердости материалов); трение скольжения из-за проскальзывания и из-за трения между гребнями бандажей и рельсами, которые уменьшаются при натяжке в режиме тяги; от ударов на неровностях пути (зависит от скорости, нагрузки на ось, зазора в стыке).

2). Сопротивление подвижного состава – трение в подшипниках (сила прямо пропорциональна диаметру оси, обратно пропорциональна диаметру колеса, зависит от коэффициента трения, площади соприкосновения, смазки).

3). Сопротивление внешней среды – впереди сжатие воздуха, боковые поверхности и крыша соприкасаются с воздухом, в промежутках между вагонами и за составом происходит разряжение, завихрение воздуха (конструктивно выполнять более обтекаемую форму).

II. Дополнительное – возникает при движении по отдельным участкам пути и в отдельные периоды времени.

1). От уклонов – эти силы создаются составляющей веса поезда, действующая на подъеме против движения поезда, а на спусках – по направлению движения.

Уклон характеризуется крутизной i, в – тысячных долях и показывает высоту подъема в метрах на каждый километр пути.

Удельная сила дополнительного сопротивления от подъема численно равна величине подъема и измеряется в ньютонах на килоньютон.

2). От кривых – под действием центробежной силы гребни бандажей колесных пар прижимаются к рельсам и появляется трение. Колесо, идущее по внутреннему рельсу, имеет проскальзывание; трение в опорах кузова, в боковых опорах. Из-за большого числа факторов и сложных зависимостей удельное дополнительное сопротивление от кривой определяется по эмпирической формуле ω_R = 700 / R, где R – радиус кривой в м.

3). При трогании с места – повышенное трение в подшипниках (смазка выдавлена, полусухое трение), большая деформация рельса и колеса.

Силы удельного дополнительного сопротивления при трогании с места определяются по эмпирическим формулам:

для подшипников скольжения ;

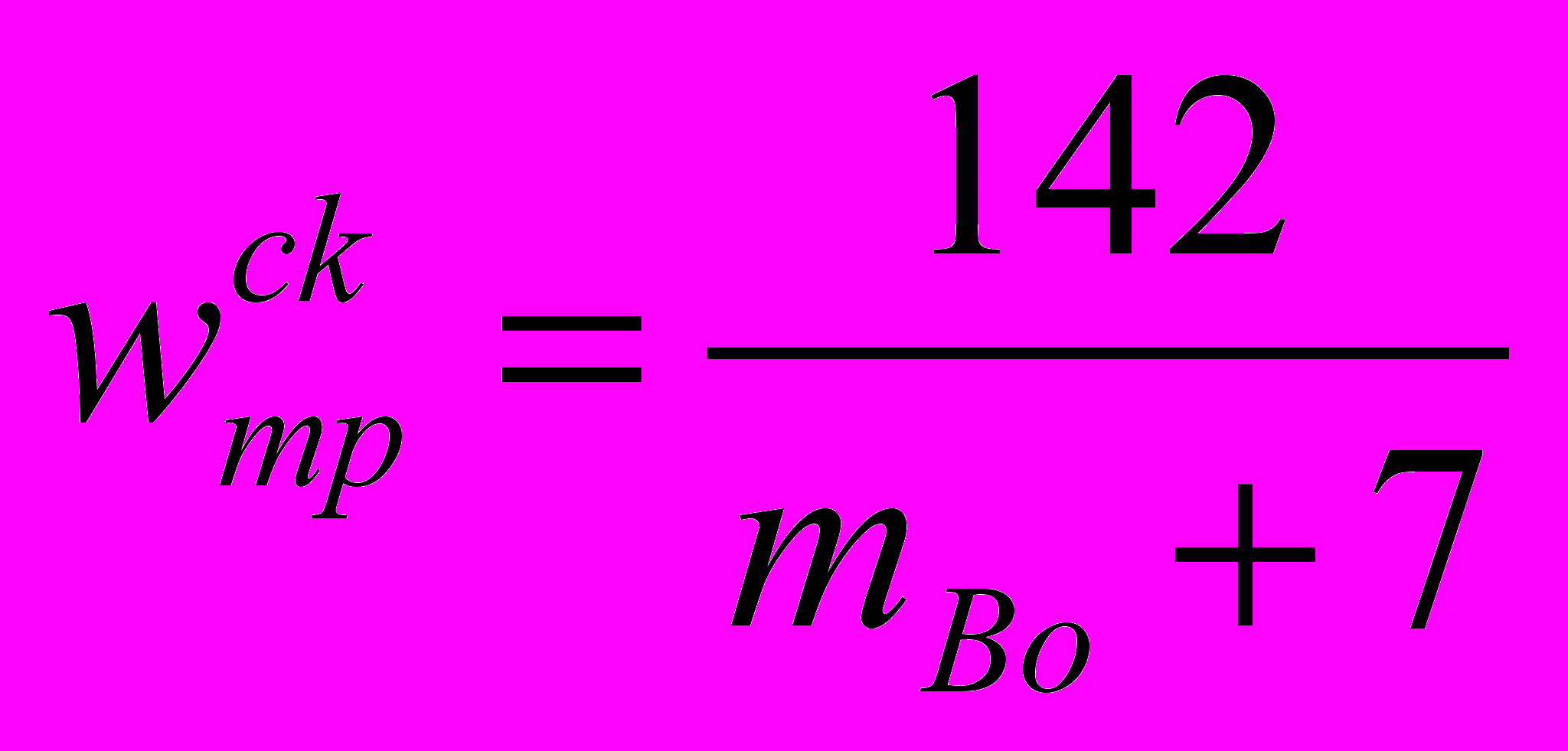для подшипников качения .

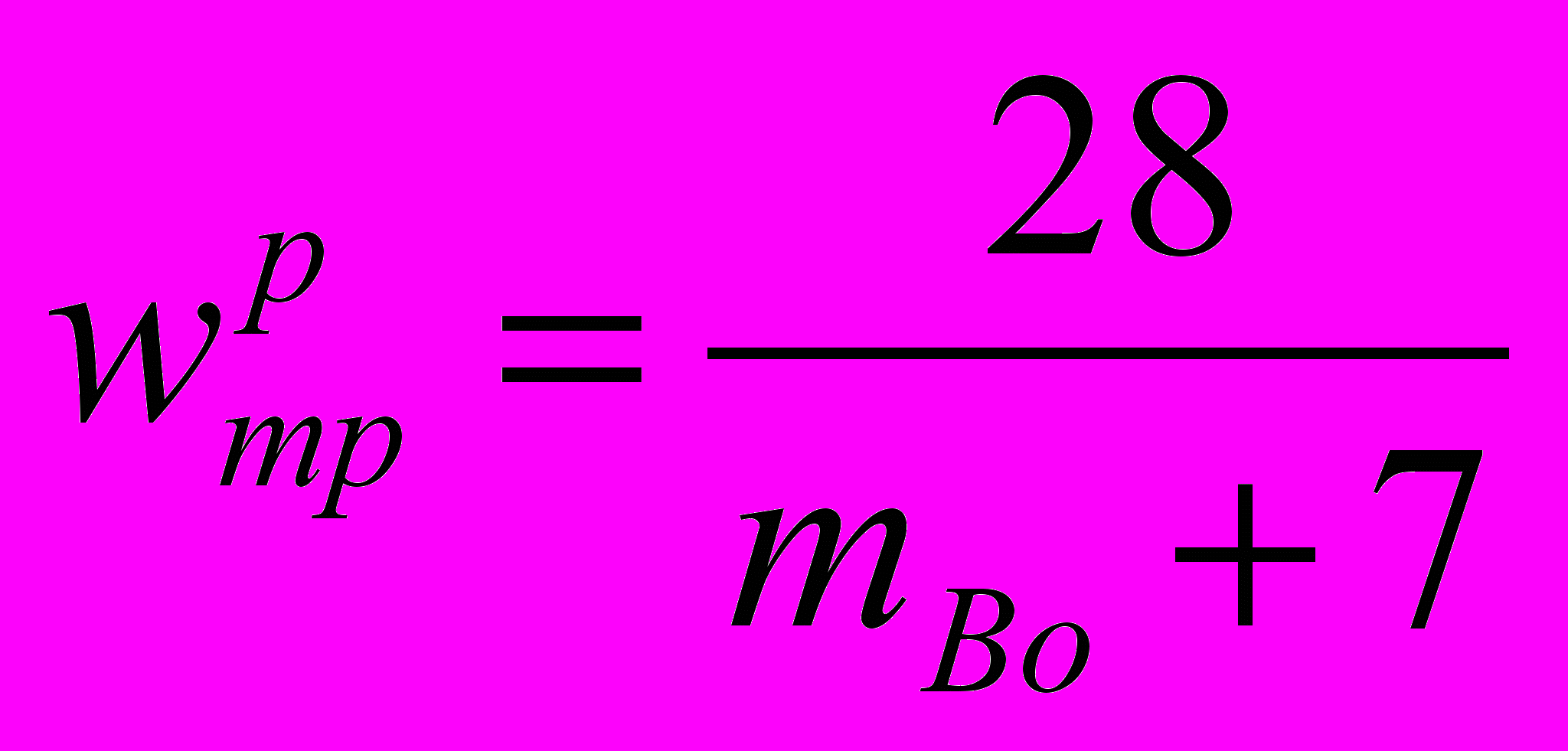m_Bo – масса вагона, приходящаяся на одну ось.

4). При низких температурах окружающего воздуха – возрастает вязкость смазки, а значит и коэффициент трения; возрастает так же и сопротивление воздушной среды; определяется по формуле ω_НТ = ω₀ (К_НТ -1), а значение коэффициента К_НТ берется из таблицы при различных низких температурах и скоростях движения для грузовых и пассажирских вагонов.

5). От ветра  - встречный и боковой ветер увеличивают сопротивление из-за трения и увеличения сопротивления воздушного потока. По таблице берется коэффициент ветра К_В и дополнительное сопротивление от ветра ω_В = ω₀ (К_В -1).

6). От подвагонных генераторов для пассажирских вагонов.

7). От движения в тоннелях.

Общее сопротивление движения поезда W_К определяется алгебраической     суммой    основного   и дополнительного сопротивлений. W_К = W₀ + W_д, в Н. Почти все виды сопротивлений пропорциональны весу поезда, поэтому рассматривают удельное   сопротивление движения   поезда ω_Н = ω₀ + ω_д в Н/кН.

Основное удельное сопротивление определяется по эмпирическим формулам в зависимости от скорости движения:

- для различных серий локомотивов;

- при движении под током;

- при движении без тока;

- в зависимости от подшипников качения или скольжения;

- в зависимости от количества осей вагона;

- для груженых или порожних вагонов;

- для стыкового или бесстыкового пути.

Общее основное удельное сопротивление определяется как .


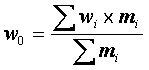22. Уравнение движения поезда.


Уравнение движения поезда позволяет оценить влияние ускоряющих и замедляющих сил, действующих на поезд, на ускорение его движения. По II закону Ньютона: F_y = m x a, где F_y – ускоряющая сила действующая на поезд в Н, m – масса поезда в кГ, а – ускорение движения в м/с². В тяге поездов масса измеряется в тоннах (нужно умножить на 1000), ускорение в км/ч² (нужно умножить на 1000 (1 км=1000 м), и разделить на 60 сек x 60 мин и в квадрате=3600) и получаем:

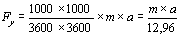 или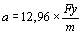

При поступательном движении поезда вместе с ним совершают поступательное движение все детали, но вращающиеся детали совершают и вращательное движение. Вращательное движение замедляет ускорение и замедляет замедление, сохраняя свое вращение.

Влияние на ускорение движения поезда вращающихся частей в расчетах оценивают коэффициентом γ и вместо массы поезда m вводят приведенную массу поезда m_n = m(1+γ). Коэффициент (1+γ) называют коэффициентом инерции вращающихся частей , показывающий увеличение массы поезда для учета действия вращающихся частей. Уравнение движения поезда будет иметь вид:

,

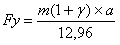Уравнение движения поезда показывает зависимость между ускорением движения поезда км/ч², ускоряющей силой Н, массой в т и коэффициентом инерции вращающихся частей. Уравнение движения поезда можно записать:

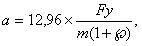
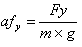   , тогда ;

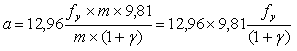п

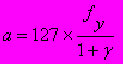
оказывает что ускорение движения поезда зависит от удельной ускоряющей силы и коэффициента инерции вращающихся частей (1+γ. Обозначим 127 / (1+γ) = ξ, получим наиболее простую форму записи: a = ξ x f_y, где ξ - ускорение поезда в км/ч² при действии удельной ускоряющей силы в 1 Н/кН.

Зная f_y = f_k - ω_k - в_т, получим a = ξ(f_k - ω_k - в_т). Значение коэффициента инерции вращающихся частей (1+γ)различно для разных видов подвижного состава. На его значение влияет и масса. Например у груженного вагона (1+γ) меньше по сравнению с порожним, т.к. при большей массе вагона меньшее влияние вращающихся частей. У локомотивов (1+γ) выше, т.к. большее число вращающихся частей. Значения (1+ γ) приводятся в таблицах. Для состава с различными типами вагонов коэффициент рассчитывают:.

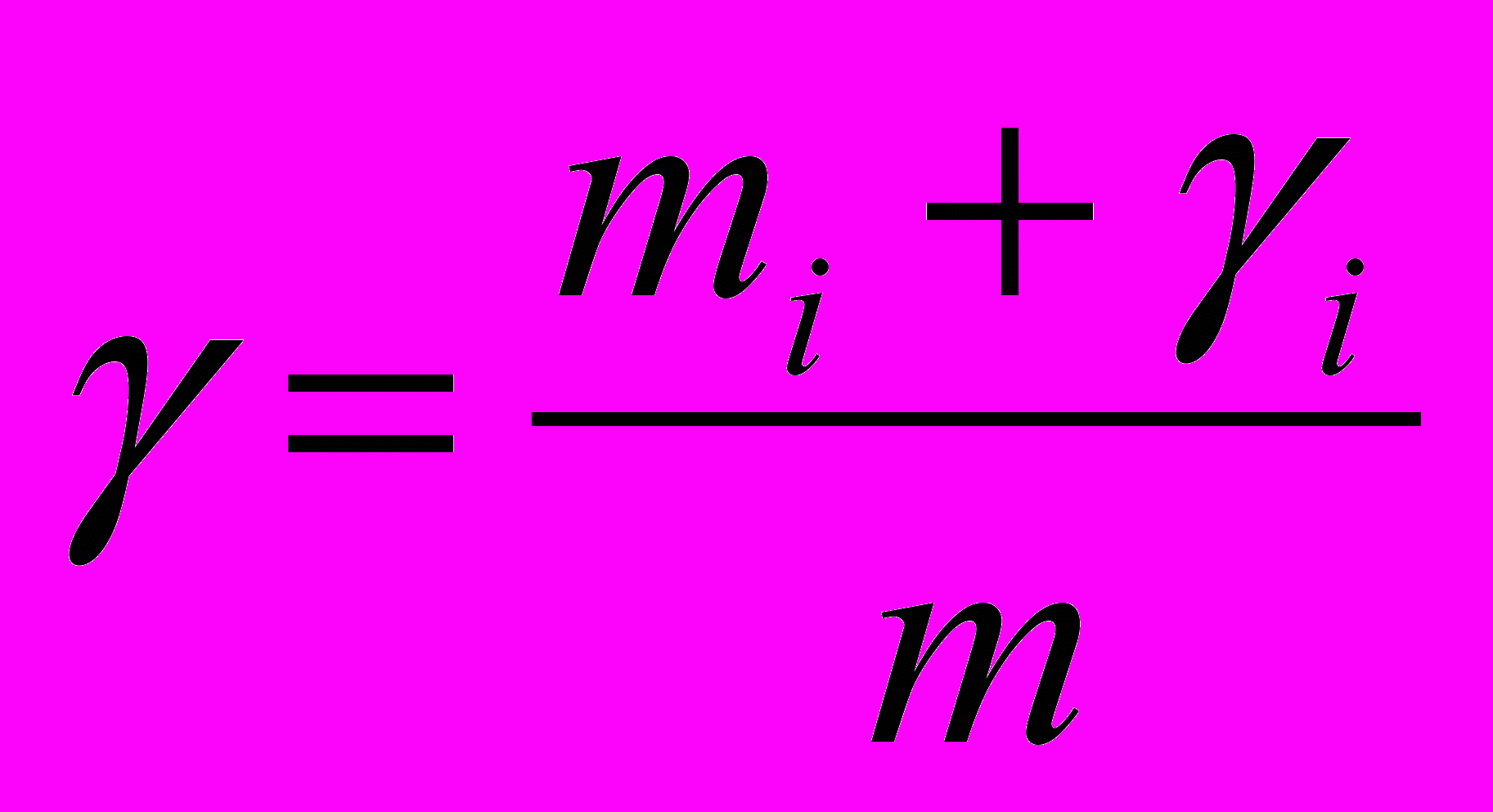Для различных грузовых и пассажирских поездов коэффициент γ  оказывается близким к 0,06 и коэффициент ξ=127/1,06=120 км/ч²/H/кН и уравнение движения поезда a = 120(f_k - ω_k - в_т)

ω₀ – основное удельное сопротивление

ω_k – общее удельное сопротивление

Уравнение движения поезда можно записать и в таком виде:

dV / dt = 120(f_k(V) - ω_k(V) - в_т(V))


23. Анализ уравнения движения поезда.


Чтобы решить уравнение движения поезда, нужно найти удельные ускоряющие и замедляющие силы, которые определяют из удельных сил тяги, удельных сил сопротивления движению и удельных тормозных сил во всех  диапазонах скоростей движения.

При движении поезда ускоряющая сила изменяется в связи с изменением режимов работы локомотива, плана и профиля пути. Наиболее общим случаем является ускоренное или замедленное движение и только в частных случаях – равномерное.

Ускоренное движение можно получить как в режиме тяги, так и в режиме выбега и торможения при следовании на спусках, когда составляющие от веса поезда окажутся больше сил сопротивления движения или суммы сил сопротивления движения и тормозной силы.

Равномерное движение наступает при равенстве этих сил.

Замедленное движение может быть и в режиме тяги при следовании по подъему, когда сила тяги окажется меньше сил основного и дополнительного сопротивлений движению.

При решении уравнения движения поезда определяют скорости движения, путь пройденный поездом за любой промежуток времени или время, необходимое для прохождения отрезков пути, в том числе и перегонов.

1)     f_y > 0 – ускоренное движение, f_y = const > 0 равноускоренное

2)     f_y < 0 – замедленное движение, f_y = const < 0 равнозамедленное

3)     f_y = 0 – равномерное движение

  Уравнение движения поезда:

для режима тяги: a = 120(f_k-ω₀-ω_д)

для режима выбега: a = 120(-ω₀-ω_д)

для режима механического торможения: a = 120(-в_т-ω₀-ω_д)