Краткий курс лекций

Вид материала

Курс лекций

Содержание Лекция №1 1.1 Предмет и метод начертательной геометрии 1.2 Основные задачи курса 2. Способы проецирования 2.1 Центральное проецирование 2.2 Параллельное проецирование 2.3 Основные свойства параллельного проецирования 2.4 Прямоугольное проецирование 3. Комплексный чертеж в трех видах

Подобный материал:

• Н. В. Рудаков Краткий курс лекций, 1552.23kb.
• В. Б. Аксенов Краткий курс лекций, 1098.72kb.
• Краткий курс лекций по медицинской паразитологии Часть Клещи, 643.33kb.
• Краткий курс лекций по философии учебно-методическое пособие для студентов всех специальностей, 2261.57kb.
• Методические указания: краткий курс лекций для студентов заочной формы обучения Санкт-Петербург, 1540.61kb.
• Краткий курс лекций учебной дисциплины «Методика преподавания начального курса математики», 631.78kb.
• И. М. Максимова теория государства и права краткий курс лекций, 2531.05kb.
• Ю. А. Фатеев логика Краткий курс лекций, 665.66kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Краткий курс лекций, 505.9kb.

Тверской государственный технический университет


Кафедра «Инженерная графика»

краткий курс лекций

В данной рукописи представлен курс лекций по начертательной геометрии, составленный на базе учебников Посвянского Александра Давидовича «Краткий курс начертательной геометрии» и читаемый с некоторыми изменениями для специальностей МАХП и МАПП.

Автор курса лекций – ст. преподаватель кафедры «Инженерная графика» Забелин А.В.


Тверь 2003 г.

ЛЕКЦИЯ №1

1. ПРЕДМЕТ И МЕТОД НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ. ЗАДАЧИ КУРСА.

2. СПОСОБЫ ПРОЕЦИРОВАНИЯ.

3. КОМПЛЕКСНЫЙ ЧЕРТЕЖ В ТРЕХ ВИДАХ.

4. ПЛОСКОСТИ УРОВНЯ И ПРЯМЫЕ ПЕРПЕНДИКУЛЯРНЫЕ К НИМ.

1.1 ПРЕДМЕТ И МЕТОД НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Начертательная геометрия, являясь одной из ветвей геометрии, относящейся к математике, имеет ту же цель, что и геометрия вообще: изучение форм предметов окружающего нас материального мира и отношений между ними, установление закономерностей и применение их к решению практических задач.

В начертательной геометрии для решения задач используется графический путь, все геометрические свойства фигур изучаются по чертежу, т.е. чертеж является основным средством изучения свойств пространственных фигур.

Для того чтобы чертеж был геометрически равноценен изображаемой фигуре (оригиналу), он должен быть построен по определенным геометрическим законам - правилам. В начертательной геометрии чертежи строятся при помощи метода проецирования, поэтому получаемые таким образом чертежи называют проекционными.

Таким образом, содержанием курса начертательной геометрии является:

• исследование способов построения проекционных чертежей;
  
• решение геометрических задач, относящихся к пространственным фигурам;
  
• применение способов начертательной геометрии к исследованию и решению практических и теоретических вопросов науки и техники.
  

В наше время нет такого вида человеческой деятельности где не применялись бы чертежи - будь то технические, строительные, географические и топографические (карты) и др. Все они строятся по правилам проецирования.

1.2 Основные задачи курса

1. Изучить теоретические основы образования чертежа.

2. Изучить алгоритмы решения позиционных и метрических задач.

Позиционные задачи - задачи на взаимную принадлежность и пересечение геометрических фигур.

В начертательной геометрии все фигуры и предметы отображаются на плоскость двумя основными способами: центральным проецированием или параллельным проецированием.

Метрические задачи-задачи на определение натуральных величин расстояний, углов геометрических фигур.

2. СПОСОБЫ ПРОЕЦИРОВАНИЯ

Геометрической фигурой называют любое множество точек. Геометрических фигур существует много, но основных только три - точка, прямая (линия) и плоскость.

2.1 Центральное проецирование

П

S

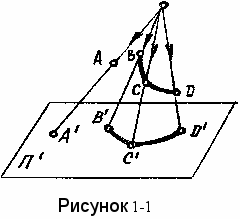
усть в пространстве дана некоторая плоскость П, которую называют плоскостью проекций, и вне этой плоскости точка S , называемая центром проецирования. Чтобы спроецировать точку А пространства на плоскость П' нужно через центр проецирования S и точку А провести прямую (проецирующий луч) до пересечения ее с плоскостью П' в точке A’ Точку А’ называют центральной проекцией точки А (рисунок 1-1).

Если возьмем произвольную криволинейную фигуру, то все проецирующие лучи образуют проецирующую коническую поверхность, поэтому этот способ проецирования называют еще коническим способом.

2.2 Параллельное проецирование

Широкое распространение в практике получил частный случай центрального проецирования, когда центр проецирования S удален в бесконечность от плоскости проекций П. Проецирующие лучи при этом практически параллельны между собой, поэтому данный способ получил название параллельного проецирования, а полученные с его помощью изображения (проекции) фигуры на плоскости называют параллельными проекциями.



Рисунок 1-2


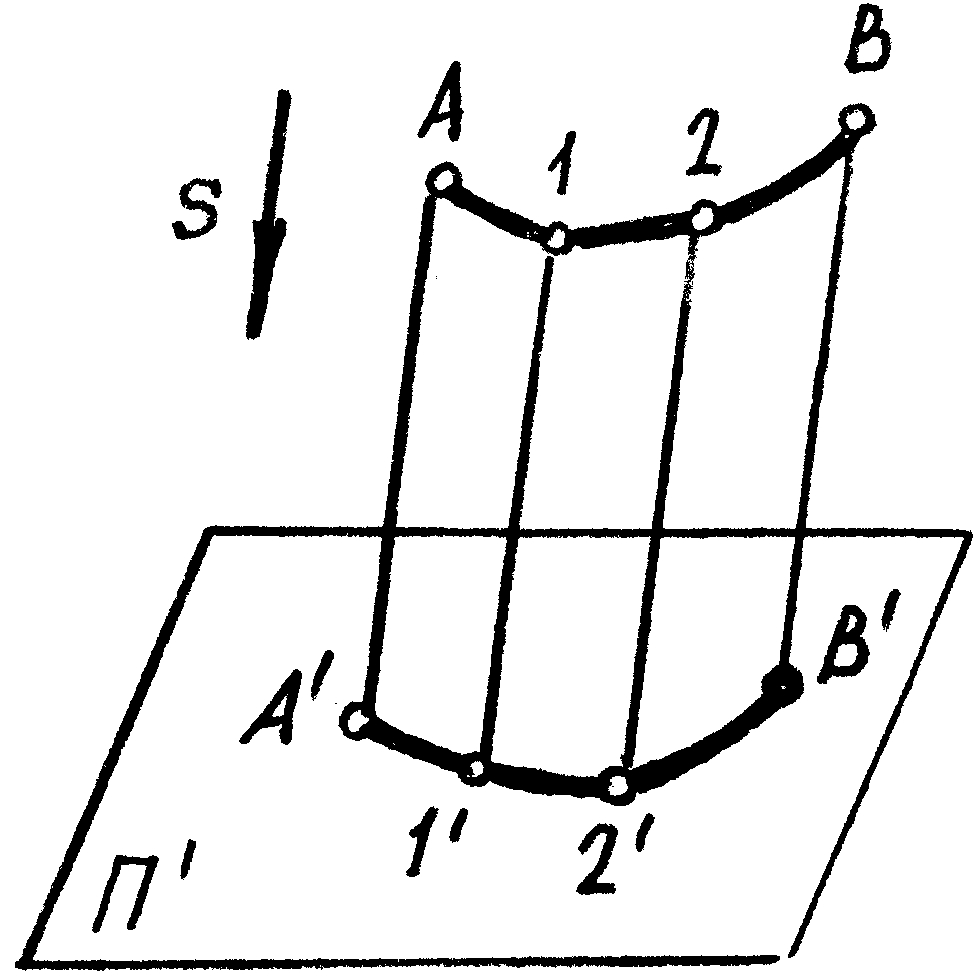
Возьмем в пространстве какую-либо фигуру, например линию АВ (рисунок1-2). Спроецируем ее на плоскость проекций П. Направление проецирования укажем стрелкой S. Чтобы спроецировать точку А на плоскость П надо провести через эту точку параллельно направлению S прямую линию до пересечения с плоскостью проекций П. Полученная точка А называется параллельной проекцией точки А. Аналогично находим проекции других точек линии АВ.

Совокупность всех проецирующих лучей определяет (представляет) в пространстве цилиндрическую поверхность, поэтому такой способ проецирования называют цилиндрическим.

2.3 Основные свойства параллельного проецирования

1) Проекцией точки является точка. АА (рисунок 1-3а).

2
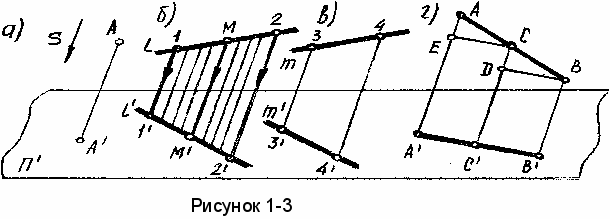
) Проекцией прямой является прямая (свойство прямолинейности).

Действительно, при параллельном проецировании все проецирующие лучи будут лежать в одной плоскости Е. Эта плоскость пересекает плоскость проекций по прямой линии l (рисунок 1-3б).

3) Если в пространстве точка принадлежит линии (лежит на ней), то проекция этой точки принадлежит проекции линии (свойство принадлежности), (рисунок 1-Зб, точка М).

4) Проекции взаимно параллельных прямых также взаимно параллельны, т.к.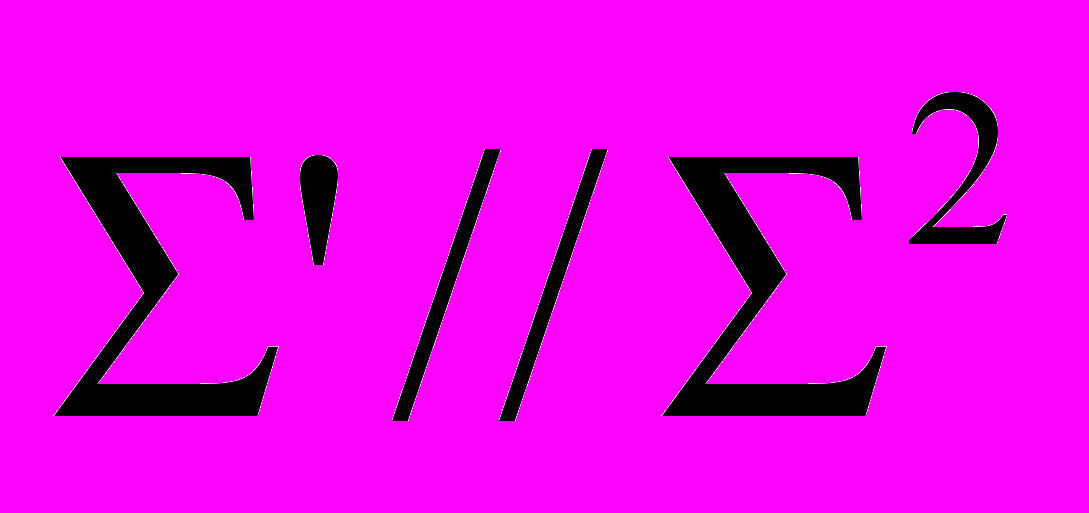(рисунок 1-3б, в), (l)ll(m) (l) II (m').

5) Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.

Докажем это: введем СЕ//A’С' и DВ//С'B', тогда 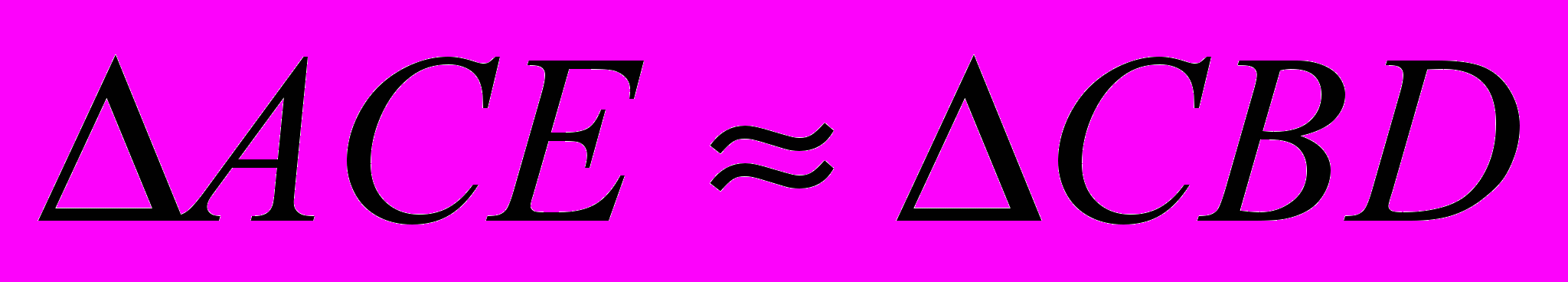. Из подобия треугольников следует, что

АС/СВ=СЕ/DB=AC/CB.

6) Параллельный перенос плоскости проекций или фигуры (без поворота) не меняет вида и размеров проекции фигуры (рисунок1-4).

2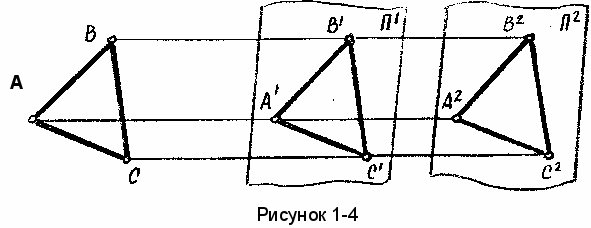
.4 Прямоугольное проецирование

Частный случай параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекций П, еще больше упрощает построение чертежа и наиболее часто применяется в конструкторской практике. Этот способ называют прямоугольным проецированием или (что тоже) ортогональным проецированием.

М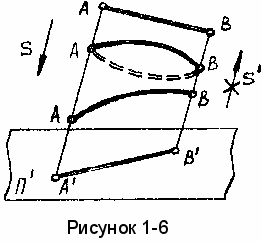етод ортогональных проекций был впервые изложен французским геометром Гаспаром Монжем, поэтому иногда его называют методом Монжа. Этот метод является основным при составлении технических чертежей, поскольку позволяет наиболее полно судить о размерах изображенных предметов. В этом случае нетрудно установить соотношение между длиной некоторого отрезка АВ в пространстве и длиной его проекции АВ(рисунок 1-5).

Рассмотренные способы проецирования позволяют однозначно решать прямую задачу - по данному оригиналу строить его проекционный чертеж. Однако только одна параллельная проекция без каких-либо дополнений недостаточна для полного представления о том, каким является этот предмет в натуре. По такому изображению (рисунок 1-6) нельзя определить не только форму и размеры предмета, но и его положение в пространстве, т.е. параллельная проекция не обладает свойством обратимости. Для получения обратимых чертежей проекционный чертеж дополняют необходимыми данными. Способы дополнения бывают различными. Мы в курсе начертательной геометрии будем рассматривать два вида обратимых чертежей:

1. комплексные чертежи в ортогональных проекциях;
   
2. аксонометрические чертежи.
   

3. КОМПЛЕКСНЫЙ ЧЕРТЕЖ В ТРЕХ ВИДАХ

Чертеж составленный из двух или более связанных между собой ортогональных проекций изображаемого оригинала называется комплексным чертежом.

Принцип образования комплексного чертежа состоит в том, что предмет ортогонально проецируется на две или три взаимно-перпендикулярные плоскости проекций (рисунок 1-7а).

Одну из плоскостей проекций П располагают вертикально перед наблюдателем, вторую П горизонтально и ниже глаз наблюдателя, П -перпендикулярно первым двум плоскостям проекций и справа от наблюдателя. Эти плоскости называются соответственно - фронтальная, горизонтальная и профильная плоскости проекций.

Спроецировав ортогонально фигуру на плоскости проекций получим, соответственно, фронтальную, горизонтальную и профильную проекции или вид спереди, вид сверху, вид слева.

Пространственная фигура имеет три измерения, называемые в начертательной геометрии - высота, глубина и широта. Необходимо отметить, что на каждом из указанных 3-х видах фигуры присутствуют по два измерения:

• на виде спереди : высота  (выше, ниже) и широта (левее-правее);
  

• на виде сверху : глубина  (дальше, ближе) и широта (левее-правее);
  

• на виде слева : высота  (выше, ниже) и глубина  (дальше, ближе).
  

В
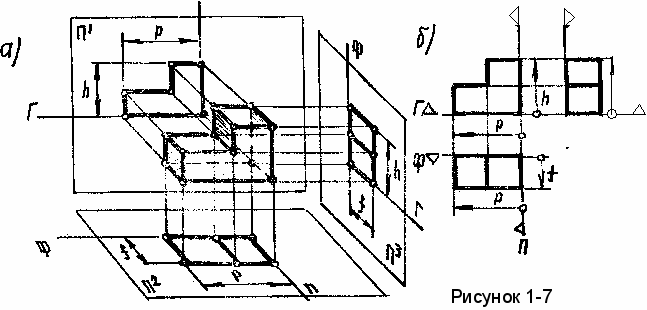
ысоту предмета h можно измерять от горизонтальной плоскости проекций, но проще и экономичнее производить замер высоты от базовой горизонтальной плоскости Г, взятой на уровне с нижним основанием (или точкой) фигуры.

Глубину фигуры f измеряют от базовой фронтальной плоскости Ф , широту - от базовой профильной плоскости П. При этом плоскости Ф и П располагают относительно фигуры определенным образом: П -на уровне с самой правой точкой, фигуры, Ф - на уровне с самой дальней точкой.

Для получения комплексного чертежа фигуры горизонтальную и профильную плоскости проекций поворачивают до совмещения с фронтальной плоскостью проекций так, чтобы широты р на видах спереди и сверху, а высоты h на видах спереди и слева находились в проекционной связи (рисунок 1-7б).

Проекции базовых плоскостей на плоскости проекций называются базами отсчета. На комплексном чертеже показаны базы отсчета: высот - Г, глубин - Ф, широт - П. Направление измерений показано стрелками. Допускается на чертеже отмечать базы отсчета знаком .

Если фигура имеет ось или плоскость симметрии удобно выбирать базы отсчета проходящими через них.

Мы рассмотрели построение комплексного чертежа для довольно непростой пространственной фигуры. Часто возникает задача построить комплексный чертеж одной точки. Он строится аналогичным образом, при этом базовые плоскости (базы отсчета) выбираются на произвольном удалении от плоскостей проекции (см. 6-е свойство) с учетом удобства расположения изображений.