Темы для изучения по предмету «Высшая математика» для студентов Iкурса (Заочное обучение, 1 семестр) Раздел Линейная алгебра
| Вид материала | Документы |
СодержаниеРаздел 2. Системы линейных уравнений. Раздел 3. Векторная алгебра Раздел 4. Аналитическая геометрия Раздел 5. Комплексные числа |
- Правительство Российской Федерации Государственное образовательное бюджетное учреждение, 416.73kb.
- Программа по дисциплине Линейная алгебра для студентов 1 курса дневного отделения факультета, 212.1kb.
- Генератор контрольных работ по курсу «высшая математика – линейная алгебра», 23.84kb.
- Контрольная работа по курсу «Высшая математика (раздел «Математическое программирование»)», 24.35kb.
- Курс: 3 Семестр: 6 Перечень вопросов к зачету: Частная методика ( математика, алгебра,, 29.41kb.
- Рабочая учебная программа дисциплины (модуля) Линейная алгебра, 227.98kb.
- Рекомендации для самостоятельной внеаудиторной работы студентов по дисциплине «Сестринское, 182.37kb.
- Рекомендации для самостоятельной внеаудиторной работы студентов по дисциплине «Сестринское, 232.55kb.
- Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая, 542.76kb.
- Программа, методические указания и контрольные задания по курсу «основы программирования, 516.11kb.
Темы для изучения по предмету «Высшая математика»
для студентов I курса (Заочное обучение, 1 семестр)
Раздел 1.Линейная алгебра
Понятие матрицы размером mn. Виды матриц: матрица-столбец, матрица-строка, треугольная, квадратная, единичная, и др. Операции над матрицами (умножение на число, сложение, вычитание, транспонирование, умножение) и их свойства. Понятие минора и алгебраического дополнения матрицы. Обратные матрицы. Условие существования и алгоритм нахождения обратной матрицы. Ранг матрицы и метод его определения. Элементарные преобразования матриц. Определители квадратных матриц и их свойства. Определители второго и третьего порядка. Схемы для вычисления определителей 2-го и 3-го порядка. Определитель порядка n.. Вычисление определителей методом разложения по строке ( столбцу).
Раздел 2. Системы линейных уравнений.
Системы m линейных уравнений c n неизвестными: различные формы записи систем, в том числе с помощью знака суммирования и в матричной форме. Совместные, несовместные, определенные и неопределенные системы. Условия существования единственного решения и бесконечного множества решений. Формулы Крамера и метод обратной матрицы для решения систем n линейных уравнений c n неизвестными. Метод Гаусса для решения систем линейных уравнений произвольного вида. Однородные системы и их решение. Общее решение неоднородной системы уравнений. Базисное решение.
Раздел 3. Векторная алгебра
Декартова система координат на плоскости и в пространстве. Определение n-мерного вектора, координаты вектора. Векторы на плоскости и в пространстве. Равенство векторов, длина, нулевой вектор. Выражение координат вектора через координаты начала и конца, орты. Операции с векторами: сумма, разность, противоположный вектор; умножение на число; проекция вектора на ось, единичный вектор. Скалярное умножение векторов: определение, свойства, геометрическая интерпретация. Нахождение угла между векторами. Векторное умножение векторов: определение, свойства, умножение в координатной форме, геометрический смысл. Смешанное произведение векторов: определение, свойства, в координатной форме, геометрический смысл. Коллинеарность и компланарность векторов, их взаимосвязь с векторным и скалярным произведениями
Раздел 4. Аналитическая геометрия
Различные формы уравнения прямой на плоскости и в пространстве. Нормальный и направляющий векторы прямой. Расстояние от точки до прямой. Угол между прямыми, угол между прямой и плоскостью. Различные формы уравнения плоскости; расстояние от точки до плоскости. Условия параллельности и перпендикулярности прямых, плоскостей, прямой и плоскости. Угол между плоскостями. Кривые второго порядка: эллипс, гипербола, парабола, окружность и их канонические уравнения. Приведение общего уравнения второй степени к каноническому виду. Поверхности второго порядка.
Раздел 5. Комплексные числа
Понятие комплексного числа, тригонометрическая и показательная формы.
Операции с комплексными числами. Комплексно-сопряженные числа и их свойства.
Задание 1. Выполнить операции с матрицами
и
| № Вар. | а) | б) | в) |
| 1 | 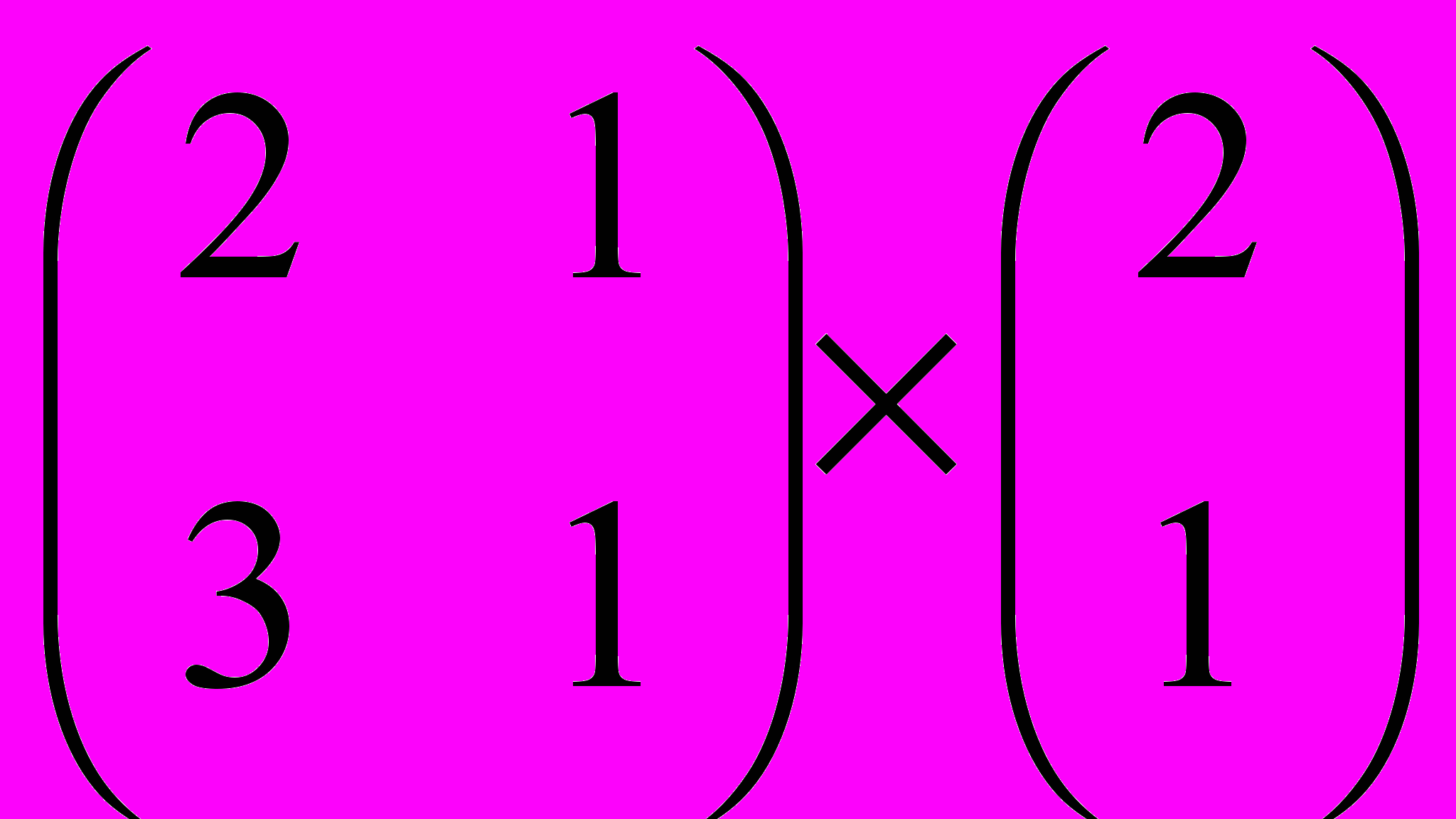 | 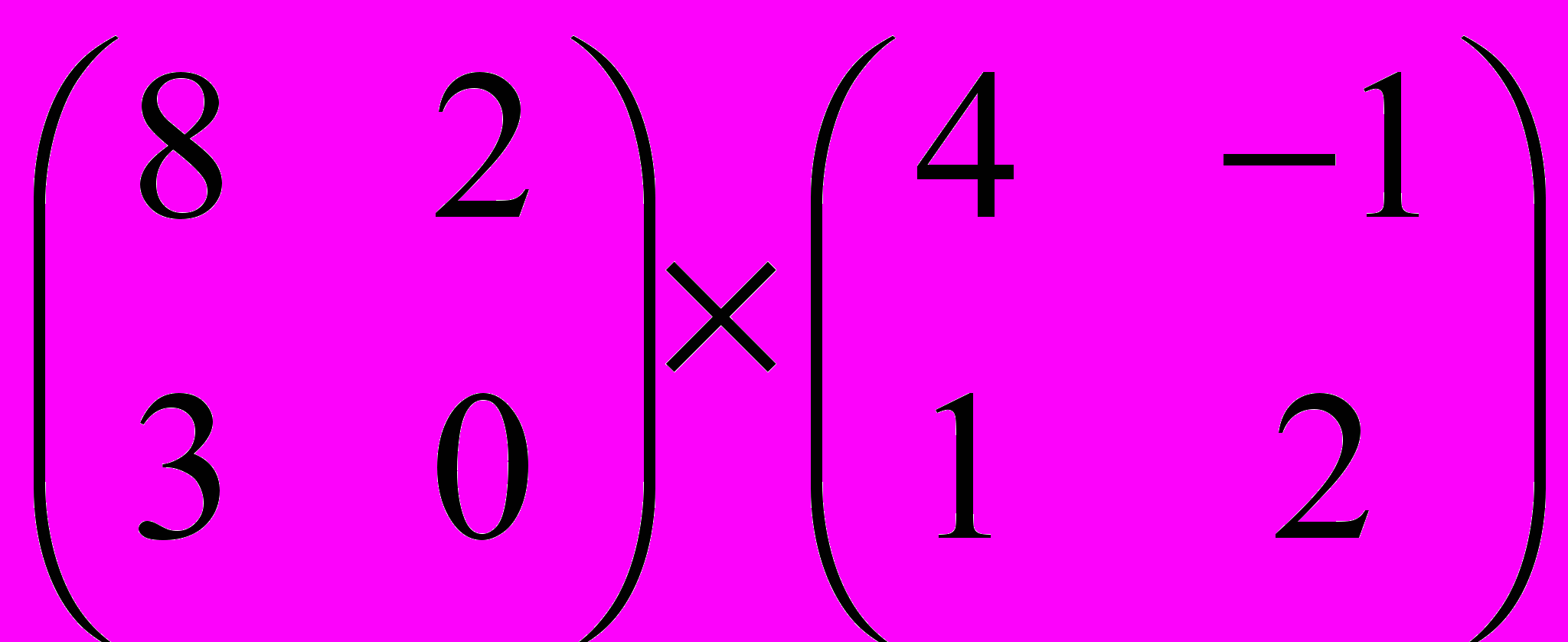 | 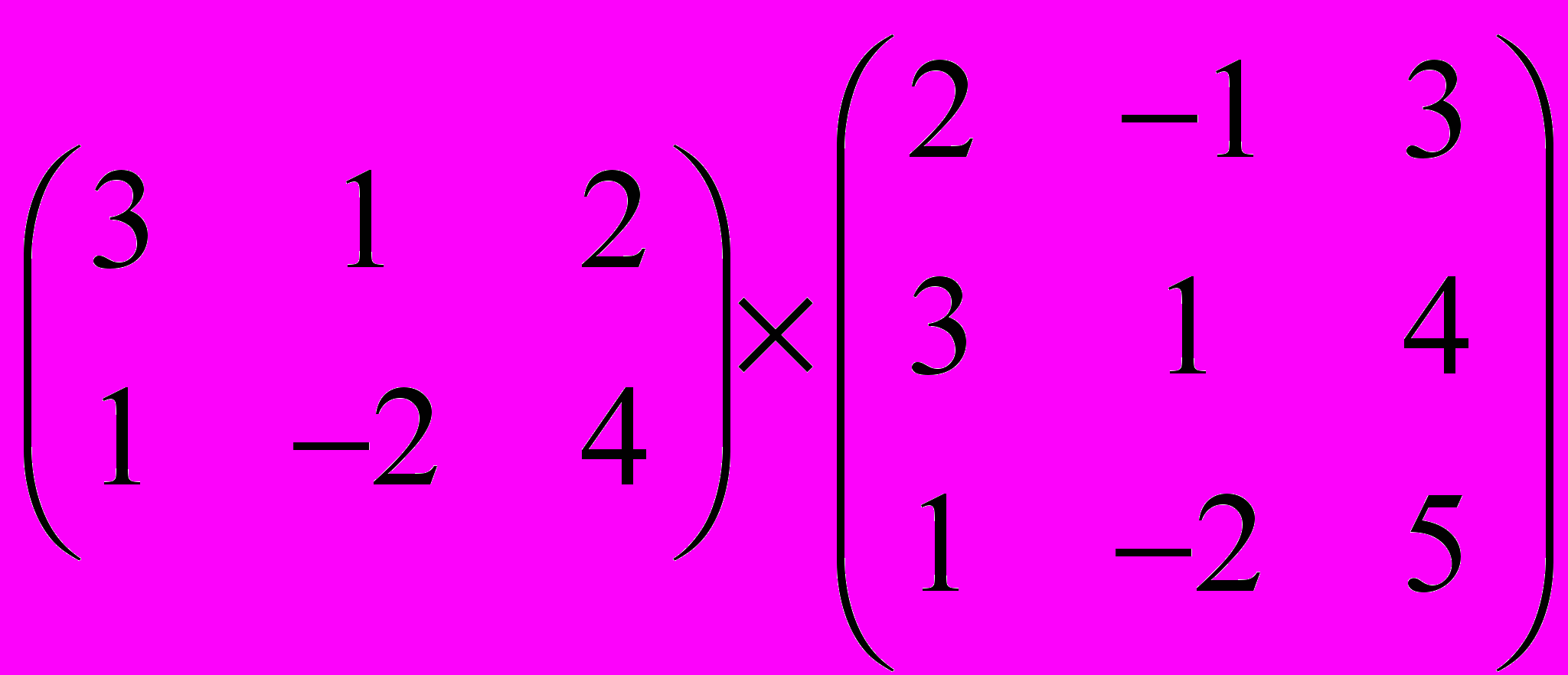 |
| 2 | 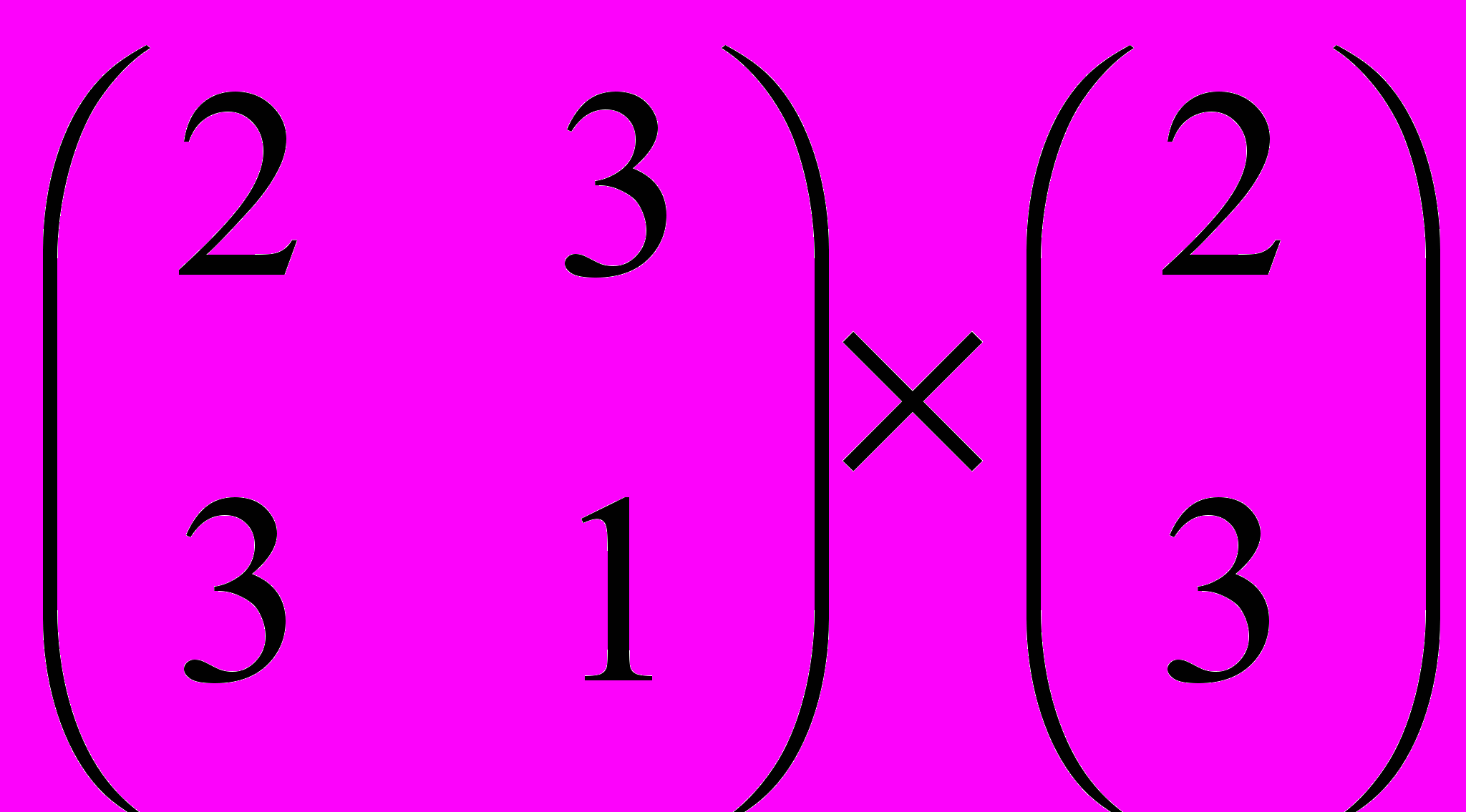 | 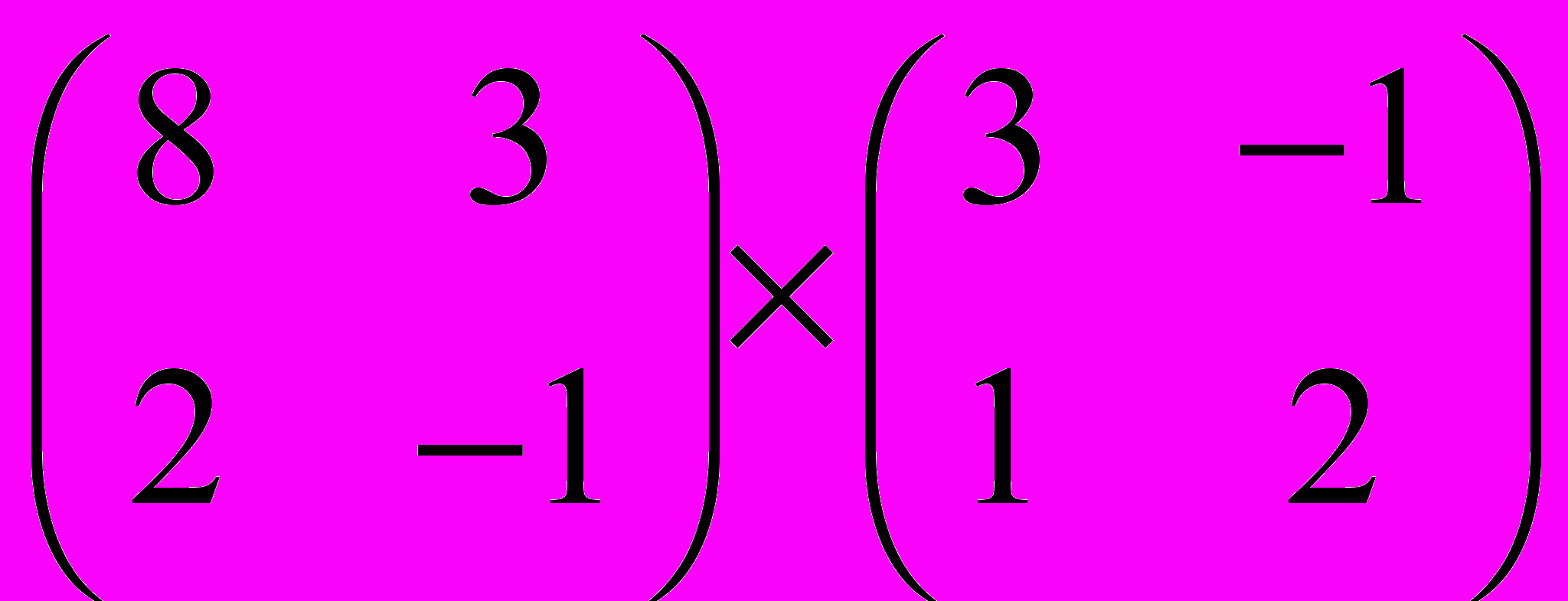 | 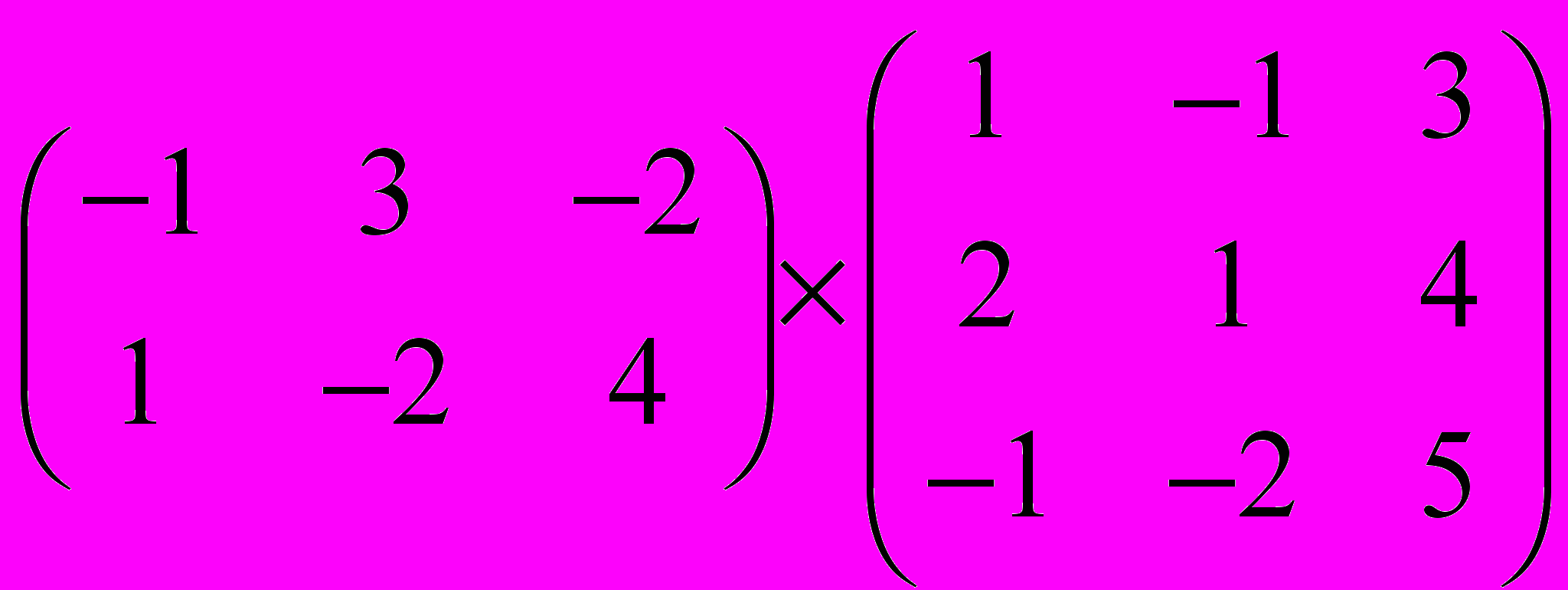 |
| 3 | 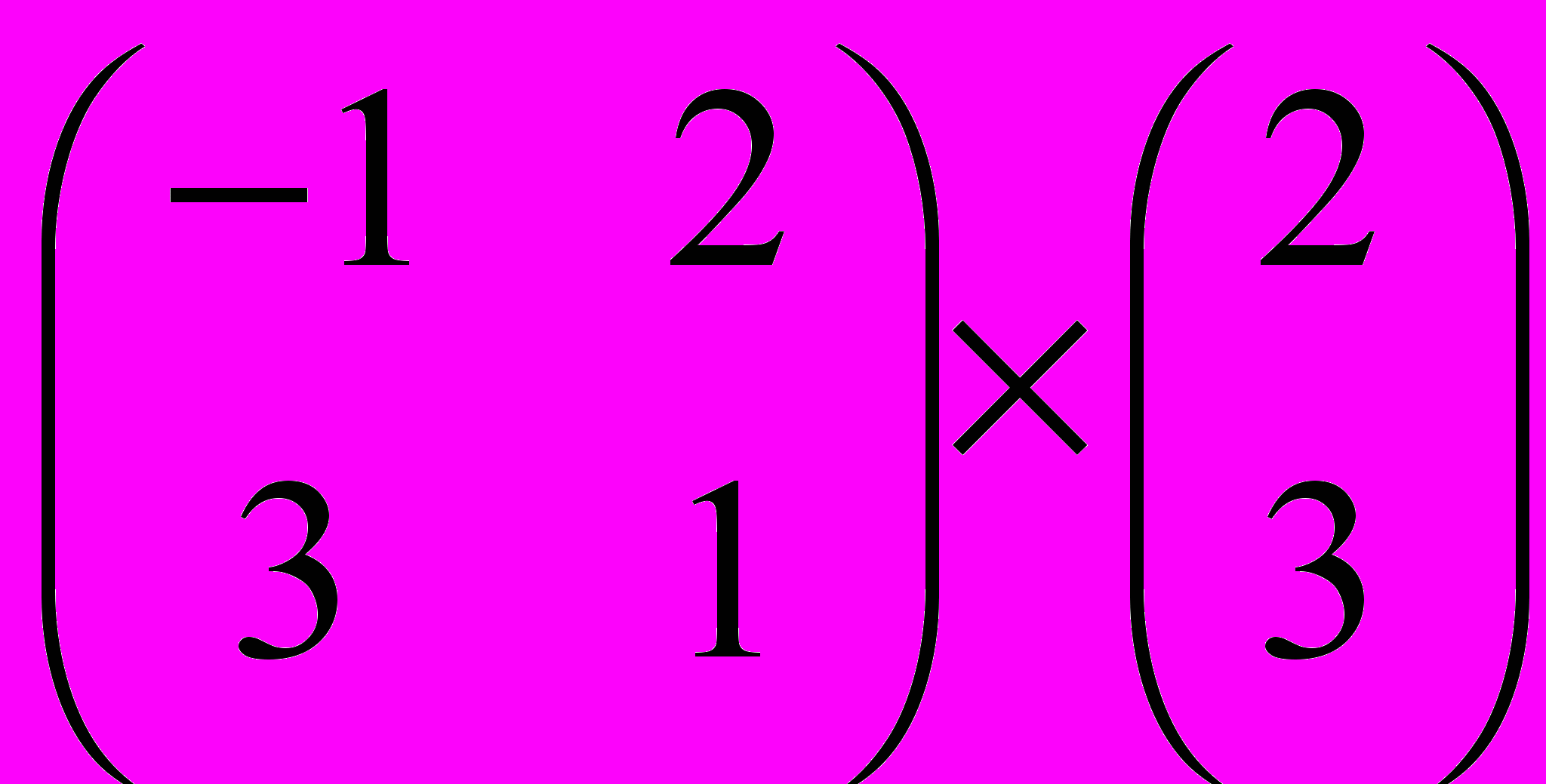 | 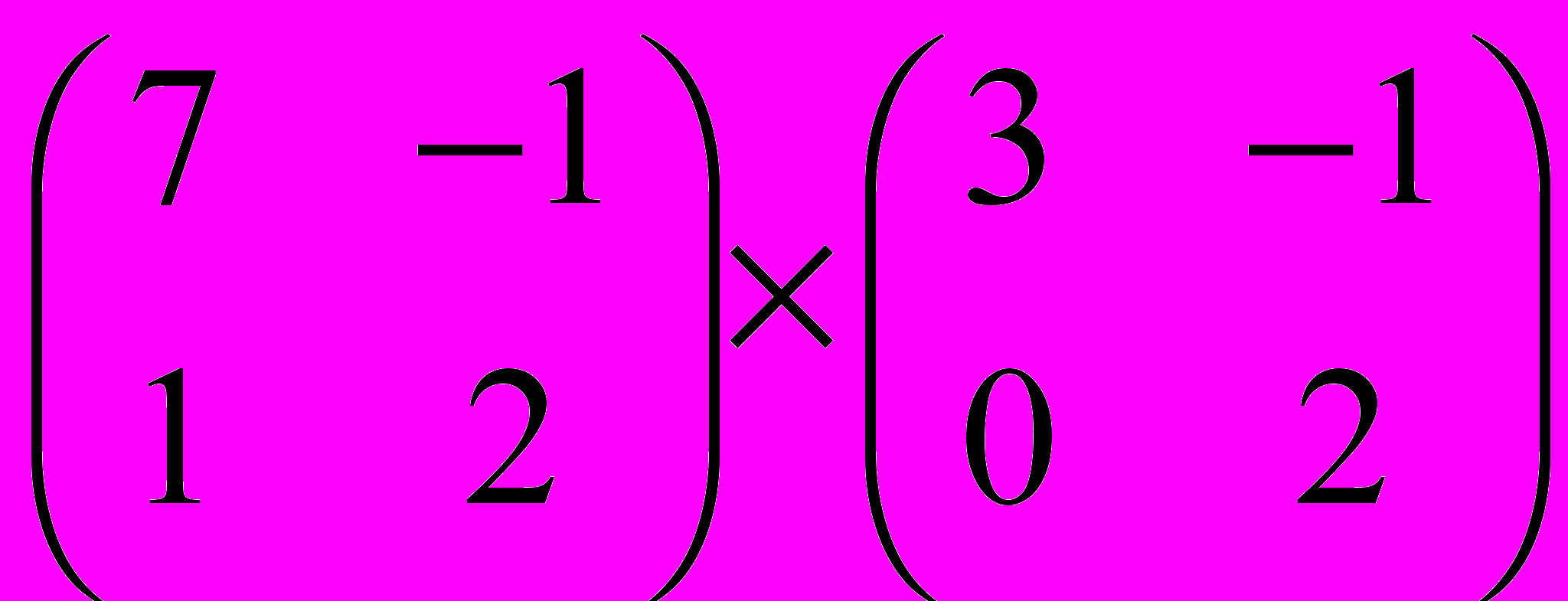 | 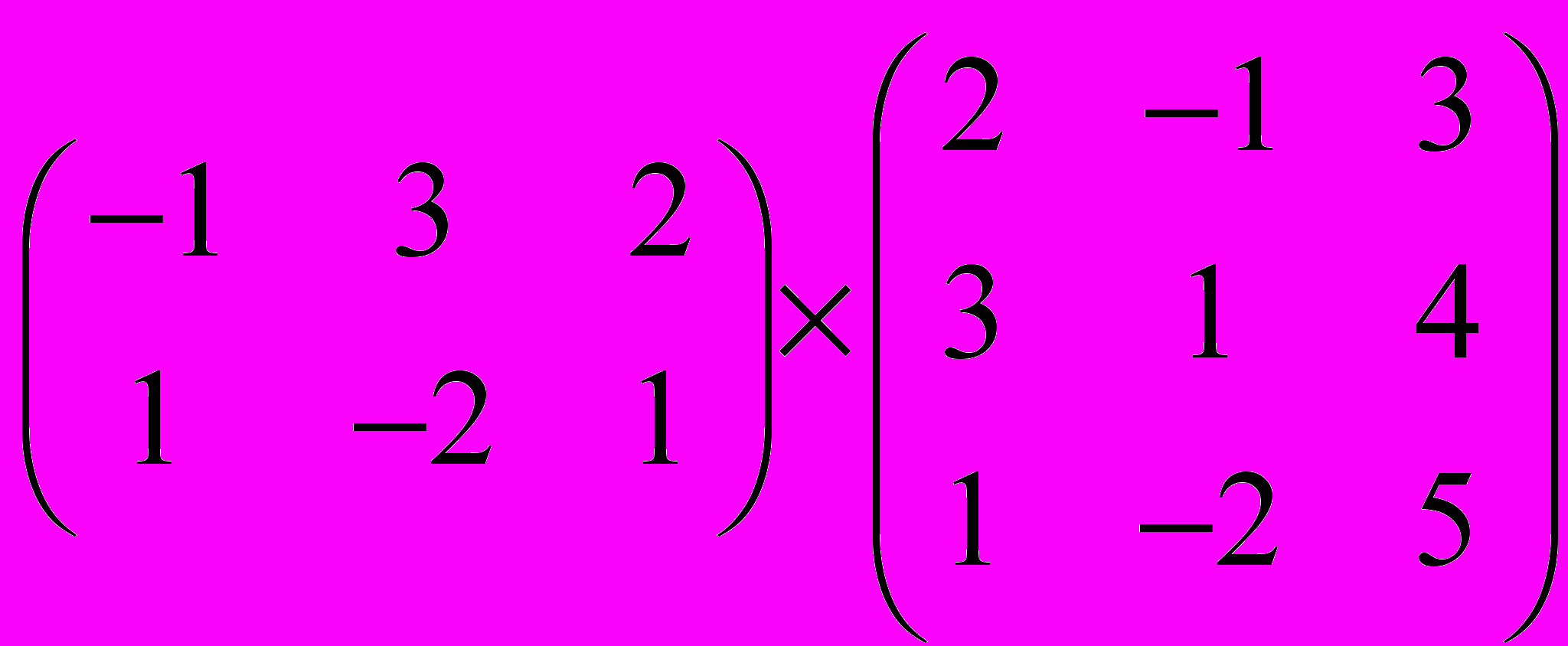 |
| 4 | 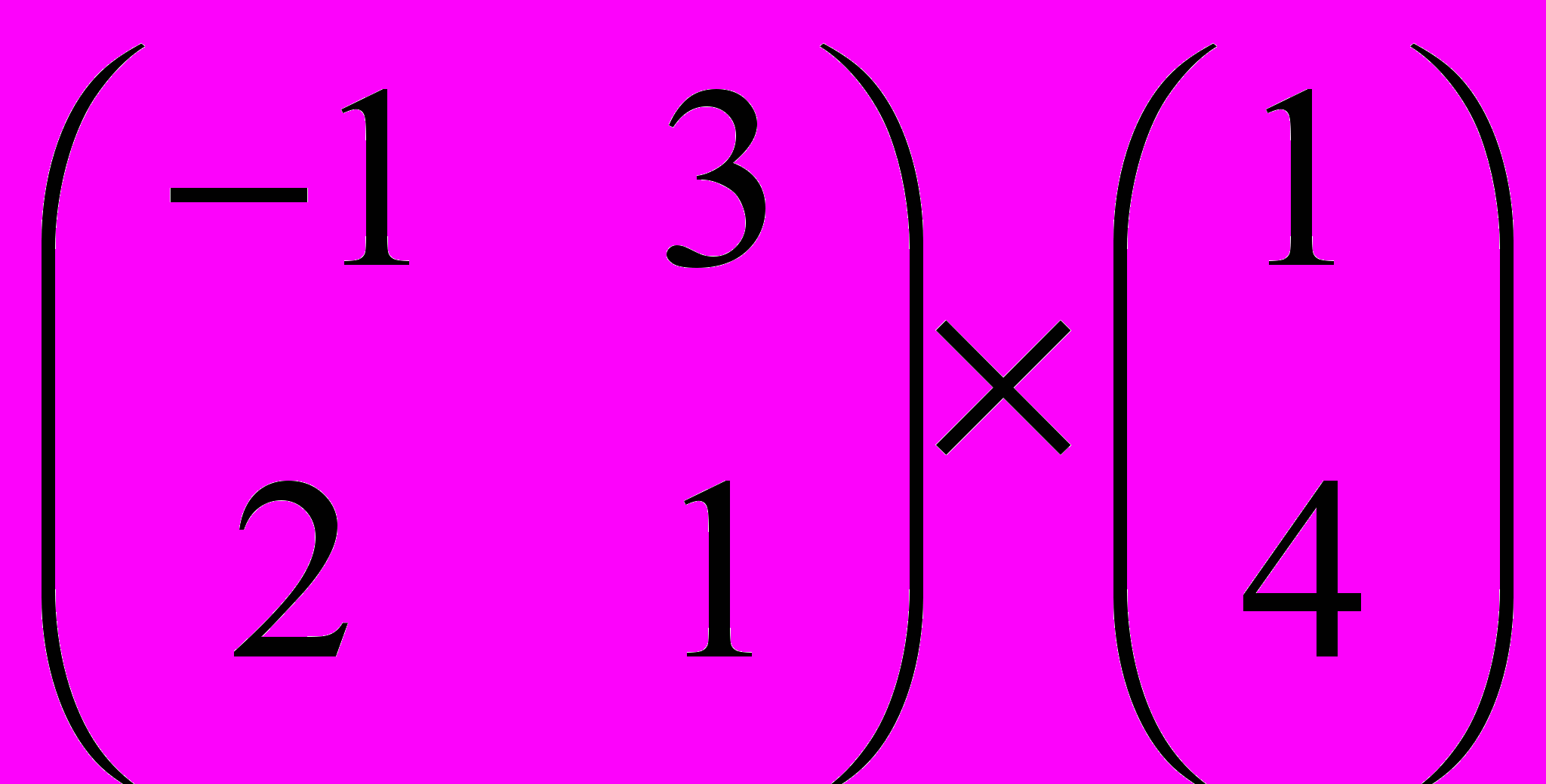 | 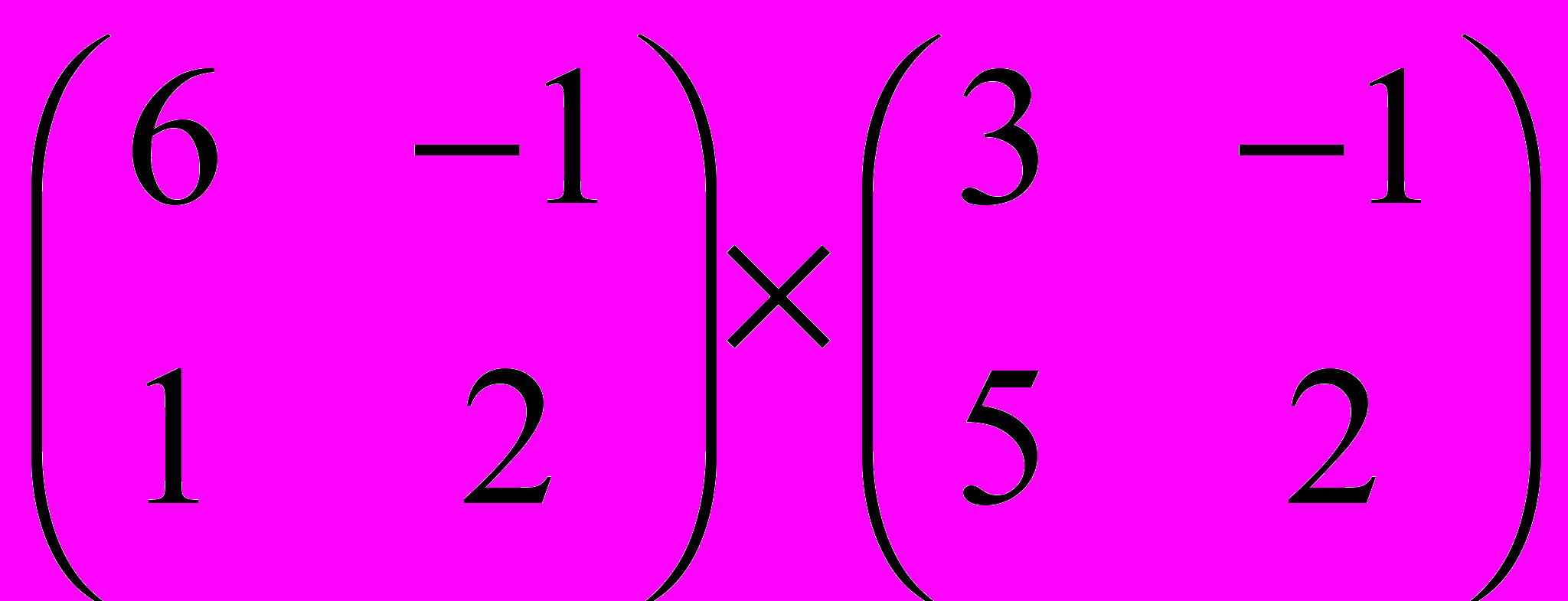 | 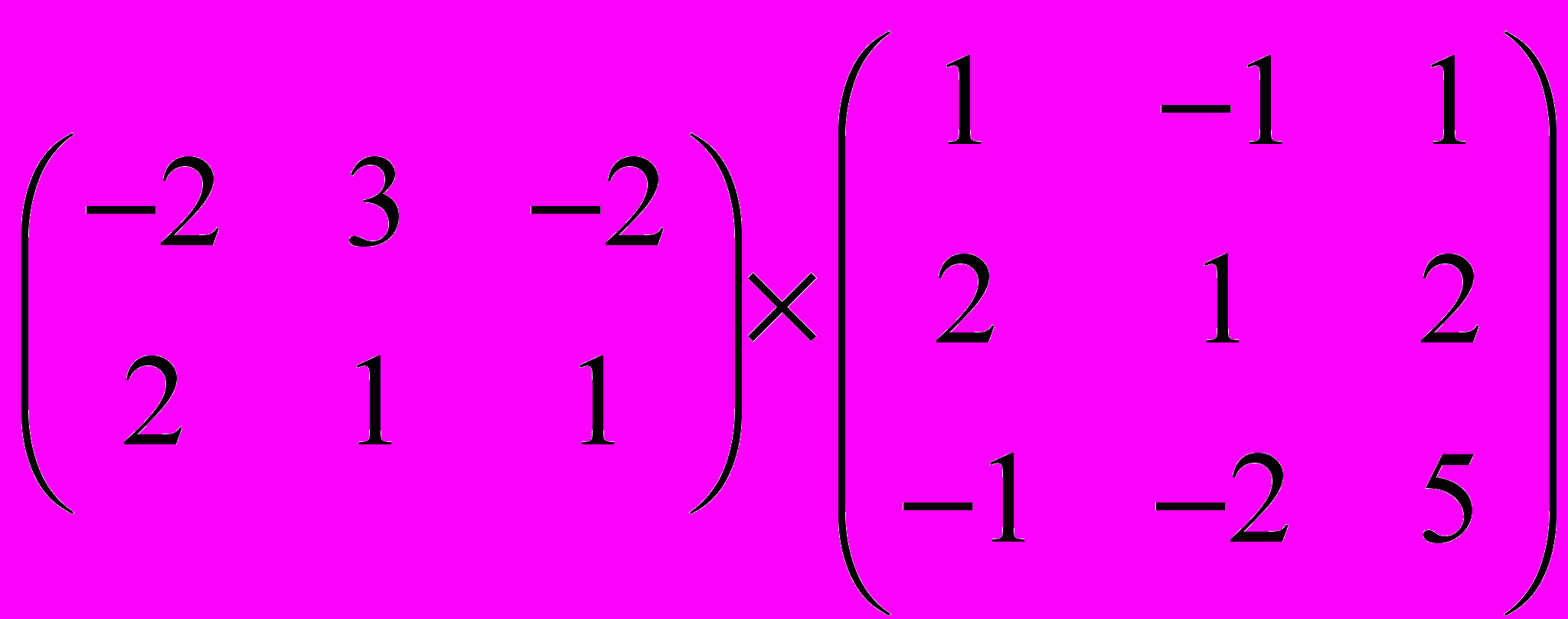 |
| 5 | 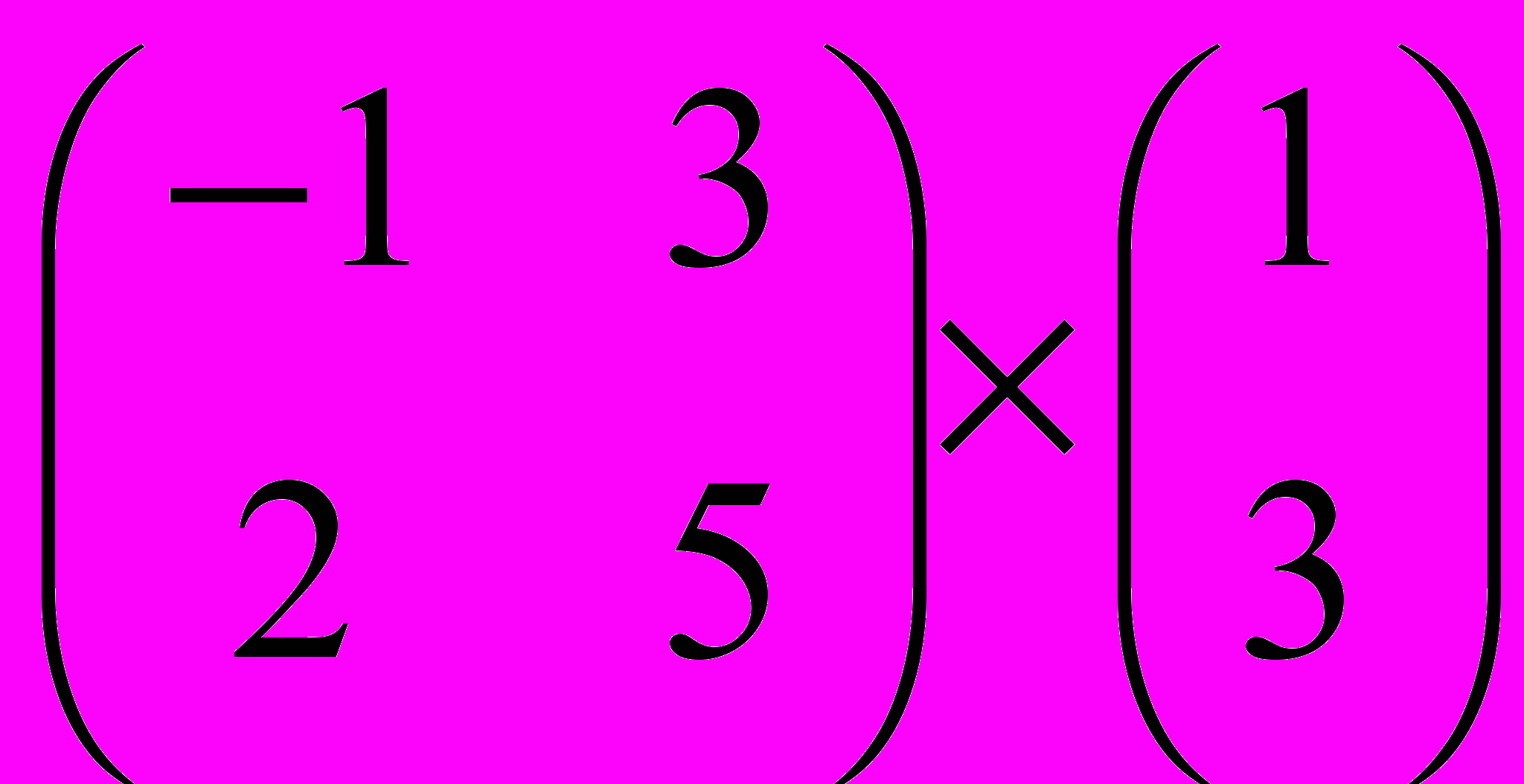 | 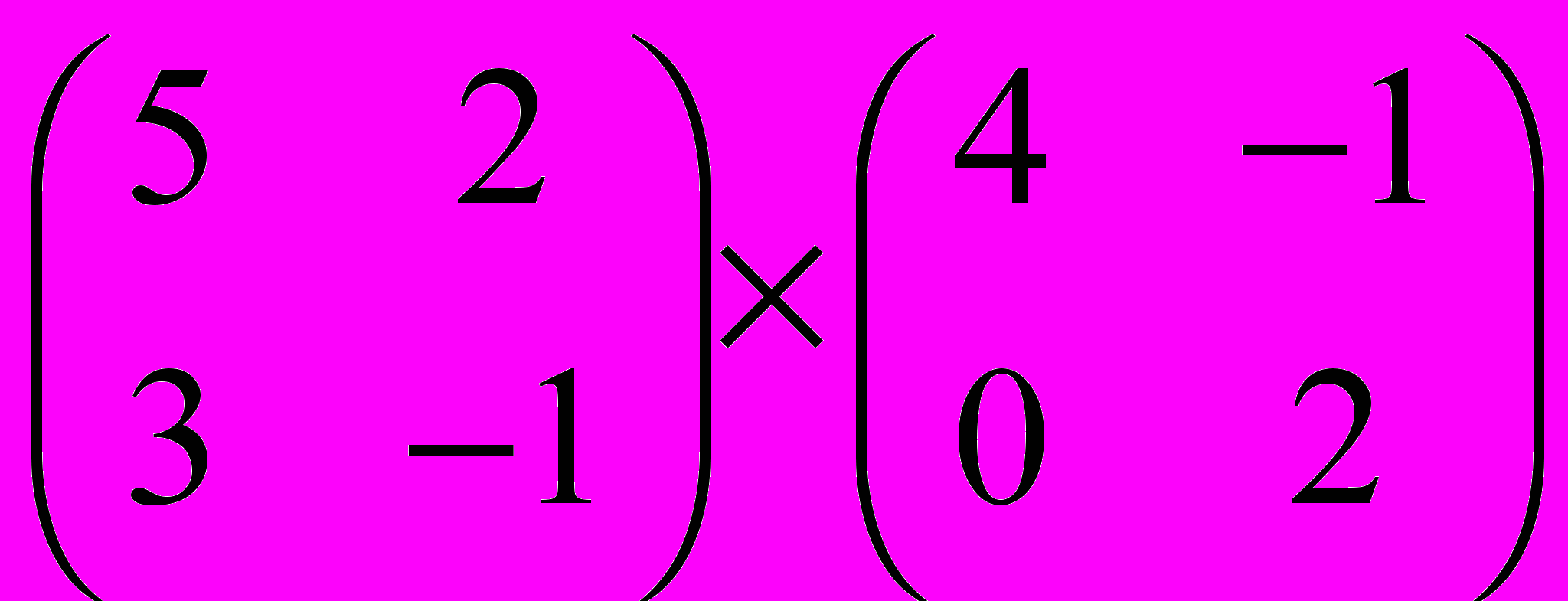 | 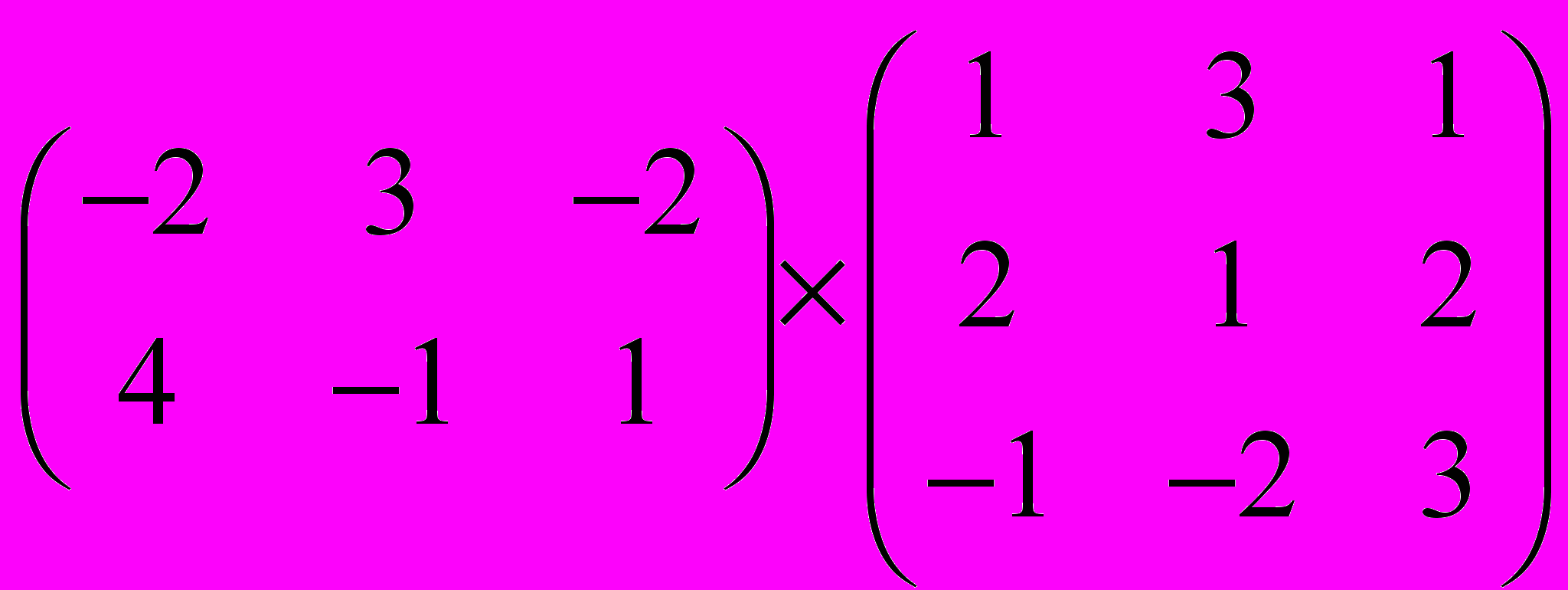 |
| 6 | 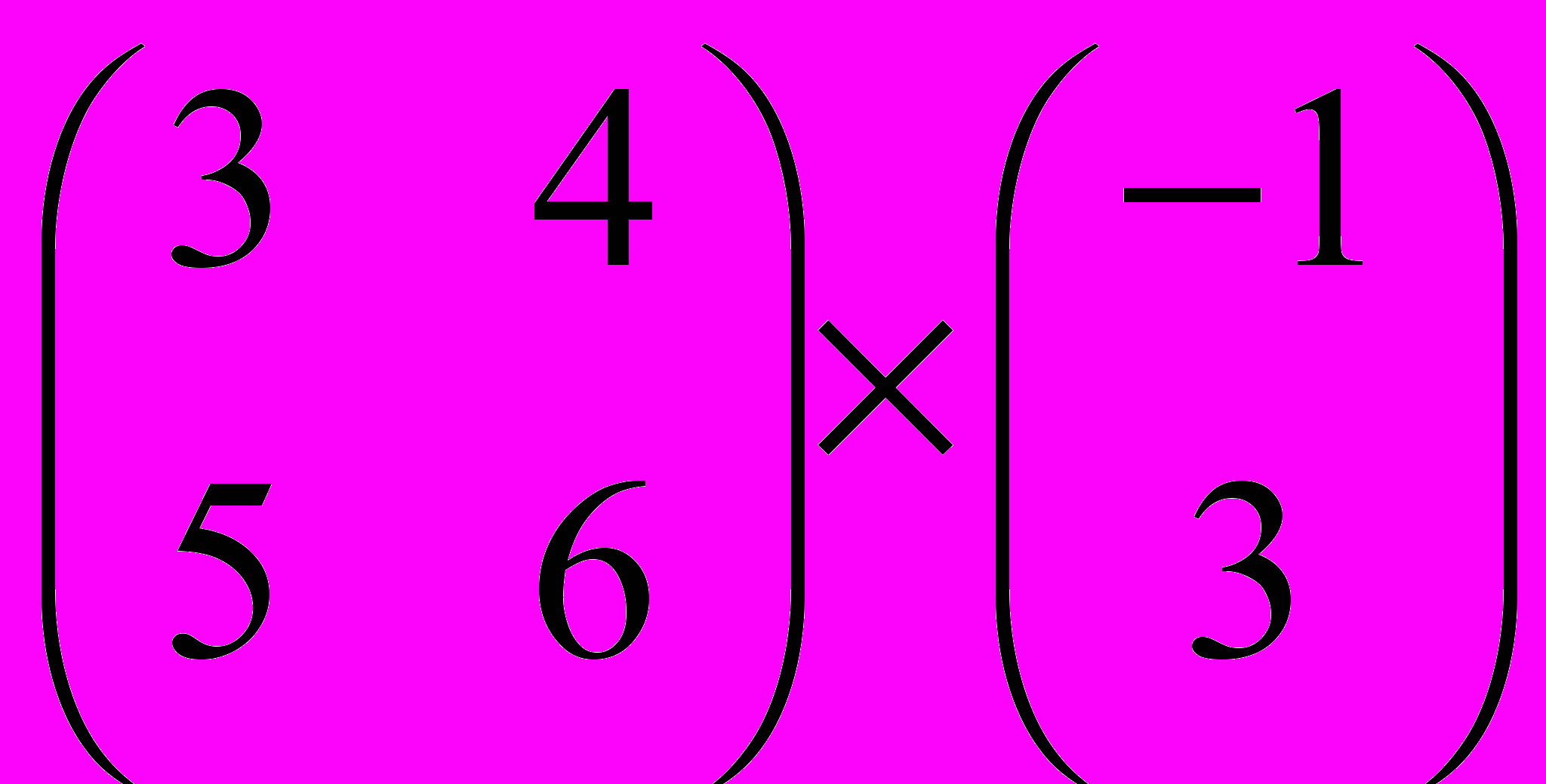 | 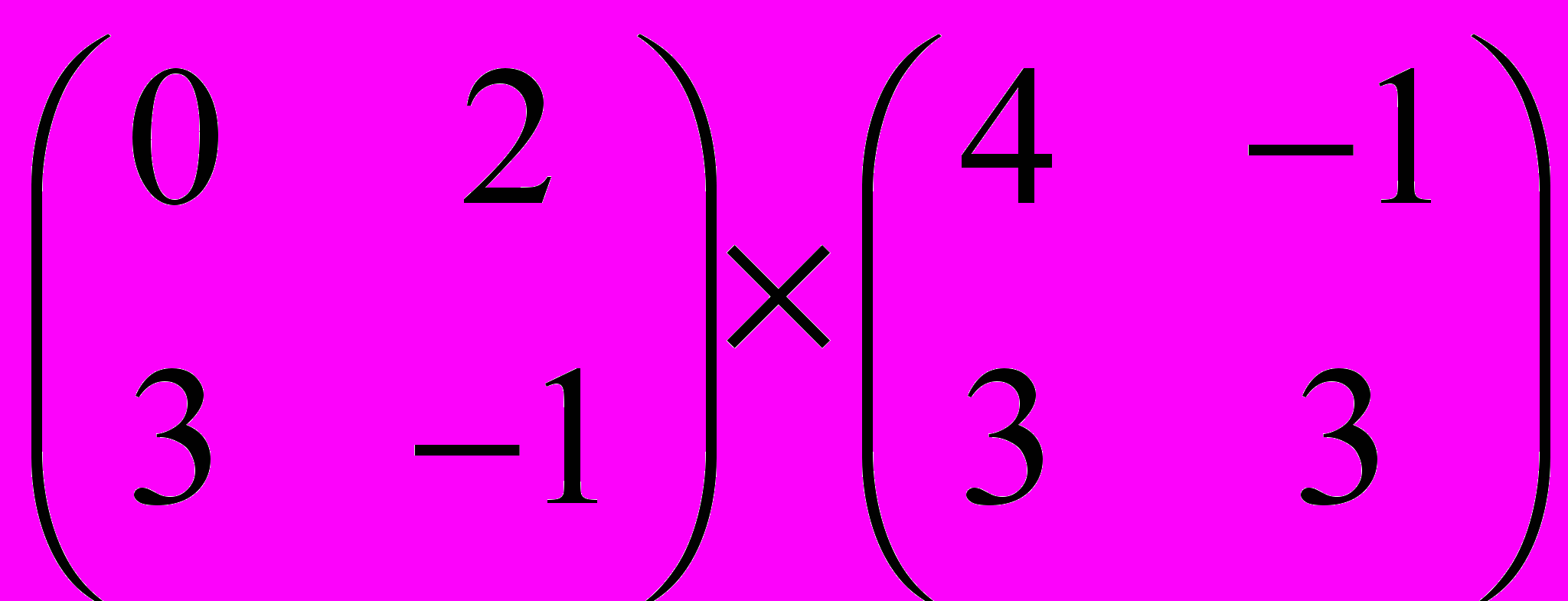 | 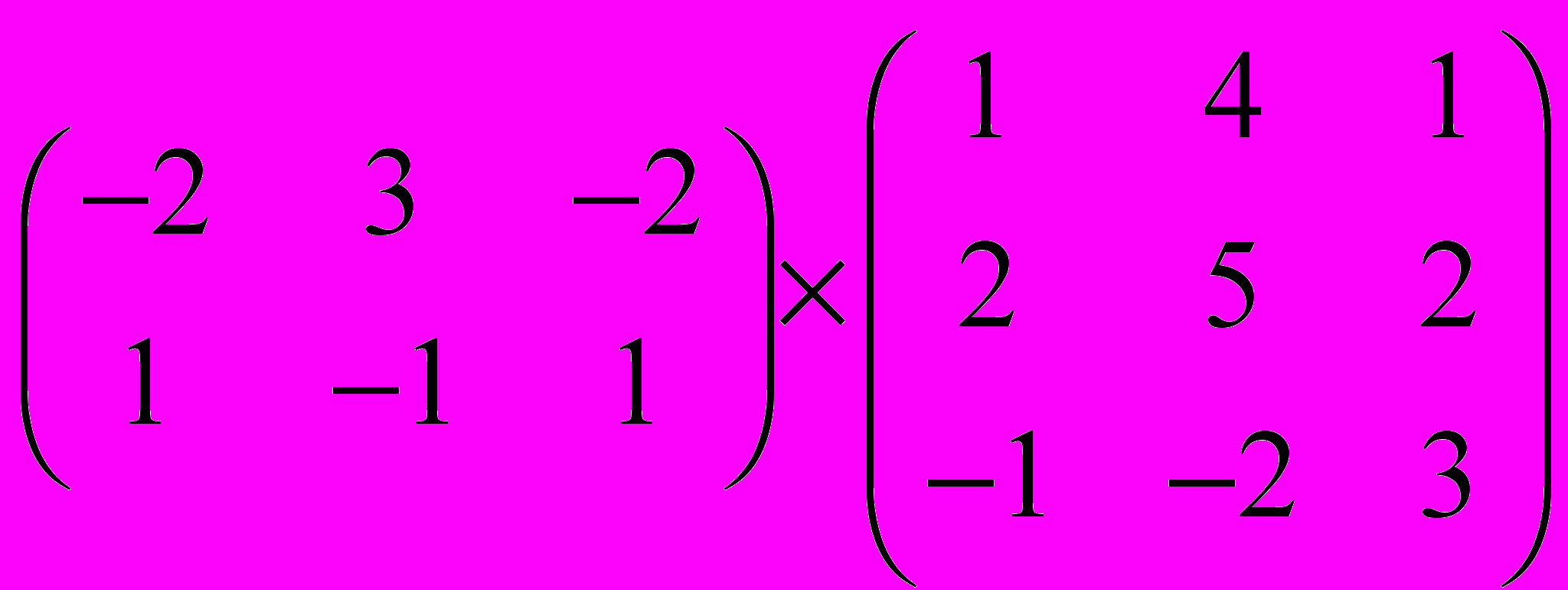 |
| 7 | 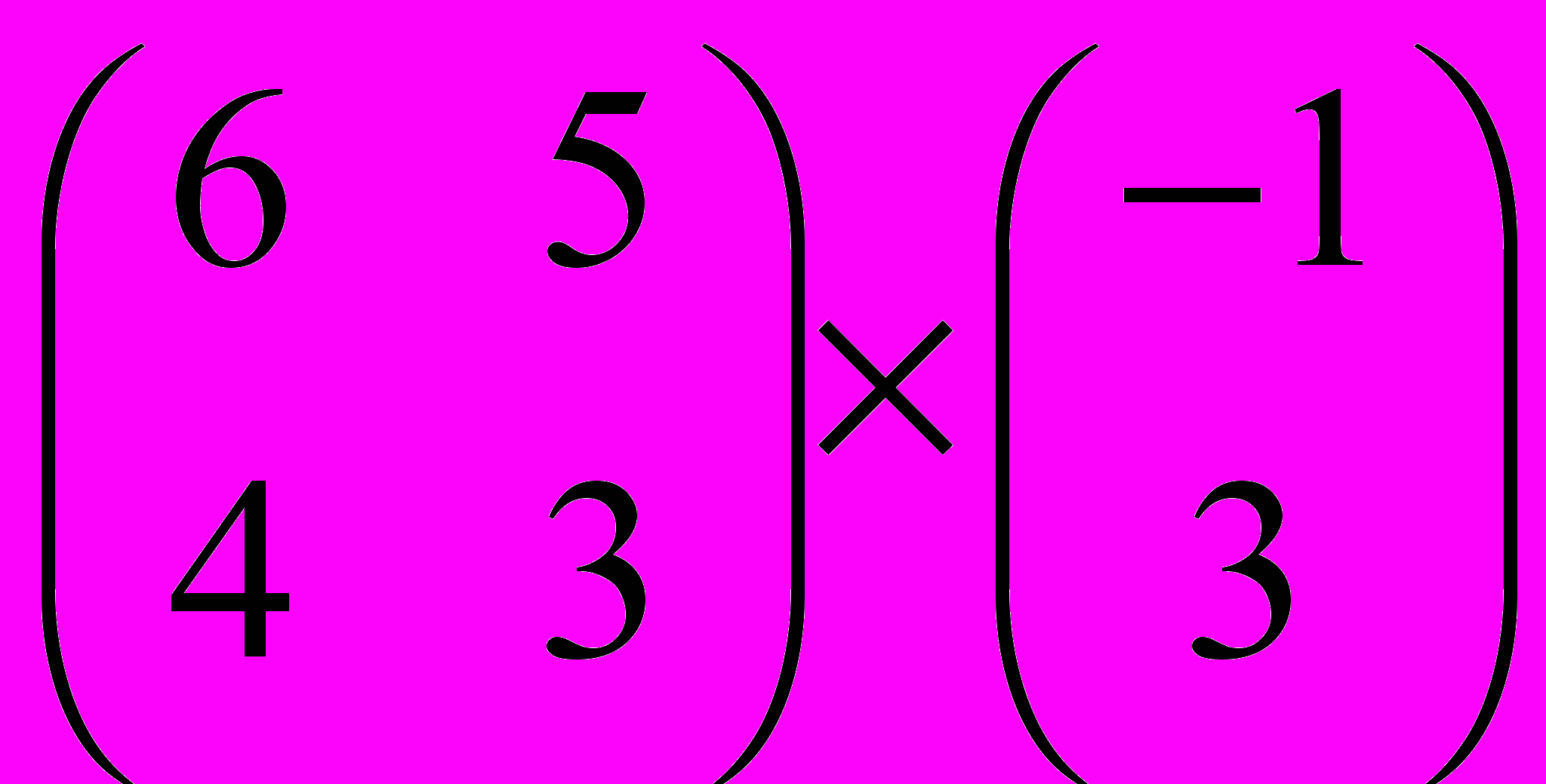 | 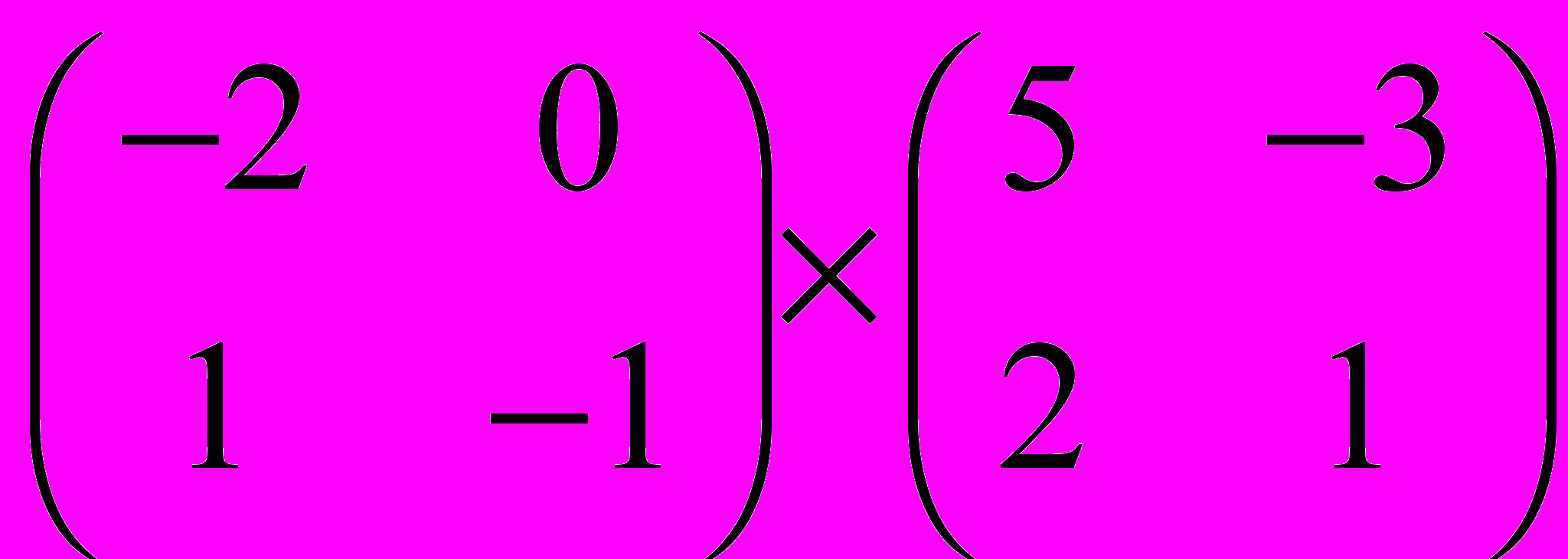 | 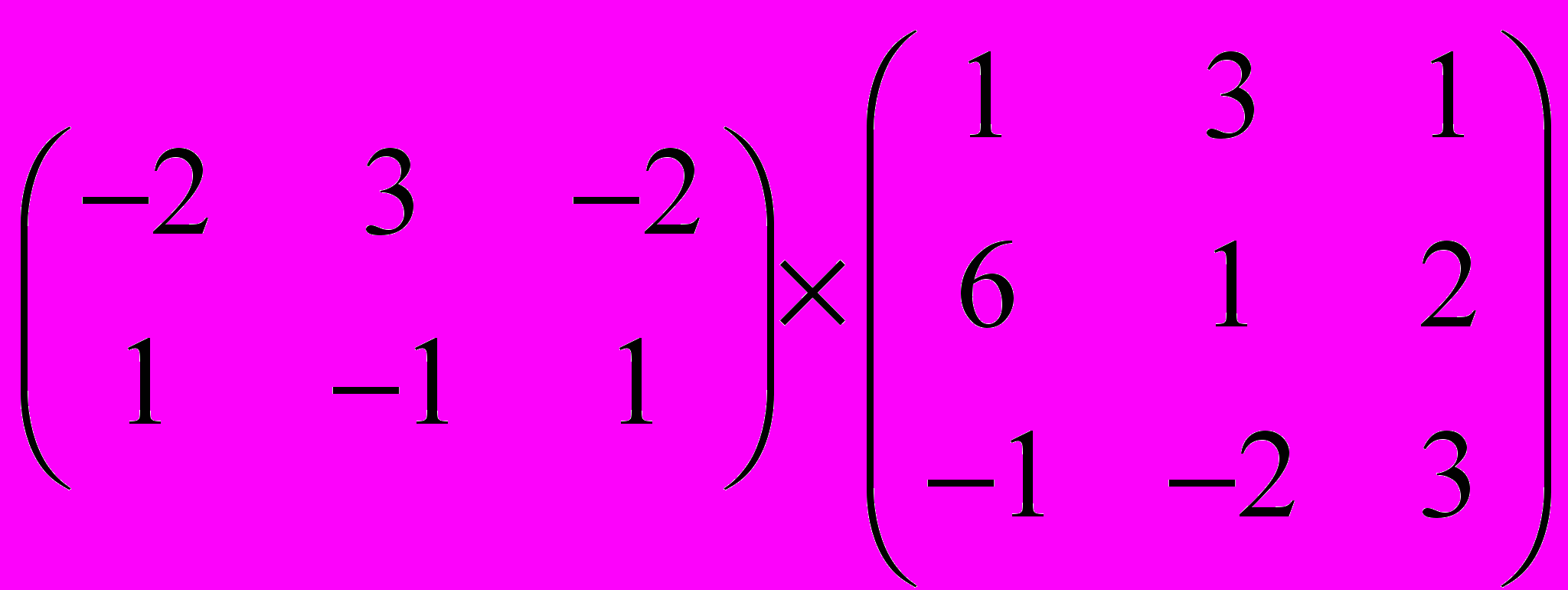 |
| 8 | 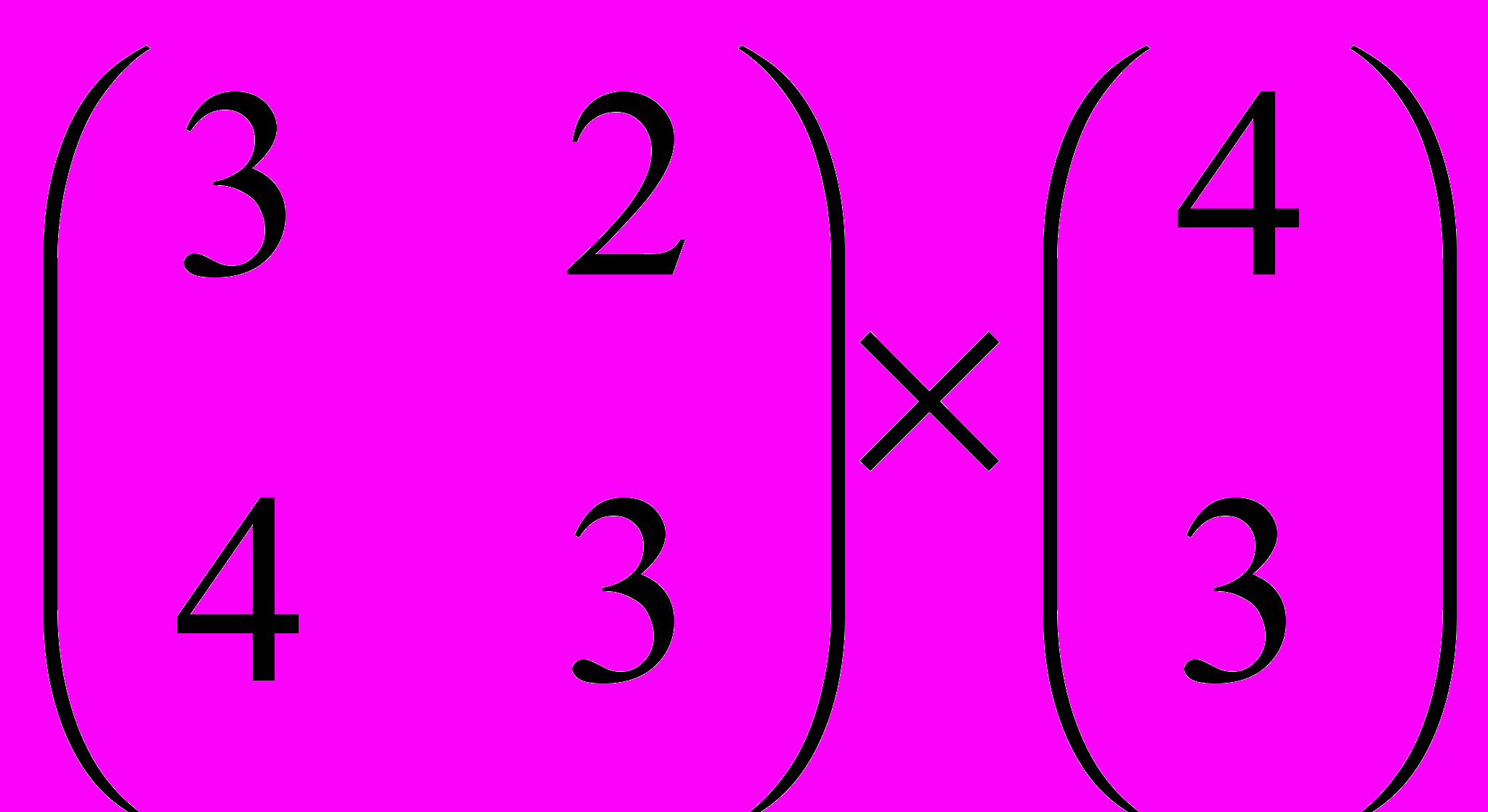 | 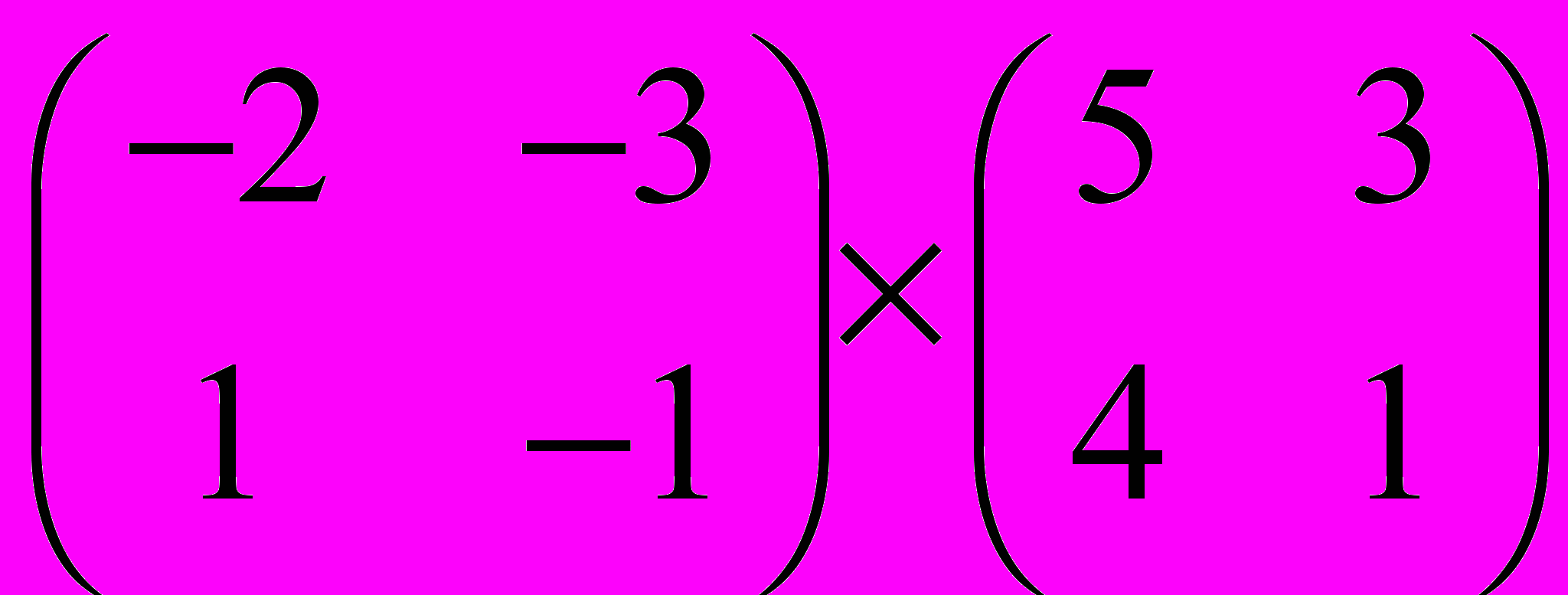 | 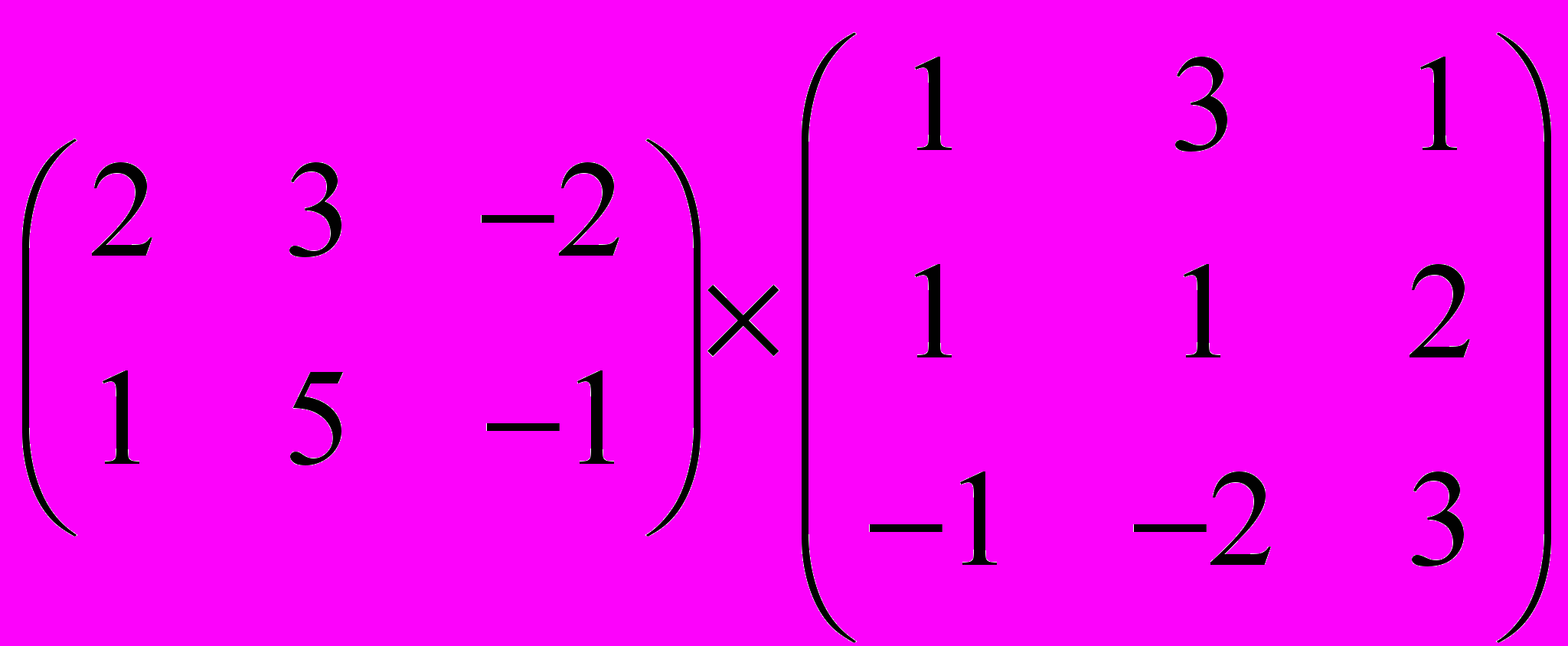 |
| 9 | 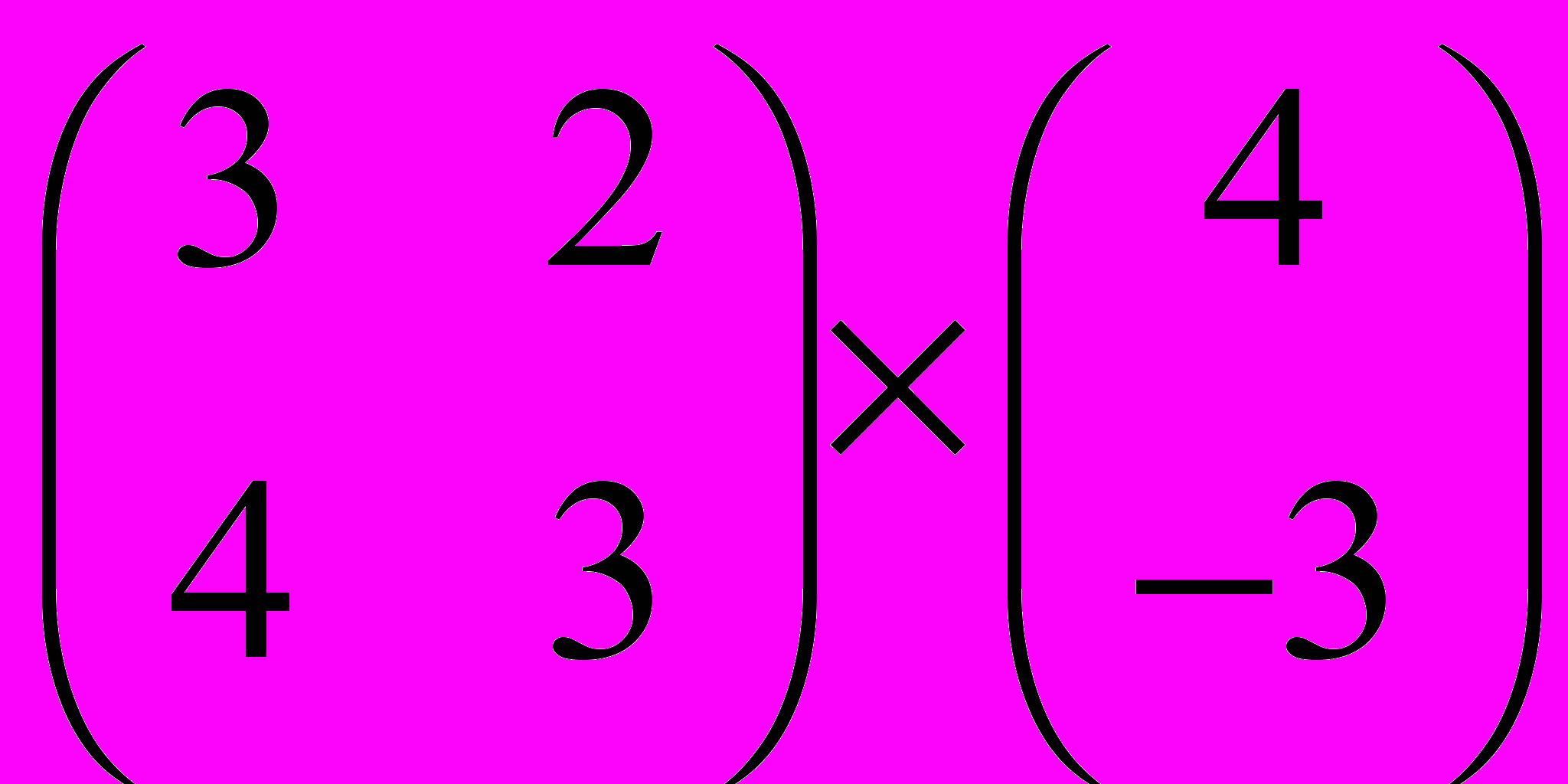 | 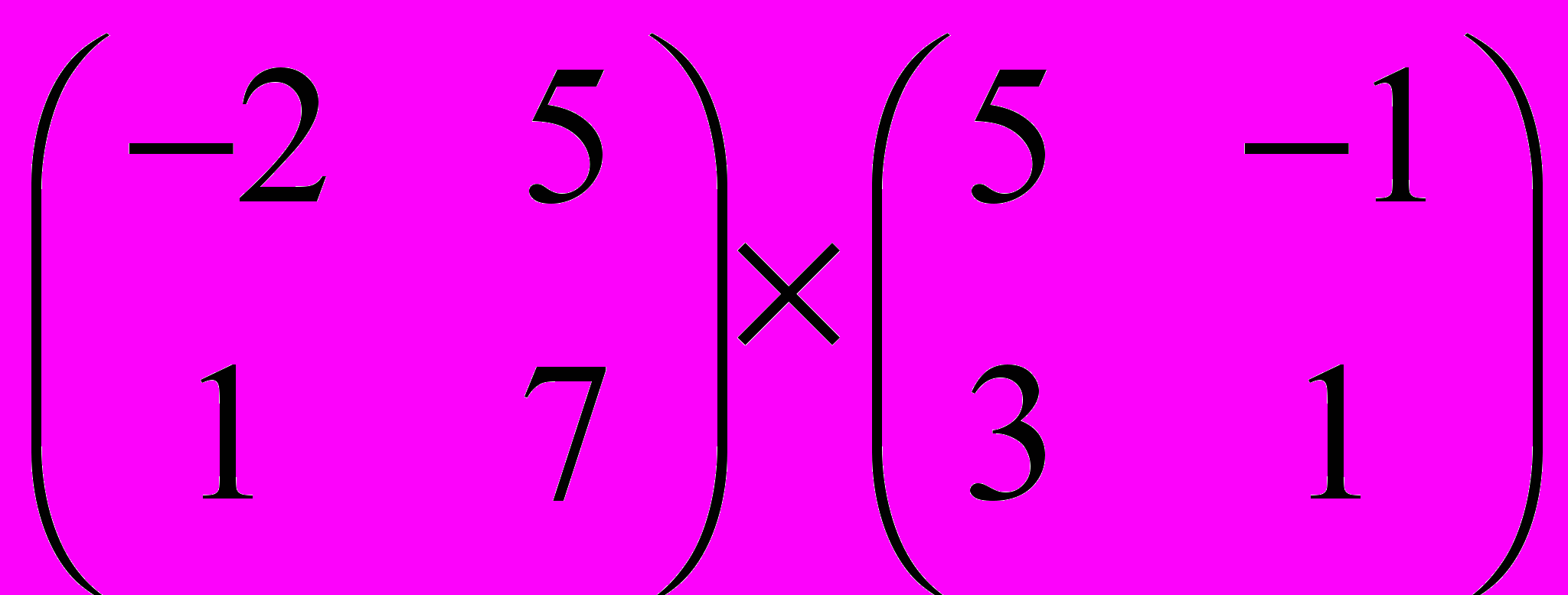 | 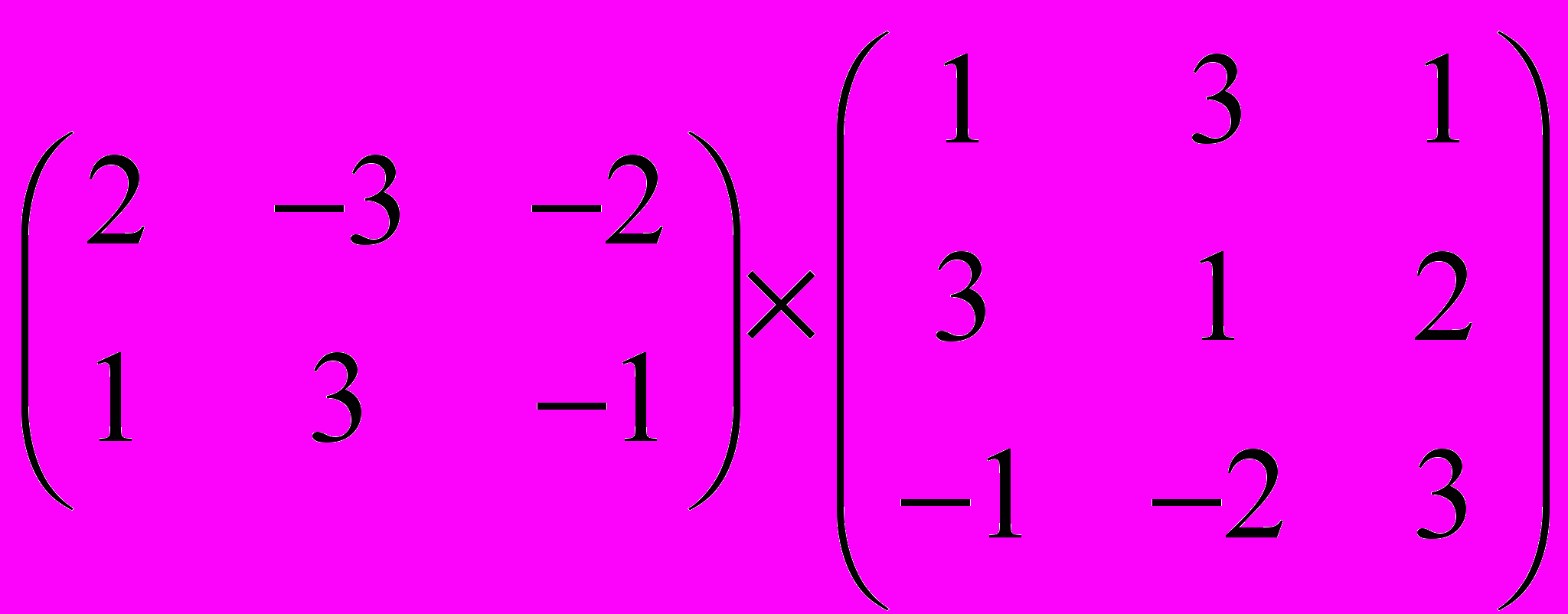 |
| 10 | 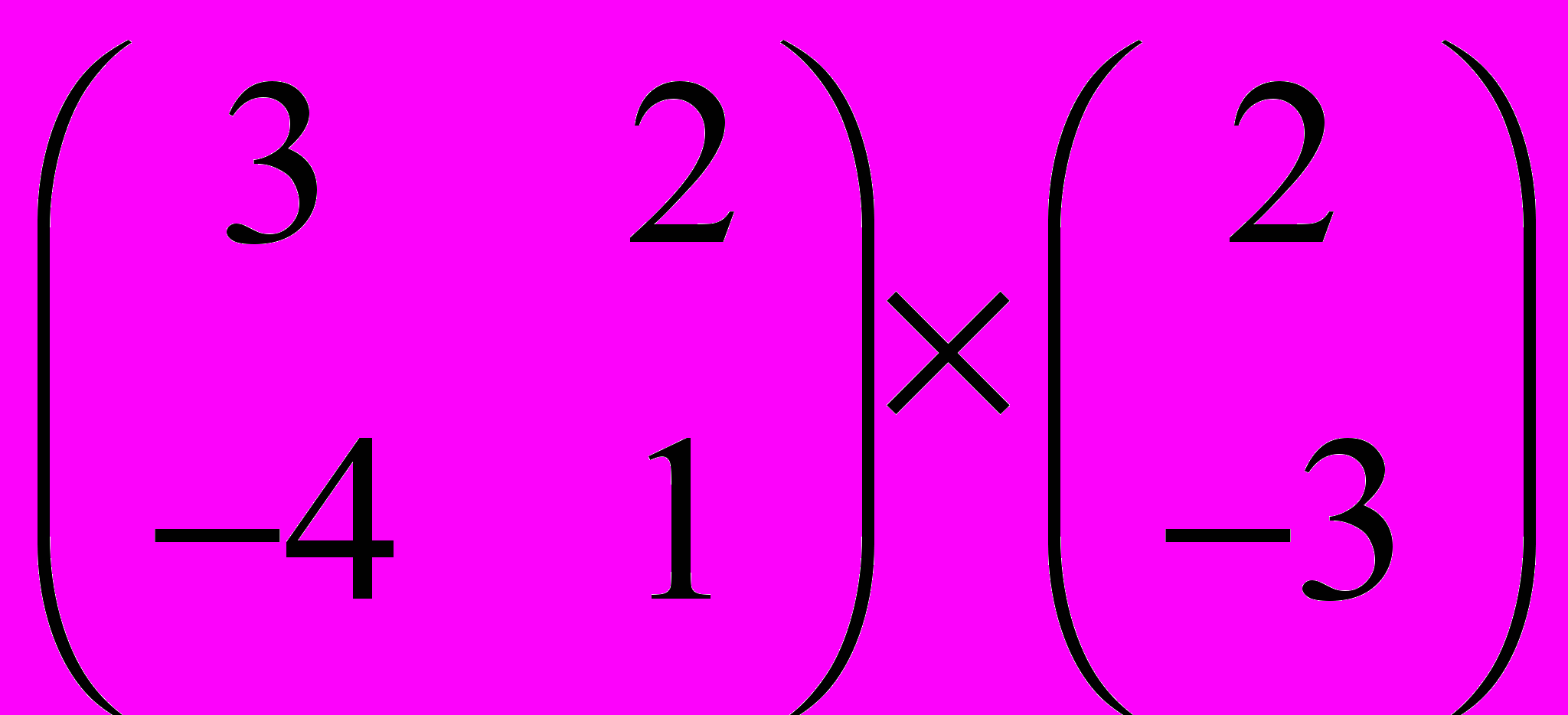 | 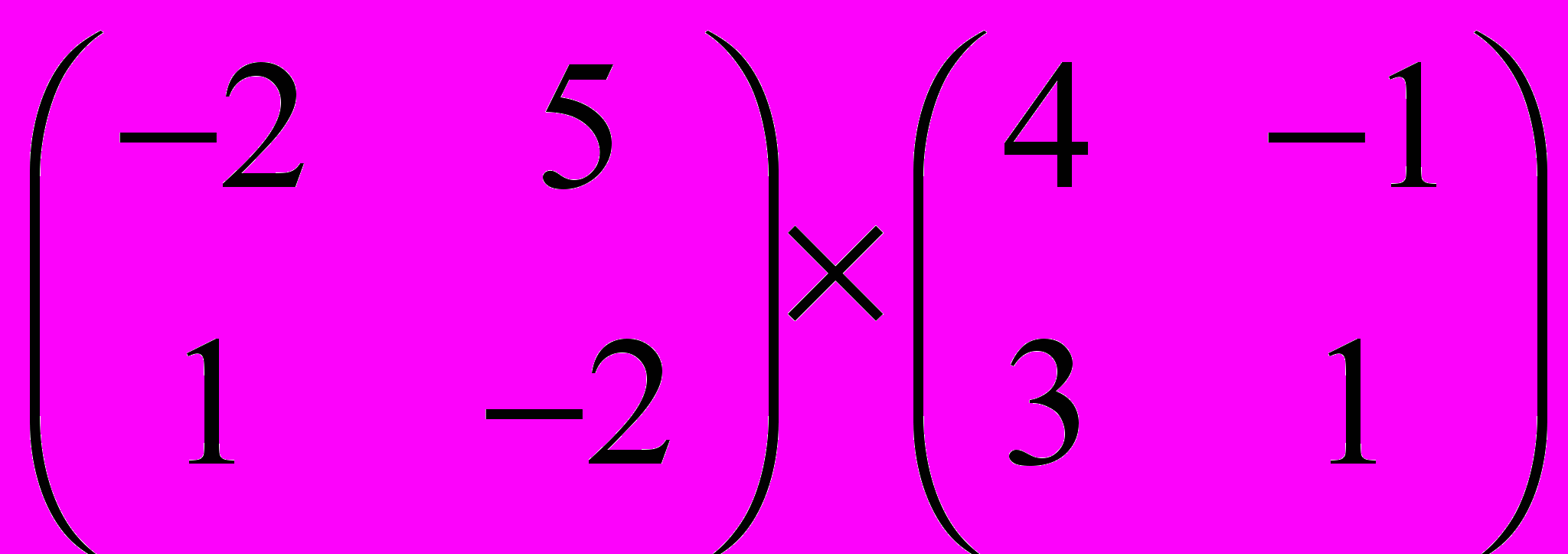 | 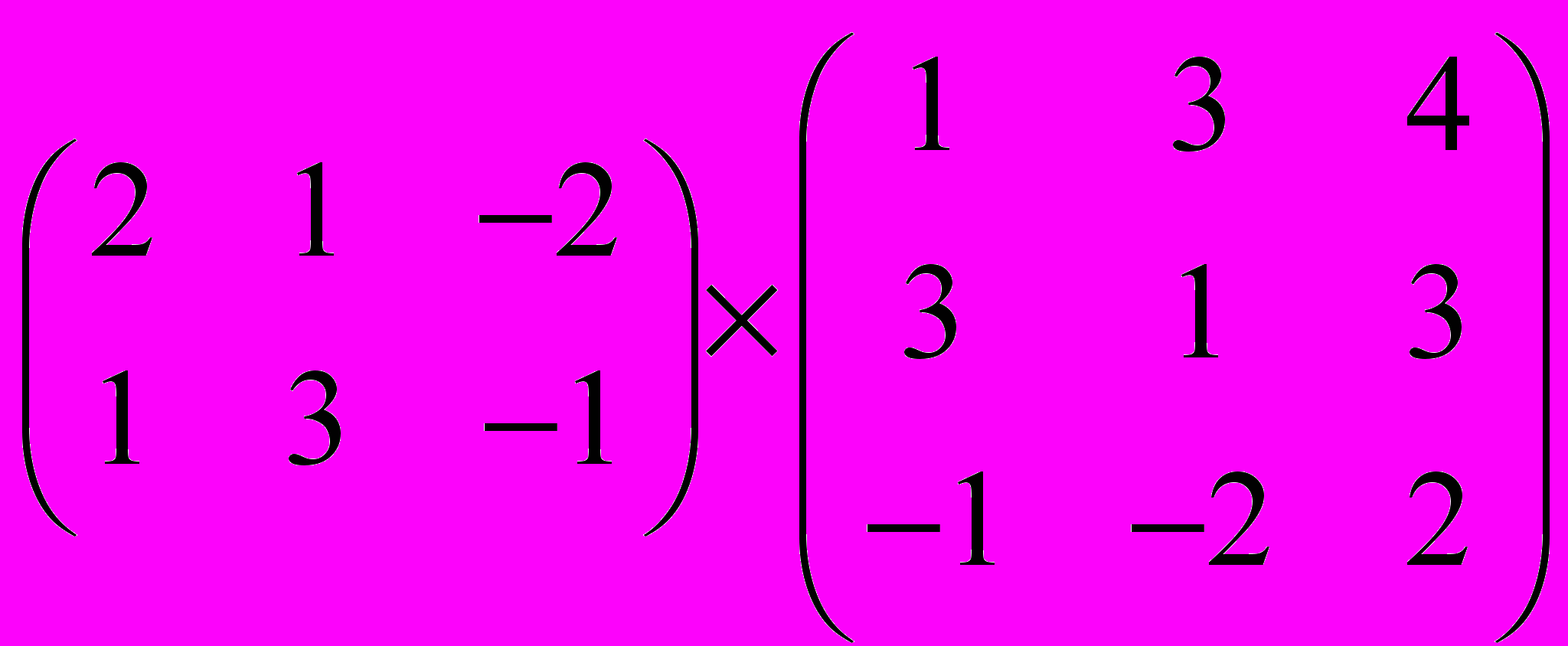 |
Задание 2. Вычислить определители методом разложения по строке или столбцу, имеющим большее количество нулей.
| № вар. | 1 | 2 | 3 | 4 | 5 |
| | 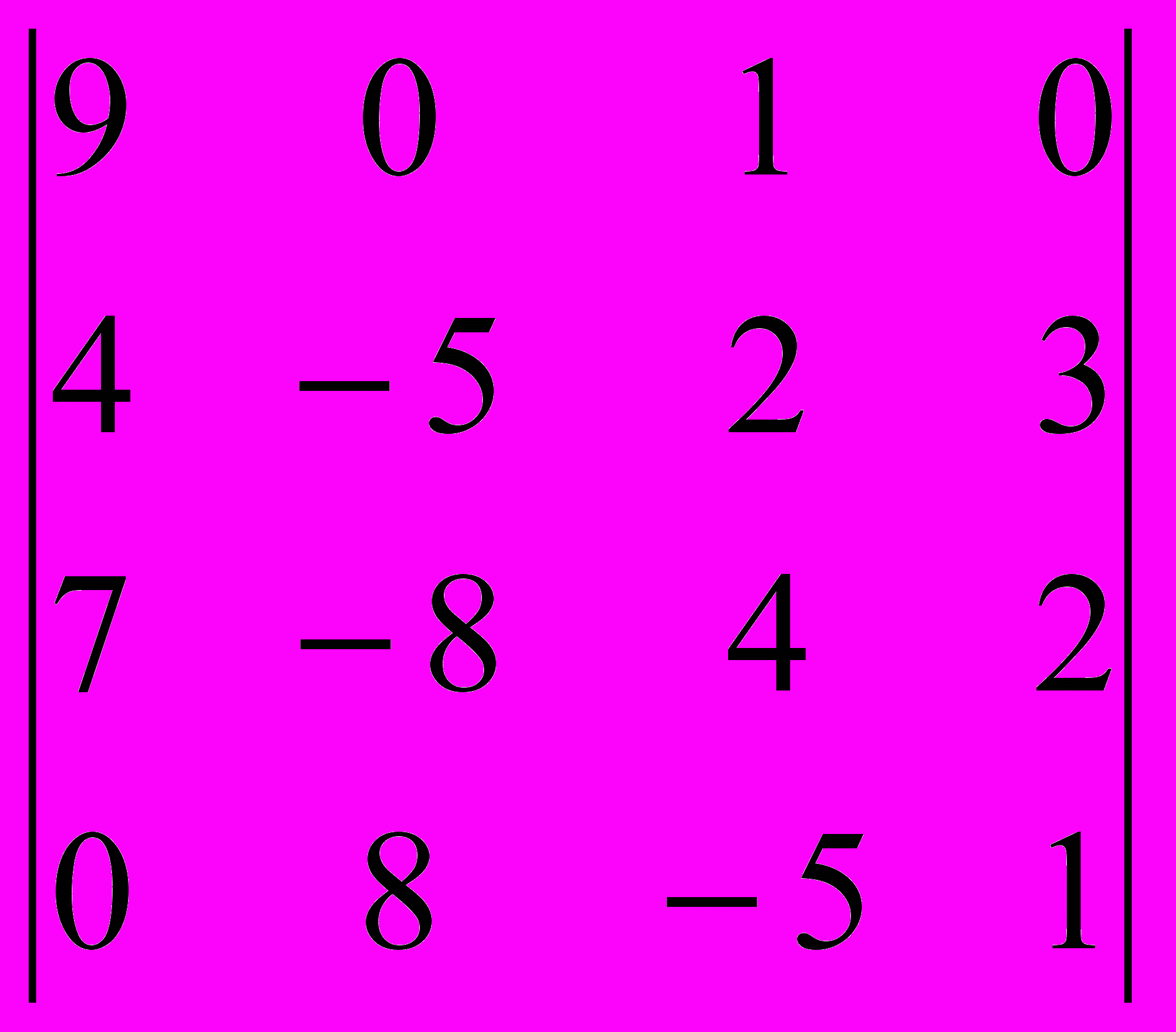 | 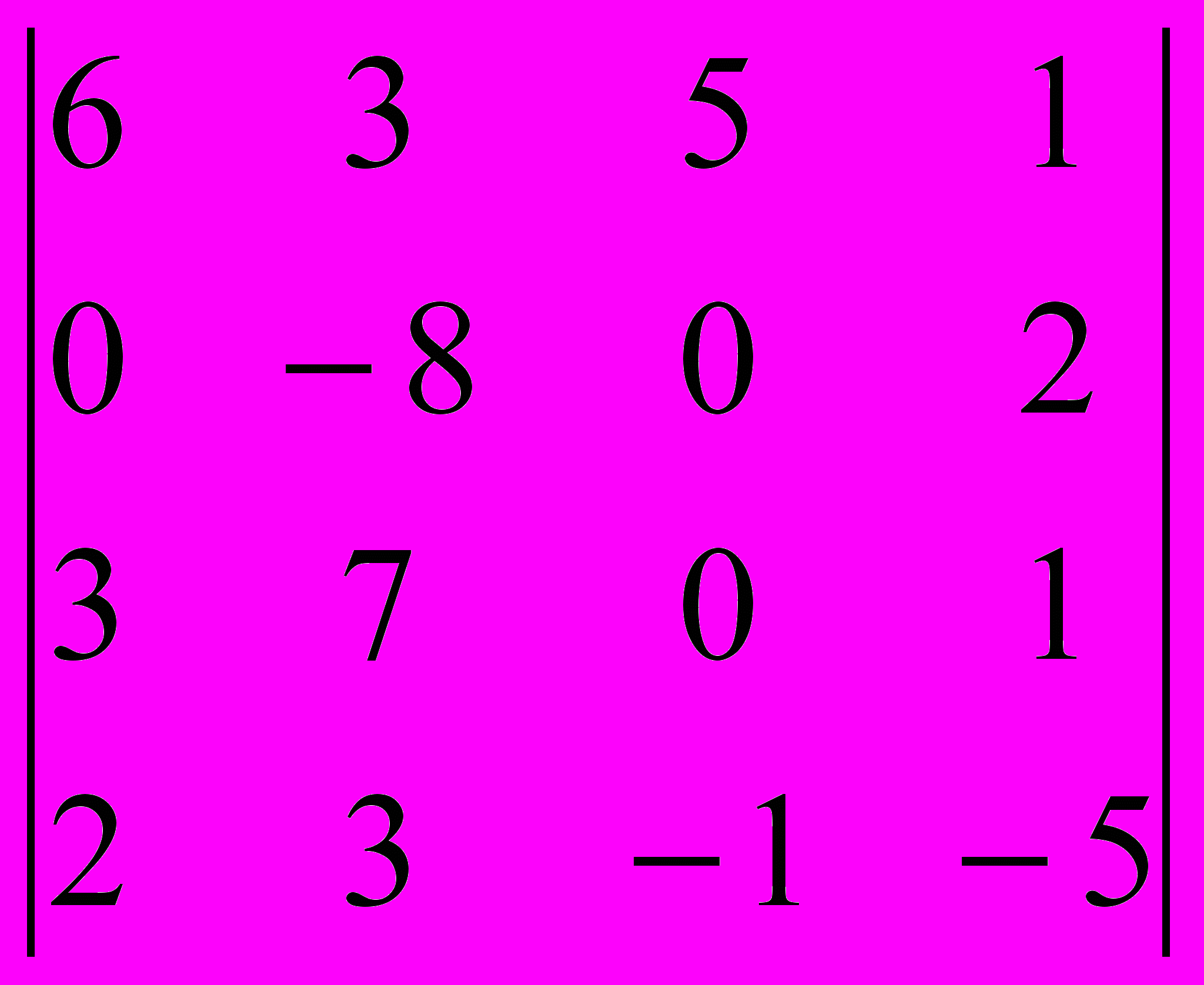 | 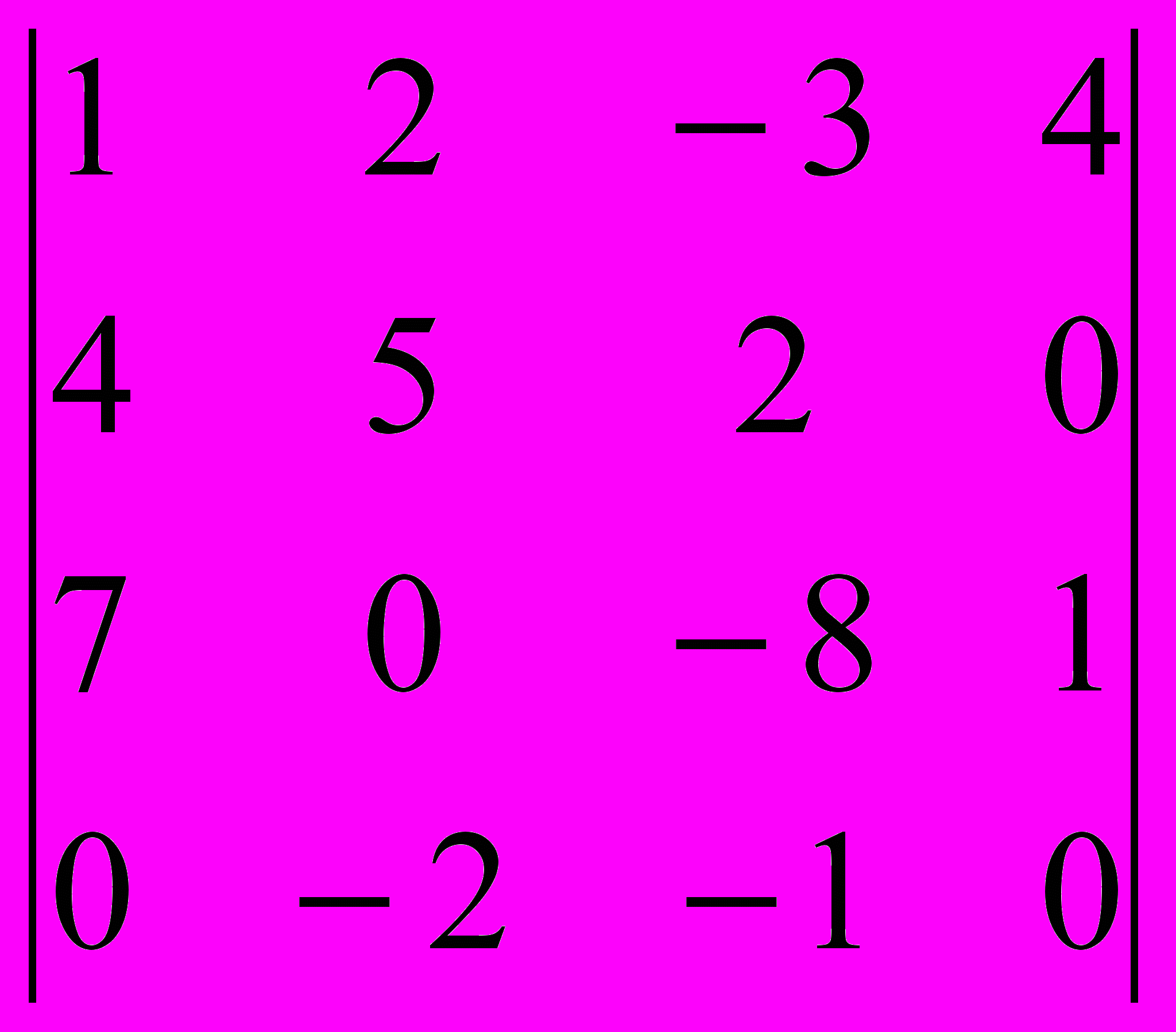 | 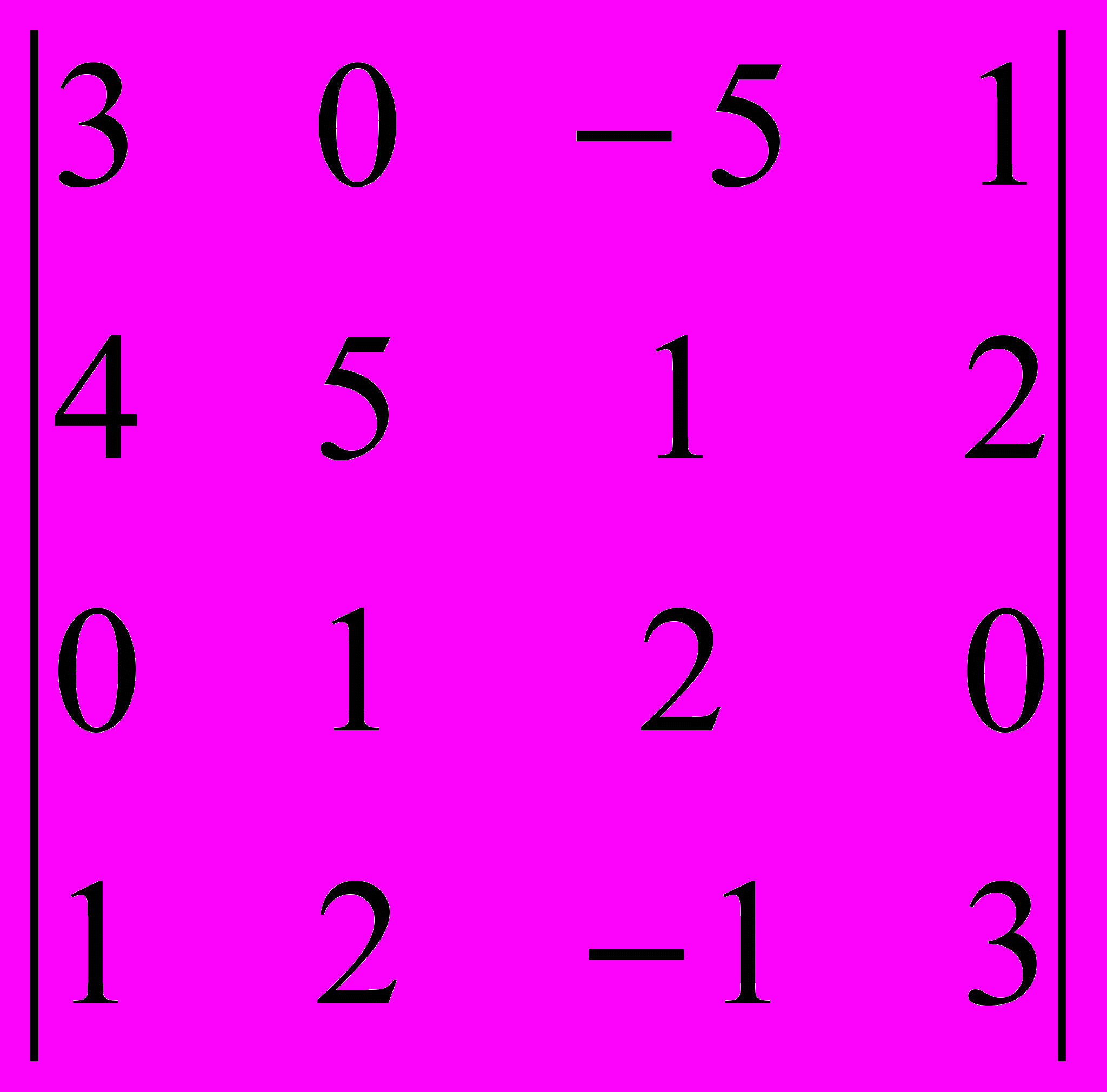 | 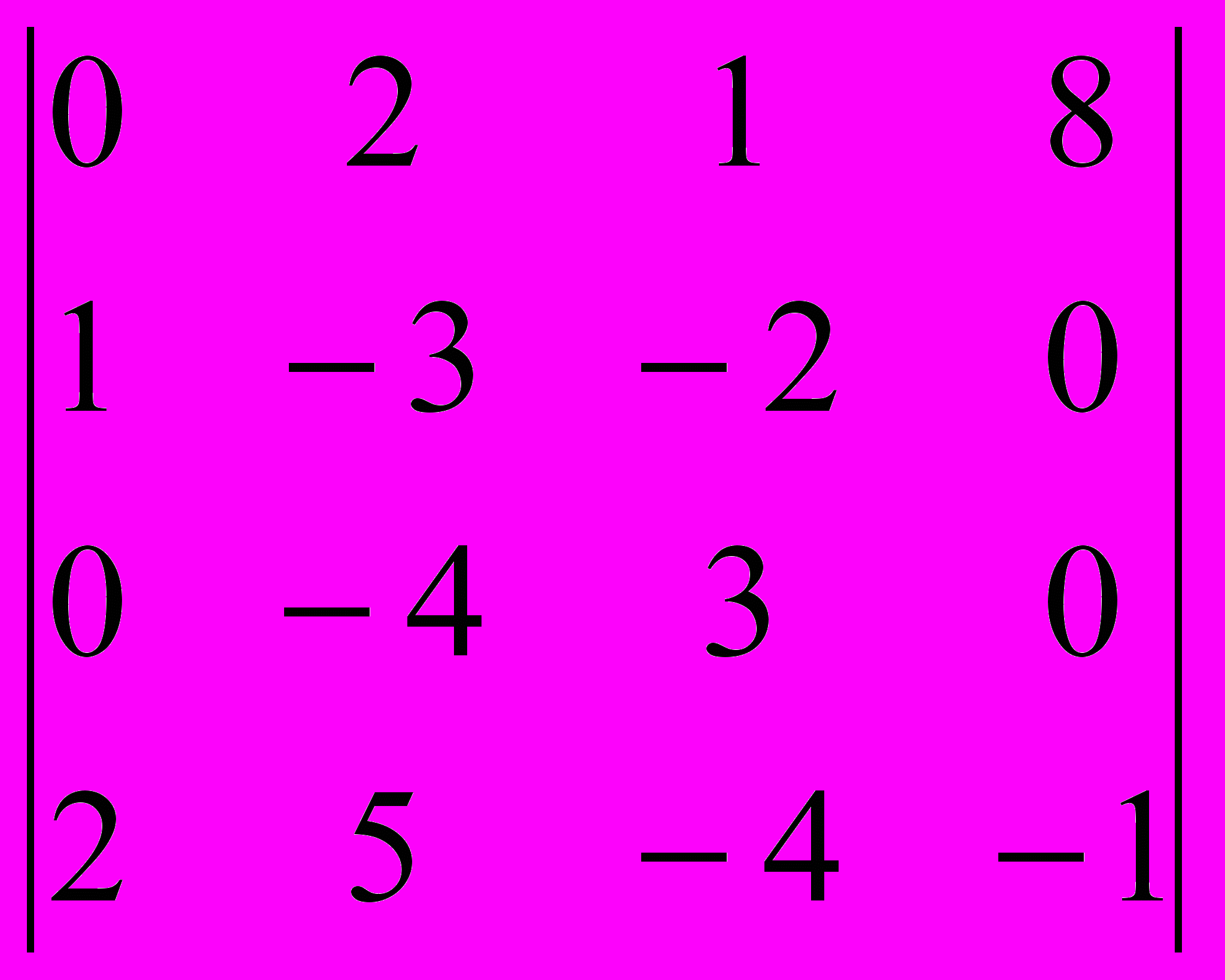 |
| № вар. | 6 | 7 | 8 | 9 | 10 |
| | 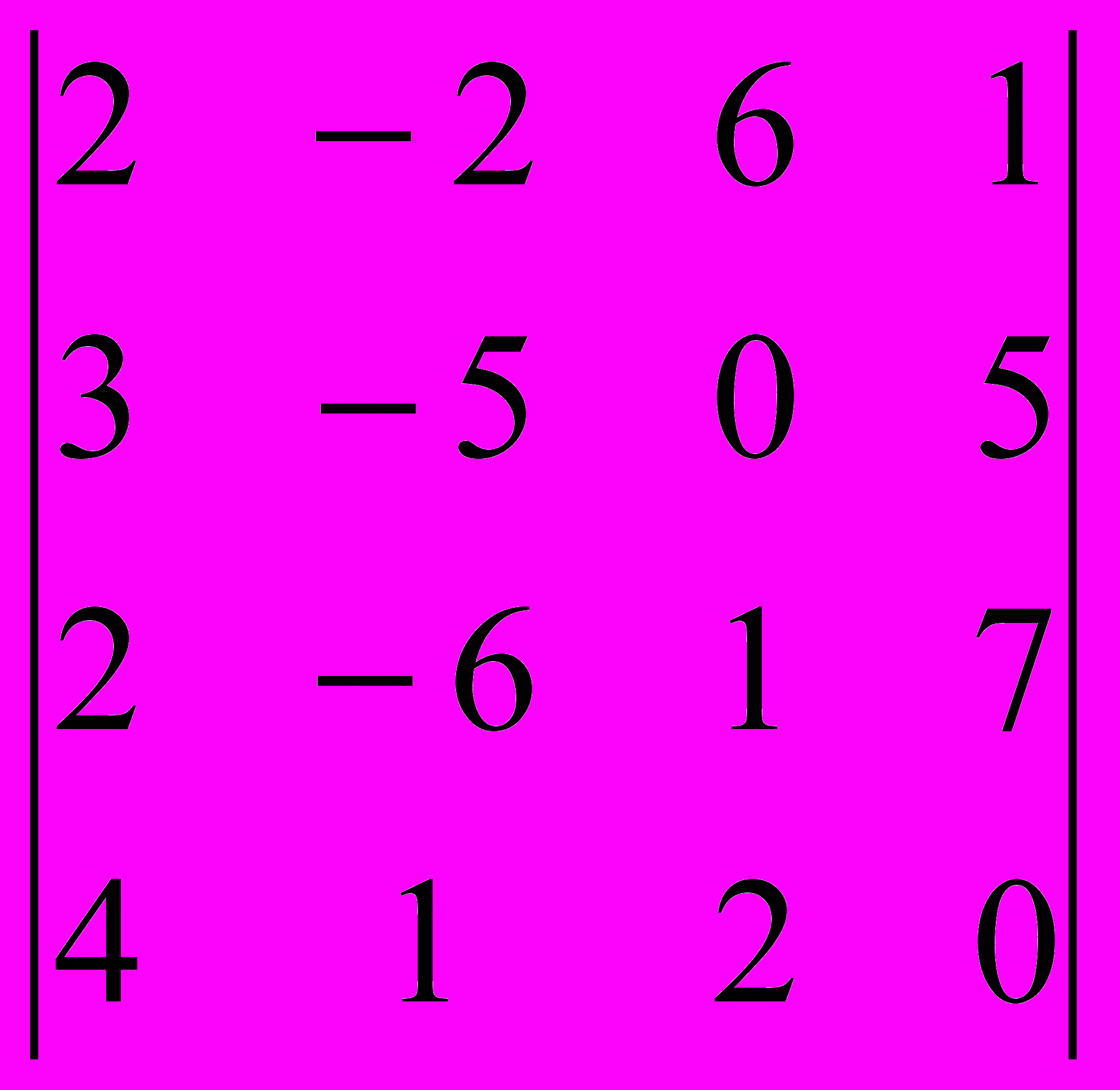 | 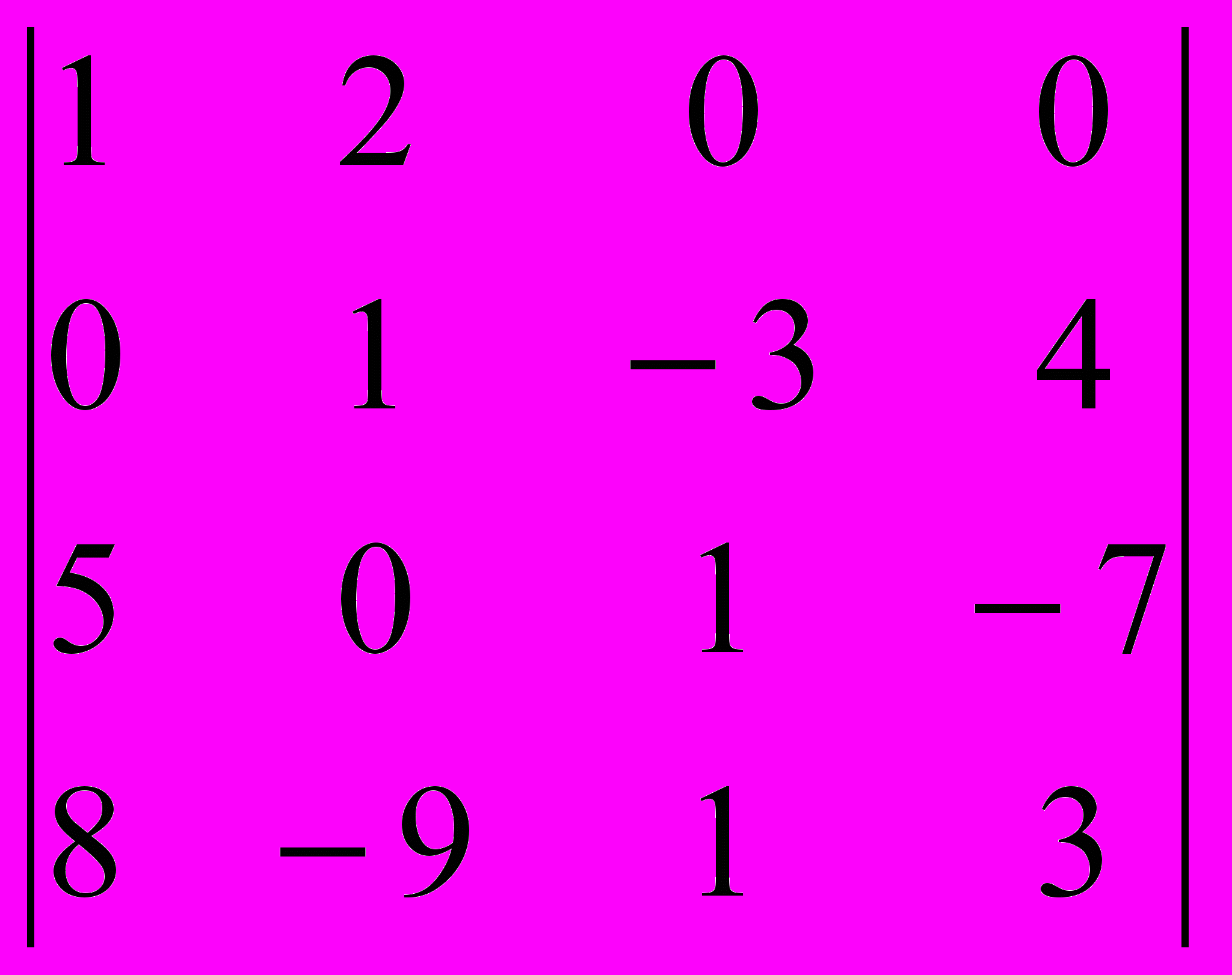 | 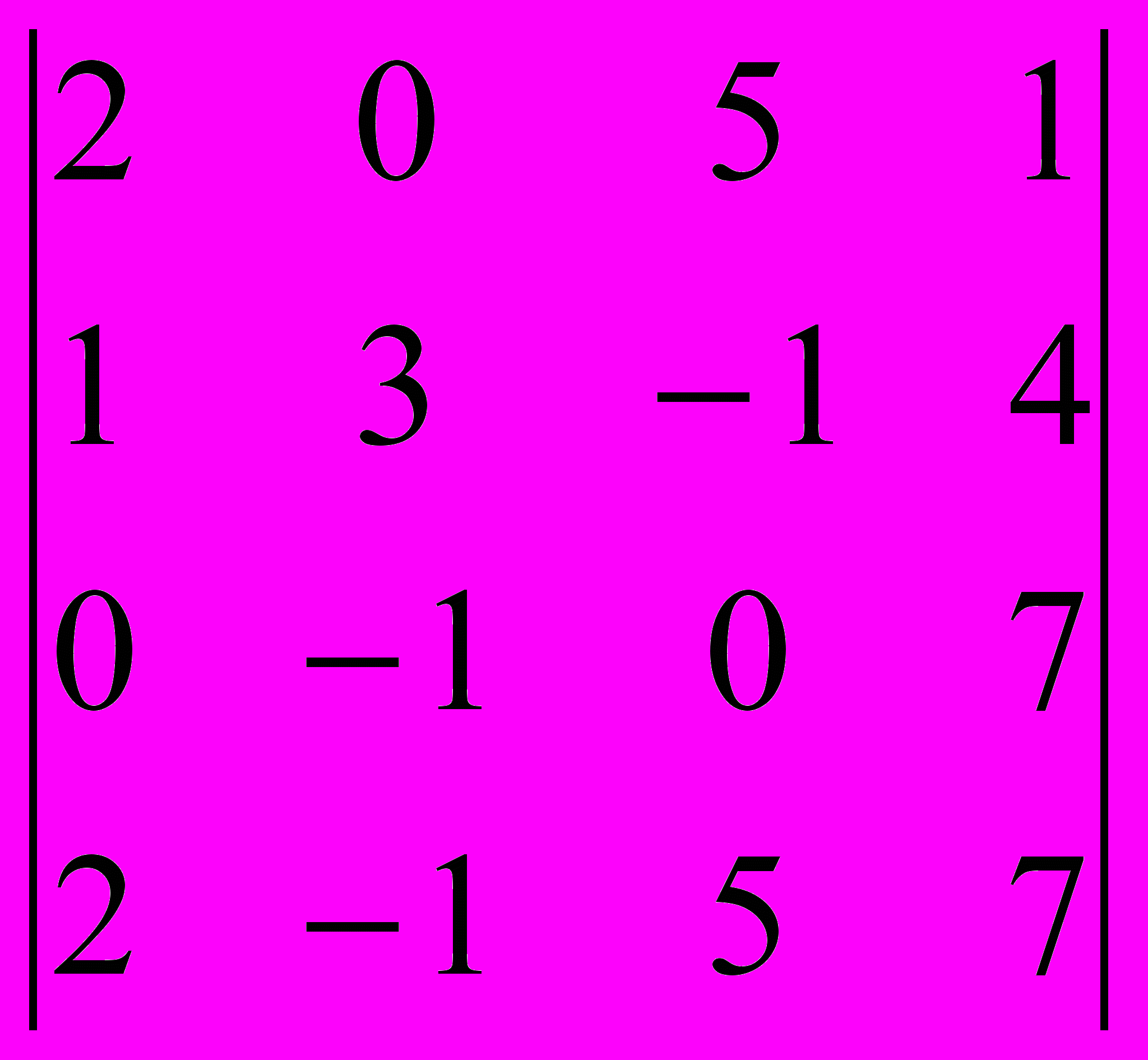 | 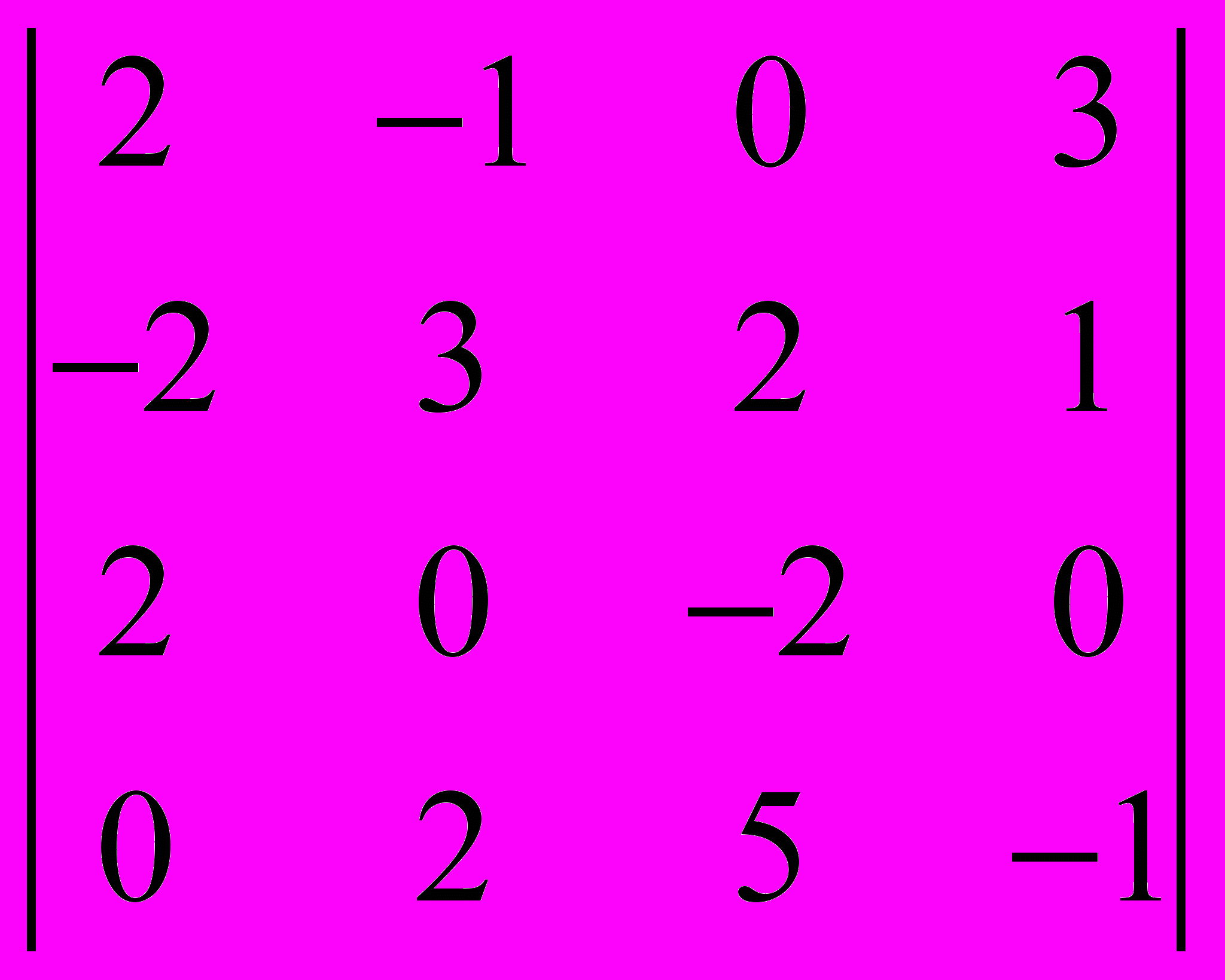 | 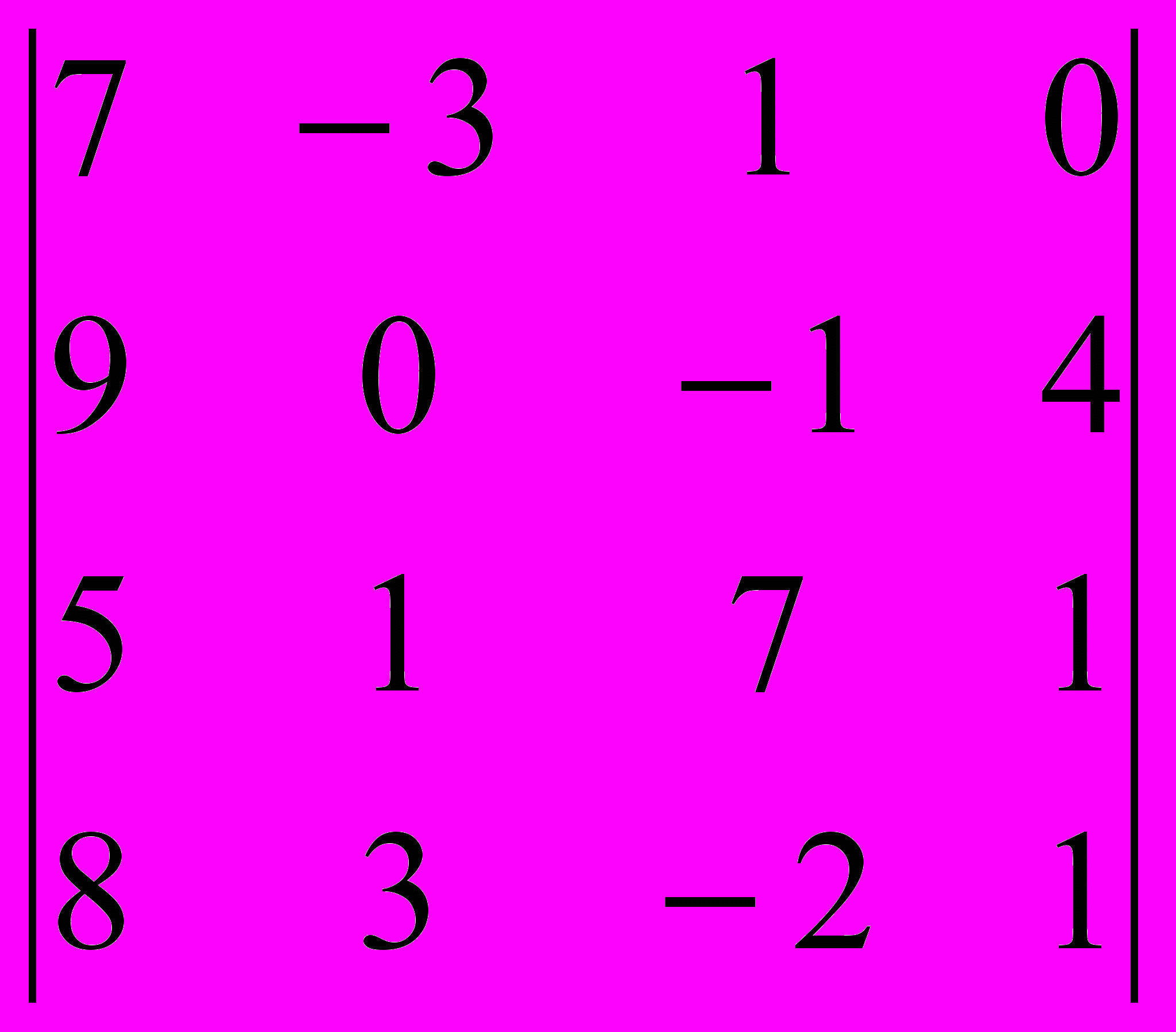 |
Задание 3. Определить, имеет ли матрица обратную, и если имеет, найти ее
| № вар. | 1 | 2 | 3 | 4 | 5 |
| | 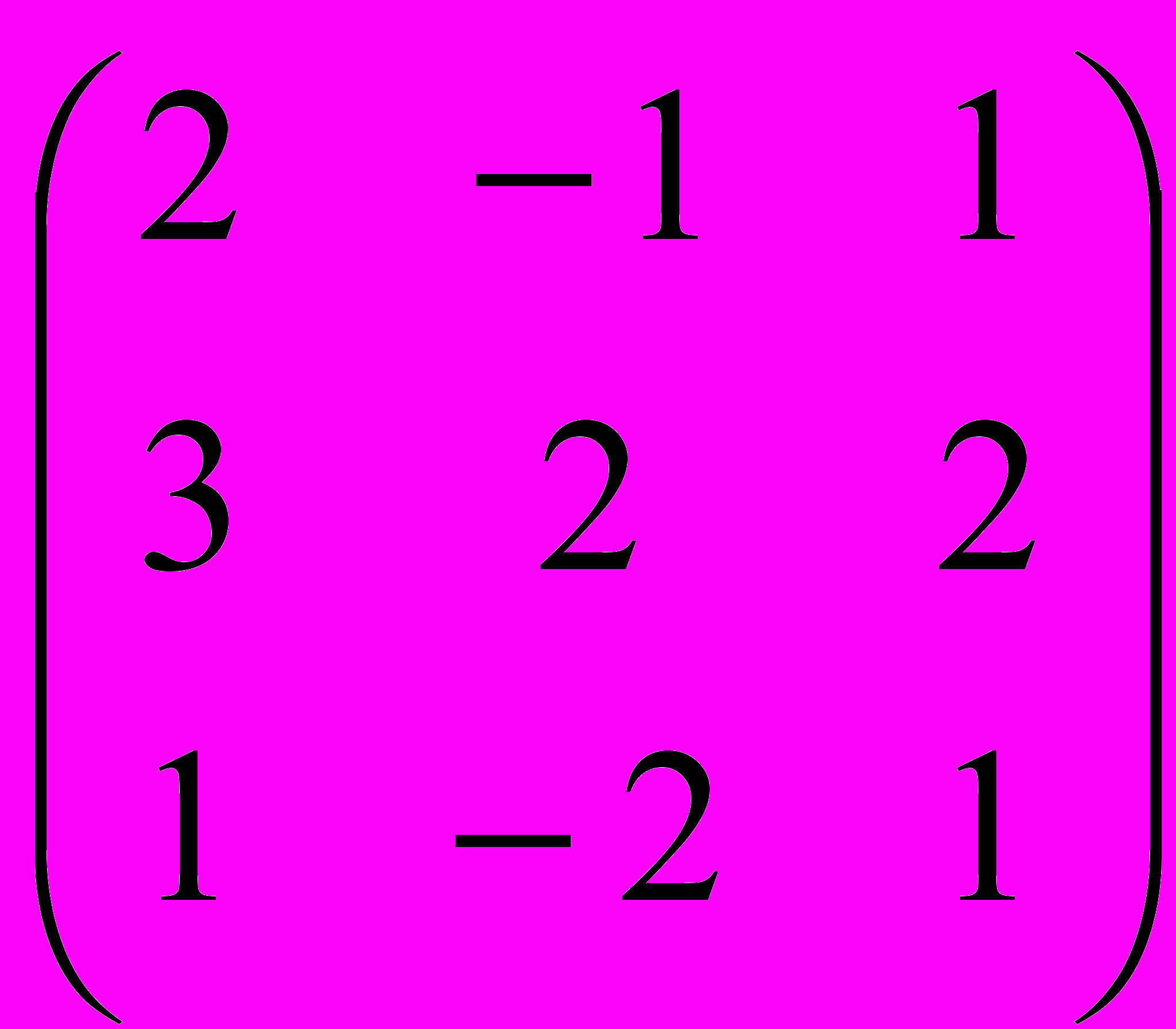 | 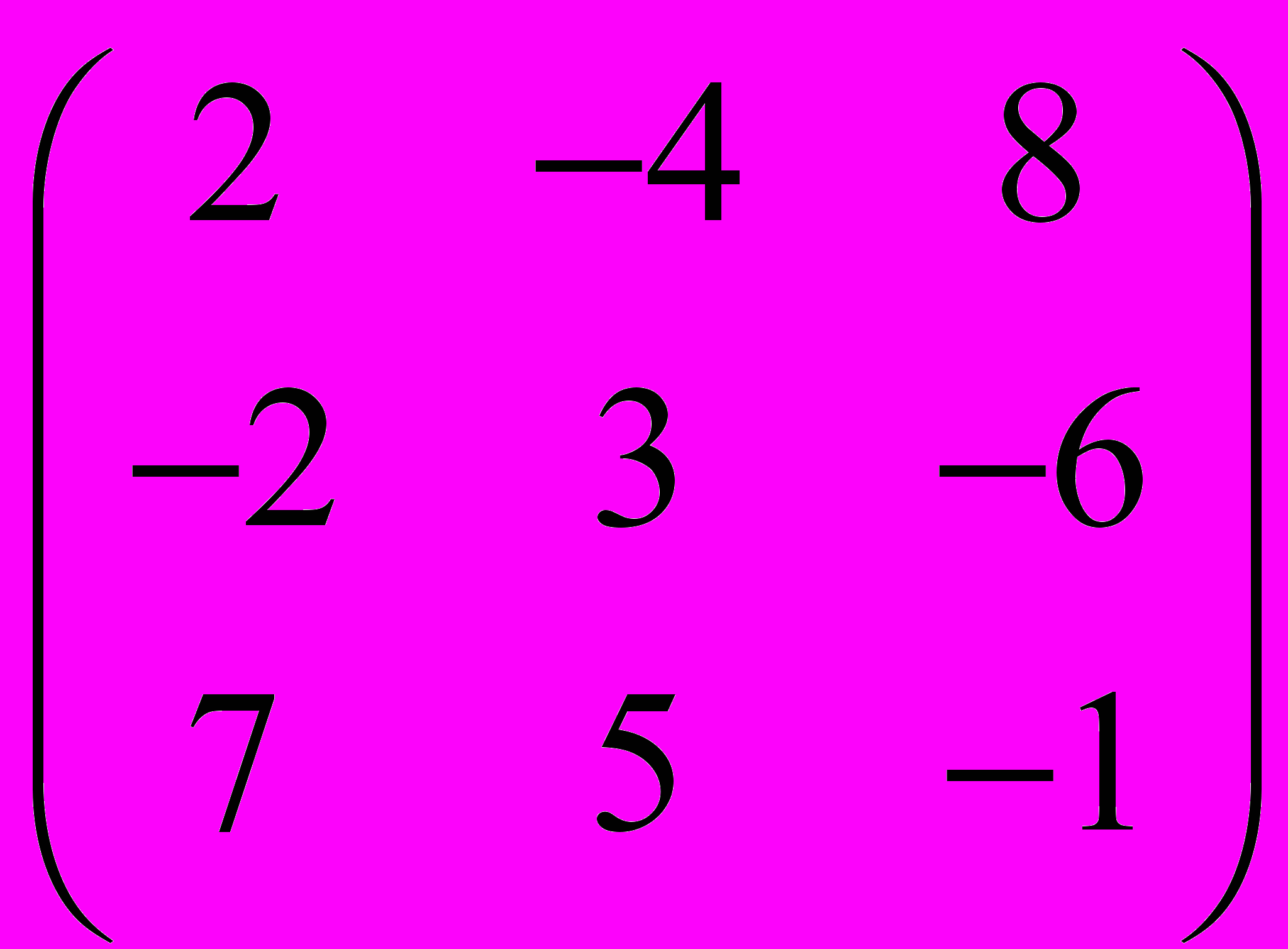 | 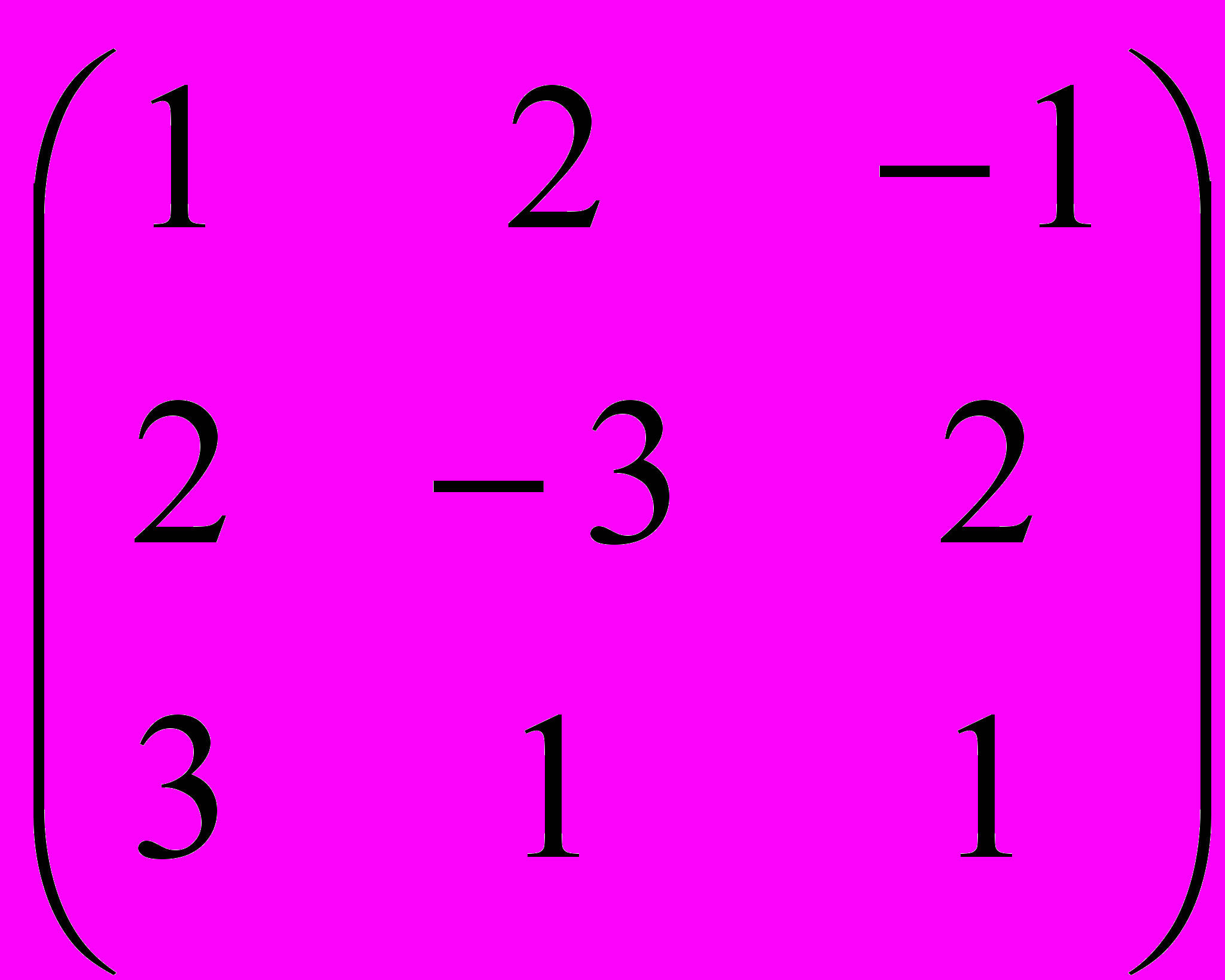 | 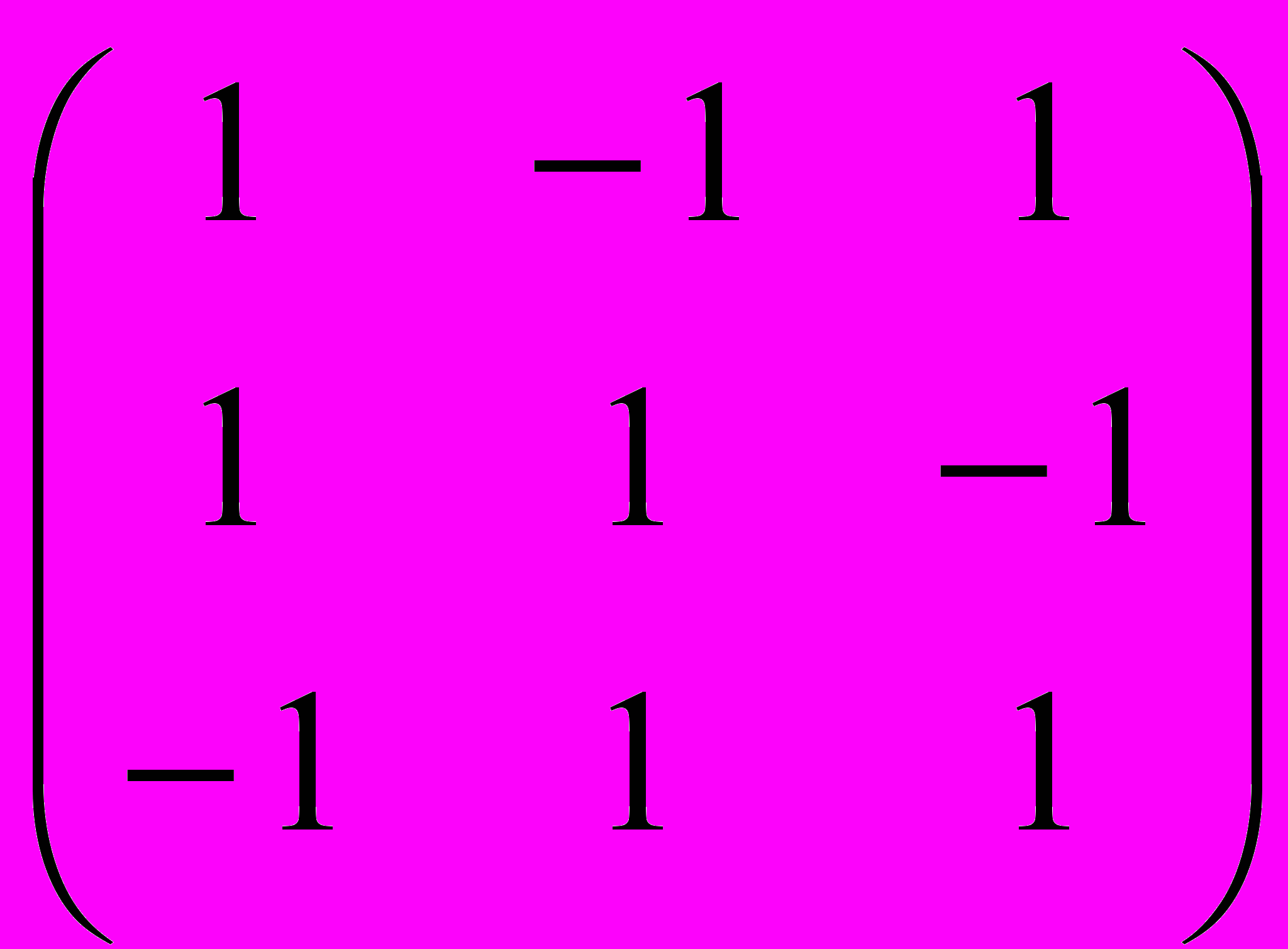 | 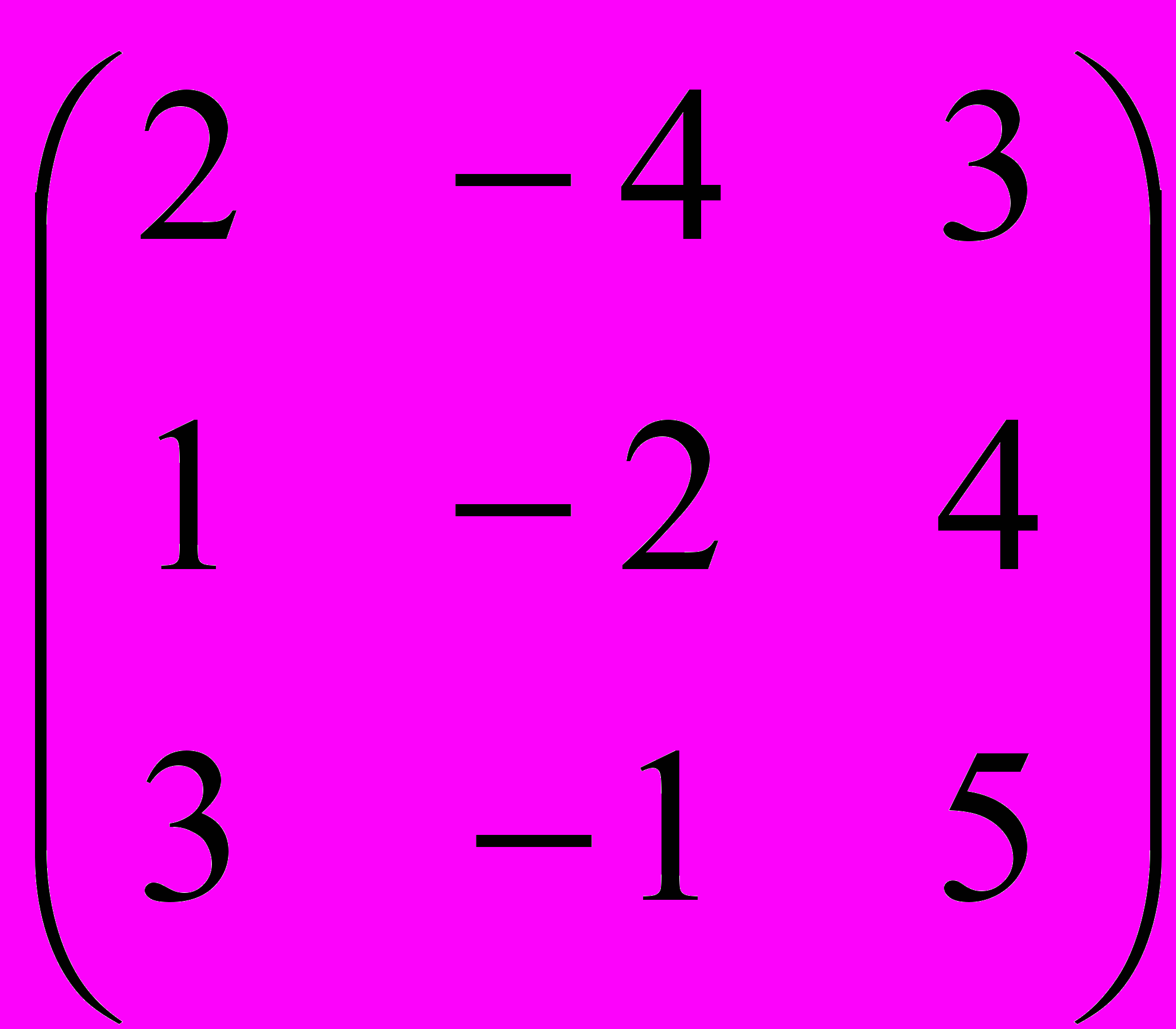 |
| № вар. | 6 | 7 | 8 | 9 | 10 |
| | 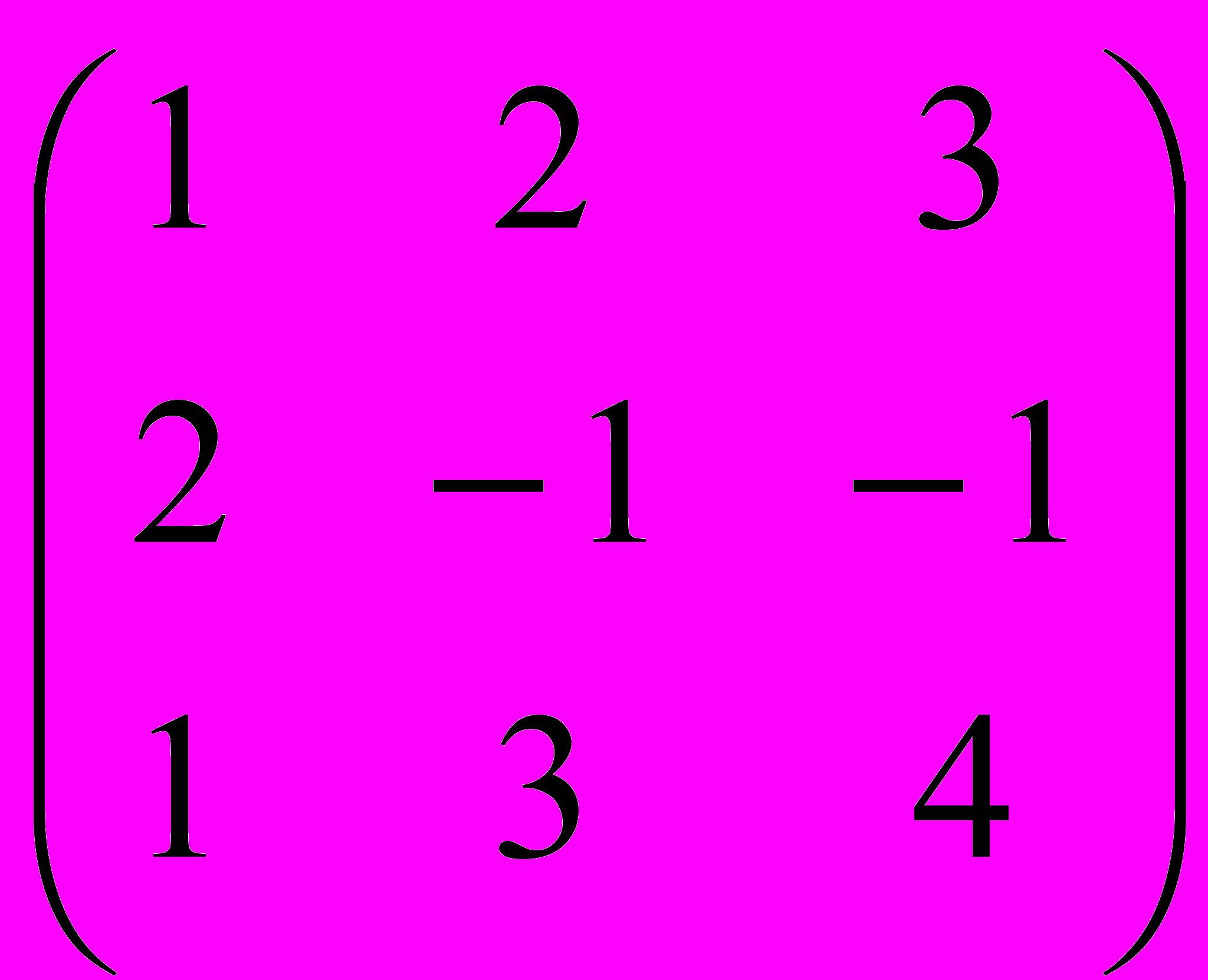 | 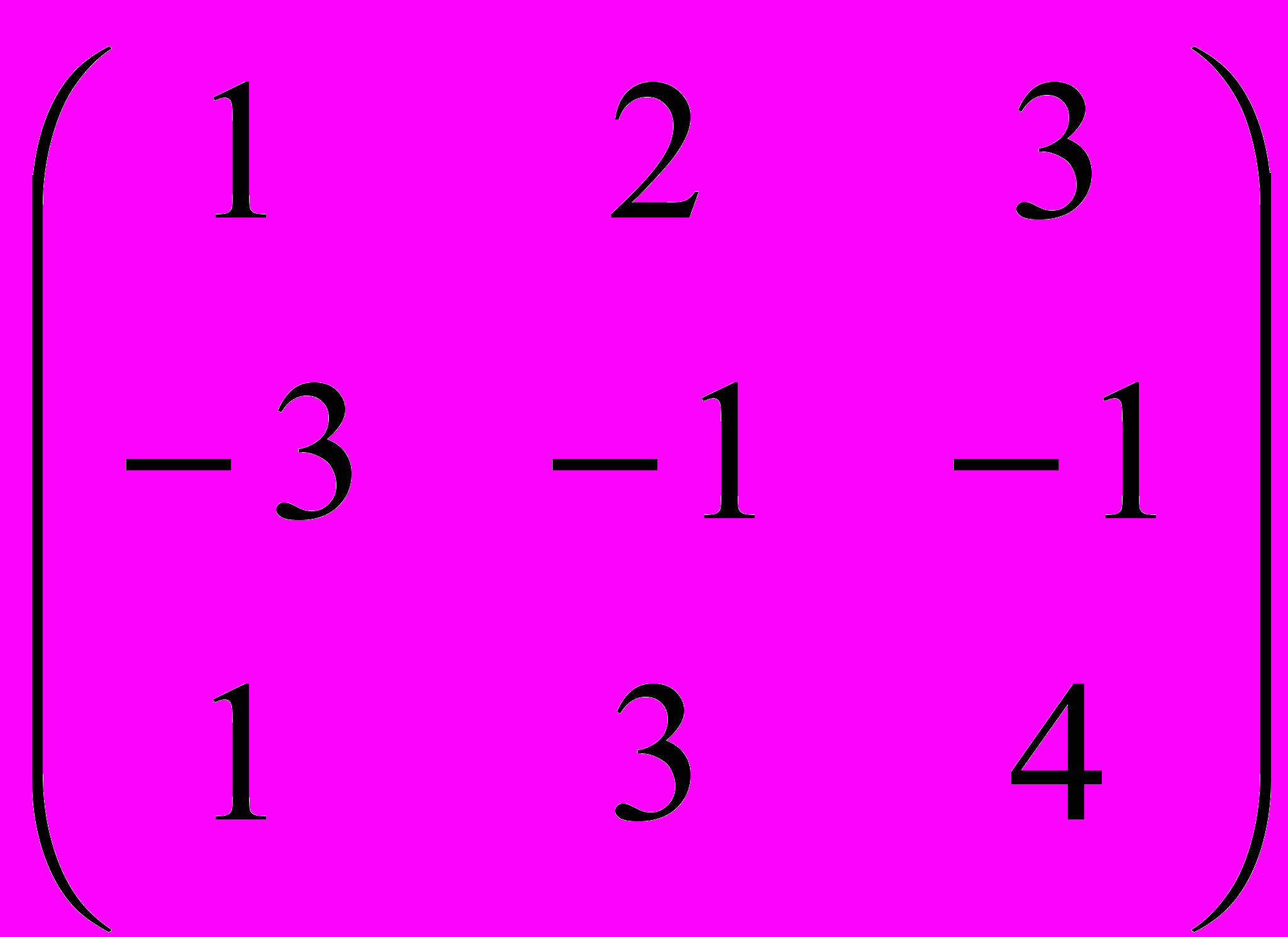 | 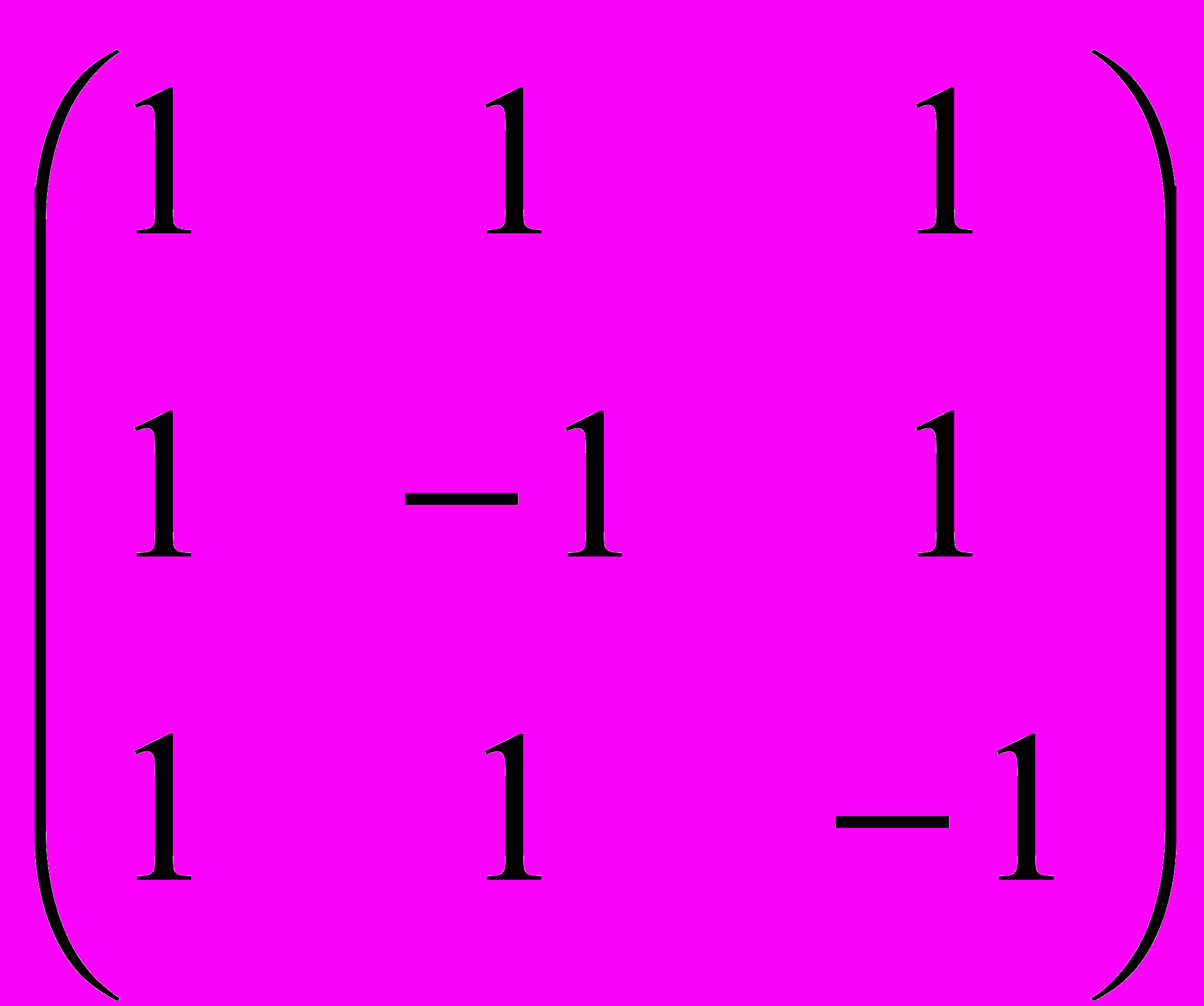 | 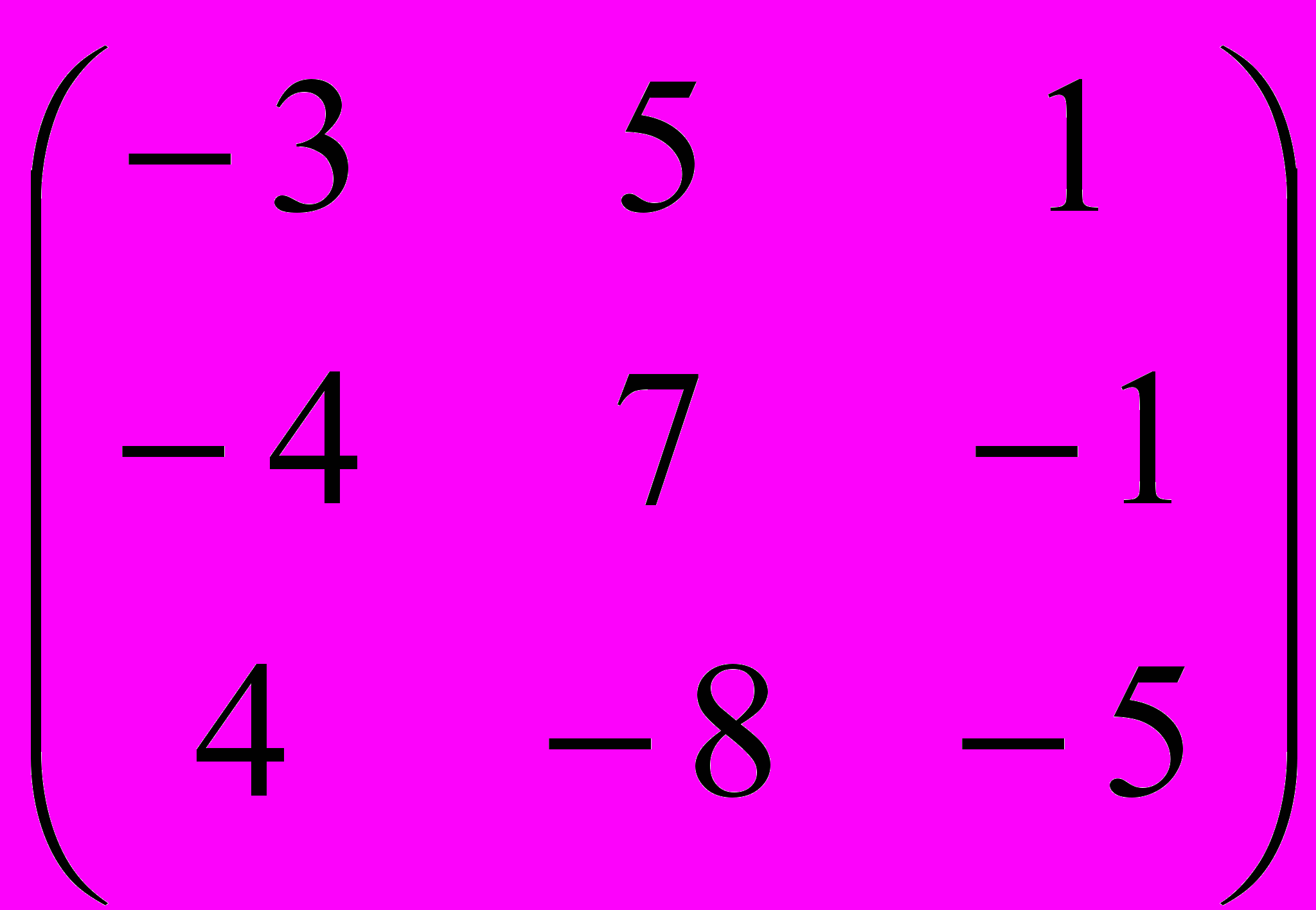 | 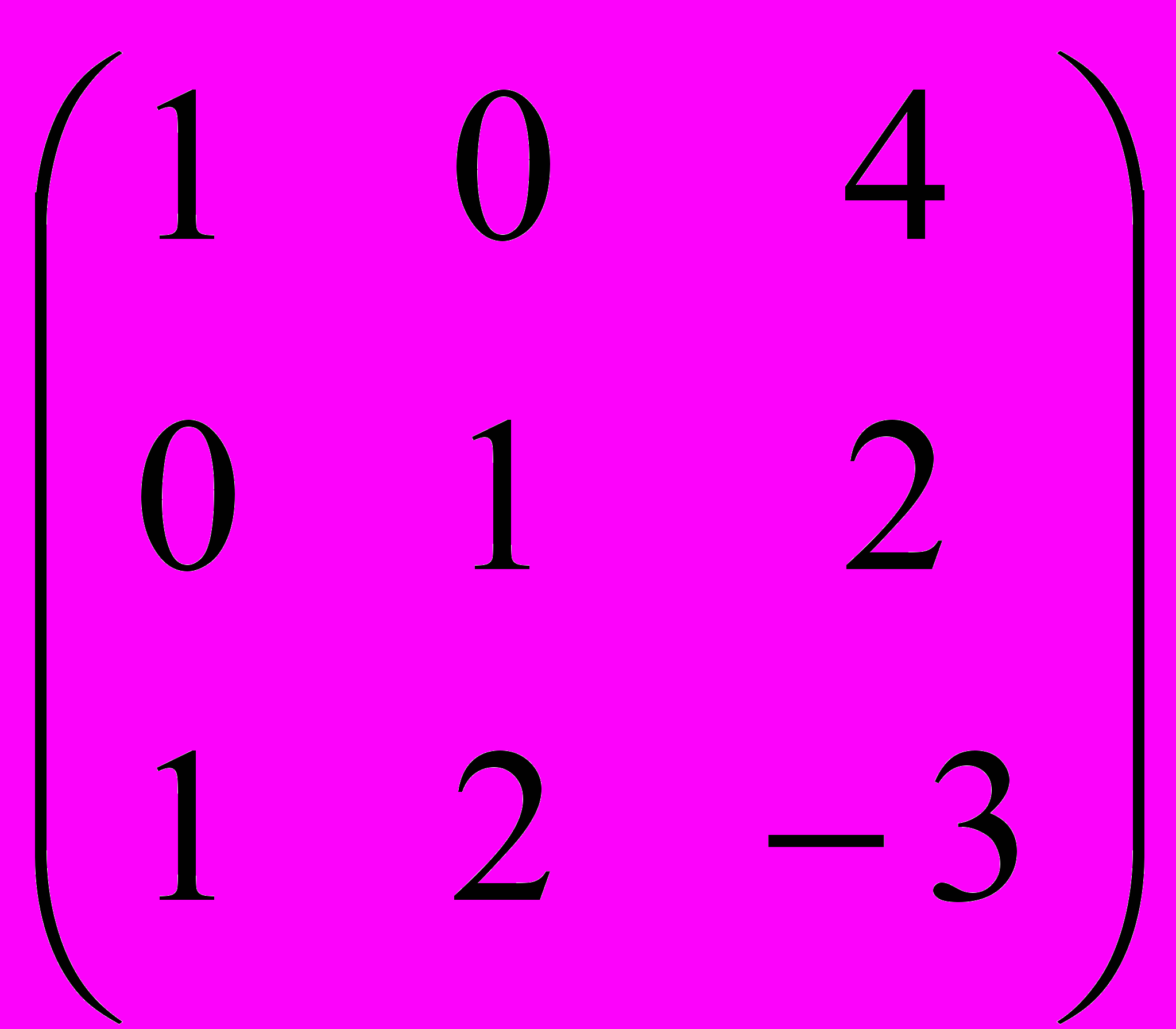 |
Задание № 4. Решить системы линейных уравнений, записанные в матричной форме,
методами Крамера, Гаусса и обратной матрицы.
| № варианта | Система линейных уравнений | № варианта | Система линейных уравнений |
| 1 | 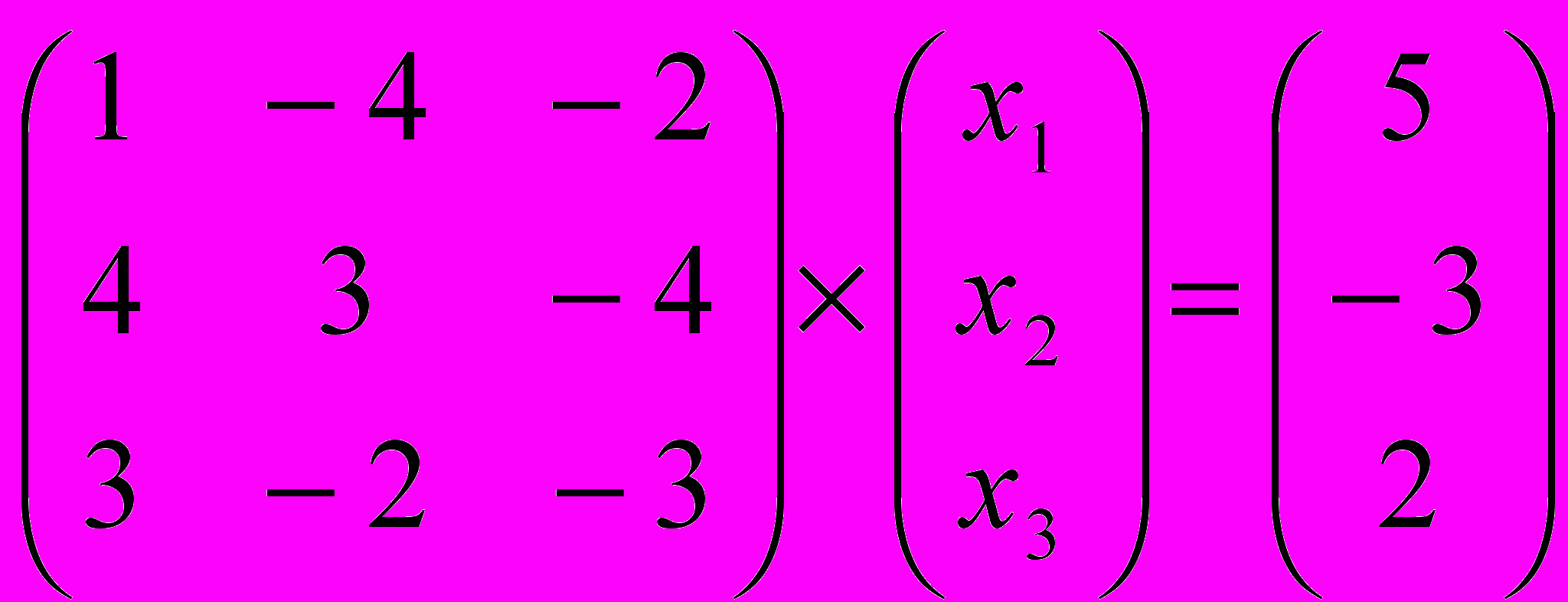 | 6 | 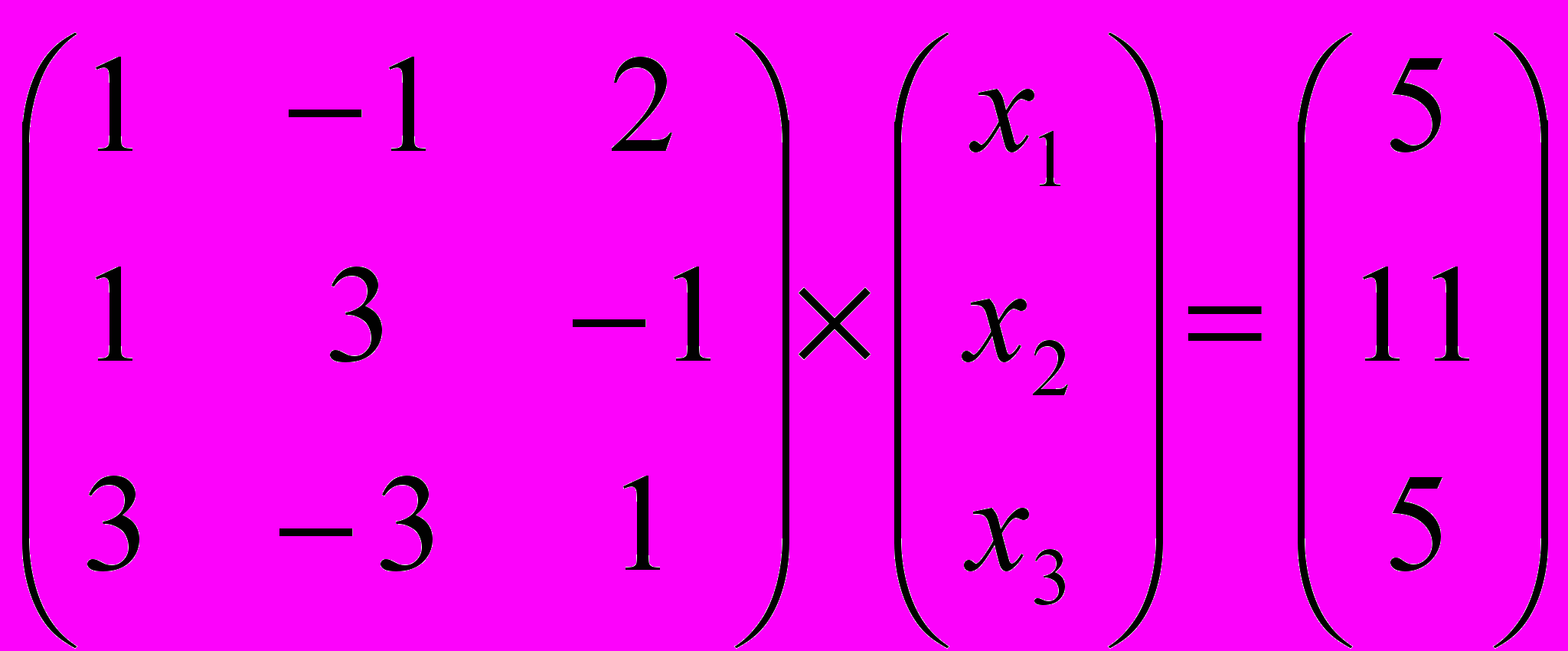 |
| 2 | 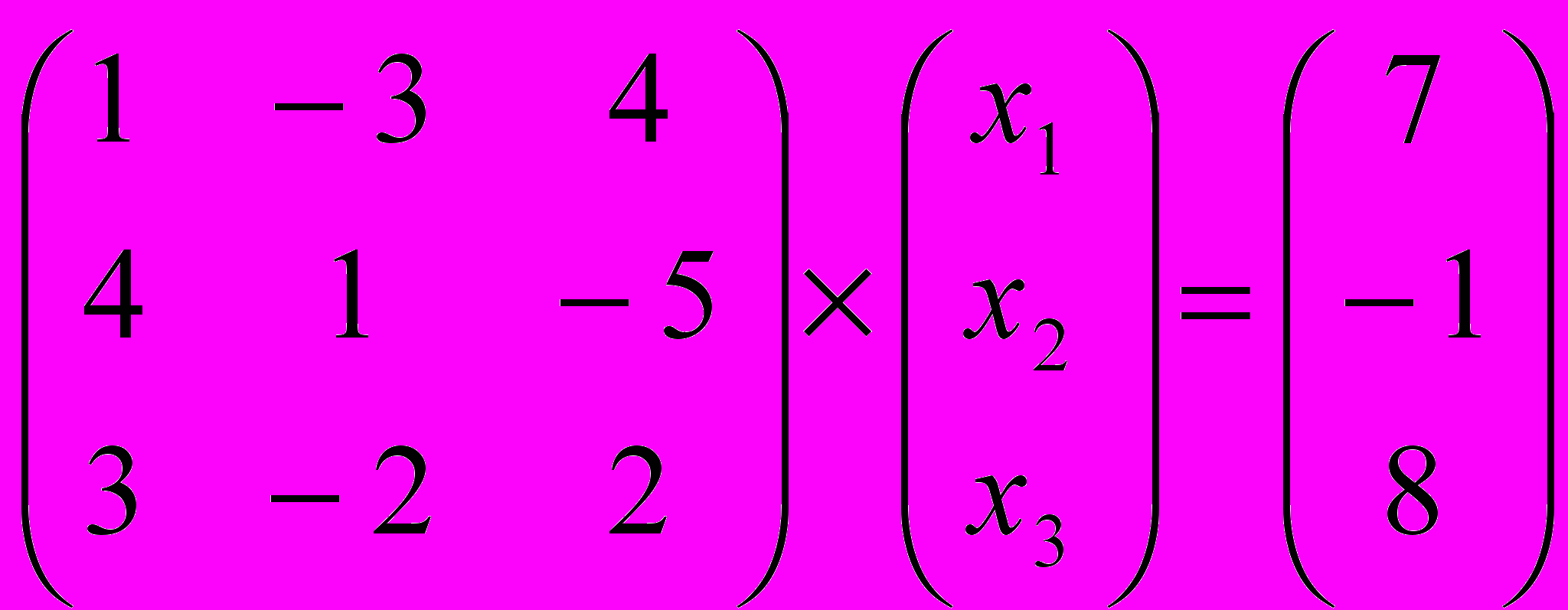 | 7 | 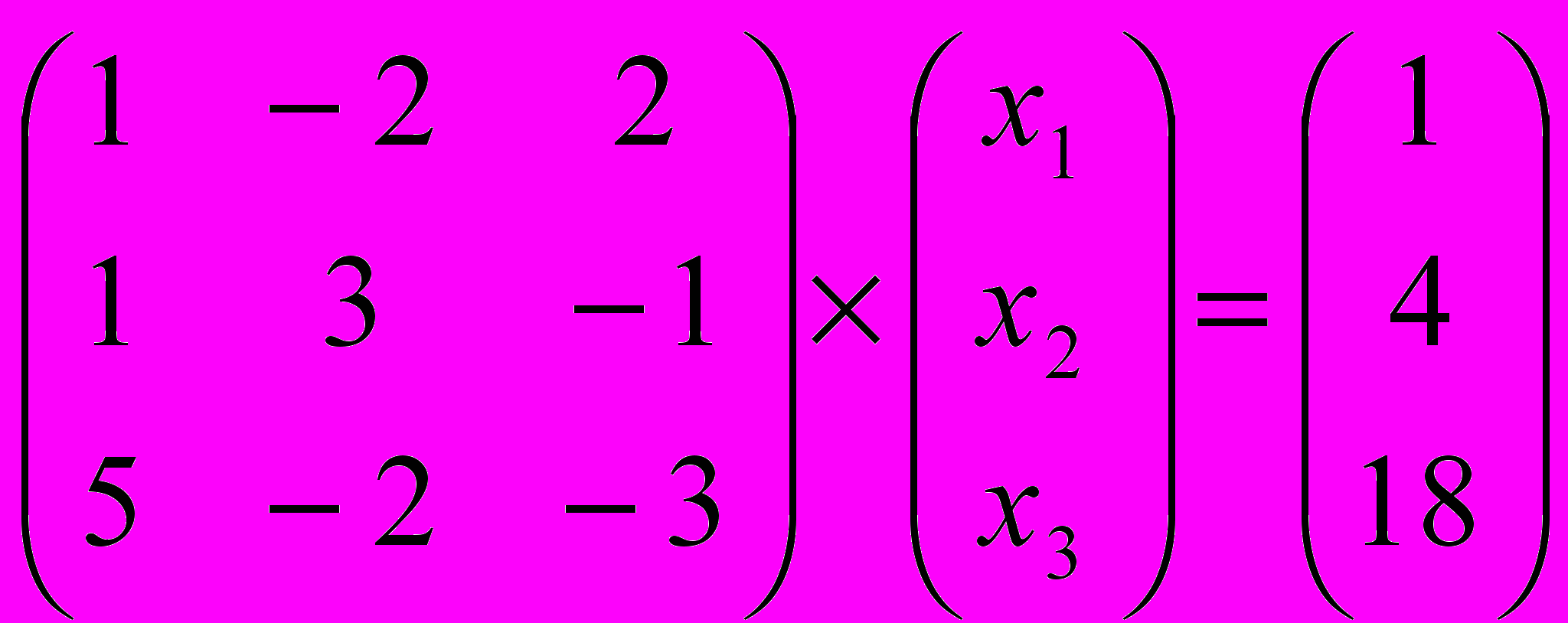 |
| 3 | 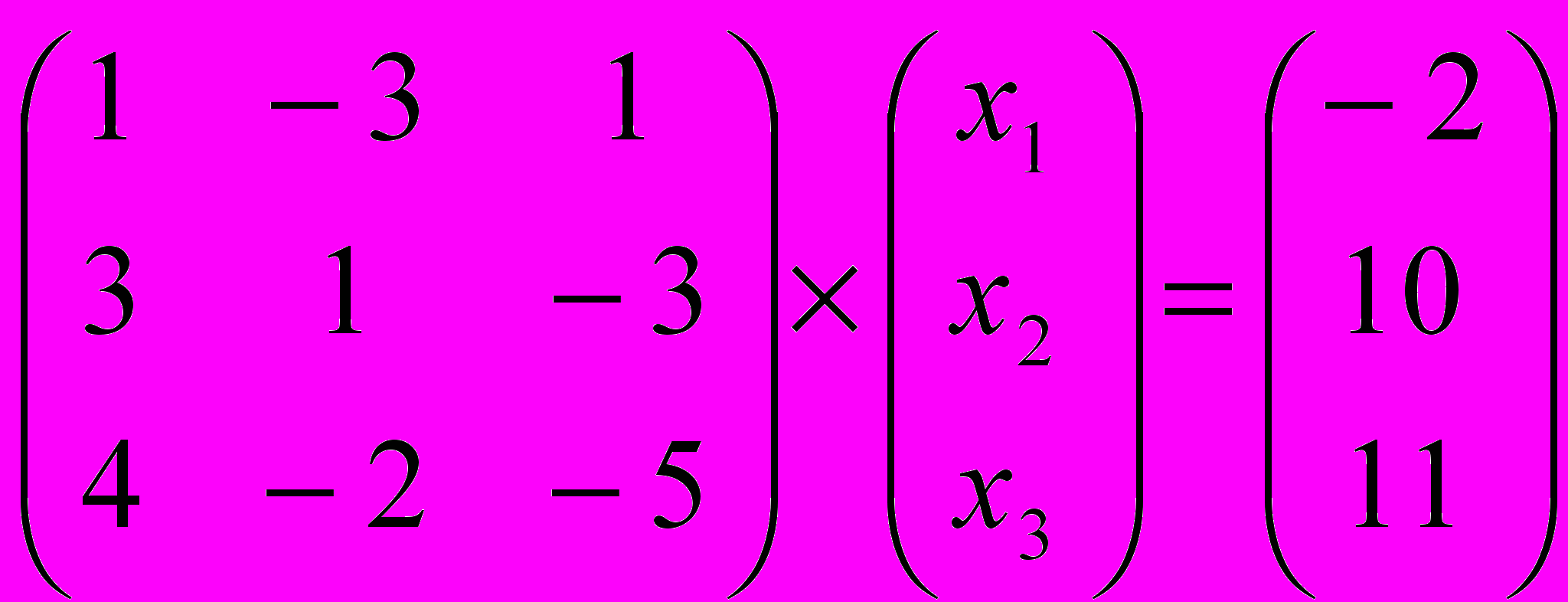 | 8 | 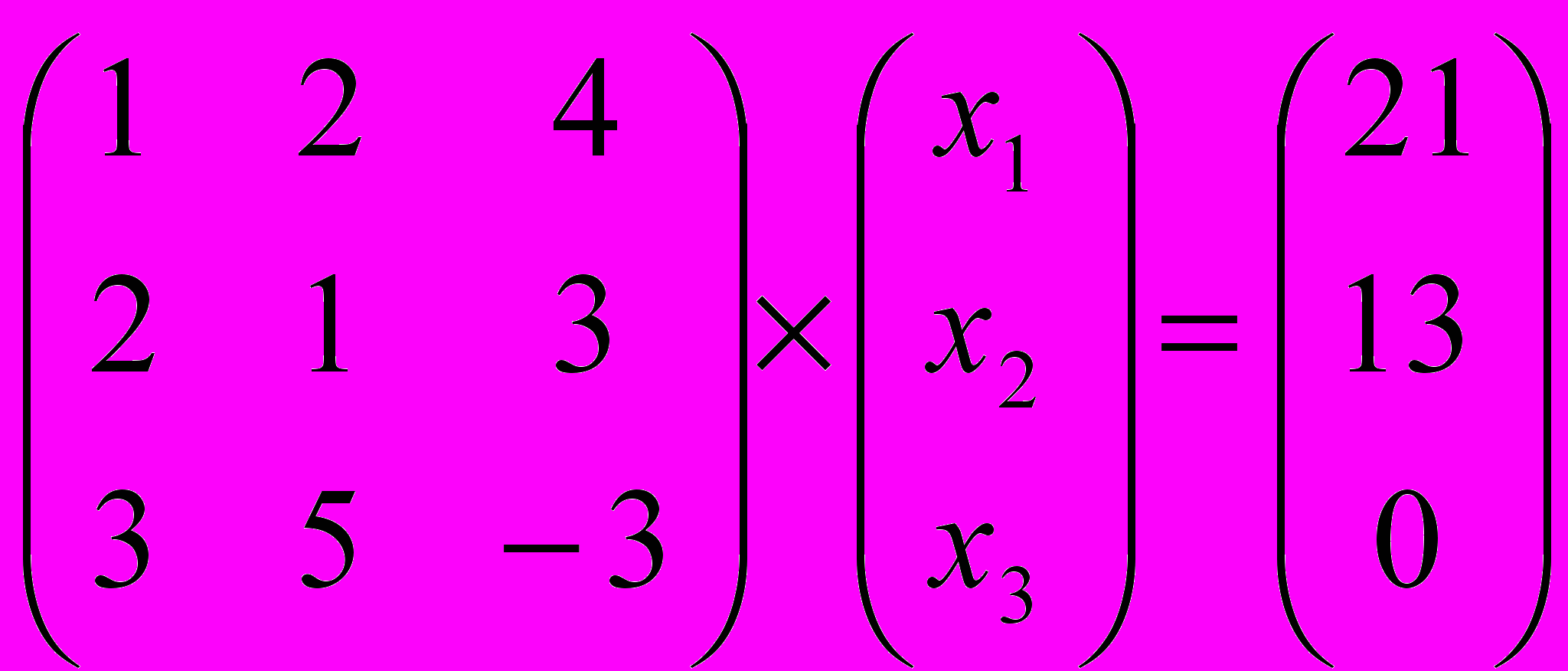 |
| 4 | 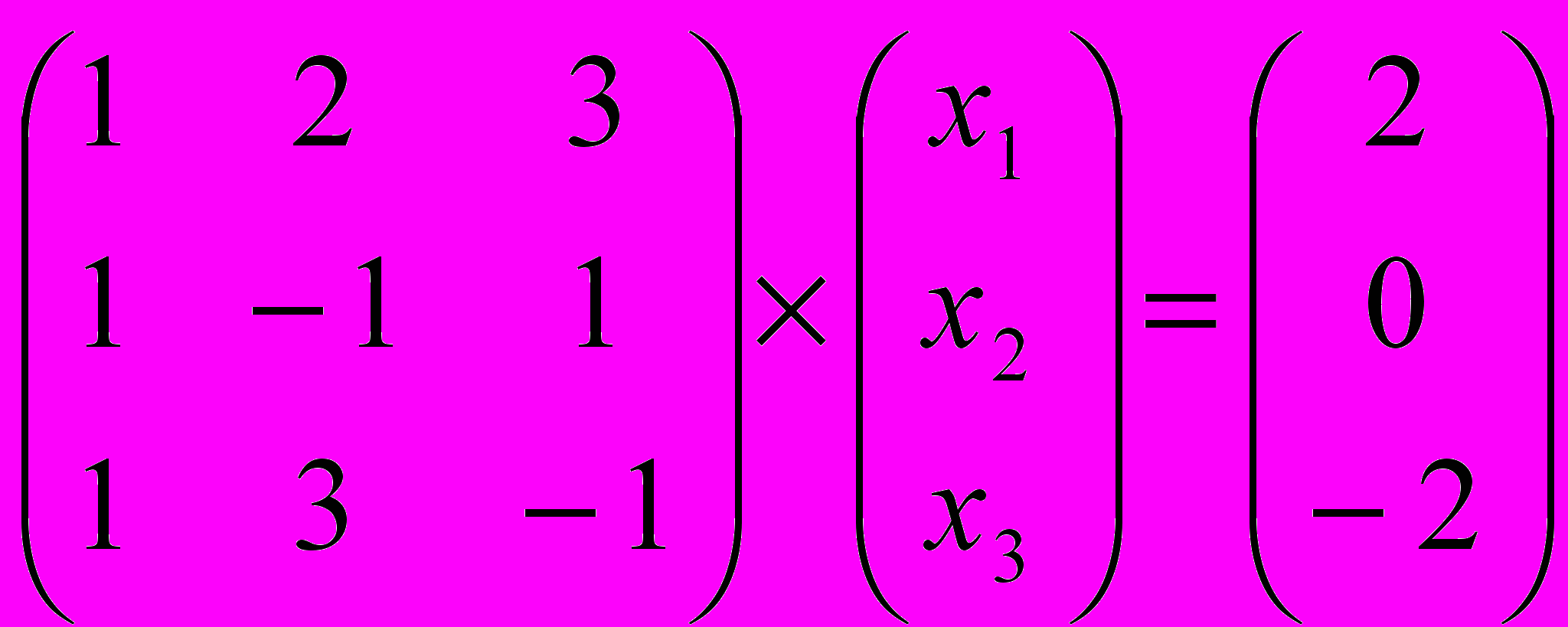 | 9 | 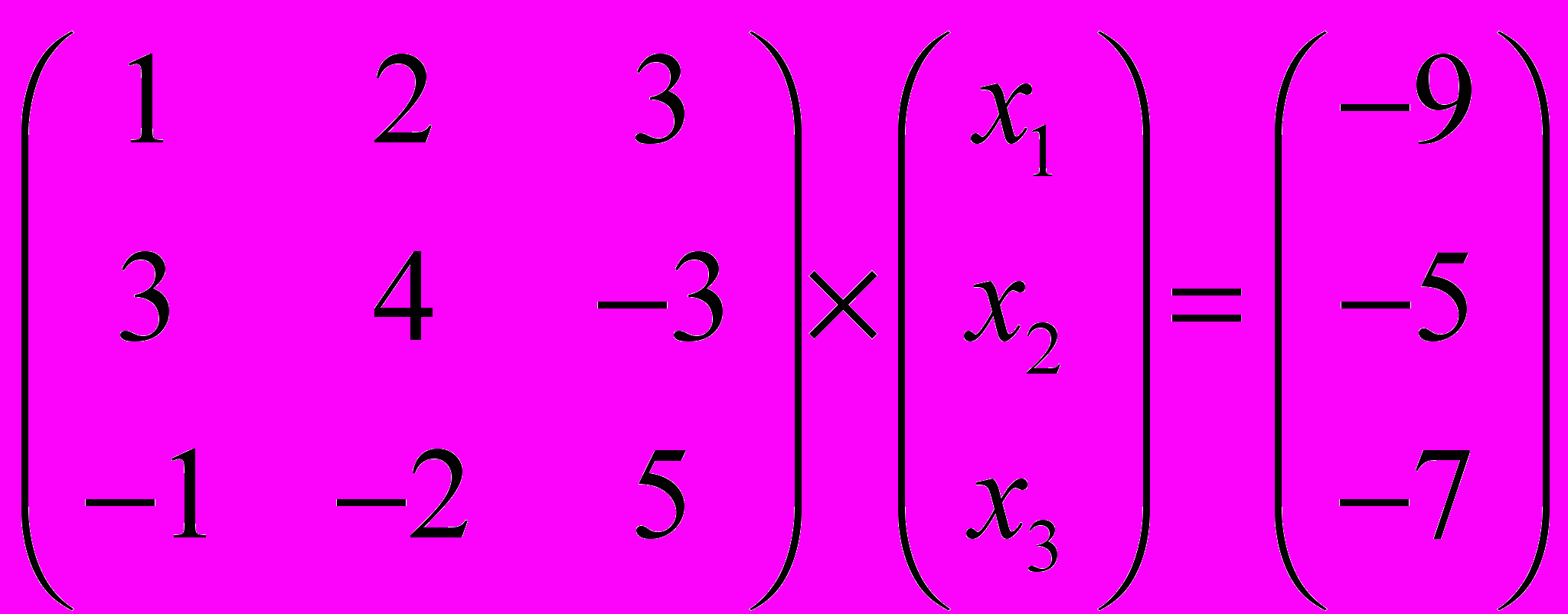 |
| 5 | 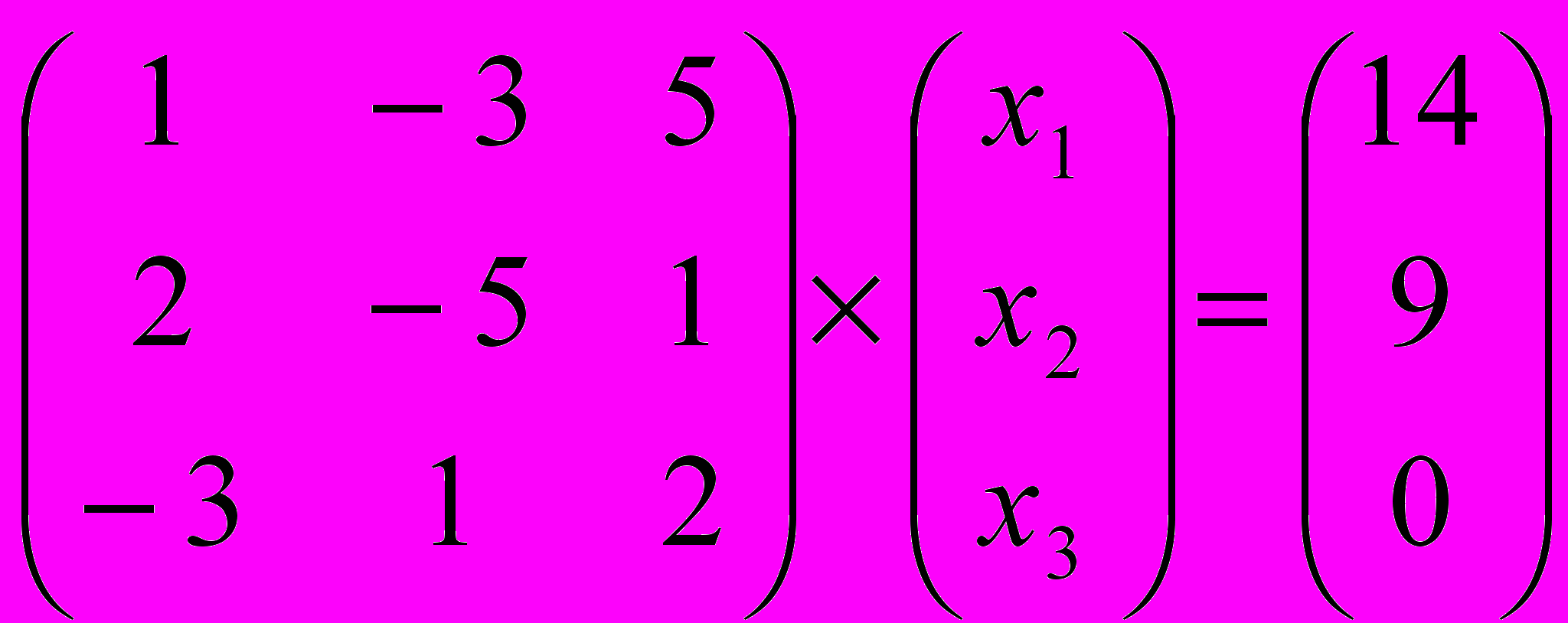 | 10 | 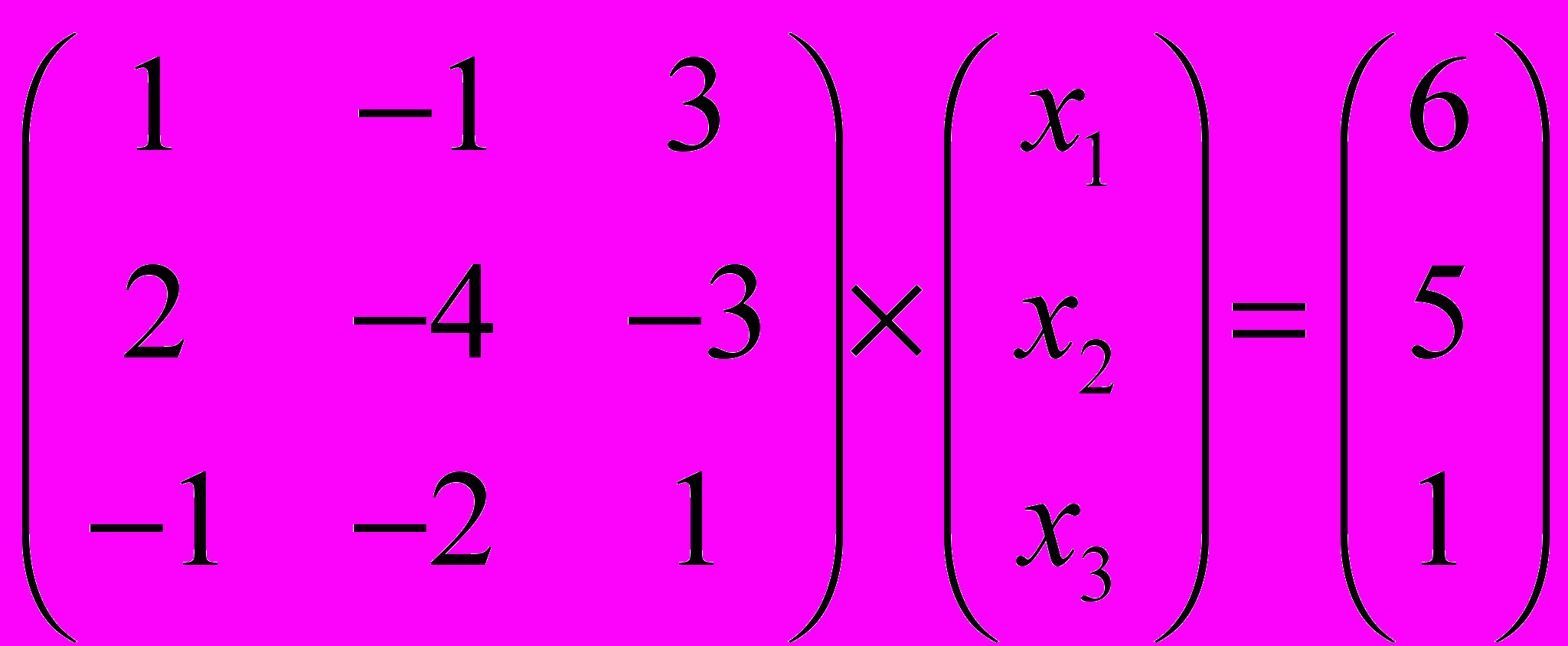 |
Задание 5. Дана прямая на плоскости. Через точку, не лежащую на этой прямой провести две прямые: параллельную и перпендикулярную данной. Начертить все три прямые и написать их уравнения.
| № варианта | |
| | 2x+3y-3=0 |
| | x–5y-1=0 |
| | 3x–y+1=0 |
| | x+y-5=0 |
| | 2x–y-6=0 |
| | –x+2y–4=0 |
| | 4x–3y-2=0 |
| | 2x–3y+5=0 |
| | 2x–2y+1=0 |
| | 2x+3y-3=0 |
Задание 6. Даны координаты вершин пирамиды А1, А2, А3, А4 .Найти:
1)угол между ребрами А1 А2 и А1А3 ;
2)площадь грани А1 А2 А3.
3) уравнение плоскости А1 А2 А3.
4) угол между плоскостями А1 А2 А3 и А1 А2 А4
5) уравнение прямой А1 А2
6) объем пирамиды.
| № варианта | А1 | А2 | А3 | А4 |
| | (-1, 2, 1) | (-2, 2, 5) | (-3, 3, 1) | (-1, 4, 3) |
| | (-2, 1, -1) | (-3, 1, 3) | (-4, 2, -1) | (-2, 3, 1) |
| | (1, 1, 2) | (0, 1, 6) | (-1, 2, 2) | (1, 3, 4) |
| | (-1, -2, 1) | (-2, -2, 5) | (-3, -1, 1) | (-1, 0, 3) |
| | ( 2, -1, 1) | (1, -1, 5) | (0, 0, 1) | (2, 1, 3) |
| | ( -1, 1, -2) | (-2, 1, 2) | (-3, 2, -2) | (-1, 3, 0) |
| | (1, 2, 1) | (0, 2, 5) | (-1, 3, 1) | (1, 4, 3) |
| | (-2, -1, 1) | (-3, -1, 5) | (-4, 0, 1) | (-2, 1, 3) |
| | (1, -1, 2) | (0, -1, 6) | (-1, 0, 2) | (1, 1, 4) |
| | (1, -2, 1) | (0, -2, 5) | (-1, -1, 1) | (1, 0, 3) |
Задание 7 Написать уравнение плоскости, проходящей через три заданные точки
| № варианта | Координаты точки 1 | Координаты точки 2 | Координаты точки 3 |
| | 1, 0, 3 | -1, -2, 1 | 3, 1, 2 |
| | 3, 1, 1 | 5, 5, -1 | -2, -3,2 |
| | -2, 4, -5 | 0, -2, 1 | 1, 3, 3 |
| | 7, 6, 7 | 5, 10, 5 | -1, 8, 9 |
| | -4, -7, -5 | 1, 0, 1 | -3, 1, 5 |
| | 1, 2, 4 | -3, -12, 10 | 2, -2, -5 |
| | 0, 6, 3 | 1,-3, -2 | 1, 8, 1 |
| | -1, 3, 1 | 2, 9, -2 | 3, 9, -4 |
| | -2, -2, -4 | 1, 3, 4 | 3, 5, 12 |
| | 1, 3, -11 | -1, 2, -4 | 2, -5, 11 |
Задание 8. Преобразованием системы координат привести уравнение кривой второго порядка к каноническому виду, найти точки ее пересечения с прямой линией и построить графики.
.
| № варианта | Уравнение кривой второго порядка | Уравнение прямой линии |
| 1 | 2x2 – 4x – 2y+3=0 | 2x – y –1=0 |
| 2 | 4х2 + 9y2 – 40 х +36y +100=0 | x – 2y -3=0 |
| 3 | x2 – 2x – y +2=0 | x – y =0 |
| 4 | x – y2 + 2y –2=0 | x + y –2=0 |
| 5 | 9х2 – 16y2 – 54 х –64y –127=0 | x – 3y –2=0 |
| 6 | x + y2 – 2y +3=0 | x + y +1=0 |
| 7 | 5х2 + 9y2 – 30 х +18y +9=0 | 2x + y – 3 =0 |
| 8 | x + 2y2 – 4y +4=0 | x – 2y +4=0 |
| 9 | 5х2 – 4y2 +30х +8y +21=0 | x – y +1=0 |
| 10 | x + 2y2 + 4y +1=0 | x + 2y + 1=0 |
Задание 9. Решить уравнения на множестве комплексных чисел. Результат представить в алгебраической, тригонометрической и показательной формах.
| № варианта | | № варианта | |
| | Z4+9Z2+20=0 | | Z2+(2i–5)Z+5–5i=0 |
| | Z8–17Z4+16=0 | | Z2 –4Z+8=0 |
| | Z4 –4Z2+20=0 | | 3Z2 – Z+2=0 |
| | Z3=1/i | | Z2 – Z+5=0 |
| | Z2 +8Z+41=0 | | Z4 –Z2 –2=0 |
| | Z4 +3Z2 –10=0 | | Z3+8i=0 |
| | Z2 –8iZ–15=0 | | Z4 +4Z2 –5=0 |
| | Z4 –Z2 –6=0 | | Z6 – 9Z3+8=0 |
