Невырожденные матрицы обратная матрица

Вид материала

Документы

Содержание A = 52. Составим присоединённую (союзную) матрицу. Для этого вычислим все алгебраические дополнения матрицы A Нахождение ранга матрицы. Метод окаймляющих миноров

Подобный материал:

• Программа для аттестационных испытаний по дисциплине: «математический анализ и линейная, 77.58kb.
• Рейтинг-план освоения дисциплины Дисциплина Математика, 240.4kb.
• Обязательный курс математика для студентов обучающихся по специальности Автомобили, 28.02kb.
• Тематическийпла н, 46.68kb.
• Контрольная работа по линейной алгебре для студентов заочного отделения рггу. Преподаватель, 8.71kb.
• Матрицы, определители, системы линейных уравнений определение матрицы. Виды матриц, 254.1kb.
• Вопросы к экзамену по дисциплине «Высшая математика», 150.21kb.
• 1. Матрица и расширенная матрица системы. Элементарные преобразования матриц. Решение, 8.16kb.
• Решение задач по тоэ, отц, Высшей математике, Физике, Программированию, 184.85kb.
• Вопросы по курсу «Дифференциальные уравнения», 19.42kb.

Тема: «НЕВЫРОЖДЕННЫЕ МАТРИЦЫ»


Обратная матрица. Матрица А^-1 наз. обратной для матрицы А , если А^-1 А = Е


Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA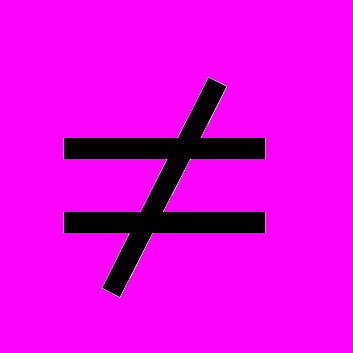0.


Элемент обратной матрицы ( А^-1)_{i j} равен алгебраическому дополнению A_{j i} матрицы А , деленному на det A : ( A^-1)_{i j} = A_{j i} / det A (индексы поменяли места) или A^-1 = (detA)^-1 ||A_ij||^T


Пример: Построить матрицу обратную к данной



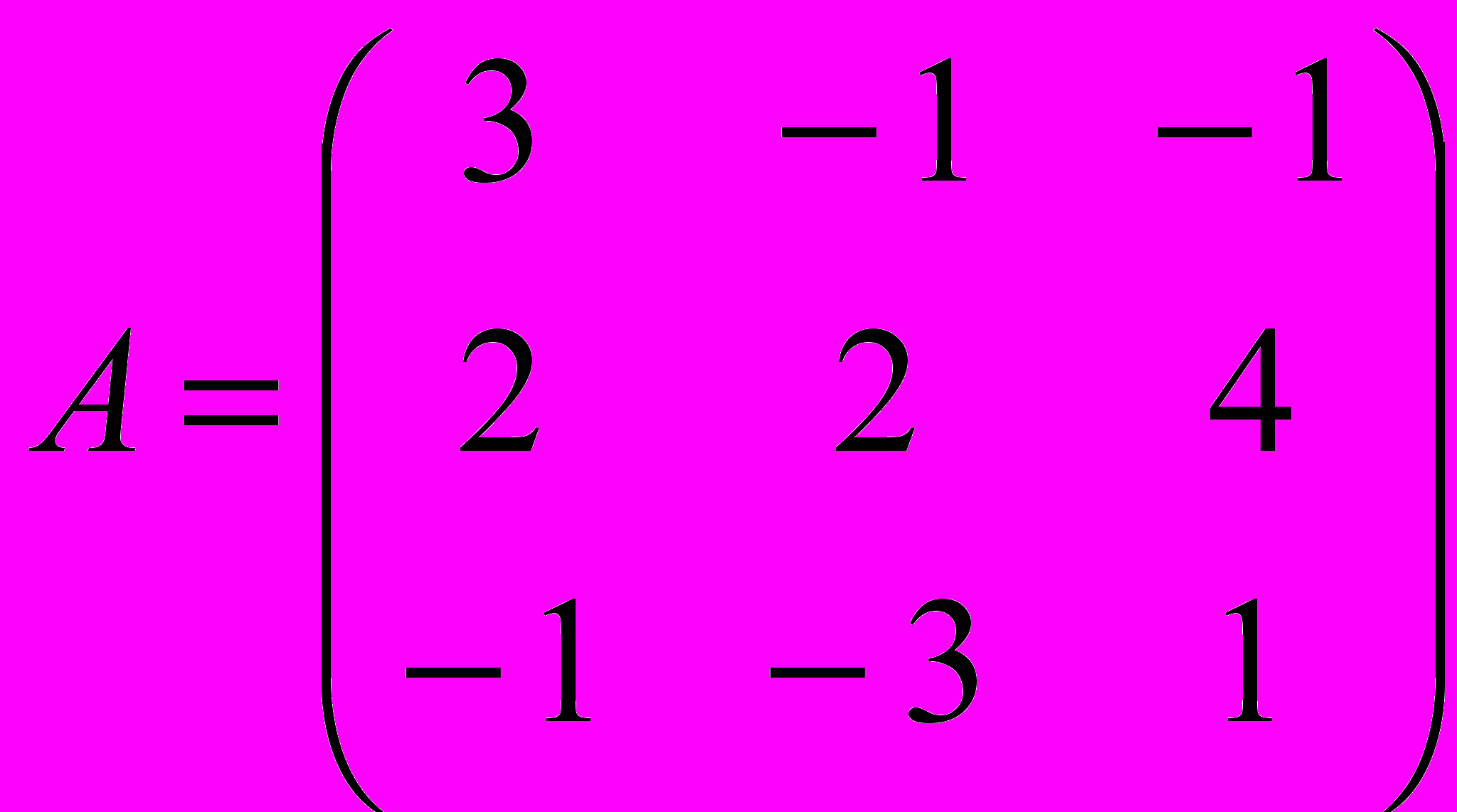
Находим определитель данной матрицы: det A = 52.

Составим присоединённую (союзную) матрицу. Для этого вычислим все алгебраические дополнения матрицы A:

A₁₁ = (–1)¹⁺¹ 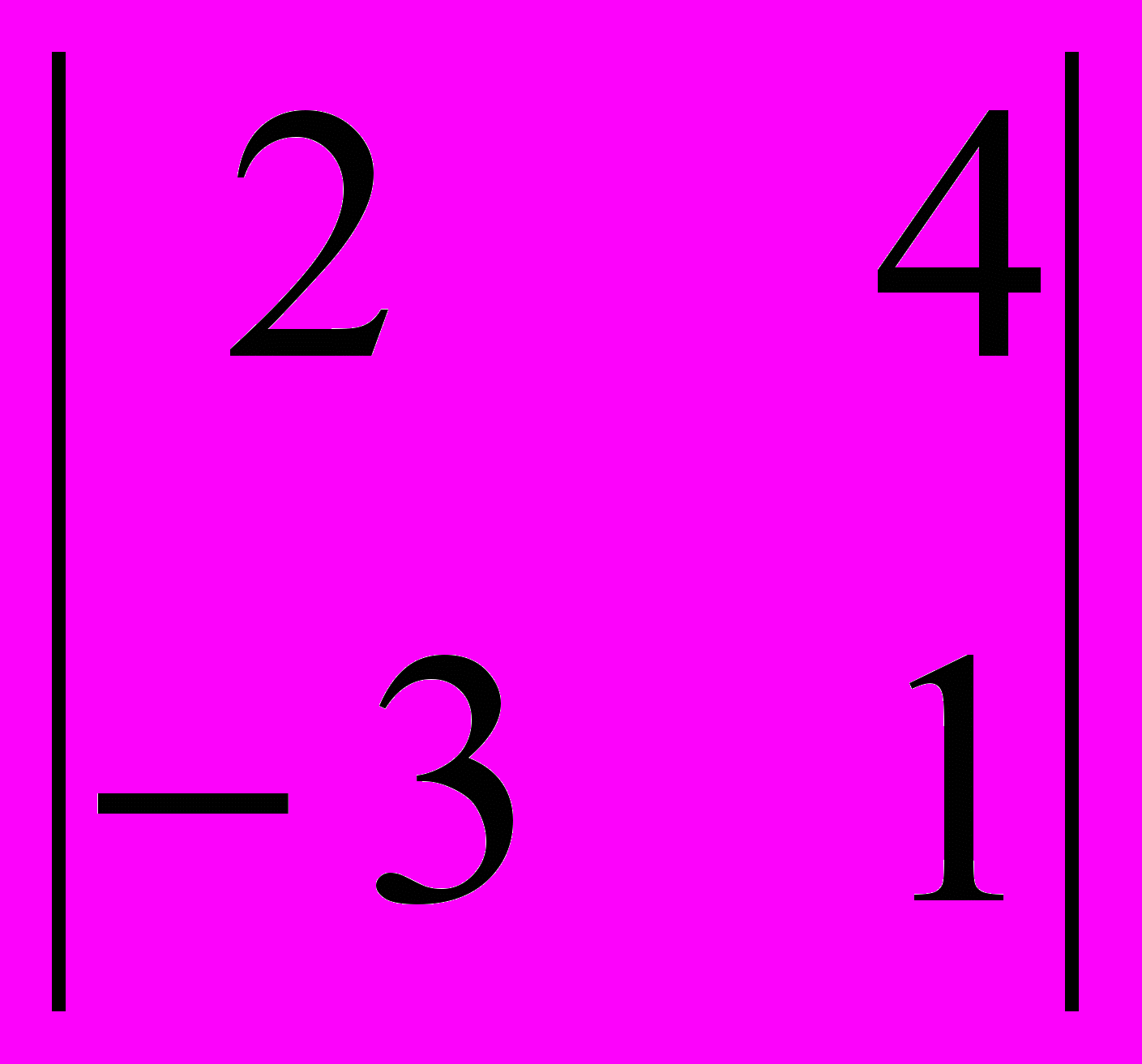= 14; A₁₂ = (–1)¹⁺² = –6; A₁₃ = (–1)¹⁺³ = –4;

A₂₁ = (–1)²⁺¹ 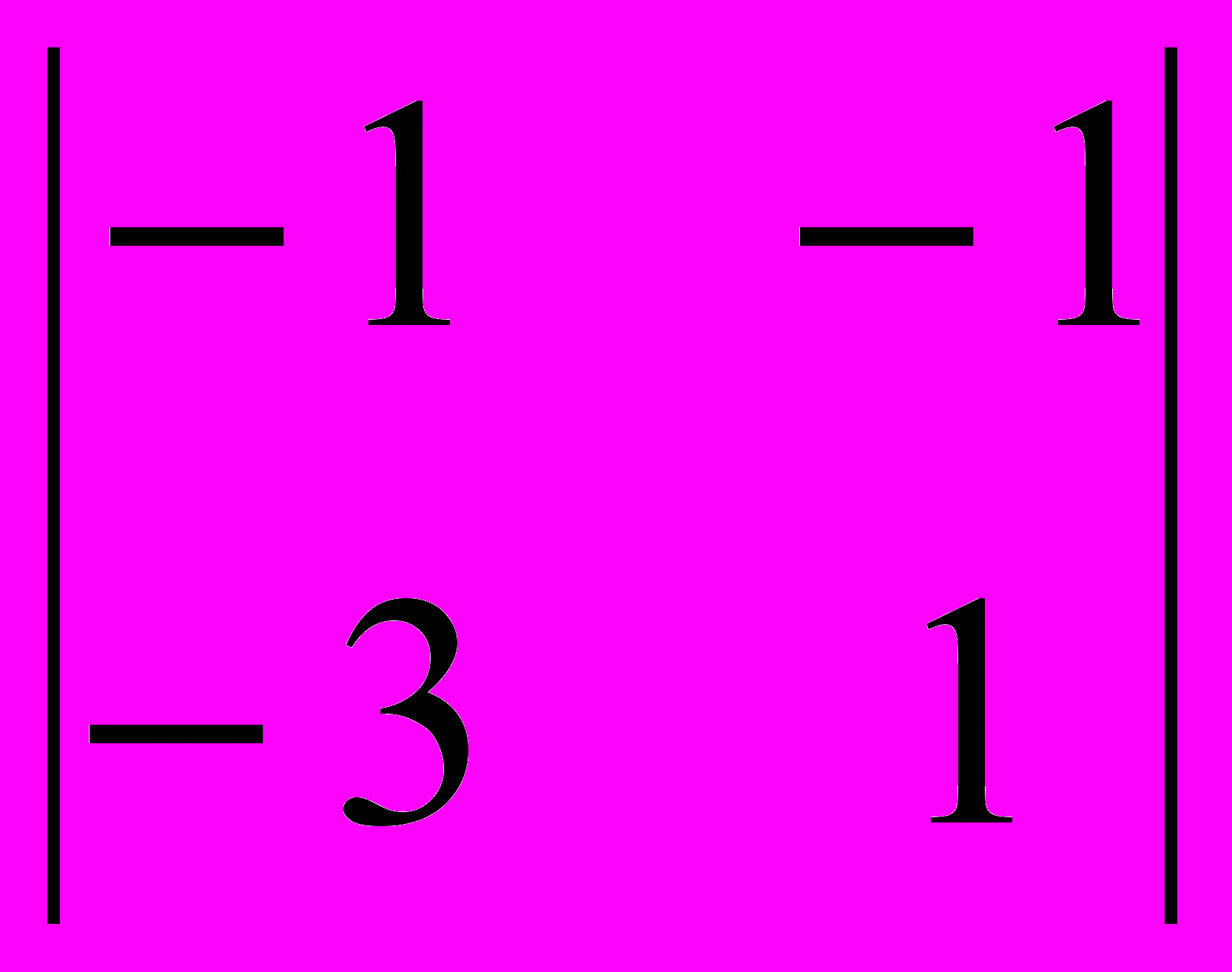= 4; A₂₂ = (–1)²⁺² 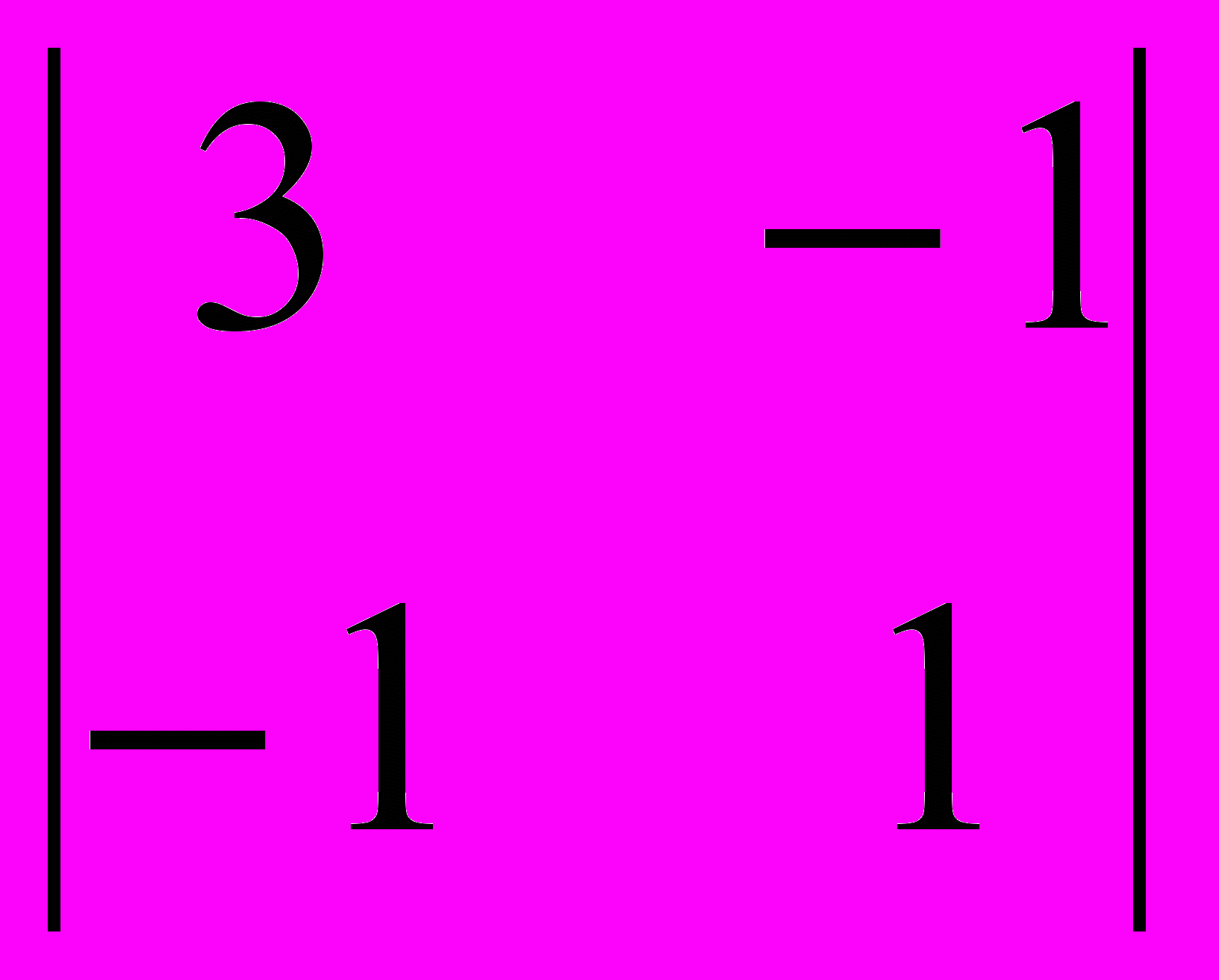= 2; A₂₃ = (–1)²⁺³ 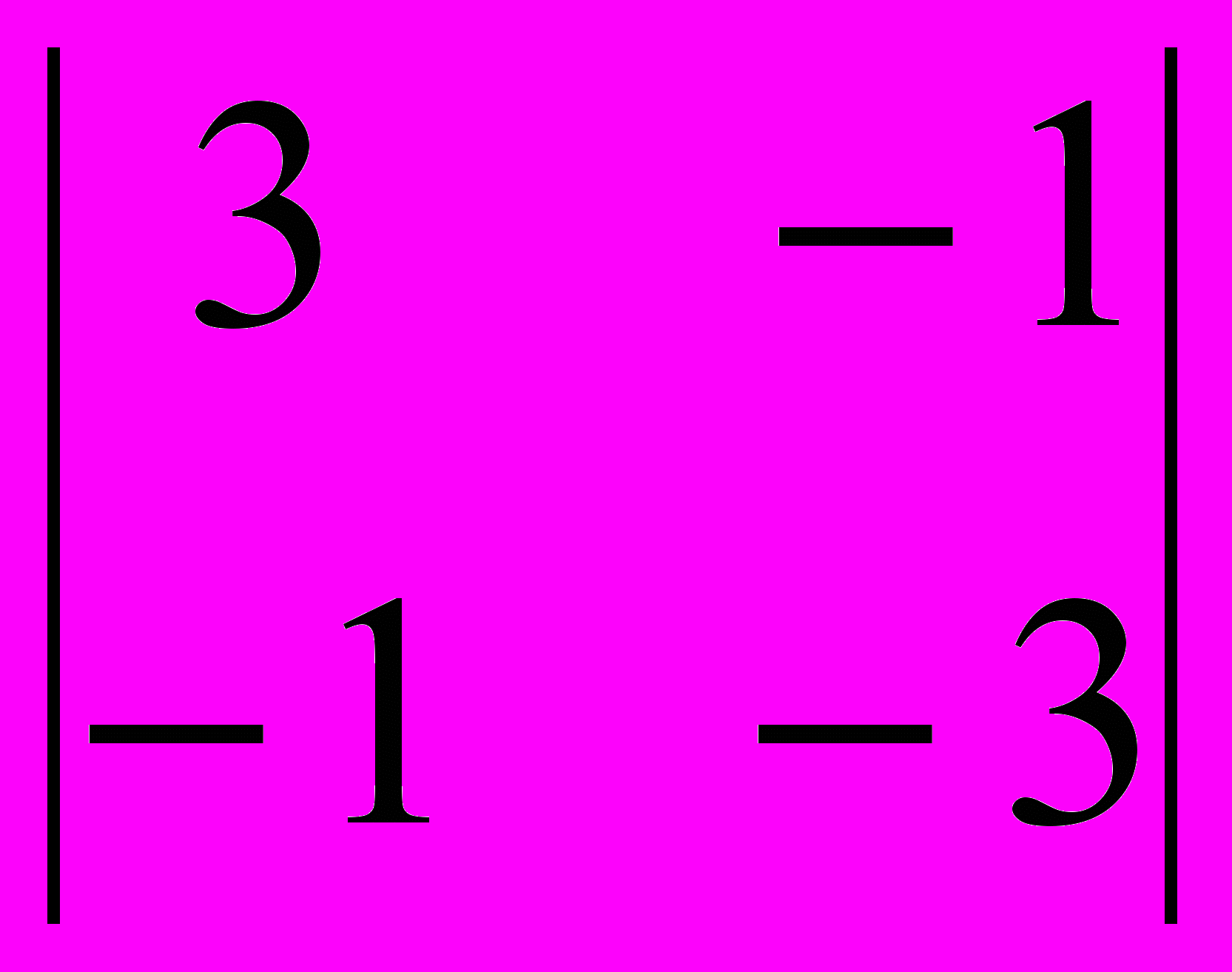= 10;

A₃₁ = (–1)³⁺¹ 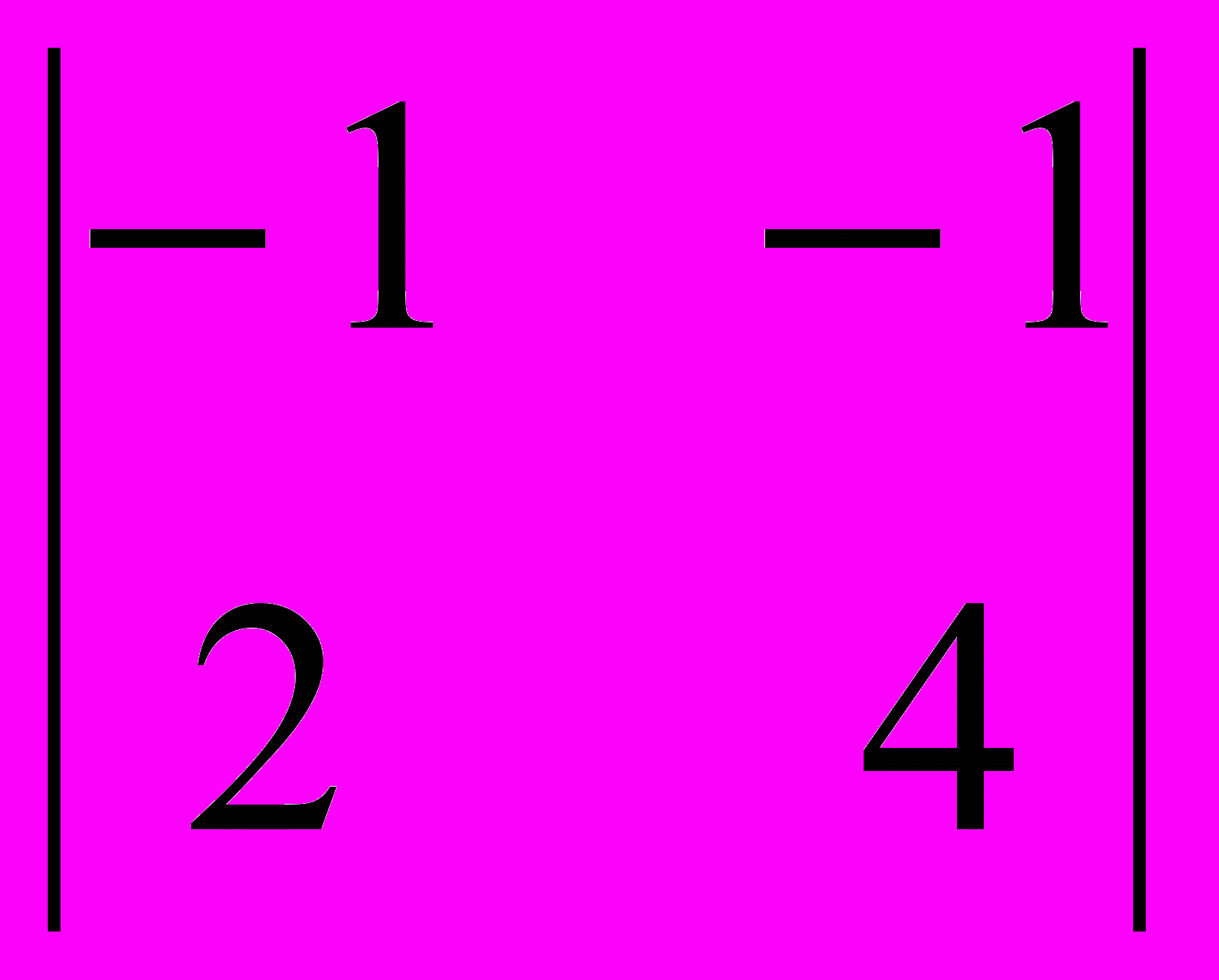= –2; A₃₂ = (–1)³⁺² = –14; A₃₃ = (–1)³⁺³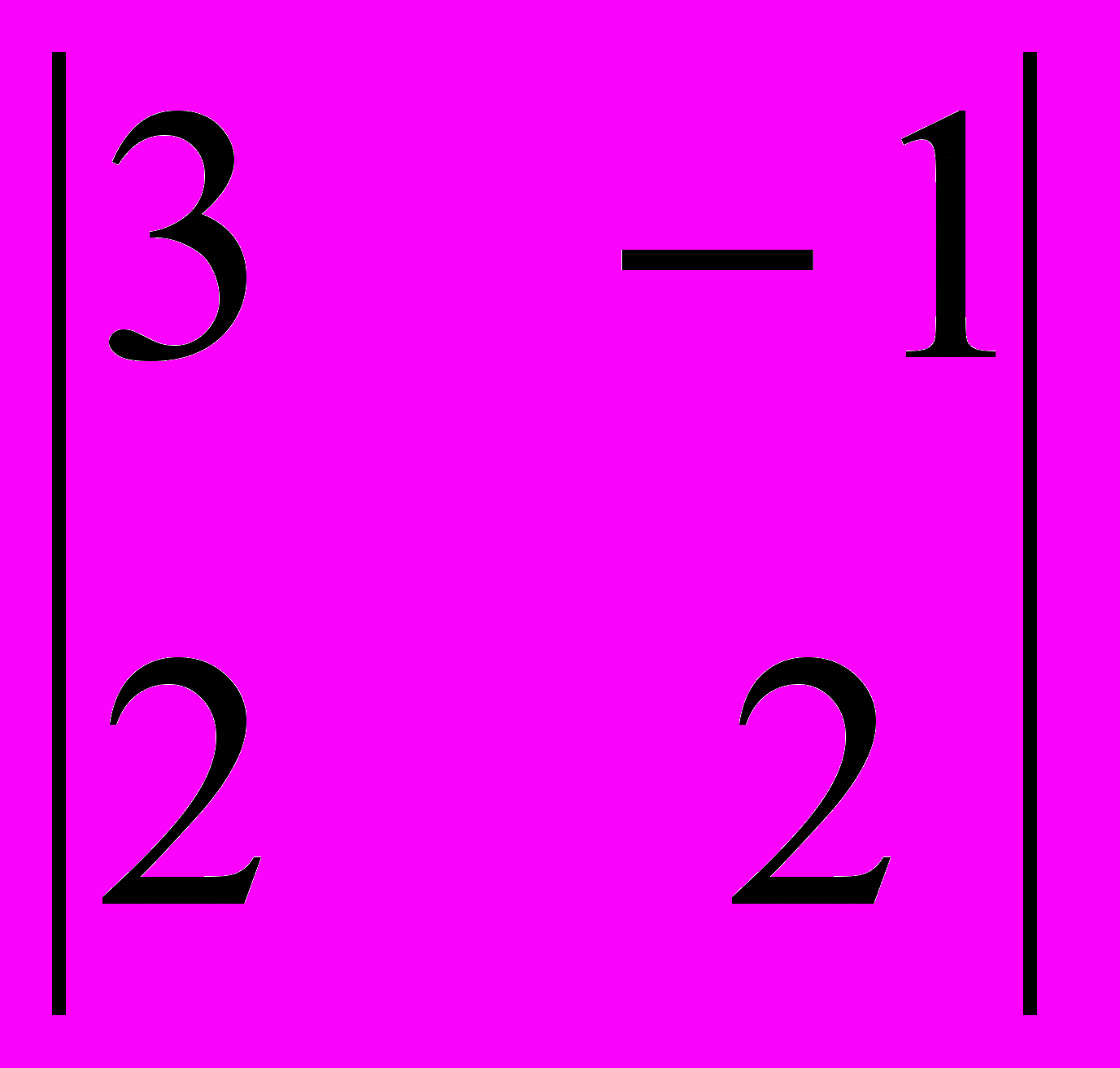 = 8.

Составим из них присоединённую матрицу 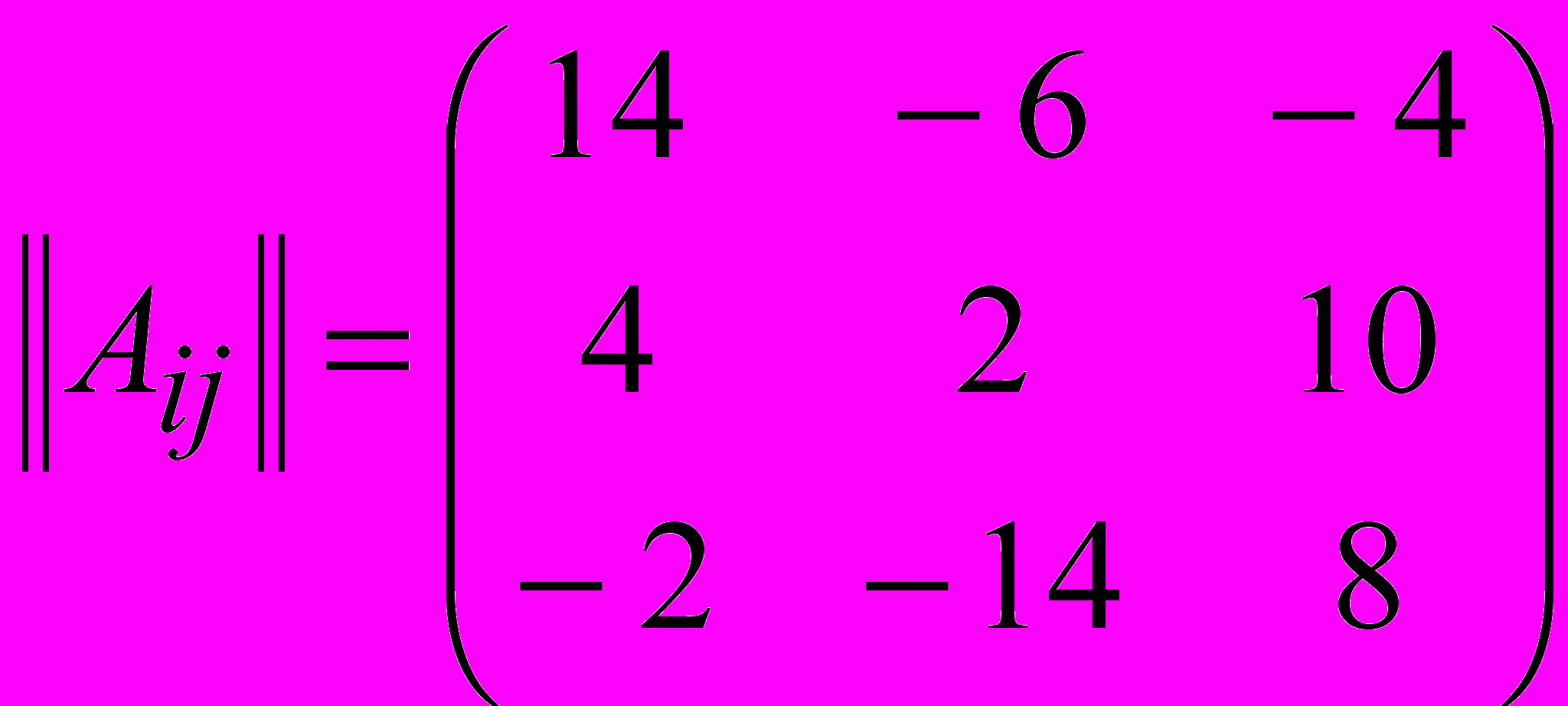и транспонируем её .

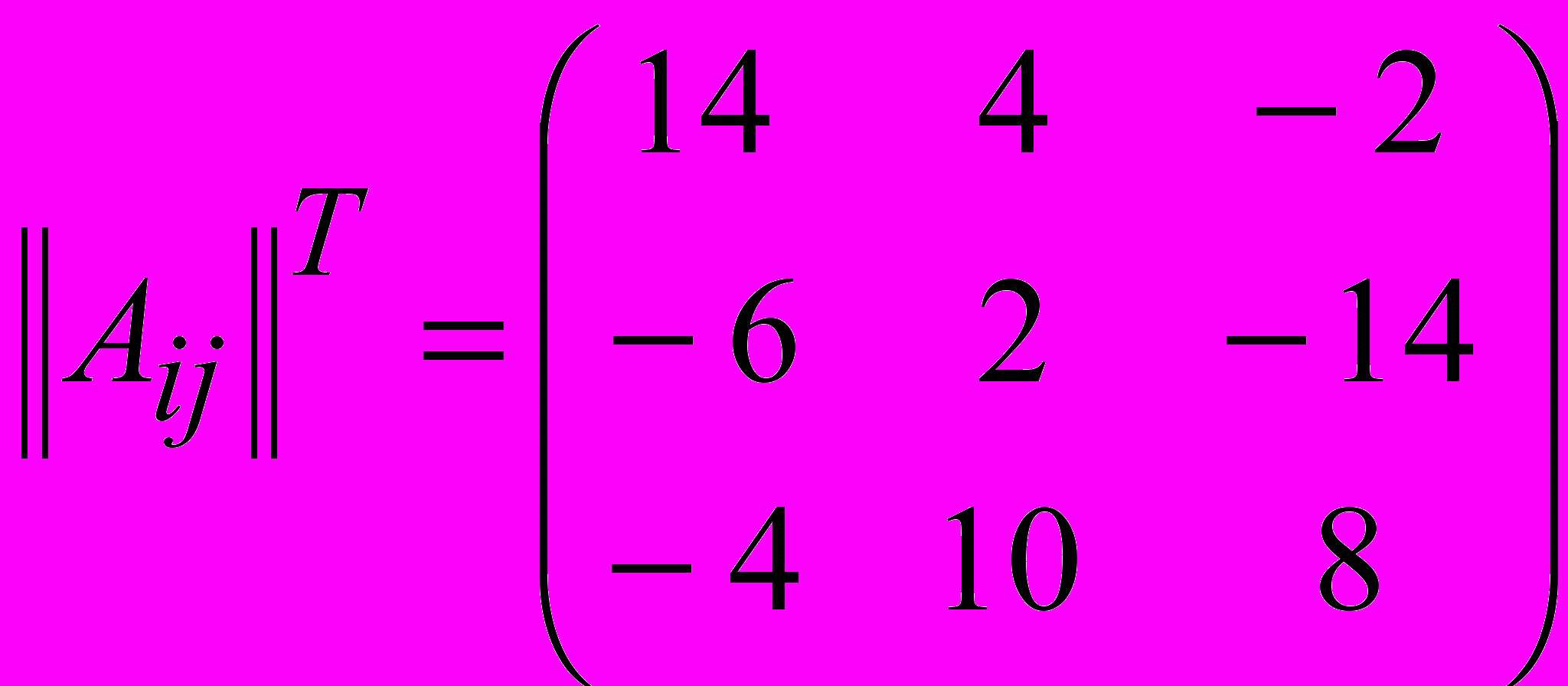Обратная матрица определяется формулой A^–1 = (detA)^–1||A_ij||^T или .

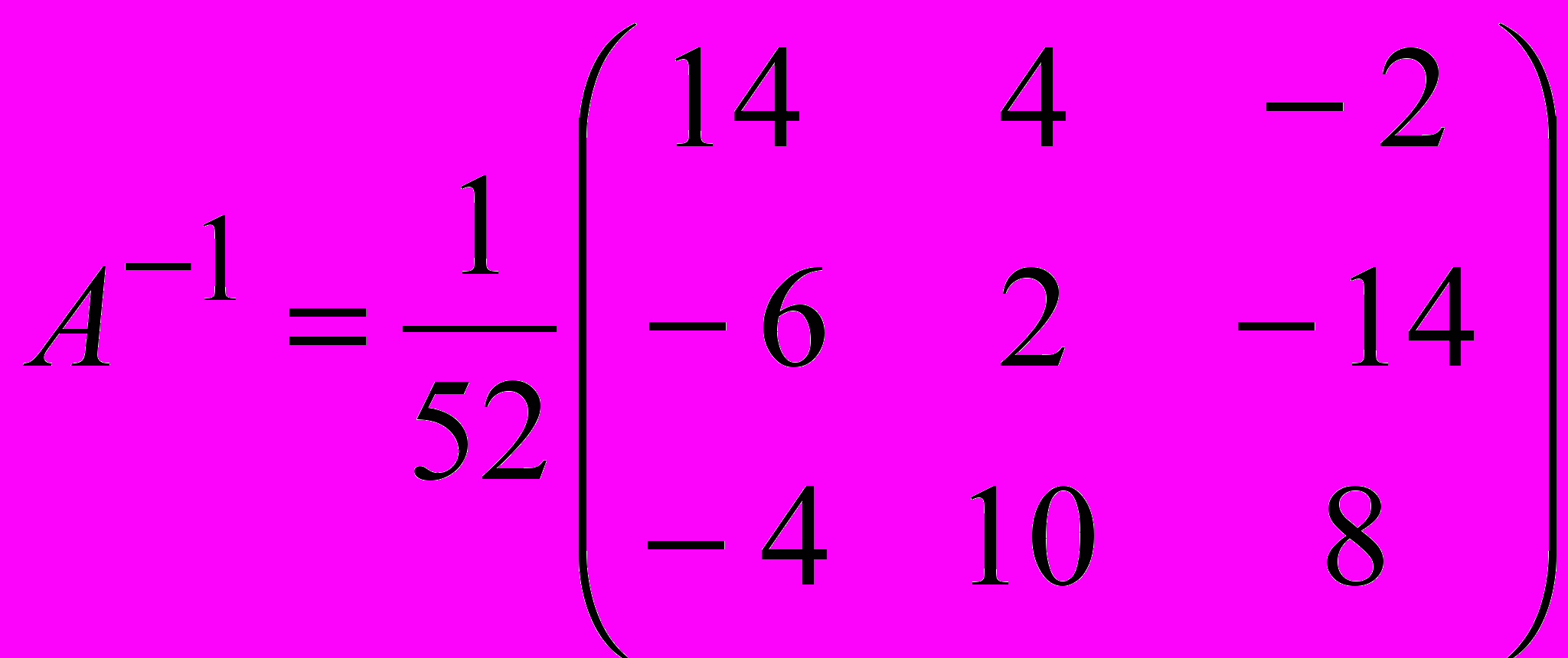Сделаем проверку. Вычислим произведение

А^–1А = =

= =

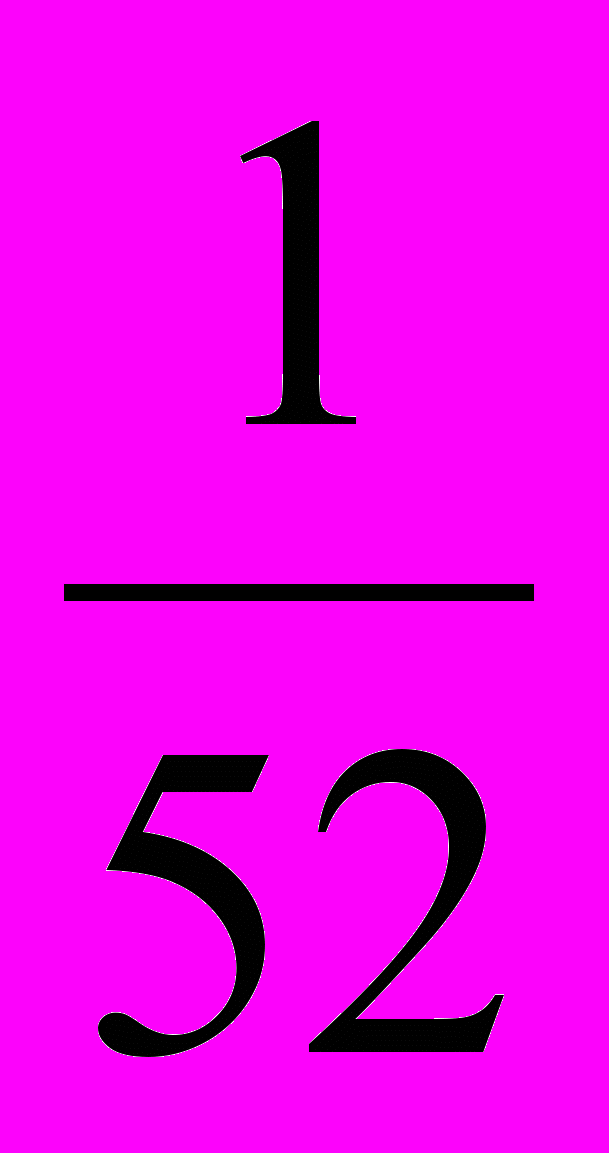
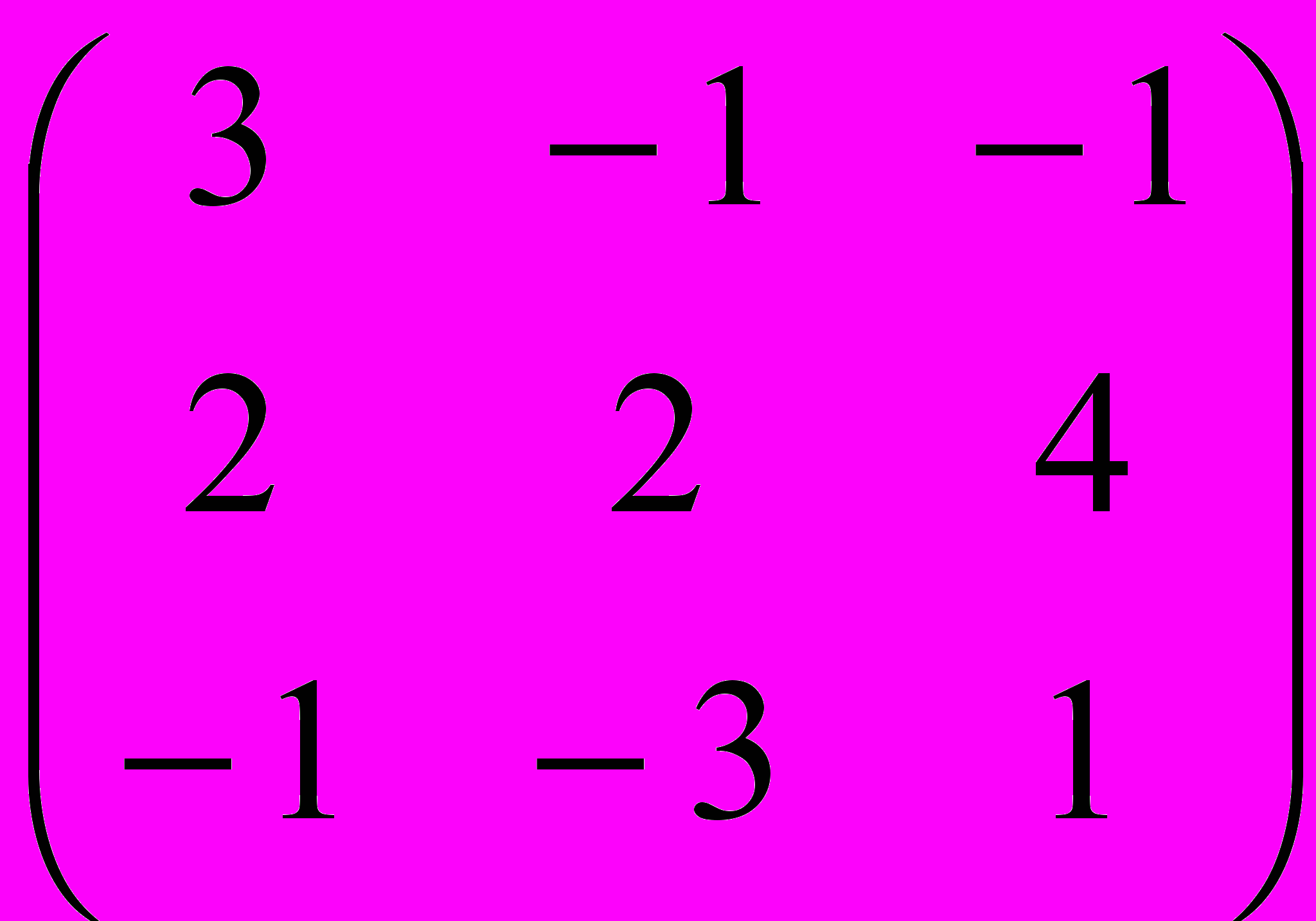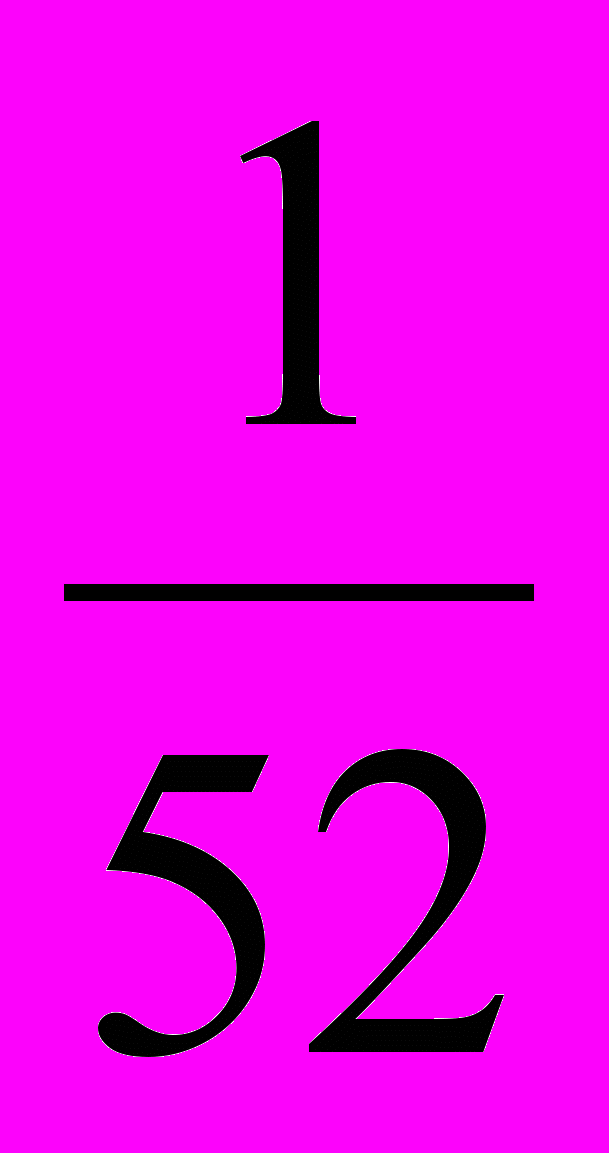
= . В ответе получили единичную матрицу, значит обратная матрица найдена верно.

Нахождение ранга матрицы.

Наивысший порядок миноров матрицы, отличных от нуля, называется ее рангом (обозначение: rang A), а любой минор матрицы, отличный от нуля и имеющий порядок r = rang A, называется ее базисным минором.

Для нахождения ранга матрицы, кроме определения используются методы окаймляющих миноров и Гаусса.

Метод окаймляющих миноров заключается в следующем: выделяют из матрицы минор М k-ого порядка, отличный от нуля. Далее рассматривают миноры (k+1) -ого порядка, которые содержат в себе (окаймляют) минор М. Если все они равны нулю, то ранг матрицы равен k, в противном случае среди окаймляющих миноров найдется ненулевой минор порядка (k+1), и вся процедура повторяется.


Пример 1. Найти ранг матрицы А методом окаймляющих миноров: .

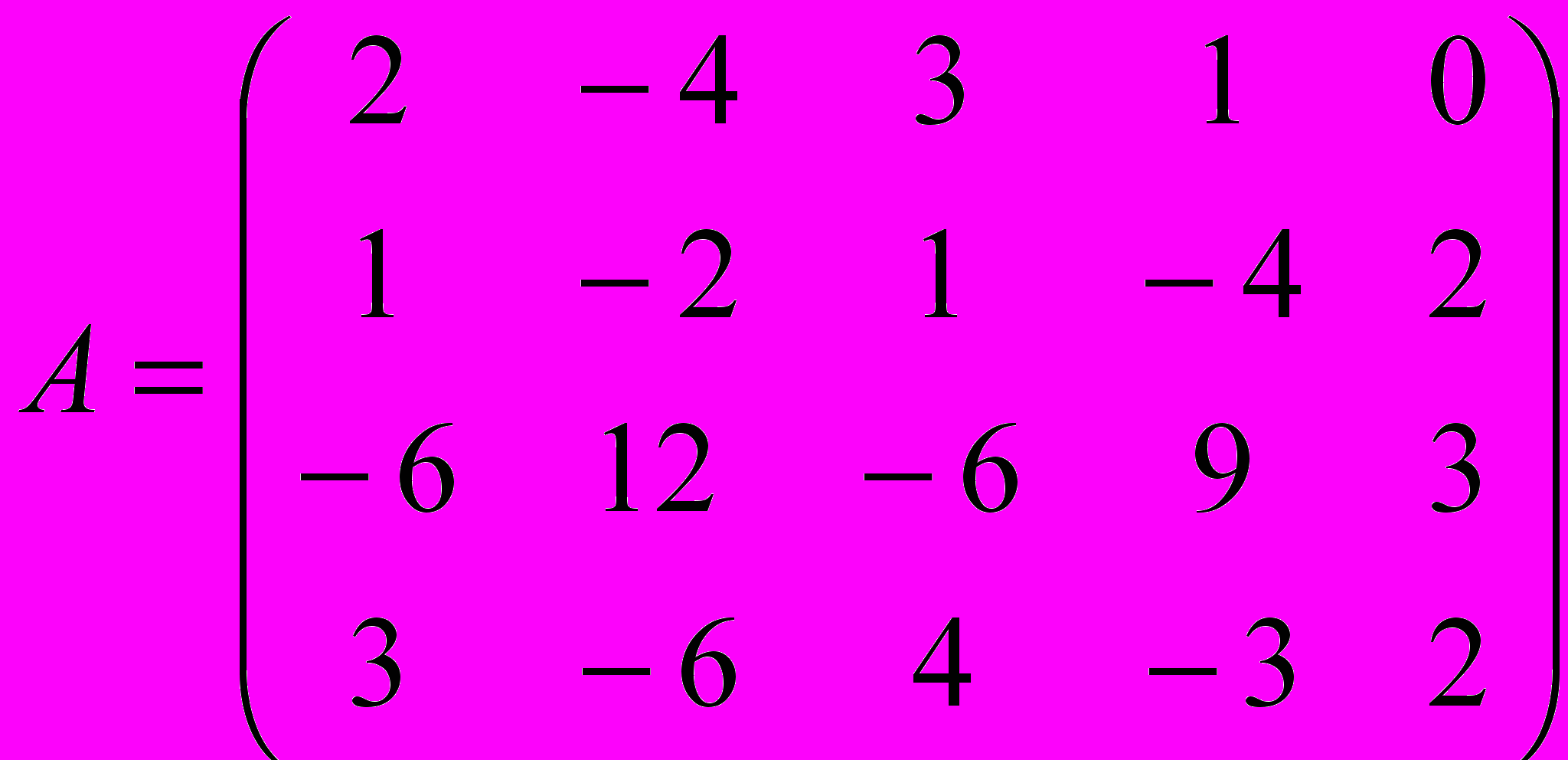Решение: Выделяем минор 2-ого порядка, отличный от нуля: 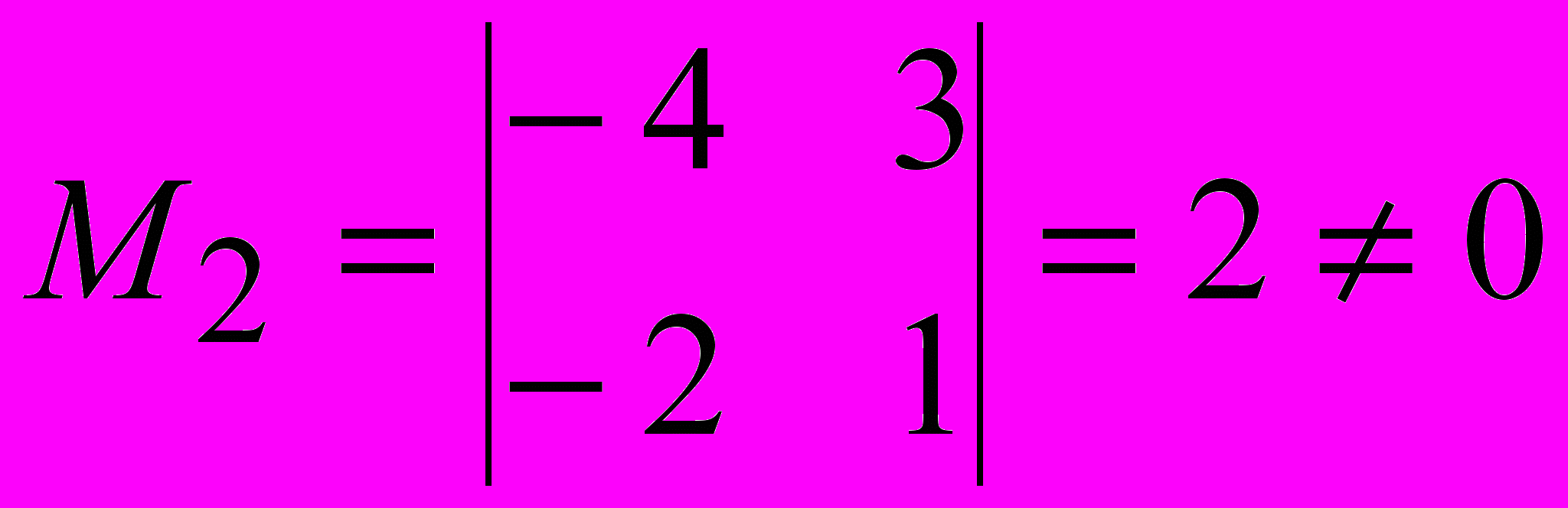. Среди миноров 3-его порядка, окаймляющие М_2, имеются ненулевые, например .

Однако, оба минора 4-ого порядка, окаймляющие , равны нулю:

.

Поэтому rang А = 3, а в качестве базисного минора можно взять .


Пример 2. А = 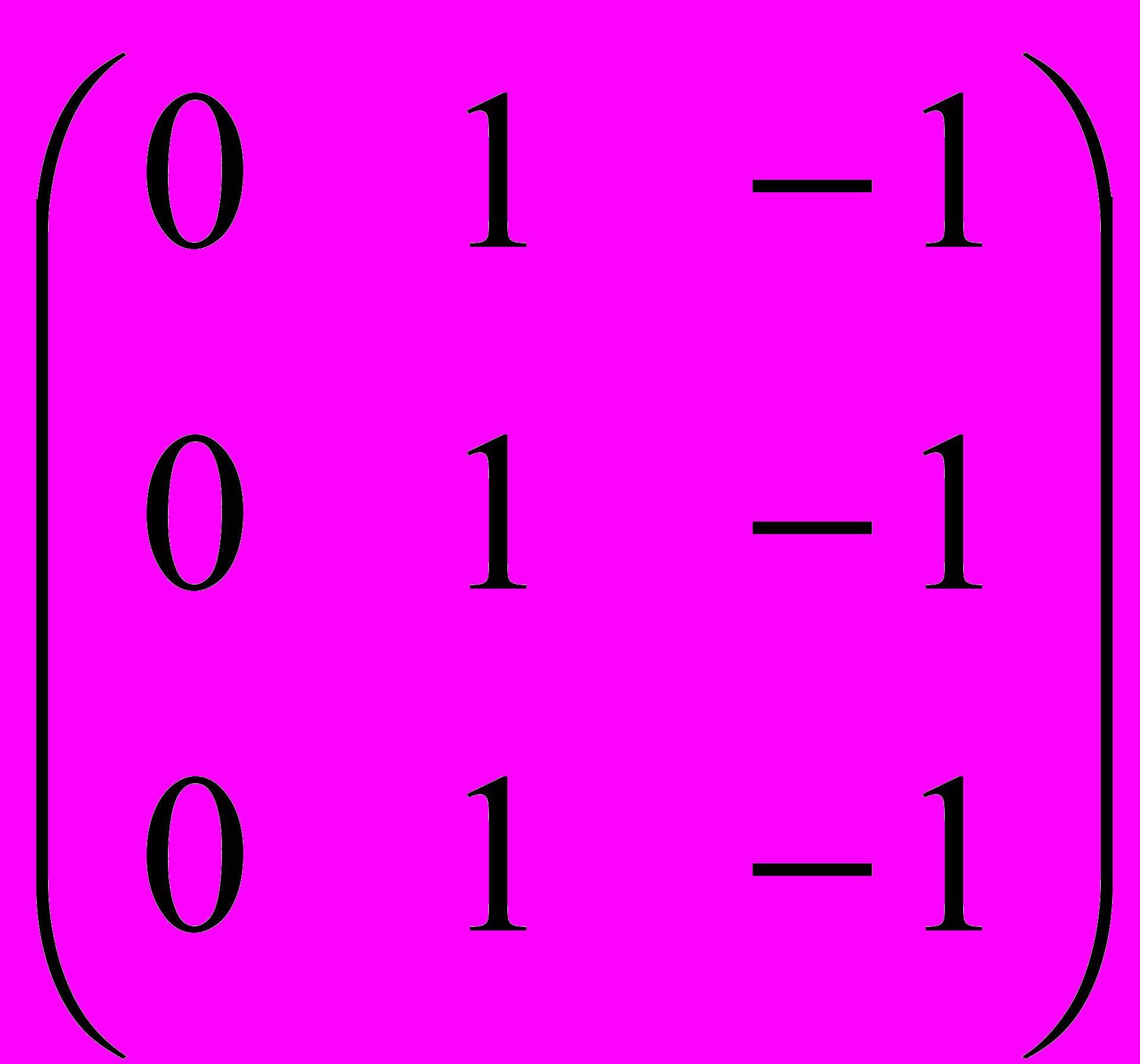B = 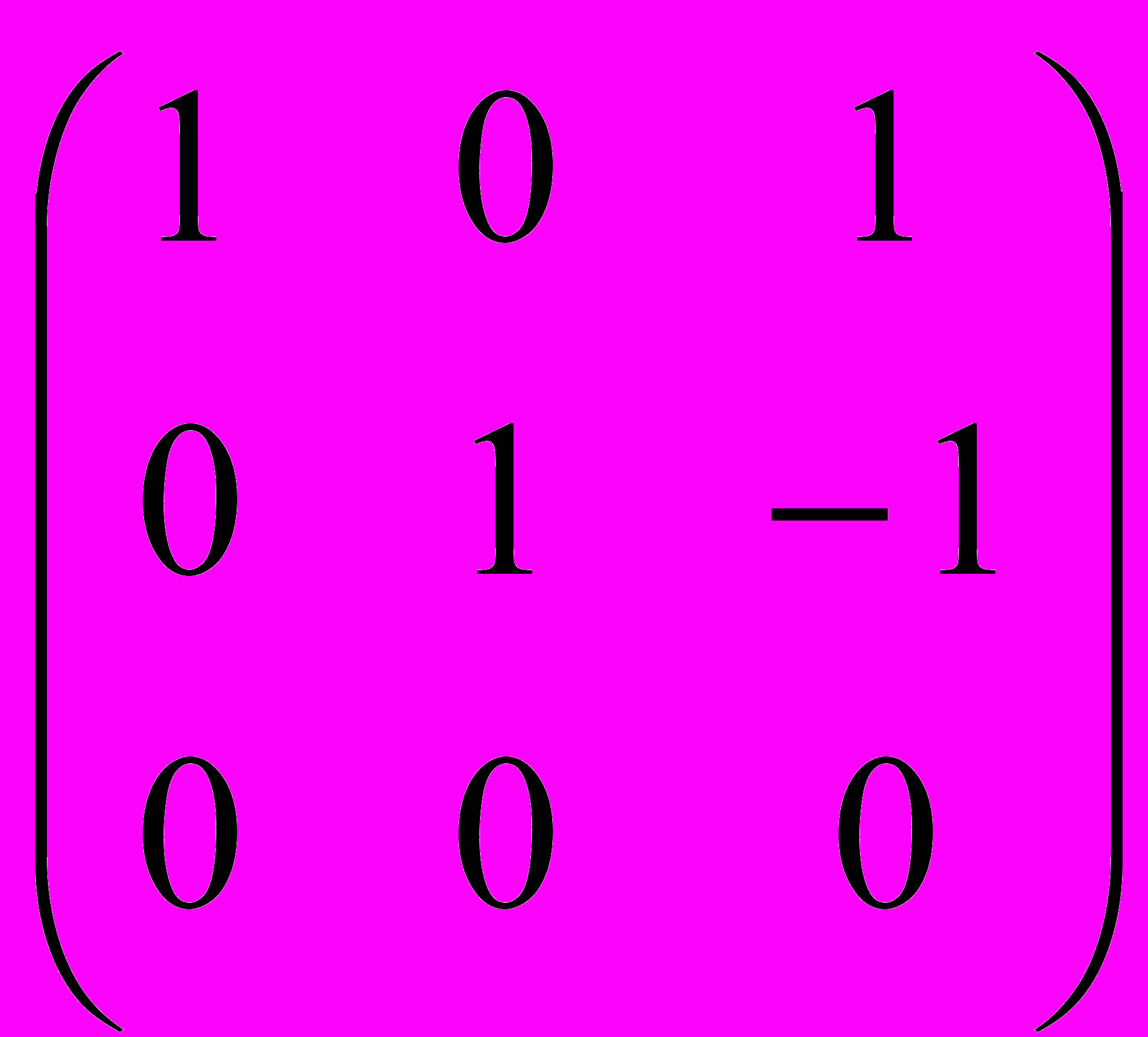rgA = 1, rgB = 2

Ранг матрицы не меняется при выполнении элементарных преобразований: сложении строк, предварительно умноженных на постоянное число. Для определения rgA удобно представить матрицу в треугольной форме. Тогда линейно зависимые строки станут нулевыми или пропорциональными друг другу


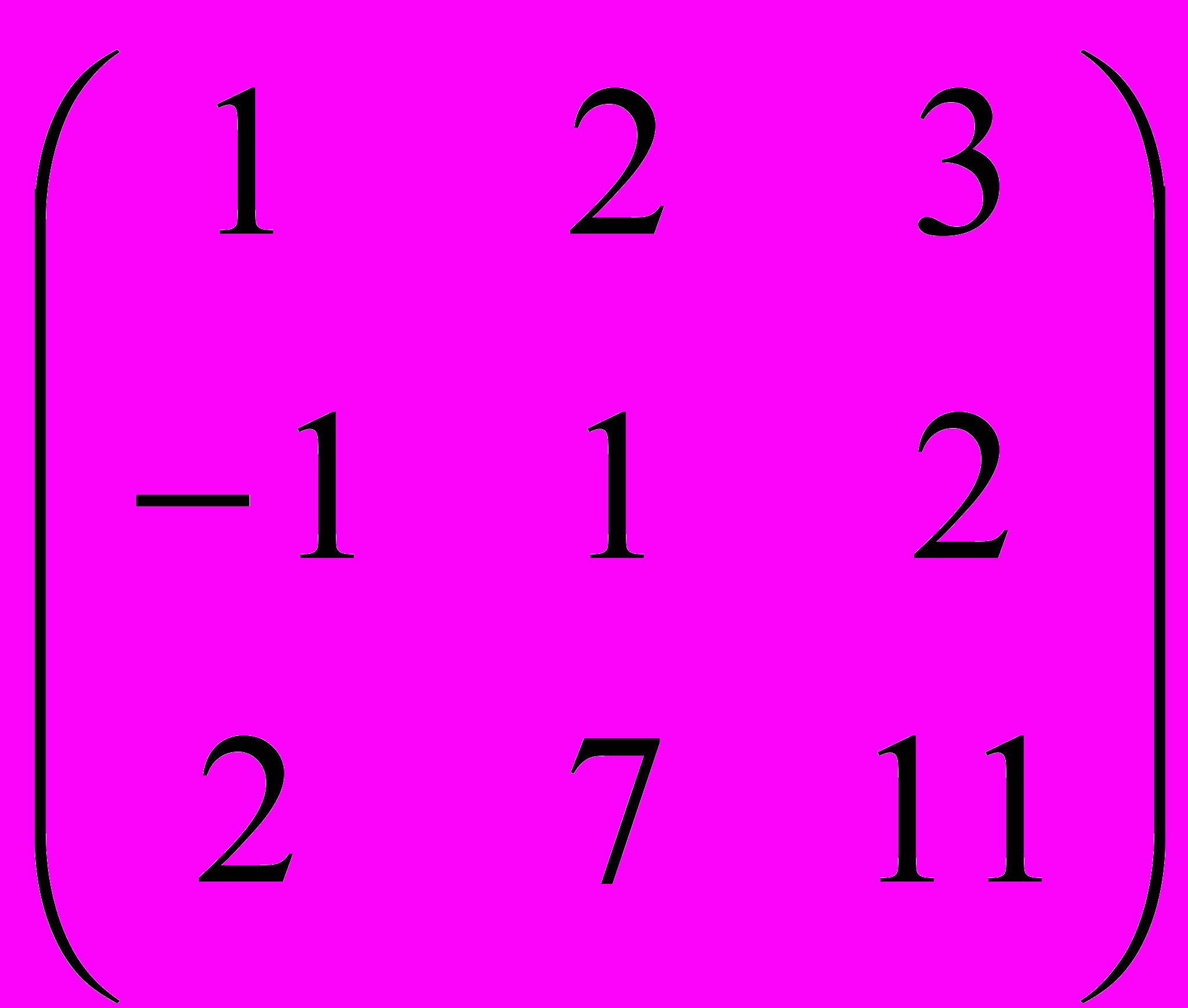
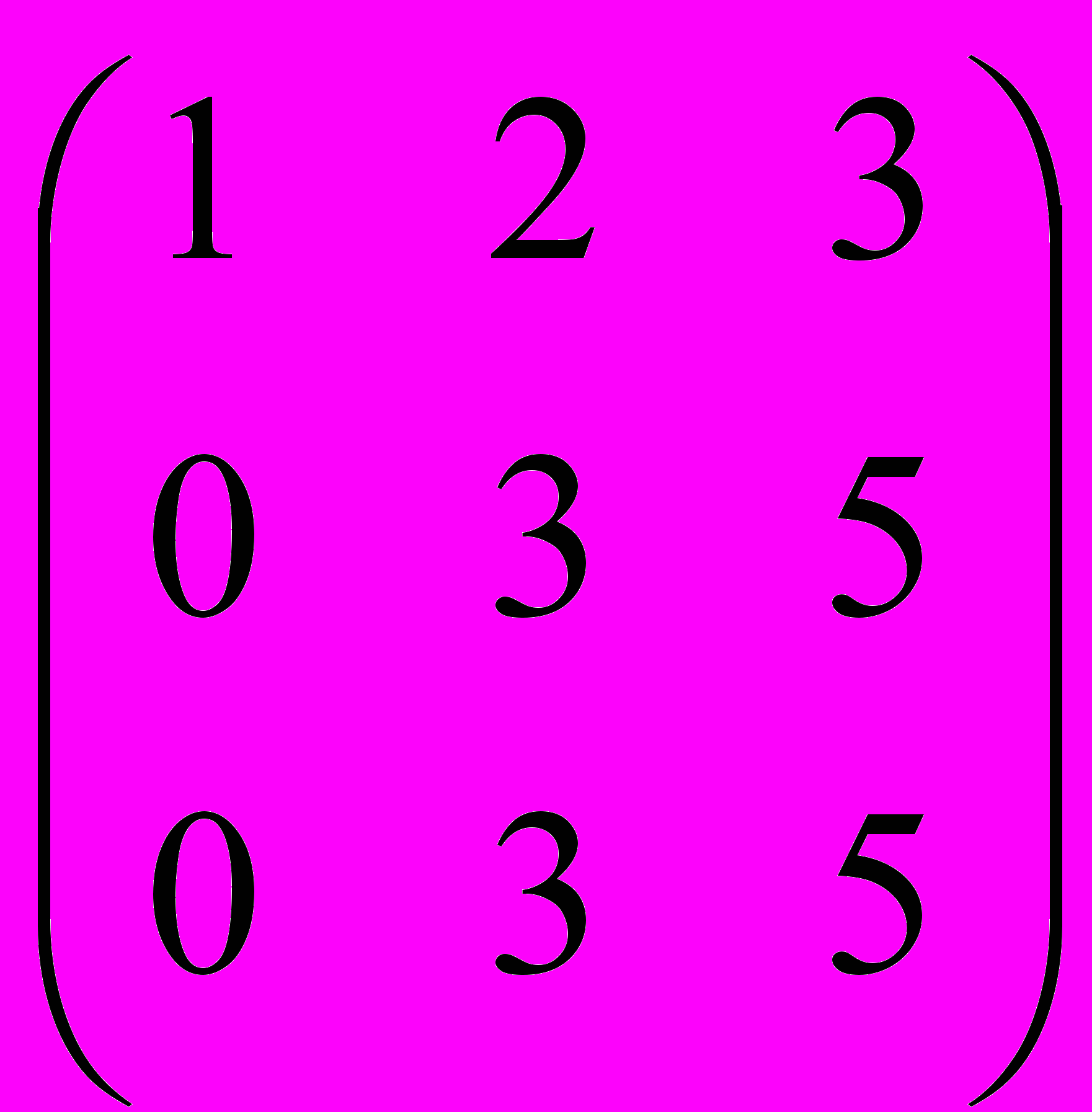
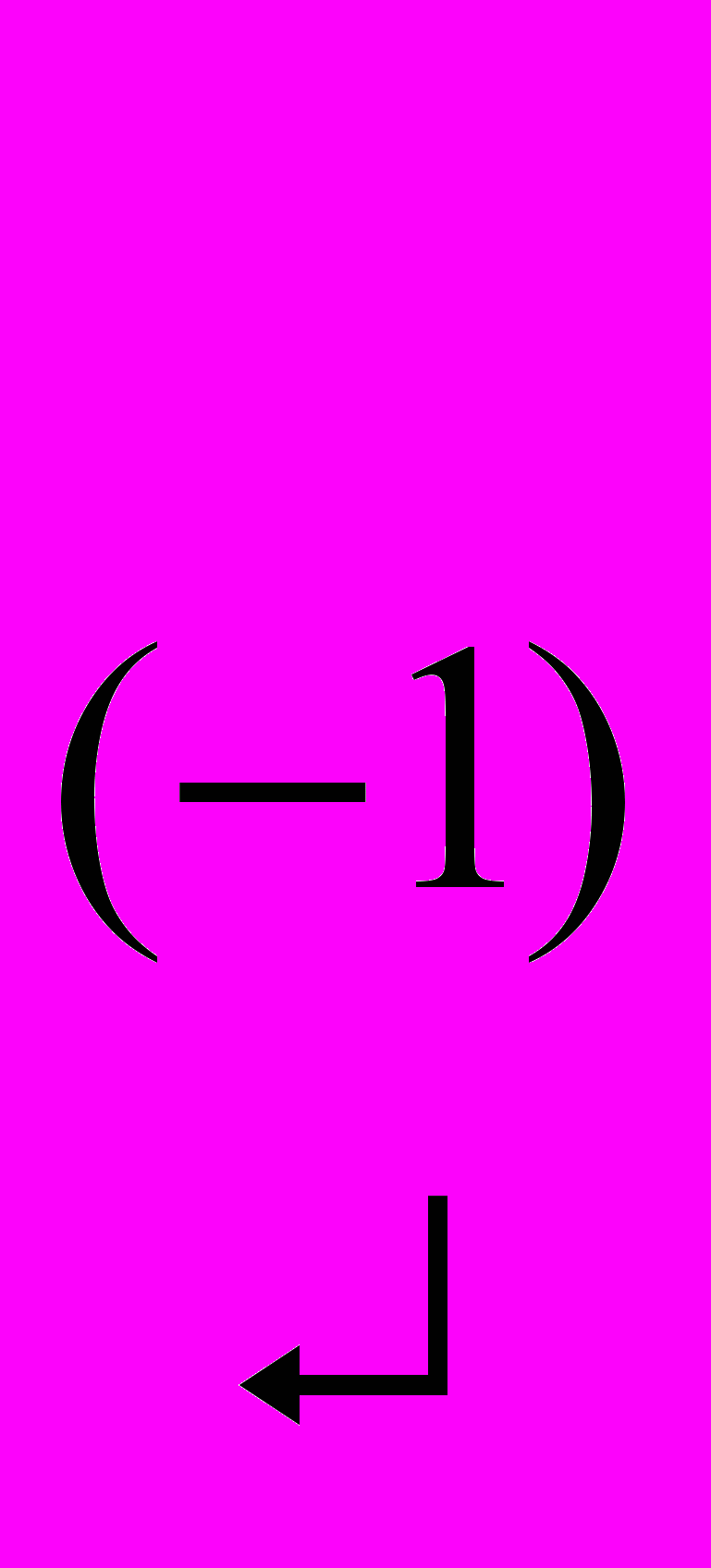
А = rgA = 2