Обязательный курс математика для студентов обучающихся по специальности Автомобили и автомобильное хозяйство
| Вид материала | Документы |
- Курс: Автомобили и автомобильное хозяйство, 18.74kb.
- Учебное пособие для преподавателей и студентов по методике организации и прохождения, 294.64kb.
- Название курса: теория механизмов, 40.16kb.
- Методические указания по курсовому проектированию для студентов специальности 15., 265.88kb.
- Яхъяев Салимсултан Магомедович, 318.1kb.
- Учебное пособие для студентов специальности 150200 «Автомобили и автомобильное хозяйство», 2263.14kb.
- Рабочая программа по дисциплине «Автомобили» для студентов 3, 4 курса очной формы обучения, 242.82kb.
- Программа для специальности 190601 «Автомобили и автомобильное хозяйство», 127.27kb.
- Методические указания к выполнению курсовой работы для специальностей 190601. 01 "Автомобили, 645.65kb.
- Программа для специальности 190601 «Автомобили и автомобильное хозяйство», 97.51kb.
Кафедра высшей математики
Факультета физико-математических и естественных наук
Обязательный курс МАТЕМАТИКА
для студентов обучающихся по специальности
Автомобили и автомобильное хозяйство (ИХС)
1й курс, первый семестр
- Линейная алгебра и аналитическая геометрия
Темы лекций по неделям
1. Определители и их свойства
2. Системы линейных уравнений. Метод Крамера. Определители и системы n-го порядка.
3. Матрицы и действия над ними. Обратная матрица. Матричный метод решения систем линейных уравнений.
4. Ранг матрицы. Теорема Кронекера-Капелли. Метод Гаусса решения систем линейных уравнений.
5. Векторная алгебра. Основные определения. Линейные операции над векторами. Проекция вектора на ось. Координаты вектора. Направляющие косинусы.
6. Теоремы о проекциях и их следствия. Разложение вектора на компоненты. Базис. Скалярное произведение векторов.
7. Векторное произведение векторов. Смешанное произведение векторов.
8. Простейшие задачи аналитической геометрии на плоскости. Полярная система координат.
9. Прямая на плоскости, общее уравнение, другие виды уравнений. Взаимное расположение двух прямых.
10. Нормальное (нормированное) уравнение прямой. Расстояние от точки до прямой.
11. Плоскость. Общее уравнение. Нормальный вектор. Уравнение плоскости в отрезках. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
12. Взаимное расположение двух плоскостей. Прямая в пространстве, общие, канонические и параметрические уравнения.
13. Эллипс, гипербола, парабола. Канонические уравнения.
14. Общее уравнение линий второго порядка. Приведение к каноническому виду.
15. Примеры приведения общего уравнения линий второго порядка к каноническому виду.
16. Поверхности второго порядка. Канонические уравнения.
17. Обзорная лекция.
18. Коллоквиум.
- Математический анализ
Темы лекций по неделям
1. Множества и операции над ними. Абсолютное значение (модуль) числа и его свойства. Переменная величина. Область изменения переменной величины.
2. Функция. Область определения. Предел функции. Предел числовой последовательности.
3. Ограниченные функции и их свойства. Бесконечно малые функции и их свойства.
4. Основные теоремы о пределах. Односторонние пределы. Предел
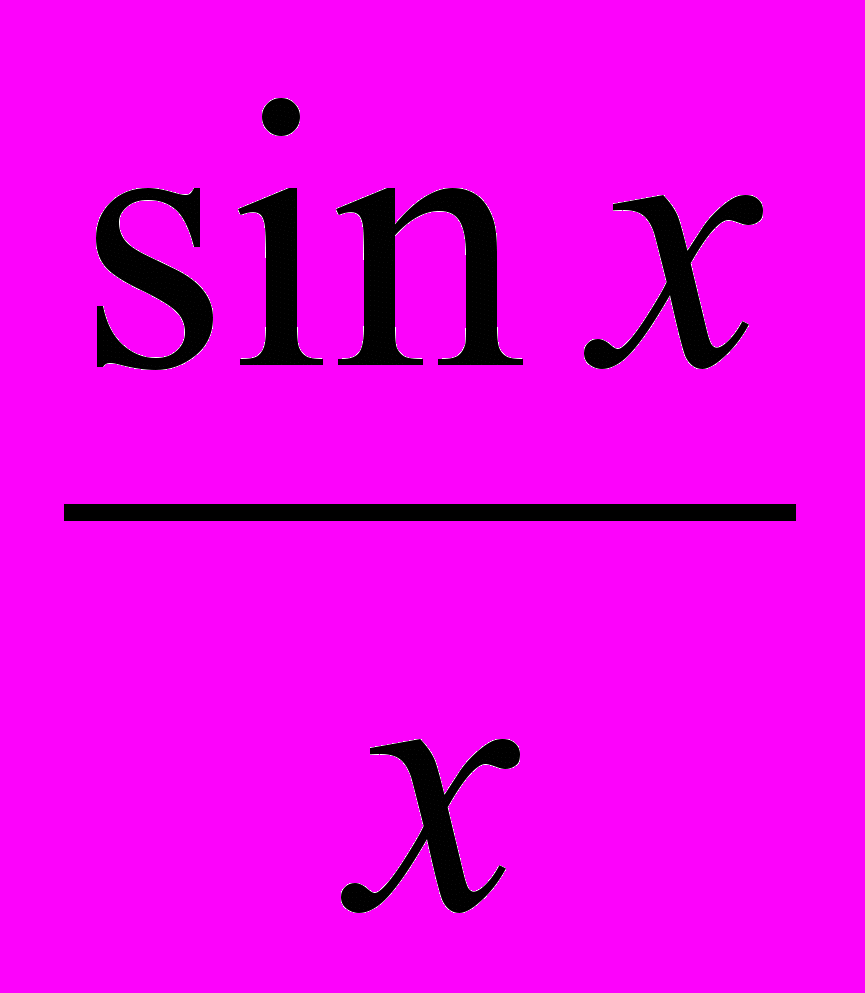при 
5. Число e (предел
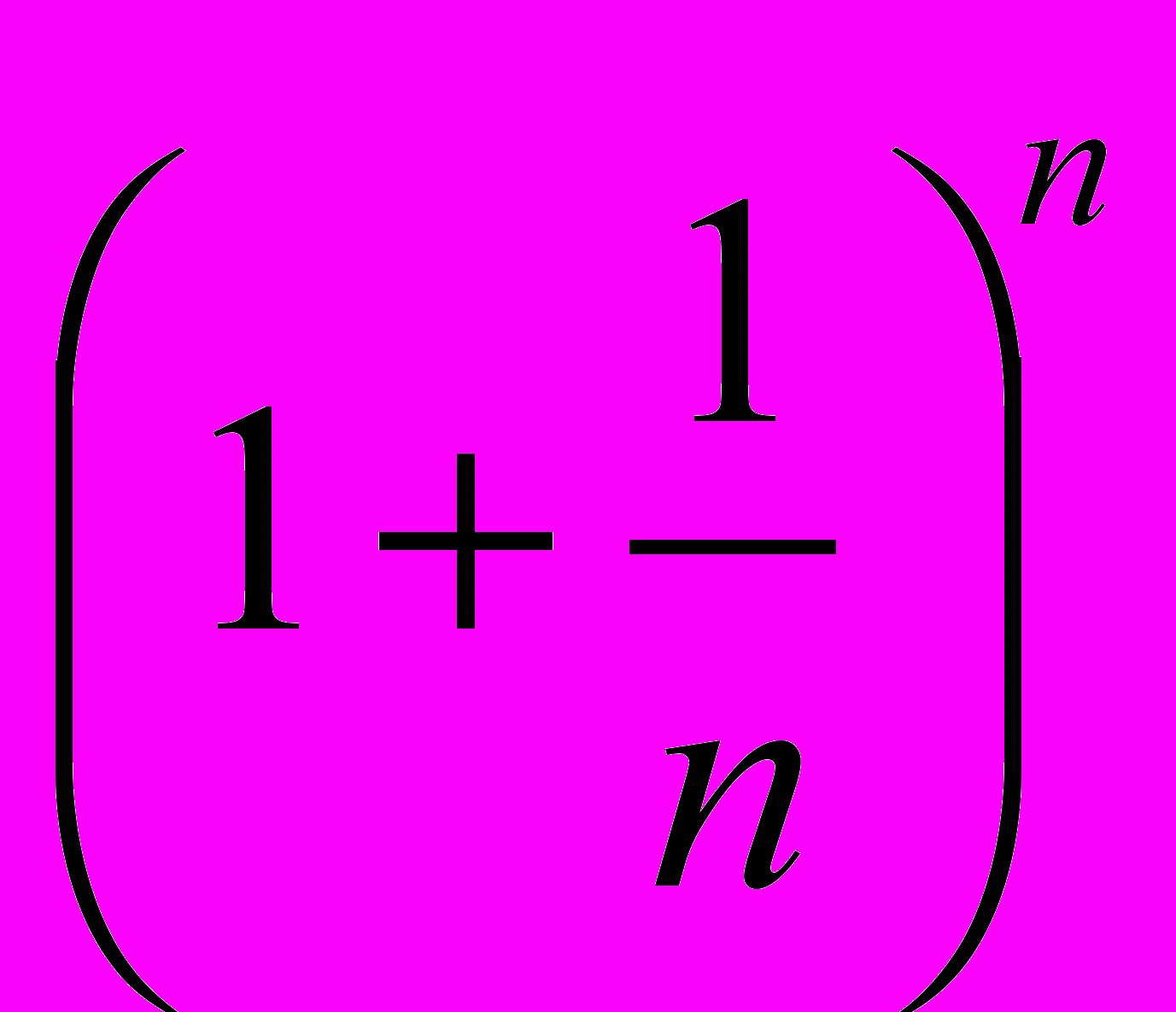при 
). Натуральные логарифмы.6. Непрерывность функций. Основные теоремы. Свойства. Точки разрыва.
7. Производная. Определение. Механический и геометрический смысл производной. Дифференцируемость функций. Дифференциал и его геометрический смысл. Уравнения касательной и нормали.
8. Основные правила дифференцирования. Производные функций:
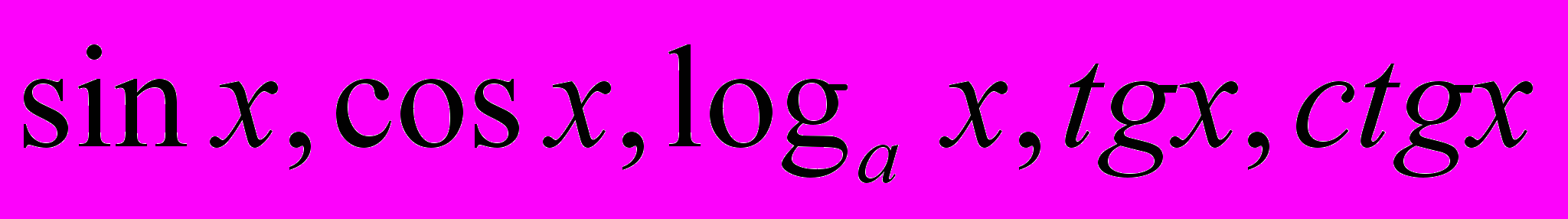. Производная сложной функции. 9. Производные степенной, показательной и сложной показательной функции. Обратная функция и ее дифференцирование. Обратные тригонометрические функции и их дифференцирование.
10. Таблица основных формул дифференцирования. Производные функций, заданных параметрически и неявно. Производные и дифференциалы высших порядков.
11. Теоремы Ферма, Ролля, Лагранжа, Коши. Предел отношения двух бесконечно малых величин (правило Лопиталя).
12. Формула Тейлора. Разложение элементарных функций по формуле Тейлора (Маклорена)
13. Возрастание и убывание функций. Экстремум. Необходимое и достаточное условие экстремума. Выпуклость и вогнутость кривой. Точки перегиба.
14. Асимптоты графика функции. Общая схема исследования функций и построения их графиков.
15. Дифференциал дуги. Кривизна. Радиус кривизны. Комплексные числа, их изображение на плоскости. Модуль и аргумент комплексного числа.
16. Тригонометрическая форма комплексного числа. Действия над комплексными числами. Формулы Муавра и Эйлера. Показательная форма комплексного числа.
17. Обзорная лекция.
18. Коллоквиум.