Матрицы, определители, системы линейных уравнений определение матрицы. Виды матриц

Вид материала

Документы

Содержание Главной диагональю Действия над матрицами B называют транспонированной A, обычно обозначают A A+B=B+A и ассоциативному (A+B C) элемент, стоящий в 1-ой строке и 3-м столбце c A на единичную матрицу E Понятие определителей Определителем второго порядка Определителем третьего порядка Свойства определителей Алгебраические дополнения и миноры Алгебраическим дополнением Теорема (о разложении определителя по заданной строке или столбцу). Обратная матрица AB=E. Аналогично можно показать, что BA=E Системы линейных уравнений Матричный метод решения систем линейных уравнений Правило крамера Теорема (правило Крамера). ... Полное содержание

Подобный материал:

• Программа курса математики, 16.23kb.
• Теоретический материал дисциплинарного экзамена (бакалавры), 215.88kb.
• Экзаменационные вопросы по курсу "Линейная алгебра", 22.34kb.
• Вопросы к зачету по ено фк: математика для студентов 111 – 116 групп, 19.15kb.
• 1. Матрица и расширенная матрица системы. Элементарные преобразования матриц. Решение, 8.16kb.
• Тематическийпла н, 46.68kb.
• Календарно-тематический план учебная дисциплина: «Математика», 53.03kb.
• Лекции пр зан, 50.82kb.
• Вопросы к экзамену по дисциплине «Высшая математика», 150.21kb.
• Тема Метод Гаусса, 94.48kb.

МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:



Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

.

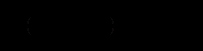Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.



Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .


ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

1. 
   
2. 
   

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,



или



Примеры. Найти сумму матриц:

1. .
   
2. - нельзя, т.к. размеры матриц различны.
   
3. .
   

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

1. 
   
2. 
   
3. .
   

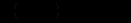
Примеры.

1. .
   
2. Найти 2A-B, если , .
   

.

3. Найти C=–3A+4B.
   

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

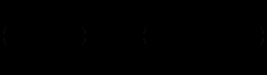Примеры.

1. Пусть
   

Найти элементы c₁₂, c₂₃ и c₂₁ матрицы C.

2. Найти произведение матриц.
   

.

3. .
   
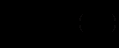4. - нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
   
5. Пусть
   

Найти АВ и ВА.

6. 
   

Найти АВ и ВА.

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

.


ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

1. 
   
2. .
   
3. Вычислить определитель матрицы D, если D= -А+2В и
   

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

.

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

1. .
   
2. .
   
3. Решите уравнение..
   

.

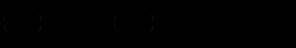(x+3)(4x-4-3x)+4(3x-4x+4)=0.

(x+3)(x-4)+4(-x+4)=0.

(x-4)(x-1)=0.

x₁ = 4, x₂ = 1.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

1. Если квадратная матрица A^T является транспонированной матрицей A, то их определители совпадают |A^T | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка .
   

Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:

2. При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,
   

Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.

.

Для определителя третьего порядка проверьте самостоятельно.

3. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, .
   

Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

4. Общий множитель строки или столбца можно выносить за знак определителя. Например, .
   

Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)

5. Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой).
   
6. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,
   

.

Доказательство - проверкой, аналогично свойству 1.

7. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например,
   

.

Докажем это равенство, используя предыдущие свойства определителя.

Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.

АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

.

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическим дополнениемэлемента a_ij определителя называется его минор M_ij, умноженный на (–1)^i+j.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1)^i+jM_ij.

Например,

Пример. Дан определитель . Найти A₁₃, A₂₁, A₃₂.



Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

.

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:



Разложим полученный определитель по элементам 1-ой строки.

.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a₂₁, a₂₂, a₂₃. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

Примеры.

1. Вычислить определитель , раскладывая его по элементам 2-го столбца.
   

2. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
   

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Доказательство:

1. Необходимость. Пусть для матрицы A существует обратная матрица A^-1. Покажем, что |A| ≠ 0.
   

Прежде всего заметим, что можно доказать следующее свойство определителей .

Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0.

2. Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть и |A| ≠ 0.
   

Покажем, что в этом случае обратной матрицей будет матрица

, где A_ij алгебраическое дополнение элемента a_ij.

Найдём AB=C.

Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,



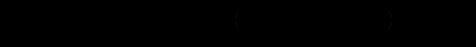
Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

Кроме того, все недиагональные элементы матрицы C равны нулю. Например,

Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A^-1.

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

где A_ij - алгебраические дополнения элементов a_ij данной матрицы A.

Итак, чтобы найти обратную матрицу нужно:

1. Найти определитель матрицы A.
   
2. Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу , элементами которой являются числа A_ij.
   
3. Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет .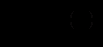
   

Аналогично для матриц второго порядка, обратной будет следующая матрица .

Примеры.

1. Найти матрицу, обратную данной . Сделать проверку.
   

|A| = 2. Найдем алгебраические дополнения элементов матрицы A.



Проверка:

.

Аналогично A∙A^-1 = E.

2. Найти элементы и матрицы A^-1 обратной данной
   

.

Вычислим |A| = 4. Тогда .

.

3. . Найдем обратную матрицу.
   

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой m линейных уравнений с n неизвестными называется система вида



где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
   
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
   
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.
   

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.


МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:



Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение



т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

1. 
   

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

2. 
   

Итак, х₁=4,х₂=3,х₃=5.

3. Решите матричное уравнение: XA+B=C, где
   

Выразим искомую матрицу X из заданного уравнения.



Найдем матрицу А^-1.



Проверка:

4. Решите матричное уравнение AX+B=C, где
   

Из уравнения получаем .



Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:



Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,



называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов



Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём



Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:



Сложим эти уравнения:



Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:



Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

1. 
   

Итак, х=1, у=2, z=3.

2. Решите систему уравнений при различных значениях параметра p:
   

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
   
2. При p = 30 получаем систему уравнений которая не имеет решений.
   
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y, yR.
   

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:



Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:



Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:



и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
   
2. умножение строки на число, отличное от нуля;
   
3. прибавление к одной строке другие строки.
   

Примеры: Решить системы уравнений методом Гаусса.

1. 
   

Вернувшись к системе уравнений, будем иметь

2. 
   

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.



Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

3. 
   

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.



Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.



Таким образом, система имеет бесконечное множество решений.

Правило Крамера

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида



Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

Примеры.

1. 
   

, а значит x=y=z=0.

2. 
   

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

,

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.



Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

Примеры.

1. Найти собственные векторы и соответствующие им собственные значения матрицы .
   

Составим характеристическое уравнение и найдём собственные значения

1. При λ₁ = –1 получаем систему уравнений
   

Если x₁ = t, то, где tR.

1. Если λ₂ = 5, то
   
1.