Решение задач по тоэ, отц, Высшей математике, Физике, Программированию

Вид материала

Решение

Содержание Высшая математика Алгебраические дополнения и миноры Алгебраическим дополнением Теорема (о разложении определителя по заданной строке или столбцу). Обратная матрица AB=E. Аналогично можно показать, что BA=E

Подобный материал:

• Решение математических задач 5-6 классы. Онлайн проверка ответов, 738.03kb.
• Программа элективный курс «Решение задач по физике», 159.48kb.
• Программа углубленного курса по физике «Решение сложных задач по физике» 11 класс, 108.16kb.
• Решение нестандартных задач по математике, 54.73kb.
• Сборник задач по логическому программированию для студентов специальности «030100 информатика», 786.39kb.
• Начало лекций по математике в 11-00, по физике в 12-45, продолжительность каждой лекции, 33.53kb.
• Факультативные занятия по физике «Решение творческих задач», 54.67kb.
• Театрализованное занятие по математике в подготовительной к школе группе "Путешествие, 36.91kb.
• Положение о районных турнирах по математике учащихся 5-7 классов и по физике учащихся, 15.76kb.
• Чеботарева Фаина Мэлсовна учитель математики высшей категории средней общеобразовательной, 155.8kb.

Решение задач по ТОЭ, ОТЦ, Высшей математике, Физике, Программированию...

Education Banner Network (Gold 468x60) - Образовательная Баннерная Сеть

Теория / Высшая математика / Лекция N 13. Свойства определителей. Обратная матрица.

Если квадратная матрица AT является транспонированной матрицей A, то их определители совпадают |AT | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка . Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа: При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например, Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка. . Для определителя третьего порядка проверьте самостоятельно. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, . Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0. Общий множитель строки или столбца можно выносить за знак определителя. Например, . Доказательство проводится проверкой, как и свойство 1. (Самостоятельно) Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой). Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например, . Доказательство - проверкой, аналогично свойству 1. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например, . Докажем это равенство, используя предыдущие свойства определителя. Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах. АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ Пусть имеем определитель третьего порядка: . Минором, соответствующим данному элементу aij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу aij будем обозначать Mij. Например, минором M12, соответствующим элементу a12, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца. Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a12, берётся со знаком “–”, т.е. можно записать, что . (1) Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков. Введём ещё одно понятие. Алгебраическим дополнениемэлемента aij определителя называется его минор Mij, умноженный на (–1)i+j. Алгебраическое дополнение элемента aij обозначается Aij. Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством Aij = (–1)i+jMij. Например, Пример. Дан определитель . Найти A13, A21, A32. Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде: . Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца. Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем: Разложим полученный определитель по элементам 1-ой строки. . (2) Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a21, a22, a23. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки. Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов. Таким образом, справедлива следующая теорема. Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения. Всё вышесказанное справедливо и для определителей любого более высокого порядка. Примеры. Вычислить определитель , раскладывая его по элементам 2-го столбца. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку: ОБРАТНАЯ МАТРИЦА Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел) Справедлива следующая теорема: Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Доказательство: Необходимость. Пусть для матрицы A существует обратная матрица A-1. Покажем, что |A| ≠ 0. Прежде всего заметим, что можно доказать следующее свойство определителей . Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0. Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть и |A| ≠ 0. Покажем, что в этом случае обратной матрицей будет матрица , где Aij алгебраическое дополнение элемента aij. Найдём AB=C. Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например, 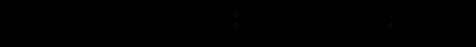Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c22 = c33 = 1. Кроме того, все недиагональные элементы матрицы C равны нулю. Например, Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A-1. Таким образом, теорема содержит способ нахождения обратной матрицы. Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом , где Aij - алгебраические дополнения элементов aij данной матрицы A. Итак, чтобы найти обратную матрицу нужно: Найти определитель матрицы A. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу , элементами которой являются числа Aij. Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет . Аналогично для матриц второго порядка, обратной будет следующая матрица . Примеры. Найти матрицу, обратную данной . Сделать проверку. |A| = 2. Найдем алгебраические дополнения элементов матрицы A. Проверка: . Аналогично A∙A-1 = E. Найти элементы и матрицы A-1 обратной данной . Вычислим |A| = 4. Тогда . . . Найдем обратную матрицу.