Конспект 2003 Комп’ютерні технології в інженерних та наукових завданнях. Для студентів спеціальностей 090220, 091601. Конспект /укл. Кондратов С. О. Рубіжне: рфсну, 2003 36 с

Вид материала

Конспект

Содержание 1 Тема хімічна інформація та її пошук 2 Тема комп’ютерні технології пошуку інформації 3 Тема хімічний графічний редактор chemwind 4 Тема хіміко-технологічні розрахунки 5 Тема первісна обробка даних в середовищі excel

Подобный материал:

• Конспект лекцій по дисципліні Інформаційні моделі "великих" систем, 1986.92kb.
• Комп‘ютерні інформаційні технології в електроенергетиці тексти лекцій для студентів, 1076.06kb.
• Робоча навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для, 204.08kb.
• Конспект лекцій 2004 Загальна теорія систем. Конспект лекцій Для студентів денної, 1136.85kb.
• Конспект лекцій з навчальної дисципліни "Комп’ютерні технології в юридичній дільності", 6139.48kb.
• Конспект лекцій з дисципліни «транспортне право» для студентів 1 курсу денної І заочної, 2079.66kb.
• Конспект лекцій для студентів спеціальностей 030508 І 030508 "Фінанси І кредит" денної, 4154.08kb.
• Опорний конспект лекцій з дисципліни „ правознавство (для студентів денної І заочної, 1124.35kb.
• Навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для студентів, 131.31kb.
• Н.І. Гордієнко Біржова І банківська справа Конспект, 3107.24kb.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ІМЕНІ ВОЛОДИМИРА ДАЛЯ

РУБІЖАНСЬКИЙ ФІЛІАЛ

ІНЖЕНЕРНО-ЕКОНОМІЧНИЙ ФАКУЛЬТЕТ

КАФЕДРА ВИЩОЇ МАТЕМАТИКИ І КОМП’ЮТЕРНИХ ТЕХНОЛОГІЙ

КОМПЮТЕРНІ ТЕХНОЛОГІЇ В

ІНЖЕНЕРНИХ ТА НАУКОВИХ

ЗАВДАННЯХ


КОНСПЕКТ


2003

Комп’ютерні технології в інженерних та наукових завданнях. Для студентів спеціальностей 8.090220, 8.091601 .Конспект /укл. Кондратов С.О. – Рубіжне: РФСНУ, 2003 – 36 с.

В конспекті містяться лекційні матеріали спеціального курсу "Комп’ютерні технології в інженерних та наукових завданнях” для студентів 5-го курсу РФ СНУ, що навчаються у магістратурі.


Схвалено на засіданні кафедри ВМКТ

Протокол № “...5....” від “..15..”.....12.. 2003 р.

Зав. кафедри д.х.н., доцент Кондратов С.О.


1 ТЕМА ХІМІЧНА ІНФОРМАЦІЯ ТА ЇЇ ПОШУК


1.1 Особливості хімічної інформації та її джерела

1.1.1 Хімічні науки як дисципліни, що динамічно розвиваються. Тенденція – постійне зростання обсягу інформації. Деякі інформаційні задачі, що доводиться вирішувати:

1. Пошук інформації про хімічні речовини:
   

а) Чи відома ця речовина раніше (пошук по назві та будові)?

б) Властивості речовини (температури кипіння, плавлення, спектральні властивості, токсичність, т.і.)

в) Методи синтезу речовини

г) Хімічні властивості речовини (в яких реакціях бере участь)

д) Галузі практичного застосування речовина

2. Пошук інформації про хімічні реакції:
   

а) Коло речовин (типів речовин), що бере участь у реакції

б) Умови перебігу реакції, розчинники, каталізатори, т.і.

г) Кінетичні закономірності, механізм реакції, зв’язок будови реагентів з реакційною здатністю

3. Пошук інформації про технологічні процеси, апарати:
   

а) Особливості конструкції апаратів

б) Математичний опис процесів

в) Математичні моделі керування процесами

г) Режими роботи обладнання (тепловий, гідродинамічний)

д) Галузі застосування процесів та апаратів

1.1.2 Традиційні джерела хімічної інформації:

• книги (підручники, монографії, дисертації, енциклопедії, словники)
  
• наукові та науково-технічні журнали
  
• реферативні журнали
  
• патенти
  
• стандарти
  
• звіти про наукову роботу
  
• рекламні та комерційні матеріали
  

1.2 Характеристика книжкової інформації


1.2.1 Монографія – достатньо велика за обсягом узагальнююча робота, що містить останні (на момент написання) досягнення у даної області. Приклади монографій. Відмінність монографій від підручників.

1.2.2 Дисертації та їх роль як джерел інформації. Види дисертацій. Структура дисертації по хімії і хімічної технології.

1.2.3 Енциклопедії як концентровані сховища інформації. Велика Радянська енциклопедія. Британська енциклопедія. Галузеві енциклопедії: Хімічна енциклопедія. Енциклопедія полімерів. Технічна енциклопедія

1.2.4 Інтернет-енциклопедії. Енциклопедія Кирила та Мефодія (km.ru), енциклопедія “Рубікон”. Електронна версія Великої радянської енциклопедії. Енциклопедичний словник Брокгауза і Ефрона.

1.2.5 Словники та довідники з дисциплін. Довідник хіміка. “Довідник інженера-хіміка” Перрі. Довідник Бейльштейна. Хімічний словник Хайльборна та Бенбері


1.3 Наукові статті як найважливіше джерело наукової інформації


1.3.1 Різновиди наукових статей: оперативна та оглядова.

1.3.1 Оглядові статті як джерело оперативних узагальнень у галузях науки і техніки. Найважливіші журнали з оглядовими статтями: “Успехи химии”, “Chemical Reviews”, Quarterly Reviews”. Оглядові статті у колективних монографіях. Серії “Успехи науки и техники”, “Органические реакции”, “Реакции и методі исследований органических соединений”.

1.3.2 Оперативні статті. Вони стосуються поточних результатів досліджень (теоретичних, експериментальних), методики проведення досліджень, т.і. Оперативні статті – основне джерело наукової інформації. Основні вітчизняні та світові журнали в галузі хімії і хімічної технології. Особливості наукових публікацій.

1.3.3 Наукові труди конференцій, відомчі науково-технічні збірники. Їх роль і місце у системі науково-технічної інформації.


1.4 Стандарти, їх роль і місце у системі науково-технічної інформації


1.4.1 Класифікація стандартів.

1.4.2 Інформація, яку можна одержати зі стандартів

1.4.3 Зарубіжні стандарти


1.5 Патентна інформація

1.5.1 Патенти як специфічна форма науково-технічної інформації. Основи патентного права. Поняття “Винахід”, “Винахідник”, “Володар патенту”. Головні принципи патентування

1.5.2 Структурні елементи патенту. Формула винаходу. Описання прототипів та їх аналіз.

1.5.3 Міжнародна патентна класифікація. Значення патентів як джерела інформації


1.6 Реферативні журнали


1.6.1 Призначення реферативних журналів

1.6.2 Найважливіші реферативні журнали: Chemical Abstracts, Реферативный журнал Химия.

1.6.3 Пошук інформації у реферативних журналах. Типи покажчиків: формульний, предметний, патентний, авторський.

1.6.4 Структура випуску реферативного журналу. Структура реферату.


1.7 Звіти про наукову роботу

1.7.1 Призначення звітів про наукову роботу. Нормативні документи, що регулюють склад і форму звітів.

1.7.2 Структура звіту про наукову роботу. Принципи укладання окремих розділів

1.7.2 Правила оформлення звітів. Оформлення переліку бібліографічних посилань.


2 ТЕМА КОМП’ЮТЕРНІ ТЕХНОЛОГІЇ ПОШУКУ ІНФОРМАЦІЇ


2.1 Техніка роботи в Інтернеті


2.1.1 Особливості сучасного Інтернету. Базові поняття: сайт, Web, протокол, ІР адрес, плагин, гіперпосилання.

2.1.2 Програма Internet Explorer. Меню, панелі інструментів. Операції, що можна проводити за допомогою меню та панелі інструментів.

2.1.2 Основні правила роботи. Увід адресу, огляд веб-сторінки, гіперпосилань. Прийоми копіювання інформації з сайту. Допоміжні програми: Flashget, ReGet, їх призначення. Програма Acrobat Reader.


2.2 Пошук інформації в Інтернеті


2.2.1 Пошукові сервери. Принципи пошуку.

2.2.2 Найважливіші пошукові сервери: Meta-Ukrraine.com, Yandex.ru, Google.com

2.2.2 Основи мови замовлень. Прості та складні замовлення. Категорії.

2.2.3 Стратегія пошуку: поступове нарощування ознак, використання синонімів. Опосередкований пошук на спеціалізованих сайтах (порталах).


2.3 Головні хімічні сервери


2.3.1 Міжнародний хімічний сервер ссылка скрыта .Порядок реєстрації на сервері.

2.3.1.1Огляд інформації, що міститься на сервері:

• “горяча” наукова інформація ї новини науки і техніки
  
• виставка журналів
  
• сервер препринтів
  
• Аlchemist
  

2.3.1.2 Бази даних на сайті. База даних Бейльштейна. Пошук рефератів статей. Правила формування запитів.

2.3.1.3 База даних американських патентів з хімії та хімічної технології на сайті ссылка скрыта. Формування запиту. Склад реферату патенту.

2.3.1.4 База даних з хімічних реакцій і правила користування

2.3.1.5 Лінки на сервері

2.3.2 Російський хімічний сервер ссылка скрыта. Огляд інформації на сервері:

• лінки відкритих журналів(Вісник МДУ, вісники декількох російських університетів, Російський хімічний журнал)
  
• електронні навчальні посібники з хімії,
  
• демонстраційні матеріали
  
• бази даних, лінки російських та зарубіжних баз даних.
  

2.4 Пошук журнальних статей та їх рефератів

2.4.1 Електронні хімічні журнали. Журнал “Компютерная химия. Бутлеровские сообщения”.

2.4.2 Соросівський освітній журнал

2.4.2 Російське видавництво “Наука”. Сайт ссылка скрыта. Огляд рефератів статей.

2.4.3 Міжнародне видавництво “John Wiley and sons”. Пошук на сайті rscience.wiley.com/search/allsearch . Порядок знаходження реферату:

• вибір категорії пошуку (Advanced search)
  
• формулювання запиту за допомогою віконців програми
  
• огляд назв статей, вибір реферату для огляду
  
• огляд і обробка реферату
  
• спроба одержати статтю (за гроши, або за допомогою E mail).
  

2.5 Пошук патентної інформації в Інтернеті


2.5.1 Сайт російського федерального інституту промислової власності ссылка скрыта. Реєстрація під логіном та паролем “guest”. Формулювання запиту. Пошук реферату патенту. Обмеження по терміну пошуку (тільки після 2003 р.)

2.5.2 Сайт патентного відомства США ссылка скрыта Особливості патентної бази даних (1790-1976 – скани, з 1976 – повні тексти). Пошук (ссылка скрыта). Категорії пошуку: Quick search, Advanced search. Правила складання запитань для Quick search: користування віконцями. Мова складання запитань для Advanced search. Особливості подальшої роботи: вибір матеріалів за назвою та їх огляд.


2.6 Пошук навчальних матеріалів та авторефератів дисертацій


2.6.1 Огляд сайтів провідних ВНЗ України, Росії, СНД.

2.6.2 Виконистання пошукових систем для пошуку навчальних матеріалів

2.6.3 Сайт Національної бібліотеки України ім. Вернадського ссылка скрыта. Доступ до авторефератів кандидатських і докторських дисертацій та інших електронних видань. Пошук дисертацій за назвою, фамілією, дисципліною.


3 ТЕМА ХІМІЧНИЙ ГРАФІЧНИЙ РЕДАКТОР CHEMWIND

3.1 Призначення редактору ChemWind. Створення хімічних формул.


3.1.1 Рисування ароматичних і гетероциклічних кілець, замісників, подвійних та потрійних зв’язків

3.1.2 “Склеювання” складних хімічних формул з простих. Використання панелі інструментів

3.1.3 Виготовлення надписів, укладання хімічних рівнянь за допомогою панелі інструментів і панелі взірців. Обмін з іншими додатками Windows


4 ТЕМА ХІМІКО-ТЕХНОЛОГІЧНІ РОЗРАХУНКИ

В СЕРЕДОВИЩІ EXCEL


4.1 Загальні відомості про табличний процесор Excel


4.1.1 Призначення, об’єкти, можливості

4.1.2 Структура робочого листа

4.1.3 Панелі інструментів

4.1.4 Принципи побудови формули комірки

4.1.5 Побудова таблиць. Виконання розрахунків у таблицях.

4.1.6 Майстер функцій, його використання для виконання розрахунків складних функцій.

4.1.7 Майстер діаграм. Побудова графіків


4.2 Методи лінійної алгебри, їх застосування Матриці і дії з ними


4.2.1. Мова сучасної науки і техніки – мова матриць Базові операції: транспонування, складання матриць, множення матриці на число, множення матриць. Вимоги до матриць, що множаться.

4.2.2 Квадратні матриці. Одинична матриця. Визначник матриці. Зворотна матриця. Умови існування зворотної матриці.

4.2..3 Вектори. Лінійна залежність векторів. Умови та наслідки рівності 0 визначника квадратної матриці.

4.2..4 Матричні функції Excel: ТРАНСП(), МОБР(), МУМНОЖ(), МОПРЕД(). Особливості уводу: виділення області, увід за допомогою комбінації клавіш + + .

4.2..5 Розв’язання системи лінійних алгебраїчних рівнянь за допомогою матричних операцій


4.3 Розрахунок складу нітросуміші


4.3.1 Постановка задачі, початкові дані.

4.3.2 Укладання рівнянь матеріального балансу, встановлення їх лінійної незалежності

4.3.3 Розв’язання задачі в середовищі Excel/


4.4 Розрахунки матеріальних балансів складних процесів


4.4.1 Типи складних процесів. Байпасування і реціклінг

4.4.2 Принципи складання рівнянь моделі балансу:

а) Закон зберігання матерії

б) Виконання співвідношення між компонентами

в) Замкненість та лінійна незалежність системи рівнянь

4.4.3 Розв’язання задачі укладання балансу в середовищі Ехсеl: запис системи рівнянь матеріального балансу та їх рішення.

4.4.4 Стандартна форма таблиці матеріального балансу. Створення таблиці та розрахунків в Еxcel.


4.5 Рішення нелінійних рівнянь. Побудова рівноважної лінії суміші

двох речовин


4.5.1 Поняття о методах рішення нелінійних рівнянь, збіжності

4.5.2 Програма “Підбор параметра” для рішення нелінійних рівнянь. Правила використання. Організація комірок на робочому листі. Одержання результатів

4.5.3 Постановка задачі про розрахунок рівноважної лінії для суміши. Припущення. Фізичні явища.

4.5.4 Використання закону Рауля та ідеально-газового наближення для одержання моделі

4.5.5 Рівняння Антуана для опису залежності тиску парів від температури. Розрахунки параметрів рівняння з експериментальних даних. Організація робочого листа для розрахунків

4.5.6 Розрахунок складу газової фази суміші виходячи з рівняння Антуана. Організація робочого листа. Побудова таблиці результатів за допомогою опції “Специальная вставка”.


4.6 Розвязання систем нелінійних рівнянь. Розрахунки складних

рівноваг


4.6.1 Поняття про метод найменших квадратів. Задача розв’язання систем рівнянь як задача мінімізації суми квадратів відхилень

4.6.2 Програма “Поиск решения” для знаходження максимальних та мінімальних значень. Структура робочого вікна програми, організація даних для уводу-виводу

4.6.3 Організація даних для рішення систем нелінійних рівнянь. Обов’язкові складові таблиць даних: початкові наближення аргументів, значення вектор-функція рівнянь, її відхилення від 0, квадрат відхилення, підсумкова сума квадратів

4.6.4 Розрахунок складу рівноважної суміші, що містить декілька рівноваг. Побудова моделі у вигляді системи рівнянь балансу та рівноваг. Перехід до логарифмів величин.

4.6.5 Побудова таблиць робочого листа. Організація даних. Оформлення результатів розрахунків.


4.7 Макроси. Задача чисельного інтегрування


4.7.1 Поняття макросу. Технологія “Програмування без програмування”.

4.7.2 Роль алгоритмізації при укладанні макросів. Викликання програми будови макросів, робота з нею. Запис макросу. Виклик макросу на виконання.

4.7.3 Автоматизація виклику макросу. Панель “Форми”. Розміщення кнопки на робочому листі і призначення неї макросу.

4.7.4 Задача чисельного інтегрування. Метод Симпсона: алгоритм і розрахункові формули. Організація вхідних даних. Організація таблиці розрахунків. Запис макросу. Організація управлінням макросом

4.7.5 Розрахунок кількості одиниць переносу. Розрахункові формули. Організація робочого листа, створення макросу.

4.8 Робота з базами даних в Excel


4.8.1 Зміст поняття “База даних “ Реляційна база даних.

4.8.2 Проектування бази даних. Ключові поля

4.8.3 Особливості організації баз даних в Excel. Заповнення за допомогою Майстра форм

4.8.3 Впорядкування бали даних за ознаками. Принципи впорядкування. Програма впорядкування за зростанням та зменшенням

4.8.4 Пошук інформації у базі даних. Авто фільтр. Фільтрування даних за ознаками

4.8.5 Робота з базами даних “Фізико-хімічні властивості”, “Температури кипіння органічних речовин” у локальній мережі РФ СНУ


5 ТЕМА ПЕРВІСНА ОБРОБКА ДАНИХ В СЕРЕДОВИЩІ EXCEL


5.1 Основні поняття статистики

5.1.1Що таке перемінні? Перемінні - це те, що можна вимірювати, чи контролювати що можна змінювати в дослідженнях. Перемінні відрізняються багатьма аспектами, особливо тією роллю, що вони грають у дослідженнях, шкалою виміру і т.д.

5.1.2 Дослідження залежностей у порівнянні з експериментальними дослідженнями. Більшість емпіричних досліджень даних можна віднести до одному з названих типів. У дослідженні кореляцій (залежностей, зв'язків...) ви не впливаєте (чи, принаймні, намагаєтеся не впливати) на перемінні, а тільки вимірюєте їх і хочете знайти залежності (кореляції) між деякими обмірюваними перемінними, наприклад, між кров'яним тиском і рівнем холестерину. В експериментальних дослідженнях, навпроти, ви варіюєте деякі перемінні і вимірюєте впливи цих змін на інші перемінні. Наприклад, дослідник може штучно збільшувати кров'яний тиск, а потім на визначених рівнях тиску вимірити рівень холестерину. Аналіз даних в експериментальному дослідженні також приходить до обчислення "кореляцій" (залежностей) між перемінними, а саме, між перемінними, на які, і перемінними, на які впливає цей вплив. Проте, експериментальні дані потенційно постачають нас більш якісною інформацією. Тільки експериментально можна переконливо довести причинний зв'язок між перемінними. Наприклад, якщо виявлено, що всякий раз, коли змінюється перемінна A, змінюється і перемінна B, те можна зробити висновок - "перемінна A впливає на перемінну B", тобто між перемінними А и В мається причинна залежність. Результати кореляційного дослідження можуть бути проінтерпретовані в каузальних (причинних) термінах на основі деякої теорії, але самі по собі не можуть чітко довести причинність.

5.1.3 Залежні і незалежні перемінні. Незалежними перемінними називаються перемінні, котрі варіюються дослідником, тоді як залежні перемінні - це перемінні, котрі чи виміряються реєструються. Терміни залежна і незалежна перемінна застосовуються в основному в експериментальному дослідженні, де експериментатор маніпулює деякими перемінними, і в цьому змісті вони "незалежні" від реакцій, властивостей, намірів і т.д. властивим об'єктам дослідження. Деякі інші перемінні, як передбачається, повинні "залежати" від дій чи експериментатора від експериментальних умов. Іншими словами, залежність виявляється у відповідній реакції досліджуваного об'єкта на послане на нього вплив. Почасти в протиріччі з даним розмежуванням понять знаходиться використання їх у дослідженнях, де ви не варіюєте незалежні перемінні, а тільки приписуєте об'єкти до "експериментальних груп", ґрунтуючись на деяких їхніх апріорних властивостях. Наприклад, якщо в експерименті чоловіка порівнюються з жінками щодо числа лейкоцитів (WCC), що містяться в крові, то Стать можна назвати незалежної перемінний, а WCC залежної перемінний.

5.1.5 Шкали вимірів. Перемінні розрізняються також тим "наскільки добре" вони можуть бути обмірювані чи, іншими словами, як багато вимірюваної інформації забезпечує шкала їхніх вимірів. Очевидно, у кожнім вимірі присутнє деяка помилка, що визначає границі "кількості інформації", яких можна одержати в даному вимірі. Іншим фактором, що визначає кількість інформації, що міститься в перемінної, є тип шкали, у якій проведене вимір. Розрізняють наступні типи шкал:

• номінальна,
  
• порядкова (ординальная),
  
• інтервальна,
  
• відносна (шкала відносини).
  

Відповідно, маємо чотири типи перемінних: (a) номінальна, (b) порядкова (ординальная), (c) интервальная і (d) відносна.

5.1.6 Характеристика типів перемінних.

а) Номінальні перемінні використовуються тільки для якісної класифікації. Це означає, що дані перемінні можуть бути обмірювані тільки в термінах приналежності до деяким, істотно різним класам; при цьому ви не зможете визначити чи кількість упорядкувати ці класи. Наприклад, ви зможете сказати, що 2 індивідуума помітні в термінах перемінної А (наприклад, індивідууми належать до різних національностей). Типові приклади номінальних перемінних - піл, національність, колір, місто і т.д. Часто номінальні перемінні називають категоріальними.

б) Порядкові перемінні дозволяють ранжирувати (упорядкувати) об'єкти, указавши які з них у більшому чи меншому ступені мають якість, вираженим даної перемінний. Однак вони не дозволяють сказати "на скількох більше" чи "на скількох менше". Порядкові перемінні іноді також називають ординальными. Типовий приклад порядкової перемінний - социоэкономический статус родини. Ми розуміємо, що верхній середній рівень вище за середнє рівня, однак сказати, що різниця між ними дорівнює, скажемо, 18% ми не зможемо. Саме розташування шкал у наступному порядку: номінальна, порядкова, интервальная являє гарний приклад порядкової шкали.

в). Інтервальні перемінні дозволяють не тільки упорядковувати об'єкти виміру, але і чисельно виразити і порівняти розходження між ними. Наприклад, температура, обмірювана в градусах чи Фаренгейту чи Цельсію, утворить інтервальну шкалу. Ви можете не тільки сказати, що температура 40 градусів вище, ніж температура 30 градусів, але і що збільшення температури з 20 до 40 градусів удвічі більше збільшення температури від 30 до 40 градусів.

г) Відносні перемінні дуже схожі на інтервалі перемінні. На додаток до усіх властивостей перемінних, обмірюваних у інтервальній шкалі, їхньою характерною рисою є наявність визначеної точки абсолютного нуля, таким чином, для цих перемінних є обґрунтованими пропозиції типу: x у два рази більше, ніж y. Типовими прикладами шкал відносин є виміри чи часу простору. Наприклад, температура по Кельвіні утворить шкалу відносини, і ви можете не тільки затверджувати, що температура 200 градусів вище, ніж 100 градусів, але і що вона удвічі вище. Інтервальні шкали (наприклад, шкала Цельсію) не мають дану властивість шкали відносини. Помітимо, що в більшості статистичних процедур не робиться розходження між властивостями інтервальних шкал і шкал відносини.

5.1.7 Зв'язку між перемінними. Незалежно від типу, дві чи більш перемінних зв'язані (залежні) між собою, якщо значення цих перемінних, що спостерігаються, розподілені погодженим образом. Іншими словами, ми говоримо, що перемінні залежно, якщо їхнього значення систематичним образом погоджені один з одним у наявних у нас спостереженнях. Наприклад, перемінні Стать і WCC (число лейкоцитів) могли б розглядатися як залежні, якби більшість чоловіків мало високий рівень WCC, а більшість жінок - низький WCC, чи навпаки. Ріст зв'язаний з Вагою, тому що звичайно високі індивіди важче низьких; IQ (коефіцієнт інтелекту) зв'язаний з Кількістю помилок у тесті, тому що люди високим значенням IQ роблять менше помилок і т.д.

5.1.8 Чому залежності між перемінними є важливими. Узагалі говорячи, кінцева мета всякого чи дослідження наукового аналізу складається в перебування зв'язків (залежностей) між перемінними. Філософія науки учить, що не існує іншого способу представлення знання, крім як у термінах залежностей між чи кількостями якостями, вираженими якими-небудь перемінними. Таким чином, розвиток науки завжди полягає в перебуванні нових зв'язків між перемінними. Дослідження кореляцій власне кажучи складається у вимірі таких залежностей безпосереднім образом. Проте, експериментальне дослідження не є в цьому змісті чимось відмінним. Наприклад, відзначене вище експериментальне порівняння WCC у чоловіків і жінок може бути описане як пошук зв'язку між перемінними: Стать і WCC. Призначення статистики полягає в тому, щоб допомогти об'єктивно оцінити залежності між перемінними.


5.2 Величина, надійність, значимість


5.2.1 Дві основні риси всякої залежності між перемінними. Можна відзначити дві найпростіші властивості залежності між перемінними: (a) величина залежності і (b) надійність залежності.

5.2.2 Величина. Величину залежності легше зрозуміти і вимірити, чим надійність. Наприклад, якщо будь-який чоловік у вашій вибірці мав значення WCC вище чим будь-яка жінка, то ви можете сказати, що залежність між двома перемінними (Стать і WCC) дуже висока. Іншими словами, ви могли б пророчити значення однієї перемінної за значеннями іншої.

5.2.3 Надійність ("істинність"). Надійність взаємозалежності - менш наочне поняття, чим величина залежності, однак надзвичайно важливе. Надійність залежності безпосередньо зв'язана з репрезентативністю визначеної вибірки, на основі якої будуються висновки. Іншими словами, надійність говорить нам про тім, наскільки імовірно, що залежність, подібна знайдений вами, буде знову виявлена (іншими словами, підтвердиться) на даних іншої вибірки, витягнутої з тієї ж самої популяції. Варто пам'ятати, що кінцевою метою майже ніколи не є вивчення даної конкретної вибірки; вибірка становить інтерес лише остільки, оскільки вона подає інформацію про всю популяцію. Якщо ваше дослідження задовольняє деяким спеціальним критеріям (про це буде сказано пізніше), то надійність знайдених залежностей між перемінними вашої вибірки можна кількісно оцінити і представити за допомогою стандартної статистичної міри (називаної чи p-рівень статистичний рівень значимості, докладніше див. у наступному розділі).

5.2.4 Що таке статистична значимість (p-рівень)? Статистична значимість результату являє собою оцінену міру впевненості в його "істинності" (у змісті "репрезентативності вибірки"). Виражаючи більш технічно, p-рівень - це показник, що знаходиться в убутній залежності від надійності результату. Більш високий p- рівень відповідає більш низькому рівню довіри до знайденого у вибірці залежності між перемінними. Саме, p-рівень являє собою імовірність помилки, зв'язаної з поширенням результату, що спостерігається, на всю популяцію. Наприклад, p- рівень = .05 (тобто 1/20) показує, що мається 5% імовірність, що знайдена у вибірці зв'язок між перемінними є лише випадковою особливістю даної вибірки. Іншими словами, якщо дана залежність у популяції відсутня, а ви багаторазово проводили б подібні експерименти, те приблизно в одному з двадцяти повторень експерименту можна було б очікувати такий же чи більш сильної залежності між перемінними. (Відзначимо, що цю не ту ж саме, що затверджувати про відому наявність залежності між перемінними, котра в середньому може бути відтворена в 5% чи 95% випадків; коли між перемінними популяції існує залежність, імовірність повторення результатів дослідження, що показують наявність цієї залежності називається статистичною потужністю плану. Докладніше про це див. у розділі ссылка скрыта). У багатьох дослідженнях p-рівень 0.05 розглядається як "прийнятна границя" рівня помилки.

5.2.5 Як визначити, чи є результат дійсно значимим. Не існує ніякого способу уникнути сваволі при ухваленні рішення про те, який рівень значимості варто дійсно вважати "значимим". Вибір визначеного рівня значимості, вище якого результати відкидаються як помилкові, є досить довільним. На практиці остаточне рішення звичайне залежить від того, чи був результат передвіщений апріорі (тобто до проведення досвіду) чи виявлений апостериорно в результаті багатьох аналізів і порівнянь, виконаних з безліччю даних, а також на традиції, що мається в даній області досліджень. Звичайно в багатьох областях результат p 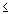0.05 є прийнятною границею статистичної значимості, однак варто пам'ятати, що цей рівень усе ще включає досить велику імовірність помилки (5%). Результати, значимі на рівні p  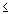0.01 звичайно розглядаються як статистично значимі, а результати з рівнем p  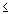0.005 чи p 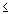0.001 як високо значимі. Однак варто розуміти, що дана класифікація рівнів значимості досить довільна і є усього лише неформальною угодою, прийнятим на основі практичного досвіду в тій чи іншій області дослідження.

5.2.6 Статистична значимість і кількість виконаних аналізів. Зрозуміло, що чим більше число аналізів ви проведете із сукупністю зібраних даних, тим більше число значимих (на обраному рівні) результатів буде виявлено чисто випадково. Наприклад, якщо ви обчислюєте кореляції між 10 перемінними (маєте 45 різних коефіцієнтів кореляції), те можна екати, що приблизно два коефіцієнти кореляції (один на кожні 20) чисто випадково виявляться значимими на рівні p 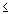 0.05, навіть якщо перемінні зовсім випадкові і некорельовані в популяції. Деякі статистичні методи, що включають багато порівнянь, і, таким чином, що мають гарний шанс повторити такого роду помилки, роблять спеціальне чи коректування виправлення на загальне число порівнянь. Проте, багато статистичних методів (особливо прості методи розвідницького аналізу даних) не пропонують якого-небудь способу рішення даної проблеми. Тому дослідник повинний з обережністю оцінювати надійність несподіваних результатів.

Величина залежності між перемінними в порівнянні з надійністю залежності. Як було вже сказане, величина залежності і надійність представляють дві різні характеристики залежностей між перемінними. Проте, не можна сказати, що вони зовсім незалежні. Говорячи загальною мовою, чим більше величина залежності (зв'язку) між перемінними у вибірці звичайного обсягу, тим більше вона надійна (див. наступний розділ).

5.2.7 Чому більш сильні залежності між перемінними є більш значимими. Якщо припускати відсутність залежності між відповідними перемінними в популяції, то найбільше ймовірно очікувати, що в досліджуваній вибірці зв'язок між цими перемінними також буде відсутній. Таким чином, чим більш сильна залежність виявлена у вибірці, тим менш імовірно, що цієї залежності немає в популяції, з якої вона витягнута. Як ви бачите, величина залежності і значимість тісно зв'язані між собою, і можна було б спробувати вивести значимість з величини залежності і навпаки. Однак зазначений зв'язок між залежністю і значимістю має місце тільки при фіксованому обсязі вибірки, оскільки при різних обсягах вибірки та сама залежність може виявитися як високо значимої, так і незначущої зовсім (див. наступний розділ)

5.2.8 Чому обсяг вибірки впливає на значимість залежності. Якщо спостережень мало, то відповідно мається мало можливих комбінацій значень цих перемінних і таким чином, імовірність випадкового виявлення комбінації значень, що показують сильну залежність, відносно велика. Розглянемо наступний приклад. Якщо ви досліджуєте залежність двох перемінних (Стать: чоловік/жінка і WCC: високий/низький) і маєте тільки 4 суб'єкта у вибірці (2 чоловіка і 2 жінки), то імовірність того, що чисто випадково ви знайдете 100% залежність між двома перемінними дорівнює 1/8. Більш точно, імовірність того, що обоє чоловіка мають високий WCC, а обидві жінки - низький WCC, чи навпаки, - дорівнює 1/8. Тепер розглянемо імовірність подібного збігу для 100 суб'єктів; легко бачити, що ця імовірність дорівнює практично нулю. Розглянемо більш загальний приклад. Представимо популяцію, у якій середнє значення WCC чоловіків і жінок одне і теж. Якщо ви будете повторювати експеримент, що складається у витягу пари випадкових вибірок (одна вибірка - чоловіка, інша вибірка - жінки), а потім обчислите різниці вибіркових середніх WCC для кожної пари вибірок, то в більшості експериментів результат буде близький до 0. Однак час від часу, будуть зустрічатися пари вибірок, у яких розходження між середньою кількістю лейкоцитів у чоловіків і жінок буде істотно відрізнятися від 0. Як часто це буде відбуватися? Очевидно, чим менше обсяг вибірки в кожнім експерименті, тим більше ймовірна поява таких помилкових результатів, що показують існування залежності між підлогою і WCC у даних, отриманих з популяції, де така залежність насправді відсутня.

Приклад: "відношення числа новонароджених хлопчиків до числа новонароджених дівчинок" Розглянемо наступний приклад. Маються 2 лікарні. Припустимо, що в першій з них щодня народжується 120 дітей, у другий тільки 12. У середньому відношення числа хлопчиків, що народжуються в кожній лікарні, до числа дівчинок 50/50. Один раз дівчинок народилося вдвічі більше, ніж хлопчиків. Запитується, для якої лікарні дана подія більш ймовірна? Відповідь очевидна для статистика, однак, він не настільки очевидний недосвідченому. Звичайно, така подія набагато більш ймовірна для маленької лікарні. Пояснення цього факту полягає в тому, що імовірність випадкового відхилення (від середнього) зростає зі зменшенням обсягу вибірки.

5.2.9 Чому слабкі зв'язки можуть бути значимі доведені тільки на великих вибірках. Приклад з попереднього розділу показує, що якщо зв'язок між перемінними "об'єктивно" слабка (тобто властивості вибірки близькі до властивостей популяції), те не існує іншого способу перевірити таку залежність крім як досліджувати вибірку досить великого обсягу. Навіть якщо вибірка, що знаходиться у вашому розпорядженні, зовсім репрезентативна, ефект не буде статистично значимим, якщо вибірка мала. Аналогічно, якщо залежність "об'єктивно" (у популяції) дуже сильна, тоді вона може бути виявлена з високим ступенем значимості навіть на дуже маленькій вибірці. Розглянемо приклад. Представте, що ви кидаєте монету. Якщо монета злегка несиметрична, і при підкиданні орел випадає частіше решки (наприклад, у 60% підкидань випадає орел, а в 40% решка), то 10 підкидань монети було б не досить, щоб переконати кого б те ні було, що монета асиметрична, навіть якщо був би отриманий, здавалося, зовсім репрезентативний результат: 6 орлів і 4 решки. Чи не випливає звідси, що 10 підкидань узагалі не можуть довести що-небудь? Ні, не випливає, тому що якщо ефект, у принципі, дуже сильний, те 10 підкидань може виявитися цілком достатньо для його доказу. Представте, що монета настільки несиметрична, що всякий раз, коли ви її кидаєте, випадає орел. Якщо ви кидаєте таку монету 10 разів, і всякий раз випадає орел, більшість людей рахують це переконливим доказом того, що з монетою щось не то. Іншими словами, це послужило б переконливим доказом того, що в популяції, що складається з нескінченного числа підкидань цієї монети орел буде зустрічатися частіше, ніж решка. У підсумку цих міркувань ми дійдемо висновку: якщо залежність сильна, вона може бути виявлена з високим рівнем значимості навіть на малій вибірці.

5.2.10 Чи можна відсутність зв'язків розглядати як значимий результат? Ніж слабкіше залежність між перемінними, тим більшого обсягу потрібно вибірка, щоб значимо її знайти. Представте, як багато кидків монети необхідно зробити, щоб довести, що відхилення від рівної імовірності випадання орла і решки складає тільки .000001%! Необхідний мінімальний розмір вибірки зростає, коли ступінь ефекту, якім потрібно довести, убуває. Коли ефект близький до 0, необхідний обсяг вибірки для його виразного доказу наближається до нескінченності. Іншими словами, якщо залежність між перемінними майже відсутня, обсяг вибірки, необхідний для значимого виявлення залежності, майже дорівнює обсягу всієї популяції, що передбачається нескінченним. Статистична значимість представляє імовірність того, що подібний результат був би отриманий при перевірці всієї популяції в цілому. Таким чином, усе, що отримано після тестування всієї популяції було б, по визначенню, значимим на найвищому, можливому рівні і це відноситься до всіх результатів типу "немає залежності".

5.2.11 Як вимірити величину залежності між перемінними. Статистиками розроблено багато різних мір взаємозв'язку між перемінними. Вибір визначеної міри в конкретному дослідженні залежить від числа перемінних, використовуваних шкал виміру, природи залежностей і т.д. Більшість цих мір, проте, підкоряються загальному принципу: вони намагаються оцінити залежність, що спостерігається, порівнюючи її з "максимальною мислимою залежністю" між розглянутими перемінними. Говорячи технічно, звичайний спосіб виконати такі оцінки полягає в тім, щоб подивитися як варіюються значення перемінних і потім підрахувати, яку частину всієї наявної варіації можна пояснити наявністю "загальної" ("спільної") варіації двох (чи більш) перемінних. Говорячи менш технічною мовою, ви порівнюєте те "що є загального в цих перемінних", з тим "що потенційно було б у них загального, якби перемінні були абсолютно залежні". Розглянемо простий приклад. Нехай у вашій вибірці, середній показник (число лейкоцитів) WCC дорівнює 100 для чоловіків і 102 для жінок. Отже, ви могли б сказати, що відхилення кожного індивідуального значення від загального середніх (101) містить компоненту зв'язану з підлогою суб'єкта і середня величина її дорівнює 1. Це значення, таким чином, представляє деяку міру зв'язку між перемінними Стать і WCC. Звичайно, це дуже бідна міра залежності, тому що вона не дає ніякої інформації про тім, наскільки велика цей зв'язок, скажемо щодо загальної зміни значень WCC. Розглянемо крайні можливості:

1. Якщо всі значення WCC у чоловіків були б точно рівні 100, а в жінок 102, то усі відхилення значень від загального середніх у вибірці цілком порозумівалися б підлогою індивідуума. Тому ви могли б сказати, що Стать абсолютно коррелирован (зв'язана) з WCC, іншими словами, 100% розходжень, що спостерігаються, між суб'єктами в значеннях WCC порозуміваються підлогою суб'єктів.
   
2. Якщо ж значення WCC лежать у межах 0-1000, то та ж різниця (2) між середніми значеннями WCC чоловіків і жінок, виявлена в експерименті, складала б настільки малу частку загальної варіації, що отримане розходження (2) вважалося б пренебрежимо малим. Розгляд ще одного суб'єкта могло б змінити чи різниця навіть змінити її знак. Тому всяка гарна міра залежності повинна брати до уваги повну мінливість індивідуальних значень у вибірці й оцінювати залежність по тому, наскільки ця мінливість порозумівається досліджуваною залежністю.
   

5.3 Статистичні критерії


5.3.1 Загальна конструкція більшості статистичних критеріїв. Тому що кінцева мета більшості статистичних критеріїв (тестів) складається в оцінюванні залежності між перемінними, більшість статистичних тестів додержуються загального принципу, поясненому в попередньому розділі. Говорячи технічною мовою, ці тести являють собою відношення мінливості, загальної для розглянутих перемінних, до повної мінливості. Наприклад, такий тест може являти собою відношення тієї частини мінливості WCC, що визначається підлогою, до повної мінливості WCC (обчисленої для об'єднаної вибірки чоловіків і жінок). Це відношення звичайне називається відношенням поясненої варіації до повної варіації. У статистику термін пояснена варіація не обов'язково означає, що ви даєте їй "теоретичне пояснення". Він використовується тільки для позначення загальної варіації розглянутих перемінних, іншими словами, для вказівки на те, що частина варіації однієї перемінної "порозумівається" визначеними значеннями інший перемінної і навпаки.

5.3.2 Як обчислюється рівень статистичної значимості. Припустимо, ви вже обчислили міру залежності між двома перемінними (як порозумівалося вище). Наступний питання, що коштує перед вами: "наскільки значима ця залежність?" Наприклад, чи є 40% поясненої дисперсії між двома перемінними достатнім, щоб вважати залежність значимої? Відповідь: "у залежності від обставин". Саме, значимість залежить в основному від обсягу вибірки. Як уже порозумівалося, у дуже великих вибірках навіть дуже слабкі залежності між перемінними будуть значимими, у той час як у малих вибірках навіть дуже сильні залежності не є надійними. Таким чином, для того щоб визначити рівень статистичної значимості, вам потрібна функція, що представляла би залежність між "величиною" і "значимістю" залежності між перемінними для кожного обсягу вибірки. Дана функція вказала б вам точно "наскільки ймовірно одержати залежність даної величини (чи більше) у вибірці даного обсягу, у припущенні, що в популяції такої залежності ні". Іншими словами, ця функція давала би рівень значимості (p -рівень), і, отже, імовірність помилково відхилити припущення про відсутність даної залежності в популяції. Ця "альтернативна" гіпотеза ( що складається в тім, що немає залежності в популяції) звичайно називається нульовою гіпотезою. Було б ідеально, якби функція, що обчислює імовірність помилки, була лінійної і мала тільки різні нахили для різних обсягів вибірки. На жаль, ця функція істотно більш складна і не завжди точно та сама. Проте, у більшості випадків її форма відома, і її можна використовувати для визначення рівнів значимості при дослідженні вибірок заданого розміру. Більшість цих функцій зв'язано з дуже важливим класом розподілів, називаним нормальним.

5.3.3 Чому важливо Нормальний розподіл. Нормальний розподіл важливо з багатьох причин. У більшості випадків воно є гарним наближенням функцій, визначених у попередньому розділі (більш докладний опис див. у “Чи усі статистики критеріїв є нормально розподілені?”). Розподіл багатьох статистик є нормальним чи може бути отримане з нормальних за допомогою деяких перетворень. Міркуючи філософськи, можна сказати, що нормальний розподіл являє собою одну з емпірично перевірених істин щодо загальної природи дійсності і його положення може розглядатися як один з фундаментальних законів природи. Точна форма нормального розподілу (характерна "дзвінообразна крива") визначається тільки двома параметрами: середнім і стандартним відхиленням.

5.3.4 Характерна властивість нормального розподілу полягає в тому, що 68% усіх його спостережень лежать у діапазоні ±1 стандартне відхилення від середнього, а діапазон ±2 стандартні відхилення містить 95% значень. Іншими словами, при нормальному розподілі, стандартизовані спостереження, менші -2 чи великі +2, мають відносну частоту менш 5% (Стандартизоване спостереження означає, що з вихідного значення віднятий середнє і результат поділений на стандартне відхилення (корінь з дисперсії)). Якщо задати z-значення (тобто значення випадкової величини, що має стандартний нормальний розподіл) рівним 4, що відповідає ймовірнісний рівень буде менше .0001, оскільки при нормальному розподілі практично всі спостереження (тобто більш 99.99%) потраплять у діапазон ±4 стандартні відхилення.




5.3.5 Ілюстрація того, як нормальний розподіл використовується в статистичних міркуваннях (індукція). Нагадаємо приклад, що обговорювалися вище, коли пари вибірок чоловіків і жінок вибиралися із сукупності, у якій середнє значення WCC для чоловіків і жінок було в точності те саме. Хоча найбільш ймовірний результат таких експериментів (одна пара вибірок на експеримент) полягає в тому, що різниця між середніми WCC для чоловіків і жінок для кожної пари близька до 0, час від час з'являються пари вибірок, у яких ця різниця істотно відрізняється від 0. Як часто це відбувається? Якщо обсяг вибірок досить великий, то різниці "нормально розподілені" і знаючи форму нормальної кривої, ви можете точно розрахувати імовірність випадкового одержання результатів, що представляють різні рівні відхилення середнього від 0 - значення гіпотетичного для всієї популяції. Якщо обчислена імовірність настільки мала, що задовольняє прийнятому заздалегідь рівню значимості, то можна зробити лише один висновок: ваш результат краще описує властивості популяції, чим "нульова гіпотеза". Варто пам'ятати, що нульова гіпотеза розглядається тільки по технічних розуміннях як початкова крапка, з яким зіставляються емпіричні результати. Відзначимо, що все це міркування засноване на припущенні про нормальність розподілу цих повторних вибірок (тобто нормальності вибіркового розподілу). Це припущення обговорюється в наступному розділі.

5.3.6 Чи всі статистики критеріїв нормально розподілені? Не всі, але більшість з них або мають нормальний розподіл, або мають розподіл, зв'язаний з нормальним і обчислюється на основі нормального, таке як t, F чи хи-квадрат. Звичайно ці критеріальні статистики вимагають, щоб аналізовані перемінні самі були нормально розподілені в сукупності. Багато спостерігаємі перемінні дійсно нормально розподілені, що є ще одним аргументом на користь того, що нормальний розподіл представляє "фундаментальний закон". Проблема може виникнути, коли намагаються застосувати тести, засновані на припущенні нормальності, до даних, що не є нормальними В цих випадках ви можете вибрати одне з двох. По-перше, ви можете використовувати альтернативні "непараметричні" тести (так називані "вільно розподілені критерії", Однак це часто незручно, тому що звичайно ці критерії мають меншу потужність і мають меншу гнучкість. Як альтернативу, у багатьох випадках ви можете усе-таки використовувати тести, засновані на припущенні нормальності, якщо упевнені, що обсяг вибірки досить великий. Остання можливість заснована на надзвичайно важливому принципі, що дозволяє зрозуміти популярність тестів, заснованих на нормальності. А саме, при зростанні обсягу вибірки, форма вибіркового розподілу (тобто розподіл вибіркової статистики критерію , цей термін був уперше використаний у роботі Фишера, Fisher 1928a) наближається до нормального, навіть якщо розподіл досліджуваних перемінних не є нормальним.

5.3.7 Як довідатися наслідку порушень припущень нормальності? Хоча багато тверджень інших розділів Елементарних понять статистики можна довести математично, деякі з них не мають теоретичного обґрунтування і можуть бути продемонстровані тільки емпірично, за допомогою так званих експериментів Монте-Карло. У цих експериментах велике число вибірок генерується на комп'ютері, а результати отримані з цих вибірок, аналізуються за допомогою різних тестів. Цим способом можна емпірично оцінити тип і величину чи помилок зсувів, що ви одержуєте, коли порушуються визначені теоретичні припущення тестів, використовуваних вами. Дослідження за допомогою методів Монте- Карло інтенсивно використовувалися для того, щоб оцінити, наскільки тести, засновані на припущенні нормальності, чуттєві до різних порушень припущень нормальності. Загальний висновок цих досліджень полягає в тому, що наслідку порушення припущення нормальності менш фатальні, чим спочатку передбачалося. Хоча ці висновки не означають, що припущення нормальності можна ігнорувати, вони збільшили загальну популярність тестів, заснованих на нормальному розподілі.


5.4 Статистичні характеристики вибірки


5.4.1Випадкові величини і їхні характеристики Величини, що у рівнобіжних спостереженнях, проведених у тих самих умовах, щораз приймають різні значення, називаються випадковими. Поняття «ті самі умови» означає, що обличчю, що проводить спостереження, відомі фактори, що істотно впливають на величину, що спостерігається. Ці чи фактори підтримуються на постійному рівні, чи, принаймні, їхні величини точно фіксуються. Однак, крім відомих факторів, на величину, що спостерігається, впливають невідомі спостерігачу фактори, що їм не фіксуються і не контролюються. Це є причиною розкиду значень величини, що спостерігається, у рівнобіжних спостереженнях.

Будь-яку випадкову величину А можна представити у виді: