Конспект 2003 Комп’ютерні технології в інженерних та наукових завданнях. Для студентів спеціальностей 090220, 091601. Конспект /укл. Кондратов С. О. Рубіжне: рфсну, 2003 36 с

Вид материала

Конспект

Подобный материал:

• Конспект лекцій по дисципліні Інформаційні моделі "великих" систем, 1986.92kb.
• Комп‘ютерні інформаційні технології в електроенергетиці тексти лекцій для студентів, 1076.06kb.
• Робоча навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для, 204.08kb.
• Конспект лекцій 2004 Загальна теорія систем. Конспект лекцій Для студентів денної, 1136.85kb.
• Конспект лекцій з навчальної дисципліни "Комп’ютерні технології в юридичній дільності", 6139.48kb.
• Конспект лекцій з дисципліни «транспортне право» для студентів 1 курсу денної І заочної, 2079.66kb.
• Конспект лекцій для студентів спеціальностей 030508 І 030508 "Фінанси І кредит" денної, 4154.08kb.
• Опорний конспект лекцій з дисципліни „ правознавство (для студентів денної І заочної, 1124.35kb.
• Навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для студентів, 131.31kb.
• Н.І. Гордієнко Біржова І банківська справа Конспект, 3107.24kb.

5. Негативна величина коефіцієнта кореляції свідчить, що значення відгуку, у середньому, убуває зі зростанням значення фактора
   

Таким чином, величина коефіцієнта кореляції свідчить про характер і силу впливу X на Y і про силу лінійної залежності між ними

Поряд з коефіцієнтом кореляції для характеристики зв'язку між вибірками використовують коефіцієнт детермінації, що представляє собою квадрат коефіцієнта кореляції.

R²=(r_XY)²

Коефіцієнт детермінації вказує, яку частку в загальну суму квадратів відхилень щодо середнього 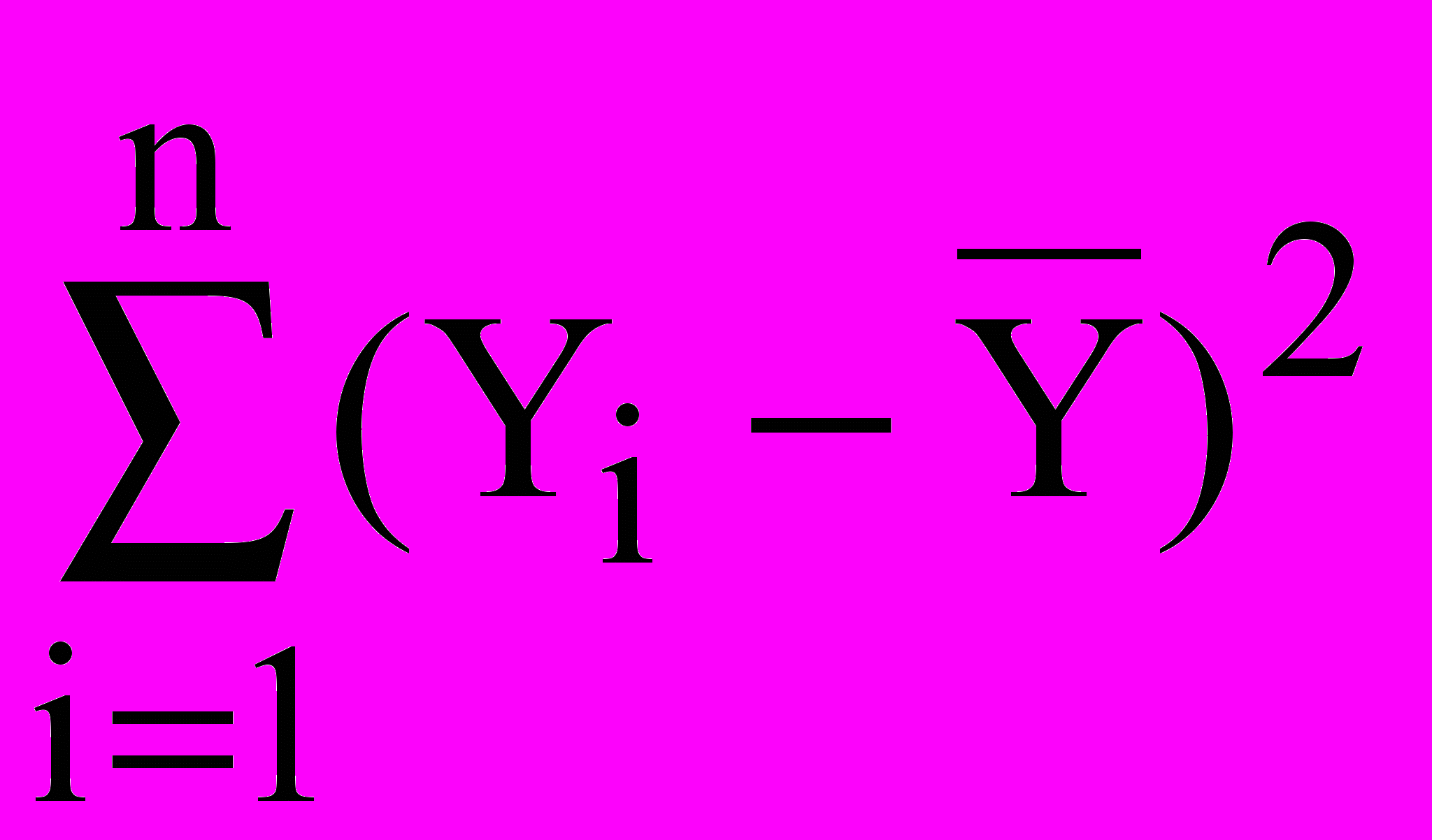вносить сума квадратів, обумовлена лінійною залежністю між Y і Х.


Перевірка значимості коефіцієнта кореляції

Оскільки коефіцієнт кореляції обчислюється, виходячи з випадкових значень відгуку, він сам є величиною випадкової.

При розрахунках коефіцієнта кореляції, особливо, якщо його значення невелике по абсолютній величині, виникає питання, наскільки значиме цей коефіцієнт, тобто, наскільки істотно він відрізняється від нуля. Іншими словами потрібно визначити, який ризик того, що, при відсутності залежності між X і Y, випадково відібрана сукупність обмеженого числа крапок групується в тім чи іншому ступені уздовж деякої прямої.

Для встановлення значимості коефіцієнта кореляції перевіряють статистичну гіпотезу r=0 при конкуруючій (альтернативної) гіпотезі r0.

1. Обчислюють випадкову величину:
   

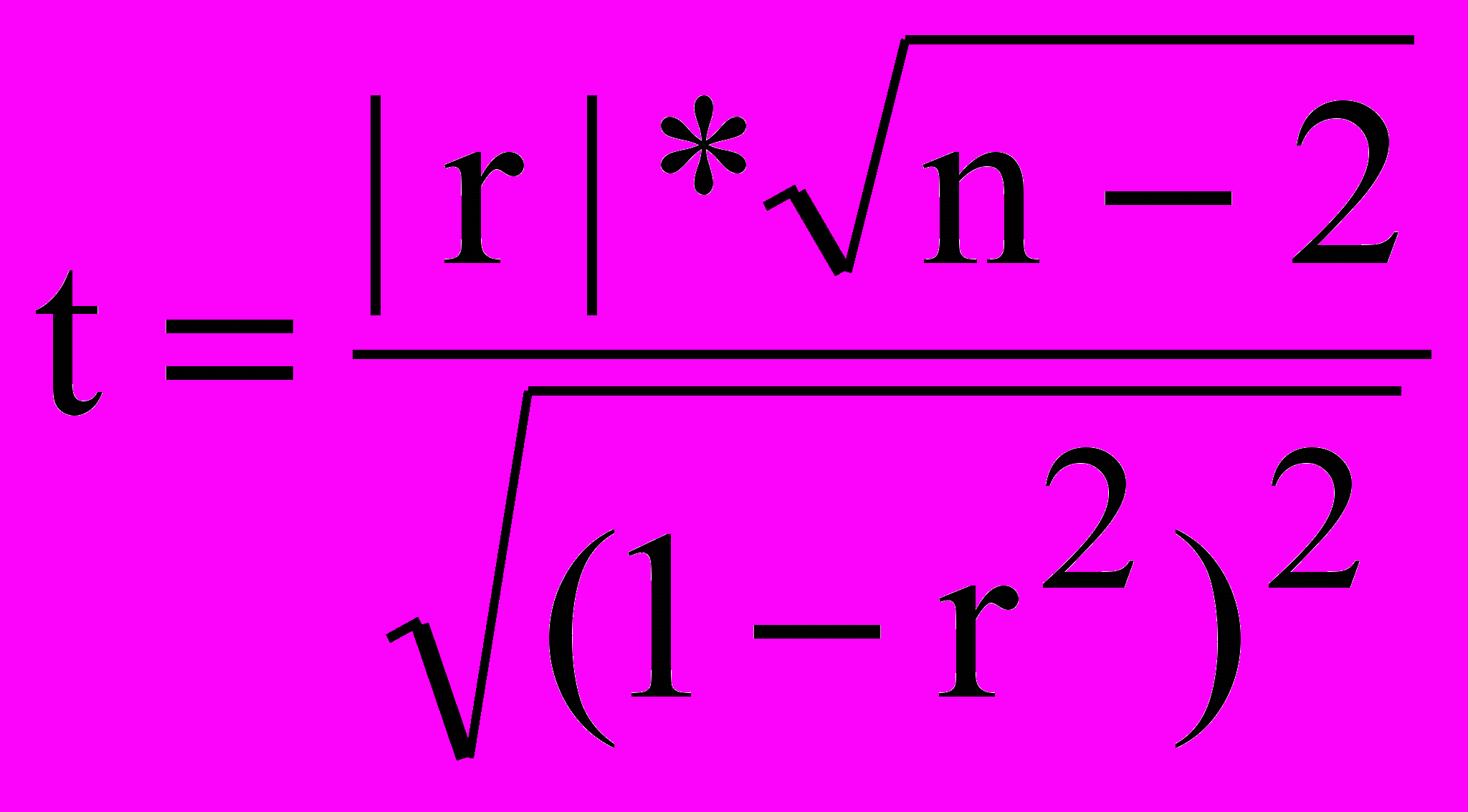
У статистику доводиться, що ця випадкова величина має розподіл Стьюдента

2. Знаходять з розподілу Стьюдента критичне значення t_q(, n-2) по заданому рівні значимості і числу крапок.
   
3. Якщо t< t_q – коефіцієнт кореляції незначимий відрізняється від нуля (відмінності від 0 з імовірністю 1- можуть бути приписані дії випадкових причин). У противному випадку коефіцієнт кореляції значимо.
   

По техніці виконання перевірка – така ж, як описана в розділі 3. Расчет характеристик выборки в среде Excel


6. Розрахунок коефіцієнтів кореляції в середовищі Excel

Розрахунок можна робити вручну, шляхом побудови таблиць і розрахунків середніх і среднеквадратических відхилень. Для зручності роботи до складу статистичних функцій Excel внесена функція КОРРЕЛ, що розраховує коефіцієнт кореляції.

Для розрахунку коефіцієнта кореляції з використанням цієї функції необхідно:

1. Побудувати таблиці значень Х и Y
   
2. Виділити осередок, у якій буде поміщений коефіцієнт кореляції.
   
3. На панелі інструментів натиснути кнопку f(x)
   
4. Викликати з меню статистичні функції
   
5. З меню статистичних функцій вибрати КОРРЕЛ
   
6. У меню функції КОРРЕЛ – натиснути на кольорову кнопку біля віконця з написом «Масив 1»
   
7. За допомогою миші виділити в таблиці дані значення Х
   
8. Натиснути на кольорову кнопку віконця, знову очутитися в меню КОРРЕЛ
   
9. У меню функції КОРРЕЛ – натиснути на кольорову кнопку біля віконця з написом «Масив 2»
   
10. За допомогою миші виділити в таблиці дані значення Y
    
11. Натиснути на кольорову кнопку віконця, знову очутитися в меню КОРРЕЛ
    
12. Натиснути кнопку ОК. Меню КОРРЕЛ зникне, у виділеному осередку з'явиться шукане значення коефіцієнта кореляції.
    

5.6 Проста лінійна регресія


Установивши наявність кореляційного зв'язку (розрахувавши коефіцієнт кореляції і переконавши в його значимості) можна вирішити задачу перебування лінійної залежності, що проходить через дану сукупність крапок деяким щонайкраще. Для рішення цієї задачі використовується метод найменших квадратів. Постановка задачі: задана сукупність з n крапок {x₁,y₁},{x₂,y₂},…{x_n,y_n}... Потрібно побудувати пряму, що проходить через ці крапки, тобто, коефіцієнти а₀,а₁ рівняння прямої y = a₀ + a₁x

Цю задачу можна вирішити однозначно, якщо шукати коефіцієнти а₀,а₁ такими, щоб зробити мінімальної суму квадратів відхилень по всіх крапках між заданими значеннями y і значеннями y, що лежать на розрахунковій прямій

Математично ця задача формулюється в такий спосіб:




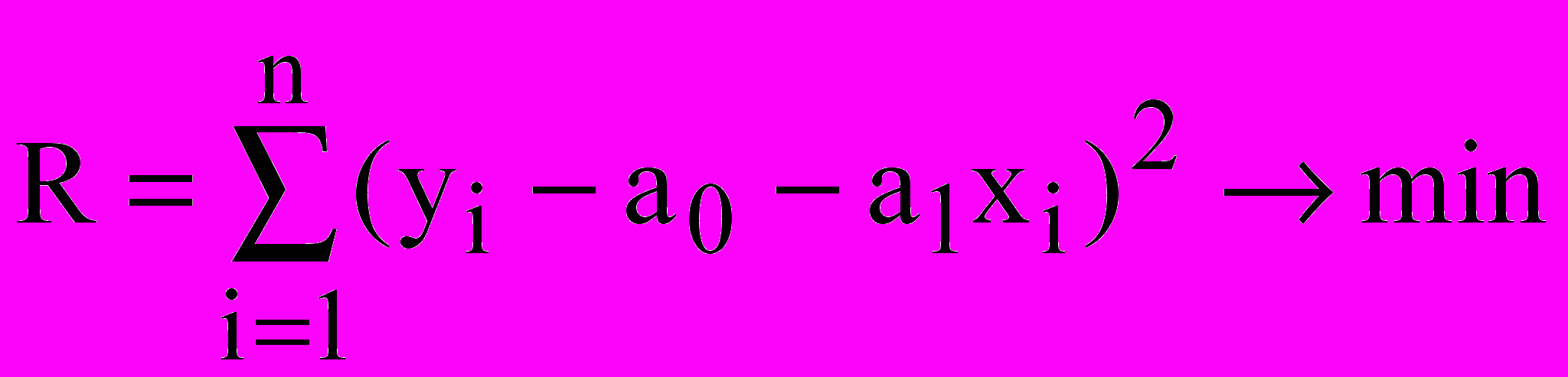
У крапці мінімуму частки похідн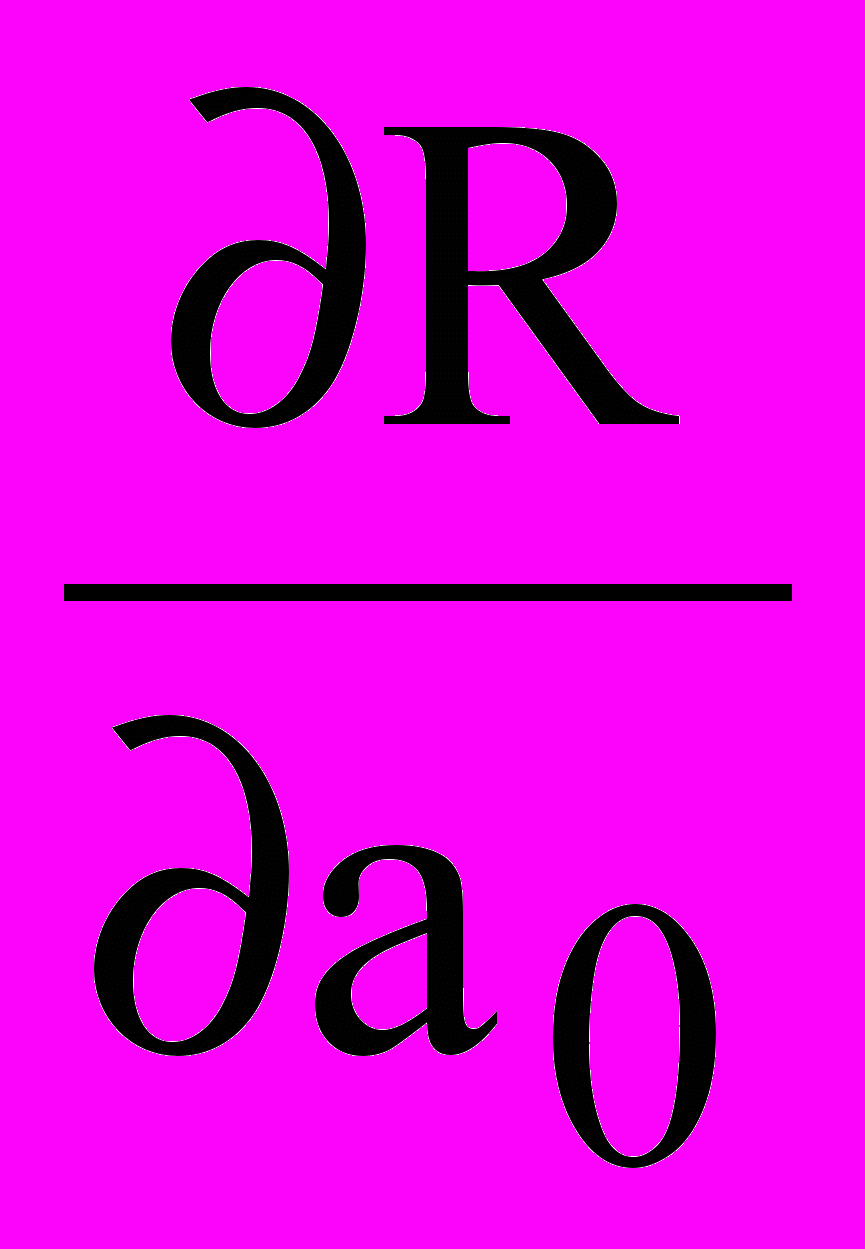і і 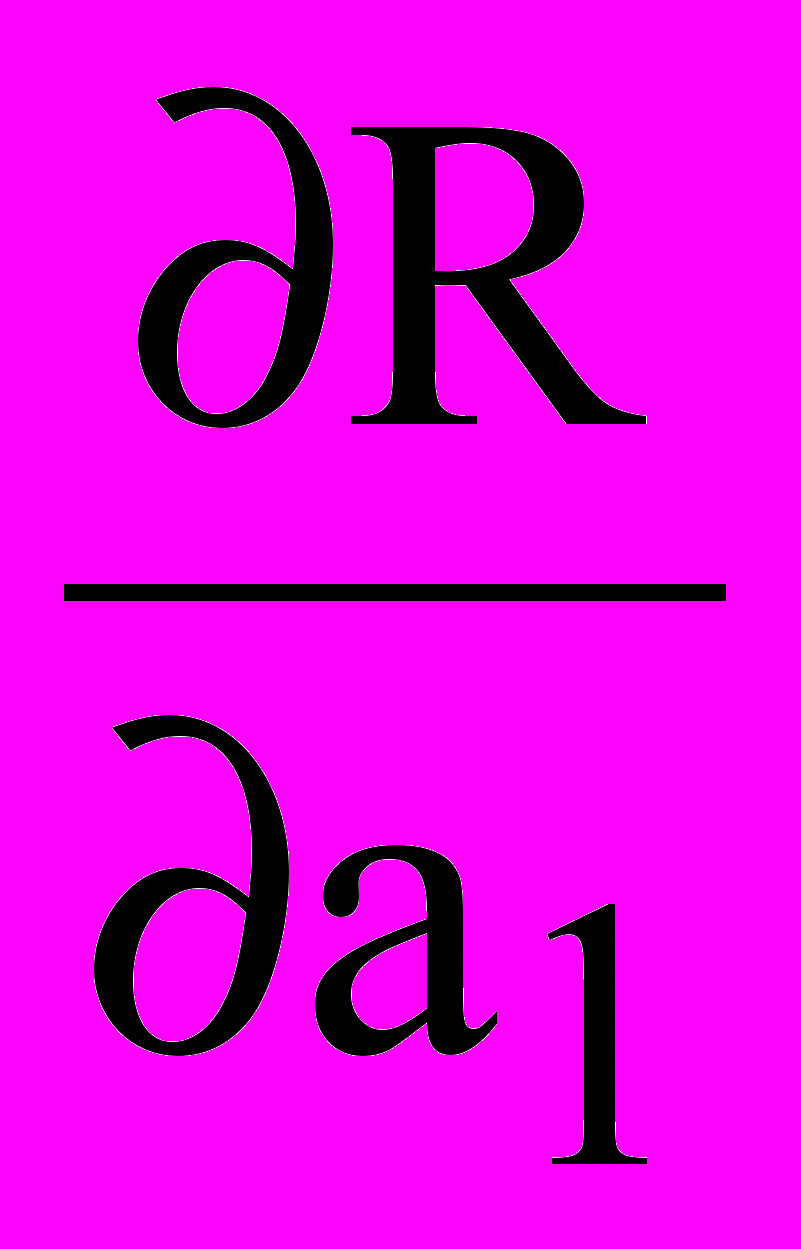дорівнюють нулю: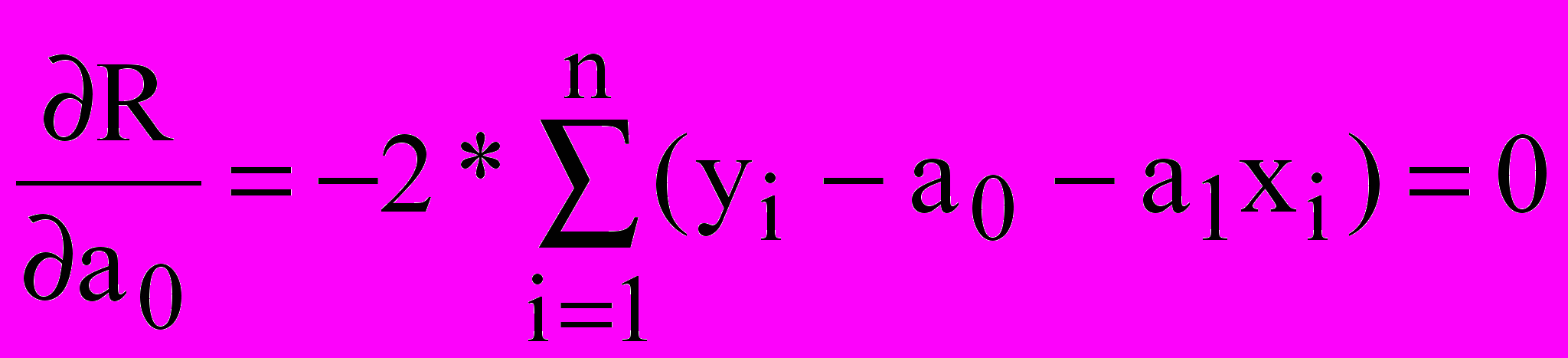






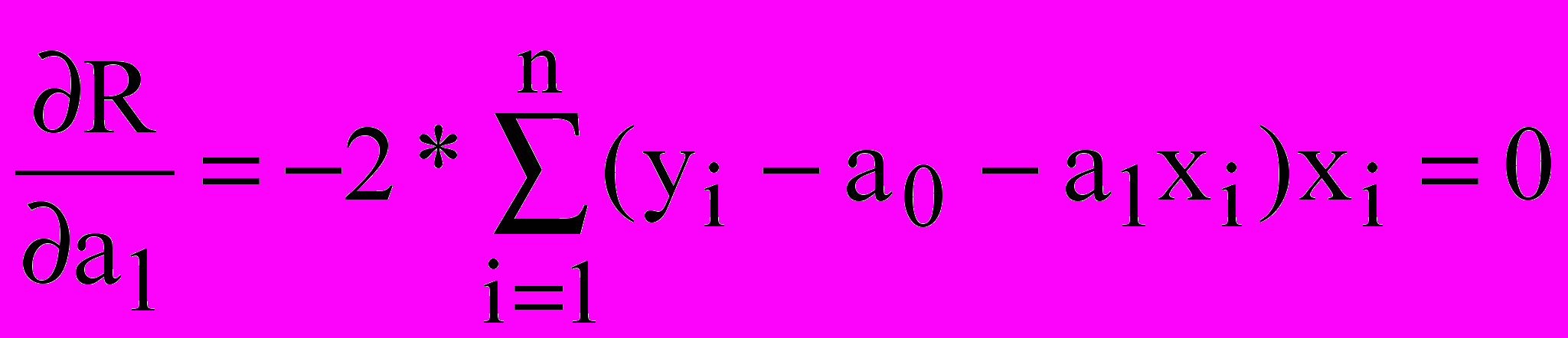
Групуючи члени, одержуємо систему лінійних алгебраїчних рівнянь із двома невідомими:




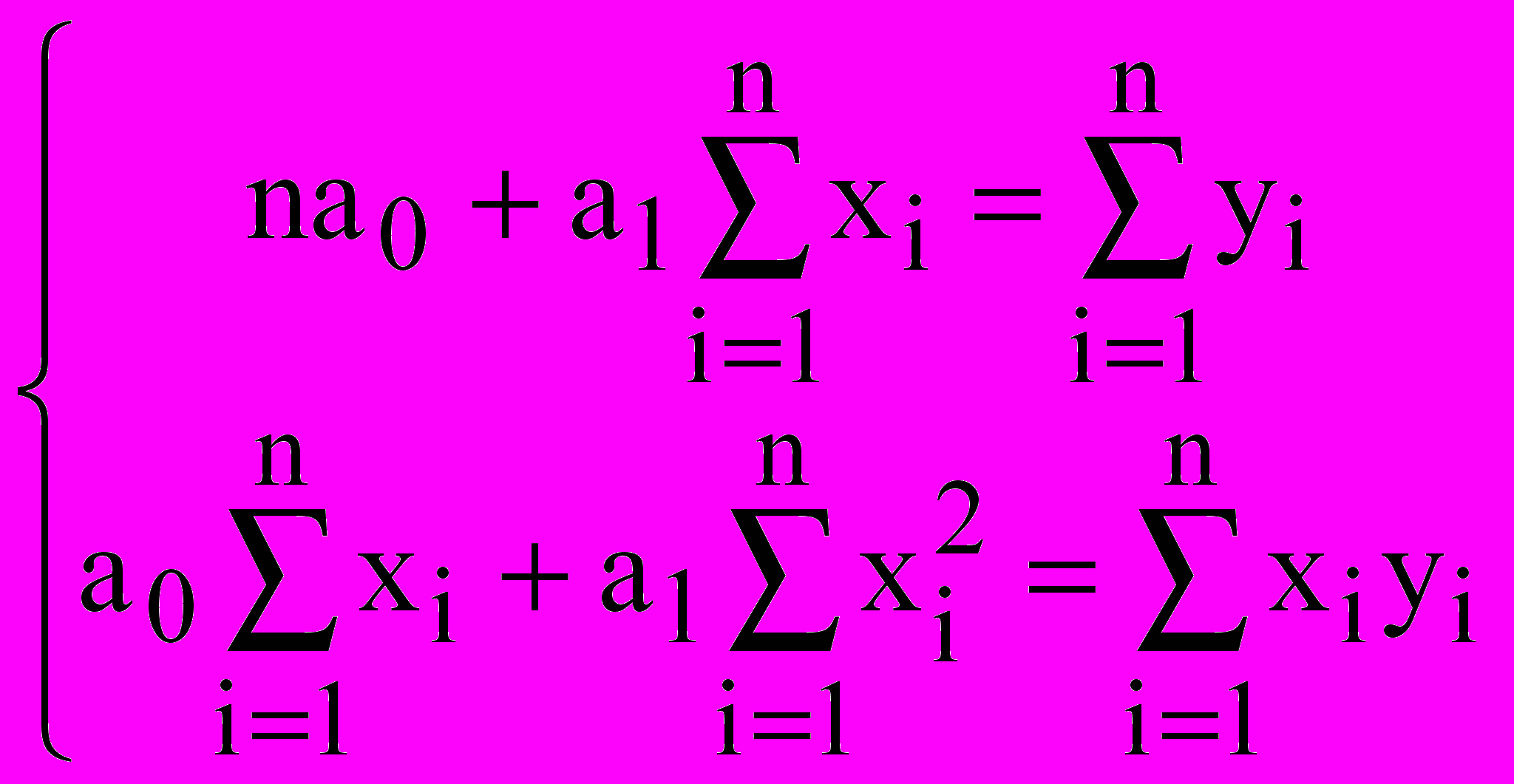
Розрахувавши всі суми і вирішивши цю систему, можна знайти коефіцієнти прямої, тобто, побудувати задану пряму на сукупності крапок.

Рівняння прямої, побудоване методом найменших квадратів, називається рівнянням регресії (простої лінійної регресії).

У середовищі Excel для побудови рівняння регресії маються статистичні функції ВІДРІЗОК і НАХИЛ.

Для перебування коефіцієнтів регресії спочатку будується таблиця значень x і y. Для розрахунку коефіцієнта а₀:

1. Виділяємо осередок, у якій буде значення коефіцієнта а₀
   
2. Викликаємо функцію ВІДРІЗОК, що знаходиться серед статистичних функцій.
   
3. Виділяємо осередок, у якій буде значення коефіцієнта а₀
   
4. У меню цієї функції – натискаємо кольорову кнопку біля вікна з написом Изв_знач_y
   
5. Виділяємо стовпець значень y, натисканням кольорової кнопки повертаємося в меню функції ВІДРІЗОК
   
6. У меню цієї функції – натискаємо кольорову кнопку біля вікна з написом Изв_знач_х
   
7. Виділяємо стовпець значень х, натисканням кольорової кнопки повертаємося в меню функції ВІДРІЗОК
   
8. Натискаємо кнопку ОК. У виділеному осередку з'являється значення коефіцієнта а₀
   

Аналогічно, шляхом виклику статистичної функції НАХИЛ, розраховується коефіцієнт а₁

5.7 Дослідження рівняння регресії


Лінію регресії можна провести через будь-яку сукупність крапок, у тому числі, через крапки з нульовим коефіцієнтом кореляції. Тому після розрахунку коефіцієнтів регресії варто провести дослідження рівняння регресії з метою з'ясування значимості цього рівняння, а також – коефіцієнтів регресії.

8.1. Установлення значимості рівняння регресії.

Найпростіша модель явища може бути побудована в припущенні, що на нього не впливають ніякі фактори, тобто, вона має вид:



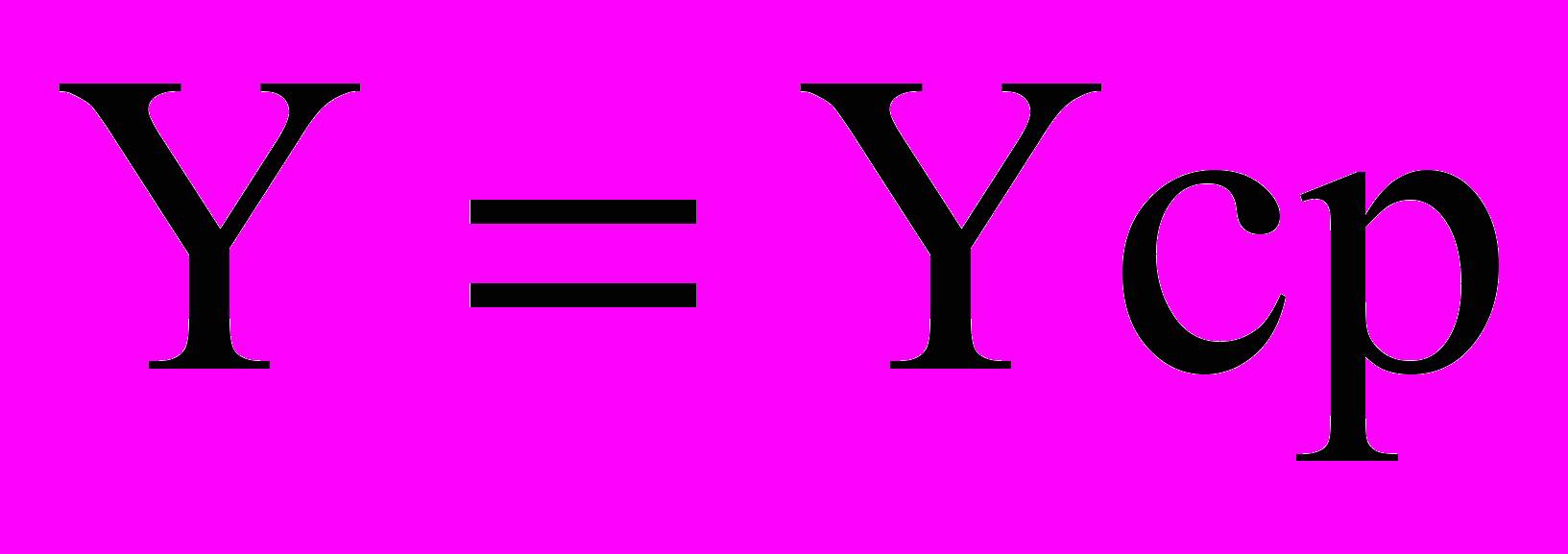
Використовуючи лінійну регресійну модель Y = A₀ + A₁*X, ми ускладнюємо картину, уводячи 2 параметри (А0 і А1) замість одного (Ycp). Установлення значимості моделі означає перевірку, наскільки істотно на якості моделі позначається це ускладнення. Якщо модель незначима – ускладнення не має змісту.

Порівняння засноване на теоремі розкладання залишкової суми квадратів щодо середнього:



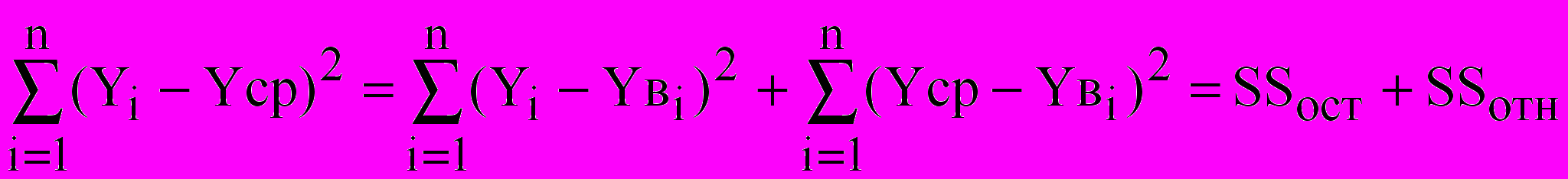
Yв_i – значення відгуку, розраховане по рівнянню регресії в i-й крапці.

Перша сума (SS_ост) зветься залишкової суми квадратів (суми квадратів відхилень, обумовлених регресією), друга – сумою квадратів щодо регресії (SS_отн). Кожне з приведених доданків має своє число ступенів волі:

Складова	Позначення	Число ступенів волі	Дисперсія
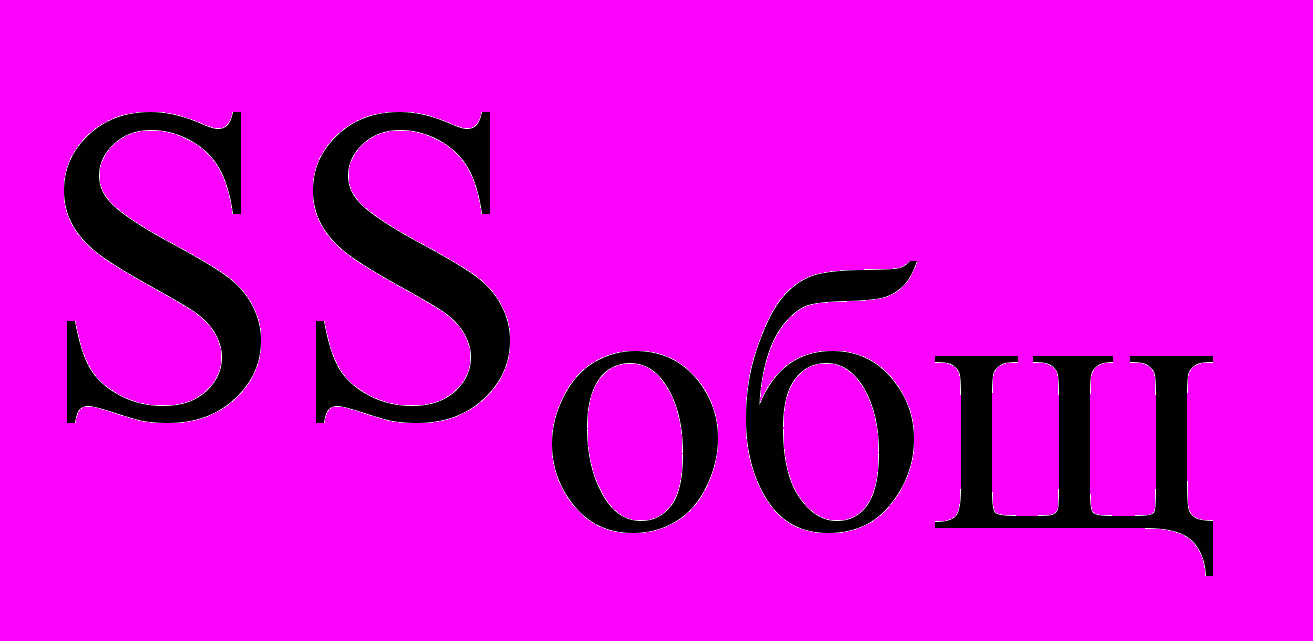		n-1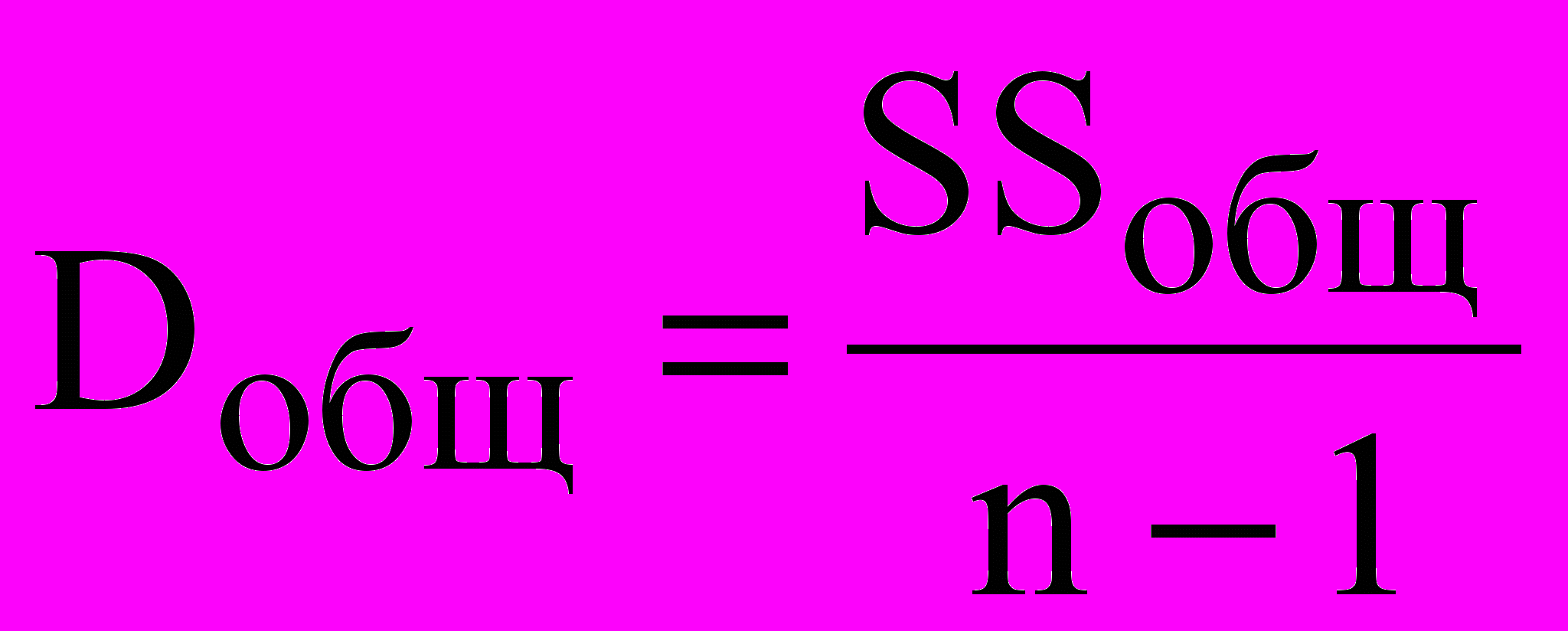
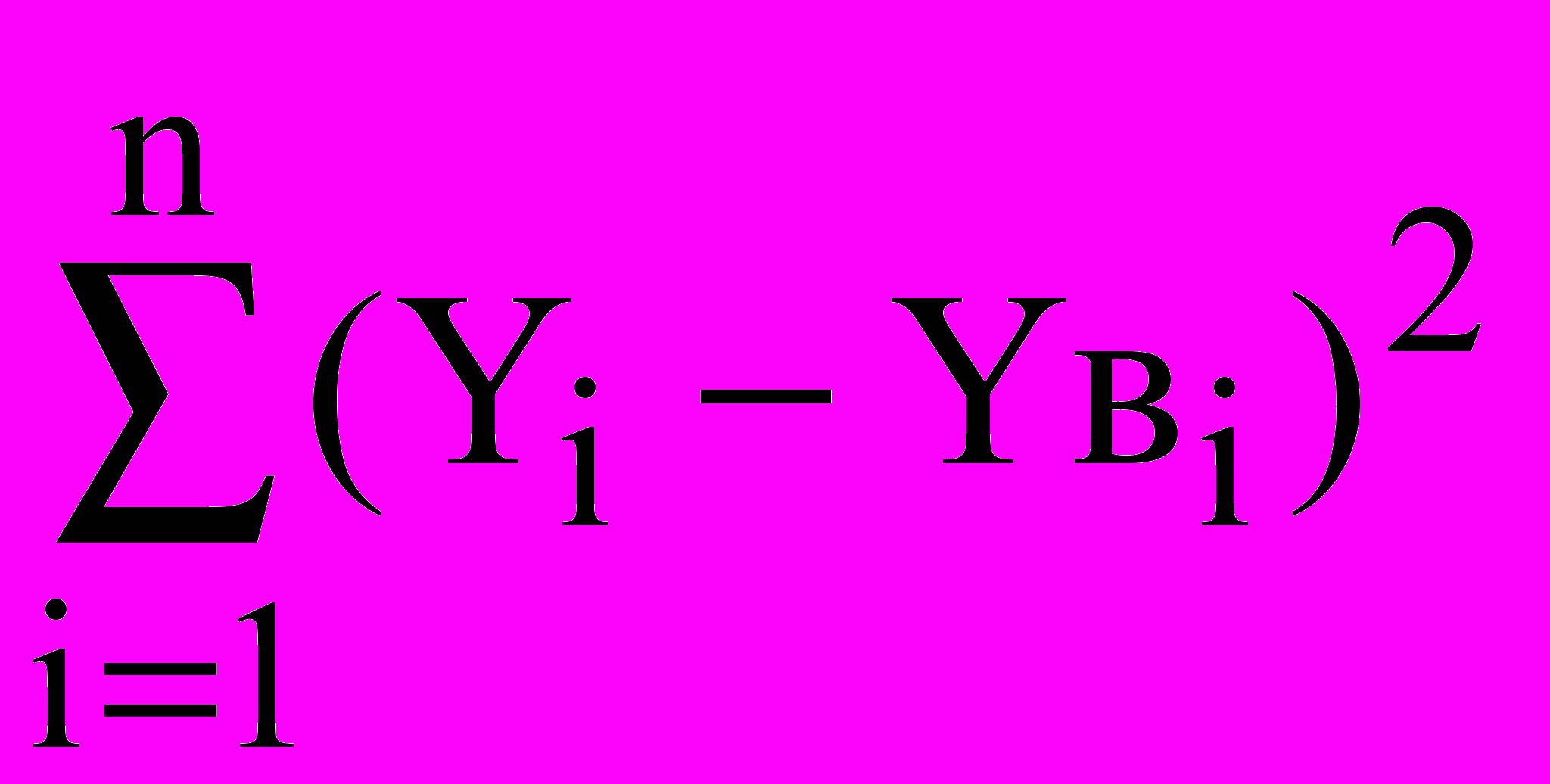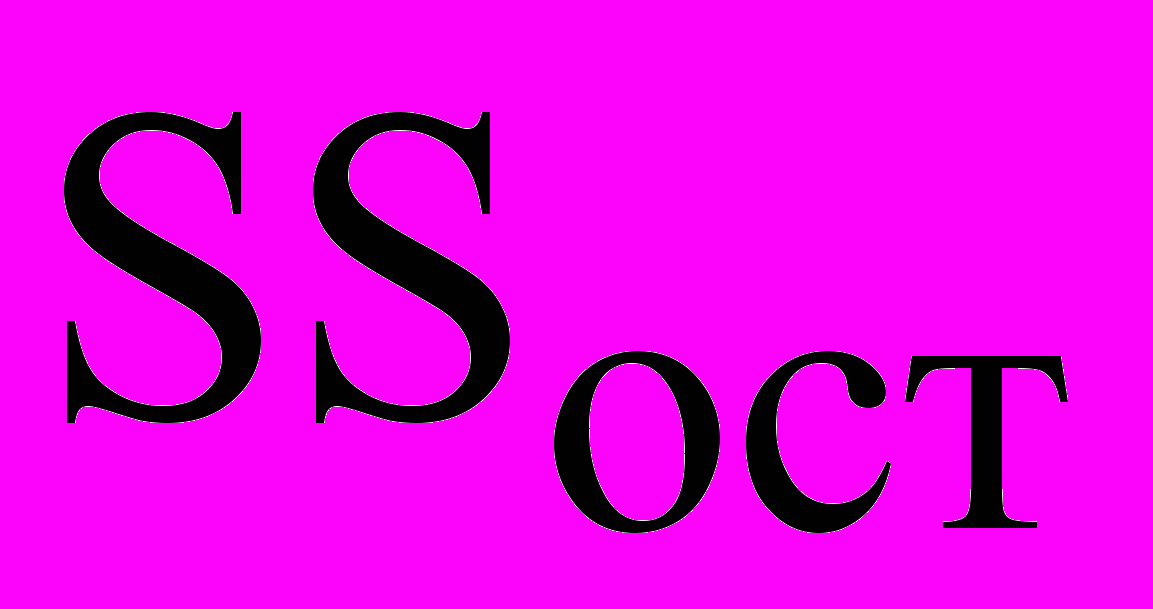		n-2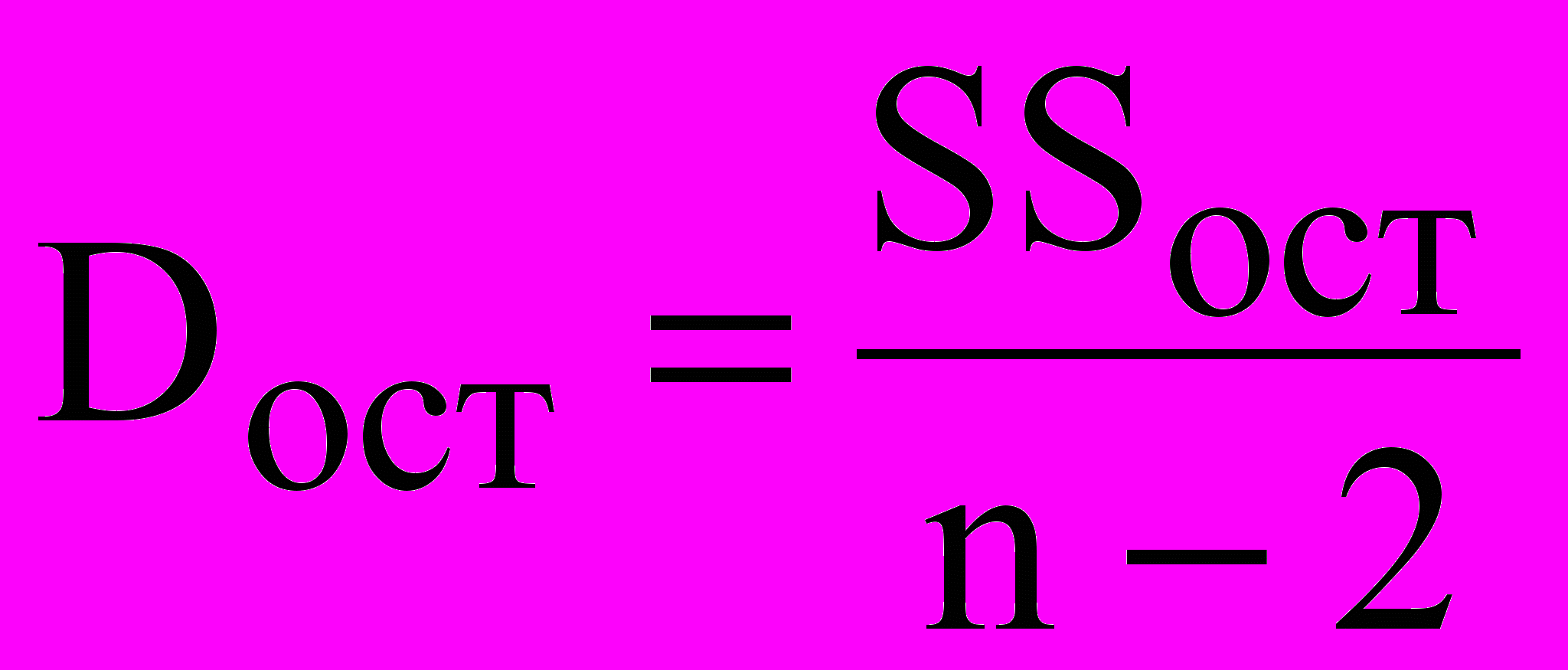
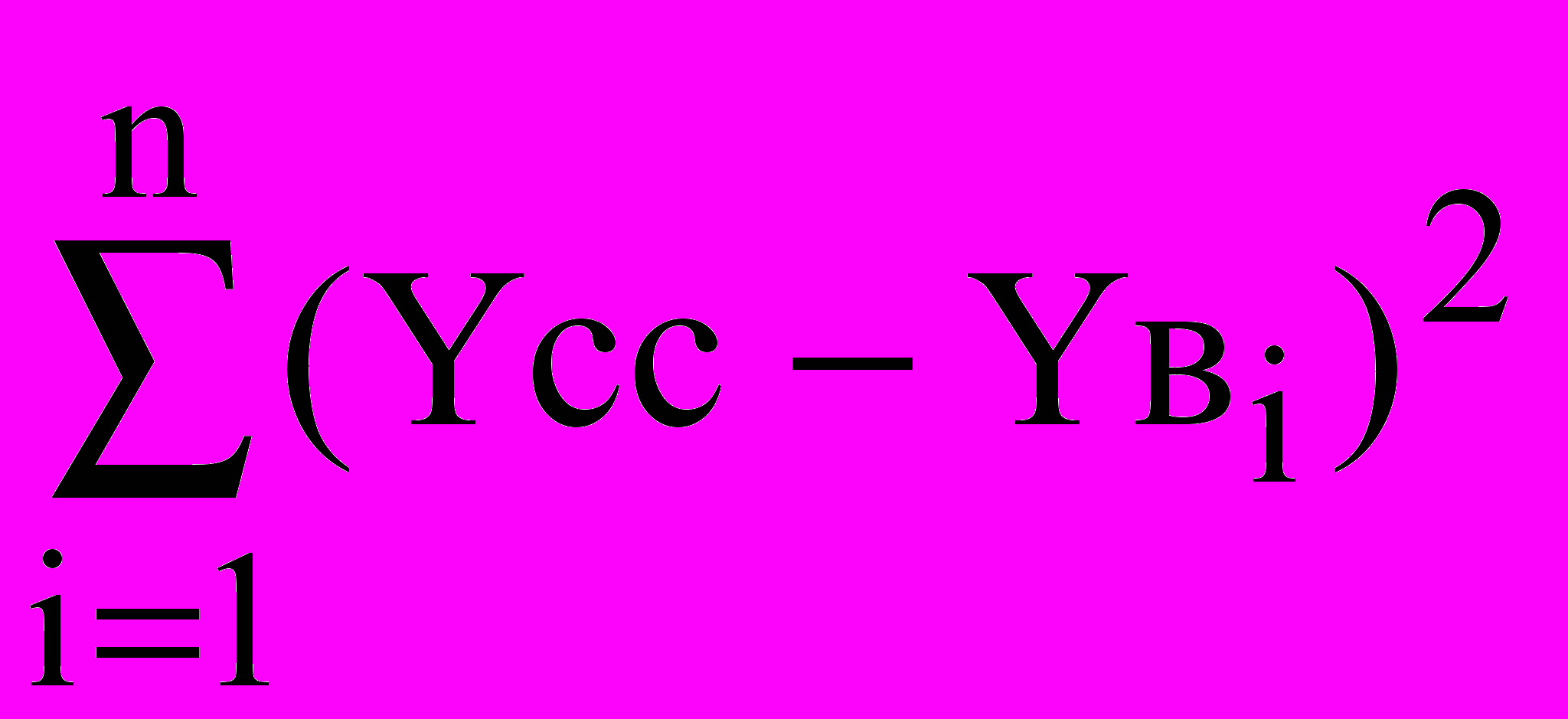		1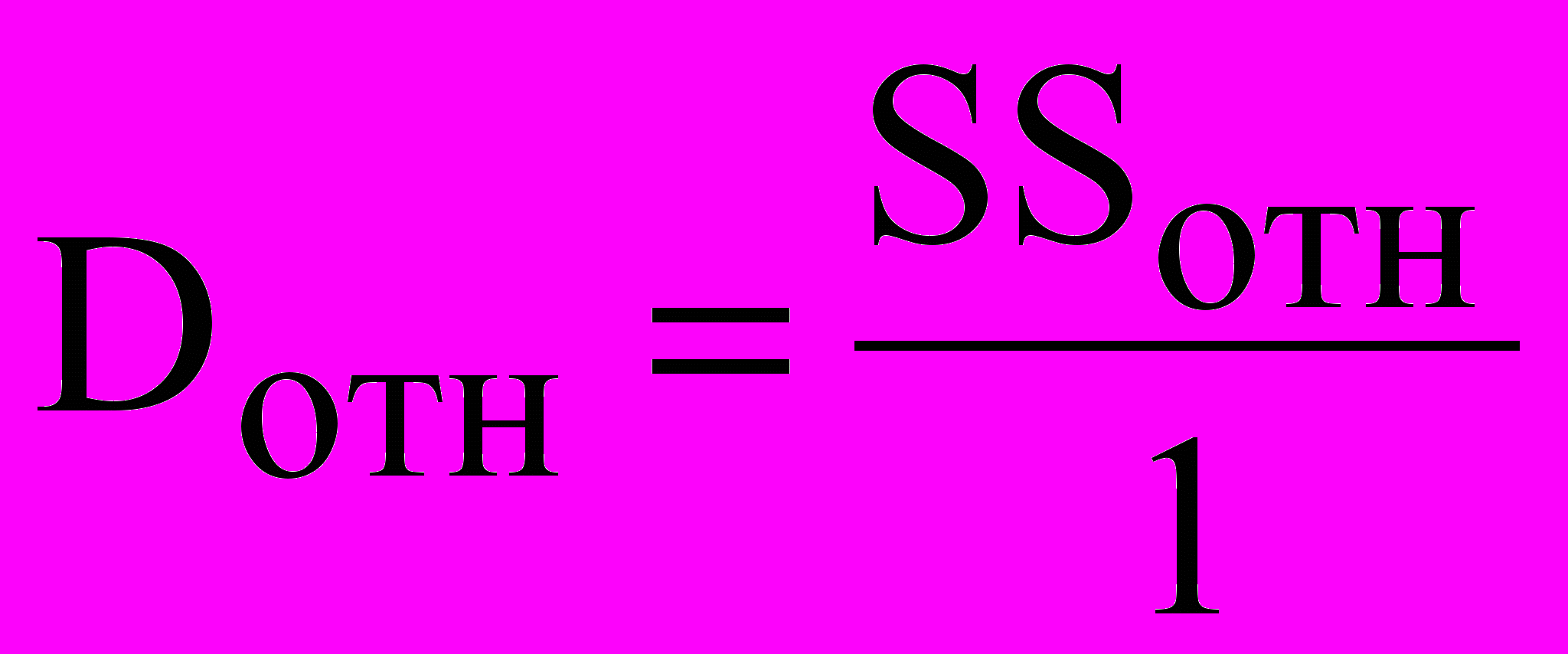

Розділивши кожну із сум на число її ступенів волі, відповідно, одержимо загальну дисперсію, залишкову дисперсію і дисперсію щодо регресії.

Сутність установлення значимості рівняння регресії полягає в перевірці гіпотезу про рівність (однорідності) двох дисперсій – дисперсії щодо регресії і залишкової дисперсії. Для цього розраховуємо так називане F-відношення – відношення більшої дисперсії до меншого (у нашому випадку – дисперсії щодо регресії до залишкової дисперсії):



Ця випадкова величина має розподіл імовірностей, називаний розподілом Фишера чи F-розподілом, що залежить від рівня значимості, а також, числа ступенів волі більшої і меншої дисперсії. У Excel можна реалізувати 2 типи перевірки: розрахувати імовірність того, то при даному F – відношенні дисперсії однакові (при заданих числах ступенів волі). Це робиться за допомогою статистичної функції FРАСПР. Якщо ця імовірність виявляється менше довірчої імовірності – гіпотеза рівності дисперсій відкидається, приймається, що рівняння регресії значиме. У противному випадку регресія незначима (розкид у даних слабко змінився в порівнянні з найпростішою моделлю).

Друга можливість – за заданим значенням числа ступенів волі і довірчої інформації розрахувати критичне значення F, вище якого гіпотеза рівності дисперсій відкидається. Це робиться за допомогою функції FРАСПА. Виклик цих функцій – такої ж, як критерію Стьюдента.

Перевірка значимості коефіцієнтів регресії

Значимість коефіцієнтів регресії означає встановлення, значиме чи ні вони відрізняються від нуля.

Коефіцієнти регресії – випадкові величини, що мають розподіл Стьюдента.

Для перевірки значимості для кожного коефіцієнта обчислюють відношення



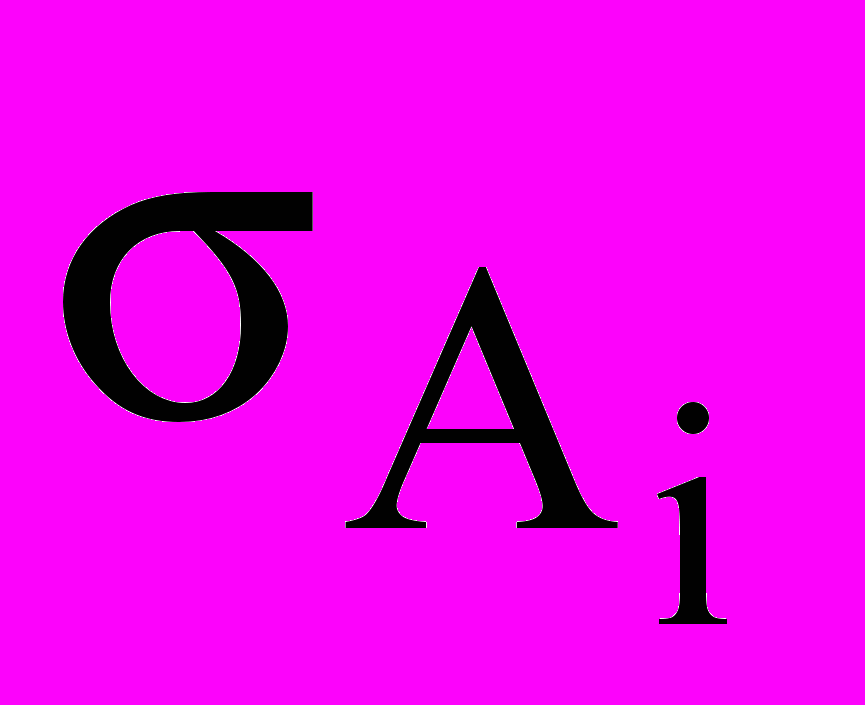- среднеквадратическое відхилення коефіцієнта А_і

Перевірку значимості проводять також, як при проверке значимости коэффициента корреляции

Якщо коефіцієнт регресії незначимо – його можна дорівняти до нуля і перерахувати дані для більш простої моделі.

Розрахунок среднеквадратических відхилень коефіцієнтів проводять по формулах:






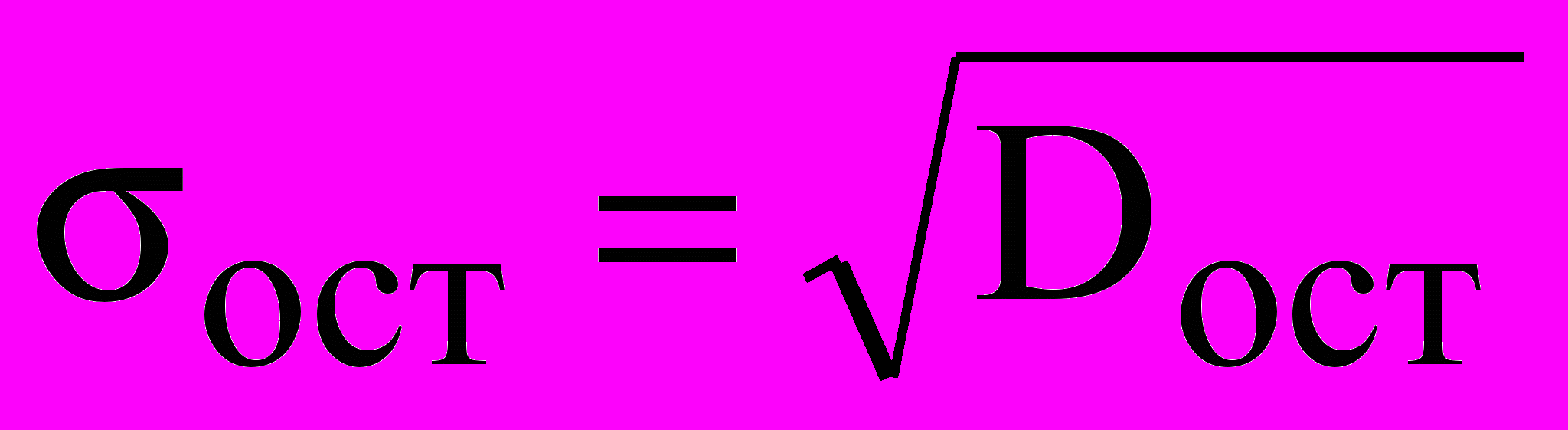- залишкове среднеквадратическое відхилення


9. Прогноз і довірчий інтервал прогнозу


Після розрахунку і дослідження рівняння регресії, у випадку його значимості, можна перейти до використання цього рівняння для прогнозування. Для цього треба підставити в рівняння регресії значення фактора, для якого проводиться прогноз (Х₀) і розрахувати прогноз Y₀

Y₀=A₀ + A₁*X₀

Оскільки прогнозне значення – випадкова величина, необхідно оцінити границі інтервалу, у яких знаходиться прогноз з визначеною імовірністю, тобто, побудувати довірчий інтервал прогнозу. Для прогнозованого значення Y₀ напівширину довірчого інтервалу в крапці Х₀



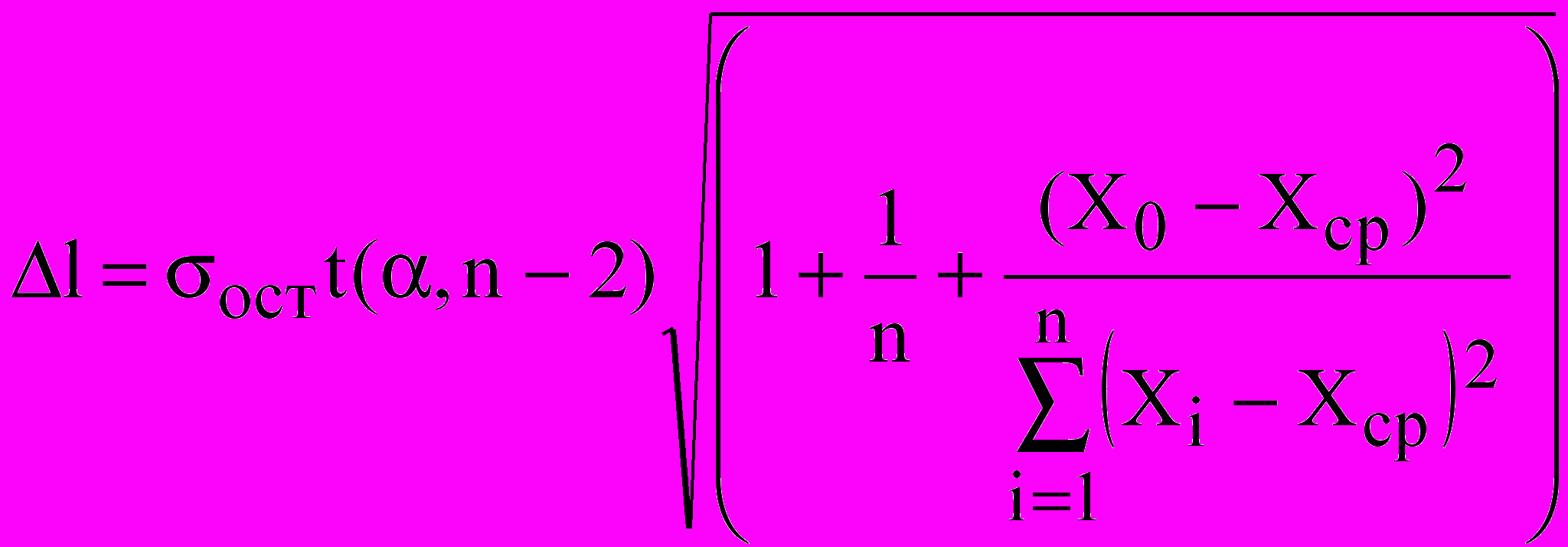
Тоді, щире значениеY з імовірністю 1- буде знаходиться між Y-l і Y+l