Конспект 2003 Комп’ютерні технології в інженерних та наукових завданнях. Для студентів спеціальностей 090220, 091601. Конспект /укл. Кондратов С. О. Рубіжне: рфсну, 2003 36 с

Вид материала

Конспект

Подобный материал:

• Конспект лекцій по дисципліні Інформаційні моделі "великих" систем, 1986.92kb.
• Комп‘ютерні інформаційні технології в електроенергетиці тексти лекцій для студентів, 1076.06kb.
• Робоча навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для, 204.08kb.
• Конспект лекцій 2004 Загальна теорія систем. Конспект лекцій Для студентів денної, 1136.85kb.
• Конспект лекцій з навчальної дисципліни "Комп’ютерні технології в юридичній дільності", 6139.48kb.
• Конспект лекцій з дисципліни «транспортне право» для студентів 1 курсу денної І заочної, 2079.66kb.
• Конспект лекцій для студентів спеціальностей 030508 І 030508 "Фінанси І кредит" денної, 4154.08kb.
• Опорний конспект лекцій з дисципліни „ правознавство (для студентів денної І заочної, 1124.35kb.
• Навчальна програма з дисципліни «комп’ютерні та інформаційні технології» для студентів, 131.31kb.
• Н.І. Гордієнко Біржова І банківська справа Конспект, 3107.24kb.

А = ( + (

 - щире значення величини, що спостерігається

 - випадкова складова, обумовленою дією неврахованих факторів.

Вивченням випадкових величин, одержуваних у результаті спостережень, займається наука математична статистика.

Співвідношення між  і  може служити мірою інформації про систему, у якій виробляється спостереження: чим більше  у порівнянні з , тим вище невизначеність системи (тим більше неврахованих невідомих факторів впливає на величину, що спостерігається,).

Виходячи з цього, конкретне значення величини, що спостерігається, в окремому спостереженні непередбачено. Однак, якщо проводити багаторазові рівнобіжні спостереження в тих самих умовах, можна одержати стійкі (тобто, що мало залежать від кількості спостережень) характеристики випадкової величини:

• математичне чекання:
  

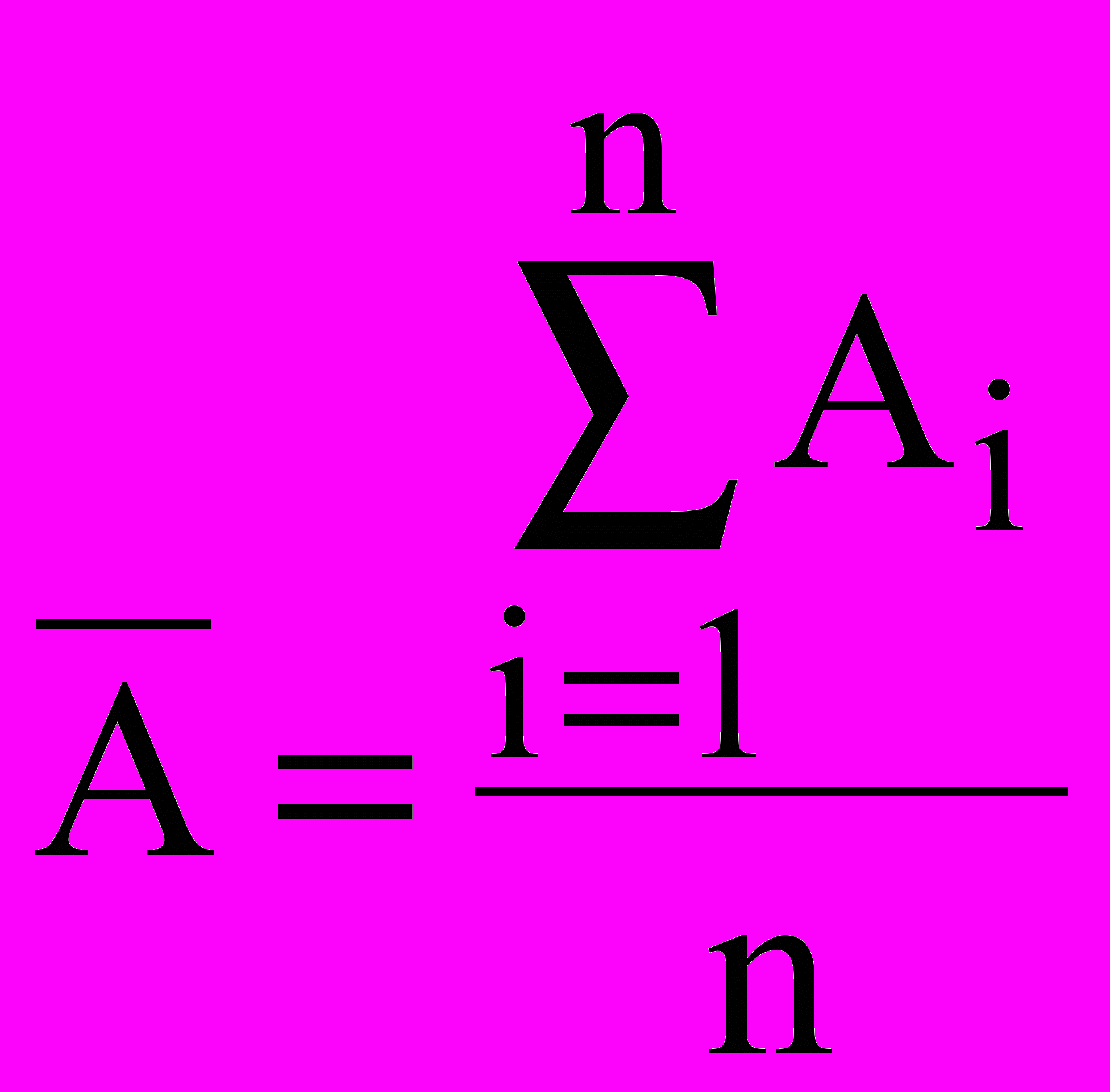
• дисперсію
  

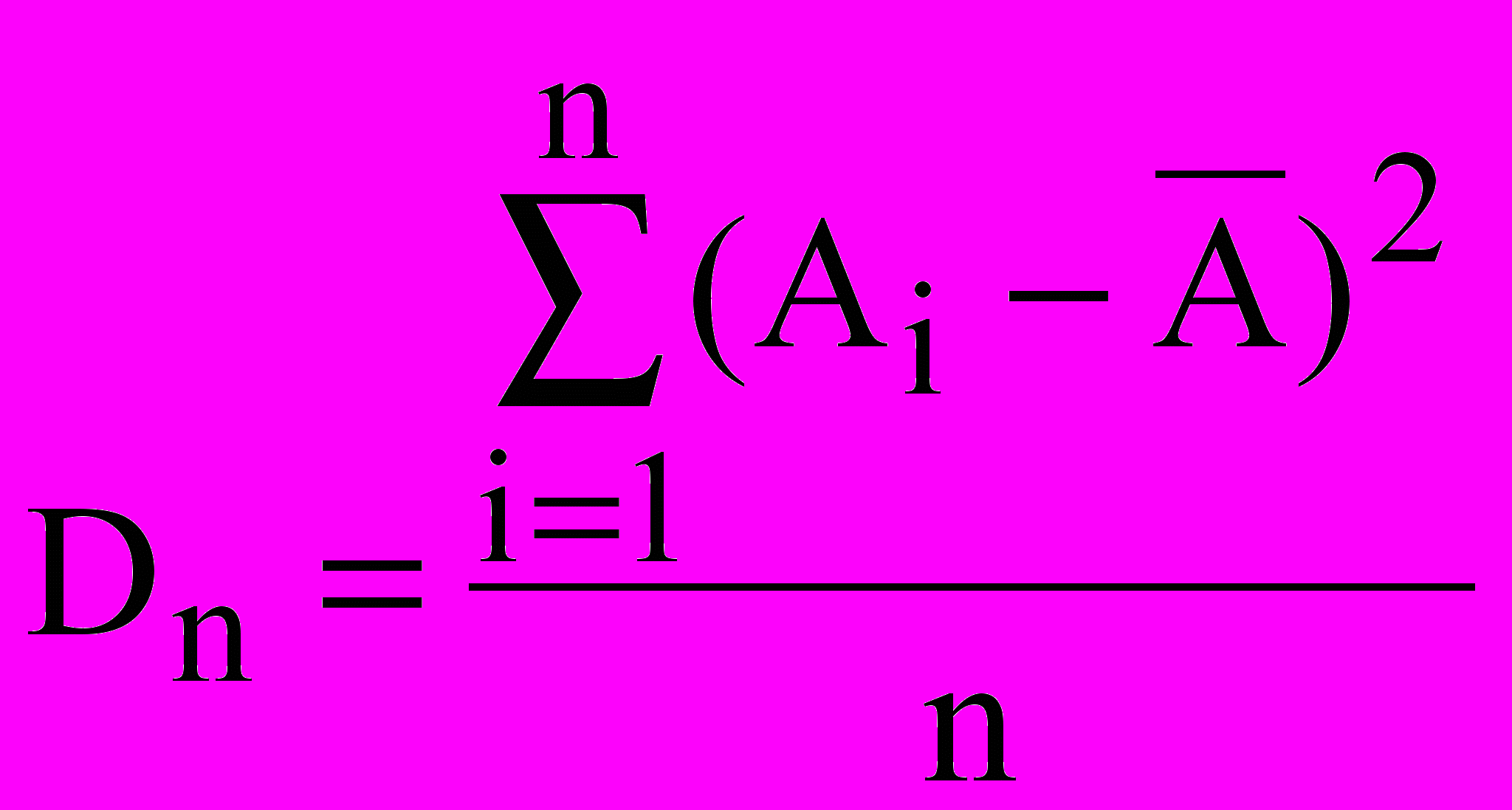
n – кількість спостережень.

Набір з n значень випадкової величини називається вибіркою.

У математичній статистиці доводиться, що величина математичного чекання (середнє арифметичне) служить оцінкою для щирого значення випадкової величини, що спостерігається. При n ця величина збігається з щирою величиною.

Дисперсія є мірою розкиду значень випадкової величини щодо середнього значення (математичного чекання). У статистичних розрахунках використовують не тільки дисперсію D_n, що називається невиправленою дисперсією, але, також, виправлену дисперсію D_n-1:



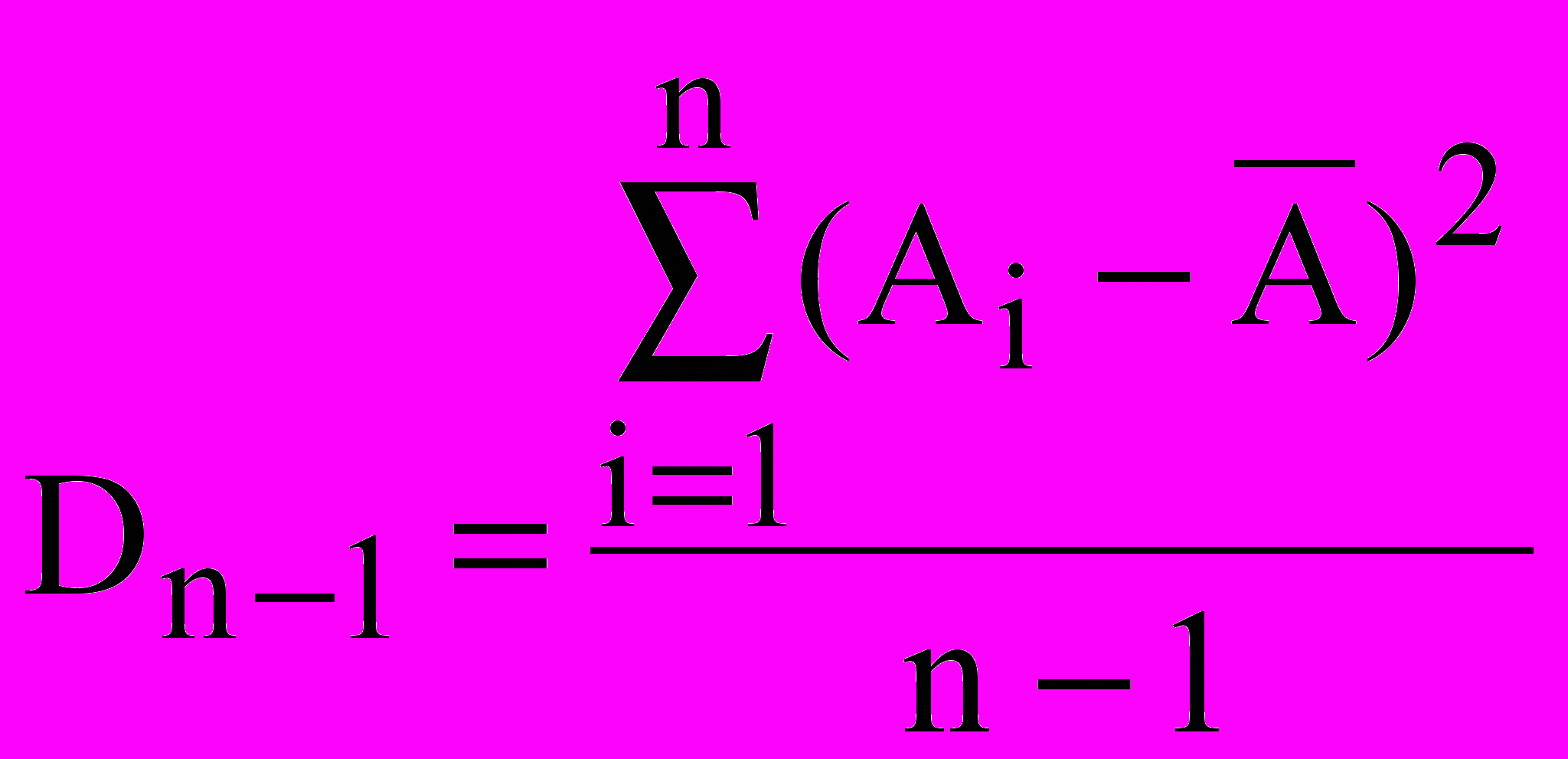
Виправлена дисперсія точніше передає розбору щодо середнього в малих вибірках

Поряд з дисперсією, як міру відхилення від середнього, використовують среднеквадратическое відхилення(виправлене чи невиправлене):



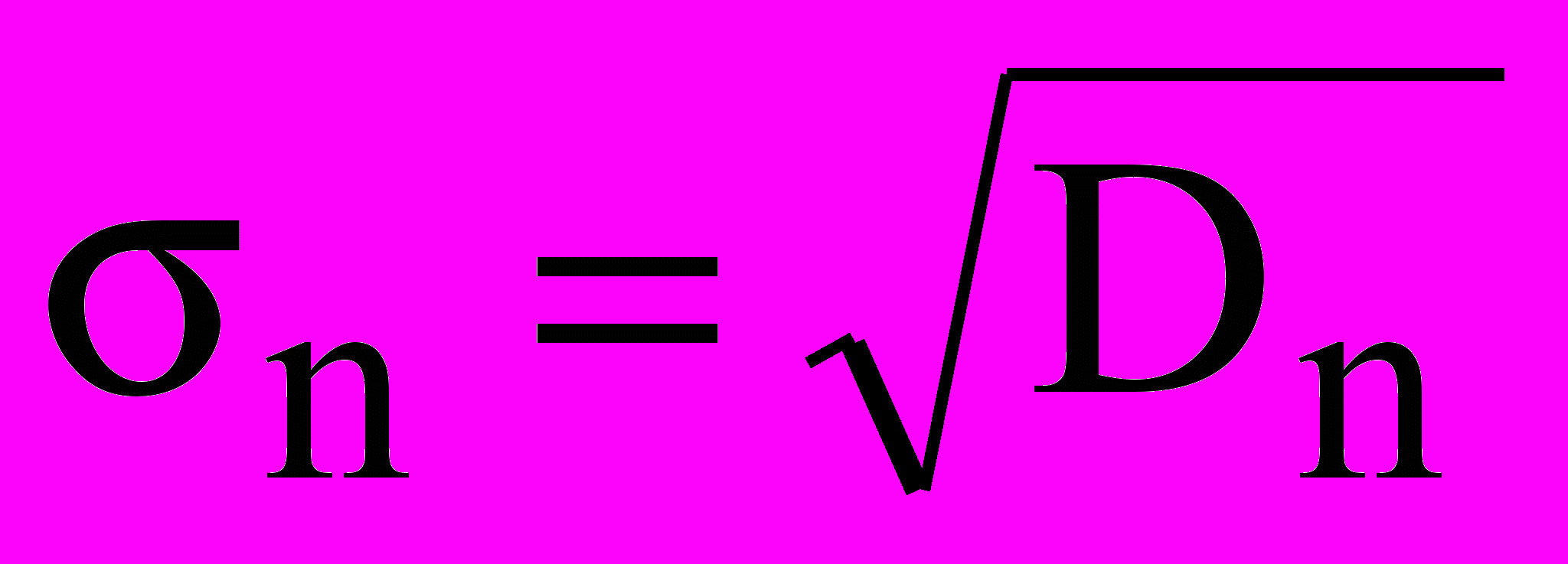
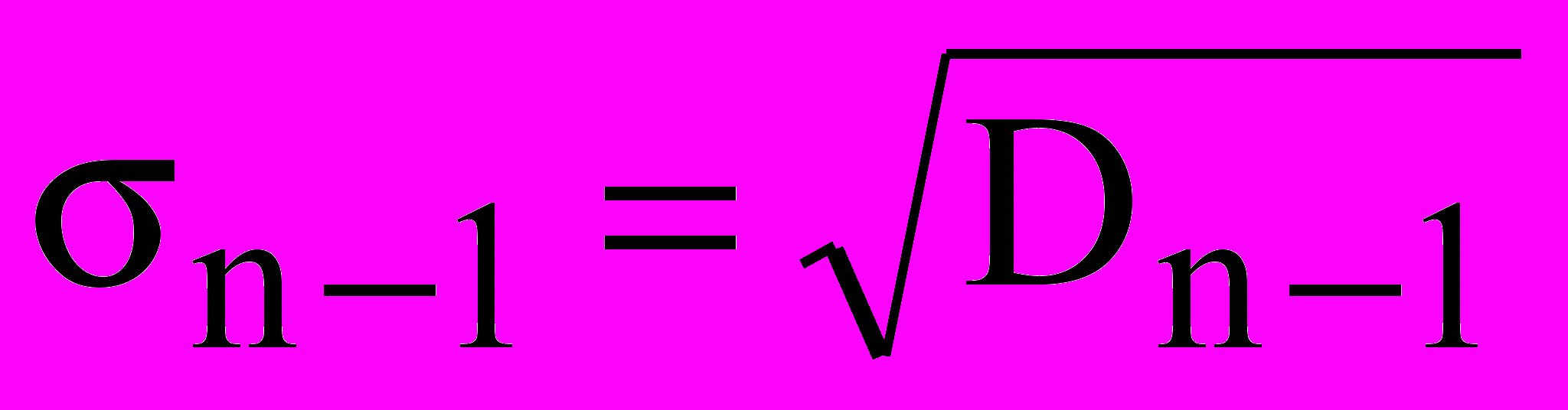
Зручність середньоквадратичного відхилення – у тім, що для розмірних випадкових величин воно виміряється в тих же одиницях, що сама випадкова величина, у той час, як дисперсія – у відповідних квадратних одиницях

2. Перевірка статистичних гіпотез. Довірчі інтервали.
   

Загальне правило роботи з випадковими величинами: усі судження про випадкові величини носять вероятностный характер, тобто, супроводжуються часткою ризику. Ця частка ризику, називана довірчою імовірністю, задається заздалегідь і характеризує імовірність того, що висловлене Вами судження щодо випадкової величини є помилковим.

Звичайно в статистичних розрахунках застосовують рівень значимості (=0,05. Тобто, у середньому, помилку можна допустити в одному випадку з 20

Судження, висловлювані про випадкові величини (їхніх значеннях у порівнянні з іншими чи величинами законах їхні розподіли) називаються статистичними гіпотезами, а встановлення їх выполнимости з заданою часткою ризику зветься перевірки статистичних гіпотез.

Особливістю статистичних гіпотез є те, що судженню, що перевіряється, (нульовій гіпотезі) обов'язково протиставляється альтернативне судження. Наприклад, якщо ми перевіряємо нульову гіпотезу «Випадкове число А=5», те цьому судженню може бути 3 альтернативи:

1. А>5
   
2. A<5
   
3. А не дорівнює 5
   

У залежності, від того, яка з цих альтернатив обрана, при заданому рівні значимості можна одержати різні результати про виконання нульової гіпотези.

Перевірка статистичних гіпотез полягає в побудові з випадкової величини, що перевіряється, деякої іншої випадкової величини, для якої відомий закон розподілу імовірностей. Виходячи з відомого закону розподілу, можна визначити, з якою імовірністю з'явилася б розрахована величина, якби була вірна перевіря не, а альтернативна гіпотеза. При цьому значення, що перевіряється, з'явилося б чисто випадково. Знайдена в такий спосіб імовірність називається критичної. Якщо критична імовірність менше довірчої – ми приймаємо нульову (тобто, що перевіряється гіпотезу). У противному випадку гіпотеза, що перевіряється, відкидається. Другий варіант перевірки – по заданій довірчій імовірності розрахувати критичне значення самої випадкової величини, якби була вірна альтернативна гіпотеза. Якщо розрахункове значення величини менше критичного – приймається основна гіпотеза, у противному випадку – альтернативна. Приклади розрахунків – у розділах

«Установлення значимості коефіцієнта кореляції»

«Установлення значимості рівняння регресії»

«Установлення значимості коефіцієнтів регресії»

Для перевірки статистичних гіпотез застосовують обоє описаних способу, причому, другий – частіше.

Знайшовши критичне значення випадкової величини, можна побудувати довірчий інтервал – інтервал, усередині якого знаходиться щире значення випадкової величини з імовірністю 1-. Приклад розрахунку – у розділі «Расчет характеристик выборки в среде Excel»

5.4.3. Розрахунок характеристик вибірки в середовищі Excel»

Задача:

По заданій вибірці визначити математичне чекання (середнє арифметичне), виправлені дисперсію і среднеквадратическое відхилення. Побудувати доверительный интервал довірчийарифметичного з надійністю 1-=0,95

Вихідна вибірка

N	1	2	3	4	5	6	7	8	9
X	2,89	1,00	1,80	1,59	0,11	3,00	2,49	1,40	0,99

Задачу розрахунку середнього і дисперсії можна вирішити двома методами: «вручную» і с использованием статистических функций.

1. Рішення вручну
   

А. Спочатку будується таблиця значень Х

Б. У нижньому осередку виробляється підсумовування (натискання клавіш Alt - +)

М. Розраховується середнє розподілом суми на число елементів вибірки

Д. Пристроюємо до таблиці графи «Різниці» і «квадрати разностей»

Е. У перших клітках нових граф створюємо формули осередку для розрахунку разностей Х-Хср і їхніх квадратів. У формулі осередку закріплюємо значення Хср за допомогою знака $.

Ж. Виділяємо отримані значення і протягаємо їх по всій таблиці

З. Розраховуємо суму квадратів відхилень і дисперсію. Витягаючи корінь – розраховуємо середньоквадратичне відхилення.

Приклад розрахунку розглянутий у таблиці 3.1

2. Розрахунок за допомогою статистичних функцій.


Розрахунок середнього.

• виділяємо осередок, у якій буде результат
  
• натискаємо кнопку f(x) на панелі інструментів
  
• вибираємо в меню Статистичні функції
  
• вибираємо серед статистичних функцій СРЗНАЧА
  
• відповідно до вказівок – виділяємо діапазон Х, натискаємо ОК, одержуємо в осередку результат-
  

Аналогічно проводяться розрахунки виправленої дисперсії (функція ДИСПА) і середньоквадратичного відхилення (функція СТАНДОТКЛОНА). Результати приведені в таблиці 3.1.


Побудова довірчого інтервалу


Довірчий інтервал будується симетрично щодо середнього арифметичних . У математичній статистиці показано, що симетричний довірчий інтервал, у якому з імовірністю 1- знаходиться - щире значення випадкової величини x_i (середнє генеральної сукупності) для вибірок невеликого обсягу n (n<50) визначається нерівністю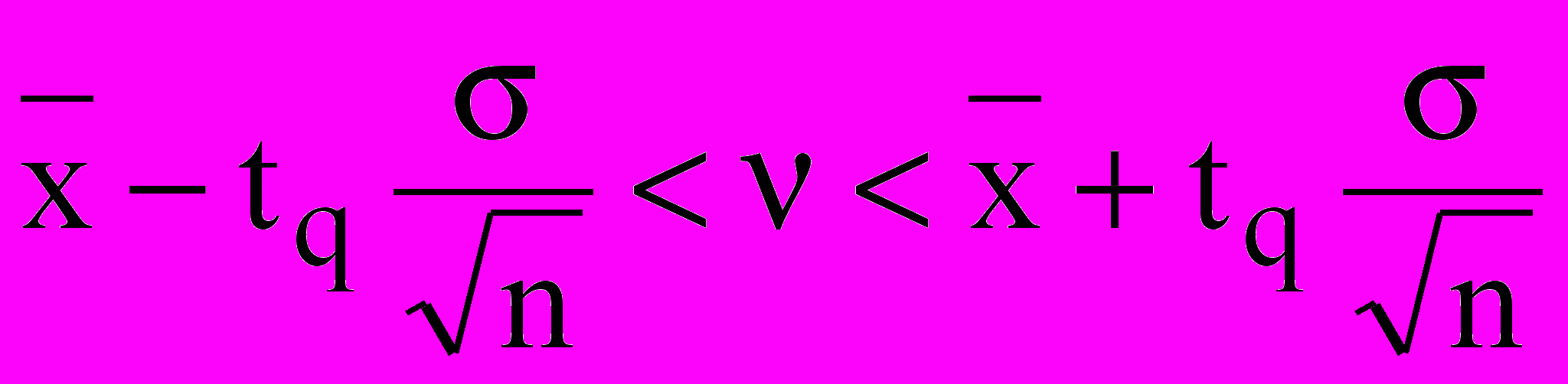



 - виправлене среднеквадратическое відхилення

t_q – критичне значення розподілу Стьюдента (критерію Стьюдента) для заданого рівня значимості  і числі ступенів волі k=n-1.

Таблиця 3.1.




Число ступенів волі випадкової величини визначається, як число значень цієї величини мінус число параметрів, обумовлених з цієї величини. З вибірки визначається один параметр – середнє арифметичне, тому, з числа крапок віднімається 1

Для практичних розрахунків у середовищі Excel критичне значення розподіл Стьюдента можна знайти в розділі «Статистичні функції» (СТЬЮДРАСПОБР). Ввівши в роботу цю функцію, Ви повинні задати рівень значимості (імовірність () і число ступенів волі, що на 1 менше числа крапок. Приклад розрахунку – у таблиці 3.1.


5.4 Зв'язані вибірки. Коефіцієнт кореляції


Часто виникає ситуація, коли потрібно перевірити, як впливає деяка величина Х на випадкову величину Y (наприклад, як впливає концентрація реагенту на швидкість реакції). Для цього проводять спостереження величини Y при різних значеннях Х. Відзначимо, що величина Х не є випадкової, вона може бути змінена і зафіксована за бажанням спостерігача. Ця величина називається фактором. Величина Y є випадковою величиною і називається відгуком.

Ми можемо розглядати Х и Y як зв'язані вибірки. Їхні значення задаються парами {x_i,y_i}, звичайно, у виді таблиць. Кожну з вибірок значень Х и Y можна обробити порізно, розраховуючи для них середнє арифметичне і среднеквадратическое (невиправлене) відхилення:






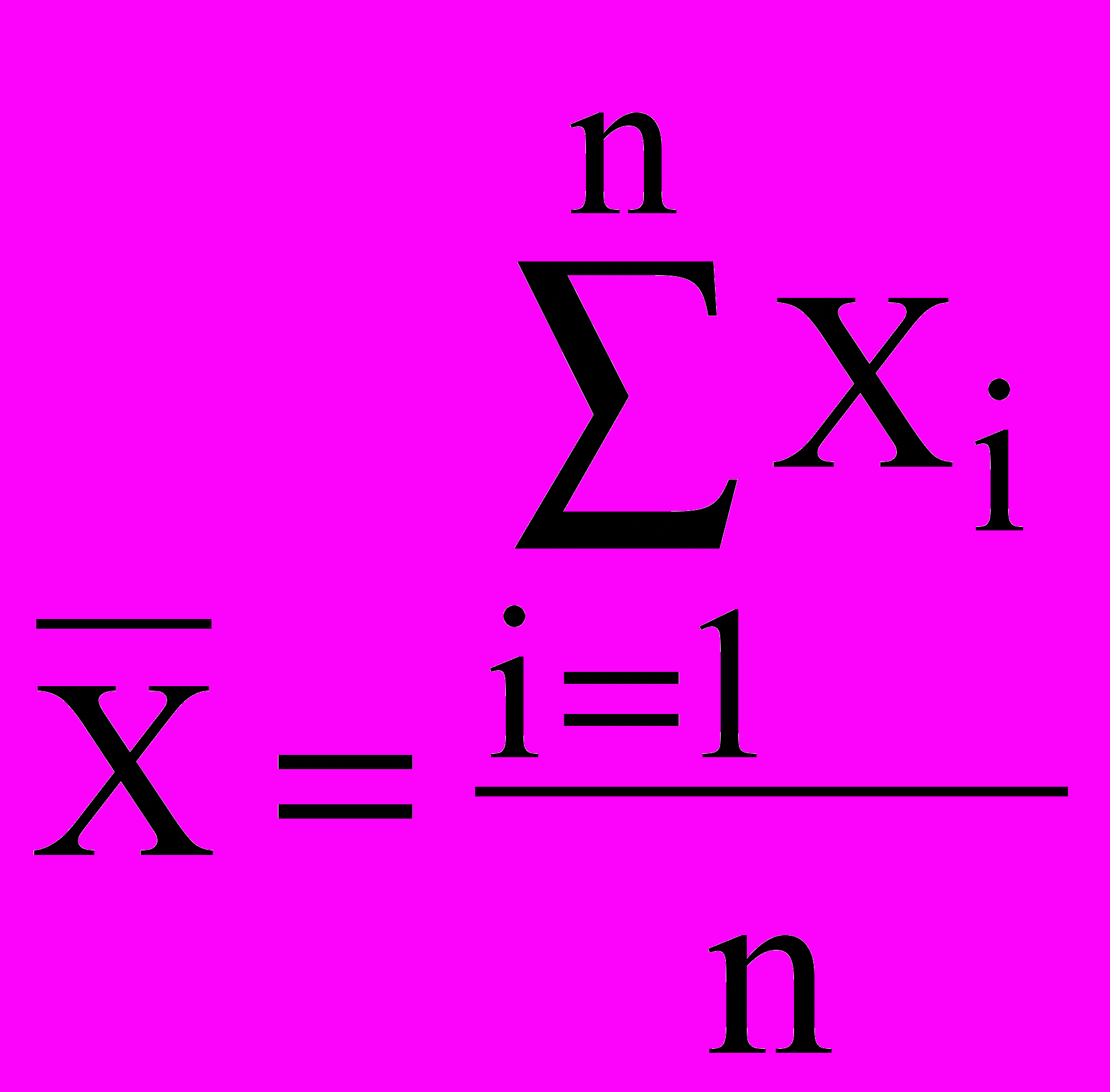
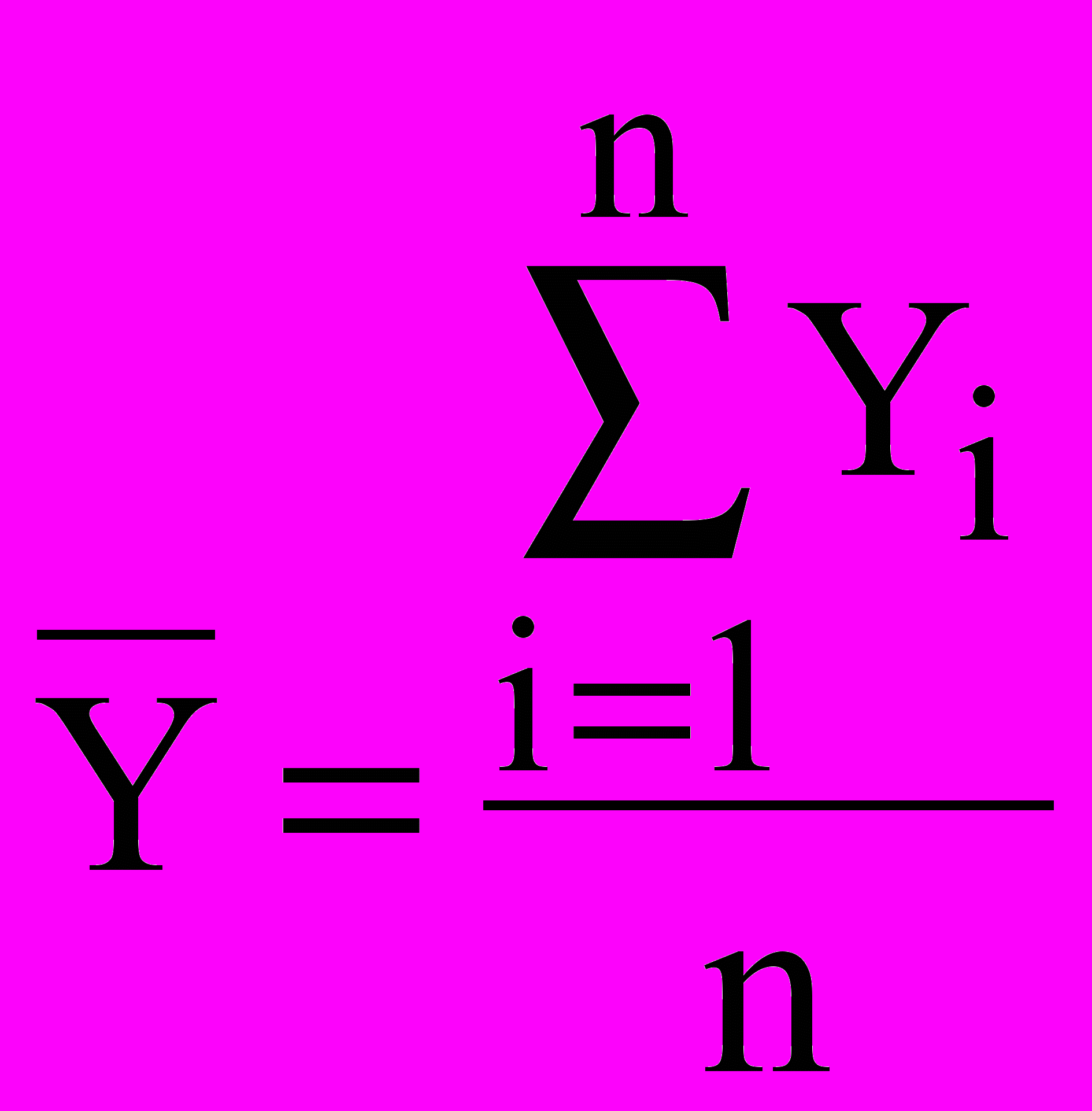
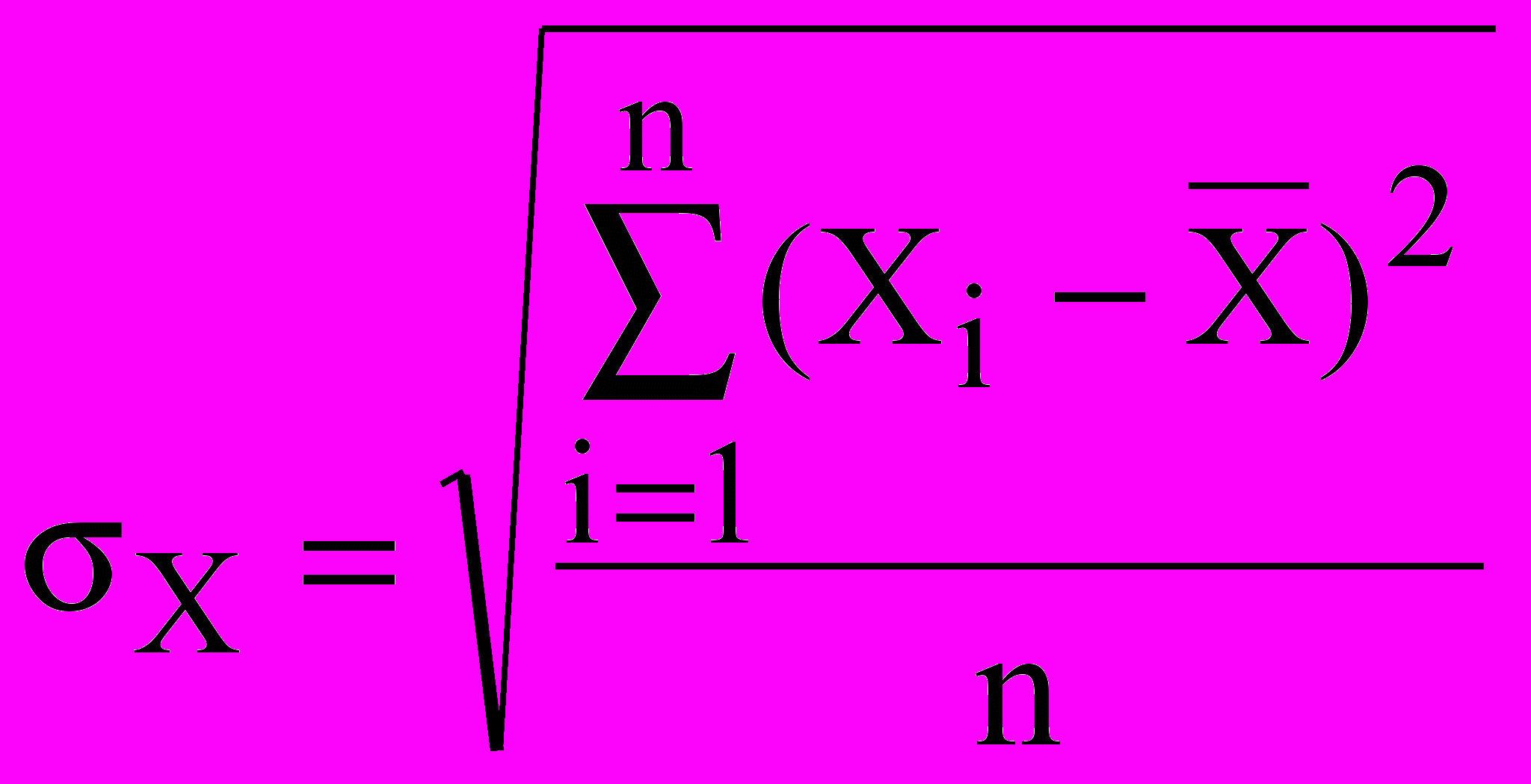
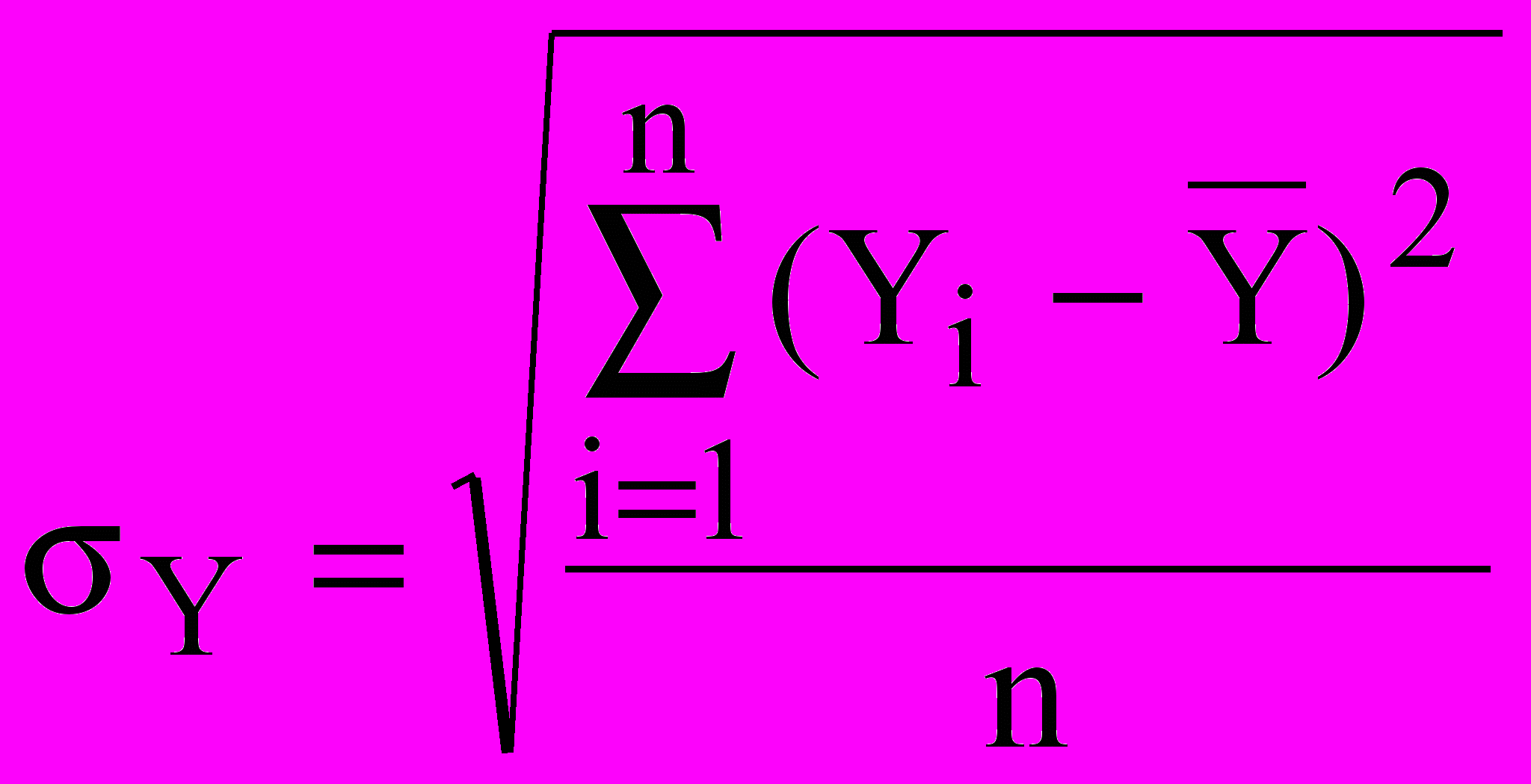
Для оцінки сили взаємодії між Y і Х розраховується коефіцієнт кореляції r_XY (його ще називають коефіцієнтом парної кореляції)



Коефіцієнт парної кореляції характеризує силу залежності між Y і Х

Властивості коефіцієнта кореляції

1. Коефіцієнт кореляції може змінюватися в інтервалі від –1 до 1
   
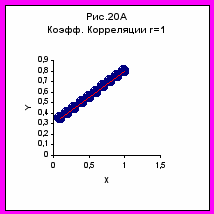
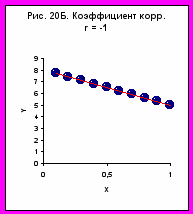
2. Якщо коефіцієнт кореляції дорівнює 1 чи –1 – це свідчить, що всі крапки залежності Y(X) ідеально лежать на прямої (рис 20А, Б)
   
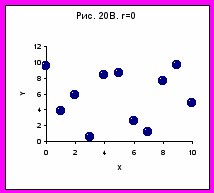
3. Якщо коефіцієнт кореляції дорівнює нулю – на графіку залежності Y від Х усі крапки лежать хаотично, між відгуком і фактором немає ніякого зв'язку (Рис. 20 В)
   
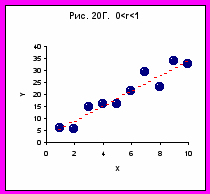
4. У проміжному випадку крапки групуються навколо деякої прямої(Рис. 20М). Тобто, між фактором і відгуком є деякий зв'язок, ускладнена дією випадкових причин.
   

Позитивна величина коефіцієнта кореляції свідчить, що зі збільшенням значення фактора значення відгуку, у середньому, зростає. Зростання в середньому говорить про тенденцію у всій сукупності крапок. При цьому, для окремих крапок можливе порушення тенденції